10 Nullmengen
Es sei (E,  , µ) ein beliebiger Maßraum. In diesem Kapitel beschäftigen wir uns mit (messbaren) Mengen, die von dem Maß µ „nicht gesehen“ werden und in diesem Sinn Ausnahmemengen sind.
, µ) ein beliebiger Maßraum. In diesem Kapitel beschäftigen wir uns mit (messbaren) Mengen, die von dem Maß µ „nicht gesehen“ werden und in diesem Sinn Ausnahmemengen sind.
10.1 Definition. a) Die (messbaren) Nullmengen sind 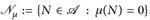 .
.
b) Eine Eigenschaft Π(x) gilt (µ-)fast überall (µ-f. ü.) oder für (µ-)fast alle x, wenn


- ► Die (Ausnahme-)Menge {x ∈ E: Π(x) gilt nicht} muss nicht messbar sein.
- ► u = w f. ü. ⇔ {u ≠ w} ⊂ N ∈
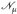 .
. - ► u, w messbar, u = w f. ü. ⇔u ≠ w} ∈
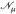 µ.
µ. - ► u = w f. ü. erlaubt z. B., dass u messbar und w beliebig ist. Dann kann {u ≠ w} ∉
 auftreten.
auftreten.
10.2 Satz. Es sei 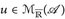 . Dann gilt
. Dann gilt
- a) ∫|u| dµ = 0 ⇔ |u| 0 f.ü ⇔ µ {u ≠0} = 0
- b) N ∈
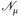 ⇒ ∫Nudµ=0.
⇒ ∫Nudµ=0.
Beweis. Wir beginnen mit b). Wegen ∣u∣∧ n ↑ ∣u∣ (n → ∞) folgt mit dem Satz von Beppo Levi (Satz 8.6) und Satz 9.3
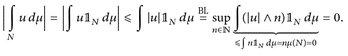
Nun zu a). Offensichtlich sind ∣u∣ = 0 f. ü., u = 0 f. ü. und µ{u ≠ 0} = 0 gleichwertig. Es genügt daher, die erste Äquivalenz von a) zu zeigen.
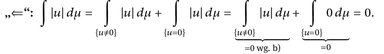
„⇒“: Hier brauchen wir die sogenannte Markov-Ungleichung: Für alle A ∈  und c >0 gilt
und c >0 gilt
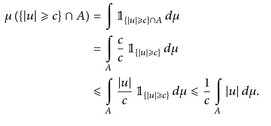
Insbesondere haben wir für A = E

10.3 Korollar. Es seien u, w ∈ 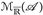 mit u = wf. ü.
mit u = wf. ü.
- a) u, w ≥ 0 ⇒ ∫udµ =∫wdµ ∈ [0, ∞]
- b)
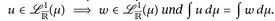
Beweis. Da u, w messbar sind, gilt {u ≠ w} ∈ 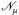 . Daher
. Daher
- a)
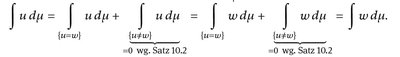
- b) u = w f. ü. gibt sofort u± = w± f. ü.; Teil a) für u±, w± zeigt die Behauptung.
10.4 Korollar. Für u ∈ 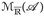 und w ∈
und w ∈ 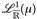 gilt
gilt
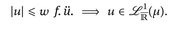
Beweis. Es ist
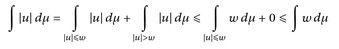
und daraus folgt dann u ∈ 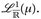
10.5 Korollar (Markov-Ungleichung). Für u ∈ 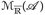 gilt
gilt
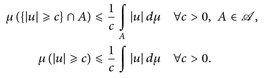
Beweis. Vgl. Beweis von 10.2.a) „⇒“.
10.6 Korollar. Jedes u ∈  ist f. ü. reellwertig. Insbesondere existiert ein ū ∈
ist f. ü. reellwertig. Insbesondere existiert ein ū ∈ 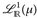 mit u =ū f.ü.
mit u =ū f.ü.
Beweis. Definiere 
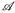 . Aufgrund der Maßstetigkeit (Satz 3.3.g) gilt
. Aufgrund der Maßstetigkeit (Satz 3.3.g) gilt

Daher erfüllt die Funktion 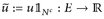 die Behauptung, wobei N = {u ≠ ū}.
die Behauptung, wobei N = {u ≠ ū}.

Konsequenz: Wir können 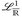 stets durch
stets durch 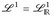 ersetzen, m.a.W.
ersetzen, m.a.W. 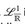 ist - bis auf Nullmengen - ein Vektorraum, und wir dürfen das „∞ - ∞“ Problem (bei allen abzählbaren Operationen!) vernachlässigen.
ist - bis auf Nullmengen - ein Vektorraum, und wir dürfen das „∞ - ∞“ Problem (bei allen abzählbaren Operationen!) vernachlässigen.
Aufgaben
- Es sei (E,
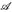 , µ) ein Maßraum und u,v ∈ ℒ1 (µ). Zeigen Sie:
, µ) ein Maßraum und u,v ∈ ℒ1 (µ). Zeigen Sie:

- In Aufgabe 10.1sei nun
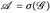 , wobei
, wobei 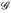 ein ∩-stabiler Erzeuger ist, so dass eine aufsteigende Folge
ein ∩-stabiler Erzeuger ist, so dass eine aufsteigende Folge  existiert. Zeigen Sie:
existiert. Zeigen Sie:

Hinweis: Eindeutigkeitssatz für Maße für G ↦ ∫G(u+ + v-) dµ und Aufgabe 10.1.
- Vergleichen Sie die beiden folgenden Aussagen:
- (a) Die Funktion u ist fast überall stetig.
- (b) Die Funktion u stimmt fast überall mit einer stetigen Funktion überein.
- Es sei (E,
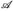 , µ) ein Maßraum. Zeigen Sie die folgenden Varianten der Markovschen Ungleichung (Korollar 10.6): Für positive Konstanten c, α > 0 gilt
, µ) ein Maßraum. Zeigen Sie die folgenden Varianten der Markovschen Ungleichung (Korollar 10.6): Für positive Konstanten c, α > 0 gilt
- (a)
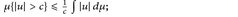
- (b)

- (c)
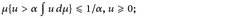
- (d)
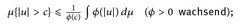
- (e)

- (f) (Chebyshevsche Ungleichung) Es sei
 ein W-Maß,
ein W-Maß, 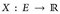 eine messbare Funktion („Zufallsvariable“),
eine messbare Funktion („Zufallsvariable“), 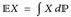 der Erwartungswert und
der Erwartungswert und  die Varianz. Dann
die Varianz. Dann 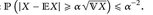
- (a)
- (Vervollständigung) Es sei (E,
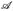 , µ) ein endlicher Maßraum. Wir definieren für jede Menge Q ⊂ E das innere bzw. äußere Maß
, µ) ein endlicher Maßraum. Wir definieren für jede Menge Q ⊂ E das innere bzw. äußere Maß
u* (Q) inf [µ(A) A ∈
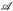 , A ⊃ Q} und µ*(Q):=sup{µ(A): A ∈
, A ⊃ Q} und µ*(Q):=sup{µ(A): A ∈ 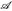 , A ⊂ Q}.
, A ⊂ Q}.Zeigen Sie:
- (a) µ* (Q) ≤{µ*(Q) und µ* (Q) + µ*(QC) = µ(E).
- (b) µ*(Q ∪ R) ≤ µ*(Q) + µ*(R) und µ* (Q) + µ*(R) ≤ µ*(Q∪R).
- (c) Zu jedem Q c E gibt es Mengen Q*, Q* ∈
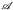 mit µ(Q*) = u*(Q) und µ(Q*) = µ*(Q).
mit µ(Q*) = u*(Q) und µ(Q*) = µ*(Q).
Hinweis: Auf Grund der Definition des Infimums gibt es messbare Mengen Qn ⊃ Q mit µ(Qn) – µ*(Q) ≤ 1/n; betrachten Sie nun ∩ Qn.
- (d) Die Familie
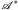 := {Q ⊂ E: µ*(Q) = µ* (Q)} ist eine σ-Algebra.
:= {Q ⊂ E: µ*(Q) = µ* (Q)} ist eine σ-Algebra. - (e) Der Maßraum (E,
 , µ) mit
, µ) mit  ist die Vervollständigung von (E,
ist die Vervollständigung von (E, 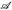 , µ) (vgl. Aufgabe 3.7, 5.4).
, µ) (vgl. Aufgabe 3.7, 5.4).
- Es sei µ ein σ-endliches Maß auf dem Messraum (E,
 ). Konstruieren Sie ein Wahrscheinlichkeitsmaß
). Konstruieren Sie ein Wahrscheinlichkeitsmaß 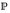 auf (E,
auf (E,  ), das dieselben Nullmengen wie µ hat.
), das dieselben Nullmengen wie µ hat.