7 Messbare Funktionen
In diesem Kapitel ist (E, 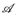 ) ein beliebiger Messraum. Im Gegensatz zum vorangehenden Kapitel betrachten wir nun messbare Abbildungen mit Werten in
) ein beliebiger Messraum. Im Gegensatz zum vorangehenden Kapitel betrachten wir nun messbare Abbildungen mit Werten in 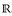 .
.
7.1 Definition. Eine messbare Abbildung u: (E, 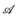 ) → (
) → (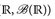 ,heißt messbare (reelle) Funktion.
,heißt messbare (reelle) Funktion.
Die Klasse der messbaren Funktionen ist für die Integrationstheorie von fundamentaler Bedeutung. Zur Erinnerung:
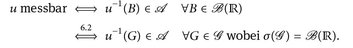
Meist werden wir 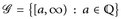 wählen; die Mengen [a, ∞) können auch durch (b, ∞), (–∞, c), (–∞, d] für b, c, d ∈
wählen; die Mengen [a, ∞) können auch durch (b, ∞), (–∞, c), (–∞, d] für b, c, d ∈  oder ∈ ℚ ersetzt werden, vgl. Bemerkung 2.9.
oder ∈ ℚ ersetzt werden, vgl. Bemerkung 2.9.
Bezeichnung. Für u, υ: E →  und B ∈
und B ∈  schreiben wir:
schreiben wir:
- ▶ {u ∈ B}:= {x ∈ E: u(x) ∈ B} = u–1(B);
- ▶ {u ≥ υ}:= {x ∈ E: u(x) ≥ υ(x)} (analog für: >, <, ≤, =, ≠);
- ▶ insbesondere ist {u ≥ a} = {u ∈ [a, ∞)} = u–1([a, ∞)).
7.2 Lemma (Messbarkeitskriterium). Eine Funktion u: (E, 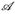 ) → (
) → (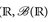 ) ist genau dann
) ist genau dann 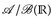 -messbar, wenn eine der folgenden Bedingungen gilt:
-messbar, wenn eine der folgenden Bedingungen gilt:
- a)
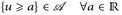 oder ∈ ℚ;
oder ∈ ℚ; - b)
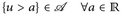 oder ∈ ℚ;
oder ∈ ℚ; - c)
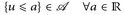 oder ∈ ℚ;
oder ∈ ℚ; - d)
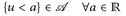 oder ∈ ℚ.
oder ∈ ℚ.
Wir werden oft in 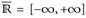 [–∞, mit den „Werten“ ±∞ rechnen. Dazu erweitern wir die üblichen Rechenregeln.
[–∞, mit den „Werten“ ±∞ rechnen. Dazu erweitern wir die üblichen Rechenregeln.
Tab. 7.1. Rechenregeln in 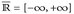 mit x, y ∈
mit x, y ∈ 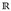 und a, b ∈ (0, ∞).
und a, b ∈ (0, ∞).


- ▶ Übliche Konvention:
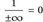 .
. - ▶ Besondere Konvention in der Maβtheorie: 0 · (±∞) = 0 (ist sonst nicht üblich).
- ▶ Nicht definiert sind: ∞ – ∞ und
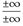 .
. - ▶
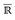 ist kein Körper.
ist kein Körper.
7.3 Definition. Die Borel σ-Algebra 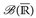 auf
auf  ist definiert durch
ist definiert durch
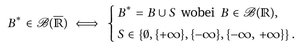
Die Definition der Borel-Mengen in 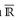 ist im folgenden Sinn verträglich mit den Borel-Mengen in IR [
ist im folgenden Sinn verträglich mit den Borel-Mengen in IR [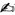 ]:
]:
7.4 Lemma. Es gilt 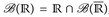 , d.h.
, d.h. 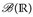 ist die Spur-σ-Algebra (vgl. Beispiel 2.3f) bezüglich
ist die Spur-σ-Algebra (vgl. Beispiel 2.3f) bezüglich 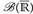 .
.
Da [–∞, a) und (b, ∞] offene Umgebungen (bezüglich der Zweipunktkompaktifizierung [–∞, ∞] von 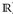 ) der Elemente ±∞ sind, gilt auch
) der Elemente ±∞ sind, gilt auch
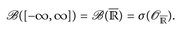
Diese Bemerkung ist für uns nicht so wichtig, wichtiger ist vielmehr die folgende Aussage.
7.5 Lemma. Die Borelmengen 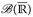 werden von allen Intervallen [a, ∞], a ∈
werden von allen Intervallen [a, ∞], a ∈ 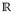 oder a ∈ ℚ, (bzw. von (a, ∞], [–∞, a), [–∞, a], a ∈
oder a ∈ ℚ, (bzw. von (a, ∞], [–∞, a), [–∞, a], a ∈ 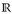 oder a ∈ ℚ) erzeugt.
oder a ∈ ℚ) erzeugt.
Beweis. Setze Σ:= σ ([a, ∞]: a ∈ ℚ). Es seien a, b ∈ ℚ und B ∈ 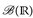 . Dann gilt
. Dann gilt
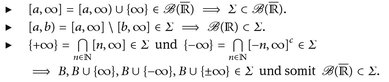
Damit ist 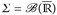 gezeigt. Die anderen Fälle behandelt man entsprechend.
gezeigt. Die anderen Fälle behandelt man entsprechend.
7.6 Definition. 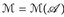 bzw.
bzw. 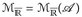 bezeichnet die Menge aller messbaren Funktionen u:
bezeichnet die Menge aller messbaren Funktionen u: 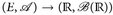 bzw.
bzw. 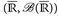 .
.
7.7 Beispiel. a) 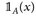 ist genau dann messbar, wenn A ∈
ist genau dann messbar, wenn A ∈ 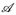 (d. h. wenn A messbar ist).
(d. h. wenn A messbar ist).

Abb. 7.1. Links: Messbarkeit der Funktion 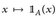 . Rechts: Messbarkeit einer Treppenfunktion (mit N = 3 Stufen).
. Rechts: Messbarkeit einer Treppenfunktion (mit N = 3 Stufen).
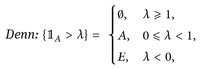
(vgl. Abb. 7.1).
b) Es seien A1, ... ,AN ∈ 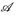 disjunkte Mengen, y1, ... yN ∈
disjunkte Mengen, y1, ... yN ∈ 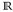 . Dann ist
. Dann ist

Denn: Offensichtlich ist g(x) = 0 für 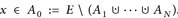 . Wenn wir y0:= 0 setzen, gilt
. Wenn wir y0:= 0 setzen, gilt 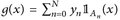 und daher ist
und daher ist  (vgl. Abb. 7.1).
(vgl. Abb. 7.1).
7.8 Definition. Eine einfache Funktion auf (E, 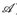 ) ist eine Treppenfunktion der Form
) ist eine Treppenfunktion der Form
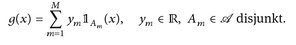
(7.1)
Gilt sogar
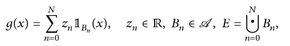
(7.2)
dann heißt (7.2) Standarddarstellung; 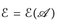 bezeichnet die Familie der einfachen Funktionen.
bezeichnet die Familie der einfachen Funktionen.

Die Darstellungen (7.1) und (7.2) sind nicht eindeutig.
7.9 Beispiel. a) Jede messbare Funktion h ∈ 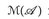 mit endlicher Wertemenge h(E) = {y1, ..., ym} ist eine einfache Funktion. Da die Mengen
mit endlicher Wertemenge h(E) = {y1, ..., ym} ist eine einfache Funktion. Da die Mengen
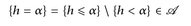
disjunkt sind, ist nämlich 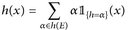 eine Standarddarstellung.
eine Standarddarstellung.
Folgerung: Jedes h ∈ 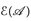 besitzt eine Standarddarstellung.
besitzt eine Standarddarstellung.
b) Es gilt f, g ∈ 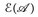 ⇒ f ± g, f · g ∈
⇒ f ± g, f · g ∈ 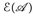 .
.
Für die Standarddarstellungen 

Beachte: (Am ∩ Bn)n,m ist die gemeinsame Verfeinerung der Partitionen (Am)m und (Bn)n. Auf jeder der Mengen Am ∩ Bn sind f und g konstant.
c) 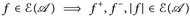 (vgl. Definition 7.10 und Abbildung 7.2).
(vgl. Definition 7.10 und Abbildung 7.2).
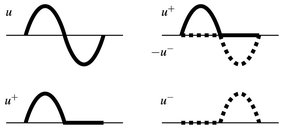
Abb.7.2. Positiv- und Negativteil einer Funktion u: E → IR. Offenbar gilt u = u+ – u–und |u| = u+ + u–.
7.10 Definition. Es sei u:  . Dann heißt
. Dann heißt
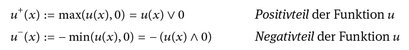
Offenbar ist jede einfache Funktion auch messbar. Wir zeigen nun, dass jede Funktion  u durch einfache
u durch einfache  -messbare Funktionen approximiert werden kann.
-messbare Funktionen approximiert werden kann.
7.11 Satz (Sombrero-Lemma). Jede  -messbare Funktion u:: E → [0, ∞] ist aufsteigender Limes einer Folge
-messbare Funktion u:: E → [0, ∞] ist aufsteigender Limes einer Folge 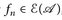 fn ≥ 0, d. h.
fn ≥ 0, d. h.
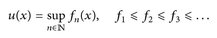
Beweis. Setze 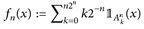 wobei
wobei
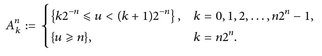
Offensichtlich (vgl. Abb. 7.3) gilt dann
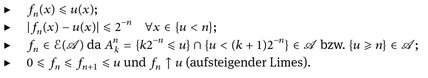
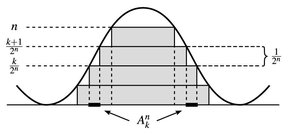
Abb. 7.3. Der Wertebereich der Funktion u wird in horizontale Stufen zerlegt.
7.12 Korollar. Für jede 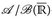 -messbaren Funktion u: E →
-messbaren Funktion u: E → 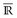 existiert eine Folge
existiert eine Folge 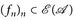 , so dass |fn| ≤ |u| und u = limn fn.
, so dass |fn| ≤ |u| und u = limn fn.
Beweis. Für messbare Funktionen gilt {u+ > λ} = {u > λ} (für λ ≥ 0) bzw. [u+ > λ} = E (für λ < 0). Das zeigt, dass u± positive messbare Funktionen sind. Die Behauptung des Korollars folgt nun, indem wir Satz 7.11 auf u± anwenden.
Die folgenden Korollare zeigen grundlegende Eigenschaften messbarer Funktionen.
7.13 Korollar. Es sei 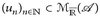 eine Folge messbarer Funktionen. Dann gilt
eine Folge messbarer Funktionen. Dann gilt
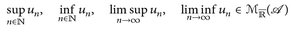
und, wenn der Limes existiert, limn→∞ un ∈ 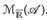 .
.

- ▶ supn un ist die punktweise definierte Funktion supn un(x) Vx ∈ E (analog: inf usw.).
- ▶ Zur Erinnerung: Der Limes inferior und superior sind folgendermaßen definiert:
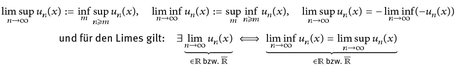
Beweis von Korollar 7.13. 1°) Behauptung: supn un ∈  . Das folgt aus der Gleichheit
. Das folgt aus der Gleichheit  die man folgendermaßen beweist:
die man folgendermaßen beweist:

2°) Es ist –un ∈  , da {–un > λ} = {un < –λ} ∈
, da {–un > λ} = {un < –λ} ∈ 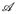 .
.
3°) 1° und 2° zeigen infn un = - supn(–un) ∈ 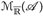 . Wegen der Definition von lim inf und lim sup ist dann
. Wegen der Definition von lim inf und lim sup ist dann
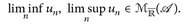
4°) Wenn limn un existiert, dann gilt 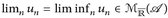 .
.
7.14 Korollar. u, υ: E → 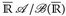 -messbar. Dann sind
-messbar. Dann sind
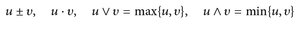
messbar – sofern diese Ausdrücke definiert5 sind.
Beweis. Nach Satz 7.11 gibt es 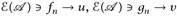 . Nun gilt
. Nun gilt
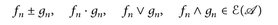
und für n → ∞ sind die Grenzwerte u ± v, u v, u v v, u ∧ v nach Korollar 7.13 messbar.6
7.15 Korollar. Es ist u ∈  genau dann, wenn
genau dann, wenn 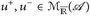 .
.
7.16 Korollar. Wenn u, v ∈ 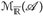 , dann sind folgende Mengen messbar:
, dann sind folgende Mengen messbar:
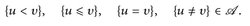
Beweis. Es gilt
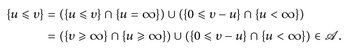
Daher sind auch {u = v} = {u ≤ v} ∩ {u ≥ v} und {u ≠ v} = {u = v}c messbar. Den Fall [u < v} erledigt man ganz ähnlich.
Am Ende dieses Kapitels zeigen wir noch ein Resultat, das für die Wahrscheinlichkeitstheorie wichtig sein wird.
7.17 ♦ Lemma (Faktorisierungslemma). Es sei 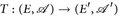 messbar. Dann
messbar. Dann

Beweis. „⇐“: Nach Definition ist T σ(T)-messbar. Also ist auch die Komposition

„⇒“: Es sei u σ(T)-messbar. Wir müssen ein geeignetes w finden.
- 1°) Angenommen
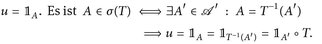 Damit erhalten wir
Damit erhalten wir 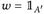 .
. - 2°) Nun sei
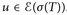 . Für eine Standarddarstellung von u finden wir mit Hilfe von 1° und der Linearität ein geeignetes
. Für eine Standarddarstellung von u finden wir mit Hilfe von 1° und der Linearität ein geeignetes 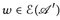 .
. - 3°) Schließlich sein
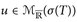 . DasSombrero-Lemma (Satz 7.11)zeigt u = limn→∞ fn für eine Folge
. DasSombrero-Lemma (Satz 7.11)zeigt u = limn→∞ fn für eine Folge 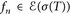 . Aus Schritt 2° wissen wir aber, dass fn = wn ∘ T für einfache Funktionen
. Aus Schritt 2° wissen wir aber, dass fn = wn ∘ T für einfache Funktionen 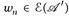 . Wir definieren w:= lim infn→∞
. Wir definieren w:= lim infn→∞ 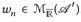 . Dann gilt
. Dann gilt
Aufgaben
- Auf
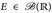 sei die Funktion
sei die Funktion 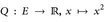 , und das Lebesgue-Maß λE:- λ(E ∩.) gegeben.
, und das Lebesgue-Maß λE:- λ(E ∩.) gegeben.
- (a) Zeigen Sie, dass Q eine
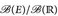 -messbare Abbildung ist (vgl. Aufgabe 2.4).
-messbare Abbildung ist (vgl. Aufgabe 2.4). - (b) Bestimmen Sie das Bildmaß ν ∘ Q-1 für E = [0, 1], v = λE und
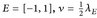 .
.
- (a) Zeigen Sie, dass Q eine
- Gegeben sei der Messraum (
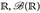 ). Finden Sie σ(u) für
). Finden Sie σ(u) für
- (a)
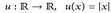 ;
; - (b)
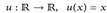 ;
; - (c)
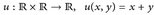 ;
; - (d)
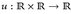 , u(x, y) = x2 + y2.
, u(x, y) = x2 + y2.
- (a)
- Beweisen Sie, dass jede lineare Abbildung
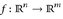 Borel-messbar ist. Gilt das auch, wenn wir
Borel-messbar ist. Gilt das auch, wenn wir 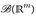 und
und 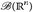 vervollständigen?
vervollständigen? - Beweisen Sie, dass
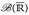 aus Definition 7.3 eine σ-Algebra ist, und zeigen Sie Lemma 7.4.
aus Definition 7.3 eine σ-Algebra ist, und zeigen Sie Lemma 7.4. -
- (a) Es sei
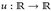 Borel-messbar. Zeigen Sie: |u|, u+, u- sind messbar. Gilt die Umkehrung?
Borel-messbar. Zeigen Sie: |u|, u+, u- sind messbar. Gilt die Umkehrung? - (b) Es sei
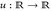 differenzierbar. Sind dann u und u′ messbar?
differenzierbar. Sind dann u und u′ messbar?
- (a) Es sei
- Es sei (fi)i∈I (I beliebig) eine Familie von Abbildungen von einer gemeinsamen Menge E nach
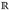 . Zeigen Sie
. Zeigen Sie
- (a) {supi fi > λ} = Ui {fi > λ};
- (b) {supi fi < λ} ⊂ ∩i {fi < λ};
- (c) {supi fi ≥ λ} ⊃ Ui {fi ≥ λ };
- (d) {supi fi ≤ λ} = ∩i{fi ≤ λ};
- (e) {infi fi > λ} ⊂ ∩i {fi > λ};
- (f) {infi fi < λ} = Ui {fi < λ};
- (g) (infi fi ≥ λ} = ∩i {fi ≥ λ};
- (h) {infi fi ≤ λ} ⊃ ∪i {fi ≤ λ}.
- Zeigen Sie, dass die Konvergenz im Sombrero-Lemma (Satz 7.11) sogar gleichmäßig ist, falls die Funktion u beschränkt ist, d. h. |u(x)| ≤ c für alle x und eine Konstante c ≥ 0.
- Zeigen Sie, dass im Beweis des Faktorisierungslemmas (Lemma 7.17) im Allgemeinen nicht mit limn wn (an Stelle von lim infwn) gearbeitet werden kann.
Hinweis: Finden Sie eine Folge von Funktionen (wn)n und eine Abbildung T, so dass (wn ∘ T)n konvergiert und (wn)n divergiert.
- Zeigen Sie, dass jede monotone Funktion
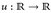 Borel-messbar ist. Wann gilt
Borel-messbar ist. Wann gilt 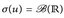 ?
? - Zeigen Sie, dass jede linksseitig (oder rechtsseitig) stetige Funktion
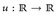 IR Borel-messbar ist.
IR Borel-messbar ist. - Auf E sei eine σ-Algebra
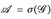 gegeben,
gegeben, 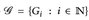 . Definiere
. Definiere  . Dann gilt
. Dann gilt 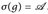 .
. - Es sei (Ω,
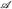 ) ein Messraum und
) ein Messraum und 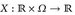 eine Abbildung, so dass
eine Abbildung, so dass 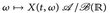 messbar ist und t ↦ X(t, w) linksseitig (oder rechtsseitig) stetig ist. Zeigen Sie, dass auch die folgenden Funktionen messbar sind:
messbar ist und t ↦ X(t, w) linksseitig (oder rechtsseitig) stetig ist. Zeigen Sie, dass auch die folgenden Funktionen messbar sind:

Hinweis: Approximieren Sie t ↦ X(t,w) durch Treppenfunktionen.
- Es sei (E,
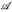 ,µ) ein Maßraum und (
,µ) ein Maßraum und (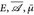 ) seine Vervollständigung (Aufgabe 3.7). Zeigen Sie, dass eine Funktion
) seine Vervollständigung (Aufgabe 3.7). Zeigen Sie, dass eine Funktion  genau dann
genau dann 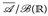 -messbar ist, wenn es zwei
-messbar ist, wenn es zwei 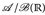 . messbare Funktionen
. messbare Funktionen 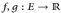 mit
mit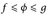 und µ{f ≠g} = 0 gibt.
und µ{f ≠g} = 0 gibt.
Hinweis: Verwenden Sie zunächst Treppenfunktionen und dann das Sombrero-Lemma.