13 Riemann vs. Lebesgue
Die Lebesguesche Integrationstheorie wurde entwickelt, weil der Riemannsche Integralbegriff sich für viele Anwendungen als zu eng erwies. In diesem Kapitel zeigen wir, dass das Lebesgue–Integral das Riemann–Integral fortsetzt. Das erlaubt es uns, in vielen Situationen Stammfunktionen „Riemannsch“ zu berechnen und so die Vorzüge beider Theorien zu verbinden. Wir werden auch eine notwendige und hinreichende Charakterisierung aller Riemann-integrierbaren Funktionen angeben (dazu benötigt man interessanterweise den Begriff der Lebesgue–Nullmenge). Wir schreiben
R- / L-integrierbar = Riemann- / Lebesgue-integrierbar,

Zunächst erinnern wir kurz an die Definition des Riemann–Integrals. Auf einem endlichen Intervall 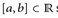 sei eine beschränkte Funktion
sei eine beschränkte Funktion 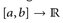 gegeben. Dann heißt
gegeben. Dann heißt

13.1 Definition. Eine beschränkte Funktion  heißt R-integrierbar, wenn
heißt R-integrierbar, wenn
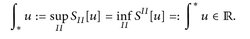
Der gemeinsame Wert (R) 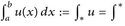 u ist das R-Integral von u.
u ist das R-Integral von u.
Offensichtlich haben wir
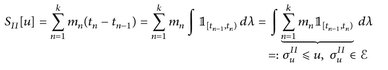
und entsprechend ist

Für jede Verfeinerung Π′ ⊃ Π der Partition Π gilt dann
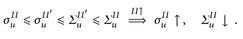
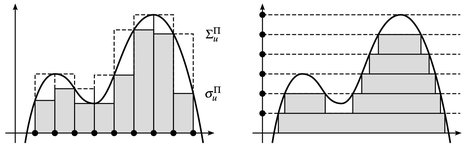
Abb.13.1. Beim R-Integral werden die Stützstellen tn im Definitionsbereich des Integranden fest gewählt, während beim Lebesgue–Integral der Wertebereich fest aufgeteilt wird, und somit die Werte von u die Partitionierung des Definitionsbereichs bestimmen.
13.2 Satz. Es sei u: 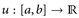 Borel-messbar und R-integrierbar. Dann
Borel-messbar und R-integrierbar. Dann
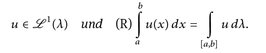
Beweis. Es sei u R-integrierbar. Dann gibt es eine Folge von Partitionen Πn mit
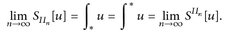
Wir dürfen o. E. annehmen, dass Πn ⊂ Πn+1 ⊂ ... (sonst betrachten wir Π1 ∪ ... ∪ Πn).
Daher gilt

und mit monotoner Konvergenz (MK) sehen wir
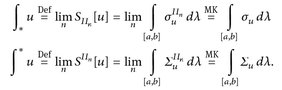
(*)
Es folgt

Da u zudem Borel-messbar war, sehen wir u ∈ ℒ1(λ).
Der Beweis von Satz 13.2 zeigt noch mehr: Wenn u R-integrierbar (aber nicht notwendig Borel-messbar) ist, dann gibt es eine messbare Funktion Σu ∈ ℒ1(λ) mit u = Σu f. ü. und 
13.3 Satz. Es sei u: [a, b] → ℝ beschränkt. Dann gilt


Die Menge der Stetigkeitsstellen {x: u stetig in x} einer beliebigen Funktion u: [a, b] → IR ist sogar eine Borelmenge, vgl. Anhang A.3.
Beweis von Satz 13.3. „⇒“: Für eine R-integrierbare Funktion u seien Πn und σu, Σu wie im Beweis von Satz 13.2. Wegen der Eigenschaften von sup und inf gilt
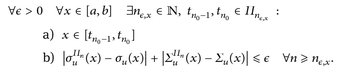
Somit erhalten wir für x ∈ [a, b] \ ∪n∈ℕ Πn und 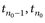 wie oben
wie oben

Nun gilt [Σu ≠ σu} ∈  da u R-integrierbar ist (vgl. Beweis von 13.2), und daher ist
da u R-integrierbar ist (vgl. Beweis von 13.2), und daher ist
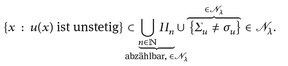
„⇐“: Umgekehrt sei {x: u(x) ist unstetig} Teilmenge einer Nullmenge.
∀x ∉ {u unstetig} ∀Π ⊂ [a, b] Partition ∃k = k(x, Π): x ∈ [tk–1, tk]
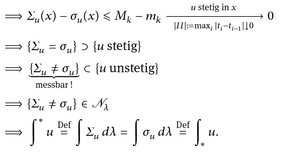
Es folgt, dass die Funktion u R-integrierbar ist.

Die Sätze 13.2 und 13.3 gelten i. Allg. nicht für uneigentliche Riemann-Integrale.
Aufgaben
- Zeigen Sie, dass
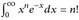 für alle
für alle 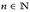 gilt.
gilt.
Hinweis: Zeigen Sie
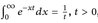 , t > 0, und differenzieren Sie diese Identität.
, t > 0, und differenzieren Sie diese Identität. -
- (a) Zeigen Sie, dass
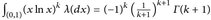 für alle k = 0, 1, 2, ... gilt.
für alle k = 0, 1, 2, ... gilt. - (b) Verwenden Sie Teil (a), um
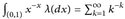 zu zeigen.
zu zeigen.
- (a) Zeigen Sie, dass
- Zeigen Sie, dass die Funktion
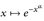 , x ≥0, für jedes α > 0 Lebesgue-integrierbar ist.
, x ≥0, für jedes α > 0 Lebesgue-integrierbar ist. - Untersuchen Sie, ob die folgenden Funktionen auf den angegebenen Intervallen Lebesgue-integrierbar sind:
- (a)
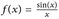 [1, ∞);
[1, ∞); - (b)
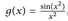 [1, ∞);
[1, ∞); - (c)
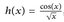 (0, 1];
(0, 1]; - (d)
 , (0,1];
, (0,1]; - (e)
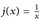 , (0, 1];
, (0, 1]; - (f)
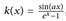 , (0, ∞).
, (0, ∞).
Was würde sich ändern, wenn wir stattdessen [
 , 2] wählen?
, 2] wählen?Hinweis: Betrachten Sie zunächst
 etc. und nutzen Sie monotone Konvergenz sowie Aussagen über den Zusammenhang von Riemann- und Lebesgue-Integralen.
etc. und nutzen Sie monotone Konvergenz sowie Aussagen über den Zusammenhang von Riemann- und Lebesgue-Integralen. - (a)
- Beweisen Sie folgende Gleichheit:
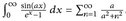 .
.
Hinweis: Verwenden Sie die geometrische Reihe und bestimmen Sie Im
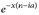 .
. - Berechnen Sieden Grenzwert
 .
. - Es sei
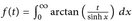 , t > 0, wobei
, t > 0, wobei 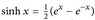 .
.
- (a) Zeigen Sie, dass ƒ auf (0, ∞) differenzierbar, dass aber ƒ′(0+) nicht existiert.
- (b) Finden Sie eine geschlossene Darstellung für f′ sowie für ƒ(0) und limt→∞ f(t).
- Finden Sie eine Folge von Riemann-integrierbaren Funktionen
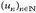 , so dass u(x) = limn un(x) für alle
, so dass u(x) = limn un(x) für alle  existiert, aber nicht mehr Riemann-integrierbar ist.
existiert, aber nicht mehr Riemann-integrierbar ist. - Eine Funktion u:
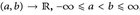 , heißt uneigentlich Riemann-integrierbar, wenn sie für alle Intervalle [c, d] ⊂ (a, b) Riemann-integrierbar ist und
, heißt uneigentlich Riemann-integrierbar, wenn sie für alle Intervalle [c, d] ⊂ (a, b) Riemann-integrierbar ist und 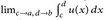 existiert. Zeigen Sie: Jede messbare, uneigentlich Riemann-integrierbare Funktion u: (0, ∞) → [0, ∞) ist Lebesgue-integrierbar.
existiert. Zeigen Sie: Jede messbare, uneigentlich Riemann-integrierbare Funktion u: (0, ∞) → [0, ∞) ist Lebesgue-integrierbar. - (Fresnelsche Integrale) Zeigen Sie, dass die folgenden Integrale als uneigentliche Riemann-Integrale existieren

Existieren diese Integrale auch als Lebesgue-Integrale?
Bemerkung: Mit Hilfe des Residuenkalküls kann man zeigen, dass beide Integrale den Wert
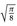 haben.
haben. - (Frullanisches Integral) Es sei ƒ:
 eine stetige Funktion mit limx→0+ f(x) = m und limx→∞ ƒ(x) = M. Zeigen Sie, dass das uneigentliche Riemann-Integral
existiert. Existiert das Integral auch im Lebesgueschen Sinne?
eine stetige Funktion mit limx→0+ f(x) = m und limx→∞ ƒ(x) = M. Zeigen Sie, dass das uneigentliche Riemann-Integral
existiert. Existiert das Integral auch im Lebesgueschen Sinne?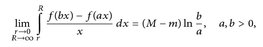
Hinweis: Mittelwertsatz für Riemann-Integrale.