8 Das Integral positiver Funktionen

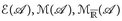In diesem Kapitel seien (E, , µ) ein beliebiger Maßraum und die Familien der einfachen bzw. messbaren Funktionen. Die positiven (d. h. „≥ 0”) Elemente dieser Mengen bezeichnen wir mit und 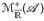. Wir wollen, dass das Integral die „Fläche unter einer Kurve“ beschreibt.

Abb. 8.1. Das Integral einer positiven Treppenfunktion.

Daher (vgl. Abbildung 8.1) ist folgende Definition naheliegend.

Problem: Ist das so definierte Integral wohldefiniert?

8.1 Lemma. Es seien 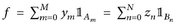zwei Standarddarstellungen von . Danngilt

Beweis. Wegen 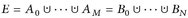gilt

und, da y_m = z_n wenn ,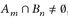

Jede positive Funktion in besitzt eine Standarddarstellung; daher ist folgende Definition sinnvoll.

 

8.2 Definition. Es sei in Standarddarstellung. Dann heißt

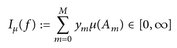
das (µ-)Integral von f.

 

Tatsächlich hat I_µ bereits die wesentlichen Eigenschaften, die wir von einem Integral erwarten.

 

8.3 Lemma. Es seien 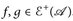. Dann gilt

Beweis. Die Eigenschaften a), b) sind klar.

c) Wenn , Standarddarstellungen sind, dann ist

auch eine Standarddarstellung (Beispiel 7.9.b). Dann gilt aber

d) Für f ≤ g gilt 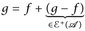und nach Teil c) ist dann

Allgemeine u lassen sich mit Hilfe des Sombrero-Lemma 7.11 durch aufsteigende Folgen von -Funktionen approximieren. Insbesondere gibt es positive einfache Funktionen unterhalb einer positiven messbaren Funktion.

8.4 Definition. Das (µ-)Integral von ist gegeben durch

(8.1)

Wenn wir die Integrationsvariable hervorheben wollen, dann schreiben wir auch

Beachte: (8.1) ist stets wohldefiniert, da wir Werte in [0, ∞] zulassen.

8.5 Lemma. Das Integral ∫ ... dµ aus Definition 8.4 setzt I_µ(∙) fort:

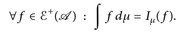
Beweis. Sei . Dann ist g:= f ≤ f zulässig im Supremum in (8.1), d. h.

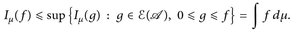
Umgekehrt gilt: , d. h.

Der folgende Satz ist der erste in einer Reihe von sogenannten Konvergenzsätzen, die die Vertauschung von Integration und Grenzwerten behandeln.

 

8.6 Satz (Beppo Levi, BL). Es sei eine aufsteigende Folge positiver messbarer Funktionen

0 ≤ u₁ ≤ u₂ ≤ u₃ ≤ ... ≤ u_n ≤ u_n+1 ≤ ...

Dann ist positiv und messbar und es gilt

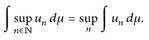
(8.2)

• ▶ u_n ≤ u_n+1 bedeutet,dass u_n(x) ≤ u_n+1, (x) für alle x ∈ E.
• ▶ u_n ↑ u ist kurz für u_n.
• ▶ u_n ↑ u, dann gilt u = lim_n u_n = sup_n u_n (aufsteigender Limes).

Beweis. In Korollar 7.13 sahen wir, dass .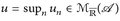

1°) Behauptung: . Wenn u ≤ w, dann gilt für jede einfache Funktion f mit f ≤ u auch f ≤ w. Daher ist

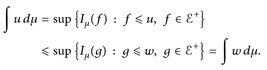
2°) Behauptung: sup_n ∫ u_n dµ ≤ ∫ sup_n u_n dµ. Nach 1°) ist das Integral monoton. Daher folgt

3°) Behauptung: 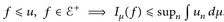. Wähle 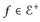mit f ≤ u und ein festes .

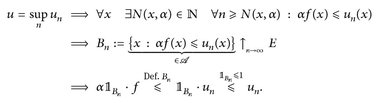
Für alle einfachen Funktionen der Form gilt nun

Die rechte Seite hängt nicht von n ab. Nach Konstruktion gilt B_n ↑ E. Wenn wir auf der linken Seite n → ∞ streben lassen, finden wir µ(B_n ∩ A_m) → µ(A_m) und daher gilt

Da die rechte Seite nicht von α abhängt, folgt die Behauptung für α → 1.

4°) Bilde in der Aussage von 3° das Supremum über alle mit f ≤ u. Dann folgt

und der Satz ist gezeigt.

Hier ist noch ein wichtiger Spezialfall von Satz 8.6.

8.7 Korollar. Sei . Dann gilt für jede Folge 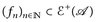mit f_n ↑ u

(8.3)

Oft wird (8.3) als Definition von ∫ u dµ verwendet. Dann hat man aber das Problem der Wohldefiniertheit: Ist das Integral unabhängig von der approximierenden Folge ? Unsere Definition (8.1) liefert das „kostenlos“. Trotzdem ist (8.3) wichtig, da es zeigt, dass das Supremum ein Limes ist, und insbesondere u ↦ ∫ u dµ linear ist.

8.8 Lemma. Es seien . Dann gilt

Beweis. Das folgt aus Lemma 8.3, Korollar 8.7 und dem Sombrero-Lemma 7.11. D

Die folgende Version des Satzes von Beppo Levi für Reihen ist oft hilfreich.

 

8.9 Lemma. Für jede Folge 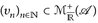ist und es gilt

Beweis. [] Hinweis: 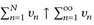für N → ∞.

 

8.10 Beispiel. a) Auf einem beliebigen Messraum (E, 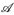) betrachten wir 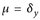für ein festes y ∈ E. Dann gilt für alle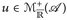

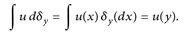
(8.4)

Denn: Für 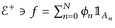in Standarddarstellung ist

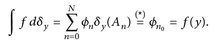
An der mit (*) gekennzeichneten Stelle verwenden wir, dass , d. h. wir finden ein n₀ mit . Aufgrund des Sombrero-Lemmas (Satz 7.11) gibt es eine Folge 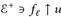, und für diese gilt

b) Es seien (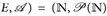) und mit α_ℓ ≥ 0. Wir wissen bereits, dass

• ► µ ein Maß auf N ist.
• ► jede Funktion u: ()) messbar ist.
• ► für eine geeignete Folge gilt.

Somit finden wir

c) Insbesondere zeigt b), dass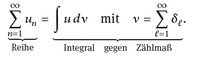

Der folgende Konvergenzsatz für positive messbare Funktionen wird „Lemma von Fatou“ genannt. Er wird häufig verwendet, um die Endlichkeit gewisser Integralausdrücke zu zeigen.

8.11 Satz (Fatou). Es sei eine Folge positiver messbarer Funktionen. Dann ist und es gilt

(8.5)

Beweis. Nach Definition ist . Korollar 7.13 zeigt, dass diese Funktion messbar ist. Wegen inf_n≥m u_n ↑u (m → ∞) gilt

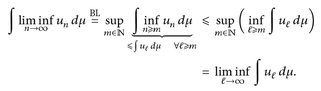
Im Beweis von Satz 8.11 wird die Positivität der u_n verwendet, um ∫ inf_n≥m u_n dµ > – ∞ sicherzustellen. Das Lemma von Fatou gilt also auch für alle Folgen , die die Bedingung u_n ≥ –w für alle und eine messbare Funktion w ≥ 0 mit ∫ w dµ < ∞ erfüllen.

Aufgaben

1. Der Satz von Beppo Levi (Satz 8.6) gilt für eine „wachsende Folge positiver Funktionen“. Zeigen Sie, dass die Aussage im Allgemeinen für „eine Folge wachsender positiver Funktionen“ falsch ist.
2. Auf einem Maßraum (E, , µ) seien eine Folge positiver messbarer Funktionen. Zeigen Sie, dass
   
   äquivalent zum Satz von Beppo Levi (Satz 8.6) ist.
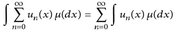
3. Auf einem Maßraum (E, , µ) sei 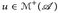. Zeigen Sie, dass , ein Maß ist.

   Hinweis: Verwenden Sie Aufgabe 8.2.

4. (Fatou) Es sei (A, 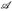, µ) ein Maßraum und . Wenn u_n ≤ u für alle und ein 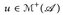mit ∫ u dµ < ∞ gilt, dann gilt auch
   
5. (Fatou für Maße) Es sei (A, , µ) ein endlicher Maßraum und . In Aufgabe 2.9 wurde der limes inferior und limes superior von Mengen eingeführt. Zeigen Sie:
   • (a)
   • (b)
   • (c) Zeigen Sie, dass die Endlichkeit des Maßes für Teil (b) wesentlich ist.
   • (d)
6. Es sei (E, 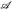) ein Messraum und µ₁, µ₂ .... abzählbar viele Maße. Zeigen Sie:
   • (a) Für jede Folge (c_i)_i ⊂ [0, ∞] ist 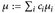ein Maß auf (E, ).
   • (b) Für jede Funktion gilt .
   • (c) Für jede Doppelfolge 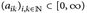gilt .

   Hinweis: Teil (c) kann elementar oder mit Hilfe des Zählmaßes und von Teil (b) bewiesen werden.

7. (Kerne) Es seien (E, , µ) ein Maßraum und (F, ℱ) ein Messraum. Ein (Maβ-)Kern oder Übergangskern ist eine Abbildung N: E × ℱ → [0, ∞], so dass

   Q ↦ N(x, Q)	ein Maß auf (F, ℱ) ist für jedes feste x ∈ E;
   x ↦ N(x, Q)	eine messbare Funktion auf E ist für jedes feste Q ∈ ℱ.

   • (a) Zeigen Sie, dass ℱ ∋ Q ↦ µN(Q):= ∫ N(x, Q) µ(dx) ein Maß auf (F, ℱ) ist.
   • (b) Für f ∈ M⁺(ℱ) definieren wir Nf(x):= ∫ f(y) N(x,dy). Zeigen Sie, dass f ↦ Nf additiv, positiv homogen und -messbar ist.
   • (c) Es sei µN das in Teil (a) definierte Maß auf (F, ℱ). Zeigen Sie, dass ∫ f d(µN) = ∫ Nf dµ für gilt.

   Hinweis: Betrachten Sie zunächst messbare Treppenfunktionen und verwenden Sie dann das Sombrero-Lemma.

8. Ein Maßraum (E, , µ) heißt σ-endlich, wenn es eine Folge mit µ(A_i) < ∞ gibt.
   • (a) Wenn (E, , µ) σ-endlich ist, dann gibt es eine strikt positive messbare Funktion f > 0 mit ∫ f dµ < ∞.
   • (b) Zeigen Sie die sog. Markovsche Ungleichung: Für gilt .
   • (c) Verwenden Sie Teil (b), um die Umkehrungvon (a) zu zeigen: Wenn es ein mit f > 0 und ∫ f dµ < ∞ gibt, dann ist (E, , µ) σ-endlich.

   Hinweis: Betrachten Sie Funktionen der Art bzw. die Mengen A_i:- {f ≥ 1/i}.