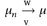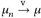25 ♦ Konvergenz von Maßen

In diesem Kapitel beschäftigen wir uns mit der schwachen und vagen Konvergenz von Maßen. Es sei (E, d) ein metrischer Raum und mit bezeichnen wir die (positiven) Maße auf (E, ℬ(E)). Weiter setzen wir

	endliche Maße,
	Wahrscheinlichkeitsmaße.

Ein Maß µ heißt lokal endlich, wenn für jedes x ∈ E eine offene Umgebung U = U(x) existiert mit µ(U) < ∞. Da wir jede kompakte Menge K mit endlich vielen derartigen Umgebungen überdecken können, gilt µ(K) < ∞ für lokal endliche Maße.

Schwache Konvergenz

25.1 Definition. Eine Folge 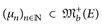konvergiert schwach gegen 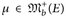(Notation: 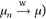, wenn

Die in Definition 25.1 eingeführte schwache Konvergenz ist nicht die aus der Funktionalanalysis bekannte schwache Konvergenz im Dualpaar wobei .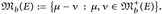

25.2 Bemerkung. Da die Familie C_b(E) maßbestimmend ist (im Sinne von Definition 21.1), sind schwache Grenzwerte eindeutig: Es seien µ, 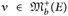und es gelte ∫ u dµ = ∫ u dν für alle u ∈ C_b(E). Für eine abgeschlossene Menge F ⊂ E bezeichnet d(x, F):= inf _y∈F d(x, y) den Abstand von x zur Menge F; dann gilt

und wir sehen mit monotoner Konvergenz

Aus dem Eindeutigkeitssatz für Maße (Satz 4.5) folgt dann µ = ν.

Für u ≡ 1 sehen wir, dass schwache Konvergenz die Gesamtmasse von Maßen erhält:

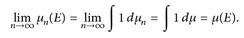
(25.1)

Andererseits kann man lim_n→∞ µ_n(B) = µ(B) nicht für beliebige Mengen B ∈ ℬ(E) erwarten. Betrachte x_n ∈ E mit lim_n→∞ x_n = x und 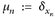sowie µ:= δ_x. Dann konvergiert 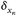schwach gegen , da

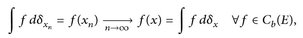
aber muss i. Allg. nicht gegen 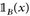konvergieren (z. B. wenn x_n ≠ x und B = {x}). Trotzdem kann man schwache Konvergenz mit Hilfe von Mengen charakterisieren. Dazu benötigen wir den Begriff des Randes einer Menge 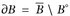, wobei den Abschluss und B° das offene Innere von B bezeichnet.

25.3 Satz (Portmanteau-Theorem). Sei (E, d) ein metrischer Raum und µ, 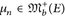, . Dann sind die folgenden Aussagen äquivalent:

• a) .
• b) lim_n→∞ ∫ u dµ_n = ∫ u du für alle gleichmäßig stetigen u ∈ C_b(E).
• c) lim sup_n→∞ µ_n(F) ≤ µ(F) für alle abgeschlossenen F ⊂ E und lim_n→∞ µ_n(E) = µ(E).
• d) lim inf_n→∞ µ_n(U) ≥ µ(U) für alle offenen U c E und lim_n→∞ µ_n(E) = µ(E).
• e) lim_n→∞ µ_n(B) = µ(B) für alle Borelmengen B c E mit µ(∂B) = 0.

 

Beweis. Die Implikation a)⇒b) ist klar. b)⇒c): Definiere für k ∈

Dann ist u_k gleichmäßig stetig (vgl. das Argument im Beweis vo0n Lemma 21.3), beschränkt und es gilt 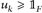sowie . Somit

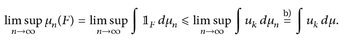
Mit monotoner Konvergenz folgt nun

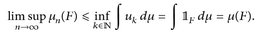
Die Masseerhaltung µ_n(E) → µ(E) haben wir schon in (25.1) gesehen.

c)⇔d): Für U c E offen ist U^c = E \ U abgeschlossen und wir finden

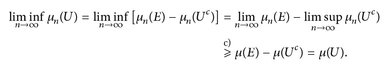
Die Umkehrung wird ganz ähnlich bewiesen.

c) & d)⇒e): Wir haben und somit

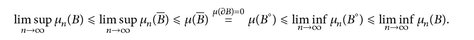
e)⇒a): Es sei u ∈ C_b (E) eine positive Funktion. Da ∂{µ ≥ t} ⊂ {u = t} und µ(E) < ∞, gilt µ(∂{u ≥ t}) > 0 für höchstens abzählbar viele t. Mit Satz 16.7, dominierter Konvergenz und der Tatsache, dass abzählbare Mengen Lebesgue-Nullmengen sind, erhält man

Der allgemeine Fall folgt nun mit Linearität.

Vage Konvergenz

Schwache Konvergenz setzt endliche Maße voraus, was für viele Anwendungen nicht erfüllt ist. Daher verwendet man oft das Konzept der vagen Konvergenz, das auf stetigen Funktionen mit kompakten Trägern C_c(E) beruht. Wir betrachten hier nur reguläre Maße, vgl. Anhang A.5: Ein Maß 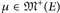∈ ist regulär, also 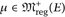, wenn

• ► µ(K) < ∞ ∀K ⊂ E kompakt;
• ► µ(B) = inf {µ(U): U ⊃ B, U offen} ∀B ∈ ℬ(E);
• ► µ(U) = sup {µ(K): K c U, K kompakt} .

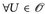25.4 Definition. Eine Folge konvergiertvag gegen 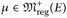∈ (Notation: 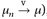, wenn

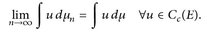
Im Gegensatz zu C_b (E) kann der Raum C_c(E) relativ klein sein. Für eine sinnvolle Theorie müssen wir weitere topologische Annahmen machen.

Eine Menge A ⊂ E heißt relativ kompakt, wenn 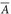kompakt ist. Ein metrischer Raum (E, d) heißt lokal-kompakt, wenn jeder Punkt x ∈ E eine relativ kompakte offene Umgebung V(x) besitzt. Unter diesen Annahmen garantiert das Lemma von Urysohn (Lemma 24.6), dass der Raum C_c(E) hinreichend reichhaltig ist.

 

25.5 Bemerkung. In lokal-kompakten Räumen E folgt — wie in Bemerkung 25.2 — mit Lemma 24.6.a) und dem Satz von der monotonen Konvergenz, dass

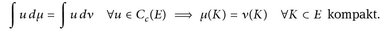
Wenn µ, ν regulär sind, dann gilt µ(B) = ν(B) für alle B ∈ ℬ(E), d. h. in sind vage Grenzwerte eindeutig.

 

Mit Hilfe von Lemma 24.6 können wir auch ein Portmanteau-Theorem für vage Konvergenz zeigen.

 

25.6 Satz. Sei (E, d) ein lokal-kompakter metrischer Raum und 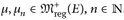. Dann sind die folgenden Aussagen äquivalent:

• a) .
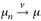• b) lim sup_n→∞ µ_n(K) ≤ µ(K) und lim inf_n→∞ µ_n(U) ≥ µ(U) für alle kompakten Mengen K c E und alle relativ kompakten offenen Mengen U c E.
• c) lim_n→∞ µ_n(B) = µ(B) für alle relativ kompakten Borelmengen B ⊂ E mit µ(∂B) = 0.

Beweis. a)⇒b): Es sei K eine kompakte Menge und 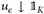mit u_ε, ∈ C_c(E) aus Lemma 24.6. Nun folgt lim sup_n→∞ µ_n(K) ≤ µ(K) wie im Beweis von Satz 25.3, b)⇒c).

Zu jeder offenen und relativ kompakten Menge U gibt es nach Lemma 24.6 Funktionen ω_∈, ∈ C_c(E) mit 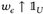. Somit

Monotone Konvergenz zeigt dann

b)⇒c)⇒a) folgt nun wie im Beweis der entsprechenden Aussagen von Satz 25.3. Beachte, dass die Mengen {u ≥ t}, t > 0, für positive u ∈ C_c(E) kompakt sind.

Im Gegensatz zur schwachen Konvergenz erhält die vage Konvergenz nicht immer die Gesamtmassen. Ein typisches Beispiel ist die Folge auf (0, ∞), die vag gegen das Maß µ ≡ 0 konvergiert.

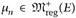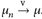25.7 Lemma. Es sei (E, d) ein lokal-kompakter metrischer Raum, µ, und . Dann gilt µ(E) ≤ lim inf_n→∞ µ_n(E).

 

Beweis. Für alle u ∈ C_c(E) mit 0 ≤ u ≤1 gilt

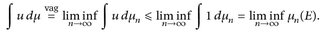
Nach Lemma 24.6 gibt es zu jedem Kompaktum K ein u ∈ C_c(E) mit 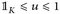. Somit

Wir schreiben 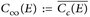für den Abschluss von C_c(E) bezüglich der sup-Norm. Da gleichmäßige Konvergenz die Stetigkeit erhält, ist u ∈ C_∞ (E) stetig. Andererseits ist die Menge {|u|, ∈} kompakt, da es nach Konstruktion ein u_ε ∈ C_c(E) mit ∥u – u_ε∥_∞, < ∈ gibt. Daher verschwindet u im Unendlichen. Man sieht leicht, dass (C_∞, (E), || · ||_∞) ein Banachraum ist.

 

25.8 Satz. Es sei (E, d) ein lokal-kompakter metrischer Raum und µ, . Dann gilt

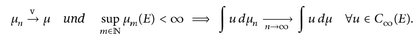
Beweis. Seien u ∈ C_∞(E) und ∈ > 0. Nach der Vorbemerkung zu Satz 25.8 und Lemma 24.6 gibt es ein χ ∈ C_c(E),0 ≤ χ ≤ 1, so dass |u| ≤ ∈ auf der Menge {χ < 1} =[X= = 1}^c. Somit

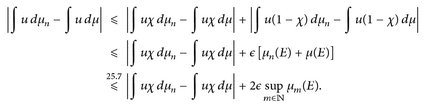
Da u_X ∈ C_c(E) ist, ergibt sich für n → ∞

Abschließend behandeln wir den Zusammenhang zwischen vager und schwacher Konvergenz.

 

25.9 Satz. Es sei (E, d) ein lokal-kompakter metrischer Raum und µ, 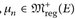. Dann sind äquivalent:

• a)
• b) µ_n → µ und Masseerhaltung: lim_n→∞ µ_n(E) = µ(E).
• c) und Straffheit: ∀∈ > 0 ∃K ⊂ E kompakt: .

Insbesondere fallen vage und schwache Konvergenz für Wahrscheinlichkeitsmaße auf lokal- und σ-kompaktem E zusammen.

Beweis. Die Implikation a)⇒b) ist offensichtlich.

 

b)⇒c) Da die Maße u_n und µ von innen regulär sind, gilt

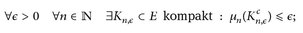
entsprechend finden wir eine kompakte Menge K_0,∈ für das Maß µ. Mit dem Lemma von Urysohn (Lemma 24.6.a) gibt es eine relativ kompakte offene Menge U_∈ ⊃ K_0,∈ und eine kompakte Menge K_∈ ⊃ U_∈, und wegen Satz 25.6.b) ist dann

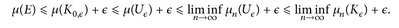
Da nach Voraussetzung µ(E) = lim_n→∞ µ_n(E) gilt, sehen wir

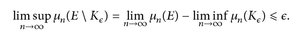
Daher gibt es ein N = N(∈) ∈ N mit sup_n>N µ_n(E\K_∈) ≤ 2∈. Da die Maße µ₁, ... , µ_N regulär sind, ist K:= K_∈ ∪ K_1,∈ ∪ ... ∪ K_N,∈ die gesuchte kompakte Menge.

c)⇒a) Sei u ∈ C_b(E), ∈ > 0 und K c E eine kompakte Menge mit sup_n µ_n(K^c) ≤ ∈ (nach Annahme) und µ(K^c) ≤ ∈ (wegen der Regularität). Mit dem Lemma von Urysohn konstruieren wir eine Funktion χ ∈ C_c(E) mit 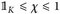. Dann ist

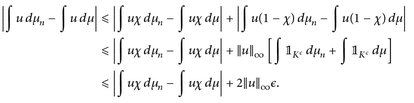
Da uχ ∈ C_c(E) ist, ergibt sich für n → ∞

Der Zusatz folgt aus der Tatsache, dass W-Maße auf σ-kompakten Räumen regulär sind, Satz A.10.

Viele Existenzbeweise lassen sich auf Kompaktheitsaussagen zurückführen. Für die vage Konvergenz (und die dadurch induzierte vage Topologie) kann man Kompaktheit durch vage Beschränktheit kennzeichnen. In allgemeinen Räumen gilt allerdings nicht, dass Kompaktheit die Existenz von konvergenten (Teil-)Folgen impliziert. Wenn aber der Raum C_c(E) eine abzählbare dichte Teilmenge enthält (also separabel ist, vgl. Satz A.14), dürfen wir mit Folgen arbeiten. Typischerweise ist C_c(E) separabel, wenn der Grundraum (E, d) selbst ein metrischer Raum mit einer abzählbaren dichten Teilmenge ist.

25.10 Lemma (Einfangtrick). Es sei (E, d) ein lokal-kompakter und σ-kompakter metrischer Raum. Dann existieren kompakte Mengen , so dass und 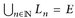gilt. Insbesondere gibt es für jede kompakte Menge K ⊂ E ein N = N(K) mit K ⊂ L_N.

 

Beweis. Da E σ-kompakt ist, gibt es eine Folge kompakter Mengen K_n ↑ E. Mit dem Urysohn-Lemma 24.6.a) finden wir Funktionen χ_n ∈ C_c(E) mit 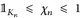; o. E. können wir χ_n ↑ 1 annehmen, sonst betrachten wir die Folge max{χ₁, ... , χ_n}.

Wir definieren nun L_n:= {χ_{n ≥} 1/n}. Diese Mengen sind abgeschlossen (χ_n ist stetig), kompakt (L_n ⊂ supp χ_n) und wegen χ_n ≤ χ_n+1 gilt auch

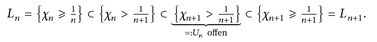
Da die Menge U_n offen ist, folgt L_n c L°_n+1 c L_n+1. Wegen χ_n ↑ 1 gilt L°_n ↑ E.

Nun sei K c E kompakt. Offensichtlich ist und wegen der Kompaktheit gibt es eine endliche Teilüberdeckung, d. h. es existiert ein N = N(K), so dass K ⊂ L₁ ∪ · · · ∪ L_N = L_N.

 

Wir kommen nun zum angekündigten Kompaktheitsresultat.

25.11 Satz. Es sei (E, d) ein lokal-kompakter und σ-kompakter metrischer Raum, so dass (C_c(E), ∥⋅∥_∞) separabel ist. Wenn 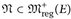vag beschränkt ist, d. h.

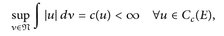
(25.2)

dann gibt es eine Folge 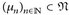und ein Maβ , so dass

 

Beweis. 1°) Mit dem Lemma von Urysohn (Lemma 24.6) und dem Einfangtrick (Lemma 25.10) konstruieren wir eine Folge mit

Es sei eine abzählbare dichte Teilmenge von C_c(E). Dann ist auch 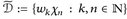eine abzählbare dichte Teilmenge von C_c(E).

2°) Mit {u₁, u₂, u₃, ... } bezeichnen wir eine Abzählung der Menge 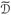aus 1°. Wir konstruieren die Folge 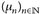rekursiv: Für 〈ν, u〉:= ∫ u dν ∫ gilt nach Voraussetzung

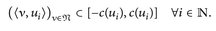
Weil die rechte Seite ein kompaktes Intervall ist, finden wir durch wiederholte Anwendung des Satzes von Bolzano-Weierstraß

Da wir die Teilfolgen immer weiter ausgedünnt haben, gilt 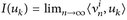für alle k = 1, ... , i. Somit erhalten wir für die Diagonalfolge

3°) Es sei u ∈ C_c(E) und ∊ > 0. Wie in Schritt 1° finden wir Funktionen w_∊ ∈ D und χ_N ∈ C_c(E), so dass für

gilt. Somit

(*)

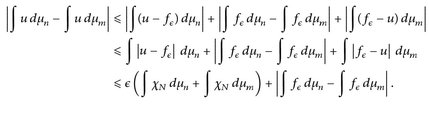
Für m, n → ∞ ergibt sich dann wegen (25.2) und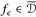

(**)

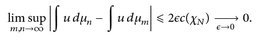
Also konvergiert I(u):= lim_n→∞ ∫ u dμ_n für alle u ∈ C_c(E) und definiert ein positives lineares Funktional. Die Behauptung folgt nun aus dem Rieszschen Darstellungssatz, Satz 24.8.

 

Wenn die Familie 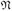aus endlichen Maßen mit 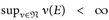besteht, dann ist die vage Beschränktheit offensichtlich erfüllt, und wir können sogar auf die σ-Kompaktheit von E verzichten. Das folgt einfach aus der Tatsache, dass wir im Beweis von Satz 25.11 an den mit (*) und (**) gekennzeichneten Stellen χ_N ≡ 1 und 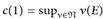wählen können.

 

25.12 Korollar. Es sei (E, d) ein lokal-kompakter metrischer Raum, so dass (C_c(E), ∥⋅∥_∞) separabel ist. Dann hat jede Folge von Maβen in eine vag konvergente Teilfolge, mit Grenzwert μ ∈ 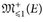. (M. a. W.: Die Familie ist vag folgenkompakt.)

 

Beweis. Wie in Satz 25.11 finden wir für jede Folge in 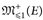(E) eine vag konvergente Teilfolge mit vagem Grenzwert . Wegen Lemma 25.7 gilt μ(E) ≤ 1 und somit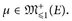

In vielen Anwendungen ist E ein σ-kompakter metrischer Raum. Dann sind nach Satz A.10 die endlichen Maße bereits regulär. Korollar 25.12 ist in der Wahrscheinlichkeitstheorie, z. B. für den Stetigkeitssatz von P. Levy oder beim Beweis der Lévy-Khintchine Formel, ein wichtiges Hilfsmittel.

Aufgaben

1. Verwenden Sie Satz 25.11, um einen weiteren Beweis für den Stetigkeitssatz von Levy (Aufgabe 24.3) zu führen. (a
   • ) Zeigen Sie (ähnlich wie in Aufgabe 24.3), dass der Grenzwert lim_n→∞ ∫ u dμ_n für alle Funktionen existiert. Da ist die Folge vag beschränkt und es gibt ein Maß μ und eine vag konvergente Teilfolge μ_n(i) → μ(vag).
   • (b) Teil (a) lässtsich auf jede Teilfolge von (μ_n)_n anwenden und es folgt, dass alle Teilfolgen wiederum vag konvergente Teilfolgen mit demselben Grenzwert μ zulassen. Daher konvergiert μ_n → μ vag.
   • (c) Mit Levys truncation inequality (Aufgabe 22.3) folgt die Straffheit der Maße (μ_n)_n, und Satz 25.9 zeigt, dass μ_n → μ schwach konvergiert.
2. Es seien (E, d) ein lokal-kompakter metrischer Raum und .Dann gilt
   

   Hinweis: Vgl. den Beweis von Satz 25.6.c).