Chapter 1
Viewing the World through the Lens of Physics
IN THIS CHAPTER
 Recognizing the physics in your world
Recognizing the physics in your world
 Getting a handle on motion and energy
Getting a handle on motion and energy
 Wrapping your head around relativity
Wrapping your head around relativity
 Mastering measurements
Mastering measurements
Physics is the study of your world and the world and universe around you. You may think of physics as a burden — an obligation placed on you in school. But in truth, physics is a study that you undertake naturally from the moment you open your eyes.
Nothing falls beyond the scope of physics; it’s an all-encompassing science. You can study various aspects of the natural world, and, accordingly, you can study different fields in physics: the physics of objects in motion, of forces, of what happens when you start going nearly as fast as the speed of light, and so on. You enjoy the study of all these topics and many more in this book.
Figuring Out What Physics Is About
You can observe plenty going on around you all the time in the middle of your complex world. Leaves are waving, the sun is shining, the stars are twinkling, light bulbs are glowing, cars are moving, computer printers are printing, people are walking and riding bikes, streams are flowing, and so on. When you stop to examine these actions, your natural curiosity gives rise to endless questions:
- Why do I slip when I try to climb that snow bank?
- What are those stars all about? Or are they planets? Why do they seem to move?
- What’s the nature of this speck of dust?
- Are there hidden worlds I can’t see?
- Why do blankets make me warm?
- What’s the nature of matter?
- What happens if I touch that high-tension line? (You know the answer to that one; as you can see, a little knowledge of physics can be a lifesaver.)
Physics is an inquiry into the world and the way it works, from the most basic (like coming to terms with the inertia of a dead car that you’re trying to push) to the most exotic (like peering into the very tiniest of worlds inside the smallest of particles to try to make sense of the fundamental building blocks of matter). At root, physics is all about getting conscious about your world.
Paying Attention to Objects in Motion
Some of the most fundamental questions you may have about the world deal with objects in motion. Will that boulder rolling toward you slow down? How fast will you have to move to get out of its way? (Hang on just a moment while I get out my calculator …) Motion was one of the earliest explorations of physics, and physics has proved great at coming up with answers.
This book handles objects in motion — from balls to railroad cars and most objects in between. Motion is a fundamental fact of life and one that most people already know a lot about. You put your foot on the accelerator, and the car takes off.
But there’s more to the story. Describing motion and how it works is the first step in really understanding physics, which is all about observations and measurements and making mental and mathematical models based on those observations and measurements. This process is unfamiliar to most people, which is where this book comes in.
Studying motion is fine, but it’s just the very beginning of the beginning. When you take a look around, you see that the motion of objects changes all the time. You see a motorcycle coming to a halt at the stop sign. You see a leaf falling and then stopping when it hits the ground, only to be picked up again by the wind. You see a pool ball hitting other balls in just the wrong way so that they all move without going where they should.
Motion changes all the time as the result of force. You may know the basics of force, but sometimes it takes an expert to really know what’s going on in a measurable way. In other words, sometimes it takes a physicist like you.
Getting Energized
You don’t have to look far to find your next piece of physics. You never do. As you exit your house in the morning, for example, you may hear a crash up the street. Two cars have collided at a high speed, and, locked together, they’re sliding your way.
Thanks to physics you can make the necessary measurements and predictions to know exactly how far you have to move to get out of the way. You know that it’s going to take a lot to stop the cars. But a lot of what?
It helps to have the ideas of energy and momentum mastered at such a time. You use these ideas to describe the motion of objects with mass. The energy of motion is called kinetic energy, and when you accelerate a car from 0 to 60 miles per hour in 10 seconds, the car ends up with plenty of kinetic energy.
Where does the kinetic energy come from? Not from nowhere — if it did, you wouldn’t have to worry about the price of gas. Using gas, the engine does work on the car to get it up to speed.
Or say, for example, that you don’t have the luxury of an engine when you’re moving a piano up the stairs of your new place. But there’s always time for a little physics, so you whip out your calculator to calculate how much work you have to do to carry it up the six floors to your new apartment.
After you move up the stairs, your piano will have what’s called potential energy simply because you put in a lot of work against gravity to get the piano up those six floors.
Unfortunately, your roommate hates pianos and drops yours out the window. What happens next? The potential energy of the piano due to its height in a gravitational field is converted into kinetic energy, the energy of motion. It’s an interesting process to watch, and you decide to calculate the final speed of the piano as it hits the street.
Next, you calculate the bill for the piano, hand it to your roommate, and go back downstairs to get your drum set.
Moving as Fast as You Can: Special Relativity
Even when you start with the most mundane topics in physics, you quickly get to the most exotic. In Chapter 12, you discover ten amazing insights into Einstein’s theory of special relativity.
But what exactly did Einstein say? What does the famous 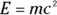 equation really mean? Does it really say that matter and energy are equivalent — that you can convert matter into energy and energy into matter? Yep, sure does.
equation really mean? Does it really say that matter and energy are equivalent — that you can convert matter into energy and energy into matter? Yep, sure does.
And stranger things happen when matter starts moving near the speed of light, as predicted by your buddy Einstein.
“Watch that spaceship,” you say as a rocket goes past at nearly the speed of light. “It appears compressed along its direction of travel — it’s only half as long as it would be at rest.”
“What spaceship?” your friends all ask. “It went by too fast for us to see anything.”
“Time measured on that spaceship goes more slowly than time here on Earth, too,” you explain. “For us, it will take 200 years for the rocket to reach the nearest star. But for the rocket, it will take only 2 years.”
“Are you making this up?” everyone asks.
Physics is all around you, in every commonplace action. But if you want to get wild, physics is the science to do it.
Measuring Your World
Physics excels at measuring and predicting the physical world — after all, that’s why it exists. Measuring is the starting point — part of observing the world so that you can then model and predict it. You have several different measuring sticks at your disposal: some for length, some for weight, some for time, and so on. Mastering those measurements is part of mastering physics.
To keep like measurements together, physicists and mathematicians have grouped them into measurement systems. The most common measurement systems you see in physics are the centimeter-gram-second (CGS) and meter-kilogram-second (MKS) systems, together called SI (short for Système International d’Unités). But you may also come across the foot-pound-inch (FPI) system. For reference, Table 1-1 shows you the primary units of measurement in the MKS system, which I use for most of the book. (Don’t bother memorizing the ones you’re not familiar with now; come back to them later as needed.)
TABLE 1-1 Units of Measurement in the MKS System
|
Measurement |
Unit |
Abbreviation |
|
Length |
meter |
m |
|
Mass |
kilogram |
kg |
|
Time |
second |
s |
|
Force |
newton |
N |
|
Energy |
joule |
J |
Keeping physical units straight
Because each measurement system uses a different standard length, you can get several different numbers for one part of a problem, depending on the measurement you use. For example, if you’re measuring the depth of the water in a swimming pool, you can use the MKS measurement system, which gives you an answer in meters; the CGS system, which yields a depth in centimeters; or the less common FPI system, in which case you determine the depth of the water in inches.
Converting between units of measurement
Physicists use various measurement systems to record numbers from their observations. But what happens when you have to convert between those systems? Physics problems sometimes try to trip you up here, giving you the data you need in mixed units: centimeters for this measurement but meters for that measurement — and maybe even mixing in inches as well. Don’t be fooled. You have to convert everything to the same measurement system before you can proceed. How do you convert in the easiest possible way? You use conversion factors. For an example, consider the following problem.
Passing another state line, you note that you’ve gone 4,680 miles in exactly three days. Very impressive. If you went at a constant speed, how fast were you going? As I discuss in Chapter 3, the physics notion of speed is just as you may expect — distance divided by time. So, you calculate your speed as follows:
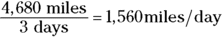
Your answer, however, isn’t exactly in a standard unit of measure. You want to know the result in a unit you can get your hands on — for example, miles per hour. To get miles per hour, you need to convert units.
In the preceding problem, you have a result in miles per day, which is written as miles/day. To calculate miles per hour, you need a conversion factor that knocks days out of the denominator and leaves hours in its place, so you multiply by days per hour and cancel out days:
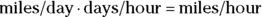
Your conversion factor is days per hour. When you plug in all the numbers, simplify the miles-per-day fraction, and multiply by the conversion factor, your work looks like this:
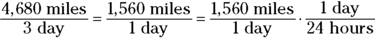
Note: Words like “seconds” and “meters” act like the variables x and y in that if they’re present in both the numerator and denominator, they cancel each other out.
When you cancel out days and multiply across the fractions, you get the answer you’ve been searching for:

So, your average speed is 65 miles per hour, which is pretty fast considering that this problem assumes you’ve been driving continuously for three days.
Nixing some zeros with scientific notation
Physicists have a way of getting their minds into the darndest places, and those places often involve really big or really small numbers. For example, say you’re dealing with the distance between the sun and Pluto, which is 5,890,000,000,000 meters. You have a lot of meters on your hands, accompanied by a lot of zeros.
Physics has a way of dealing with very large and very small numbers. To help reduce clutter and make these numbers easier to digest, physics uses scientific notation. In scientific notation, you express zeros as a power of ten. To get the right power of ten, you count up all the places in front of the decimal point, from right to left, up to the place just to the right of the first digit. (You don’t include the first digit because you leave it in front of the decimal point in the result.) So you can write the distance between the sun and Pluto as follows:
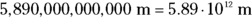
Scientific notation also works for very small numbers, such as the one that follows, where the power of ten is negative. You count the number of places, moving left to right, from the decimal point to just after the first nonzero digit (again leaving the result with just one digit in front of the decimal):

If the number you’re working with is greater than ten, you’ll have a positive exponent in scientific notation; if it’s less than one, you’ll have a negative exponent. As you can see, handling super large or super small numbers with scientific notation is easier than writing them all out, which is why calculators come with this kind of functionality already built in.
Knowing which digits are significant
In a measurement, significant digits are those that were actually measured. So, for example, if someone tells you that a rocket traveled 10.0 meters in 7.00 seconds, the person is telling you that the measurements are known to three significant digits (the number of digits in both of the measurements).
If you want to find the rocket’s speed, you can whip out a calculator and divide 10.0 by 7.00 to come up with 1.428571429 meters per second, which looks like a very precise measurement indeed. But the result is too precise. If you know your measurements to only three significant digits, you can’t say you know the answer to ten significant digits. Claiming as such would be like taking a meter stick, reading down to the nearest millimeter, and then writing down an answer to the nearest ten-millionth of a millimeter.
In the case of the rocket, you have only three significant digits to work with, so the best you can say is that the rocket is traveling at 1.43 meters per second, which is 1.428571429 rounded up to two decimal places. If you include any more digits, you claim an accuracy that you don’t really have and haven’t measured.
What if a passerby told you, however, that the rocket traveled 10.0 meters in 7.0 seconds? One value has three significant digits, and the other has only two. The rules for determining the number of significant digits when you have two different numbers are as follows:
-
When you multiply or divide numbers, the result has the same number of significant digits as the original number that has the fewest significant digits.
In the case of the rocket, where you need to divide, the result should have only two significant digits — so the correct answer is 1.4 meters per second.
-
When you add or subtract numbers, line up the decimal points; the last significant digit in the result corresponds to the right-most column where all numbers still have significant digits.
If you have to add 3.6, 14, and 6.33, you’d write the answer to the nearest whole number — the 14 has no significant digits after the decimal place, so the answer shouldn’t, either. To preserve significant digits, you should round the answer up to 24. You can see what I mean by taking a look for yourself:
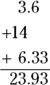
 Always remember to stick with the same measurement system all the way through the problem. If you start out in the MKS system, stay with it. If you don’t, your answer will be a meaningless hodgepodge because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems. (Imagine baking a cake where the recipe calls for two cups of flour, but you use two liters instead.)
Always remember to stick with the same measurement system all the way through the problem. If you start out in the MKS system, stay with it. If you don’t, your answer will be a meaningless hodgepodge because you’re switching measuring sticks for multiple items as you try to arrive at a single answer. Mixing up the measurements causes problems. (Imagine baking a cake where the recipe calls for two cups of flour, but you use two liters instead.) When you round a number, look at the digit to the right of the place you’re rounding to. If that right-hand digit is 5 or greater, you should round up. If it’s 4 or less, round down. For example, you should round 1.428 to 1.43 and 1.42 down to 1.4.
When you round a number, look at the digit to the right of the place you’re rounding to. If that right-hand digit is 5 or greater, you should round up. If it’s 4 or less, round down. For example, you should round 1.428 to 1.43 and 1.42 down to 1.4.