Chapter 2
Taking Vectors Step by Step
IN THIS CHAPTER
 Adding and subtracting vectors
Adding and subtracting vectors
 Putting vectors into numerical coordinates
Putting vectors into numerical coordinates
 Dividing vectors into components
Dividing vectors into components
You have a hard time getting where you want to go if you don’t know which way to go. That’s what vectors are all about. Too many people who’ve had tussles with vectors decide they don’t like them, which is a mistake. Vectors are easy when you get a handle on them, and you’re going to get a handle on them in this chapter. I break down vectors from top to bottom and relate the forces of motion to the concept of vectors.
Getting a Grip on Vectors
Vectors are a part of everyday life. When a person gives you directions, she may say something like, “The hospital is 2 miles that way” and point. She gives you both a magnitude (a measurement) and a direction (by pointing). When you’re helping someone hang a door, the person may say, “Push hard to the left!” That’s another vector. When you swerve to avoid hitting someone in your car, you accelerate or decelerate in another direction. Yet another vector.
Looking for direction and magnitude
Visually, you see vectors drawn as arrows in physics, which is perfect because an arrow has both a clear direction and a clear magnitude (the length of the arrow). Take a look at Figure 2-1. The arrow represents a vector that starts at the foot and ends at the head.

FIGURE 2-1: The arrow, a vector, has both a direction and a magnitude.
You can use vectors to represent a force, an acceleration, a velocity, and so on. In physics, you use A to represent a vector. In some books, you see it with an arrow on top:
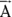
The arrow means that this is not only a scalar value, which would be represented by A, but also something with direction.
Take a look at Figure 2-2, which features two vectors, A and B. They look pretty much the same — the same length and the same direction. In fact, these vectors are equal. Two vectors are equal if they have the same magnitude and direction, and you can write this equality as 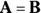 .
.
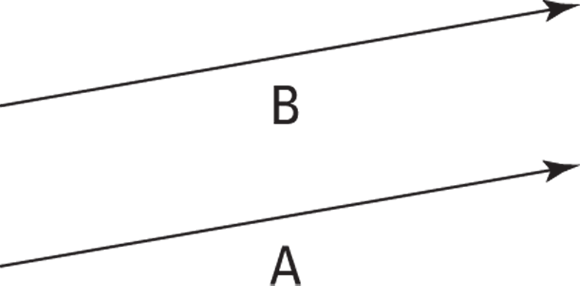
FIGURE 2-2: Two arrows (and vectors) with the same magnitude and direction.
You’re on your way to becoming a vector pro, but there’s more to come. What if, for example, someone says the hotel you’re looking for is 20 miles due north and then 20 miles due east? How far away is the hotel, and in which direction?
Adding vectors
You can add two direction vectors together. When you do, you get a resultant vector — the sum of the two — that gives you the distance to your target and the direction to that target.
Assume, for example, that a passerby tells you that to get to your destination, you first have to follow vector A and then vector B. Just where is that destination? You work this problem just as you find the destination in everyday life. First, you drive to the end of vector A, and at that point, you drive to the end of vector B.
When you get to the end of vector B, how far are you from your starting point? To find out, you draw a vector, C, from your starting point to your ending point, as Figure 2-3 shows. This new vector, C, represents the result of your complete trip, from start to finish.
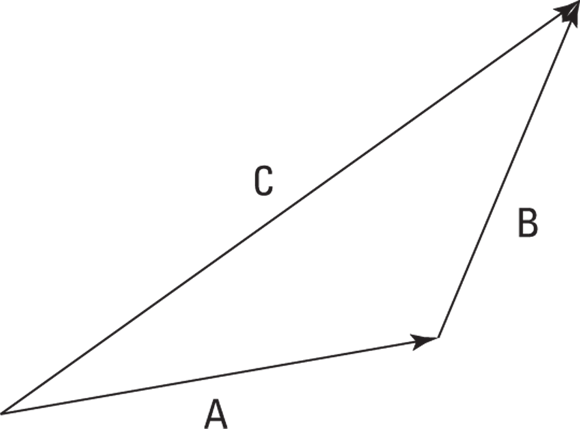
FIGURE 2-3: Take the sum of two vectors by creating a new vector.
Subtracting vectors
What if someone hands you vector C and vector A from Figure 2-3 and says, “Can you get their difference?” The difference is vector B because when you add vectors A and B together, you end up with vector C. So to arrive at B, you subtract A from C. You don’t come across vector subtraction that often in physics problems, but it does pop up sometimes.
To subtract two vectors, you put their feet (the nonpointy parts of the arrows) together and draw the resultant vector, which is the difference of the two vectors. The vector you draw runs from the head of the vector you’re subtracting (A) to the head of the vector you’re subtracting it from (C). To make heads from tails, check out Figure 2-4.
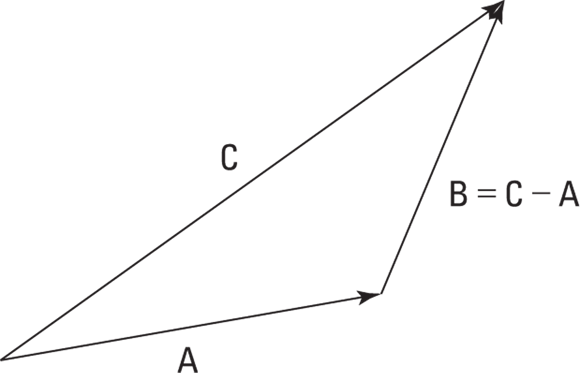
FIGURE 2-4: Subtracting two vectors by putting their feet together and drawing the result.
As you can see, both vector addition and subtraction are possible with the same vectors in the same problems. In fact, all kinds of math operations are possible on vectors. That means that in equation form, you can play with vectors just as you can scalars, like 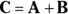 ,
, 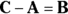 , and so on. This approach looks pretty numerical, and it is. You can get numerical with vectors just as you can with scalars.
, and so on. This approach looks pretty numerical, and it is. You can get numerical with vectors just as you can with scalars.
Waxing Numerical on Vectors
Vectors may look good as arrows, but that’s not exactly the most precise way of dealing with them. You can get numerical on vectors, taking them apart as you need them. Take a look at the vector addition problem 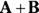 shown in Figure 2-5. With the vectors plotted on a graph, you can see how easy vector addition really is.
shown in Figure 2-5. With the vectors plotted on a graph, you can see how easy vector addition really is.
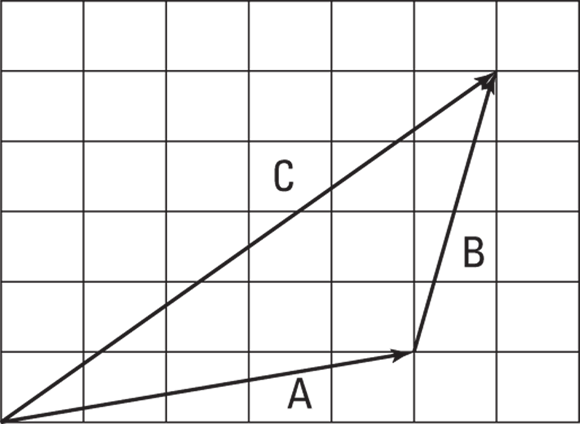
FIGURE 2-5: Use vector coordinates to make handling vectors easy.
Assume that the measurements in Figure 2-5 are in meters. That means vector A is 1 meter up and 5 to the right, and vector B is 1 meter to the right and 4 up. To add them for the result, vector C, you add the horizontal parts together and the vertical parts together. The resulting vector, C, ends up being 6 meters to the right and 5 meters up. You can see what that result looks like in Figure 2-5.
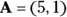
And because B is 1 meter to the right and 4 up, you can express it with (x, y) coordinates like this:
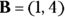
Having a notation is great because it makes vector addition totally simple. To add two vectors together, you just add their x and y parts, respectively, to get the x and y parts of the result:
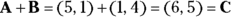
Now you can get as numerical as you like because you’re just adding or subtracting numbers. It can take a little work to get those x and y parts, but it’s a necessary step. And when you have those parts, you’re home free.
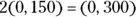
Now you’re flying along at 300 miles per hour in the same direction. In this problem, you multiply a vector by a scalar.
Working with Vector Components
Physics problems have a way of not telling you what you want to know directly. Take a look at the first vector you see in this chapter: vector A in Figure 2-1. Instead of telling you that vector A is coordinate (4, 1) or something similar, a problem may say that a ball is rolling on a table at 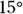 with a speed of 7.0 meters per second and ask you how long it will take the ball to roll off the table’s edge if that edge is 1.0 meter away to the right. Given certain information, you can find the components that make up vector problems.
with a speed of 7.0 meters per second and ask you how long it will take the ball to roll off the table’s edge if that edge is 1.0 meter away to the right. Given certain information, you can find the components that make up vector problems.
Using magnitudes and angles to find vector components
You can find tough vector information by breaking a vector up into its parts or components. For example, in the vector (4, 1), the x-axis component is 4 and the y-axis component is 1.
Typically, a physics problem gives you an angle and a magnitude to define a vector; you have to find the components yourself. If you know that a ball is rolling on a table at 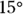 with a speed of 7.0 meters per second, and you want to find out how long it will take the ball to roll off the edge 1.0 meter to the right, what you need is the x-axis direction. So, the problem breaks down to finding out how long the ball will take to roll 1.0 meter in the x direction. To find out, you need to know how fast the ball is moving in the x direction.
with a speed of 7.0 meters per second, and you want to find out how long it will take the ball to roll off the edge 1.0 meter to the right, what you need is the x-axis direction. So, the problem breaks down to finding out how long the ball will take to roll 1.0 meter in the x direction. To find out, you need to know how fast the ball is moving in the x direction.
You already know that the ball is rolling at a speed of 7.0 meters per second at 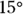 to the horizontal (along the positive x-axis), which is a vector: 7.0 meters per second at
to the horizontal (along the positive x-axis), which is a vector: 7.0 meters per second at 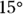 gives you both a magnitude and a direction. What you have here is a velocity: the vector version of speed (more about this topic in Chapter 3). The ball’s speed is the magnitude of its velocity vector, and when you add a direction to that speed, you get the velocity vector v.
gives you both a magnitude and a direction. What you have here is a velocity: the vector version of speed (more about this topic in Chapter 3). The ball’s speed is the magnitude of its velocity vector, and when you add a direction to that speed, you get the velocity vector v.
Here you need not only the speed, but also the x component of the ball’s velocity to find out how fast the ball is traveling toward the table edge. The x component is a scalar (a number, not a vector), and it’s written like this: 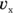 . The y component of the ball’s velocity vector is
. The y component of the ball’s velocity vector is 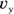 . So, you can say that
. So, you can say that
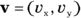
That’s how you express breaking a vector up into its components. So, what’s 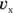 here? And for that matter, what’s
here? And for that matter, what’s 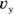 , the y component of the velocity? The vector has a length (7.0 meters per second) and a direction (
, the y component of the velocity? The vector has a length (7.0 meters per second) and a direction (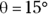 to the horizontal). And you know that the edge of the table is 1.0 meter to the right. As you can see in Figure 2-6, you have to use some trigonometry (oh no!) to resolve this vector into its components. No sweat; the trig is easy after you get the angles you see in Figure 2-6 down. The magnitude of a vector v is expressed as v (you sometimes see this written as |v|), and from Figure 2-6, you can see that
to the horizontal). And you know that the edge of the table is 1.0 meter to the right. As you can see in Figure 2-6, you have to use some trigonometry (oh no!) to resolve this vector into its components. No sweat; the trig is easy after you get the angles you see in Figure 2-6 down. The magnitude of a vector v is expressed as v (you sometimes see this written as |v|), and from Figure 2-6, you can see that
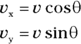
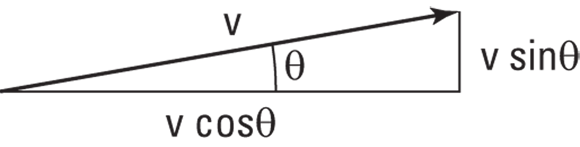
FIGURE 2-6: Breaking a vector into components allows you to add or subtract them easily.
You know that 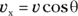 , so you can find the x component of the ball’s velocity,
, so you can find the x component of the ball’s velocity, 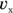 , this way:
, this way:
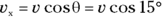
Plugging in the numbers gives you
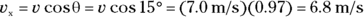
You now know that the ball is traveling at 6.8 m/s to the right. And because the table’s edge is 1.0 meter away,
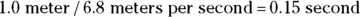
It will take the ball 0.15 second to fall off the edge of the table. What about the y component of the velocity? That’s easy to find, too:
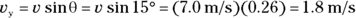
Using vector components to find magnitudes and angles
Sometimes, you have to find the angles of a vector rather than the components. For example, assume you’re looking for a hotel that’s 20 miles due north and then 20 miles due east. What’s the angle the hotel is at from your present location, and how far away is it? You can write this problem in vector notation, like so (see the section “Waxing Numerical on Vectors”):
- Step 1: (0, 20)
- Step 2: (20, 0)
When adding these vectors together, you get this result:
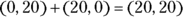
The resultant vector is (20, 20). That’s one way of specifying a vector — use its components. But this problem isn’t asking for the results in terms of components. The question wants to know the angle the hotel is at from your present location and how far away it is. In other words, looking at Figure 2-7, the problem asks, “What’s h, and what’s  ?”
?”
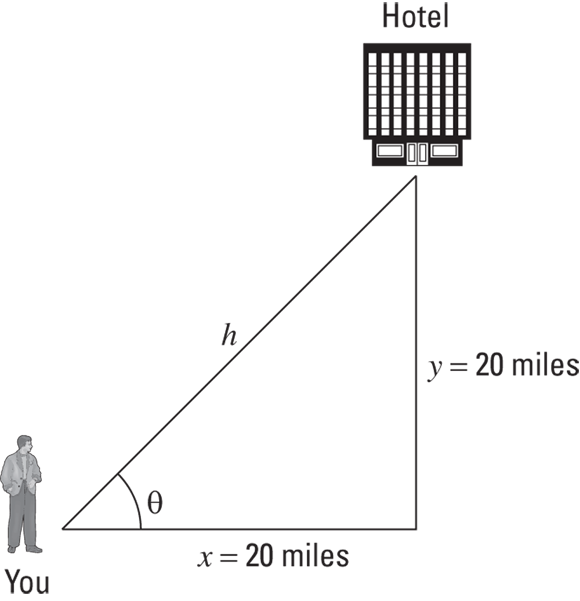
FIGURE 2-7: Using the angle created by a vector to get to a hotel.
Finding h isn’t so hard because you can use the Pythagorean theorem:
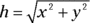
Plugging in the numbers gives you
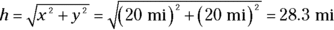
The hotel is 28.3 miles away. What about the angle 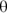 ? Because of your superior knowledge of trigonometry, you know that
? Because of your superior knowledge of trigonometry, you know that
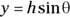
In other words, you know that
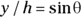
Now all you have to do is take the inverse sine:
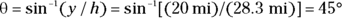
You now know all there is to know: The hotel is 28.3 miles away, at an angle of 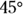 . Another physics triumph!
. Another physics triumph!
 Plenty of situations in your life display vectors, and plenty of concepts in physics are vectors too — for example, velocity, acceleration, and force. You should snuggle up to vectors because you see them in just about any physics course you take. Vectors are fundamental.
Plenty of situations in your life display vectors, and plenty of concepts in physics are vectors too — for example, velocity, acceleration, and force. You should snuggle up to vectors because you see them in just about any physics course you take. Vectors are fundamental. When you have a vector, you have to keep in mind two quantities: its direction and its magnitude. Forces that have only a quantity, like speed, are called scalars. If you add a direction to a scalar, you create a vector.
When you have a vector, you have to keep in mind two quantities: its direction and its magnitude. Forces that have only a quantity, like speed, are called scalars. If you add a direction to a scalar, you create a vector.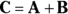 . C is called the sum, the result, or the resultant vector. But if having only one option bores you, there are other ways of combining vectors, too — you can subtract them if you want.
. C is called the sum, the result, or the resultant vector. But if having only one option bores you, there are other ways of combining vectors, too — you can subtract them if you want.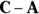 ) and use vector addition. In other words, start with the first vector, C; put the reversed vector’s (A’s) foot at the first vector’s head; and draw the resulting vector.
) and use vector addition. In other words, start with the first vector, C; put the reversed vector’s (A’s) foot at the first vector’s head; and draw the resulting vector.