Chapter 4
Studying Circular Motions
IN THIS CHAPTER
 Staying steady with uniform circular motion
Staying steady with uniform circular motion
 Circling with centripetal acceleration
Circling with centripetal acceleration
 Getting angular with displacement, velocity, and acceleration
Getting angular with displacement, velocity, and acceleration
Circular motion can involve rockets moving around planets, racecars whizzing around a track, or bees buzzing around a hive. The previous chapters discuss concepts like displacement, velocity, and acceleration; now you find out how these concepts work when you’re moving in a circle.
You have circular equivalents for each of the concepts I’ve mentioned, which makes handling circular motion no problem at all — you merely calculate angular displacement, angular velocity, and angular acceleration. Instead of dealing with linear displacement here, you deal with angular displacement as an angle. Angular velocity indicates what angle you sweep through in so many seconds, and angular acceleration gives you the rate of change in the angular velocity. All you have to do is take linear equations and substitute the angular equivalents: angular displacement for displacement, angular velocity for velocity, and angular acceleration for acceleration.
Time to get dizzy with circular motion.
Understanding Uniform Circular Motion
An object with uniform circular motion travels in a circle with a constant speed. Practical examples may be hard to come by, unless you see a racecar driver with his accelerator stuck or a clock with a seconds-hand that moves in constant motion. Take a look at Figure 4-1, where a golf ball tied to a string is whipping around in circles. The golf ball is traveling at a uniform speed as it moves around in a circle (not with a uniform velocity because its direction changes all the time), so you can say it’s traveling in uniform circular motion.
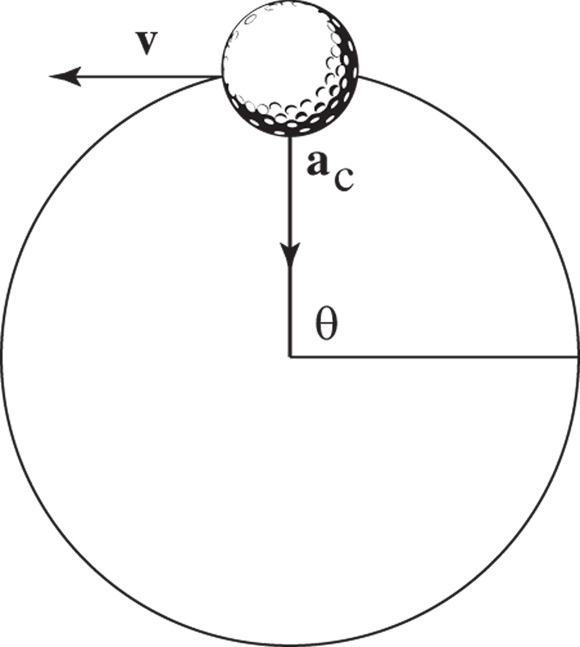
FIGURE 4-1: A golf ball on a string travels with constant speed.
Any object that travels in uniform circular motion always takes the same amount of time to move completely around the circle. That time is called its period, designated by T. You can easily relate the golf ball’s speed to its period because you know that the distance the golf ball must travel each time around the circle is the circumference of the circle, which, if r is the radius of the circle, is 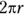 . So, you can get the equation for finding an object’s period by first finding its speed:
. So, you can get the equation for finding an object’s period by first finding its speed:
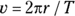
If you switch T and v around, you get
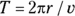
For example, say that you’re uniformly spinning a golf ball in a circle at the end of a 1.0-meter string so that it makes one revolution every half-second. How fast is the ball moving? Time to plug in the numbers:
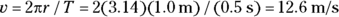
The ball moves at a speed of 12.6 meters per second. Just make sure you have a strong string!
Creating Centripetal Acceleration
To keep an object moving in circular motion, its velocity constantly changes direction, as you can see in Figure 4-2. Because of this fact, acceleration is created, called centripetal acceleration — the acceleration needed to keep an object moving in circular motion. At any point, the velocity of the object is perpendicular to the radius of the circle.
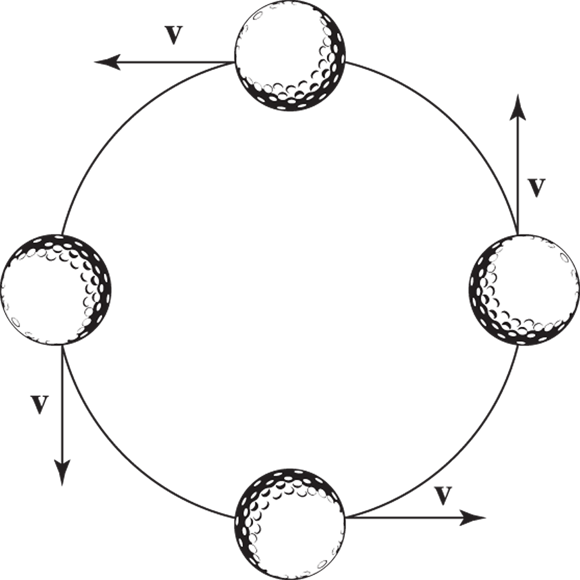
FIGURE 4-2: Velocity constantly changes direction to maintain an object’s uniform circular motion.
If the string holding the ball in Figure 4-2 breaks at the top, bottom, left, or right point you see in the illustration, which way would the ball go? If the velocity points to the left, the ball would fly off to the left. If the velocity points to the right, the ball would fly off to the right. And so on. That’s not intuitive for many people, but it’s the kind of physics question that may come up in introductory courses.
Seeing how centripetal acceleration controls velocity
Here’s what’s special about uniform circular motion: When an object travels in circular motion, its speed is constant, which means that the magnitude of the object’s velocity doesn’t change. Therefore, acceleration can have no component in the same direction as the velocity; if it could, the velocity’s magnitude would change.
However, the velocity’s direction is constantly changing; it always bends so that the object maintains movement in a constant circle. To make that happen, the object’s centripetal acceleration is always concentrated toward the center of the circle, perpendicular to the object’s velocity at any one time. The centripetal acceleration changes the direction of the object’s velocity while keeping the magnitude of the velocity constant. You can see the centripetal acceleration vector, 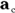 , in Figure 4-1.
, in Figure 4-1.
If you accelerate the ball toward the center of the circle to provide the centripetal acceleration, why doesn’t it hit your hand? The answer is that the ball is already moving. The acceleration you provide always acts at right angles to the velocity and therefore changes only the direction of the velocity, not its magnitude.
Calculating centripetal acceleration
You always have to accelerate an object toward the center of the circle to keep it moving in circular motion. So, can you find the magnitude of the acceleration you create? No doubt. If an object is moving in uniform circular motion at speed v and radius r, you can find the centripetal acceleration with the following equation:
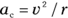
For a practical example, imagine you’re driving around curves at a high speed. For any constant speed, you can see from the equation 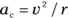 that the centripetal acceleration is inversely proportional to the radius of the curve, which you know from experience. On tighter curves, your car needs to provide a greater centripetal acceleration.
that the centripetal acceleration is inversely proportional to the radius of the curve, which you know from experience. On tighter curves, your car needs to provide a greater centripetal acceleration.
Finding Angular Equivalents for Linear Equations
You can actually describe circular motion in a linear fashion, but doing so takes a little getting used to. Take a look at the ball in Figure 4-1; it doesn’t cover distance in a linear way. You can’t chart the x-axis or y-axis coordinate of the golf ball with a straight line. However, its path of motion provides one coordinate that you can graph as a straight line in uniform circular motion: the angle, 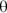 . If you graph the angle, the total angle the ball travels increases in a straight line. When it comes to circular motion, therefore, you can think of the angle,
. If you graph the angle, the total angle the ball travels increases in a straight line. When it comes to circular motion, therefore, you can think of the angle, 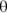 , just as you think of the displacement, s, in linear motion. (See Chapter 3 for more on displacement.)
, just as you think of the displacement, s, in linear motion. (See Chapter 3 for more on displacement.)
If you have 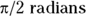 and you want to know how many degrees that converts to, here’s the conversion:
and you want to know how many degrees that converts to, here’s the conversion:
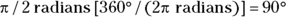
You calculate that 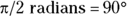 .
.
The fact that you can think of the angle, 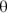 , in circular motion just as you think of the displacement, s, in linear motion is great because it means you have an angular counterpart for each of the linear equations from Chapter 3. Some such linear equations include
, in circular motion just as you think of the displacement, s, in linear motion is great because it means you have an angular counterpart for each of the linear equations from Chapter 3. Some such linear equations include
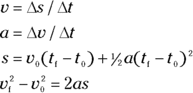
To find the angular counterpart of each of these equations, you just make substitutions. Instead of s, which you use in linear travel, you use 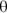 , the angular displacement. So, what do you use in place of the velocity, v? You use the angular velocity,
, the angular displacement. So, what do you use in place of the velocity, v? You use the angular velocity, 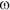 , or the number of radians covered in one second:
, or the number of radians covered in one second:

Note that the previous equation looks close to how you define linear speed:
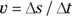
Say, for example, that you have a ball tied to a string. What’s the angular velocity of the ball if you whirl it around on the string? It makes a complete circle, 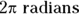 , in
, in 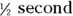 , so its angular velocity is
, so its angular velocity is
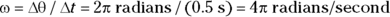
Can you also find the acceleration of the ball? Yes, you can, by using the angular acceleration, 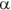 . Linear acceleration is defined this way:
. Linear acceleration is defined this way:
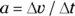
Therefore, you define angular acceleration this way:
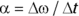
The units for angular acceleration are 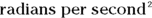 . If the ball speeds up from
. If the ball speeds up from 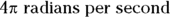 to
to 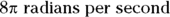 in 2 seconds, for example, what would its angular acceleration be? Work it out by plugging in the numbers:
in 2 seconds, for example, what would its angular acceleration be? Work it out by plugging in the numbers:
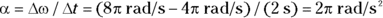
Now you have the angular versions of linear displacement, s, velocity, v, and acceleration, a: angular displacement, 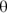 , angular velocity,
, angular velocity, 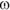 , and angular acceleration,
, and angular acceleration, 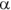 . You can make a one-for-one substitution in velocity, acceleration, and displacement equations (see Chapter 3) to get:
. You can make a one-for-one substitution in velocity, acceleration, and displacement equations (see Chapter 3) to get:
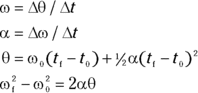
If you need to work in terms of angle, not distance, you have the ammo to do so for constant angular acceleration. To find out more about angular displacement, angular velocity, and angular acceleration, see the discussion on angular momentum and torque in Chapter 9.
 This rule holds true for all objects: The velocity of an object in uniform circular motion is always perpendicular to the radius of the circle.
This rule holds true for all objects: The velocity of an object in uniform circular motion is always perpendicular to the radius of the circle.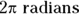 , which is also
, which is also 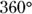 , so
, so 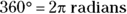 . If you travel in a full circle, you go
. If you travel in a full circle, you go 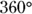 , or
, or 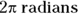 . A half-circle is
. A half-circle is 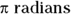 , and a quarter-circle is
, and a quarter-circle is 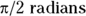 .
. How do you convert from degrees to radians and back again? Because
How do you convert from degrees to radians and back again? Because 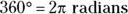 (or 2 multiplied by 3.14, the rounded version of
(or 2 multiplied by 3.14, the rounded version of  ), you have an easy calculation.
), you have an easy calculation.