Chapter 6
Falling Slowly: Gravity and Friction
IN THIS CHAPTER
 Getting up to speed on gravity
Getting up to speed on gravity
 Looking at angles on an inclined plane
Looking at angles on an inclined plane
 Taking the forces of friction into account
Taking the forces of friction into account
Gravity is the main topic of this chapter. Chapter 5 shows you how much force you need to support a mass against the pull of gravity, but that’s just the start. In this chapter, you find out how to handle gravity along ramps and include friction in your calculations.
Dropping the Apple: Newton’s Law of Gravitation
Sir Isaac Newton came up with one of the heavyweight laws in physics for us: the law of universal gravitation. This law says that every mass exerts an attractive force on every other mass. If the two masses are 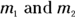 , and the distance between them is r, the magnitude of the force is
, and the distance between them is r, the magnitude of the force is

where G is a constant equal to  .
.
This equation allows you to figure the gravitational force between any two masses. What, for example, is the pull between the Sun and the Earth? The Sun has a mass of about  , and the Earth has a mass of about
, and the Earth has a mass of about  ; a distance of about
; a distance of about 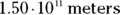 separates the two bodies. Plugging the numbers into Newton’s equation gives you
separates the two bodies. Plugging the numbers into Newton’s equation gives you

For an example on the land-based end of the spectrum, say that you’re out for your daily physics observations when you notice two people on a park bench, looking at each other and smiling. As time goes on, you notice that they seem to be sitting closer and closer to each other each time you take a glance. In fact, after a while, they’re sitting right next to each other. What could be causing this attraction? If the two lovebirds weigh about 75 kg each, what’s the force of gravity pulling them together, assuming they started out  apart? Your calculation looks like this:
apart? Your calculation looks like this:

The force of attraction is roughly five millionths of an ounce — maybe not enough to shake the surface of the Earth, but that’s okay. The Earth’s surface has its own forces to deal with.
The equation for the force of gravity —  — holds true no matter how far apart two masses are. But you also come across a special gravitational case (which most of the work on gravity in this book is about): the force of gravity on the surface of the Earth. Adding gravity to mass is where the difference between weight and mass comes in. Mass is considered a measure of an object’s inertia, and its weight is the force exerted on it in a gravitational field. On the surface of the Earth, the two forces are related by the acceleration due to gravity:
— holds true no matter how far apart two masses are. But you also come across a special gravitational case (which most of the work on gravity in this book is about): the force of gravity on the surface of the Earth. Adding gravity to mass is where the difference between weight and mass comes in. Mass is considered a measure of an object’s inertia, and its weight is the force exerted on it in a gravitational field. On the surface of the Earth, the two forces are related by the acceleration due to gravity:  .
.
Can you derive g, the acceleration due to gravity on the surface of the Earth, from Newton’s law of gravitation? You sure can. The force on an object of mass 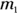 near the surface of the Earth is
near the surface of the Earth is

By Newton’s second law (see Chapter 5), this force must also equal the following, where  is the radius of the Earth:
is the radius of the Earth:
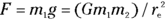
The radius of the Earth,  , is about
, is about  , and the mass of the Earth is
, and the mass of the Earth is 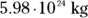 , so you have
, so you have
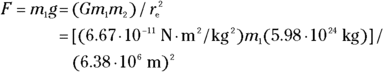
Dividing both sides by 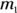 gives you
gives you
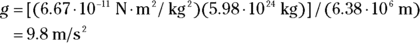
Newton’s law of gravitation gives you the acceleration due to gravity on the surface of the Earth: 9.8 meters per second2.
You can use Newton’s law of gravitation to get the acceleration due to gravity, g, on the surface of the Earth just by knowing the gravitational constant G, the radius of the Earth, and the mass of the Earth. (Of course, you can measure g by letting an apple drop and timing it, but what fun is that when you can calculate it in a roundabout way that requires you to first measure the mass of the Earth?)
Down to Earth: Dealing with Gravity
When you’re on the surface of the Earth, the pull of gravity is constant and equal to mg, where m is the mass of the object being pulled by gravity and g is the acceleration due to gravity:
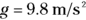
Acceleration is a vector, meaning it has a direction and a magnitude (see Chapter 2), so this equation really boils down to g, an acceleration straight down if you’re standing on the Earth. The fact that 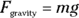 is important because it says that the acceleration of a falling body doesn’t depend on its mass:
is important because it says that the acceleration of a falling body doesn’t depend on its mass:

In other words,

This discussion sticks pretty close to the ground, er, Earth, where the acceleration due to gravity is constant. For the purposes of this chapter, gravity acts downward, but that doesn’t mean you can use equations like  only to watch what goes up when it must come down. You can also start dealing with objects that go up at angles.
only to watch what goes up when it must come down. You can also start dealing with objects that go up at angles.
Leaning Vertically with Inclined Planes
Plenty of gravity-oriented problems in introductory physics involve ramps, so ramps are worth taking a look at. Check out Figure 6-1. Here, a cart is about to roll down a ramp. The cart travels not only vertically but also along the ramp, which is inclined at an angle 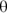 .
.

FIGURE 6-1: A cart on a ramp with a force vector.
Say, for example, that 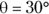 and that the length of the ramp is 5.0 meters. How fast will the cart be going at the bottom of the ramp? Gravity will accelerate the cart down the ramp, but not the full force of gravity. Only the component of gravity acting along the ramp will accelerate the cart.
and that the length of the ramp is 5.0 meters. How fast will the cart be going at the bottom of the ramp? Gravity will accelerate the cart down the ramp, but not the full force of gravity. Only the component of gravity acting along the ramp will accelerate the cart.
What’s the component of gravity acting along the ramp if the vertical force due to gravity on the cart is 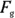 ? Take a look at Figure 6-1, which details some of the angles and vectors. (See Chapter 2 for a detailed discussion of vectors.) To resolve the vector
? Take a look at Figure 6-1, which details some of the angles and vectors. (See Chapter 2 for a detailed discussion of vectors.) To resolve the vector  along the ramp, you start by figuring out the angle between
along the ramp, you start by figuring out the angle between  and the ramp. Here’s where having a knowledge of triangles comes into play: A triangle’s angles have to add up to
and the ramp. Here’s where having a knowledge of triangles comes into play: A triangle’s angles have to add up to  . The angle between
. The angle between  and the ground is
and the ground is  , and you know that the ramp’s angle to the ground is
, and you know that the ramp’s angle to the ground is 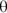 . And from Figure 6-1, you know that the angle between
. And from Figure 6-1, you know that the angle between 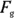 and the ramp must be
and the ramp must be  , or
, or  .
.
Physics instructors use a top-secret technique to figure out what the angles between vectors and ramps are, and I’m here to let you in on the secret. The angles have to relate to 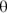 in some way, so what happens if
in some way, so what happens if  goes to zero? In that case, the angle between
goes to zero? In that case, the angle between 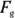 from the example in the previous section and the ramp from the previous section is
from the example in the previous section and the ramp from the previous section is 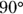 . What happens if
. What happens if 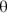 becomes
becomes 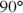 ? In that case, the angle between
? In that case, the angle between  and the ramp is
and the ramp is  .
.
Now you’re wondering, “What’s the component of 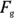 along the ramp?” Now that you know the angle between
along the ramp?” Now that you know the angle between 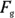 and the ramp is
and the ramp is 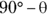 , you can figure the component of
, you can figure the component of 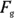 along the ramp (called resolving
along the ramp (called resolving 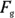 along the ramp):
along the ramp):

If you love trigonometry as much as the normal person, you may also know that
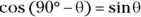
(Hint: It isn’t necessary to know this; the previous equation works just fine.) Therefore,
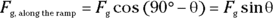
This makes sense; when  goes to zero, this force goes to zero as well because the ramp is horizontal. And when
goes to zero, this force goes to zero as well because the ramp is horizontal. And when 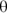 goes to
goes to 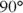 , this force becomes
, this force becomes 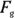 because the ramp is vertical. The force that accelerates the cart is
because the ramp is vertical. The force that accelerates the cart is 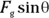 along the ramp. What does that make the acceleration of the cart, if its mass is 800 kg? Easy enough:
along the ramp. What does that make the acceleration of the cart, if its mass is 800 kg? Easy enough:
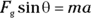
Therefore,

This equation becomes even easier when you remember that  :
:
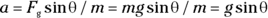
Facing Friction
You know all about friction. It’s the force that holds objects in motion back — or so it may seem. Actually, friction is essential for everyday living. Imagine a world without friction: no way to drive a car on the road, no way to walk on pavement, no way to pick up that ham sandwich. Friction may seem like an enemy to the hearty physics follower, but it’s also your friend.
Friction comes from the interaction of surface irregularities. If you introduce two surfaces that have plenty of microscopic pits and projections, you produce friction. And the harder you press those two surfaces together, the more friction you create as the irregularities interlock more and more.
Physics has plenty to say about how friction works. For example, imagine that you decide to put all your wealth into a huge, gold ingot, which you see in Figure 6-2, only to have someone steal your fortune. The thief applies a force to the ingot to accelerate it away, as the police start after him. Thankfully, the force of friction comes to your rescue because the thief can’t accelerate away nearly as fast as he thought — all that gold drags heavily along the ground.

FIGURE 6-2: The force of friction makes it tough to move large objects.
So, if you want to get quantitative here, what would you do? You’d say that the pulling force,  , minus the force due to friction,
, minus the force due to friction, 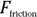 , is equal to the net force in the x-axis direction, which gives you the acceleration in that direction:
, is equal to the net force in the x-axis direction, which gives you the acceleration in that direction:
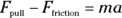
That looks straightforward enough. But how do you calculate  ? You start by calculating the normal force.
? You start by calculating the normal force.
Figuring out the normal force
The force of friction,  , always acts to oppose the force you apply when you try to move an object. Friction is proportional to the force with which an object pushes against the surface you’re trying to slide it along.
, always acts to oppose the force you apply when you try to move an object. Friction is proportional to the force with which an object pushes against the surface you’re trying to slide it along.
As you can see in Figure 6-2, the force with which the gold ingot presses against the ground is just its weight, or mg. The ground presses back with the same force. The force that pushes up against the ingot is called the normal force, and its symbol is N. The normal force isn’t necessarily the same as the force due to gravity; it’s the force perpendicular to the surface an object is sliding on. In other words, the normal force is the force pushing the two surfaces together, and the stronger the normal force, the stronger the force due to friction.
In the case of Figure 6-2, because the ingot slides along the ground, the normal force has the same magnitude as the weight of the ingot, so  . You have the normal force, which is the force pressing the ingot and the ground together. But where do you go from there? You find the force of friction.
. You have the normal force, which is the force pressing the ingot and the ground together. But where do you go from there? You find the force of friction.
Finding the coefficient of friction
The force of friction comes from the surface characteristics of the materials that come into contact. How can physics predict those characteristics theoretically? It doesn’t. You see plenty of general equations that predict the general behavior of objects, like 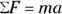 (see Chapter 5). But detailed knowledge of the surfaces that come into contact isn’t something that physics can come up with theoretically, so it wimps out on the theoretical part here and says that the characteristics are things you have to measure yourself.
(see Chapter 5). But detailed knowledge of the surfaces that come into contact isn’t something that physics can come up with theoretically, so it wimps out on the theoretical part here and says that the characteristics are things you have to measure yourself.
What you measure is how the normal force (see the previous section) relates to the friction force. It turns out that to a good degree of accuracy, the two forces are proportional, and you can use a constant,  , to relate the two:
, to relate the two:
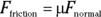
Usually, you see this equation written in the following terms:

This equation tells you that when you have the normal force, all you have to do is multiply it by a constant to get the friction force. This constant, 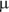 , is called the coefficient of friction, and it’s something you measure for a particular surface — not a value you can look up in a book.
, is called the coefficient of friction, and it’s something you measure for a particular surface — not a value you can look up in a book.
The coefficient of friction is usually between zero and one. The value of zero is possible only if you have a surface that has absolutely no friction at all. You won’t often see coefficients of friction greater than one, unless you’re a fan of drag racing.
 isn’t a vector equation (see Chapter 2) because the force due to friction,
isn’t a vector equation (see Chapter 2) because the force due to friction,  , isn’t in the same direction as the normal force,
, isn’t in the same direction as the normal force, 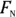 . As you can see in Figure 6-2,
. As you can see in Figure 6-2,  and
and  are perpendicular.
are perpendicular. 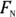 is always at right angles to the surfaces providing the friction because it’s the force that presses the two surfaces together, and
is always at right angles to the surfaces providing the friction because it’s the force that presses the two surfaces together, and 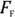 is always along those surfaces because it opposes the direction of sliding.
is always along those surfaces because it opposes the direction of sliding.
Okay, are you ready to get out your lab coat and start calculating the forces due to friction? Not so fast! It turns out that you must factor in two different coefficients of friction for each type of surface.
Bringing static and kinetic friction into the mix
The two different coefficients of friction for each type of surface are a coefficient of static friction and a coefficient of kinetic friction.
The reason you have two different coefficients of friction is that you involve two different physical processes. When two surfaces are static, or not moving, and pressing together, they have the chance to interlock on the microscopic level, and that’s static friction. When the surfaces are sliding, the microscopic irregularities don’t have the same chance to connect, and you get kinetic friction. What this means in practice is that you must account for two different coefficients of friction for each surface: a static coefficient of friction, 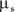 , and a kinetic coefficient of friction,
, and a kinetic coefficient of friction,  .
.
Getting moving with static friction
Between static friction and kinetic friction, static friction is stronger, which means that the static coefficient of friction for a surface, 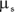 , is larger than the kinetic coefficient of friction,
, is larger than the kinetic coefficient of friction, 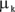 . That makes sense because static friction comes when the two surfaces have a chance to fully interlock on the microscopic level. Kinetic friction happens when the two surfaces are sliding, so only the more macroscopic irregularities can connect.
. That makes sense because static friction comes when the two surfaces have a chance to fully interlock on the microscopic level. Kinetic friction happens when the two surfaces are sliding, so only the more macroscopic irregularities can connect.
For example, say that the static coefficient of friction between the ingot from Figure 6-2 and the ground is 0.3, and that the ingot has a mass of 1,000 kg (quite a fortune in gold). What’s the force that a thief has to exert to get the ingot moving? You know from the section “Finding the coefficient of friction” that
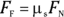
And because the surface is flat, the normal force — the force that drives the two surfaces together — is in the opposite direction of the ingot’s weight and has the same magnitude. Therefore,
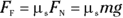
where m is the mass of the ingot and g is the acceleration due to gravity on the surface of the Earth. Plugging in the numbers gives you

Pretty respectable force for any thief. What happens after the burly thief gets the ingot going? How much force does he need to keep it going? He needs to look at kinetic friction.
Staying in motion with kinetic friction
The force due to kinetic friction, which occurs when two surfaces are already sliding, isn’t as strong as static friction. But that doesn’t mean you can predict what the coefficient of kinetic friction is going to be, even if you know the coefficient of static friction; you have to measure both forces.
Say that the ingot (from Figure 6-2), which weighs 1,000 kg, has a coefficient of kinetic friction,  , of 0.18. How much force does the thief need to pull the ingot along during his robbery? You have all you need — the kinetic coefficient of friction:
, of 0.18. How much force does the thief need to pull the ingot along during his robbery? You have all you need — the kinetic coefficient of friction:

Putting in the numbers gives you
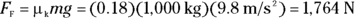
The thief needs 1,764 N to keep your gold ingot sliding while evading the police — not exactly the kind of force you can keep going while trying to run at top speed, unless you have some friends helping you. Lucky you! Physics states that the police are able to recover your gold ingot. The cops know all about friction. Taking one look at the prize, they say, “We got it back; you drag it home.”
Dealing with uphill friction
The previous sections of this chapter deal with friction on level ground, but what if you have to drag a heavy object up a ramp? Say, for example, you have to move a refrigerator.
You want to go camping, and because you expect to catch plenty of fish, you decide to take your 100-kg refrigerator with you. The only catch is getting the refrigerator into your vehicle, as shown in Figure 6-3. The refrigerator has to go up a 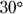 ramp, which happens to have a static coefficient of friction of 0.2 and a kinetic coefficient of friction of 0.15 (see the previous two sections for these topics). The good news is that you have two friends to help you move the fridge. The bad news is that you can supply only 350 N of force each, so your friends panic.
ramp, which happens to have a static coefficient of friction of 0.2 and a kinetic coefficient of friction of 0.15 (see the previous two sections for these topics). The good news is that you have two friends to help you move the fridge. The bad news is that you can supply only 350 N of force each, so your friends panic.

FIGURE 6-3: You must battle different types of force and friction to push an object up a ramp.
“Don’t worry,” you say, pulling out your calculator. “I’ll check out the physics.” Your two friends relax. The minimum force needed to push that refrigerator up the ramp,  , has to counter the component of the weight of the refrigerator acting along the ramp and the force due to friction. I tackle these issues one at a time in the following sections.
, has to counter the component of the weight of the refrigerator acting along the ramp and the force due to friction. I tackle these issues one at a time in the following sections.
Calculating the component weight
To start figuring the component of the weight of the refrigerator acting along the ramp, take a look at Figure 6-3. The weight of the refrigerator acts downward. The angles in a triangle formed by the ground, the ramp, and the weight vector must add up to 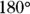 . The angle between the weight vector and the ground is
. The angle between the weight vector and the ground is 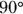 , and the angle between the ground and the ramp is
, and the angle between the ground and the ramp is  , so the angle between the ramp and the weight vector is
, so the angle between the ramp and the weight vector is

The weight acting along the ramp will be

The minimum force you need to push the refrigerator up the ramp while counteracting the component of its weight along the ramp and the force of friction,  , is
, is

Determining the force of friction
The next question: What’s the force of friction, 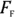 ? Should you use the static coefficient of friction or the kinetic coefficient of friction? Because the static coefficient of friction is greater than the kinetic coefficient of friction, it’s your best choice. After you and your friends get the refrigerator to start moving, you can keep it moving with less force. Because you’re going to use the static coefficient of friction, you can get
? Should you use the static coefficient of friction or the kinetic coefficient of friction? Because the static coefficient of friction is greater than the kinetic coefficient of friction, it’s your best choice. After you and your friends get the refrigerator to start moving, you can keep it moving with less force. Because you’re going to use the static coefficient of friction, you can get 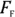 this way:
this way:
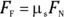
You also need the normal force, 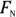 , to continue. (See the section “Figuring out the normal force” earlier in this chapter.)
, to continue. (See the section “Figuring out the normal force” earlier in this chapter.) 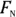 is the component of the weight perpendicular to (also called normal to) the ramp. You know that the angle between the weight vector and the ramp is
is the component of the weight perpendicular to (also called normal to) the ramp. You know that the angle between the weight vector and the ramp is  , as shown in Figure 6-4.
, as shown in Figure 6-4.

FIGURE 6-4: The normal and gravitational forces acting on an object.
Using some trigonometry, you know that

You can verify this by letting  go to zero, which means that
go to zero, which means that  becomes mg, as it should. Now you know that
becomes mg, as it should. Now you know that

All you have left is plugging in the numbers:

You need 660 N to push the refrigerator up the ramp. In other words, your two friends, who can exert 350 N each, are enough for the job.
 Therefore,
Therefore, 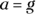 , no matter the object’s weight. (A heavier object doesn’t fall faster than a lighter one.) Gravity gives any freely falling body the same acceleration downward (g near the surface of Earth).
, no matter the object’s weight. (A heavier object doesn’t fall faster than a lighter one.) Gravity gives any freely falling body the same acceleration downward (g near the surface of Earth). Based on this info, you can make a pretty good case that the angle between
Based on this info, you can make a pretty good case that the angle between 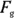 and the ramp is
and the ramp is 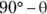 . So, when you’re at a loss as how to figure out an angle with respect to another angle, let the other angle go to
. So, when you’re at a loss as how to figure out an angle with respect to another angle, let the other angle go to 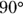 and then
and then 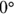 and see what happens. It’s an easy shortcut.
and see what happens. It’s an easy shortcut. . This equation holds for any object gravity accelerates down a ramp, if friction doesn’t apply. The acceleration of an object along a ramp at angle
. This equation holds for any object gravity accelerates down a ramp, if friction doesn’t apply. The acceleration of an object along a ramp at angle  to the ground is
to the ground is 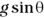 in the absence of friction.
in the absence of friction.