FIGURE 11.1 Block diagram of a generic quadcopter control system.
In this chapter, I will discuss both enhancements and future projects that you may want to consider for your quadcopter. Several of the concepts that were introduced in earlier chapters will now be integrated into these discussions. You might want to go back and refresh your knowledge regarding these concepts as you read about them. I have endeavored to point out the appropriate chapters in which they were first discussed. You will also find some new material about advanced sensors that will add significant flexibility and capability to your quadcopter flight operations.
Determining the quadcopter’s geographic position is relatively easy using the GPS system. In Chapter 10, I described and demonstrated a simple, real-time GPS system that continuously sent the GPS coordinates back to the ground-control station (GCS). These coordinates were then displayed on an LCD screen in a latitude and longitude format. In that discussion, I showed how these coordinates could be manually entered into the Google Earth program to provide a real image of where the quadcopter was positioned in the nearby terrain. GPS data can also be used onboard the quadcopter to direct the aircraft to travel to a previous location or to a new location. Unfortunately, I cannot show you how to implement a GPS positioning system onboard the Elev-8, since the flight-control software in the Hoverfly Open flight-control board is proprietary (as I mentioned in Chapter 3). I can, however, outline a proposed approach on how to implement a virtual system that will position a generic quadcopter by using GPS data.
This generic quadcopter will be a very simple one consisting of four motors driven by four electronic speed controllers (ESCs) that are, in turn, controlled by the virtual flight-control system (VFCS), which is implemented by the Parallax Board of Education (BOE). For this project, I will assume that the VFCS will respond to R/C control signals from the GPS module and also from an electronic compass. Figure 11.1 shows a block diagram of my generic quadcopter control system that I just described.
In Chapter 10, I described the onboard GPS module. In the new configuration, the GPS module’s signals will be connected directly to a BOE instead of a Prop Mini. In addition, there will be another sensor input from an electronic compass that I describe and demonstrate in the following section.
I use the Parallax Compass Model HMC5883L with the Parallax part number 29133. This module is described as a sensitive, three-axis electronic compass with sensors that are very capable of detecting and analyzing the Earth’s magnetic lines of force. This module is shown in Figure 11.2 and is quite small and compact.
The module uses the basic physics principle of magnetoresistance in which a semiconductor material changes its electrical resistance in direct proportion to an external magnetic flux field that is applied to it. (The effect was first discovered in 1851 by William Thomson, who is more commonly known as Lord Kelvin.)
The HMC5883L utilizes the Honeywell Corporation’s Anisotropic Magnetoresistive (AMR) technology that features precision in-axis sensitivity and linearity. These sensors are all solid state in construction and exhibit very low cross-axis sensitivity. They are designed to measure both the direction and the magnitude of Earth’s magnetic fields, from 310 milligauss to 8 gauss (G). Earth’s average field strength is approximately 0.6 G, well within the range of the AMR sensors. Figure 11.3 is a close up of the three-axis sensor used in the compass module.
Three magnetoresistive strips are mounted inside the module at right angles to one another in a way that enables them to sense the X-, Y- and Z-axes. It is probably easiest to picture the X-axis aligned with the Earth’s north-south magnetic lines of force, which then makes the Y-axis an east-west alignment. The Z-axis can now be thought of as the altitude, or depression. Figure 11.4 shows these axes superimposed on the Earth’s lines of force.
The figure is a bit hard to decipher, as there is a lot being shown. The bold line labeled H represents a magnetic line of force vector that can be decomposed into three smaller vectors that are aligned with the X-, Y-, and Z-axes. I have shown only the Hx and Hy components, for clarity’s sake.
The angle between the plane formed by Hx and Hy components and the H vector is called the declination and is usually represented by the Φ symbol. Note that it is also important to compensate for the tilt of the compass in order to achieve an accurate bearing.
Fortunately, all the compensation and calculations are nicely handled for us within the HMC5883L module. Figure 11.5 shows a block diagram of what constitutes the main electronic components within the module.
The module communicates with the host microprocessor using the I2C bus that was discussed in Chapter 6. It takes a total of only four wires to connect the compass module to the BOE. These connections are detailed in Table 11.1. The physical connections can be seen in Figure 11.6.
We now need software to test the compass module with the BOE. I downloaded a very nice demo program named HMC5883.spin from the Parallax OBEX website, which I have discussed in previous chapters. This program contains all the test code necessary to demonstrate the compass functions as well as the I2C driver software that communicates between the compass module and the BOE. In addition, the program uses the FullDuplexSerial object, which provides a terminal display using the Propeller Serial Terminal (PSerT). This program is also available from this book’s website, www.mhprofessional.com/quadcopter.
The first portion of the test program with comments is shown below.


Much of this program code simply controls how the data is displayed on the PSerT. The actual program used in the VFCS will be much more condensed, since there is no need for a human readable display to be implemented.
Figure 11.7 shows the demonstration circuit in operation. I have included a traditional compass in the figure to illustrate magnetic north. The whole BOE has been oriented such that the compass module is pointing to magnetic north. Figure 11.8 is a PSerT screenshot confirming that the compass module is indeed pointing north.
It is time to examine the latitude and longitude calculations now that I have established how to measure real-time magnetic bearings. These background discussions will set the foundation for your understanding of how quadcopter operations tasks, such as return to home base, can be accomplished.
I need to review some fundamental principles regarding latitude and longitude that you might have missed if you snoozed during fifth-grade geography class. The horizontal lines in Figure 11.9 are lines of latitude and the vertical lines are lines of longitude. Lines of longitude are also known as meridians, and lines of latitude are sometimes referred to as parallels.
If you were to cut the Earth along a line of longitude, it would result in a circle, from which you would conclude that the planet is a spheroid, but it is not. However, for our purposes, I will make the reasonable assumption that the Earth is a sphere, since the computed distances in quadcopter operations are miniscule with regard to the radius of Earth. Any errors introduced by this assumption are too small to be realistically determined.
All the cross-sectional circles cut on longitude lines have the same diameter, which makes path determination easy for true north-south travel directions. Cutting along the horizontal latitude lines, however, results in circles that diminish in size, which you should be able to envision readily as you travel from the Equator (the maximum-diameter circle) to either the true North or South Poles (minimum-diameter circles). This change in diameter greatly complicates distance determination, but it is handled by a series of calculations (shown later in this section).
All the latitude and longitude circles are further divided into degrees, minutes, and seconds to establish the geographic coordinate system. The zero degree (0°) line of longitude is defined by international standards to run through Greenwich, England. Vertical lines to the left of the 0° line are designated as west while lines to the right are designated as east. The lines continue to the opposite side of the Earth ending at 180° for both east and west lines of longitude. The 0° line of longitude is also known as the Prime Meridian.
Figure 11.10 shows how the distance between lines of longitude narrows as it travels north from the 0° line of latitude, which is also known as the Equator. The same holds true for traveling south from the Equator. Table 11.2 shows precise measurements of longitudinal arcs at selected latitudes.
The ± 0.0001° measurement is of the most interest for quadcopter operations because it will be the typical scale for flight operations. This means that the degree measurements of latitude and longitude must be accurate to at least four right-hand-side decimal points.
The distances between lines of latitude, or parallels, will be the same no matter at which specific latitude they are measured. For instance, at the Equator, a 1° of latitudinal length is 111.116 km, which is almost exactly the same as 1° of longitudinal length. The following equation holds true for all latitudinal length calculations:
Latitudinal length = π × MR × cos(Φ)/180
where:
MR = 6367449 m (Earth’s radius)
Φ = angle subtended in degrees
For a 1° angle subtended and substituted into the above equations, the result is: (3.14159265 × 6367449 × .9998477)/180 = 111116.024 m or 111.116 km or about 68.9 statute miles (sm).
Computing longitudinal length is a bit complex as I mentioned above. I used the haversine formula to calculate the great circle distance between any two points on the Earth’s surface. Great circle distance is often called as the crow flies, meaning the shortest distance between two points. The haversine formula was first published by Roger Sinnott in the Sky & Telescope magazine in 1984. The formula is actually in three parts, where the first step is to calculate the a parameter. Technically, a is the square of half of the chord between the two coordinate positions. The second step computes c, which is the angular distance expressed in radians. The last step is to compute d, which is the linear distance between the two points. The complete haversine formula is shown below:
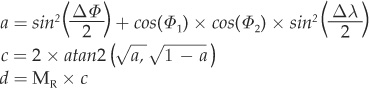
where:
Φ = Latitude
λ = Longitude
MR = Earth’s radius (mean radius = 6371 km)
I am sure that it is possible to calculate this distance manually; however, you have to be very careful in extending the precision of the numbers involved, since some may become very small. I chose to write a Java program to test how the haversine formula actually works with the computer by keeping track of all the tiny numbers involved in the calculations. I did want to mention for those readers with some math background that the two-parameter atan2 function is used in the second step to maintain the correct sign, which is normally lost when using the single parameter atan trignometric function.
I set up a simple test to compare the performance of the haversine formula in determining the path length with Google Earth’s straight-path feature. I arbitrarily choose the following coordinates for this test:
position 1—53° N 1° W
position 2—52° N 0° W
You should have immediately realized that since one of the positions was on the Prime Meridian, the test must be located in England. Figure 11.11 is a screenshot of Google Earth with the path clearly delineated and the path length shown in the Dialog Box as 130.35 km.
The Java test class named DistanceDemo.java was created using the Eclipse integrated development environment (IDE) and is shown below:


Figure 11.12 is a screenshot of the output from the Eclipse IDE console after the program was run. You can see the coordinates entered as well as the calculated distance of 130.175 km.
I actually believe the results from the Java program are more accurate than the results from Google Earth because the Google Earth path distance depended on how accurately I set the beginning and end points, which is tough to do with the computer’s touch pad. In any case, the results differed by about 0.1%, which was enough to convince me that the haversine formula functioned as expected.
There is one more formula that I need to show you in order to complete this navigation discussion. This formula computes the bearing between two coordinates and will be used in conjunction with the electronic compass to guide the quadcopter on the proper path.
This formula does not appear to have a formal name, but it is used to calculate the initial bearing between two coordinates by using the great-circle arc as the shortest path distance.
![]()
where:
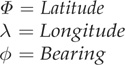
This formula, while not nearly as complex as the haversine, will still be demonstrated using a Java program that I aptly named BearingDemo.java. The program code is shown below:

Figure 11.13 is a screenshot of the output from the Eclipse console after the BearingDemo program was run with the same coordinates as those used in the DistanceDemo program. I measured the bearing with a protractor on a printed copy of Figure 11.11 and estimated the true bearing at 148°, which matches the calculated bearing. Ignore the minus sign on the bearing value, since it is simply a result of the atan2 function. The two Java programs used above are available on the book’s companion website www.mhprofessional.com/quadcopter.
One more item that must be discussed regarding the bearing is the difference between true bearing and magnetic bearing. True bearings are always taken with respect to the true North (or South) Pole. This is normally the vertical or straight up and down direction on most maps. Magnetic bearings are taken with respect to the magnetic poles, which deviate from the true poles. Called magnetic deviation, its value is dependent on where you are taking a compass reading on the earth’s surface. In my locale, the deviation is approximately 17° W, which means that I must add 17° to a true bearing in order to determine the equivalent magnetic bearing. For the test location that I used for the program demonstrations, the magnetic deviation was approximately 7° W, thus making the magnetic bearing between the two coordinate positions 155° instead of 148° for the true bearing. There are also magnetic deviations that are classified as east (E); these must be subtracted from the true bearing to arrive at the correct magnetic bearing. An old memory aid that pilots and navigators use to help remember whether to add or subtract is the following:
“East is least and West is best” (subtract for East; add for West)
There is also another compass compensation that usually has to be accounted for in non-electronic compasses. This is magnetic declination, or the angle between the Earth’s magnetic lines of force and the measuring compass. Fortunately, we do not need to be concerned with this compensation, as it is done automatically by the electronic compass module.
This concludes the navigation fundamentals discussion. You should now have sufficient knowledge regarding how the quadcopter can be guided between geographic coordinate points.
The discussion in this section is based on my vision of how the VFCS functions in a return-to-home scenario. There are commercial flight-control systems that incorporate this type of operation. How the system’s designers implement this function is usually proprietary, and thus, not available for analysis. I am guessing that some may use a simple type of dead-reckoning system in which the quadcopter records the angles turned and the time of flight while not turning, and then simply “plays” back these flight motions to return to base. This type of dead reckoning may be perfectly adequate for close-in operations in which distances are short and there is little to no wind to push the quadcopter off its commanded course. The system I envision is much more robust and could easily counter crosswinds and much longer path lengths. It is also suited for autonomous operations that I discuss later in this chapter.
A return-to-home flight command first requires that the coordinates of your initial launch place be stored in the flight controller. This could be done automatically when the quadcopter is first powered on or through a sequence of R/C transmitter commands that the flight controller is programmed to respond to within a predetermined time interval. It could even be implemented by pressing a dedicated button on the quadcopter. Whatever the means, the quadcopter needs to know the start point or home coordinates.
The quadcopter is then flown through whatever flight operations are desired until it receives the command to return home. Sending this command can be done in a fashion similar to the one previously described for storing home coordinates except, of course, for pressing a button on the quadcopter. Let us assume a dedicated R/C channel is used to initiate this operation. This approach is probably the most reliable, although you may not have the luxury of access to an uncommitted channel, especially if you are using an R/C system with six or fewer channels.
1. The first step in returning home is to compute both the path distance and the bearing from the quadcopter’s current position to the already stored home position. The bearing is really the most important computation of the two parameters. Path length is nice to know and will be used to slow down the quadcopter; however, you can always manually slow down the quadcopter as it zooms over your home position, as long as it is on the right course.
2. The second step is to command a yaw until the quadcopter is pointed to the correct computed magnetic bearing. Remember that the true bearing is done by the formula, and the appropriate magnetic variation must be added or subtracted to arrive at the correct magnetic bearing.
3. The third step is to command the quadcopter to proceed in the forward direction at a reasonable speed. The path length should be continually recomputed until it reaches a predetermined limit near zero.
4. The fourth step is to slow down and stop the forward motion once the quadcopter is within a reasonable distance of the home coordinates. I would suggest +/– 50 m (54.7 yd) as a good selection.
5. The fifth and final step would be to slowly reduce the throttle-power setting until the hovering quadcopter touches down. This could be done either automatically or under manual control.
The five-step process shown above assumes the existence of little to no crosswind that would push the quadcopter off course. The five-step process could be altered a bit to account for the crosswinds. The bearing would have to be continually recomputed during flight by using the current position. Some minor aileron commands would then be needed to slightly turn the quadcopter to the new home bearing. I would definitely not try to yaw the quadcopter while it is in straight and level flight.
Most likely, you have already seen online videos of quadcopters flying in formation. If not, I would suggest viewing this video, http://makezine.com/2012/02/01/synchronized-nano-quadrotor-swarm/.
Formation flying has been a hot-topic research item for several years. The research focuses on the swarming behavior of insects as they act in a collective manner. There are important goals that researchers are trying to achieve, in which groups or teams of quadcopters can accomplish tasks simply not possible with a single quadcopter. The General Robotics, Automation, Sensing, and Perception (GRASP) Lab at the University of Pennsylvania has been the predominant organization in this field. One of its chief researchers is Professor Vijay Kumar, who gave an excellent 15-minute Technology, Entertainment, Design (TED) presentation back in February, 2012 that I strongly urge you to view before proceeding in this chapter. Here is the link http://www.ted.com/talks/vijay_kumar_robots_that_fly_and_cooperate.html. This informative video provides a wealth of information on quadcopter performance and swarming behavior.
At present, two technologies are used to implement swarming behavior: motion capture video (MoCap) and close-proximity detection. First, I will discuss MoCap technology and then the close-proximity detection technology.
In the TED video, the MoCap cameras can be seen mounted high on the GRASP Lab walls where they have a clear field of view of the flight area. Each quadcopter also has some reflective material mounted on it to provide a good light target for the cameras. Each MoCap camera is networked to a host computer that has been programmed to detect the reflective targets and determine all the quadcopter positions in 3D space. It is probable that only one of the quadcopters has been designated as the lead quadcopter and that sensors and decentralized control allow the others to follow it. The host computer would likely control the lead quadcopter through some type of preprogrammed flight path, and all the others would just follow the leader. However, the video http://www.geeky-gadgets.com/quadcopters-use-motion-capture-to-fly-in-formation-video-17-07-2012/ shows a situation in which all the quadcopters are under direct MoCap control as they execute formation flying.
In this case, the MoCap cameras capture all of the quadcopter’s reflective markers and send the images to the host computer, which then calculates the position and attitude for each quadcopter. Precise repositioning to within 1 mm is then transmitted to each quadcopter. The control frequency is 100 Hz, which means that position and altitude are recalculated every 10 ms to prevent collisions.
In the GRASP Lab experiments, each quadcopter had a means of determining how close it was to its neighbor(s) and repositioning itself if the distance was too small. I believe that distance was only several centimeters, which is very tight but not as tight as the full MoCap positioning as described above.
I will discuss the Parallax Ping sensor as a typical unit that can serve as a close-proximity sensor. The Ping sensor is shown in Figure 11.14. It has the overall dimensions of 1¾ × ¾ × ¾ in, which is a bit on the large size for a sensor.
The Ping sensor uses ultrasonic pulses to determine distances. It works in a way similar to a bat’s echo-location behavior. This sensor may be thought of as a subsystem in that it has its own processor that controls the ultrasonic pulses used to measure the distance from the sensor to an obstruction. Figure 11.15 is a block diagram for this sensor. The sensor has a stated specification range of 2 cm (0.8 in) to 3 m (3.3 yd), which I verified by using the test setup described later in this section.
The Ping sensor uses a one-wire signal line by which the host microprocessor (BOE) emits a two-microsecond pulse that triggers the microprocessor on board the sensor to initiate an outgoing acoustic pulse via an ultrasonic transducer.
The test code was downloaded from the Parallax product Web page for product number 28015. The test program is named Ping_Demo_w_PST.spin. The program continually outputs the distance measured by the sensor in both inches and centimeters. This program also uses a Spin library object named Ping.spin that acts as a driver and is listed below:

The following code snippet from the above listing generates the initial pulse that is sent to the sensor. The onboard sensor then sets the signal line high and then listens for the return pulse with another ultrasonic transducer. The echo-return acoustic pulse causes the onboard processor to change the signal line from high to low. The Ping code measures the time interval, in microseconds, that has elapsed while the signal level was going from high to low. The system-clock counter value is stored in the variable cnt1 when the high value is detected and in the variable cnt2 when the sensor changes the signal-line level to low. The difference, cnt2 - cnt1, must then be the elapsed time in the units of system-clock cycles.

The test code also incorporates a provision to activate two LEDs, depending upon the measured distance. The LED connected to P1 will turn on when the distance is less than 6 inches. The other LED connected to P2 will turn on when the distance exceeds 6 inches. The P1 LED will also turn off when the distance exceeds 6 inches. The test code is shown below:

Figure 11.16 shows the setup of the test components on the BOE solderless breadboard. The P1 LED is at the top of the breadboard, and P2 is near the bottom. A book was placed 8 in from the Ping sensor to reflect the ultrasonic pulses. A PSerT screenshot shown in Figure 11.17 illustrates the results of the test setup shown in Figure 11.16.
A Ping sensor can also be mounted on the underside of the bottom chassis plate, pointing straight down, which would provide near-to-ground altitude measurements. The maximum Ping sensor range is 3 m (3.3 yd), which is more than enough to provide good above-ground readings for hovering or for approach-to-landing operations. Figure 11.18 shows a Ping sensor that is mounted on the bottom chassis plate and has a clear field of view of the ground.
It could also be used as part of the close-proximity sensor set discussed in the section on formation flying. In such a situation, it would provide vertical clearance measurements between it and any quadcopter flying below it.
There are some conditions that you should be aware of if you want to use an ultrasonic sensor successfully for close-proximity detection. These conditions are listed and discussed below:
• Wind turbulence
• Propeller acoustic noise
• Electrical noise both conducted and radiated
• External radio interference
• Frame vibration
Wind turbulence is created by the propellers. The only realistic solution to minimize this type of interference is to mount the sensor as far as possible from any propeller.
Propeller acoustic noise adds additional acoustic energy to the sensor, which generally reduces the overall ultrasonic transducer sensitivity. Careful sensor placement reduces this effect along with avoiding a direct structural mount near any motor.
The ultrasonic sensor’s electrical power supply should be directly connected to the same power source used by the flight-controller board. In the Elev-8 configuration, the HoverflyOPEN controller-board power is supplied through the BEC lines (as I described in Chapter 5). The AR8000 receiver, in turn, is powered from the flight-control board. Using the power-distribution board actually helps reduce the interference by providing a ground-plane-shielded power source for the ESCs, which are primary potential noise sources.
Strong interference may also be present as conducted electrical noise. This type of noise is often eliminated by using a simple resistor/capacitor (RC) filter. Figure 11.19 shows an RC filter that can be connected at the sensor power inputs to eliminate any conducted electrical noise interference.
Electrical currents that flow through wires produce an electromagnetic (EM) field. Strong currents that also carry noise pulses produce what is known as radiated electrical noise. The ultrasonic-sensor power leads should be twisted to mitigate any possible radiated noise interference. You also might need to use a shielded power cable if the interference is particularly severe. Ground only one end of the shielded cable at the host microprocessor side to stop any possible ground loop current from forming.
There are also several radio transmitters on board the Elev-8 that can generate lower levels of EM interference. Usually they will not be an issue provided you have taken some or all of the control measures already mentioned.
The final interference might come from frame vibrations, which can upset the sensor’s normal operation. This type of interference is easily minimized by securing the sensor in a small frame that, in turn, is mounted on the quadcopter’s frame with rubber grommets. This is precisely the same type of mounting arrangement that is used to mount the HoverflyOPEN control board on the Elev-8.
Maintaining position in a formation is really a matter of providing very slight control inputs to shift the quadcopter’s position a few centimeters. Ping sensors mounted at the ends of each quadcopter boom are easily programmed to provide an output on two pins that can signal to the flight controller that the quadcopter is either closer to or farther away from a neighboring quadcopter than it should be. The precise control inputs that are needed will probably be determined by trial and error, since only small shifts in rotor rotation speeds would be required to accomplish centimeter-scale movements. It would make no sense to actually bank or pitch the quadcopter for tiny lateral movements. Massive control inputs, such as banking or pitch changes, would result in excessivly large displacements, which are definitely not required. Instead, just changing the rotation speeds on one or two motors by 100 to 200 r/min may very well accomplish the required shifts. Such precise control will likely need to be repeated 10 to 20 times per second to maintain accurate positioning.
Several other manufacturers provide ultrasonic sensors that will function quite well for close-proximity detection. Figure 11.20 shows the MaxBotix HRLV-Max Sonar®–EZ1™, model MB1013, which is a very compact sensor with overall dimensions of approximately ¾ × ¾ × ¾ in.
This versatile sensor has many more operational functions than the Ping sensor. The following summary in Table 11.3 was extracted from the MaxBotix data sheet, to provide you with some additional background on this sensor type. The pin connections for this sensor are shown in Figure 11.21.
Real-Time Range Data—When pin 4 is low and then brought high, the sensor will operate in real time, and the first reading that is output will be the range measured from this first commanded range reading. When the sensor tracks that the RX pin is low after each range reading and then the RX pin is brought high, unfiltered real-time range information can be obtained as quickly as every 100 ms.
Filtered Range Data—When pin 4 is left high, the sensor will continue to range every 100 ms, but the output will pass through a 2-Hz filter, through which the sensor will output the range, based on recent range information.
Serial Output Data—The serial output is an ASCII capital R, followed by four ASCII digit characters representing the range in millimeters, followed by a carriage return (ASCII 13). The maximum distance reported is 5000 mm. The serial output is the most accurate of the range outputs. Serial data sent is 9600 baud, with 8 data bits, no parity, and one stop bit.
One important constraint that you must be aware of is the Sensor Minimum Distance or No Sensor Dead Zone. The sensor minimum reported distance is 30 cm (11.8 in). However, the HRLV-MaxSonar-EZ1 will range and report targets to within 1 mm (0.04 in) of the front sensor face; however, they will be reported as at a 30-cm (11.8 inches) range.
Another close-proximity sensor that you might consider using is one based on invisible light pulses. This sensor is the Sharp GP2D12, which is an infrared (IR) light-ranging sensor. It is shown in Figure 11.22.
The IR light pulses used by this sensor are similar to the IR pulses used in common TV remote controls and are rather impervious to ambient light conditions. The pinout for this sensor is shown in Figure 11.23 and it has only three connections, as was the case for the Ping sensor. The VCC supply range is from 4.5 to 5.5 V, and the output is an analog voltage that is directly proportional to the target range. Figure 11.24 shows a graph of the Vo pin voltage versus the target range.
This type of output means that you must use an analog-to-digital converter (ADC) to acquire the numerical range value. The range precision will also be dependent on the number of ADC bits. The Parallax Propeller chip uses 10-bit sigma-delta ADCs, which means a 1024-bit resolution over the input voltage range. Figure 11.23 indicates a maximum output of 2.6 V at 10 cm (3.94 in), which incidentally, is also the minimum range the sensor will detect. I would probably use the VCC as an ADC reference voltage, since it is readily available and encompasses the maximum expected input voltage.
The precision calculations would be as follows:
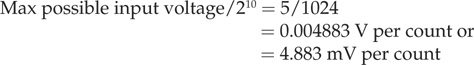
The maximum range is 80 cm (31.5 in), which generates a 0.4 V output. Therefore, the total voltage change for the specification range of 10 to 80 cm must be:

Next divide 2.2 V by 70 to arrive at volts per centimeter (Note: I am assuming linearity, which is not actually the case, but it will have to suffice without overly complicating things.)
![]()
Now using the 4.883 mV per count calculated above, it is easy to see that the ultimate precision is:
![]()
This means each centimeter in the interval can be resolved to approximately one sixth of a centimeter or about 16 mm (0.63 in), which should be sufficient for most close-proximity operations.
The above calculations are fine, but you are likely puzzled as to the actual numbers that you could expect from the ADC. Three values are shown below that represent the minimum, midpoint, and maximum ranges:

I always like to do a sanity check on my calculations, which follows:

I did mention in the above calculations that I assumed that analog voltage versus distance curve was linear or a straight line, which it is obviously not. If you desire absolute precision, you would have to develop either a lookup table or an analytic equation that modeled the curve. The latter is actually not hard to do by using the Microsoft Excel feature that automatically creates best-fit equations from a data set, but that is best left for another time.
One more special type of proximity sensor I would like to discuss is a LIDAR. The term LIDAR is a combination word made from the words light and radar. It uses an IR laser beam to detect, and many times, map out distant objects. Until recently, LIDAR sensor systems were bulky, consumed substantial power, and were very expensive. But that has changed recently, to the point where very capable systems are now available that can be mounted on a quadcopter. They are also relatively inexpensive. LIDAR is able to range distant objects at or beyond 3 km (1.86 mi) because it uses high power and IR laser pulses of very short duration. The reflected pulses are detected by sensitive, optical-photo receivers, and the distances are computed by precisely the same method used by traditional radar systems.
Figure 11.25 shows a LIDAR kit, model ERC-2KIT, that is sold by Electro-Optic Devices. The kit contains a single-board ranging controller as well as the transmitter and the receiver boards, as shown in the figure. It does not come with a laser diode, which must be purchased separately. Diode selection depends upon the intended LIDAR application because diodes are available in a range of both wavelength and power capacity. Common wavelengths are 850 and 905 nanometers (nm), both of which are in the IR range. Power ratings can vary from a low of 3 W to a high of 75 W, which is a very powerful laser that can cause severe eye injury if not used carefully.
Figure 11.26 shows the OSRAM SPL PL85 LIDAR-capable laser-pulse diode that is rated at 10 W and capable of ranging up to about 1 km (0.62 mi). LIDAR pulses are very short in time duration, typically some tens of nanoseconds. However, the current pulse can easily exceed 20 A.
Electro-Optic Devices provides a test and control board for their LIDAR ERC-2KIT, which is very useful for development purposes. Electro-Optic Devices calls this board the BASIC Programmable Laser Ranging Host Module, model EHO-1A, and it is shown in Figure 11.27.
FIGURE 11.27 BASIC Programmable Laser Ranging Host Module, model EHO-1A, from Electro-Optic Devices.
This board uses a Parallax Basic Stamp II (BS2) as a controller, which fits nicely into the whole Parallax controller discussion that has been ongoing in this book. The BS2 uses a derivative of the BASIC language named PBASIC to implement its microcontroller functions. BASIC, as most of you already know, is procedural and not object oriented as is the Spin language used for the Parallax Propeller microcontroller. Nonetheless, it is more than adequate for this application, and it is really very easy to program in BS2 BASIC. The BS2 also uses The Basic Stamp Editor, which is a different integrated development environment (IDE) from the Propeller chip IDE. It is freely available to download from the Parallax website.
The PBASIC instructions in the following section are excerpted from the Electro-Optic Devices’s EHO-1A manual to illustrate how to display data on the LCD screen and how to read from and write to the peripheral modules.
The LCD display must be written to serially from the BS2. The BS2 instruction SHIFTOUT accomplishes this task. There are four LCD-oriented subroutines available in each example program. They are:
1. DSP_INIT—Initializes the LCD Display
2. DSP_TEXT—Sends a text string to the LCD
3. DSP_CLR—Clears the LCD
4. DSP_DATA—Displays binary data on the LCD (up to 4 digits)
At the top of each example program is a section for EEPROM DATA. ASCII string data is stored in this location to be written to the LCD by the DSP_TEXT subroutine. The LCD string format is as follows:
![]()
The LABEL can be any valid name for the string. DATA indicates to the tokenizer that this information will be stored in EEPROM. L#P# is the line number (1 or 2) and position number (1–16) where the first character of text is to be located in the LCD. LENGTH is the number of characters that follow inside the quotation marks. For the above example, this program line might look like this:
![]()
When the DSP_TEXT subroutine is called after the message pointer MSG is set to the string’s label: MSG = T_STRG, the text message “STRING INFO” is displayed at the first position of line 2 on the LCD. Similarly, BCD data can be written to the LCD using the DSP_DATA subroutine. A binary number to be displayed in the range of 0–9999 must be stored in VALUE. The LCD location pointer LOC must be set to the location of the first digit of a four-digit result. Before calling the DSP_DATA subroutine, a selection must be made between the two decimal point formats for the four-digit display (NNNN or NNN.N). Two examples follow:
1. To display the number 1234 beginning at character position 10 in line 1 of the LCD:

2. To display the number 456.7 beginning at character position 3 in line 2 of the LCD:

The example programs each have slight differences in the data acquisition subroutines and should be examined closely before writing your own. The ECH-4 is especially unique, since it uses a single bidirectional serial bus. The basic procedure is described in the following section.
Set the COMMAND variable to the command or data byte to be written to the module, for example:
COMMAND = $00
Next, bring the chronometer select signal ![]() low to enable communication with the module. Now use the BS2 SHIFTOUT instruction to send the byte to the module,
low to enable communication with the module. Now use the BS2 SHIFTOUT instruction to send the byte to the module,
SHIFTOUT HDO, HCLK, MSBFIRST, [COMMAND]
Now bring ![]() back high to disable communication and acknowledge the end of a write.
back high to disable communication and acknowledge the end of a write.
Each module has its own manner of indicating that data is available to be read. See the individual examples for more information. Generally, the read is performed similarly to the write. Bring the chronometer select signal (![]() ) low to enable communication with the module. Now use the BS2 SHIFTIN instruction to read the byte from the module:
) low to enable communication with the module. Now use the BS2 SHIFTIN instruction to read the byte from the module:
SHIFTIN HDI, HCLK, MSBPRE, [DATABYTE]
Now bring ![]() back high to disable communication and acknowledge the end of a write. The read information is now stored in the variable DATABYTE.
back high to disable communication and acknowledge the end of a write. The read information is now stored in the variable DATABYTE.
Autonomous behavior happens when the quadcopter performs tasks without direct human operator control. A common autonomous task might be to fly a preset path, which could even include taking off and landing without any human intervention. Such a task would necessarily have to have predetermined coordinates already programmed into the flight-controller’s memory. These coordinates are normally called waypoints and are just a series of latitude and longitude coordinate sets that the quadcopter will fly to in a preset sequence. Of course, flying a preset path without any other function would be fairly meaningless beyond giving you the satisfaction of being able to do it. Taking video or periodic still photographs while flying the path would be a much more meaningful experience and would illustrate the versatility of the quadcopter. Photographic aerial damage assessment after a natural disaster would be a good fit for an autonomous quadcopter mission.
Creating a virtual map of an indoor environment is another interesting task that is currently being developed by a number of organizations. The quadcopter would be equipped with a type of LIDAR as discussed above. The LIDAR would usually be mounted on an automated pan-and-tilt mechanism. A typical and rather inexpensive mount is shown in Figure 11.28.
Using the ERC-2KIT requires only that the lightweight transmitter and receiver boards be mounted with a pair of signal cables connected to the ranging controller. In a video shown in Professor Kumar’s TED presentation, you can see mapping being done by a quadcopter within a building. Incorporating artificial intelligence (AI) within the flight controller helps the quadcopter avoid obstacles and keeps it from being trapped in a room. This important topic is discussed further in the next section because it is a vital component to the successful completion of an indoor mapping task.
Artificial intelligence is an extremely interesting topic that I have studied for a number of years. I will not present a full AI discussion but instead will focus on the essential ideas that are directly applicable to quadcopter operations in a confined space. The essential goal for this specific AI application is to equip the quadcopter controller with sufficient “reasoning” capability so that it can autonomously avoid obstacles.
Researchers have already determined that the AI methods of Fuzzy Logic (FL) and, more specifically, Fuzzy Logic Control (FLC) are particularly well suited for autonomous robotic operations. Let me start by stating that there is nothing “fuzzy” or “confused” about this AI field of study; it is simply a name applied to reflect that it incorporates decision ranges in lieu of traditional, discrete, decision points of yes/no, true/false, equal/not equal, and so on. I need to show you some basic FL concepts before proceeding any further.
Professor Lufti Zadeh invented FL in 1973. He applied set theory to traditional control theory in such a way as to allow imprecise set membership for controlling purposes instead of using normal, precise, numerical values, as was the case before FL. This impreciseness allows noisy and somewhat varying control inputs to be accommodated in ways that were not previously possible.
FL relies on the propositional logic principle, Modus Ponens (MP), which translates to “the way that affirms by affirming.” An equivalent logical statement is:
IF X AND Y THEN Z
where X AND Y is called the antecedent and Z is the consequent.
Next, I will use a simple room-temperature-control example to demonstrate the fundamental parts that make up an FLC solution. Normally, you might have the following control algorithm in place to control an indoor room:
IF Room Temperature < = 60° F THEN Heating System = On
This reflects precise measurements and a definitive control action. It is also easily implemented by a “dumb” thermostat. Transforming the above control statement into an FL type statement might lead to:
IF (Room too cool) THEN (Add heat to room)
You should readily perceive the input statement’s impreciseness, yet there is a certain degree of preciseness in the outcome or output action. However, do not make the mistake of thinking that FL does not use numerical values; it does, but they are derived from a set of values.
Room temperatures may be grouped or categorized into regions with the following descriptors:
• Cold
• Cool
• Normal
• Warm
• Hot
If you were to survey a random group of people, you would quickly find that one person’s idea of warm might be another person’s idea of hot, and so forth. It quickly becomes evident that some type of membership value must be assigned to different temperatures in the different regions. In addition, a graph of temperature-versus-membership value could take on different forms, depending upon how the survey was taken. Triangular and trapezoidal are the two graph shapes that are normally used with membership functions and that vastly simplify FL calculations. Membership values range from 0 to 100%, where 0 indicates no set members are present, while 100% shows all set members are within the region. By set members, I mean the discrete temperatures on the horizontal axis. Figure 11.29 shows the five membership functions for the five temperature regions.
The use of these shapes for membership functions avoids arbitrary thresholds that would unnecessarily complicate passing from one region to the next. It is entirely possible, and in fact desirable, that a given temperature have membership in two regions simultaneously. Not every temperature point has to have dual or even triple membership, but temperatures on the region’s edges should be so assigned except for the extremis ones associated with the very cold and the very hot trapezoidal regions, for example, tmin and tmax of Figure 11.29. This format allows the input variable to gradually lose membership in one region, while increasing membership in the neighboring region. The translation of a specific temperature to a membership value in a selected region is known as fuzzification. The complete set of membership values for the input temperature is also referred to as a fuzzy set.
The combination of fuzzy sets and Modus Pons relationships are the needed inputs to a rule set that decides what action to take for the control inputs. FLC may be analyzed as three stages:
1. Input—This stage takes sensor input and applies it to the membership function to generate the corresponding membership values. Values from different sensors may also be combined for a composite membership value.
2. Processing—Takes the input values and applies all the appropriate rules to eventually create an output that goes to the next stage.
3. Output—Converts the processing result to a specific control action. This stage is also called defuzzification.
The processing stage may have dozens of rules, all in the form of IF / THEN statements. For example:
IF (temperature is cold) THEN (heater is high)
The antecedent IF portion holds the “truth” input value that the temperature is “cold,” which triggers a “truth” result in the heater-output fuzzy set that its value should be “high.” This result, along with any other valid rule outputs, is eventually combined in the output stage for a discrete and specific control action: so called defuzzification. You should also note that, as a given rule, the stronger the truth-value is for an input, the more likely it will result in a stronger truth-value for the output. The resultant control action may not be the one expected, however, since control outputs are derived from more than one rule. For instance, in the example of the room heating and cooling system, if a fan were used, it is entirely possible that the fan’s speed might be increased, depending upon the rule set and whether or not the heater is set on high.
The AI core of FL lies in the construction of the rule set, which basically encapsulates the knowledge of problem-domain experts in crafting all the rules. Typically, subject matter experts (SMEs) would be asked a series of questions, such as “if so and so happened, what would your response be?” These questions and the SME answers would then constitute the rules set as a series of IF/THEN statements. The usefulness of an FLC solution is totally dependent upon the quality of the SME input.
This concludes my FL basics introduction, and I will now return to how FLC is used with quadcopters.
There are two common types of FLCs:
1. Mamdani
2. Sugeno
Mamdani types are the standard FLCs, in which there are membership shapes for both their input and output. Defuzzification of the output fuzzy variables is done by using a center-of-gravity, or centroid, method. Sugeno types are simplified FLCs, in which only inputs have membership shapes. Defuzzification is done by the simpler weighted average method. I will be discussing only the Mamdani FLC because that seems to be the most popular approach for quadcopter FLC.
FLC commonly uses the term error (E), which is the actual output minus the desired output. I will use Z as the variable for the error input. It is also very common to use the rate of change of the error variable as an input, which I will show as dE where the d represents the time derivative of E. Finally, accumulated error should be accounted for. It will be represented by iE where the i represents the error integrated (summed) over a time interval. If all this looks vaguely familiar, I will refer you back to Chapter 3 where the proportional, integral, and derivative (PID) controller was introduced. FLC controllers function as PID controllers with some additional pre- and postprocessing to account for the FL components.
The input variables Z, dE, and iZ also need to be multiplied by their gains, GE, GDE, and GIE respectively. The output variable will be designated Z, and it also has a gain of GZ.
Matlab® is a powerful, scientific-modeling and math computational system that will be the basis for the rest of this discussion. Matlab® has a variety of toolkits that expand its capabilities, including a Fuzzy Logic Toolkit. This toolkit has the following characteristics:
• Mamdani inference.
• Triangular central membership function with the rest as trapezoidal shapes.
• The FL rules set will follow this form:
if (Ez is E) and (dEz is DE) and (iEz is IE) then (Z is Zz), where E, DE, IE, and Zz are fuzzy sets.
• Defuzzification method is centroid or center of gravity.
• AND operator implemented as the minimum.
• Implication is a minimum function.
• Tuning of input and output gains will be done by trial and error.
Figure 11.30 is a block diagram of a Matlab® quadcopter control system. There are four FL controllers shown in the diagram: Z, roll, pitch, and yaw. The Z controller acts as a kind of master because it controls altitude or height above the ground. Obviously, if the quadcopter is not above the ground, it is not flying; and the three other controller actions are moot. Each FL controller takes the four inputs that are the same primary ones first mentioned in Chapter 3:
1. Throttle
2. Elevator
3. Aileron
4. Rudder
Each FL controller also has four outputs, one for each of the quadcopter motors. You may be able to see the membership functions drawn as three generic-triangle shapes in each of the FL controller blocks. They simply symbolize that each block constitutes an input stage. The Aggregation block is a combination processing and output stage that holds all the fuzzy set rules as well as the logic to combine all four FL controller outputs.
The Z controller always has equal power supplied to each motor so that only vertical travel is allowed. If Fz is one output, then 4Fz must be supplied to all four motors. This power level must always be maintained if the quadcopter is to remain at a commanded altitude. Other controllers can require certain motors to speed up and others to slow down in order to achieve a yaw, pitch, or roll, but the net overall power will always result in a net of 4Fz. It is entirely possible that the sets of fuzzy rules will limit or prohibit certain combinations of control inputs, since they would be physically impossible to perform.
The Z controller is probably the easiest to understand because it controls motion along only one axis. Let’s say that the proportional control input (E) is an error signal that is the difference between the commanded altitude and the actual altitude. Also present will be the derivative (dE) and integral (iE) inputs that makeup the totality of the PID control system. The likely proportional input fuzzy sets might be:
• Go up
• Hover
• Go down
The derivative and integral input fuzzy sets might be:
• Negative
• Equal
• Positive
The output fuzzy set, assuming a Mamdani setup, might be:
• Go up a lot
• Go up
• No change
• Go down
• Go down a lot
Figure 11.31 shows the probable fuzzy set membership functions for the Z parameter using the listed control actions. Notice that four out of five membership shapes are trapezoidal and only the No Change is sharply triangular, thus reflecting the expert opinions that most often some control action is needed to maintain altitude.
Table 11.4 shows the probable rules outputs given all nine combinations for the three Z output variables Z, dZ, and iZ. Remember that these outcomes are suggested by SMEs given the stated conditions for the membership variables. Sometimes this rule table is referred to as an inference table, reflecting the MP background.
Of course, the relative results of the error terms depend very much upon the gains associated with their PID inputs. A larger gain will add more weight to a specific input, which could cause somewhat of a biased operational result. Too much gain can, and often will, result in unstable or oscillatory behavior that makes the quadcopter unflyable.
ViewPort™ is a software development tool for the Propeller chip that was developed and marketed by myDancebot.com, a Parallax partner. ViewPort™ contains a fuzzy logic view as part of the ViewPort™ Development Studio software suite. You can incorporate FL objects into your programs with this tool. It will greatly enhance your ability to create quadcopter FLCs based on the Propeller chip and the Spin language.
The following discussion has excerpts from the ViewPort™ manual to help clarify how FL could be incorporated into Spin programs.
ViewPort comes with a Graphical Control Panel view found in the Fuzzy view, and a Fuzzy Logic Engine implemented in the fuzzy.spin object. ViewPort’s fuzzy logic implementation consists of fuzzy maps, fuzzy rules, and fuzzy logic functions.
Figure 11.32 is a screenshot of the ViewPort™ program running a Lunar-Lander simulation that uses an FLC. In the lower pane, you should also be able to see the three-input-variable membership function graphs, which represent altitude, velocity, and thrust. I also extracted a portion of Figure 11.32 to show you a close-up view of the resultant rules matrix that shows all the possible outcomes for the velocity and altitude variables, as applied to the relevant rules.
Figure 11.33 shows this resultant rules matrix with the altitude and velocity both in the positive region. When you look at the shaded matrix area, it appears that the combined output would be approximately 3. It also appears that the ViewPort™ FL output does not use the centroid, or center-of-gravity approach but relies more on a weighted average. I really do not believe it greatly affects the overall FLC operation, at least in this case.
This last section concludes my AI and FL discussion and also finishes this book. I hope that you have gained some knowledge of and insight on how to build a quadcopter and how it functions. I have tried to provide you with a reasonable background that explains how and why the quadcopter performs as it does and also how to modify it to suit your own personal interests.
Remember, have fun flying the quadcopter, but also be aware of your own and others safety!
I began the chapter by discussing how a virtual quadcopter could return to its start position, or home. To accomplish this feat, the quadcopter would need an electronic compass sensor, which I both described and demonstrated.
I followed the introduction with a brief discussion of what longitudinal path lengths are and how to calculate them. Next, we explored the haversine formula and how it could be used to compute the great-circle path length between two sets of geographic coordinate pairs. We then looked at how to compute the relative true bearing between these coordinates. I next showed how to derive the magnetic bearing once the true bearing was determined, as the electronic compass mentioned earlier works only with magnetic bearings.
A discussion on formation flying followed that included specific close-proximity sensors, which partly enabled this type of precision quadcopter flying. A demonstration was shown, using a Parallax ultrasonic sensor, that permitted quadcopters to operate within 2 cm (0.79 in) of each other. I also discussed some concerns that you should be aware of regarding using this type of sensor on a quadcopter.
I next discussed a very small analog ultrasonic sensor that could also be used for close-proximity operations. I showed how this sensor could be connected to and used with one of the Parallax Propeller analog-to-digital inputs.
The next section included an introduction to LIDAR, which is a combination word for light and radar. It is a very powerful sensor system that is capable of both obstacle detection and carrying out long-range mapping operations to over 3 km (1.86 mi). LIDAR has also been used in many autonomous robotic projects.
I next discussed fuzzy logic (FL), which is a branch of the artificial intelligence (AI) field of study that is particularly well suited for quadcopter control applications. I tried to provide a somewhat comprehensive introduction to FL and fuzzy logic control (FLC) by using a room heating and cooling example. In this example, you saw input and output membership functions as well as the rule set. The rule set captures and encapsulates human expertise such that it can be applied to provide “intelligent” decisions based upon a given set of input values from the membership functions.
An FLC application was next shown to illustrate how FL could be applied to an operating quadcopter. I also used a Matlab® project to further illustrate quadcopter FLC operations.
The chapter concluded with an introduction to ViewPort™, which is a complementary Propeller-chip development environment that happens to have built-in FL functions. Using ViewPort™ makes Propeller FLC development very straightforward, especially because it already does most of the complex programming for you.