CHAPTER IV

The Metric System

1. BACKGROUND

The genius of liberty has at last made its appearance, and has put this question to the genius of science: What is the unit that is fixed and invariant, independent of any arbitrary element, a standard such that there is no need to move it from place to place in order to know its value, and such that it may be verified at any time and place? Estimable scientists, it is through you that the Universe will owe this benefit to France. You have drawn your theory from nature. Among all the lengths that have been determined, you have chosen two, the measurement of the pendulum and above all the measurement of the meridian, the only two for which the combined result is most absolute. Relating thus the one to the other, your zeal has matched your sagacity in the dual comparison of time with the dimensions of the earth. By virtue of their mutual confirmation, you will have won the glory of discovering for the benefit of the whole world this stable unit, this beneficial truth, which will be a new boon to all nations and one of the most useful conquests of mankind.

Response of the abbé Grégoire to the Academy of Sciences, assembled before the bar of the Convention, 25 November 1792.¹

The father of a family may take a certain pleasure in being able to say to himself, “The field that enables me to support my children is such or such a fraction of the world. I am to that degree a coowner of the world.”

Address delivered before the Legislative Body in the name of the Institute, 4 messidor an VII.²

In the regular doings of scientists and other people, the metric system of weights and measures remains the most pervasive legacy of the French Revolution. Its units serve requirements of three sorts: standardization, decimalization, and a particular definition of the meter, the basic magnitude. Standardization governs every activity involving measurement throughout the modern world. The scope of decimalization, though large, is limited by certain exceptions. Angular and temporal subdivisions everywhere continue to be sexagesimal. More parochially, in the United States and much of the British Commonwealth, ordinary transactions are still conducted in avoir-dupois, while the metric system, which answers general purposes throughout the rest of the world, is largely reserved to science.

With respect to definition of the magnitudes, it will be well to begin by recalling the main features of the linear, volumetric, and gravimetric units that American children encounter when they leave inches, feet, pints, and pounds at home and enter the school laboratory. The basis, so they learn, is linear, the meter being approximately 39 inches in length. They are not often told that the original specification was that it should measure one ten-millionth of the quadrant of the meridian of the earth. Larger and smaller units are in decimal multiples or divisions, 1,000 meters to the kilometer, 100 centimeters and 1,000 millimeters to the meter. Units of area and volume are derived by squaring and cubing, the hectare being 10,000 square meters and the liter 1,000 cubic centimeters. Units of weight, finally, are obtained by assigning the value of one gram to one cubic centimeter of water at 4Centigrade, the temperature at which its density is a maximum, so that a cubic vessel ten centimeters on a side holds one liter at a weight of one kilogram.

Generally adopted throughout the scientific world by the end of the nine-teenth century, and largely so in the civic world throughout Europe, the metric system has been much praised in French textbooks as a scientific incarnation of the values of universality, equality, and naturalism, at once Cartesian and revolutionary. Nothing is sacred, however. The bicentennial of the Revolution itself produced a spate of revisionism rather than celebration. Mingling political skepticism with populist social sympathies, certain historians formerly of a leftist persuasion came half circle to what were once counter-revolutionary tenets and tend to deplore the actions of the revolutionary protagonists.³ The great programs, whether constitutionalist, Girondist, or Jacobin, are held to have imposed a set of political and economic abstractions upon a populace whose real interests are better grasped in categories of anthropology than in those of political theory.

So it is with the metric system, for much historiography of science has become as sociopolitical in vein as ordinary history, and certain of its practitioners discount the claims of science to be the rational mediator between humanity and nature. Instead, such authors explain the success or failure of theories as a function of the structure of power and attribute the choices scientists make, not to technical factors, which are taken as pretenses to be seen through, but to their interests, more or less disguised. The metric system has thus come to have something of a bad press, both politically and technically.⁴

The instance of modern America shows that it is not essential to the functioning of a modern economy and of a scientific enterprise that they make use of the same system of measurement. Both commercial and scientific units are standard, however. Not so in commerce or in agriculture in the old regime, and not altogether so in science: “In France,” wrote Arthur Young in 1787, “the infinite perplexity of the measures exceeds all comprehension. They differ not only in every province, but in every district, and almost in every town, and these tormenting variations are found equally in the denominations and contents of the measures of land and corn. To these sources of confusion is added the general ignorance of the peasantry, who know nothing of the Paris arpent or the Paris septier, the most commonly received measure of the Kingdom.”⁵

The contemporary attribution of this “Gothic diversity of our measures,” as Bureaux de Pusy called it, to that “feudality which no one longer dared defend” (Delambre’s words) was perfectly correct as far as it went.⁶ Only in the matter of coinage had the French monarchy succeeded in gathering into its hands the manifold juridical, fiscal, and administrative functions that pertain to sovereignty in the modern state, as the crown had done in England since Tudor times. Compounding feudal particularism, manorial custom in the countryside and the corporative practice of guilds in towns had produced agrarian and commercial as well as political layers of dimensional discrepancy. The size of a unit, the aune or ell for cloth, the boisseau or bushel for grain, and many another, varied not only with the locality but with the commodity being measured, often very considerably. These mani-fold conventions, this complexity of measures, put a greater premium on knowing one’s business than can well be imagined nowadays when lengths, weights, and volumes are everywhere standard. Clearly, however, the traditional measures did work after a fashion, the fashion of the old regime, in which commerce and science both did well, after all. It is to this that apologists for those usages point, taking up in the modern literature a refrain among its artisanal defenders.

The apology goes deeper into life than the mere practicality of sticking to workable conventions, and partakes of the anthropological penchant for discerning the wisdom embodied in folkways. Not only did linear units take their dimensions from the measure of man, the foot, the ell, the six-foot toise, and so on. Beyond that, which is obvious, the magnitude of agrarian and commercial units was functional in origin. The extent of a tract of forest would be estimated in terms of the number of quarter-hours it took to walk around the perimeter. A journal of arable land would be the area that a man could sow, or plow, or scythe, depending on local custom, in a day. It would vary in size according to the crop and the fertility of the field. A similar logic deriving from conditions of transport and marketing underlay other apparent inconsistencies. If the minot of wheat contained three bushels and the minot of oats five, it was because the densities of the two grains are such that a minot of either weighed the same, 27.3 kilograms in each case. And so on indefinitely if not ad infinitum.⁷

Inconvenience and uncertainty thus afflicted economic exchanges at all levels, and standardization was among the most prominent reforms demanded in the cahiers de doléances drawn up in the constituencies prior to convocation of the Estates-General convened in April 1789: “One King, One Law, One Weight, One Measure.”⁸ What practical men had in mind was not a scientific system, but a fair and honest one. That the portion of grain owed to the lord of the manor should be measured out in the lord’s standard bushel, for the use of which the peasant had to pay a fee (and which was commonly suspected of growing in capacity over time); that persons in authority buying or taxing oats should decide whether a container in such or such a transaction should be filled flat, rounded, or heaped; that the value of wheat sold to the miller, of cowhides to the tanner, of leather to the shoe-maker, of wine to the wine merchant, of pigiron to the blacksmith, in short that the worth of all commodities, both agrarian and manufactured, should be determined by weights and measures of arcane definition in the hands of the most powerful of the parties to the affair, whether tax-collector, lord, or great merchant—all this was of a piece with the presence in manorial muni ment rooms stocked with inscrutable registers, deeds, and charters containing the record, unverifiable by the peasant, of everything owing to lord and overlord, clerical and secular.

According to legend, uniformity of weights and measures had obtained throughout the Carolingian empire, and before that in the metric golden age of ancient Rome and Egypt. From the time of François I^er, successive royal edicts imposing such standardization throughout the realm largely failed of effect beyond the Ile-de-France.⁹ The official weights and measures employed in Paris itself, to which the seigneurial and municipal standards in the provinces would in principle have been subordinated, were of haphazard definition. Legally the fundamental linear unit was the pied du roi, contained six times in the cubit, the Toise de Pâris. In the eighteenth century the actual standard was a graduated iron bar, the Toise du Châtelet, mortised into the wall at the foot of the great staircase in that edifice. It served the public for the verification of appropriate measuring rods and rulers. There it had been emplaced in 1668, an improvement upon an ancient standard, which had buckled with the settling of the pillar. Over the years the Toise du Châtelet, a trifle shorter than its predecessor, rusted in its setting. In 1759 an alert and civic-minded laborer, noticing that it had worked loose, took a sledge and pounded the ends back into the masonry. Jean-Jacques Dortous de Mairan, of the Academy of Science, found it bent firmly into position, reported the curvature to the Academy, and returning to verify the situation, saw that in the meantime it had been further secured by hammering along the lower flange.

Fortunately, La Condamine had had a duplicate made prior to the expedition he led to Peru in 1735 in order to survey the length of a degree of latitude at the Equator. On 16 May 1766, acting on advice tendered by the Academy of Science eight years previously, the government ordered eighty replicas made of this Toise de Pérou. Marked off in feet and inches, the bars were distributed about Paris and to the provincial capitals, where they might or might not be respected and utilized. They served officially, therefore, as the final linear referent of the old regime.¹⁰

The standard of marc weight had known fewer vicissitudes. It consisted of a Chinese nest of cylindrical weights totaling fifty marcs, or twenty-five pounds. This Pile de Charlemagne, which in fact dated from the fifteenth century, was kept at the Mint, along with the dies for coinage.¹¹ As for units of capacity and of yardgoods, and those such as the dram, the carat, and the grain, which pertained to highly skilled trades, the appropriate guild corporations, the Mercers, the Grocers, the Apothecaries, the Jewelers, and so on had the standards in their (very jealous) keeping, the more important of them in quarters assigned to the respective Jurés-mesureurs in the Hôtel de Ville.

Like the juridical procedures in which it was embedded, such metrical practice derived from precedent. Even so, it was little if at all detrimental to the conduct of most of science in the eighteenth century. Only in geodesy, of which the Cassini map of France was the grandest achievement, did it matter that measurements from scattered places be referrable to a common, invariant standard. In the experimental or observational practice of a Franklin, of a Nollet, of a Herschel, even of a Lavoisier or a Coulomb, the reliability of a single instrument or set of instruments was essential. As long as Lavoisier’s weights were faithful to themselves, it did not signify what proportion they bore to the components of the Pile de Charlemagne, whereas the necessity to convert into his terms units employed in London or Uppsala was at worst an inconvenience attending the repetition of experiments.

Thus it was no accident that the movement for a general scientific reform of weights and measures should have taken its impetus from the geodesists, from La Condamine, specifically, on his return from Peru. Adopting a suggestion by Huygens in Horologium oscillatorium (1673), La Condamine read a memoir at the public meeting of the Academy of Science in April 1748, in which he outlined a project for basing a universal system of measures on a unit to be determined by the nature of things.¹² The most convenient magnitude would be the length of a simple pendulum that beats seconds at the equator.

Nothing was done. The idea remained in the air, however, and although the decision ultimately taken based the meter rather on a fraction of the length of the meridian, the geodetic survey undertaken in 1792 to establish its value was in effect a resumption of the operation of triangulation through which La Condamine’s successors, both French and British, linked the observatories of Paris and Greenwich in 1787 and with them the Cassini map of France to what became the Ordnance Survey of Britain.¹³

In contrast to the clarion demands for uniform and honest standards of commercial measurement contained in the cahiers de doléances at the outset of the Revolution, the initial indications of scientific interest in metrical reform, as in other political questions, were tentative and muted. An entry in the register of the Academy of Science for 27 June 1789 records appointment of a committee composed of Lavoisier, Brisson, Laplace, Tillet, and Leroy “for a piece of work on weights and measures.” No record remains of their deliberations, if any, and the subject received no further mention in the Academy until 14 August, ten days after the night-long session of the Constituent Assembly in which noble members renounced their privileges. On that date Leroy urged that the moment was ripe to erect a properly scientific structure of weights and measures on the ruins of feudal diversity.¹⁴

Whether he was speaking for himself or for the committee is unclear. Jean-Baptiste Leroy, an experimentalist in electricity and champion of Benjamin Franklin’s one-fluid theory, was the son of a famous clockmaker and himself less noteworthy for his science than for his articles on scientific instruments in the Encyclopédie. His more prominent colleagues who had given serious thought to metrology, notably Condorcet, Lavoisier, and Laplace, preferred to operate behind the scenes for the time being, where (as will appear) they were developing the scheme that Talleyrand, acting as the spokesman of enlightened science, presented to the Constituent Assembly on 6 May 1790.

By that time a number of other proposals had already been submitted. Since it was assumed, at this initial stage, that weights and measures pertained primarily to commerce, all such projects were referred routinely to the Committee on Agriculture and Commerce.¹⁵ The two most interesting among them, in part because of the authorship, were a memoir by a pair of veteran civil servants, L.-P. Abeille and Matthieu Tillet, writing on behalf of the Royal Society of Agriculture, and another by Claude-Antoine Prieur, future member of the Committee of Public Safety. The former was submitted to the Constituent Assembly on 6 February 1790.

Evidently, the Committee had requested the opinion of the Society of Agriculture on a still earlier discussion of uniform weights and measures by one Villeneuve, who was concerned mainly with public order. Rather than limiting themselves to that, Abeille and Tillet seized the moment to review the entire subject of metrology from a practical point of view.¹⁶ Abeille was seventy years of age in 1789. He had served as private secretary to Vincent de Gournay, the Intendant of Commerce in the 1750s whose precepts had been the inspiration of economic liberalism at mid-century. Converted by later experience of office to belief in the need for moderate regulation, Abeille was one of the founders of the Royal Society of Agriculture in 1761. He remained a principal figure in its counsels until his death in 1807.

Tillet also had been of the circle of agronomists that included Duhamel de Monceau, Fougeroux de Bondaroy, and Broussonet, then serving as Permanent Secretary of the Society of Agriculture. Tillet had the further qualification of long service as Director of the Mint at Troyes. In 1774 Turgot had commissioned him to collaborate with the young Condorcet in what was, in effect, the latter’s introduction to the subject, preparation of a plan for standardization of weights and measures. The project was one among many for which the statesman’s scant two years in office failed to suffice. That abortive experience, it may be conjectured, is likely to have reinforced if it did not generate Tillet’s distrust of abstract approaches to concrete practices.

In composing their Observations, Abeille and Tillet were well aware that a scientific plan was in the making. They begin by opposing anything of the sort. If only there were an immutable natural standard, it would indeed provide a bulwark against error, whim, and chicanery. But no such object is known. To be sure, scientists of a rational disposition do aspire to measure the length of the seconds pendulum for that purpose. “It is in the character of genius to reach for distant prospects, often beyond the limits of our grasp, and not to hesitate to flatter itself that success is near and will be complete.”¹⁷ However attractive, the notion of a natural standard is altogether visionary in present circumstances. The nations of the world would never adopt such a scale. Consider how many centuries elapsed before they agreed on the Gregorian Calendar. In any case, determinations of the pendulum are susceptible of nothing like perfect precision. The force of gravity varies from place to place, and may also be inconstant at a given location. Even were gravitational force assumed to be invariant, different observers would never arrive at precisely the same figure for a pendulum of unit length. Still, suppose for the sake of argument that an absolute value could be established. Fabricating perfect replicas would still prove impossible.

The only practical recourse, therefore, must be to standards agreed upon as pure conventions. Most obviously is that true of the manifold exchanges of commerce and daily life. Why regret it? Such transactions require nothing more exact than the approximations that suffice for ordinary buying and selling. The important thing is that people should know what quantity to expect in this commodity bought at that price, that they should be able to calculate by rule of thumb how much flour they will obtain from so many bushels of wheat, and so on and so on.¹⁸ “The idea of buying and selling, of weights, of measures, always entails the comparison of the thing bought or sold with the standard of measurement or weight that serves to fix the price. Into what confusion would it throw people who have constantly to be buying and selling if they were suddenly to be deprived of their accustomed means of comparison.”

The essential thing is immediately to establish a uniform and usable system without disrupting the operation of the market. Nothing more is needed than to standardize the existing weights and measures of Paris throughout the kingdom, and nothing more should be attempted. “Let us scrupulously distinguish our everyday measures from our scientific measures.” ¹⁹ Let us reflect, even with respect to the latter, that absolute perfection, of whatever sort, always escapes our efforts.

So far, Abeille and Tillet sound very like a preview of the modernday critique of the conception of the metric system. When their essay is read straight through, however, inconsistencies appear. They too were men of their time, after all, and it turns out to have been on the score of practice, important though that was, that they were taking unnamed scientists to task. As to principle, they entirely agree that units should ultimately be referrable to nature. Their argument is simply that this was already true of the Toise of Peru. The prototype of that bar had been employed in measurements of the pendulum, at Quito and at Paris. Those had been scrupulous determinations. Units currently in use need only be calibrated against the original standard, itself a natural magnitude. Abeille and Tillet recommend that the ratio be engraved on each of the replicas distributed to all the main cities.

Beyond that, study of the literature has persuaded our authors that, despite all the confusion, it may well be true, as certain learned scholars hold, that a universal metric system had indeed existed in antiquity.²⁰ Everything leads them to believe that what German counterparts would have called this Ursystem still underlies the corrupted usages of the moderns. If so, it will suffice to scrape away the rust. It would then appear that the peoples of antiquity “made use of weights and measures of which the standard of reference, taken from nature, has always been the same.”²¹ As their final recommendation, Abeille and Tillet propose that a joint commission of the Academy of Inscriptions and Belles-Lettres and the Academy of Science be named in order to investigate the question. If the proposition should turn out to be true, it should not be difficult to recover the elementary prototype of the measures of the peoples of Europe, and perhaps of all peoples living in organized societies.

Abeille and Tillet submitted their report on 6 February 1790. Prieur followed them by three days, presenting his memoir on the ninth. Having composed it in Dijon, at a provincial remove from Paris, he was probably unaware that a scientific project was in the wind. Only two months later did he send a copy to the Academy of Science, apparently as an afterthought.²² A graduate of the Royal Engineering School at Mézières, Prieur calls himself “ci-devant du Vernois” on the title page. For he had not quite consigned to oblivion the style that he, a favored nephew, had appropriated from an aunt married into the minor nobility, nor had he yet adopted the designation “de la Cote d’Or.” He was a twenty-seven-year old first lieutenant in 1790, a slightly lame young man, the impecunious son of a spendthrift father.²³

Despite the insecurities of his personal situation, Prieur betrayed little or nothing of the frustration experienced by fellow officers in the Corps of Engineers, intellectually in the case of Coulomb, professionally in that of Lazare Carnot.²⁴ He was a generation behind the one, and ten years younger than the other, and perhaps he did not feel thwarted. For he had proved less than assiduous in his duties, even by the relaxed standards of the Corps. He spent barely three months annually on post in the several garrisons to which he was assigned.

A native Burgundian, Prieur passed most of every year in Dijon. There he formed a life-long liaison with the grocer’s wife with whom he lodged and by whom he had a son. It happened that his father and Guyton de Morveau were cousins. Having abandoned the law for chemistry in the 1780s, Guyton was the leading figure scientifically in the Royal Academy of Sciences, Arts, and Letters of Dijon. The youthful Prieur assisted his eminent cousin in preparing the famous balloon ascent of 1784, the first to be tried outside Paris after the maiden Montgolfier flights of the previous autumn. He improved what he had learned of chemistry at Mézières by attending Guyton’s course of lectures. Prieur was himself elected to membership in the Academy, the forum for the vigorous cultural and scientific life that distinguished the Burgundian capital where, as in Bordeaux, in Lyons, in Toulouse, in Montpellier, in still other provincial centers, the literary, the scientific, and the social strains of thought commingled in preparing minds all ignorant of the immediate future for the events of 1789.²⁵

Prieur, outwardly a dilettante, inwardly a well-trained engineer, made his entrance into those events by writing his pamphlet on weights and mea sures. He did so, he acknowledged, at the suggestion of Monsieur de Morveau, who had provided valuable advice and information. In accordance with legislative usage, the title does the work of an abstract:

Memoir on the necessity and the means for rendering uniform throughout the kingdom all measures of extension and of weight; for establishing them on fixed and invariant bases; for regulating all multiples and subdivisions according to the decimal order; finally, for assimilating all moneys in circulation to the new order of things.

And as a consequence of this reform to simplify accounting and calculation, in the physical sciences as well as in finance and commerce.

Prieur nowhere pretends to originality. He has drawn the material to-gether from the writings of “true scientists” with a view to familiarizing the layman with the best thinking on the subject. Scientists, he says, had always wanted a universal system of weights and measures, but particularly so “since they have committed themselves to bringing the greatest precision into the physical sciences.”²⁶ Until now science has perforce made do with units drawn from commercial practice. The central thrust of Prieur’s pro-posal, and the basic wish of the scientific community, is to reverse that dependency, to the benefit of all parties.

Units of measurement are of five sorts. Those of the first class depend on conventions yielding values that are merely relative, such as the gradations on the scale of a thermometer, the degrees of a circle, and the number of carats indicating the hardness of jewels and the purety of gold. Those of the second type mark the passage of time in hours, minutes, and seconds. Beyond observing that decimal subdivision would be a convenience, Prieur has nothing to say about these intensive, angular, and temporal magnitudes, for the reason that they were already standard throughout Europe.

His main concern is with measurements of extension and of weight, the third and fourth types. It was there that confusion reigned. There, too, lay the clearest opportunity for reform, since linear and gravimetric units are indeed capable of absolute and not merely relative or arbitary definition. Prieur cites Bailly’s Histoire de l’astronomie moderne as his authority for the belief that the units of antiquity had been referred to the length of a degree taken along a meridian of the globe.²⁷ That possibility remained the first of two alternatives on which a natural system might be founded. Surveying the base would be difficult and expensive, however, and it was uncertain how accurately the job could be done. For these reasons, Prieur preferred the second option, the length of the seconds pendulum. It would be for the Academy of Science to decide where that value should be determined, but the most convenient spot would seem to be the Observatory of Paris. The location was known very exactly, and the temperature of the cellars always held steady at a constant 10.

The new linear standard would then be divided into thirds to give a unit very close to the pied du roi. The “national foot,” it could be called. No doubt foreigners would name it the French foot—no matter, “Scientists will make it a universal foot.” There is no need to fear, as La Condamine had done, lest the jealousy of other nations impede adoption: “Liberty, advancing day by day across our globe, makes all men cosmopolitan.” The foot would be divided decimally into inches, lines, and points. Gravimetric stan-dards would then be derived from linear units by defining the pound as the weight of ten cubic inches of water.²⁸

Prieur apologizes for, or rather justifies, the proposal to retain the word “foot.” He recognizes that ideally names should express things. Guyton, after all, was a principal author of the reform of chemical language. “Today,” acknowledged Prieur, “the most distinguished scientists are convinced that the improvement of the sciences is inseparable from that of their nomenclature.” ²⁹ But it was no less important to spare popular sensibilities so far as was consistent with the substance of needed change. For that reason he advocated writing decimals as 4^pi,89 rather than 4,89. People want to know what is being numbered. Prieur was equally circumspect with respect to money, there too without sacrificing decimal reform to duodecimal habit. In the old system, there were 20 sous to the pound and 12 deniers or pennies to the sou. The smallest coin in circulation was the liard, worth three sous. He would call the new sou the demi-dixième, half a tenth of the pound, and the two-sou piece the dixième. The liard would be replaced by a centième, trivially different in value at a hundredth rather than an eightieth of the pound.

The Prieur pamphlet may be taken as an index to what would have satisfied the general run of technically informed opinion. The essential mat-ter was uniformity, of equal importance commercially and scientifically, rather than a generalized reform. The basis, however, should be a natural magnitude determined by scientific procedures, and not a mere convention. Only so could verification and correction of standards be conducted inde-pendently of the play of special interests of any sort, whether national, re-gional, commercial, or vocational. Finally, multiples and fractions must be decimal. Facilitating calculation generally was incomparably more important than the shopkeeper’s preference for the base twelve because of its divisibility into halves, thirds, and quarters.

2. PROPOSALS

These considerations, or most of them, inform the proposal that the National Assembly initally enacted into law. It was presented, not by some drudge of a functionary, such as Tillet, nor by an unknown aspirant for notice, such as Prieur, but by one among the luminaries of that body, Charles-Maurice de Talleyrand-Périgord, bishop of Autun. The intervention of a noble prelate in the discussion over weights and measures was less incongruous than might appear. At this juncture in his protean career, Tal-leyrand was among the aristocrats, along with La Rochefoucauld, Noailles, Lafayette, Mirabeau, and for that matter Condorcet, who championed the early Revolution in a show of enlightened noblesse oblige. As we have seen, he was also the author, a year later, of the first comprehensive plan for a national system of education.³⁰

Throughout the 1780s, the leadership of the Academy of Science had normally enlisted aristocratic participation in its several ventures into re-forms affecting public policy. It has long been supposed, and was at the time, that Talleyrand had received coaching for his report on weights and measures. He acknowledges having consulted “as was my duty” practical men, “les personnes de l’Art.” He is aware, however, that their knowledge is insufficient, and he presumes that the National Assembly will not wish to proceed without first ascertaining the views of the Academy of Science, “to which so properly belongs the right of determining opinions in matters of this sort.”³¹

Who might his principal interlocutor have been? On the specific subject of the integration of gravimetric with volumetric and linear units, he cites Lavoisier’s procedure for determining the weight of a given quantity of dis-tilled water at standard temperature. More generally, in discussing the back-ground he notes that Turgot had intended unification of weights and measures: “You will accomplish today what this great man to his regret did not achieve.”³² Since it was Condorcet whom Turgot had commissioned to study the problem, it is reasonable to surmise that he, rather than Lavoisier, may have been the one at Talleyrand’s elbow. So, indeed, he proves to have been: recent research among Condorcet’s manuscripts has uncovered a fragment so close in phrasing to a lengthy passage in Talleyrand’s proposal that the sim-ilarity can scarcely admit of mere coincidence.³³ Talleyrand was too tactful to tax the patience of his fellow deputies by actually reading his proposal on the floor of the National Assembly. Instead, he had it printed prior to pre-senting it formally on 9 March 1790.

Opening with the contrast between the orderly glories of antiquity and the scandals of the present, Talleyrand overwhelms any petty concern for respecting usage and insists on the necessity of a clean break with the corruptions of the past. The revolutionary moment was to be seized. A fundamental reform based upon nature would be true to the general cause of submerging all relics of feudal diversity in national uniformity. The Assem-bly had already accomplished the task with respect to other sectors of gov-ernance such as taxation and legislation. Let the suppression of feudal rights and privileges clear the way for naturalizing weights and measures. (Though he does not mention it, Talleyrand clearly had in mind the law of 15 March 1790, which specified the dues to be eliminated in implementing the general abolition of feudalism decreed on the night of 4 August 1789.)

How, then, define the linear basis for a natural system of units? The first of two possibilities would be the sixty-thousandth part of the length of a degree of latitude measured along the meridian and bisected by the forty-fifth parallel. That distance, as determined by Lacaille in the 1740s, was 57,030 toises. The new unit would thus differ only slightly from the old. Talleyrand calls it the milliaire since one thousand would constitute the mille. That is as far as he goes with either nomenclature or decimalization. Three miles would make a league, so that there would be twenty leagues to the degree, while the milliaire would be divided into six feet.

Surveys were complicated to run, however, and they involved an irreduc-ible margin of error, which expert estimates placed at 34 toises per degree of latitude. (This figure was a gross exaggeration, and can scarcely have come from Condorcet or Lavoisier.) For those reasons, Talleyrand opted for the simpler alternative of the seconds pendulum. Its length, calculated to be 36 inches, 8.52 lines at the 45th parallel, was to be verified at that latitude. The most convenient site would be Bordeaux. This natural dimension would henceforth define the aune and be contained twice in the toise, which was to be subdivided in the conventional manner into feet, inches, and lines. The pound, also close to current values, would be defined, and this is where the Lavoisier determinations come in, as the weight of distilled water at the temperature of 14.4Réaumur filling a cubic vessel three inches on a side.

In effect, then, the Talleyrand proposal was modest enough. Stripped of the rhetoric of clean breaks, it limited the reform of weights and measures to unification and naturalization. Did he ignore Condorcet’s advice in thus eschewing decimalization and renaming? Was it with an eye to popular sen-sibilities that his system was radical only in principle, reducing in practice to the conventional? Or was it in order to bring in the British? Or for both those reasons? Ever the diplomatist, he attached great importance to the latter consideration.

Talleyrand made no doubt that England would join in. Her astronomers had already collaborated with Cassini in the 1787 survey linking the obser-vatories of Paris and Greenwich.³⁴ Commercial relations strengthened the common interest in a unification of weights and measures to be based on a joint determination of the seconds pendulum. The enterprise would be an example to all Europe: “Perhaps it is even permissible to see in this cooperation of two nations investigating nature together . . . the principle of a political union brought about through the intermediary of science.”³⁵

As for implementation, commissioners were already engaged in organizing the reformed system of local government throughout the country. It would be easy for them to inform the Academy of Science concerning the standards everywhere in use. The Academy would meanwhile appoint a commission with the task of determining the precise ratio of the new stan-dards to the myriad old units. Copies of the former would then be dis-tributed to the local authorities, along with instructions for making the conversion.

It was a foregone conclusion that Talleyrand’s would be the proposal pre-ferred by the Committee on Agriculture and Commerce. Occupied with grittier, more immediate matters, it never so much as considered any of the others. When the chairman of the ad hoc subcommittee, the marquis de Bonnay, brought in his report, adopted by the Constituent Assembly on 8 May 1790, the terms were an entire endorsement couched in language even more extravagant than Talleyrand’s.³⁶ To all appearances, then, the issue between standardizing customary units and determining scientific units from a natural magnitude was settled in favor of the latter solution, while the new metric system was to be based on the seconds pendulum.

So it proved with respect to the naturalistic principle. Not so with respect to the linear base. Ten months elapsed. On 19 March 1791 the Academy of Science sent the Assembly its own recommendation. Still in the role ofspokesman, Talleyrand read out the covering letter written by Condorcet as Permanent Secretary.³⁷ Condorcet was also the author of the report itself, which was enacted into law without change on 26 March. This was the central provision: “The quadrant of the terrestrial meridian . . . will be taken as the real unit of measurement, and its ten-millionth segment will serve as the practical unit.”³⁸

Such was the change of mind, not indeed unauthorized by the decree of 8 May 1790, but certainly unanticipated, which has exposed the Academy to charges of bad faith, both then at the hands of disgruntled persons whose own projects were passed over, and since by critics who take a certain pleasure in catching science out playing politics on feet of clay.³⁹ Together with Condorcet, the members of the Commission that drew the report were Borda, Lagrange, Laplace, and Monge, an experienced navigator and sea-captain and three eminent mathematicians. They must certainly have under-stood (it is said) that any standard unit is a convention, that what matters is definition and agreement, and that there is no such thing as a naturalistic metrology.

This general point is simply incorrect. It was the hallmark of the Enlight-enment, and theirs was its last generation, that reasonable people really did believe that true standards of all sorts, moral as well as physical, are to be found in nature. The business of science is to obtain knowledge of how things fit. That scientists and mathematicians were not so naive as to sup-pose that perfect knowledge is attainable, or that the meridian, or the sec-onds pendulum, or anything else, is capable of a perfect determination, does not make them crypto-positivists. Truths are to be approximated and error reduced so far as technically possible. Sir John Riggs Miller, the foremost advocate of metrical reform across the Channel, can have had no interest in deceiving the French National Assembly. Yet his reasoning is exactly that of the academicians in Paris:

The qualities of a Standard are of two kinds, viz., those which are essential, and those which are only eligible. The essential qualities, which every Standard should possess, are, that it should be taken from Nature, or connected with something in Nature, and not from any work of art, which must necessarily decay, nor from anything that is merely arbitrary, and which has no other right to be a standard, than that it is kept in a house, which is called the Exchequer or Guildhall and which has certain marks upon it, and a certain name given to it.⁴⁰

Still, the pendulum would have satisfied those requirements, and the question remains, why another survey of the meridian? The concealed mo-tivations for this otherwise gratuitous enterprise, so say the skeptics, were, first, the desirability of improving the geodetic data relevant to calculating the shape of the earth, a favorite problem in celestial mechanics since the launching of the expeditions to Lapland and Peru in the 1730s; and, second, the opportunity to make trial on a global scale of the surveying instrument, the repeating circle, invented by Borda and used with great success by the French team in the 1787 Paris-Greenwich triangulation.⁴¹

That the former was the main reason was stated by Laplace’s disciple, Jean-Baptiste Biot, writing in 1803.⁴² In 1790 Biot was a sixteen-year-old pupil reading the classics at the Collège Louis-le-Grand and can hardly have been party to the deliberations of the commission. He gravitated into La-place’s orbit after graduating from the Ecole Polytechnique in 1797. It is plausible to suppose that what he had been told then or surmised later was correct, and that the prospect for improved data regarding the shape of the earth had indeed been a factor in the preference for a geodetic survey. The matter was extremely technical. In a memoir of 1785, Laplace had obtained expressions (since called Laplace’s functions) which permitted comparing the value for the force of gravity measured by means of the pendulum with that calculated from the inverse square law of attraction. The comparison could be made at any point where geodetic measurements along the meridian permitted determination of the radius.⁴³

As for Borda’s repeating circle, it is true that Jean-Baptiste Delambre, the astronomer upon whom fell the lion’s share of the labor, later mentioned having suspected that one of the reasons for preferring the quadrant had been a desire to enhance the reputation of that novel and very clever device.⁴⁴ Only a single such instrument existed in 1790–91, the one used in 1787. At least one other, and preferably several, would have to be commissioned for the metric survey.⁴⁵ Delambre never suggests or even implies, however, that instrumentation was the compelling, and certainly not the only, consideration motivating the academic inner circle to measure the great circle of the earth rather than to calibrate a pendulum oscillating at the seashore near Bordeaux. Not that the latter project was abandoned—in tacit accordance with Laplacean theory, the project called for verifying the two sorts of deter-mination, one against the other.

In short, the charge of duplicity is probably unfair. Those who actually ran the survey, Delambre and Méchain, had little to gain, having already proved themselves, and much to lose—time, domestic peace and quiet, quite possibly their lives. Also, even if the sponsors left certain, highly tech-nical considerations unstated, it does not follow that the reasons of a more general sort that they did advance, which were suited to the comprehension of the legislators who composed the Constituent Assembly, were either facti-tious or insincere. Honorable people may well believe what they say, after all, while not finding it politic to say all they believe.

It does, on the other hand, have to be admitted that the language of Condorcet’s report is unconvincing in hindsight and must have been unclear at the time. He rehearses (less cogently than Riggs Miller) the importance of excluding everything arbitrary from the determination of a natural unit. The objection to the seconds-pendulum is that its determination depends on a parameter in time, which is both arbitrary and extraneous: arbitrary because the second is simply the 86,400th part of a day; extraneous because even if it were agreed to resort to the hypothetical pendulum with a frequency of one oscillation per day (the day being the smallest natural unit of time), and then to divide that length by ten million for the basic unit, even so the linear determination would depend on the force of gravity at the surface of the earth.

Now, if it were possible to have a linear unit which depends on no other quantity, it would seem natural to prefer it. Moreover, a mensural unit taken from the earth itself offers another advantage, that of being perfectly analogous to all the real measurements which in ordinary usage are also made upon the earth, such for example as the distance between two places or the area of some tract. It is far more natural in practice to refer geographical distances to a quadrant of a great circle on the earth than to the length of a pendulum. . . .⁴⁶

As usual when the question partook of technicality, Laplace expressed himself more clearly than did Condorcet. In April 1795, at which time the metric survey had been resumed after being interrupted, as we shall see, under the Terror, he put the point very simply in a lecture before the École Normale:

The length of the pendulum and that of the meridian are the two principal means offered by Nature for fixing the unity of linear measures. Both being independent of moral revolutions, they can undergo no detectable alteration short of enormous changes in the physical constitution of the earth. The first method is easily applicable, but has the disadvantage of making the measurement of distance depend on two elements that are heterogeneous to it, gravity and time, the division of [the latter of] which, moreover, is arbitrary. It was decided, therefore, to adopt the second method, which appears to have been employed in early antiquity, so natural is it for man to relate the units of distance by which he travels to the dimensions of the globe that he inhabits. In moving about this globe, he may thus know by the simple denomination of the distance the proportion it bears to the entire circumference of the earth. This has the further advantage of making nautical and celestial measurements correspond. The navigator often needs to deter-mine, one from the other, the distance he has traversed and [the length of] the celestial arc lying between the zenith at his point of departure and that at his destination. It is important, therefore, that one of these magnitudes should be the expression of the other, with no difference except in the units. But to that end, the fundamental linear unit must be an aliquot part of the terrestrial meridian, which corresponds to one of the divisions of the circumference. Thus, the choice of the meter came down to that of the unity of angles.⁴⁷

Laplace can have had no interest in deceiving the students assembled on the benches of that portentous if abortive institution. That the reasoning had been shared among his colleagues is confirmed by a manuscript of Lagrange, still less open to the imputation of special pleading since it remains unpublished: “We judged that the length of the meridian was preferable [to the pendulum] with respect to itinerary distances and to maritime measures, because it will give immediately and without any reduction the route trav-elled as parts of the meridian, and consequently the difference in latitude of departure and arrival.”⁴⁸

In the previous November, as we know from a letter of Condorcet to the President of the National Assembly, the Academy was still planning to base the system on the pendulum.⁴⁹ The commission that recommended the change, those named above, was appointed on 16 February 1791. It was one of several ad hoc committees of the Academy that considered the elements of metrical reform throughout the year following the decree of 8 May 1790, and its shift from the pendulum to the meridian was only one, albeit the most important one, among the modifications and implementations enacted by the National Assembly.⁵⁰

The decree of 8 May 1790 was, indeed, an enabling law, never taken to be the last word. For one thing, it contained no provision for decimalization. For another, probably related, its terms presupposed British participation. That never happened, despite the efforts of Riggs Miller, whether because of recalcitrance on one side of the Channel or chauvinism on the other. Only on 22 August did the 8 May law receive royal assent. Its main significance in practice was to shift responsibility for bringing in a reform from the Committee on Agriculture and Commerce to the Academy of Science. On 25 June the Committee accepted the motion of the marquis de Bonnay to forward the entire file to the Academy.⁵¹ Apparently Prieur’s memoir had languished in a folder, as did some twenty others, for five months until it was singled out for examination by a commission composed of Laplace, Borda, Coulomb, Tillet, and chaired by Lavoisier, who began a reading before the Academy of Science on 13 July 1790.⁵²

Lavoisier, again, took the lead in making arrangements with local authori-ties for submitting their standards to Paris for verification.⁵³ The administrators of the Department of La Nièvre, for example, objected (as did their colleagues elsewhere) that it would be impossible to collect and send all the weights and measures currently in service. Lavoisier agreed. The Academy, he replied, recognized the impracticality of a literal interpretation of the 8 May decree and would seek permission to collect one standard of each type.⁵⁴ On Condorcet’s request, the National Assembly enacted the recommendation into law on 8 December 1790.⁵⁵ In that connection, Mercklein fils de-vised and won approval of an instrument for precise calibration of linear measures.⁵⁶ Despite his opposition in principle, Tillet, still an official of the mint at Troyes, took an active and apparently constructive part throughout the deliberations, particularly with respect to the integration of monetary reform with metric reform.

Among the provisions of the decree of 8 May was a request for the opinion of the Academy on the regulation of coinage and on the most appropri-ate scale of division for money, and also for weights and other measures. The commission appointed to draw up a response consisted of Borda, Lagrange, Lavoisier, Tillet, and Condorcet. Lavoisier knew finance. Tillet and Condorcet knew the Mint.

The questions concerning coinage (no doubt planted in advance) were whether the proportion of precious to base metal in the alloy should be held constant, so that coins would differ only in their weight, and whether the tolerance in composition (le remède) should always be in excess rather than sometimes in defect of the reputed fineness. Submitting its report on 27 October 1790, the Commission came down, predictably enough, on the side of sound money and consistency.⁵⁷ Explaining the technical reasons for the very slight uncertainty of composition of the alloys—between two to three parts in 576 for silver coins and one to two parts in 768 for gold—the commissioners suggested in a footnote that the use of pure metals would simplify matters. The supposition that the alloys, being harder, are more durable had never actually been tested, and the Academy initiated a series of experiments to decide the question.⁵⁸ Preliminary results indicated that metallic discs of pure gold or silver resisted friction better than alloys when rubbed together but less well when jingled against coins currently in use.

Turning to subdivision, the immediate problem was the monetary system of the old regime that, like its British offshoot of pounds, shillings, and pence, derived from Carolingian times. There were 20 sous in the livre and 12 deniers in the sou. Higher denominations were the silver écu and the gold louis d’or, worth 6 and 24 livres, respectively. The term franc—if we may look ahead for a moment—was coming into use before it officially replaced the livre by the law of 18 germinal an III (7 April 1795). A further measure of 15 August 1795 fixed the value at 5 grams of silver. Anticipating these changes, the Convention on 7 December 1793 had already decreed the sub-division of the livre into décimes and centimes. Thus, the earliest, indeed much the earliest, application of the principles of the metric system was to money, and—to return now to the monetary commission of 1790—that was the connection in which the Academy first made the case for decimal-ization in general.

Its report calls for adoption of the “arithmetical” (or decimal) scale for subdivision of all units, whether of money, length, surface, volume, weight, or capacity. The simplification of procedures would be enormous. As it was, the man who could reckon his sous and deniers was not thereby able to figure in toises, pieds, pouces, and lignes, let alone in livres, onces, gros, and grains. Anybody used to calculating in any of these systems would easily learn to use decimals, while the converse was certainly not true. Certain experts had urged the duodecimal scale, since the base would be evenly divisible into thirds and quarters as well as halves. But the disadvantages were formidable. Two extra digits would have to be denominated. People unaccustomed to calculation, in other words the whole population, would have to be trained to think in steps of twelve instead of ten when combining numbers. Anyway, division by four was no serious impediment to use of decimals. Shoppers buying a quarter of a pound would easily grow accus-tomed to receiving two ounces five gros. The indivisibility of ten into thirds remained awkward. Still, the inconvenience would be trivial compared to the massive confusion into which a novel arithmetical scale would plunge the public.

The National Assembly did not act separately on this report, which was sent to it on 27 October 1790. Instead, decimalization became incorporated, not to say smuggled, into the metric reform as a corollary of the law of 26 March 1791 basing the system on the measurement of the meridian. The report points out in the opening passages that defining unit length as the ten millionth part of the quadrant necessarily entails abandoning the traditional partition of the arc into degrees, minutes, and seconds. The justification is that sexagesimal division could not be retained “without vitiating the unity of the system of measurement, since decimal division, which corre-sponds to the arithmetical scale, is to be preferred for all purposes.”

The reasoning would appear to be a classic, and perhaps unconscious, example of answering a question by begging it, or reaching a solution by assuming it, for no authority higher than the Academy had prescribed the preferability of decimals. Nothing in the system is arbitrary, the commis-sioners insist, except the choices, first, of the arithmetical scale, and second, of water as the substance of which the specific gravity would define unit weight. The latter is dictated by physical convenience, and the former “by the fear lest any change there, added to all the others, would jeopardize the success of the entire operation.”⁵⁹

A new survey, the report acknowledged, would cover the same ground that the abbé Lacaille had traversed half a century before in measuring the meridian from Dunkerque to Perpignan.⁶⁰ So much the better. Redoing his triangles (nearly 800 in all) would either confirm or improve the accuracy, while extending them the relatively short distance across the Pyrenees and down to Barcelona would anchor both ends at sea level. Meanwhile, new and precise determination of the length of the seconds pendulum would yield a standard for comparison permitting ready verification of the new and still unnamed unit. The merits of both alternative bases for a natural stan-dard would thus be combined in one. Finally, the report alludes to, though without emphasizing, the most material of the considerations behind the preference for the meridian. Reverting to and perfecting the Lacaille trian-gulation would make of the new scale a grid to be laid conformably over the map of France.

Completed, except for Brittany, the Cassini Map of France had, in effect, been fleshed out on the skeleton, or rather the spinal cord, of the Lacaille survey. That great compilation had already stood the Revolution in good stead politically and administratively. The cartographers who in 1790 partitioned the country into 83 departments, and the departments into cantons and districts, worked their task on the surface of its 170-odd sheets. Now it might serve in the finer, more intricate, and more contentious detail of land registry and tax assessment.

There had never been a Domesday book in France. No national registry recorded the boundaries, the type of exploitation, and the revenue of land-holdings, and no basis existed for equitable assessment of land taxes. A cadastre, as such an instrument was called, had been assembled in certain pays d’état, in Dauphiny in the fourteenth century, in Provence in the fif-teenth, and in Languedoc in the fifteenth and sixteenth centuries. These documents were merely descriptive, however, tabular rather than graphic in form, and provincial in scope. Throughout the country, the incidence of taxes on real property varied enormously from region to region, and from one locality to another, often nearby. As in other aspects of the relevance of science for administrative reform, Turgot had anticipated revolutionary de-velopments in basing a cadastre for the Limousin, where he was intendant in the 1760s, on a proper set of surveys. Demands for nation-wide rational-ization appeared in many cahiers de doléances in 1789.

The initial call in the Constituent Assembly for creation of a thorough and uniform cadastre came from Pierre-François Aubry Dubochet during a debate on taxation generally in September 1790. Something of a specialist in government finance, he was a member both of the Committees of Finance and of the Constitution. He had spent the previous six months with a team of technicians verifying the detail of the new departmental and district sub-divisions on the map of the Academy, as the Cassini map was generally called. Its excellence was everywhere recognized, although in Aubry’s plan new sheets at double the scale would have to be drawn for a cadastre.⁶¹ His ideas were systematic and in no way original. Informed opinion simply as-sumed that a set of proper maps was a precondition to equitable assessment of land tax in a post-manorial countryside. Aubry supposed that a provi-sional cadastre could be set up within a year, but that institutionalizing such a bureau, equivalent to a ministry of state, would require seven years.

Meanwhile the Treasury needed money. Pending a thorough-going re-form, the Constituent Assembly on 1 December 1790 voted a general tax to be levied on all real property, rural and urban, in proportion to the net revenue produced. The law required owners to declare the extent and value of their holdings. Assessments were thereupon to be set by municipal offi-cials out of their sense of fairness (“en leur âme et conscience”).⁶² At the same time, every declaration was to be open to inspection by any taxpayer in the community. Like the procedures of the old regime, the measure thus depended on the participation of taxpayers controlled by the jealous scrutiny of neighbors. It was meant to be a stopgap.

Legislation establishing the Bureau du Cadastre was ready for passage on 16 September 1791.⁶³ Named Director on 5 October was the brightest among the rising lights in the Corps des Ponts et Chaussées, Gaspard Riche de Prony. He had, evidently, been conferring regularly throughout months of preparation with officials of the Ministry of Finance (Contributions Publi-ques), with his own colleagues among civil engineers, and with the Academy’s Commission of Weights and Measures. A memoir of 10 October gives a comprehensive and detailed plan fully developed at the very outset.⁶⁴

A thorough cadastre would be an exact instrument of national self-knowledge, demographic, topographic, fiscal, and economic. It would comprise precise information on the population, on the productivity, and on the boundaries of all territorial divisions from the departmental level right down to every piece of property in every commune. As to demography, the place to begin would be the remarkable series of memoirs on the population of France published by the Academy of Sciences at the end of the old regime.⁶⁵ The estimates would have to be transposed to accord with the new subdivision of the country. With regard to natural resources, regional productions, agricultural particulars, and transportation, getting a handle on the immense mass of existing information was more urgent than accumulating more facts.⁶⁶

Since the Cassini map was to be the framework of the whole enterprise, the most fundamental task would be to verify the location of the church steeples and other vantage points which had served as posts of observation. The detail, moreover, was insufficient. The areas triangulated were too large for a cadastre and the scale too small for showing property lines. Local surveys would be needed covering every canton. Piecing them together, the central office would insert a fine-grained network of secondary triangles into the master plan of a corrected Cassini map. All baselines would be measured with full astronomical accuracy. Finally, the cadastre would necessarily be correlated with the metric system, since the new measurement of the merid-ian would perfect the entire chain of primary triangles. Meanwhile, the data, the instruments, the surveyors, everything and everyone still depended on the old units, and Prony began thinking hard about the problems of conver-sion. The thorniest turned on the standard tables of trigonometric functions that had been calculated from the sexagesimal division of the circle.

Prony engaged personnel, installed an office, and early in 1792 prepared a provisional Instruction laying out the above task in general. He submitted it in the first instance to the Minister of Finance, Etienne Clavière, who, as was normal procedure, requested the opinion of the Academy of Science. It named a commission consisting of Laplace as chairman together with Borda, Lagrange, and Monge. This was the point at which Laplace took over scien-tific leadership with respect to the metric system, a role that he resumed after the interruption of the Terror, and maintained in later years. His commission held several meetings with deputies in the Legislative Assembly, which had named an expert on taxation, Jean-Baptiste Jolivet, to report on the cadastre.

A preliminary recommendation was ready on 12 May 1792. Since compre-hensive verification of Cassini’s points of reference would require the utmost accuracy and take a long time, the commission confined itself to the most urgent matters within its competence. These were the geodetic and trigo-nometric procedures to be employed in local surveys, which were already being demanded in adjudication of tax claims. Laplace and his colleagues approved Prony’s intention to make use of a new instrument, which combined the advantages of a theodolite with those of Borda’s circle by permit-ting reduction of angles to the plane of the horizon and repetition of measurements at all points of the circumference. The commission further noted Prony’s intention to measure bases by means of chains similar to the ones used on Hounslow Heath and Romney Marsh in 1787, though less expen-sive. They would be six toises in length, and divided decimally in order that measurements might be mapped on a scale of 1:20,000. But, objected the commission, since these plans would long outlast the reform of weights and measures, “what is to prevent fabricating them as of now on the scale to which they will soon have to be reduced?” The distance between the lati-tudes of Perpignan and Dunkirk was sufficiently well known so that the forty millionth part of the circumference of the earth along the meridian could serve as the unit with all the accuracy needed for these local surveys. And the Commission asks that Prony be so advised and the Instruction modified accordingly.⁶⁷

If the new unit were to be used, however, it would have to have a name, and that is the main subject of the full recommendation. Laplace presented it on 11 July 1792. The Academy, runs his draft, strongly desired that the units of measurement employed in the great operation of the cadastre should be drawn from the universal standard. For that purpose, and in order that they might pass into general use, the Academy was seizing the occasion to define and name them. The Academy has therefore resolved that the linear standard shall be called the mètre. In the reckoning of long distances, the millaire, a thousand meters, would replace the league. Since intervening multiples of ten and one hundred served no useful purpose, they need not have names. The subdivisions were another matter, for they would be in constant use. The Commission recognized that there was an argument for coining easy, one syllable words. Such terms could only be arbitrary, how-ever, whereas general principles of scientific nomenclature called for expressing the thing in the name. Accordingly, the Commission chose decimeter, centimeter, and millimeter. Similarly, an area 100 meters square would be an are, subdivided into deciaires and centiares. “We settled finally for this latter approach as the simplest, and because by our adopting it for measures of area, volume, capacity, weight, and money, the entire system of denominations would be uniform for all measures and composed of the least possible number of arbitrary words.” It was to be hoped, for these same reasons, that other peoples might equally accept the terminology, with whatever trivial variations differences of language should require.⁶⁸

The example of the new chemical nomenclature showed how readily words catch on with use. In the same way, the operations for the cadastre, involving a large number of intelligent people, will soon spread the new system throughout the country and greatly facilitate its applicability to di-mensions other than those of line and surface. For that reason, the Commis-sion concludes, it had decided to postpone further denominations until the ground should be thus prepared.

That decimalizaton should have been introduced in connection with the currency, and nomenclature with the cadastre, is evidence that the dimen-sions of the metric system were to be coextensive with the whole polity. The prospect of a set of simple standards, drawn from and referrable to nature, and adapted to transactions of every sort, not only buying and selling in the market, nor merely weighing and measuring in the laboratory, but also those involving finance, taxation, navigation, cartography, land registry, and de-mography—that vista unfolded before successive commissions of scientists dealing with the several aspects throughout the two years of discussion that ensued between preparation of the Talleyrand plan in the summer of 1790 and the Laplace report in the summer of 1792. In such a comprehensive scheme, citizen calculators would move from the angular observations of astronomy to linear measurements of the earth’s surface by a simple inter-change of units involving no numerical conversions; from these to units of area and capacity by squaring and cubing; thence to units of weight by means of the principle of specific gravity; and finally from amount to price by virtue of the value of gold and silver in alloys held invariant in composition through a rigorous fiscal policy.

The goal of a unified metric in a science bent on maximizing the fit with nature while minimizing the arbitrary in all things may, perhaps, be likened to the dream of a unified communications network in a science bent on information for all and all for information. It may have been visionary, naturalistic rather than realistic. Indeed, it was.

But not discreditable.

3. METHODS AND INSTRUMENTS

Effecting the reform of weights and measures had in common with other enlightened programs initiated in the revolution, whether social, political, constitutional, economic, educational, moral, or technical in nature, that nothing went smoothly, that circumstances forced compromise, that suspi-cion bred violence, that habits changed more slowly than principles, but that, nevertheless, the outcome taken all in all fitted into the foundations of the way we live now.

Upon passage of the definitive law of 26 March 1791, the Academy re-ceived a grant of 300,000 livres to carry out the metric project. On 13 April it named five subcommittees on weights and measures, assigning to each a set of the tasks to be accomplished.⁶⁹ The first, and by far the most important, was to survey the length of the meridian from Dunkirk to Barcelona. Initially appointed were Cassini, Méchain, and Legendre, the team that had joined Calais to Dover in the triangulation linking the observatories of Paris and Greenwich in 1787⁷⁰ Legendre, the complete mathematician, had no wish to go into the field again, and withdrew on 17 March 1792.⁷¹ Cassini, out of tune with revolutionary politics, also begged off and was replaced by Jean-Baptiste Delambre on 5 May 1792.⁷² Once the operation was under way Delambre and Méchain shared the danger equally, but it was Delambre, coming on stage only toward the end of the prologue, who turned out to be the protagonist in the whole metric drama.

Delambre was in his forty-fourth year, and newly elected to the Academy of Science, when he replaced Cassini on the Commission of Weights and Measures. His career until then might seem that of an astronomical journey-man. Thus, Herschel discovered the planet Uranus in 1781, while Delambre computed the elements of its motion in competition for a prize set by the Academy in 1790. Similarly, he followed in the wake of Laplace’s theoretical resolution of the planetary inequalities of Jupiter and Saturn, and of his theory for the satellites of Jupiter, by constructing the tables of motion for those heavenly bodies, and also for the sun. There is a whole sociology of science implicit in Delambre’s appreciation of his colleague, Méchain, à propos of what they both took for granted—that only people of means could enjoy an observatory: “Observation is a recreation for the astronomer, in spite of its fatigues. Computations are far longer and above all more boring. They require a different vocation, a type of courage not very charac-teristic of men who have some fortune.”⁷³

The opportunity for such recreation was afforded Delambre by generous patrons, the d’Assy family, whose son he tutored and who installed an obser-vatory for him (it still exists) in their Paris townhouse, rue du Paradis. The son of a clothier in Amiens, he had excelled in Greek and Latin in the local college. Delambre’s teacher, the abbé Delile, recognized his quality and en-couraged the boy to pursue classical studies at the Collège du Plessis in Paris. Lalande’s course on astronomy at the Collège de France thereupon opened the avenue along which the young Delambre escaped the lot of a clerical schoolmaster. His education stood him in good stead. The history of astronomy in six volumes that he composed in later years is the work of an accomplished Hellenist and Latinist no less than an astronomer, a scholar intent on getting things right.⁷⁴ His Base du système metrique, appearing in three large volumes between 1806 and 1810, contains his narrative of the survey together with the record of the observations from his registers. Anyone who wishes to verify the computations, or to recalculate the original meter, will find the data there.⁷⁵

Five years older than Delambre, Méchain also came from modest circum-stances, his father having been a master plasterer. He too had had a minor career prior to the metric survey. Another protégé of Lalande, and one who drew closer to their patron than Delambre ever did, Méchain came to as-tronomy by way of mapmaking in the naval bureau of hydrography. The dramatic return of Halley’s Comet on schedule in 1759 had set astronomers to wondering whether other comets might exhibit an equally interesting periodicity. Two in particular, observed in 1532 and in 1661, seemed to differ sufficiently little in their elements that they might be one and the same. In 1780 Lagrange proposed a new method for calculating perturbations, and the Academy set a prize for an analysis of the two paths in question. Méchain won the contest with a proof that the comets of 1532 and 1661 were not identical, and that no return could be expected in 1790. The event, or rather its absence, proved him right. In the meantime, he had served under Cassini and Legendre as the junior member of the team of 1787, assigned to use a quadrant for the angles that they measured with the Borda circle. The purpose was to test the superiority of the latter.⁷⁶ Beginning in 1785, Méchain edited Connaissance des temps and lodged with his wife and three children in very cramped quarters at the observatory.

The assignments of the remaining four subcommittees were auxiliary and less arduous than the prospect for Delambre and Méchain. No great urgency was felt, there being no need to complete these supporting measurements before the survey of the meridian should be well advanced. Monge and Meusnier were to measure the two bases to which the triangulation would be referred, and of that more in a moment. Borda and Cassini, who replaced the aging Coulomb, were to verify the length of the seconds pendulum. They ran those experiments at the observatory between 15 June and 4 August 1792. The technique consisted of comparing the oscillation of a bob suspended on a twelve-foot wire with those of a pendulum clock accurately beating seconds. Equipped with a spotting scope, Borda observed and timed the coincidences of the bob and the clock pendulum at the low point. Since the frequency of the bob was slightly less than half that of the clock, the coincidences were widely enough spaced so that the times could be recorded accurately. The length of a simple seconds pendulum could then be readily deduced from the duration of the interval between coincidences. It came to 440.5593 lignes, or 3 feet, 8.5593 lignes.⁷⁷ Lavoisier and Haüy refined determinations of the weight of a unit volume of water at fixed temperature, reporting their results in January 1793.⁷⁸ Finally, Tillet, Brisson, and Vandermonde were to carry through a comprehensive comparison of provincial measures to standard units of Paris, as called for by the legislation. Tillet died in December 1791, Vandermonde in 1796, and no systematic inventory was ever made.

Nothing could begin in the field before Etienne Lenoir had constructed the instruments both for triangulation and for determination of the linear bases. The repeating circle of 1787 was divided sexagesimally and was, in any case, in a bad state of repair. The Academy ordered four new circles, to be graduated in 4,000 angular units, 1,000 to the quadrant as compared to the 5,400 minutes of the old instrument.⁷⁹ In addition, Borda designed rules of an altogether new type for measurement of the bases.

Like the circles, these instruments were very beautiful. The greatest source of inaccuracy in previous surveys was the expansion or contraction of measuring rods with rise or fall in temperature. One that was a certain length in the cool of a summer morning would be longer by noon and shorter in the winter. It was for this reason that General Roy had preferred glass rods on Hounslow Heath in 1787. Borda’s solution exhibited, as did the principle of his repeating circle, the elegance of accepting a problem rather than the ingenuity of circumventing its effects. His rules were to be made of plat-inum, the least expansible of metals. Each was twelve feet long by six lines (half an inch) wide by one line thick. (It would have begged the question to define them metrically.) He enclosed the platinum strip, almost as flexible as a piece of wire, in a snug sleeve of copper six inches shorter. The platinum core and the copper casing were attached at one end. The other end of each was free to move according to the coefficient of expansion of the metal.

As the day grew warmer, the surveyor could read the extent to which the copper crept along the platinum off a scale on the platinum strip that, together with a vernier on the copper sleeve, made the device in effect a thermometer, indicating the temperature at any moment by the excess of the dilation of the copper over the platinum. He could then reduce the differential expansion of the two to the absolute expansion of the platinum. The measuring rods would thus be self-correcting for variations in temperature. Each was equipped with a coupling to attach it to the next so that they might be laid precisely end to end. Lenoir constructed four such rules, two for each of the bases to be measured, together with a fifth of simpler design for the determination of the seconds pendulum. He also built an elaborate measuring table on which to establish the zero of each rule, the coefficients of expansion of the metals, and the correction to be applied to the verniers and couplings.⁸⁰

The construction required over two years. Lavoisier then joined with Borda and Lenoir himself in calibrating these fine instruments. On leaving the Arsenal he had taken a house at 243 boulevard de la Madeleine. Lenoir installed his equipment in the garden.⁸¹ There they labored on a task requiring the utmost precision throughout the last week of May and the first week of June 1793. Midway through their labors, the streets around them filled with the crowd that forced the Convention to expel its Girondist mem-bers on 1 June. This was the last scientific determination Lavoisier ever undertook.

By then Monge and Meusnier were no longer available to make the measurements assigned to them at the outset. Monge had long since been drawn into politics and briefly into government. He was Minister of the Navy for eight months, from the overthrow of the monarchy on 10 August 1792 until

10 April 1793, while Meusnier, called to active duty with the Corps of Engi-neers, died on 17 June 1793 of wounds sustained during the Prussian siege of Mainz. Determination of the bases eventually devolved on Delambre along with the major part of the triangulation.

Not everyone, perhaps, is familiar with the elements of surveying, and a brief reminder of the trigonometric principles presupposed by such operations as those of Delambre and Méchain may be in order. AZ represents the distance to be determined along a segment of the meridian. The surveyor’s first step would be a reconnaissance in order to find elevated vantage points, B, C, D, E, etc., on either side of AZ from which to measure the angles of the triangles ABC, BCD, CDE, etc. Each of the stations at the corner of each triangle had to be visible from the other two. In most locations, of course, the choice fell on a church steeple. Otherwise a turret or roof corner on some other structure would be picked, for terrain features were seldom well enough defined.

Setting out with his instruments, the surveyor would measure the angles of the triangle ABC. He would then check his accuracy by verifying that the triangle closes, which is to say that the sum of the interior angles is 180°. Before moving on to the next triangle, BCD, he would determine the azi-muth, or direction with respect to the meridian, of one side of ABC. He would also determine the latitude of A, the beginning of the chain. When all triangles were completed, he would have to anchor the entire network to a measured distance by actually taping the length of a base on the ground.

In principle one side of any triangle in the chain might serve. In practice difficulties of terrain normally dictated running an auxiliary triangle of which one side would lie in relatively level, open ground. Finally, knowing the length of the base, and all the angles in the chain, the surveyor could calculate the distances Aa, aa, ab, bc, etc. along the meridian. In the case of a large survey, two bases would be measured, one near either end. The length of each would then be calculated from the other, and the closeness of agreement would indicate the degree of accuracy of the whole operation. Verifying latitudes and azimuths at intervals along the line provided a series of interim controls. Given suitable terrain, trigonometry, patience, endur-ance, accuracy, adequate funds, and instruments, a surveying team might multiply triangles as far as desired.⁸²

That is a mere schematization. In practice none of these measurements was a simple matter of looking at two steeples through a telescope and reading the angle between them off a scale. Delambre’s account of the actual manipulation of Borda’s intricate, finely tooled, and very ingenious instrument occupies eighty closely written quarto pages of the Base du système métrique.⁸³ He there covers only the instructions an astronomer would need for using the repeating circle. An artisan would require a whole volume of drawings and specifications in order to make one.

As for us, it is scarcely possible to appreciate the seriousness of the metric survey without a sense of the steps required to establish each type of deter-mination among the thousands it entailed. In sextants and quadrants of a traditional sort, the instrument maker could improve precision only at the expense of portability. The splendid theodolite constructed by William Ramsden for the junction of the Greenwich and Paris observatories in 1787 weighed 200 pounds. Not so the Borda circle, a foot in diameter, 18 inches high, 15 pounds in weight, which achieved accuracy by permitting multiple but independent observations of the same angle.

Two traversing telescopes were mounted on the shaft, one centered above a graduated limb or circle and the other attached excentrically beneath it. Either or both might share the rotation of the circle. Suppose that BAC (fig. 1) represents the angle between the directions of Watten (B) and Cassel (C) that Delambre is measuring from the tower at Dunkirk (A). Setting the upper scope at zero on the circle, he takes a sighting on the steeple (B) to his right, at Watten. With the upper scope fixed at that point on the circle, he shifts his eye to the lower scope and sets it on the turret at Cassel (C) to his left. But contrary to what might be expected, he takes no reading. In-stead, he turns the circle carrying both scopes clockwise until he has (B) at Watten in the lower scope. The whole head has thus traversed the angle to be measured. Only the positions of the upper scope may be read off the scale, however. His last step, therefore, is to free the upper scope, and turn it counter-clockwise past (B) at Watten to (C) at Cassel, swinging it back through twice the angle. The reading would thus be double the value to be determined. He then repeats the same steps to measure quadruple the angle, sextuple the angle, and so on around the circle as many times as he desires, diminishing observational error progressively with every multiple.

Readings made with a conventional quadrant or sextant could be repeated only after returning the setting to zero. That might verify but did not im-prove an observation. Moreover, measuring angles wider than 60°or 90°, respectively, required moving the instrument. Doing so displaced its center with respect to the center of the observation post, whereas the center of the Borda circle remained fixed. The Borda circle suffered from only one important disadvantage. Repetition of angles was of no avail in perfecting direct astronomical readings of azimuths. For that purpose Delambre would have preferred a quadrant of much larger radius, the more so that only at five locations did he and Mechain need to measure the azimuth of one side of a triangle, at Dunkirk and Montjouy, the northern and southern termini of the survey, and, for verification, at three points in between, Paris, Evaux, and Carcassonne.⁸⁴

The inclination of the plane of every triangle in the chain had to be determined by observations at each station, however. In that operation, too, the Borda circle was preferable. The head could be tilted 90°for measurement of vertical angles. A bubble-level that does not show in the illustration sufficed to establish the horizontal for these observations, though Delambre insisted on a plumb bob when shooting the North Star and other circumpo-lar stars in the critical determinations of latitude that accompanied the azimuthal measurements at the same five locations.

So much in brief for the instrument. That was only the beginning. The raw data had to be corrected by measurements and calculations of three sorts. The first, as just indicated, involved variation in altitude. For this purpose, a series of ten readings at each position normally sufficed. After determining the angle that every side of every triangle made with the verti-cal (“the distance to the zenith”), Delambre reduced his values for the inter-nal angles of each triangle to those of the corresponding figure in the plane of the horizon. A by-product of the metric survey was thus a series of values for the altitude of all stations in the chain of triangles. Méchain could observe the horizon of the Mediterranean directly from most of the Catalonian stations. For Delambre only Dunkirk, Cassel, and Wattel were within sight of the Channel, and so hazy was it that he relied on an engineering survey of the altitude of the base of the Dunkirk tower above the beach at low tide. He then calculated the difference between each station and the succeeding ones down the entire length of the meridian. In the event, the values agreed almost exactly with altitudes computed from Méchain’s end.

Precision was of still greater moment in the triangulation itself. Under the most favorable conditions Delambre and his team regularly made twenty readings of each angle in the chain, and took correspondingly more where conditions were adverse, as they often were. Here the most important correction concerned the exact location of the point of observation. All too rare were the stations in which the repeating circle could be located exactly at the point to be observed from the other two corners of the triangle. That was never possible in a belfry—the bells were hung right under the spire. “Re-duction to the center” was the second type of correction to be applied to each set of readings. Delambre was especially proud that his and Méchain’s was the first geodetic operation in which these corrections were laid before the public. His predecessors had given only adjusted figures, with no indication of how they had been obtained.⁸⁵

The third set of reductions was also unprecedented except in the case of the Anglo-French expedition joining the observatories of Paris and Green-wich in 1787, of which the metric survey was, technically speaking, the continuation and completion. Prior to that, surveyors had employed plane trigonometry, in effect treating their data as if the earth were flat and ne-glecting the inconvenience that the sum of the angles of a spherical triangle is greater than 180°. Less easily satisfied was Legendre, the mathematical member of the French team, whose analysis of the operations served Delambre and Méchain as the theoretical basis of their work. Legendre there proves a theorem concerning spherical triangles of which the sides are very small by comparison to the radius of the sphere. If one-third the excess of the sum of the three angles over 180be subtracted from each angle, the angles thus diminished may be considered those of a rectilinear triangle.⁸⁶ Delambre took advantage of this finding to construct tables that permitted systematically adapting the formulas of spherical trigonometry to the flat-land of geodetic problems. The error amounted to less than two feet over an arc of four to five degrees.⁸⁷

It is not necessary to have run a traverse in order to imagine the quality of those moments when the surveyor closes a triangle. Does it check out? Or was the mist too thick? The wind too strong? His fingers too cold? The twilight too deceptive? The signal from the next station too faint after night had fallen? Or did the inadvertent jolt knock the instrument off center there in the last steeple, where he had had to corkscrew himself between the joists to get at the eyepiece?

Infinitely more tense is the final verification of one base from the other. In the case of the metric survey, as will appear, it was not until 1798 that it proved possible to measure both bases using Borda’s rules. Aided by Laplace, Delambre completed the northern base at Melun after six weeks of work on 3 June 1798. He then traveled the 850 kilometers to Perpignan and measured the southern base on his own between 22 July and 21 September 1798. Each was just over 6,000 toises or about ten kilometers in length, and (if an anticipation may be pardoned) the length of the Perpignan base calculated from that at Melun differed from the measured value by ten to eleven inches. That is to say, the linear error was on the order of one part in 37,000. In the angular measurements the average departure from the mean was 1.3 seconds. This result is to be compared to the best experience of previous surveys, except again for the Paris-Greenwich junction of 1787. In no other was the average angular error less than ten to thirteen seconds, about ten times as great.⁸⁸ Perhaps that may dispose of the question whether the entire project was a lengthy redundancy.

4. OPERATIONS IN THE FIELD

The length of the meridian from Dunkirk to Barcelona subtends an angle of just over nine degrees. Planning called for Delambre to take the northern portion from Dunkirk to Rodez, and Méchain the southern from Rodez to Barcelona. It was estimated that the respective distances would be about 380,000 and 170,000 toises, roughly 750 and 335 kilometers, respectively, and the division of labor about equal. Delambre would be triangulating ground that had already been covered twice, by Cassini II in 1718 and Lac-aille in 1739–40. He would thus be making his observations from stations most of which were identified in advance, whereas the Spanish part would be entirely new and the Pyrenees difficult.

On 25 June 1792, barely a month after Delambre’s appointment, Lenoir put the final touches on three of the four circles ordered over a year earlier. Mechain, with farther to go, departed Paris that very day with two of the instruments. Delambre elected to use the third for the stations in and ad-joining the capital rather than to await completion of the fourth.

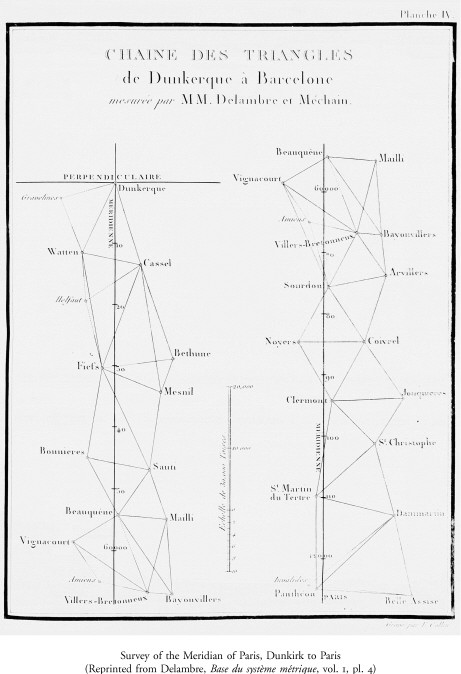
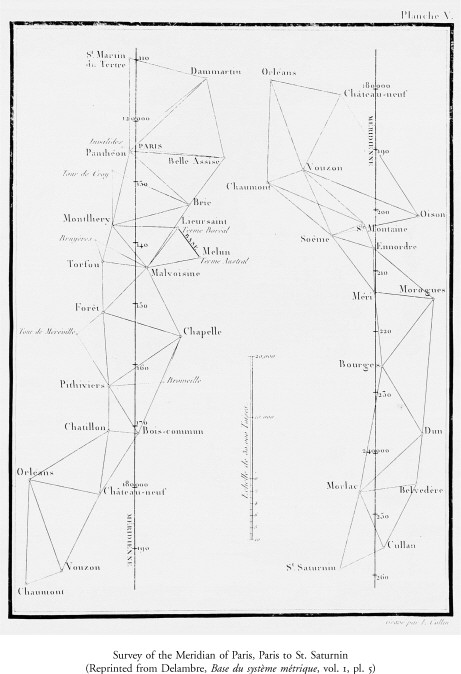
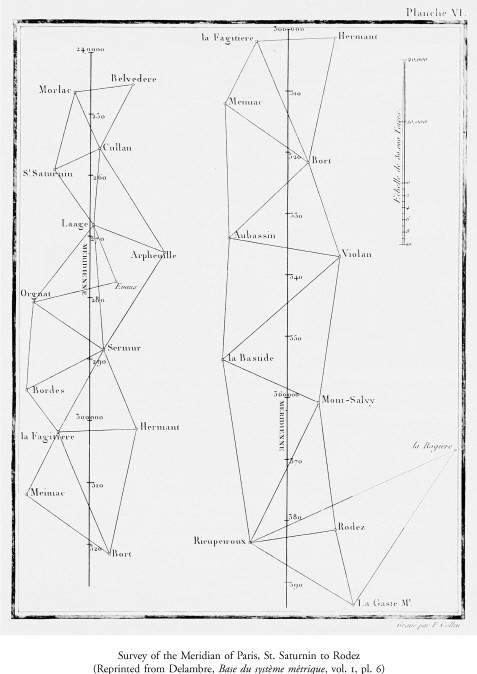
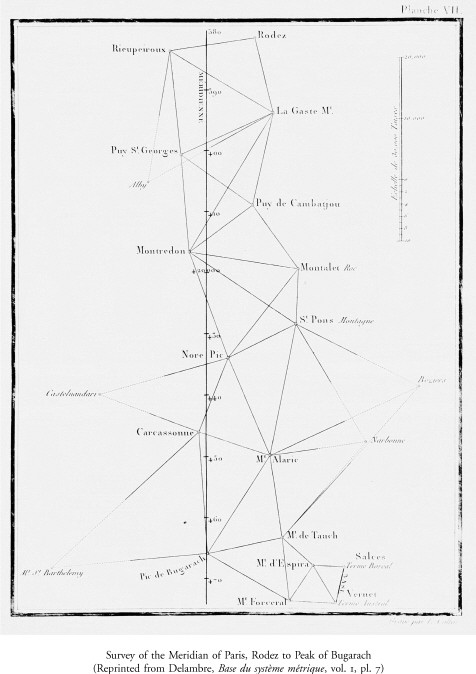
Both parties were furnished by Roland, Minister of the Interior, with documents identifying them as members of the Academy of Science, author-izing them to requisition supplies in the name of government, and bespeaking the cooperation of local authorities. They also carried a proclamation signed by Louis XVI and dated 10 June. Copies had preceded them to the chief cities of the departments they would traverse. The timing could hardly have been worse. The King and royal family survived the rising of 20 June and the mob invasion of the Tuileries only by taking refuge with the National Assembly. In the remaining weeks before overthrow of the monarchy on 10 August, the political temper of Paris and the surrounding region alter-nated between the fever of patriotism and the chill of suspicion.

At the outset Méchain was more fortunate than Delambre. True, he was arrested the very first day, at Essonne, compromised in the eyes of vigilant patriots by the mysterious instruments in his carriage. The authorities did respect his papers, however, and managed to secure his release. Thereafter, his difficulties diminished in proportion to his distance from Paris, until he arrived in the Pyrenees. He had left Paris with two assistants. The first was a cartographer and civil engineer called Tranchot, who had run the survey of Corsica for the Cassini map of France. The second, Esteveny, was a skilled artisan in charge of maintaining the instruments. The Academy had arranged that they should be joined at the border by two Spanish military engineers, Alvarez and Planez. On the French side popular distrust again fermented, heightened by the presence of these foreign officers. Méchain thought it prudent to defer the frontier stations until the political weather should clear and to begin in Spanish territory.

There they met with no trouble whatever. This was new ground altogether, never before surveyed or mapped scientifically. The party of five worked very fast among the mountains and down into the Catalonian plain. By the end of September 1792 they had reconnoitered their route, chosen stations for triangulation, and constructed observation towers, erecting stone cairns in the mountains and scaffoldings of timber wherever no church or castle offered in the flat country. By 29 October they had surveyed their way down the nine stations they needed in order to reach the southern anchor of the entire meridional chain of triangles. That was the fortress of Mont Jouy, or Jouich, on the coast just south of Barcelona.

There Méchain decided to settle in for the winter of 1792–93, taking advantage of his leisure to make precise azimuthal measurements and determinations of latitude in the season of the winter solstice.⁸⁹ He fixed on three stars in addition to the sun in order to measure their respective distances from the zenith along the arc of the meridian. His choices were Polaris, Beta of Ursa minor, and Alpha of Draco. The resulting figures for latitude agreed to 0.2", giving him 41°21'45.06"for Montjouy. He later trained the scope of his circle also on Zeta of Ursa major. That figure was 41°21'40.97", a difference of 4.09". Still, that star passed across the meridian at an altitude of only 7°15, at which height Bradley’s formula for refraction was accurate only to 8". Méchain thus decided to ignore that finding in favor of the close agreement among his three primary series of observations.

Méchain also explored the feasibility of a favorite project taking form in his mind. This was to exceed the terms of his mission by extending the survey of the meridian out into the Mediterranean as far as the Balearic Islands. He made a few experimental sightings of Majorca from points fur-ther down the coast, the last of them on 2 April 1793. By then it was time to return to the Pyrenees in order to complete the junction with the frontier stations he had skipped in France, and thence to work north to his goal at Rodez. There are only nineteen stations in the completed work, not counting the two in the base at Perpignan. Most of the ground had been covered by the surveys of 1719 and 1740. He should easily have finished by the end of the summer of 1793, and might well have advanced into the segment assigned to Delambre and met his colleague somewhere between Rodez and Paris.

He suffered, instead, a grievous accident. Méchain had made friends with a physician in Barcelona, an enthusiast for mechanical inventions who had been kind to him throughout the lonely winter, and whom he could not disappoint. For months the doctor had been pressing Méchain to visit the country house where he had installed a new type of pump. A day was fixed for the expedition, 1 May 1793, on the brink of Méchain’s intended depar-ture for France. Nothing was ready. The horses that were to supply power were nowhere to be found. In gallant Spanish fashion, the doctor and his servant undertook to manhandle the machine. They placed Méchain at a point of vantage and set to turning the capstan. Méchain admired the vast flow of water. It was too vast. He heard cries. The back pressure had over-powered the two men, who were in danger of being drawn into the gears. Méchain sprang to their help even as they let go. A spoke of the capstan whipped around and knocked him to the wall, where he lay in a bloody heap, unconscious, with three ribs broken, his collarbone smashed, and the appearance of a fractured skull.

After three days he came to his senses, running a high fever and in agonizing pain. For months he had no use of his right arm. In June he tried shooting the sun left-handed at the summer solstice. The effort put him into a faint. He took the baths at Caldas. Only in September was he fit enough, and then barely, to set out for the Pyrenees in order to complete the border stations he had postponed in the threatening political climate of the previous autumn. It did not simplify his prospects that in the meantime, on 1 February 1793, the French Republic had declared war on the Spanish mon-archy along with England and Holland.

Nevertheless, General Ricardos, commanding in Catalonia, at first made no difficulty about Méchain’s resuming operations in the field. On the con-trary, he urged that the task be brought to completion. Equally accommodating were the officials of the Department of Pyrénées-Orientales in Perpignan, where Méchain had the good fortune to be acquainted with the Procurator-General, one Lucier. Permissions were forthcoming from both sides. Méchain was to undertake the Puy Camellas just south of the border, and Tranchot to make the more strenuous climb to the top of the Puy de Stella in the French Pyrenees. Trouble arose, not this time with vigilant patriots, but with mountain brigands. A band of miquelets took Tronchet prisoner and led him, hands bound, to the nearest town. The local authori-ties transported him to Perpignan, where the president of the Department had him released forthwith. Tranchot was immediately authorized to erect the signals needed for the next triangles to the north on the peaks of Bugarach and Mount Forceral and then to return to Puy de Stella and afterward to rejoin Méchain in Spain. He wound up his observations at Puy de Stella on 3 December 1793, the same day that Méchain completed his at Camellas.

It remained only to measure the angles at Perpignan, Bugarach, and For-ceral, and the junction between French and Spanish triangles would be complete. Tranchot, Méchain, and their assistant Esteveny thereupon made their way back to Barcelona to gather up their effects, expecting to take their leave of Catalonia and proceed northward to Évaux, where they hoped to observe the distance of the key stars from the zenith at the winter solstice. Should all go smoothly, they might still advance the chain of triangles beyond their original terminus at Rodez as far as Sermur, or even Bourges, and join up with Delambre early in July. Thus would the great operation be completed in the span of two years, despite all the accidents and delays.

That was not to be. General Ricardos had had second thoughts, or per-haps his superiors in Madrid had them for him. On returning from the Pyrenees to Barcelona in early December 1793, Méchain and his party were met with orders interning them for the duration of the war. The knowledge they had acquired of the frontier might, it was suddenly feared, prove useful to the enemies of Spain.⁹⁰

Let us turn attention back to Paris now, and to Delambre. He for his part had set out the day after Méchain, on 26 June 1792. Lenoir had still to complete the second of his Borda circles as well as the parabolic mirrors for night signals. Rather than waiting for everything to be ready, Delambre decided to begin with a reconnaissance of the stations in Paris and its surroundings and a preliminary verification of the angles of Picard’s survey in 1668–70 and of Cassini’s and Lacaille’s in 1739–40. His party consisted of two assistants, one Bellet and Lefrançais de Lalande, nephew of the astronomer, and a servant, Michel. Besides the single Borda circle, they were equipped with a telescope, two magnifying glasses, a tripod with plumb bob, two levels, two clocks, one with a second-hand and one with a bell, two barometers, two copper-mounted and two glass-mounted thermome-ters, four lamps, tools for maintenance, and two cases of reference books, one of them in English. Two carriages were needed, one for the instruments and one for themselves.

Climbing the bluff of Montmartre to what should have been the very first station, he was dismayed to find that the belfry that had afforded a 360° view of the countryside in 1739 had been demolished. His first thought was to shift to the Panthéon, but La Rochefoucauld, president both of the Acad-emy of Science and also of the department of Paris in these last days of the monarchy, warned that alterations were pending on the dome. Returning to Montmartre, Delambre thought he could use the belvedere Flécheux re-cently constructed on the brow of the hill.

Moving next to stations south of the city, he found the tower at Montlhéry in much the same state as in the time of Cassini and Lacaille. Since the mass was too irregular and too wide to be sighted accurately, he had a carpenter construct a twelve-foot pyramid of scaffolding on the top. It was destroyed the same day, and though the procurator of the commune made the vandals rebuild it at their own expense, someone knocked it over again and chopped it into pieces a few days later.

At Malvoisine the trees had grown and obscured the farmhouse chimney that had served Lacaille in 1739. After his experience at Montlhéry, and Méchain’s at nearby Essonne, it seemed unwise to erect anything on the roof, and Delambre contented himself with having the flue raised a good six feet. No obstacles arose at Torfou or Brie, but at Montjai the tower had been so ruinous over a century before, in 1670, that Picard had not dared climb it a second time to correct a ten-inch error in the closing of his triangle. Again Delambre engaged a carpenter to put up a pyramidal scaffolding atop one corner of the ruins. Armed with muskets, the villagers drove him off, and here the authorities dared not intervene.

By 15 July Lenoir had the second circle ready. In view of the difficulties of his reconnaissance to the south, Delambre decided to begin definitive observations with the stations north of Paris. On the eighteenth he arrived at Jonquières, his first stop. The mayor seemed cordial. Delambre took the precaution, nevertheless, of seeking out an old man in the village who remembered Lacaille’s operation in 1740, and had him tell of it in the square as the villagers came trouping around. Delambre found the recital naive and charming, but it failed of the desired effect. At sight of the instruments the people began murmuring, and the municipal representatives asked De-lambre to desist until he could obtain clearance from the departmental au-thorities at Beauvais.

Returning the next day, he moved on to Clermont. The fine 67-foot steeple of earlier times had fallen, and he had to make do with a miserable 8½ foot turret at the corner of a wall some 42 feet distant from the previous station. At Saint-Christophe everything went smoothly. Not so at Dammar-tin, where the church had been sold. The new owner was about to demolish it to make room for something profitable but did allow Delambre to make his observations. There it became immediately apparent that at a distance the belvedere Flécheux was indistinguishable from the neighboring houses on Montmartre.

Off to Paris went Lefrancais Lalande with the purpose of shining a re-flecting lamp from the belvedere the next evening. The date was 10 August. Neither he nor Delambre could know what was occurring in the Tuileries. Delambre watched from the condemned belfry in Dammartin until ten that evening, seeing only the glow of houses on fire in the Carrousel. Lefrançais Lalande had encountered no trouble in entering Paris, but Montmartre was then a suburb, and no one was allowed to leave the city. The colleagues whom he asked to intervene with the Commune thought him out of his mind. He did obtain a permit the next day, however, and managed a faltering light about 8:30 in the evening of the eleventh. On the twelfth and thirteenth Delambre saw nothing. Only on the fourteenth was his young assistant able to make another flickering signal. Two other reflectors would have been needed in order to complete the triangle, one at Saint-Martin-du-Tertre and one at Saint-Christophe, and Lenoir had not yet furnished those. It was fortunate he had not, noted Delambre later. There was no telling what might have been the consequences of such imprudent observations.

Montmartre thus eliminated, he needed another objective in Paris and decided to try the Invalides. The next station south of Dammartin should have been Montjai, the site where the inhabitants had already prevented construction of a scaffolding on the roof of the old tower. Delambre’s appeal to the district authorities at Meaux failed to overcome their resistance, and he moved to the nearby chateau of Belle-Assise, where the steep pyramidal roof of an outbuilding seemed made to order. Before being noticed, his small team succeeded in measuring the angles that the direction of the In-valides made with the directions of Dammartin and Brie, respectively. Luck failed to hold. As they were packing their gear to move on, a detachment of the national guard arrived from Lagny, recognized them as the suspects who had tried to make a signal at Montjai, and demanded their passports. Dated in May, these documents produced no good effect. Still less did the proclamation of the King, from which Delambre read out passages.

Delambre tells how this was received in a letter to his patroness, Mme d’Assy. “A good sans-culotte took offense at our title of Academician. ‘There is no more Cademy’ he said [anticipating its suppression by almost exactly a year], and kept repeating ‘Plus de Cadémie: everybody is equal. You come with us.’”⁹¹ It had begun to pour. Off they were marched across muddy fields to Lagny to be incarcerated at midnight in an inn called l’Ours. Two musketeers were stationed at their door. A special delivery letter to the district authorities at Meaux secured their release, with apologies, the next day.

The sequence of their operations called for making their way next to Saint-Martin-du-Tertre, passing through the ancient pays de France to the north of Saint-Denis. Every commune along the route was in the same state of permanent alert. Arrested in one after the other, they realized that it would be impossible to proceed without republican passports. Again Lefrançais Lalande repaired to Paris on that errand. Delambre dared not appear in the capital lest he be told to postpone the whole enterprise until more tran-quil times. Should that happen, he feared, it might never be resumed.

Instead, he requested interim credentials from the district officers at Saint-Denis, who gave him a paper readily enough while warning it would not take him half a league. They were right. He was stopped in Épinay. Again the instruments were what alarmed. Watchful patriots found them insufficiently described in his passport, and required Delambre to demon-strate the construction and operation of the Borda circle in the public square. No one understood him. Even so, he was made to begin over each time some new citizen joined the throng. In vain did he seek to enlist the support of two professional surveyors among the crowd. After three hours of debate, his party was ordered into its carriage and conducted under guard back to Saint-Denis.

“Vive la nation,” cried the escorts as they arrived before the District of-fices, “Voici des aristocrates.” Volunteer soldiers surged about in the square, awaiting the muskets to be issued them before flying to the defense of the frontiers. Delambre and his team were delivered over to the very Procurator-General who had warned of the inefficacy of his protection. That official disappeared to enlist the support of higher authority, showing Delambre the back door and advising him to escape if he, the procurator, should be long delayed. Delambre was summoned instead to the square again and required to resume the course in geodesy he had begun in Épinay.

I was not very favorably heard. Evening began to draw on. It became almost too dark to see. The audience was very numerous. Those up front heard without understanding. Further back they could see less and hear nothing at all. Impatience began to rise and murmurs to circulate. Several voices rose above the crowd suggesting one of those expeditious solutions often resorted to at the time, which cut through all difficulties and put an end to all doubts.⁹²

Fortunately, the president of the district had presence of mind. Taking advantage of the darkness, he proposed delaying further examination of the instruments until the morning. All this occurred on 6 September. Delambre and Bellet slept that night in an armchair in the procurator’s office. They had contrived to send the servant, Michel, to Paris with a letter to the president of the National Assembly. The zoologist Lacepède was serving at the moment on its Comité de surveillance. He succeeded in eliciting from that committee a decree in the name of the National Assembly enjoining “administrative bodies, municipalities, and national guards, in all localities where Delambre and Méchain feel they should pursue their operations, to ensure that no obstacle impede their work, to guarantee free transportation of whatever instruments they need to use, and to procure them all the facilities in their power, in order that they may the more speedily conclude the mission with which they are entrusted.” That sufficed, together with the publicity that attended the arrest. On the tenth Delambre was back in Paris, regrouping.

On delivery of the new, republican papers, the entire team set off again for Saint-Martin-du-Tertre. The belfry in that dismal village had fallen into wobbly disrepair since the 1739 survey. Worse, the sighting from Paris had evidently confounded some other object with the steeple, for the dome of the Invalides was masked by a rise in the ground. The Panthéon was per-fectly visible, however, and although that meant redoing the observations at Dammartin and Belle-Assise, there was no alternative. Moving on south to the stations reconnoitered in the summer, Torfou and Montlhéry, Forêt and Tour le Craye, the party was impeded by the rains and fogs of October and November. The direction of Boiscommun from Chappelle-la-Reine was the last determination Delambre proposed to make before stopping for the win-ter. For four days he strove to discern the steeple by the dull light of late December—in vain, until its image rose to view in the momentary clearing of the sunset, a vertical thread visible above the horizon for a few minutes. Five rainy days passed before the reading could be verified. Then the fugi-tive steeple reappeared fleetingly, again as dusk fell. The phenomenon re-minded Delambre of the refraction of rays from the setting sun in the surface layer of the atmosphere that on an occasional evening brings the mountains of Corsica into view from Genoa and from coastal points in Provence.

Now that the Pantheon was to be the station in Paris, it was urgent to take the directions of Dammartin and Malvoisine from there before the church should be demolished at the former and the raised chimney tumble at the latter. What, therefore, was Delambre’s dismay on returning to Paris from Chappelle-la-Reine in early January 1993 to find the cupola gone. The alterations of which La Rochefoucauld had warned were under way, one of the few items of public works to transpire on schedule that winter. Con-structing a temporary observation platform on top of the dome consumed another month, and not until 28 February 1793 was Delambre able to finish those observations. Thus, it had taken him eight months, from June 1792 until March 1793, to complete the fourteen stations on either side of the capital, while Méchain, working under the Catalonian sun and in the security of monarchical Spain, had got through his first nine stations in less than two.

Ready at last to move north, Delambre requested passports from the Ministry of the Interior. By then, however, the Commune of Paris had arrogated such functions to itself. Unanimously it rejected his application. For six weeks he lobbied. Eventually a colleague, the mathematician Cousin, serving on the municipal Comité des subsistances , proved able to exert influence. Papers were delivered on 3 May at noon, and at two o’clock Delambre and his party were on their way, past Saint-Denis and Épinay to the more tranquil regions of Picardy and Flanders, partially insulated by a little dis-tance from the high political tension of the capital in a country where security was threatened mainly by war. Delambre carried a letter commending his operations to the protection of the general commanding the Army of the North, Philippe Custine, with whom he lodged for several nights in Béthune. This was, he later said, the most agreeable part of the whole survey. The belfries were in good repair across that cultivated land. Its gently rolling prospects were unobscured by forests. Repeating and perfecting the triangulation of 1740 was a pleasant chore throughout the spring and summer of 1793.

That was just the time when Méchain was recuperating from his accident and preparing the operations in the Pyrenees that culminated in his internment in early December. Though restricted to Barcelona, he was free to move about within the city and took rooms in the Fontana de Ora. The inn was comfortable. Not so his situation. His injuries still ached. No money could come from France. His remaining funds were sequestered as enemy property in the bank where he had deposited them. A long letter of 21 nivose an II (10 January 1794) addressed to Borda, chairman of the Commission of Weights and Measures, is part cri de coeur and part report on the mission thus aborted by his internment.⁹³ On 17 July he had received a letter from Lavoisier authorizing him to complete the operations in Catalonia. It was dated 15 June. He had heard nothing since from Paris. He is apprehensive lest the long delay be attributed to sloth on his part or to some putative reluctance to return. Were his continuing absence to be thus misinterpreted, he fears for the situation of his wife and children and for his own position at the Observatory as well as his job with the Navy.

“I put my cause in your hands,” he writes, begging Borda to explain his predicament to the Commission of Weights and Measures, to defend his interests, and to protect and comfort his family.⁹⁴ If nothing could be done for him by diplomatic channels, could not something be attempted for his associates, Tranchot and Esteveny? Esteveny was not even an educated man. Concerned only with the instruments, he had made no observations. The thousands of shepherds who follow their flocks freely back and forth across the border know the passes far better than he, or indeed his superiors. As for more general matters, Méchain reads alarming reports in the Spanish press about bloody scenes in Paris. He hears rumors to the effect that the Acad-emy of Sciences has been abolished and its membership dispersed, that their mission no longer has any object, that if unity of weights and measures is achieved, it will be on the basis of the seconds pendulum, and so on.

But enough—Méchain pulls himself together and turns to reporting on what he has accomplished. With this letter he enclosed a table giving the angles of all his triangles from Montjouy to Forceral and Bugarach. The ten Catalonian triangles were complete, the two requiring observations at Per-pignan, Forceral, and Bugerach were incomplete, and the whole chain was based on the latitude determined at Montjouy in December 1792.

Until he should be released from detention, there was nothing more Méchain could do to fulfill his mission. In order to while away the time and render his “slavery” useful at least to astronomy, if not to the metric survey, he was, so he informs Borda, putting in hand observations to determine the obliquity of the ecliptic. He would then compare his results with the value he had found the previous year at Montjouy. The only observation post available to him was the terrace of the Fontana de Oro. Montjouy being a military installation, he was no longer permitted to visit the tower there and would need to determine the small difference in latitude trigonometrically.

Only after sending off his report to Borda did Méchain complete these observations. The first results were gratifying. Two of the three circumpolar stars that had agreed so beautifully for the latitude of Montjouy, Polaris and Beta of Ursa Minor, were equally in accord for Barcelona. He decided that the third, in Draco, would be superfluous. What was even more reassuring, Zeta of Ursa Major exhibited the same anomaly as at Montjouy, minus about four seconds. Now came another shock, the worst yet, difficult though it is to imagine that any blow could be more severe than those Méchain had already suffered. So it was, however, for this one was astronomical.

Triangulation showed the Fontana da Ora and the citadel of Montjouy to be 1094 toises apart. The difference in latitude was 949.80 toises, a bit over a mile, or in angular terms approximately 1 minute of arc. Calculated from the data of December 1992 for Montjouy, the latitude of Barcelona should have been 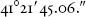.Calculated from the observations of Polaris and Ursa Minor on the terrace of the Fontana de Oro, it was 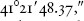412148.37,a scan-dalous 3.31" higher than predicted. This was no single slip. Méchain had made 326 and 288 observations, respectively, of the two stars in question at Montjouy and 208 and 226 of each at the Fontana de Oro.

Méchain made renewed, and now desperate, appeals to be allowed to revisit the tower on Montjouy and to redo his observations there, though without acknowledging that they were the anchor for the entire chain of triangles he had just sent off by a special, confidential route to Paris. He was refused. There was no way to resolve the anomaly. His state of mind can be imagined. He was at best a timid man, in Delambre’s account, self-doubting and secretive, a superlative observer and a good calculator, so obsessed with precision that he would never use the labor-saving formulas Delambre had devised for the reduction of angles. Nor would he let anyone see his raw data. His registers contain only the average of the many observations he made on every sighting. With such a temperament, Méchain kept the dreadful secret of his results for Barcelona to himself, determined that no one must know, not even his assistant Tranchot, until he should somehow find a way to return to Montjouy to redo his initial observations. He never managed that, and eventually died in the attempt, in 1804.

Delambre learned of the Barcelona data only thereafter, on Madame Méchain’s turning over to him her husband’s papers some time after his death in 1804. Six years previously, in 1798, the nations of Europe had gathered in congress in order, so went the rhetoric, to accept the meter from the hands of France. Thereupon Delambre composed and saw through the press the first volume of Base du système métrique, knowing and using only the figures that Méchain had communicated for Montjouy, the southern terminus of the survey.

Fortunately, as it turned out, those figures were beyond reproach. When Delambre learned the facts, he recalculated all the Barcelona data to see whether he might resolve the discrepancy. He could not, and reports his attempts in the second volume of his great book on the basis of the metric system, published in 1807. He could only speculate about the reason. Local variations in the force of gravity resulting from irregularities in the crust of the earth may affect the plumb bob and the level. The refractive properties of light may be slightly different over sea and over land. Possibly, and this seems a startling suggestion for the time, it may be gratuitous to suppose that light always travels in straight lines.⁹⁵ At all events, he concluded, not only had the agony of Méchain’s last years been quite unnecessary, it was a shame that he had not called attention to so interesting an anomaly instead of hiding it. Others might have been inspired to undertake investigations that would have explained it.

Taking every occasion to praise Méchain’s accuracy as an observer, Delambre wrote charitably of the misfortunes that had overtaken his colleague in the wake of that unlucky pump handle.⁹⁶ Perhaps, he suggested, Méchain could have told himself that the Barcelona observations were not part of his mission, since he had performed them on the side, to fill in time during his confinement and to satisfy his own curiosity. Perhaps. In any case, “The good fortune that had accompanied him for the first nine months seemed to have abandoned him forever, and the four years that followed his accident brought him only a series of contretemps, cross-purposes, and afflictions, which transformed him into an extremely unhappy man.”⁹⁷

At the end of the summer of 1794, Méchain finally succeeded in getting passports for Tranchot and himself, though for Italy, not for France. Barely escaping the Barbary pirates, their ship took them to Livorno, whence they made their way to Genoa in September 1794. There he lingered in a state of indecision extremely puzzling to his family and colleagues, who thought to welcome him momentarily back to a Paris no longer in the grip of political Terror. But at least his mission did not suffer from these particular hesitations. For the metric survey had in any case been in abeyance since the start of the (old-style) year 1794.

It was put in that state by one of the very few decrees of the Committee of Public Safety to touch science directly:⁹⁸

Extract of the Register of the Committee of Public Safety of the National Convention.

The third day of nivôse in the second year of the French Republic, one and indivisible.

The Committee of Public Safety, considering how essential it is for the improvement of public spirit that those who are entrusted by the government neither delegate functions nor give missions except to menworthy of confidence through their republican virtues and their hatred of kings; after having consulted the members of the Committee of Public Instruction particularly concerned with weights and measures, decrees that from this day on Borda, Lavoisier, Laplace, Coulomb, Brisson, and Delambre shall cease to be members of the Commission of Weights and Measures, and shall immediately deliver to the remaining members the instruments, calculations, notes, memoirs, and in general everything in their hands related to the operation of measures, together with an inventory; And decrees, in addition, that the members remaining to the Commission of Weights and Measures inform the Committee of Public Safety as soon as possible which persons are indis-pensably needed to continue its work, and that it communicate at the same time its views on the means for giving all citizens the use of the new measures as quickly as possible, taking advantage of the revolutionary impetus.

The Minister of the Interior will see to the execution of this decree.

C.-A. Prieur, B. Barère, Carnot, Billaud-Varenne, R. Lindet.

The old-style date was 23 December 1793. Delambre had completed his triangles in the north by the end of September. Doubling on his tracks, he then made his way south of Paris, reaching the Loire Valley by the end of the autumn. He reported throughout to the Commission of Weights and Measures named by the former Academy of Science, redesignated Commis-sion Temporaire on 18 September, following the suppression of the Academy on 8 August. After the purge on 23 December, the rump Commission con-sisted of Lagrange, Monge, Haüy, Vandermonde, and (in absentia) Méchain. Haüy continued as Secretary, and an unnerved Lagrange replaced Borda in the chair. Meeting on the very day of the decree, the survivors requested that Prony and Hassenfratz be joined to their number. Five days later, the Committee of Public Safety gave a limited consent, stipulating that they might be added, but only as “cooperators.” They would draw the same retainer as the others, 10 livres per day, when actually performing duties.⁹⁹ Also named to the Commission, for political reasons and as a full-fledged member, was Jean-Nicolas Pache, Hébertist mayor of Paris, and intimate friend of Monge.

To Prony fell the ungrateful task of informing Delambre that he was to be relieved of his duties. A letter of 29 December, directing Delambre to put his papers, accounts, and instruments in order and to terminate his operations, reached him at Vrigny, in the Department of Loiret. He was in the midst of joining Pithiviers and Boiscommun with Orléans and Châteauneuf. Having just had a fifty-four-foot observation tower constructed in the Forest of Orléans, he was halfway through the observations required there and also needed to measure the angles at Pithiviers, Orléans, and Châteauneuf. His reply of 2 January 1794 asks to be allowed to complete those triangles.

Prony arrived on the scene a few days later.¹⁰⁰ Delambre’s account identi-fies him only as a member of the Commission, one who was tactful enough to hover about noncommittally until observations at those stations were finished. Their encounter appears to have been altogether correct and colle-gial, even cordial. That someone else, no doubt Prony himself, would con-tinue the work, was assumed on both sides. Having had to do the calculations at night for the most part, Delambre would require three months of hard work to complete them and to put his registers in final order. He supposed he would be accorded that time. “Pray submit these reflections to the Commission of Weights and Measures and kindly inform me of their decision as soon as possible. If you should have only a refusal to impart, it will be much softened by the pleasure of receiving another letter from you. I am much touched by the sentiments you were good enough to express to me. I salute you and embrace you fraternally.”¹⁰¹

The formal instructions Prony carried were of a different order. The tri-angles once completed, he delivered a sealed packet into Delambre’s hands to be opened on his departure, and left forthwith. The envelope contained a copy of the decree of 3 nivôse (above) with a covering letter from the Commission dated 7 January 1794. The message was, Delambre remarked, “in the style of the times.”¹⁰²

15 nivôse an II

Citizen,

The Commission of Weights and Measures has instructed one of its members to deliver to you the decree of the Committee of Public Safety which concerns you, and to concert measures with you for closing out your operations in such a way that the signals will remain useless. It invites you to finish up your calculations and to copy your observations, as you have proposed.

5. THE PROVISIONAL METER

The draft of the 3 nivôse decree is in the handwriting of Prieur de la Côted’Or. His own early proposal for weights and measures, discussed above, had been one among the many to which, after hearing Lavoisier read it out in July 1790, the Academy had preferred its own design.¹⁰³ He was twenty-nine years old when he eliminated the leading scientists of France from the metric Commission, having been a member of the Committee of Public Safety for four months. To understand how that came about, it will help to look back briefly at the political history of the metric project during the time since its enactment by the Constituent Assembly on 26 March 1791.

Prieur had been elected a deputy to the Legislative Assembly in Septem-ber 1791, and served on its Committee of Public Instruction. His earliest official involvement with the metric system was in that capacity. In April 1792 Roland, Minister of the Interior, impatient that over a year had elapsed with nothing to show for it, proposed to the Assembly that, pending completion of the academic system, provisional standards be adopted to facilitate circulation of grain and other commodities. A deputy thereupon moved that the Executive require an account of the state of the Academy’s work, begun “a long time ago.” In response to Roland’s memoir, the Academy prepared a propitiatory extract to be published from its minutes.¹⁰⁴ It could do little else, for Delambre and Méchain were not yet in the field. The Committee of Public Instruction thereupon named Prieur to examine all these papers.¹⁰⁵

The Academy improved the situation as soon as word from Méchain on his first rush of triangles down through Catalonia provided concrete evi-dence of progress toward “equality of weights and measures.”¹⁰⁶ On 25 No-vember 1792, a deputation from the Academy came before the Bar of the Convention, submitted a report by Borda on the organization and progress of the metric system, and offered in homage the entire collection of the Academy’s publications from the beginning. In all this, said Lalande, who made the presentation, “the Academy has shown a consistent preference for everything that promises immediate and tangible utility.”¹⁰⁷ To which bit of special pleading the representatives of the nation replied, through the person of the abbé Grégoire, their president, in words that stand at the head of this chapter.

Further moves in the displacement of scientific by political authority took place a little over three weeks later, on 21 December 1792. The Committee of Public Instruction then designated four of its members to join with the commissions of the Academy concerned respectively with the reform of the calendar and of weights and measures. The calendar, politically the more sensitive topic, will have to await the next chapter. As for weights and mea sures, assigned “to join in the work of the Academy of Sciences” were Prieur again and the Strasbourg mathematician L.-F.-A. Arbogast.¹⁰⁸ Although Pri-eur did not lose interest, indeed far from it, he rotated off the Committee in January 1793, leaving Arbogast to exercise the authority of Representative of the People in the Academy’s Commission of Weights and Measures.

The same day, 21 December 1792, also brought the Academy an inquiry from the Convention’s Committee on Assignats and Currency. In concert with the ministerial commission on the Mint, its members were framing the monetary system. They say nothing either of the Academy’s October 1790 memoir on that subject, or of the July 1791 report on the cadastre. They may not have known them, for they ask about matters already covered in those documents, namely the denominations of the new linear units, their relationship to units of weight, and the ratio of the latter to the pound-weight and the marc. They had read Borda’s report of three weeks previously, however, and were especially struck by his experiments on the seconds pen-dulum. Had the work advanced sufficiently to provide an invariant mone-tary standard?¹⁰⁹

This was an inquiry that was bound to throw the Academy into a dilemma. On the one hand, its commissioners had themselves tied the justification for the meridional survey to monetary reform by way of decimalization and to the cadastre by way of nomenclature and angular measurement. On the other hand, they could scarcely expect France to await a proper monetary system or a fair tax base until such time as Delambre and Méchain should have completed their work. At that moment, Delambre was still extricating himself from the toils of revolutionary Paris while Méchain would soon be interned in Barcelona. Only on one subsidiary item was the Academy in a position to respond definitively in short order. This inquiry was what prompted Lavoisier and Hauy to perform their determinations of the density of water.¹¹⁰

Working more rapidly than usual, the Academy’s Commission of Weights and Measures returned its reply on 19 January 1793. Its members had de-cided to compromise on the basis of the metric system in order to save its structure. A provisional meter, they reported, could be based on Lacaille’s data from the 1740 survey. Its length would be three feet, 11.44 lignes. The probable error would be approximately one part in 4,500, less than one-tenth of a ligne in the meter.

To the main question, which concerned monetary standards, the academic commission responded with a lengthy account of the determination, which Lavoisier and Haüy had hastened to perform, of the weight of a cubic foot of distilled water. Reducing that value to the weight of a cubic decime-ter (liter), they found that the grave, as unit weight would be called, would equal two pounds, zero ounces, five gros, and five grains of marc weight, and that the margin of error in the measurements could not exceed one part in twelve hundred, or three and five-sixths grains per marc. That degree of precision would amply suffice for founding the denominations of a new monetary system on the value of a fixed weight of metal. The Academy proposed the silver décigrave, as it would have been called, equivalent to 40 sous, 10.6 deniers of legal specie.

The Commissioners improved the occasion by suggesting that the existing monetary system be decimalized forthwith. Let the Convention simply decree that after a certain date, say 1 October of that same year, all public accounts and all government contracts be framed in livres, dixièmes, et centièmes instead of livres, sols, et déniers. Monetary reform would thus prepare the way for the changeover in weights and measures generally when the metric system should be ready for application.¹¹¹

These abstruse considerations can scarcely have won much attention in the anterooms or on the floor of the Convention. They were submitted to the Committee of Public Instruction on 19 January 1793. The Convention was in the midst of the debate over the execution of Louis XVI. The King’s sentence had been voted two days previously and was carried out two days later. Forwarded on to the Committee on Assignats and Money, the Academy’s reply to its inquiry nevertheless proved satisfactory. It was the foundation for the scheme of monetary reform, modeled arithmetically on the new monetary system of the United States, that was brought before the Convention on 17 April 1793.¹¹²

A week later, on 10 April 1793, Borda, Lagrange, and Monge delivered a report on the entire metric project before the springtime open meeting of the Academy, destined to be the last of its public sessions. The Academy was on the defensive. Political tensions were running high. Monge resigned as Minister of the Navy that very day. Addressing themselves to the educated public, he and his colleagues insisted on the importance of decimalization and emphasized its convenience for navigation and geography. They repeated the 19 January finding, based on analysis of the Lacaille survey of 1740, that the length of the meter would be 3 feet, 11.44 lignes. For this audience they did not even mention that the figure was an approximation.

On nomenclature they beat a retreat. Given the temper of the public, it has to be thought a tactical, though not a strategic, retreat. The Academy had been discussing fine points of terminology since the previous July, when the Laplace report on the cadastre introduced the term “meter.” The system that had emerged from these deliberations was logical and Condillacian. That approach has prevailed, although many of the words were changed in 1795—gram and kilometer replaced grave and millaire, for example.

Nevertheless—so report Borda, Lagrange, and Monge—the Academy had had second thoughts. It would require mental gymnastics, they now acknowledge, for people to seize the meaning of words such as centimeter and millimeter. The Academy had also given consideration to an alternative possibility, one that would accommodate the common understanding, and which it now preferred. That scheme preserved the essentials of the metric system—its basis in the meridian, its decimals, and its meter—while avoiding abstract neologisms. The units would bear one-syllable names, some suggestive of their magnitude, such as palme for decimeter, doigt for centi-meter, trait for millimeter, and mille for 1,000 meters; some simply traditional, such as pinte for a cubic palme (liter) and livre (kilogram) for the weight of that volume of water.

According to the 10 April report, the Academy then reversed its earlier position and adopted this alternative. There is no formal documentation to that effect, but the records for those months are very spotty, and it may indeed have done so. What appears more likely is that the full Commission of Weights and Measures, recognizing that the locus of power had shifted on matters once within the purview of the Academy, decided to play safe and leave the decision to higher authority. On 29 May the commissioners for-warded both systems to the Comité d’Instruction Publique in order that it might choose which one to propose to the Convention. Rationalism still prevailed on that Committee. On 4 July it opted for the abstract and deno-tative nomenclature that the Academy had originally preferred.¹¹³

In the activist summer of 1793, it had become politically inadmissible that there were as yet no things, no workable units, to which these new words might be attached. Amid the urgency of that season Arbogast, in effect deputy on mission to the Commission of Weights and Measures, pre-empted the initiative from the academicians among whom he had beensitting since early in the winter. He may well have been fortified by Monge in thus taking matters into his own hands. The elements of a policy lay ready to hand. Almost a year had passed since Roland in his impatience had suggested the notion of a provisional standardization. The Academy had gone back to the Lacaille data of 1740 and calculated the approximate length of the meter for its 19 January reply to the Convention’s Committee on Assignats and Currency. On 30 July Arbogast handed up to the Convention on behalf of the Committee of Public Instruction the draft of a law adopting that length as the provisional meter. It passed on 1 August. The accompanying report rehearses the advantages of uniformity and natural lengths:

Your Committee of Public Instruction comes before you to fix the attention of the Convention for a few moments on an object of univer-sal beneficence. The uniformity of weights and measures has long been desired by philanthropists. It is required both by science and the arts, both by commerce and the useful man who lives by the work of his hands, and who, being the most exposed to fraud, is least of all in a position to withstand its effects. This new means of cementing the unity of the Republic offers still further occasions for esteem and liai-son between the French and other peoples, between the present generation which confers the benefit, and that posterity which will enjoy it, or verify its basis.¹¹⁴

The last clause carries the thrust, and Arbogast goes on to pay lip service to the Academy’s public spirit and zeal in geodetic and astronomical operations:

But this work, which will imprint upon the determination of the new units the ultimate degree of precision, is of such a nature that it cannot be completed promptly. Nevertheless, the interests of the Republic and of commerce, the projects under way on reforming the currency and on the cadastre of the whole of France—all these matters require that adoption of the new system of weights and measures be no longer delayed.¹¹⁵

Eight days later the Academy was suppressed, in circumstances that will concern the next chapter. Those of its responsibilities deemed to be in the public interest devolved upon the Committee of Public Instruction. “I do not know,” wrote Lavoisier to Delambre, then at Amiens, “whether I still have the right to call you my colleague,” assuring him, however, that some way would be found to continue the survey.¹¹⁶ On 11 September, as we have seen, the ci-devant Academy’s commission was redesignated the Temporary Commission of Weights and Measures. Reporting henceforth to the Execu-tive Council of Ministers, it was assigned quarters near the Convention in order that deputies might keep it under surveillance.¹¹⁷

In principle the Commission was to consist of all those members of the Academy who had been concerned with weights and measures. Tillet and Meusnier were dead. Condorcet was in hiding. Those remaining until the December purge were, to recapitulate, Borda, Brisson, Cassini, Coulomb, Delambre, Haüy, Lagrange, Laplace, Lavoisier, Méchain, Monge, and Van-dermonde. Sitting for the Committee of Public Instruction were Arbogast and Fourcroy, the latter a former academician. Finally, Prieur de la Cote d’Or, now the member of the Committee of Public Safety who was taking technology for his province, joined himself to their deliberations to repre-sent the regime.¹¹⁸

There Prieur sat, then, a colleague of Lavoisier, Laplace, and Lagrange. The Temporary Commission elected the same officers as formerly, Borda to be chairman, Haüy to be secretary, Lavoisier to be treasurer. Never one to shirk responsibility, Lavoisier had had custody of the funds granted for the metric system since September 1791. His arrest along with the entire company of Tax Farmers came on 24 November 1793. At the instance (almost certainly) of Borda, the Temporary Commission dared intervene on his behalf. On 18 December it addressed a petition to the Committee of General Security asking that Lavoisier be paroled during the mornings under the guard of a gendarme in order that he might continue his collaboration in the work on weights and measures.¹¹⁹

There is no evidence that Prieur opposed the move in open committee. In Delambre’s view, however, and in that of his colleagues, the purge of the Temporary Commission five days later on 23 December was retribution for this démarche:

The secret reason was that Prieur de la Côte-d’Or, member of the Committee of Public safety and a man altogether worthy of the confi-dence of the government of which he was a part, had taken some share in the initial work of the Commission, that he had even presented a nomenclature for the new decimal system, and that he attended all the meetings that were held at Lavoisier’s house; that after these confer-ences, it often happened that they would talk politics; that rather sharp debates arose between those who no longer merited any confidence and the member of the Convention who has distinguished himself by his hatred for kings; that in these discussions Prieur would most often find himself alone against everyone and that the force of the reasons that he opposed to his adversaries did not sufficiently repair his disadvantage in point of numbers; in consequence he nourished a profound resentment, especially against Lavoisier and those of his colleagues who, like Borda and Coulomb, had shown themselves most ardent, most intel-ligent, or wittiest in the disputes. Such were the motives that dictated to Prieur the decree which has just been cited and which for the sake of form, he dressed out with the signatures of his colleagues Barère, Robespierre, Billaud-Varenne, etc., whose names appear after that of Pri-eur de la Côte-d’Or.¹²⁰

It is to be noted, in deciding what credence to give these suspicions, that Delambre had not been present at the gatherings in question. He attributed the honor of finding himself in such distinguished company to the intention, already hinted in the law of 1 August, to abandon the survey of the meridian altogether and to adopt the provisional meter as definitive.

Perhaps the intention does not much matter, however. For in effect the purge of the Temporary Commission brought a halt, or at least a hiatus, not only to the meridional survey, but to the policy of a provisional reform. The very day of the purge, Prieur himself was sent on an information mission to determine the needs of the Army of the North and to take measures of general security at his discretion.¹²¹ Left to the passive chairmanship of Lagrange, the “regenerated” Commission, as Monge called it in a report thanking the Committee of Public Safety, lapsed into inactivity, and the execution of the law of 1 August calling for a provisional meter fell into abeyance along with the survey of the meridian between “Barcelona and Dune-Libre.”¹²²

1 PVCd’IP 1, pp. 241–242.

2 Cited in Delambre, Base du système metrique décimal (3 vols., 1806–10), 3, 582. Hereafter cited as Base.

3 For a review of the historiography of the bicentennial, see Kaplan (1993), part 4.

4 The revisionism was anticipated by Favre (1931). John L. Heilbron, “The Measure of Enlightenment,” in Frängsmyr, Heilbron, and Rider (1990), pp. 207–242, is the clearest and most comprehensive brief account. The classic social history of weights and measures is Kula (1970), translated into French (1984) and English (1986). Two recent French collections, both examples of the anthropological trend in current social history, contain much detail on partic-ular practices: Garnier, Hocquet, and Woronoff (1989); Garnier and Hocquet (1990). Another, very useful, collection, Debarbat and Ten (1993) contains papers on the Spanish operations as well as those in France.

5 Arthur Young, Travels in France during the Years 1787, 1788, 1789 (1792), quoted from Cambridge University Press edition (1929), pp. 406–407. For a modern overview, see Zupko (1978).

6 Bureaux de Pusy in an opinion attached to marquis de Bonnay, Rapport fait au nom du Comité d’Agriculture et de Commerce sur l’uniformite à établir dans les poids et mesures(6 mai 1790), BN, Le29.633; Delambre, Base 1, p. 14.

7 For excellent summary discussions, see E. Gruter, “Le concept de mesure,” in Garnier, Hocquet, and Woronoff (1989), pp. 3–42; and J.-C. Hocquet, “Introduction,” in Garnier and Hocquet (1990), pp. 9–20.

8 Kula (French edition, 1984), pp. 170–210. Such demands may be sampled in AN: F12. 1288.

9 J.-B. Hocquet, “Le Roi et la reglementation des poids et mesures en France,” and M. Touzery, “Contribution à la géographie des mesures agraires: Le travail des arpenteurs de Bertier de Sauvigny, 1776–1790,” in Garnier and Hocquet (1990), pp. 23–34, 63–84.

10 Charles Marie de La Condamine, “Remarques sur la Toise-étalon du Châtelet,” MARS (1771/Pt I, 1774), pp. 482–501.

11 M.-C. Chabalian, J. Forien, B. Garnier, “Balances et poids,” in Garnier, Hocquet, and Woronoff (1989), pp. 101–167.

12 La Condamine, “Nouveau projet d’une mesure invariable propre à servir de mesure commune à toutes les nations,” MARS (1747/1752), pp. 489–514.

13 Gillispie (1980), pp. 122–130.

14 PVAS, 27 June and 14 August 1789, fol. 170, 207.

15 For the proceedings, see Fernand Gerbaux and Charles Schmidt, eds., Procès-verbaux des Comités d’Agriculture et du Commerce de la Constituante, de la Législative, et de la Convention (4 vols., 1896–1910). Collection de documents inédits sur l’histoire économique de la Révolution francaise. Hereafter PVCA&C.

16 Observations de la Société Royale d’Agriculture sur l’uniformité des poids et des mesures (Le 4 février 1790). BN, Vz 1685 and Vz 1792. To this pamphlet is appended an attack by the astronomer Lalande, always something of a maverick, upon “the new system of measurement” that his colleagues intended to propose.

17 Ibid., pp. 9–10.

18 Ibid., pp. 25–26.

19 Ibid., pp. 25–26.

20 They cite A.-J.-P. Paucton, Métrologie, ou traité des mesures, poids et monnaies des anciens peuples et des modernes (1780), and Jean-Baptiste Romé de l’Isle, Métrologie, ou tables pour servir à l’intelligence des poids et mesures des anciens (1789).

21 Abeille and Tillet, op. cit., n. 16 above, pp. 118–119.

22 PVAS, 17 April 1790, fol. 91. The commissioners were Laplace, Coulomb, Lavoisier, Borda, and Tillet. There is no record of a report.

23 The standard biography is Bouchard (1946).

24 Gillispie (1980), pp. 529–533.

25 For the provincial academies, see Roche (1978), who is concerned entirely with their social role, however, and not at all with their actual proceedings.

26 Prieur, Mémoire sur la necessité de rendre uniforme . . . toutes les mesures d’étendre et de pesanteur (1790), pp. 9–10, n. 2.

27 3 vols. (1779–82), 1, p. 154.

28 Ibid., p. 15.

29 Ibid., p. 19, n.3.

30 Above, chapter 2, section 3.

31 Talleyrand, Proposition faite à l’Assemblée Nationale, sur les poids et mesures, par M. l’évêque d’Autun (1790) (BN, Le29.632). The Avertissement containing these preliminary observations is not contained in the text printed in AP (9 March 1790), 1 ^ere série, 12, pp. 104–108, which gives the body of the proposal and the draft of the law.

32 AP, 1 ^ere série, 12, p. 105.

33 Champagne (1979), pp. 133–134. The two texts are printed side by side in this doctoral dissertation, the purpose of which is to specify the contributions of Condorcet, Laplace, Lagrange, Legendre, and Monge to the creation of the metric system. Besides accomplishing that purpose, it is a mine of precise historiographical detail.

34 Gillispie (1980), pp. 117–130.

35 Ibid., p. 107.

36 Charles-François marquis de Bonnay, Rapport fait au nom du Comité d’Agriculture et du Commerce sur l’uniformité à établir dans les poids et mesures, to which is annexed Opinion de M. Bureaux de Pusy sur le même sujet, the two printed together by order of the National Assembly, 6 May 1790. A copy is in AN: ADVIII, 36. A military engineer and contemporary of Lazare Carnot at École Royale du Génie at Mézières, Jean-Xavier Bureaux de Pusy was much occu-pied with the division of France into departments and with reorganization of the Corps of Engineers.

37 AP, 1^ére série, 24, Séance du 26 mars 1791, p. 379.

38 ”Rapport fait à l’Académie des Sciences sur le choix d’une unité des mesures,” HARS (1788/91), pp. 7–16.

39 Marat, Les charlatans modernes (1791); on Cassini’s attitude, see Devic (1851), pp. 155–159. For modern critics, see Favre (1931), 114–130; Heilbron, “The Measure of Enlightenment,” in Frängsmyr, Heilbron, and Rider (1990), pp. 207–242; Dhombres (1992), pp. 26–30.

40 Riggs Miller, Speeches in the House of Commons upon the Regulation of the Weights and Measures of Great Britain (London, 1790), pp. 37–38.

41 Gillispie (1980), pp. 122–130; Sven Widmalm, “Accuracy, Rhetoric, and Technology: The Paris-Greenwich Triangulation, 178–88,” in Frängsmyr, Heilbron, and Rider (1990), pp. 179– 206.

42 Jean-Baptiste Biot, Essai sur l’histoire générale des sciences pendant la Revolution Francaise (1803), p. 36. Biot changed his tune when he was invited, along with Arago, to extend the survey of the meridian from Barcelona to the Balearic Islands. Their data, completed in 1807, gave a value for the meter that agreed with the official determination to within 0.0001 lignes. “This agreement,” he now concluded, “proves that the meter as deduced from the size of the earth is henceforth well known, and that whatever operations of this sort are made in the future, if indeed anything so considerable is ever undertaken, could not require any change. ” Recueil d’observations géodésiques, astronomiques, et physiques (1821). For the Biot-Arago expedition, see below, chapter 7, section 3.

43 ”Théorie du mouvement et de la figure elliptique des planètes,” MARS (1782/85). Laplace read the memoir before the Academy on 11 August 1784. He incorporated it with little change into Mécanique céleste (Book III, chapters 1–4), where he made no use or mention of data obtained in the metric survey. See Gillispie (1997a), pp. 113–123.

44 Grandeur et figure de la terre, p. 203.

45 Observatoire de Paris, MSS du Bureau des Longitudes, MSS Delambre, Z 137 (2). Un-dated note.

46 “Rapport fait à l’Académie des Sciences sur le choix d’une unité des mesures,” HARS (1788/91) 7–16, pp. 9–10. The later observations of J.-G. Tralles, a Swiss mathematician who was a member of the international commission on the meter in 1798–99 (below, chapter 7, section 3), convey the thinking of contemporary physicists. “The length of the pendulum is too complex an idea to serve as the unit of length. In making that determination it is impossi-ble to avoid considering the period and motion of the earth’s rotation. A thing entirely deter-mined in nature is thus made complicated and in part arbitrary. That would be to follow an unsystematic course contrary to the spirit of exact science, because what is purely geometric would be preceded by mechanical and astronomical considerations. Force and time would be the fundamental quantities, and they would have to be known before length could be defined. “Rapport . . . sur l’unité de poids,” Base 3, pp. 559–560.

47 For the text of Laplace’s lecture, see Dhombres (1992).

48 Quoted in Champagne (1979) from Manuscrits de Lagrange, Bibliothèque de l’Institut de France, Mss. 910, fol. 3v.

49 Condorcet to the president of the National Assembly, 11 November 1790. AN, ADVIII, 36. Jefferson, he goes on to say, had agreed to accept a determination at the 45th instead of the 38th parallel, and Spain had sent an envoy to Paris to follow the work in order that a comparative determination might be undertaken at a latitude of 45° south in the New World.

50 PVAS, 29 September; 6, 13, 20 October 1790, 109, fol. 224–225.

51 PVAC&C, 359.

52 PVAS, 13 July 1790, 109, fol. 143. For a collection of these proposals, see AN: ADVIII, 36.

53 PVAS, 10 November 1790, 109, fol. 233.

54 Lavoisier to Conseil du Departement de la Nièvre, 7 December 1790. OL, Correspon-dance 6, pp. 205–206.

55 Condorcet to the president of the National Assembly, 11 Nov. 1790, AN, ADVIII.36; AP 21, p. 323.

56 PVAS, 15 December 1790, p. 109, fol. 258.

57 “Rapport fait à l’Académie des Sciences, par MM Borda, Lagrange, Lavoisier, Tillet, et Condorcet,” le 27 octobre 1790, HARS (1788/1791), pp. 1–6.

58 The commission consisted of Borda, Coulomb, Darcet, and Lavoisier together with Tillet, who made the tests. See PVAS, 15 January 1791, 109, fol. 267.

59 Borda, Lagrange, Laplace, and Condorcet, “Rapport fait à l’Academie des Sciences, sur le choix d’une unité de mesures,” 19 March 1791, HARS (1788–1791), p. 11. On decimilization, see Heilbron (1998), pp. 96–97.

60 Gillispie (1980), pp. 114–115.

61 AP (23 Sept. 1790), 1ére série 19, pp. 148–155; the full text of Aubry’s proposal is an annex to the session of 15 December, 20, pp. 493–507.

62 AP (23 Nov. 1790), 1 ^ere série, 20, pp. 698–721.

63 Dreux (1933), p. 16.

64 “Réflexions sur la carte et le cadastre de la France, Bibliothèque de l’École Nationale des Ponts et Chaussées,” MSS 2147.

65 Gillispie (1980), pp. 45–47; Brian (1994), pp. 256–286.

66 Ms. cited n. 64, and also a later report, “Situation du travail du Bureau du Cadastre et Transport au 30 frimaire de l’an deuxième,” loc. cit., MSS 2402. On the work of the cadastre, see below, chapter 7, section 3.

67 PVAS, 12 May 1792, 109 (2), fol. 147–150.

68 PVAS, 11 July 1792, 109 (2), fol. 204–207. The report is in the pochet for that session.

69 PVAS, 6, 9, 13 April 1791, 109 fol. 318–321. Cf. HARS (1788/91), pp. 17–20.

70 Gillispie (1980), pp. 122–130.

71 PVAS, 17 March 1792, 109 (2), fol. 101; cf. Gillispie (1980), pp. 126–127.

72 PVAS, 5 May 1792, 109 (2), fol. 139.

73 Delambre, Histoire de l’astronomie au dix-huitième siècle (1827), vol. 6 of his Histoire de l’astronomie.

74 Delambre, Histoire de l’astronomie (1817–27). The title varies from volume to volume so as to specify the period covered.

75 Delambre also gathered materials for an uncompleted history of geodetic surveys in-tended to be volume 7 of Histoire de l’astronomie. Edited by G. Bigourdan with the title Grandeur et figure de la terre (1912), it contains several confidential bits of information that he would have been indiscreet to publish in Base du Système Métrique, which was conceived by Delambre to be at once the completion of his task and its history. For a catalogue of Delambre’s manuscripts, see Michelle Chapront-Touzé (1985).

76 Delambre, Histoire de l’astronomie, 6, pp. 756–757.

77 “Expériences pour connoître la longueur du pendule qui bat les secondes à Paris, par MM Borda et Cassini,” Base 3, pp. 337–401.

78 “Expériences de Lavoisier et Haüy, du 4 janvier 1793,” Lavoisier, OL 6, pp. 683–685. This is a very summary report. A more complete one by Borda, Lagrange, Condorcet, and Laplace appeared in “Rapport fait à l’Académie des Sciences, le 19 janvier 1793, sur l’unité des poids et mesures & sur la nomenclature de ses divisions,” Annales de Chimie 16 ( Jan. 1793), pp. 267– 282.

79 Though not given in the Procès-Verbaux, Borda’s report was printed in Extrait du registre de l’Académie Royale des Sciences du 2 mai 1792, BN Le33.3U. Also AN, ADVIII, 36; cf. AP, 1 ^ére série, 43, pp. 260–263, séance du 11 mai 1792.

80 Borda, “Expériences sur les règles destinées à la mesure des bases de l’arc terrestre,” in Base 3, pp. 313–335. Cf. Delambre’s account of measuring the bases, 2, pp. 1–62. He gives drawings in Plates I–V.

81 Base 1, p. 21; Borda, “Expériences sur les règles destinées à la mesure de l’arc terrestre,” Base 3, pp. 313–336.

82 Adapted from Bigourdan (1901), pp. 109–113.

83 Base 2, pp. 160–240.

84 Grandeur et figure de la terre, pp. 202–203.

85 For these corrections in general, see Base 1, pp. 112–145, and for the correction tables Delambre constructed and used, 1, pp. 167–175. Delambre gave an account of his mathemati-cal techniques in Méthodes analytiques pour la détermination d’un arc du méridien (An VII, 1799).

86 “Mémoire sur les opérations trigonometriques dont les resultats dépendent de la figure de la terre,” MARS (1787/89), pp. 352–383, on p. 358. Cf. Itard, “Legendre,” DSB 8, pp. 135–136.

87 Base 1, pp. 176–180; 2, pp. ix–xiii, 683–712.

88 Base 1, p. 93; 3, pp. 415–433. For the measurement of the bases, see below, chapter 7, section 3.

89 Méchain reported his observations in a letter to Borda, 13 February 1793, of which a copy is conserved in the Bibliothèque de l’École des Ponts et Chaussées, MS. 1504.

90 Méchain to Borda, 21 nivôse an II (10 January 1794). A copy of this important letter is in the Bibliothèque de l’École des Ponts et Chaussees, MS 1504. Cf. Delambre, “Éloge de Méchain,” MIF 6 (1806), pp. 11–14.

91 Delambre to Madame d’Assy, 5 September 1792, in Bigourdan (1901), pp. 119–122.

92 Base 1, 33–34. For Delambre’s narrative of this phase, see also Grandeur et figure de la terre, pp. 210–212.

93 On 30 November 1793 Méchain sent a detailed accounting to Lavoisier in the latter’s capacity as Treasurer of the Commission of Weights and Measures. Lavoisier could never have seen it, for he had been arrested the previous week, on 24 November. Méchain summarized it in his letter to Borda of 14 January 1794. (Bibliothèque de l’École des Ponts et Chaussees, MS. 1504.)

94 Ibid.

95 Base 2, pp. vii–x, 563–631; Grandeur et figure de la terre, p. 234.

96 He was less charitable in the memoir published long after his death, where he expresses the bitterness he privately felt over Méchain’s secrecy and the delays caused in 1796 and 1797 by his then inexplicable efforts to return to Barcelona instead of cooperating in the completion of the triangulation in southern France and in the measurement of the base at Perpignan. Grandeur et figure de la terre (1912), pp. 219–225.

97 Base 1, p. 41.

98 AN, AF*56, 8; printed in PVCd’IP 3, p. 239.

99 8 nivôse an II. The decree is signed by Carnot, Robespierre, Barère, Billaud-Varenne, R. Lindet, and Couthon. A copy is in the Bibliothèque de l’École des Ponts et Chaussées, MS. 724.

100 Base 1, p. 49. Prony’s orders from Paré, Minister of the Interior, are dated 18 nivôse an II (7 January 1794). Bibliothèque de l’École des Ponts et Chaussées, MS 724.

101 Delambre to Prony, 13 nivôse an II, Bibliothèque de l’École des Ponts et Chaussees, MS 7211.

102 Base 1, p. 49.

103 Above, section 2.

104 AN, ADVIII, 36; also F17.1095, dossier 2, pièce 3; PVAS, 21 April 1792, fol. 119; also 2 May 1792, fol. 138.

105 PVCd’IP (L), 14 May 1792, pp. 294–295.

106 PVAS, 17 November 1792, fol. 295.

107 PVCd’IP 1, p. 241.

108 PVCd’IP 1, p. 227.

109 PVAS, 21 December 1792, fol. 323–324. For Borda report, see above, n. 77.

110 Above, n. 78.

111 Rapport fait à l’Académie des Sciences, le 19 janvier 1793, sur l’unité des Poids & sur la nomenclature de ses divisions. PVAS, 19 January 1793, fol. 327–335. Never printed by the Academy, this report was published in Annales de Chimie 16 ( Jan. 1793), pp. 267–282.

112 Précis historique sur l’uniformite des poids et mesures, suivi de deux projets de décret et de quinze tables propre à faciliter l’application du Systême Decimal, aux Poids, aux Mesures, aux Monnoies, et aux Temps. The authors of this interesting pamphlet were two deputies, Frécine of the Loire-et-Cher and Loysel of the Aisne. It goes further than any of the scientific texts in giving a detailed tabulation for converting hours, minutes, and seconds into decimal subdivisions of a ten-hour day, 100 minutes to an hour and 100 seconds to a minute. The only copy I have seen is in the Bibliothèque de l’École des Ponts et Chaussées, MS 2149.

113 PVCd’IP 2, pp. 9, 17; No record of the Borda, Lagrange, Monge report is to be found in the Procès-Verbaux of the Academy. It was printed in Annales de Chimie 18 ( July 1793), pp. 137–162. The authors do not state that the report was delivered at the séance publique on 10 April, but a reference by Delambre, Base 1, p. 59, makes it virtually certain that such was the case. For the initial rejection of this alternative scheme, see above, this section.

114 PVCd’IP 2, pp. 14–20.

115 Ibid., p. 15.

116 Lavoisier to Delambre, ca. 9 August 1793, Fric copy.

117 PVCd’IP 2, pp. 384–385.

118 Ibid., pp. 386–387; Bouchard (1946), pp. 294–298.

119 PVCd’IP 3, p. 237. On 21 December, the Convention’s Comité des Assignats et Monnaies petitioned the Committee of Public Safety in the same sense, acting (it would appear from the text) at the instance of the Commission Temporaire (PVCd’IP, 3, 238).

120 Grandeur et figure de la terre (1912), p. 213. Note that in fact the signatories were Prieur, Barère, Carnot, Billaud-Varenne, and Lindet (above, section 4). Delambre in Base 1, pp. 49– 50, gives them as “Barère, Robespierre, Billaud-Varenne, Couthon, Collot d’Herbois, etc.” He now says, “In transcribing the text of this decree, . . . I suppressed the signatures of those who were still living, while reserving the intention of disguising nothing if I should one day have occasion to write the full history of our survey.” This may explain the omission of Prieur, Carnot, and Lindet in the earlier account, but not of Carnot and Lindet in the later, nor the inclusion of Robespierre, Couthon, and Collot d’Herbois in either of them.

121 AN, AF*56, 8.

122 Monge, “Adresse de la Commission des Poids et Mesures à la Convention Nationale,” PVCd’IP 3, pp. 249–252.