CHAPTER IX

Positivist Science

1. DISCIPLINE FORMATION

The sciences that emerged phoenix-like and transformed from the fires of revolutionary change have been well studied for themselves and will continue to be.¹ Let us attempt in conclusion not a full, documented account but a summary portrayal of the character of the scientific action—“mouvance” says it better—in this, the second generation of French preeminence in science.

With respect to organizational aspects, the keynotes were professionalization and discipline formation. Although the two were intimately connected, the one concerns primarily the situation of science in the larger society, the other primarily the practice of science within itself. Professionalism, indeed, was to the Republic of Science what citizenship was to the Republic proper, the signet of self-governance and collective self-esteem within the respective contexts. Factors differentiating the status of science in 1815 from what it had been in 1789 were the constitutional and civic basis of institutions formerly qualified as royal, the opening of careers that afforded a livelihood for research combined with teaching, and—perhaps most important—the creation of higher education in science.²

Not only the mathematical physicists of the coming generation, but even the mathematicians, Lazare Carnot, Cauchy, and Poncelet, had been trained as engineers. In like manner, in chemistry, those with a bent to industry—Berthollet, Chaptal, Gay-Lussac, Leblanc, Clément, Desormes—came to the fore. Similarly, in medical arts, hands-on clinical practice stemmed largely from surgery. The pattern is evident. It inheres in the advancement to professional dignity and even to leadership of skills, now become disciplines, that had been relegated in earlier times to the status of trades.

Professions are defined by their social role and disciplines by their content. Membership in a profession presupposes mastery of the relevant discipline, but until the turn of the nineteenth century, only the three classic disciplines of theology, law, and medicine were fully professional. Mathematics and astronomy were not. Nor had chemistry fully reached that stage in Lavoisier’s lifetime. In point of practice and method, mathematics and astronomy were little changed by professionalization, and chemistry not fundamentally. Medicine, however, was transformed in those respects, but not with respect to its professional standing. By contrast, the disciplines that mainly concern us in what follows, comparative anatomy, experimental physiology, and mathematical physics, took form concurrently with the professionalization of science in general. The formation of disciplines and their professional standing have entailed, in a certain sense, the partial separation, or perhaps insulation, of science from the larger society.

A related complementarity in science generally, that between theory and practice, is relevant, although in different ways, both to professionalism and discipline formation. Insofar as members of the general public at large take any interest in science beyond its applications to technology and medicine, they seek to comprehend what can be conveyed of its current theories concerning the structure and functioning of nature: gravity, evolution, relativity, the big bang, the genome, and so on. Laymen take very little interest in actual scientific practice, except when a scandal involves misconduct. The distinction between theory and practice also pertains to scientific revolutions, and in the same manner that a distinction between ideology and civic practice does to the political revolution. We argue in the Introduction that the lasting changes in the functioning of the body politic wrought by the French Revolution were structural in kind rather than ideological. To be sure, revolutionary leaders and their followers were motivated by the succession of theories about man in society that moved the Revolution ever left-ward until its consolidation following the fall of Robespierre and prior to the First Consul’s self-conversion into an Emperor. But none of those theories outlived their day. Their significance, and it was great at the time, quickly became historical and has, indeed, fascinated historians more than have the work-a-day changes that proved permanent.

In these concluding pages we shall argue that a comparable distinction obtains between, on the one hand, the actual practice of the scientists who formed the modern disciplines of a rigorous biology and a mathematical physics, and on the other hand the theories that motivated and divided them. Others beside the present author may wish to consider whether the point is relevant to the differentiation between normal science and scientific revolutions that figures in the profound analysis of the latter by his close friend and longtime colleague, the late Thomas S. Kuhn. There can in any case be no doubt but that disputes in zoology between Cuvier and Lamarck turned on theory of species and those between Cuvier and Geoffroy Saint-Hilaire on theory of morphology; or that Xavier Bichat’s preoccupation with vital forces offended Francois Magendie’s sense of the necessity to achieve a rigorous physiology; or that Laplace and his disciples thought to reduce the world picture of Newtonian astronomy to the action of forces of attraction and repulsion acting at a micro-distance on point masses, whereas their opponents constructed quite other models in analyzing problems of light, sound, heat, and electricity and magnetism. In the case of heat, Fourier preferred no model at all, which may be the reason that his analysis, though of seminal importance in mathematics, had virtually no influence on physics. Nor, finally, can there be any doubt but that models such as a mass-free elastic aether and interconvertibility of work and energy (which neither Laplacians nor their opponents considered) became staples of nineteenth-century physics.

As in the case of political theory in the Revolution, these issues did motivate the actors and are what have chiefly interested historians. They have in consequence been well explored and need no further exposition here. Those disagreements were not, however, what drove the formation of the respective disciplines. What did was rather agreement on the practice and conduct of science, to wit the application of mathematics, vivisection, and comparative anatomy to problems of physics, physiology, and zoology.

It will be evident in the following remarks, and perhaps from the foregoing, that I have found the reading and rereading of Cours de philosophie positive very suggestive. Drawn from the practice of science, not from the theories advanced by scientists, Comte’s historicist scheme of knowledge may not have withstood the test of time as well as have the epistemologies of such as Plato, Leibniz, Hume, or Kant, and few philosophical injunctions are less appealing than the authoritarian political prescriptions Comte would lay down for governors to put in place when “social physics,” the science of society, should enter the positive stage in its turn. All that apart, historians of science may well find Comte, X-1814, rewarding as an acute, attentive, and informed critic of the science of his own time. He was more so, curiously enough, for the biological sciences than for the exact sciences in which he had been trained, perhaps because he could see more clearly from outside. With respect to both, however, he is a philosopher and goes deep.

In contrast to the reports that Delambre and Cuvier prepared for Napo-leon in 1809 on the progress of the physical sciences and life sciences since 1789,3 Comte penetrates beneath the surface to what was fundamentally at issue with respect both to methods and results. Once a science enters the positive stage, its goal is no longer a metaphysical quest for truth nor a rational theory purporting to represent physical reality. There is no longer any question of classifying information about the world in a manner consonant with the nature of things. Science is composed of laws, not theories. Laws are correlations of observable facts. The goal of science is to make accurate predictions based on exact knowledge of the facts. We know in order to predict. We predict in order to control events within the limits of the possible. Like the scientists of whom Comte writes, and also like Bonaparte, he was a product of his times. Rigorous attention to gathering facts and to forming policies that get results were watchwords of the men of affairs in public and private life who, whatever the carryover from the old regime, built the institutions of a modern polity on foundations laid down once the ground was cleared.

2. COMPARATIVE ANATOMY

As is well known, the word biology was a neologism embracing topics stemming from natural history on the one hand and medicine on the other. The sciences of life, wrote Comte in 1833, are capable of stating general laws in the measure that they address themselves to analyzing the relation between the diversity of organic forms and the physical milieu in which each form exists. “Formulated as mathematically as possible,” he continued, “the dual problem of biology may be posed in these general terms: given the organ, or organic modification, find the function and action, and reciprocally.”⁴ Over the years many biologists would have agreed with Comte’s definition, prominent among them Cuvier, from whose practice Comte took it. Among their many colleagues in disageement would have been Lamarck and Treviranus. They were the ones who in 1802 had coined the word independently of each other and in a spirit very different from Comte’s. They called for a comprehensive study of the phenomena of life. Although that is what biology does, it has never taken on an identity comparable to that of astronomy, physics, and chemistry, its predecessors in the positivist sequence. Development of the field has prospered amid a tension between the poles of vitalism and mechanism, holism and reductionism, although neither pair quite reduces to the other. Phases of its history are marked by the successive emergence of subdisciplines, each in its turn a candidate for the role of cutting edge: histology, morphology, embryology, cytology, pathology, evolution, heredity, genetics, molecular biology, genomics. All the while, and to a degree earlier, the umbrella terms zoology and botany designated study of phenomena that natural history assigned to the animal and vegetable kingdoms.

Whatever the emotional appeal of vitalism and holism, and however fruitful much of the work produced under such inspiration, Comte did identify the dynamic that ultimately drove the science. He focused his anal-ysis on the areas where the action then was: comparative anatomy and experimental physiology. Based in the Muséum, Cuvier, Lamarck, and Geoffroy Saint-Hilaire were the foremost practitioners of comparative anatomy. In their hands it became a keen analytical tool serving the purposes of taxonomy. Working out of the Hôtel-Dieu, the Faculty of Medicine, and the Collège de France, Bichat and Magendie, both trained in surgery, were the principal founders of experimental physiology as a scientific discipline in its own right. In their hands physiology became an experimental science practiced on animals and not merely a set of theories about bodily functions or a collection of descriptive observations of specific pathologies in human beings. There was no conjunction of comparative anatomy and experimental physiology in our period, but the protagonists in each field were aware of work in the other. Commitment to rigor resonated between them in the ambience of the Institut de France.

A passing observation by Lamarck in Histoire naturelle des animaux sans vertèbres will convey the theme of our discussion of comparative anatomy. “It is,” he wrote, “fairly curious to notice how, in spite of differences in enlightenment and intelligence, and in spite too of the confidence everyone has in preferring his own opinion to that of others, unanimity is nevertheless virtually complete among zoologists in their ordering of the best established classes among animals.”⁵ How, given what we know about their theoretical disagreements, was such consensus possible? Perhaps a historical thought experiment may suggest an answer. Let us imagine that Cuvier had died two years before he did, say in 1830. He would still have grown corpulent, arrogant, and oracular in his later years, but would not have had time to compose the insulting éloge of Lamarck that has offended all Lamarckians and many others. Nor would he have engaged in the acrimonious debate with Geoffroy Saint-Hilaire, his friend and partner in their slim, inquiring youth, concerning unity of type, a quarrel trumpeted to the world by Goethe. Absent those events, neither Cuvier nor Lamarck would have contributed less than he did to positive scientific knowledge. As for Geoffroy, had his work stopped in 1830, he would have gone less far down the largely blind alley of his later memoirs on teratology. Had all that been the case, the historical perspective on their scientific relations would be formed, not by the quarrels of old age, but by reading the work of their prime and the writings of their colleagues. The image of three antagonistic proponents of mutually irreconcilable research programs would not then have taken center stage, or rest on anything more substantial than gossip.

On the contrary, the first colleague cited by Lamarck in Histoire naturelle des animaux sans vertèbres was Cuvier, à propos of a fairly abstract difference of opinion over the definition of animal. He there identifies Cuvier as “the most celebrated zoologist of our time and, in effect, the most distinguished.”⁶ The two first cited by Cuvier in Le Règne animal were Lamarck and Geoffroy, who, he acknowledges, had left him little to do on shellfish and quadrupeds, respectively.⁷ As for Geoffroy, in Philosophie anatomique he first tips his hat to Newton. The next he names is Cuvier, whom Geoffroy thanks for having recognized in a memoir read before the Institute in 1812 that Geoffroy had suggested to him original views on the composition of the cranium in vertebrates.⁸ Later, in 1828, Cuvier stated in the preface to the second edition of Le Règne animal that the most important debt he owed on the subject of mammals was to the work on which Geoffroy and Frédéric Cuvier, his younger brother, had collaborated.⁹ It is evident from reading the major works of our three authors, as well as the memoirs they published in journals, that the pair Cuvier-Lamarck, followed by the pair Cuvier-Geoffroy Saint-Hilaire, cited each other more frequently than either did any other zoologist. There was, however, little overlap between the work of Geoffroy and Lamarck.

It is further evident from such a reading that the method of analysis came from Cuvier, the major division between vertebrates and invertebrates from Lamarck, and the increasing attention given to morphology (the name was not yet coined) from Geoffroy. In that last respect, however, the more detailed and thorough work of Savigny on the mouth parts of insects and arthropods was what permitted integration of morphology into the overall enterprise of a systematic classification.¹⁰ Cuvier and Lamarck agreed on the merit of his research on alcyons, finding that “the observations of M. Savigny are epoch-making.”¹¹

For it is not a question only of the three major figures. We here meet with the most substantial collective body of work to be encountered in all history of science until that time. Its origin may be placed precisely. In 1795, a youthful Geoffroy and youthful Cuvier, the latter new to the Museum, collaborated on a memoir on mammals. They there expressly rejected the Linnean method of classifying species according to easily recognizable external features, and initiated a program of classification based on internal anatomical organization.¹²

Its execution presupposed a radical new departure in technique, namely dissection and not merely description of their specimens. The background of anatomy was surgery, not natural history. Until then a scalpel was the surgeon’s tool, not the naturalist’s. There had been nothing systematic about the “tripailles” with which, in the eyes of most readers, Daubenton had disfigured Buffon’s charming and (except for those plates) beautifully illustrated Histoire naturelle. Cuvier’s ensuing Leçons d’anatomie comparée in five volumes (1799–1805), far more technical and less widely read than Le Règne animal, was arguably his scientific masterpiece. But it was not his alone. He called on Constant Duméril for assistance in preparing the first two volumes and on Georges Duvernoy for help with the last three. Composing Le Régne animal some ten years later, he recognized that Opel and Henri Ducrotay de Blainville had preceded him in the anatomical preparations on which he there based the division of reptiles. Attending Blainville’s lectures was Auguste Comte’s inroduction to biology. Cuvier turned to Pierre Latreille to prepare the third volume of Le Régne animal, which treated insects. Lamarck had also thought of Latreille, but too late, to do the same parts of Histoire naturelle des animaux sans vertèbres. Both Lamarck and Cuvier studied the fossils of the Paris basin, Lamarck the invertebrates and Cuvier the vertebrates, on which the latter collaborated with Alexandre Brongniart for the aspects having to do with geology. Savigny’s plates in the Description de l’Égypte were prepared by Victor Audouin, while Geoffroy’s son, Isidore, did his father’s. Cuvier’s last work, on fish, was edited and completed by Achille Valenciennes.¹³

In scanning the entire literature of zoology from 1800 to 1830—major treatises, the Annales du Muséum, more or less important articles in other journals, the three dictionaries of natural history14—and taking account of authors who cite each other, one arrives at the number of some fifty-odd serious researchers. That is without counting twenty-odd foreign contributors and some fifteen botanists, whose field was closely related. The whole constituted in effect a scientific community based on the Muséum as its principal locus for research and communication.

There were, of course, differences of interpretation expressed, for the most part, in prefaces, notes, and occasional obiter dicta in the body of their works. What historians normally call the conflicting theories of the trio of principal authors—transformism, branchings, unity of composition—were in their own vocabulary philosophical standpoints. The word always appears with a modifier, as in Lamarck’s Philosophie zoologique and Geoffroy’s Philosophie anatomique. The differences between the three leading figures are manifest, not only in the content of their work, but also, and perhaps in a more revealing fashion, in the relation of theory to observation in its development.

In Lamarck’s view, what we call theory had precedence over observation. It would be an exaggeration to say that theory was independent of observation, but it involved considerations on a higher plane. In his enormous introduction to Histoire naturelle des animaux sans vertèbres, he distinguished between the art of zoology and biological philosophy. The one concerns the classification of animals, the other the order of living nature. Lamarck sees in the latter a progression in the forms of life, not only in the past but continuing in the present. The temporal chain of being has, so to say, the dimensions of an escalator of being. Transformation of species over time is only one aspect of that vision, and not the most important. Throughout a long life, Lamarck never changed his outlook, but only its application. As early as Flore française in 1778, he made the same distinction between an artificial classification of plants and their natural order. There too he affected a certain scorn for the lowly task of taxonomy, to which however he devoted the major share of his time. Exactness was important so that naturalists might understand one another, but the main interest of natural history was not there.

In Geoffroy’s case, by contrast, philosophical motivation took precedence over observation in mid-career rather than at the outset. From the time that he was in Egypt, he began to meditate on the great forces of nature that are at the root of phenomena of light, heat, electricity, and life. He there also exhibited special enthusiasm for the more bizarre creatures, such as the polyptère bichir, the crocodile, the great Nile tortoise, the silure trembleur, and the torpedo ray. Only after he was recognized as an anatomist, however, did his dissections, which were always exactly performed and precisely described, begin to concern problems of morphology rather than taxonomy, about which he too came to express a certain disdain.

As for Cuvier, the four branchings, “embranchements”—vertebrates, mollusks, articulata, radiata—into which stationary categories he distributes species little variable in form—date only from a memoir of 1812, the year when his major book on paleontology, Recherches sur les ossemens fossiles, also appeared.¹⁵ There is every reason to believe that he then felt obliged to react against what he thought to be the more and more exaggerated views of his colleagues. However that may have been, the system of branchings had no more effect on his distribution of species into class, order, and genus than did transformism on Lamarck’s taxonomy. For that, they worked in effect as a tacit pair, the one on vertebrates, the other on invertebrates, not in harmony, but in tandem.

That is how they were perceived in the next generation. It was not to advance either of their theories that Cuvier’s and Lamarck’s successors gave themselves the trouble of republishing their principal works in the 1830s and 1840s. The eleven disciples who prepared the second edition of Le Règne animal pay little attention to the branchings.¹⁶ As to Histoire naturelle sans vertèbres, Henri Milne-Edwards and C.-P. Deshayes were the two most important of the four editors.¹⁷ The one had never believed in transformism, and the other renounced it. Apropos Lamarck’s discussion of motion among the infusoria, Milne-Edwards remarks: “As to the physico-physiological theory on which the hypothetical views of our author depend, it appears to us useless to discuss it.”¹⁸ Why, then, republish Cuvier and Lamarck, with all the corrections and additions that the progress of zoology entailed? Evidently because nothing as complete, as clear, as descriptive, and as comprehensible as were the two great syntheses had appeared in the interval since their initial publication. The history of modern taxonomy for the rest of the century is a series of additions, reattributions, and modifications in detail of classifications requiring only transposition to the time dimension and the operation of natural selection to become the outcome of the evolutionary process. It is, parenthetically, to be noted that Geoffroy’s Philosophie anato-mique never had a second edition.

The central feature of the method Cuvier developed for basing a taxonomy on comparative anatomy was that classification depends on the relation of function to form and arrangement in internal as well as external anatomical structures. The general problem is the relation of the structure of an animal to the life it leads. Cuvier begins his Anatomie comparée with vital functions. First are those relative to the external world. The categories are two, sensibility and locomotion. Second are functions relative to the internal economy of the creature, namely digestion, absorption, circulation, respiration, transpiration, excretion, and generation. The puzzle then is to identify the organs proper to each: serving sensibility are nervous system, eyes, ears, nose, tongue; serving locomotion are skeleton, legs, paws, hooves, fins, wings; serving digestion are mouth, esophagus, stomach, intestines, liver—and so on for all the rest. The actual work consisted in dissecting specimens of every species known in order to make a systematic comparison, species by species, of the presence or absence, form, function, and relation to other structures in the body, of each organ in every animal, and further to give an account of the variation and relative importance of each structure from species to species. This was an enormous task. It might at its level be compared to the genome project of the present day. Clearly, it required a team effort.

The goal was a taxonomy arranging animals in a natural series on the model of the botanical systematics of Jussieu’s Genera Plantarum of 1789. For that purpose the signal characteristics of each species had to be determined in order of importance. The first cut establishes classes—mammals, birds, reptiles, fish, mollusks, and so on, each of which exhibits certain gross anatomical features that distinguish it. At the successively lower levels of orders, genera, and species, differences of physiological function in the several systems of organs and even individual organs become the telling factors. Cuvier stated the guiding principle, which Jussieu before him had called Subordination of Characters, though in a more restricted anatomical sense, as follows:

Since the parts of any being must fit together [avoir une mutuelle convenance], there are certain characteristics of configuration that exclude others; there are others, however, which necessitate them. When we know such and such characteristics in a living being, we can calculate those that coexist with others, or those that are incompatible with them. The parts, the properties, or the characteristics of configuration that have the largest number of these relations of incompatibility or of coexistence with others, or in other words which exert the most marked influence on the whole being, are what we call important characteristics, dominant characteristics; the others are subordinate characteristics, and they are so in varying degree.¹⁹

For example, an animal whose digestive tract can handle only meat must have a certain form of teeth to seize its prey; must also be capable of running fast; must have strong jaws, paws, and claws; must have keen eyes and/ or nose, and so on. It is, indeed, possible to deduce all these structures from any one of them, and also the absence of others. Incisor and cuspid teeth are never found in animals with horns. Every animal with hooves is herbivorous. “It is on the mutual dependence of functions,” Cuvier writes elsewhere, “that the laws which determine the relation of their organs is founded, laws of which the necessity equals that of mathematical or metaphysical laws.”²⁰

Such was Cuvier’s mastery of detail that he was able to trace the telling similarities or distinctions at the finer levels of systems of organs and individual organs that permitted dividing orders into genera and identifying individual species. The regulative as distinct from the methodological principle he called the Correlation of Parts:

Every organized being forms a whole, a closed and unique system whose parts mutually correspond and conduce to the same definitive action by their reciprocal reaction. None of these parts can change without the others changing also, and in consequence each of them, taken separately, indicates and gives all the others.²¹

This principle in turn derives from what he defines as Conditions of Existence (Comte took the term from the Le Règne animal ):

Since nothing can exist if it does not join together the conditions that make its existence possible, the different parts of each being must be so coordinated as to make possible the entire being, not only in itself, but in its relations with what surrounds it. The analysis of these conditions often leads to general laws as demonstrable as those deriving from calculation or experiment.²²

Here is how Lamarck stated the same principle in Système des animaux sans vertèbres:

I could here pass in review all classes, all the orders, all the genera, all the species of animals that exist, and demonstrate that the conformity of the individual and of their parts; their organs, their faculties, etc.,etc., are entirely the result of the conditions to which each race of each species finds itself subjected by nature.²³

As for Geoffroy, his methodological statements, if not his ideas, were less general, but his comments on the relation of structure to function in particular cases come down to the same thing. With respect to the oxygenation of veinous blood, for example, he writes “The respirable element [i.e., oxygen] is disseminated in two fluids [air and water] that are very different in nature and density. Thus an ordinate of the external world determines the condition of their respiratory organ; hence, two modes of respiration and, in consequence, two groups of animals according to whether they live in air or in the water.”24

3. EXPERIMENTAL PHYSIOLOGY

In completing his comparative anatomy, Cuvier reaches out to physiology and expresses hope for a rapprochement between the two sciences. The pre condition, in Comte’s view, was that the one should liberate itself from natural history and the other from medicine. On the side of physiology, the new departure dates from the work of Xavier Bichat, whose meteoric career, Napoleonic in its trajectory, transpired between 1795 and his death at the age of thirty-one in 1802.25 Institutionally, Bichat succeeded his mentor, Desault, chief surgeon of the Hôtel-Dieu, who died suddenly in 1795, and whose example he followed in leading troops of students from bedside to operating table in the new teaching of clinical medicine. Scientifically, he transcended that and set out to investigate, not merely the location and pathology of organs and structures, but their functioning and contribution to processes of life, disease, and death. In the seven packed years of his career, he published five treatises, the most famous of which are Recherches physiologiques sur la vie et la mort (1799) and the four-volume Anatomie générale, appliquée à la physiologie et à la médecine (1801).

The former seizes the reader’s attention with the opening statement: “Life is the ensemble of functions that resist death.” Part I of Recherches physiologiques treats of life, part II of death. Neither is a simple matter. Life has two divisions, organic and animal. The functions of organic life, which are common to all living things, animal and vegetable, are birth, nutrition, growth, and death. They are internal to the organism. The functions of animal life are sensitivity, perception, volition, and mobility. They relate the creature to the world. Categorical distinctions differentiate the two lives. The most obvious is the form of the respective sets of organs. Those supporting animal life—brain, eyes, ears, nose, mouth, vocal cords, voluntary muscles, and skeletons—are bilaterally symmetrical. Those carrying out the functions of organic life—heart, blood vessels, stomach, intestines, bladder, liver are irregular in form or, in kidneys and lungs, imperfectly balanced.

Bichat’s Recherches physiologiques was a transitional book. The first part, in a philosophical vein, reads like an eighteenth-century treatise of physiology. At the center of his thinking is the unbridgeable difference between vital laws and physical laws. Nevertheless, he rejected all efforts, such as those of Van Helmont, Stahl, and Barthez, to reduce the phenomena of life to a single, ineffable principle. The term pluravitalism, if such a coinage be allowed, may be said to encapsulate his standpoint. He followed Bordeu in holding that every organ is endowed with its own share of the sum of the vital forces that animate the organism.

Unlike Cabanis, Bichat wrote with an economy and immediacy such that in the first part of his book, one is a little surprised and somehow pleased to recognize the functioning of one’s own body in his account of its various systems. One feels like part of the story, in which passing remarks pique attention. Plants, for example, may be thought of as incomplete drafts of animals, a sort of canvas that “need only be dressed out with an apparatus of external organs suitable for establishing relations with the world.”²⁶ Let us not, he warns, confuse physical laws with those of social life. Both are solid but different. The onset of old age is precisely what we have observed in our parents and dread for ourselves. Bichat’s vein throughout Part I is observational. His material is drawn from medical knowledge, wide reading, and many autopsies. The information adduced from opening cadavers is subsidiary, however, and merely anatomical rather than functional in nature.

The second half of his book, treating physiological researches on death, is another matter. The vein is experimental, and graphically so. Deaths are of two sorts, natural and unnatural. Bichat gives short shrift to natural death, that which the ensemble of living functions resists until it prevails. It simply happens. Unnatural deaths are of two sorts, caused by terminal illness or by accident. Study of the former is very difficult. Diseases that affect human beings can rarely be reproduced in animals. Experiment is thus out of the question. Nor can observation be conclusive, since the progress of a fatal illness denatures the phenomena to be studied. For these reasons Bichat declares himself to be incapable of addressing precisely how diseases cause death. His interest in any case, though he would not have put it this way, was not medical. The deaths he does study through their effects on particular organs are accidental to the animal, but not to him. He caused them in order to determine in the negative the function of the organ he modified or excised. Vivisection was his principal tool, as it was of the first generation of experimental physiologists who followed his lead.

Prominent among those followers was Julien Legallois, who also died young, and who justified the method thus succinctly:

Experiments on living animals are among the greatest lights of physiology. There is an infinity between the dead animal and the most feebly living animal. . . . It does not suffice to observe the simultaneous play of all the functions in the healthy animal; it is above all important to study the effects of the cessation of such and such a function. It is in the determination by this analysis of the function of such and such an organ and its correlation with other functions that all the art of experiment on living animals consists.²⁷

In the always discriminating judgment of Georges Canguilhem, Legallois, but not Bichat is to be considered the earliest fully positive physiologist.²⁸ The spirit of his research was analytic rather than programmatic. Impressed with the exactitude of Cuvier’s comparative anatomy, he limited his problems, defined their parameters with exceptional care, and achieved precise determinations that, unlike many of Bichat’s generalizations, have stood the test of time. The two most notable were, first, the locus of the brain’s control of respiration in the medulla oblongata, and, second, the metameric properties of the spinal cord.

The four volumes of Bichat’s Anatomie générale followed Recherches physiologiques within two years. It is a work of systematization rather than experimentation. The central argument is that the fundamental building blocks of the human body are not, as commonly held, its several organs, but rather the tissues of which the organs are composed. The basic membranes have the same character and are subject to the same diseases whatever the organ in which they figure. Tissues are to general anatomy what the elements of matter are to chemistry, the constituents of bodily organs in the one case and of chemical compounds in the other. Thus the stomach is an assemblage of mucous tissue in the lining, serous tissue on the outside, and muscular tissue in between. Muscles consist for the most part of muscular tissue attached by fibrous tissue to the bones and are bounded by synovial tissue where they slide across other structures. Bones are mainly bony tissue with cartilaginous tissue at either end and marrow in the core. Not to list them all, Bichat distinguished twenty-one systems of tissue falling into two divisions. The first comprises those that pervade the entire organism, such as fleshy matter, the nervous system, the arterial and venous systems, and what would now be called metabolic systems. The second division comprises tissues pertaining to particular organs and functions such as the bony, cartilaginous, muscular, and glandular systems. Later anatomists have modified the identity and number of such systems in many ways. But the identity of histology as a subdiscipline of biology dates from Bichat’s work. The full title, Anatomie générale appliquee à la physiologie et à la médecine, would be more accurate if it were reversed. His great book is the work of a physiologist who had learned the body as a surgeon. He gives detailed descriptions of the texture and structure of all tissues while developing his treatment along functional lines. General anatomy was an analysis and in no sense a topography of the body. There are no plates, no diagrams of any sort. In that respect it may not be far fetched to compare it to another famous work of analysis, Lagrange’s Mécanique analytique.

Bichat’s originality has on occasion been called into question, most severely in careful studies by Othmar Keel.²⁹ Bichat himself acknowledged that he had the idea for the two lives from Bordeu. Underlying the definition of life in Recherches physiologiques was the widespread vitalist notion of a tension, even a conflict, between physical forces and life forces. He also recognized that reading the first edition of Pinel’s Nosographie philosophique (1798) had fixed his attention on tissues rather than organs as the locus of certain types of inflammation. In the second edition of that work, Pinel in turn paid tribute to the extension Bichat had given the matter in his early Traité des membranes (1798). He, Pinel, had drawn on that while improving his classification and account of diseases in the second edition.³⁰

Bichat in turn developed Pinel’s nosological criteria of tissue pathology into what in the next generation became the subdiscipline of histology. Published before the words biology or histology existed, Anatomie générale could appear at all only as a medical work. Bichat saw it that way himself. His vocabulary speaks unconsciously to the point, however. The word “tissues,” not all of which are membraneous, displaces membranes as the general term. Tissues are his subject, not diseases or their classification as in Pinel, but tissues, their character and structure, their physiological role in the functioning of the organism, their anatomical role in the constitution of its organs. The pathological state of tissues and therapeutic application of his findings are little prominent. Unlike Pinel, Bichat never practiced medicine nor ever treated patients. He taught anatomy and physiology to medical and surgical students, but did so in the manner, not of a healer and physician, but of what, in the parlance of a slightly later day, would be called a medical scientist.

Bichat’s originality was in the architecture of his work, not in its details, and his impact owed as much to its dynamism as to its content. Its influence was threefold, philosophical, physiological, and biological. Even while deploring the vitalist spirit of Recherches physiologiques sur la vie et la mort, Comte put Bichat on a high pedestal in the positivist pantheon. Treating objectification of the will in Die Welt als Wille und Vorstellung, Schopen-hauer considered that “nothing is more pertinent in confirming and clarifying the argument of the current chapter than the justly celebrated work of Bichat, Sur la vie et la mort. His considerations and mine reciprocally support each other. His provide the physiological commentary to mine, mine being the philosophical commentary on his. If we are read at the same time, we will be better understood.”³¹ Specifically, Schopenhauer’s dichotomy between the unconscious will to live and conscious volition corresponded to that between organic life and animal life.

Lamarck does not acknowledge Recherches physiologiques, but what energizes the evolutionary process in Zoologie philosophique is the force of living nature striving against destruction by forces of physical nature. Bichat was not the first to do experimental physiology (one need think only of Harvey), but the second part of Recherches physiologiques was far and away the most general and systematic experimental exercise yet to have been undertaken. It was Magendie’s starting point in transforming physiology from a theoretical and speculative to an experimental discipline and in securing its autonomy from medicine. In the critical footnotes Magendie added to the fifth edition (1822), he runs along the bottom of page after page pointing up to the absurdity of the ideas and the excellence of the work. Finally, and most important, Bichat’s initiation of the study of tissues was the first step in the two-hundred year sequence through which experimental analysis has penetrated the living organism to fix its elements successively in tissues, cells, nuclei, chromosomes, genes, and proteins, just as physical science has done (not in chronological order) in atoms, protons, neutrons, electrons, and quarks, with neither end anywhere in sight.

To no other physiologists of Bichat’s time, and only to leading scientists of any time, has it been given, whether by genius or by circumstances or by genius in the circumstances, to reach thus far beyond the bounds of their research.

In the estimate of John Lesch, whose account of the emergence of experimental physiology is the standard work, the medical people occupied to a greater or lesser extent with physiology in Paris between 1800 and 1820 were seventeen in number. Four among them (Nysten, Dupuytren, Legallois, and Magendie) were directly inspired by Bichat and undertook experimental investigations. The total number of qualified persons involved in experimental physiology was greater than that, however. Commissioners named by the Institute to report on particular researches (themselves well informed) mention at least half a dozen other investigators. Staff members in the veterinary schools of Alfort and Lyons also engaged, and very actively, in vivisectional research.³²

Nevertheless, experimental physiology had yet to become a viable specialty. Nor did it do so within the institutional structure of medicine, which was exclusively educational and clinical. There were no chairs of experimental physiology, no hospital posts, no recognized pattern for a career, no incentives for research beyond curiosity. Bichat and Legallois died young before beating out a professional path that others might follow. In order to make a living, Nysten abandoned research and concentrated on medical practice. Dupuytren’s career reversed the pattern of Bichat’s. Driven by ambition, he quit physiology and won the fame accruing to great performances on the surgical stage.

It was left to Magendie to make of experimental physiology rather a scientific than a medical discipline. That he was able to do so was owing individually to his skill, enterprise, and single-mindedness and contextually to the interest his work held for the Institute. He was far from alone in submitting his findings to its judgment. Pinel, Bichat, Dupuytren, Legal-lois—all followed that course. They had no choice. Prior to reincarnation of the Société Royale de Médecine as the Académie de Médecine in 1820, the only forum for receiving and recognizing medical research was the Société Médicale d’Émulation, an entirely unofficial voluntary body founded by Bichat and other youngsters barely out of medical school. The scientific cast of French medicine has thus an institutional as well as an intrinsic explanation.

It has been surmised that reacting against the familial, political, and professional disorder in which Magendie grew up inculcated in him the pro-found respect for facts, the aggressiveness about finding them, and the skepticism about theory that characterized his career.³³ That may well be correct, the more so that a rigorously empirical attitude was in keeping with the positivist tenor of the times. In any case Magendie made his debut in print with a programmatic declaration comparable in point of prescience to the sealed note in which Lavoisier had laid out a program for the reform of chemistry before beginning his research in 1773.34 In 1809 the journal of the Société Médicale d’Émulation, unfaithful for the moment to the memory of Bichat, published Magendie’s essay, “Quelques idées générales sur les phénoménes particuliers aux corps vivans.”³⁵ Physiology, declared the young Magendie, lagged behind the exact sciences for two reasons. First, phenomena were badly observed and ill defined. The bulk of so-called facts would have to be verified and refined by precise experiments before the subject could become a discipline. Second, imaginary concepts and constructs multiplied entities in violation of the principle of economy in scientific explanation. Albrecht von Haller had established what became the received wisdom, to wit that sensibility and contractility are the basic properties of living matter in animals. Magendie would have none of that. He insisted instead that physiological phenomena are to be understood, not as the manifestation of innate properties, but as functions of anatomical structures organized in certain ways species by species. Without denying the validity of reducing those structures to the level of tissues, he scornfully rejected the multiplicity of vital forces with which Bichat had invested those elements.

In Magendie’s thinking, the features common to animal life come down to operations of two sorts: nutrition (the processes by which the body composes and decomposes itself materially) and movement (not merely locomotion, but the activity of heart, lungs, digestive system, and so on). His formulation of the uniformity of nature in the case of living things clearly owes much to his reading of Cuvier’s comparative anatomy and may be taken as the credo of modern biology: “Two living bodies having the same organization will display the same vital phenomena; two living bodies having different organizations will display vital phenomena the diversity of which will always be in direct proportion to the difference in organization.”³⁶ Magendie’s early attitudes and his later practice were thus what has often been considered mechanist. Nevertheless, his position, even like Cuvier’s views on species, is an illustration that a mechanist versus vitalist dichotomy seldom sorts physicians or biologists cleanly into mutually exclusive categories. For Magendie did admit the concept of a vital force. When and if it could be related to a precise law, as the principle of attraction was to the inverse square law of gravity, its role would be similar, that of a universal principle to be known by its effects and unknowable in its essence. The goal was not in sight, but he set out to work toward it.

Magendie’s experimental investigations have often been described, and we need not follow the entire sequence. In the course of a long lifetime he established the responsibility of many particular structures for important generalized functions: of the cerebellum for maintaining equilibrium, of the fifth pair of cranial nerves for the sense of touch, of the roots of motor and sensory nerves in the medulla, of the absorption of nutrition both in the lymphatic and circulatory systems, of the role of the liver in detoxification, to mention only outstanding examples. His signet was the acumen and skill with which he would pinpoint the site of a specific, often minor organic function and exhibit the general physiological consequences that followed from its inactivation. The reasoning moved from effects to causes in a probabilistic vein rather than from considerations of overall design to the purpose served by the parts. The density and variation of experiments he performed in order to establish each finding was unequalled among contemporary medical scientists, and perhaps among predecessors.

His style is better described as activist, interventionist, even invasive rather than as mechanistic in some external sense. It would be only a small exaggeration to characterize his work as a kind of physiological engineering. His purpose was not so much to quantify, or even analyze, his problems as to get inside them, to take control of the functions he was investigating, to turn them off or on at will. To be sure, he modeled his methods on those of physics and chemistry but always adapted to the qualitatively different complexity of living organisms. He was attentive not only to the methods of the physical sciences, but also to their content where relevant to physiology and, what may have been professionally most important, to leading chemists and physicists of the Institute prior to his election in 1821, and also afterward.

In his laboratory he employed not merely the scalpel, but newly discovered vegetable drugs, several of which he himself isolated and identified. He thus extended the reach of physiological inquiry beyond the frontier of medical research proper into the fields of botany, pharmacology, chemistry, and even physics.

After publishing his critical and programmatic essay in 1809, Magendie inaugurated his research by reaching out to other sciences. Appearing before the Institute in the same year, he read a pair of papers, one on 14 April and the sequel on 7 August.³⁷ Although the design of the experiments was largely his, he had conducted them in collaboration with a botanist, Alyre Raffenau-Delille, a veteran of the Egyptian expedition. The subject of the first mem-oir was the action on the spinal cord of an unknown drug. One of the botanists of the Baudin expedition to the South Seas had brought back a few twigs of a bush called upas tieuté in Java and Borneo, where hunters and warriors smeared a bit of the poison extracted from it on their spears and arrowheads. A.-L. de Jussieu, who was a member of the commission reporting on the memoir, identified the plant as one belonging to the genus strychnine.

Thus informed, Magendie and Delille put in hand experiments with extracts of two well-known species of the genus, nux vomica and St. Ignatius bean, which confirmed the identification. The dire effects of upas itself, however, were the main subject. Magendie dipped a splinter of wood into the mixture and inserted the merest drop under a dog’s skin. He reports in vivid detail the progress, from spine, to legs, to lungs, of the tetanus it induced, with remissions at each stage. The poison worked, Magendie expressly showed, on the spinal cord. Separating the medulla, at the top of the spinal cord, from the brain did not suppress the symptoms. Destroying the medulla did, and the animal survived—totally paralyzed. The commission reporting on the demonstration concluded that the memoir would have merited inclusion in the Savans étrangers series had its publication not been so dangerous.³⁸

In the research that followed, Magendie threw in his lot with a pair of pharmacologists, Joseph Pelletier and Joseph Caventou. In so doing he joined forces with a companion discipline the practice of which was rising in prestige from the stage of trade to that of profession. Apothecaries were henceforth pharmacists formed no longer by apprenticeship, but in the new École Supérieure de Pharmacie (not yet a faculty), directed after its foundation in 1803 by Fourcroy’s onetime protégé, the now eminent chemist Nicolas Vauquelin. The subject matter, formerly materia medica, would henceforth be pharmacology, which, even like physiology, was in the initial stage of developing an experimental component.

Scion of a family of apothecaries, Pelletier qualified for his license at the École de Pharmacie in 1810. He had inherited the business from his father, who had taken over Rouelle’s apothecary shop and died in 1797, when his son was nine years old. The Pharmacie Pelletier is still in business on the rue Jacob. Caventou and he followed the course in chemistry given by Jacques Thenard at the École de Pharmacie and focused attention on the chemistry of vegetable substances. Pelletier proceeded to the degree of Docteur-ès-Sciences in 1812. A paper on the chemical nature of opoponax appeared in 1811. Later in the year he published the first memoir of a series reporting his analyses of further gum resins—bdellium, myrrh, asafetida, galbanum, and sagapenum—and of other naturally occurring substances such as amber, sarcocolla, toad venom, and sandalwood.³⁹

None of this had any bearing on drugs or on their physiological effects. It was just such a problem that led Magendie to initiate a collaboration. In an investigation in 1813 of the mechanics of vomiting, he found that the muscles of the diaphragm cause regurgitation and that the role of the stomach is passive. He there left unasked the question of the mode of action of the emetics he had employed.⁴⁰ Medical practitioners made wide use of ground ipecacuanha root as an emetic, and Magendie now enlisted Pelletier’s chemical skills in undertaking an analysis. Dissolving out the components of the plant tissue one by one, they isolated the active principle, which Magendie dubbed emetine. Impressed, Thenard in his report to the Institute recommended that a systematic program of analysis of other medical compounds be undertaken.⁴¹ Pelletier and Caventou, the latter still Thenard’s student, took up the challenge. In close cooperation with Magendie they identified the poisonous component of upas as a salifiable base, which Magendie named strychnine. Over the next half-dozen years they proceeded to analyze the chemical constitution of other medicinal plants and isolated the active principles, notably brucine, veratrine, cinchonine, and most important, morphine and quinine, all salifiable bases or alkaloids.⁴² Magendie on his own determined the medicinal properties of iodine and prussic acid.

Magendie had been appointed in 1811 to the post of demonstrator at the Faculty of Medicine, where he taught anatomy and surgery but not physiology. Constant frictions with colleagues ensued, particularly with his immediate superior, François Chaussier, the professor of anatomy, and with Dupuytren, who took Magendie for a dangerous rival. It did not ease matters that Magendie himself could be abrupt, rude, and scornful on occasion. At all events, in 1813 he abandoned anatomy, resigned from the faculty, and set out to earn his living from the practice of medicine while focusing his research on experimental physiology. In Claude Bernard’s view, that decision marked the beginning of the “new physiology.” In his account, “Magendie joined example to precept. He undertook private courses in experimental physiology based on vivisections. He attracted numerous students, among whom were a number of foreigners. It was from this center that young physiologists carried the seeds of the new experimental physiology into the neighboring schools, where it then developed with prodigious rapidity.”⁴³ Not only foreigners were attracted. Magendie’s demonstrations were soon the talk of Paris. After a visit to England in 1824 they also became the scandal of London, where the reaction of animal sympathizers breathed life into the fledgling Anti-Vivisection Society.

The early papers Magendie presented to the Institute beginning in 1809 were refereed by medical members of the First Class. In the ensuing years, however, his determination to develop physiology into an experimental science aroused the interest of the whole Academy of Science. Cuvier was among the commissioners, as was Humboldt, who reported on the memoir on the mechanics of vomiting absorption in 1813.44 He served too, in company with Biot and others, on the commissions that reviewed an 1813 memoir on the esophagus and the first volume of Magendie’s only comprehensive work, the Précis élémentaire de physiologie (1816–17).⁴⁵ Suggestions by Cuvier were almost surely responsible for Magendie’s undertaking comparative studies of the lymphatic systems in birds, while Geoffroy Saint-Hilaire examined the memoir on the “Organes propres aux oiseaux et aux réptiles.”⁴⁶

As befitted a physicist, Biot collaborated with Percy in a comprehensive review of the 1817 memoir on “L’action des artères sur la circulation.” Magendie’s vivisections there settled in the negative the question whether muscular contractions in the arteries synchronous with the pulse supplement the pumping of the heart in propelling the bloodstream. Cuvier supplied him with an example of the largest blood vessel in nature, the aorta of a deceased elephant in the menagerie of the Muséum. Neither embedded in its tissues nor surrounding them was there anything of a muscular tunic capable of exerting contractions. Instead, elasticity of the walls of the arteries is the property that enables the heart to do all the pumping. Magendie compared the elastic role of the arteries to that of the reservoir of air in hydraulic systems powered by alternating force pumps. They serve the mechanical principle that intermittent action may be converted into continuous action by using the driving force to compress a spring that exerts steady pressure in reacting.⁴⁷ Following out of Magendie’s study of arterial action, J.-L.-M. Poiseuille, an 1816 graduate of the École Polytechnique, undertook an investigation of the hydrodynamics of the circulatory system and developed it into the thesis that qualified him for the degree of doctor of medicine in 1828. He devised a haemodynamometer, adaptations of which instrument have been used ever since. It measured blood pressure by the height to which it lifted a column of mercury.⁴⁸

In what might be taken as a personal vote of confidence from the side of the exact sciences, Laplace chose Magendie to be his doctor. It was almost surely Laplace, moreover, who persuaded baron de Montyon to endow an annual award for experimental physiology, a prize won by Pelletier and Caventou in 1827. Laplace and Berthollet were instrumental in securing Magendie’s appointment to the Bureau central des hospices de Paris in 1818.49 More formally indicative of Magendie’s growing scientific reputation was the membership of the commission named by the Academy of Science in 1820 to report on the memoir treating the mechanism of venous absorption in warm-blooded animals. With respect to the lymphatic alternative, only fictitious hypotheses and “nothing positive” had ever been proposed. Not a single life scientist was among the academic referees who, instead, were Berthollet, Thenard, and Gay-Lussac. After a review of Magendie’s previous research on this, the earliest of his general problems, they reported on the convincing experiments performed in their presence. “In this memoir,” they conclude, “M. Magendie gives new proofs of the sagacity with which he strives to introduce the rigorous methods of the physical sciences into physiology and to banish everything hypothetical.”⁵⁰ To that appreciation may be added Magendie’s procedural remark in a footnote to his memoir on arterial elasticity: “In science, to express an opinion, to think [croire], is nothing but to be ignorant. In effect, what do we really mean when we say, I believe, I think, my opinion is that such or such a phenomenon happens like this? That means only, I suspect, I conjecture that the thing takes place in such a way. In fact, when you suspect, when you make conjectures, you don’t know. You might as well say: you believe, therefore, you don’t know.”⁵¹

Magendie’s election to the Academy of Science followed in 1821. The triumph was personal, however, rather than institutional. Defense of turf defeated Geoffroy Saint-Hilaire’s proposal for a reorganization of the structure of the Academy in order to create a section for physiology, the experimental aspect of which had scarcely existed at the time of its foundation in 1795. Instead, Magendie was named to the section of Medicine and Surgery.⁵² What signaled the emergence of a new discipline was not yet institutionalization, but the success of the journal Magendie launched in the same year, Journal de physiologie expérimentale, to which he added et pathologique in the second volume. There in the fullness of his powers he published experimental researches in the ensuing decade. Notable are those that issued in his part of the Bell-Magendie Law, his most famous finding. It states that the anterior and posterior roots of the spinal cord in the medulla have different functions, and that the former govern mobility while the latter control sensibility. (Current parlance designates the two sets as ventral and dorsal, respectively.) Magendie also published translations of Bell’s papers in his journal. The joint naming represents eventual compromise in a priority dispute with Sir Charles Bell. It would be Magendie-Bell if primacy were given to depth and cogency rather than to the heuristic effect of a partial anticipation.⁵³

Other papers in the field of neurophysiology treat the role of the cerebellum in maintaining equilibrium; the gyrations of animals when the cerebellar peduncle is severed; and the composition, circulation, and function of the cerebrospinal fluid.⁵⁴ There too appeared papers of other, mostly younger medical people, and several veterinaries, doing what was clearly physiology, experimental or pathological or both. The number of such authors throughout the 1820s comes to approximately one hundred in France and abroad, for there were numerous translations from English and German. The figure may reasonably be considered a rough measure of the population of active contributors to the field. Indicative of its scientific standing was the participation of specialists in other disciplines who published on problems of physiology: from chemistry, Vauquelin and Chevreul as well as Pelletier and Caventou; from physics, Pouillet, Savart, Poisson, and Coriolis. Notable among such outside names were those of Cuvier, Humboldt, Bory de St. Vincent, and Larrey.

Membership of the Institute gave Magendie the standing to secure the two positions in which he exerted formal influence. In 1830 he became head of the women’s ward in the Hôtel-Dieu. Later in the same year he won election to a still more important post, the chair of Medicine in the Collège de France. Magendie there impressed an audience wider by far than ever had heard or read the many memoirs presented before the Academy of Science. The series he delivered between 1832 and 1838, and published in 1842, transformed the perception of physiology among the educated public. His subject was the physical phenomena of life. The purpose was twofold. On the scientific side, he put all possible emphasis on physical explanations of the functioning of living creatures. On the medical side, he insisted on the necessity of basing therapeutics on exact knowledge of normal and pathological physiology.⁵⁵ At the same time he was now in a position to form a new generation of students who later peopled the new discipline of experimental physiology in direct consequence of their training.

It might, perhaps, be said that Magendie’s most important contribution to the science he had the largest part in launching was his role in the education of Claude Bernard, who in 1842 became his laboratory assistant in the Collège de France. For the present purpose, however, it will be fitting to conclude discussion of Magendie with a passing remark in the fourth edition of Précis élémentaire in 1836, at which time Comte was publishing Cours de philosophie positive . Magendie there identifies his discipline with biology: “Physiology, or Biology, that vast natural science which studies life wherever it exists and investigates its general characters.”⁵⁶

4. MATHEMATICAL PHYSICS

In portraying the character of mathematical physics in its formative stage, we shall have to widen the angle of vision. What distinguishes the writings to be considered, and many subsidiary contributions, is that the reasoning was mathematical and that, with one exception (Sadi Carnot’s Réflexions sur la puissance motrice du feu), the findings are expressed in formulations of mathematical physics.

The same cannot be said of any body of physics generated by a community of scientists prior to 1800 in France or to the late 1830s elsewhere. D’Alembert, to take an eminent example, would have regarded the phrase “mathematical physics,” if not quite a contradiction in terms, at least as a conflation of unlike divisions of knowledge. The Discours préliminaire (1751) to the Encyclopédie distributes the sciences into two main branches, “Mathématiques” and “Physique générale et particulière.” To the former belong geometry, arithmetic, and algebra, which d’Alembert calls “Pures,” and also mechanics, astronomy, and geometric optics, which he designates as “Mixtes. ” All other knowledge of nature is “Physique,” where the best to be expected is a “recueil raisonné,” an organized collection of observations and experiments.

These distinctions still governed the design of the curriculum when the École Polytechnique opened its doors in 1794. “Physique générale” was a relatively trivial course treating the properties of bodies. “Physique particulière” was simply chemistry. Neither had anything to do with mathematics. Nor did Haüy’s standard textbook Traité élémentaire de physique (1803). In Delambre’s 1809 report to the Emperor on the progress of “Sciences Mathématiques” since 1789, there is one fairly minor section entitled “Physique mathématique.” Delambre saw the beginnings of the developments that were to transform the science of physics very differently from the way they appear to later scrutiny. In his eyes what was gained for mathematics (he says “géométrie”) was lost to physics. He mentions “light, gravity, motion and laws of impact, even the phenomena of magnetism and electrostatics, which some have tried to subject to calculation.” The new phenomena of galvanism might possibly compensate physics for some of these deprivations. What Delambre had in mind in writing “Physique mathématique” was quantitative data developed by means of exact instruments, such as Coulomb’s torsion balance, Volta’s electric battery, Borda’s repeating circle, and Ramsden’s theodolite—physical investigations carried out with what were

To return, then, to the École Polytechnique: What can have led certain members of the first generation of graduates, and of staff, to do what they were never taught to do, and what Delambre instinctively took as a deprivation for physics, and attack its main problems in mathematical terms? Clearly, we do not have to do with the accommodation or extension of some signal accomplishment. There is no single focus such as Copernicus’s De Revolutionibus, Newton’s Principia, Planck’s quantum of action, or Einstein’s relativity. Instead, the inauguration of mathematical physics occurred in a large sense in consequence of the state of the art, both in mathematics and in physics. Analysis had developed virtuosity enough so that it could be applied to physical phenomena. Experimental and observational technique had developed to the point that data could be obtained with sufficient precision to serve in the production and verification of formulas. Still, it will not do to say that mathematical physics came into being simply because it could. Those same technical conditions, necessary but not sufficient, obtained over a much longer period and a much wider range of activity—say from the prime of d’Alembert and Euler in the 1750s and 1760s down to the emergence of British and German theoretical physics in the 1840s. Historically, the question is, what precipitated matters in France between 1800 and 1830?

One explanation has won a considerable and deserved following. In 1974 Robert Fox published an excellent paper, “The Rise and Fall of Laplacian Physics.”⁵⁷ The rise consists of Laplace, become the lawgiver of the scientific establishment, gathering disciples into a school following publication of the fourth volume of Mécanique céleste in 1805 and associating them and himself with Berthollet’s protégés in the Society of Arcueil. Its research program was reduction of the Newtonian world picture to the dimensions of corpuscular physics by applying its laws mathematically to the phenomena of light, heat, sound, electricity, and magnetism. The summons was more than intellectual. The program consisted of a concrete policy for setting problems, favoring the right people for appointment—Biot, Malus, Poisson, Arago—defining and awarding prizes offerred by the Institute, steering members of the younger generation, and shaping their careers—in a word, patronage.

The fall consisted in the failure of this dogmatic and overbearing program. A supple modern physics was then born amid a rebellion of young Turks, and some not so young—a turncoat Arago, Fresnel, Fourier, Ampère, Sophie Germain, Sadi Carnot—against the Newtonian-Laplacian ortho-doxy. The displacement of a corpuscular by a wave theory of light is usually taken to be the paradigm shift in this scientific revolution, if such it was. With respect to those concepts, Fox’s schematization is illuminating. How well the interpretation fits experimentation and practice as distinct from theory, even in optics, remains to be considered, as does the more general question of its adequacy as an explanation of mathematization in the other sectors that came together with optics to constitute the modern science of physics.

First of all, what did it mean to be a Newtonian in the latter part of the eighteenth century? The term is not quite equivalent to physical scientist. To suppose, as is often done, that Newtonian mechanics had completely routed Cartesianism among French “géomètres,” as mathematicians still called themselves, is an exaggeration. A principle of equilibrium based on conservation of momentum still went by Descartes’s name. D’Alembert in the Discours préliminaire exhibits a certain wistful nostalgia for the model of planets swirled about the sun in cosmic vortices. More generally, scientific values were strongly marked, not to say defined, by the cognitive primacy of mathematics. Apart from Cartesianism, it is important to recognize that the legacy of seventeenth-century physical science did not all pass through Newton’s head and hands. Statics, laws of impact and collision, and the infinitesimal calculus did not require Newton to mediate between Stevin, Huygens, and Leibniz, who respectively formulated these disciplines, and the successors who were doing rational mechanics in the eighteenth century.

Nevertheless, such was the power and generality of Philosophiae Naturalis Principia Mathematica (1687) that the figure of Newton towered over the eighteenth century. There are three senses in which a scientist of the Enlightenment may be said to have been a Newtonian. The first pertained to astronomy. A strong, essentially Newtonian research program consisted in perfecting planetary theory by comparing calculations based upon the theory of gravity to observational data on the positions of known planets and satellites such as Jupiter, Saturn, and the moon and newly detected bodies such as Uranus, the asteroids, and many comets. By no means was the correspondence between theory and observations always exact, and the question remained open whether irregularities derived from inaccuracies in the observations, imperfections in the calculations, or higher order inadequacies in the theory itself. Laplace’s principal purpose in the many memoirs gathered into Mécanique céleste was to exhibit mathematically that such perturbations in orbital motion resulted from mutual gravitation among the planets themselves and thus confirmed rather than invalidated Newtonian theory.

The second sense of Newtonianism pertained to physics. The world picture was more general than the theory of gravity, which applied only to astronomy. That theory presupposed two considerations of wider, indeed of universal, scope that were rather hypotheses than matters of demonstrated fact. The first, action at a distance, was a precondition: mechanical effects do not require contact between a moved body and a moving agent, but are capable of being produced by forces acting across empty space. The second was an extrapolation: Forces of attraction, and a fortiori of repulsion, operate not only between gross bodies such as planets, but between all the particles in the universe. Such was the research program of so-called Laplacian physics. It may be noted, parenthetically, that the appeal of a model of the solar system in microphysics was not exhausted by the failure of that program, if failure it was. The atom imagined a century later by Niels Bohr at the start of the old quantum theory in 1912 consisted of electrons orbiting at fixed levels a nucleus of protons and neutrons. Moreover, the strategy of miniaturizing the range of Newtonian forces was never a monopoly of physics. A similar inspiration has guided many an investigation of the nature of the chemical bond, of the form of minerals, and even of the structure of the living cell.

The third sense is methodological. The Principia is primarily a book of mathematics applied to the solar system. Formally the laws—in analytical terms, equations—of motion of the planets are derived mathematically from first principles of mechanics, Newton’s three laws of motion stated as axioms. The success of that procedure gave a more powerful impetus than the merely philosophical assertions of Descartes to the notion of mathematics as the preferred mode of scientific reasoning and to mechanics as the fundamental discipline. Thus would Lavoisier at the end of his life hold up mathematicization as the grail that chemistry should strive to win. In this sense everyone who considered that mathematicization was the goal of science was a Newtonian, whether his science was ready for it, as Haüy’s crystallography was, or whether it was not, as in the case of chemistry.

It must not be supposed, however, that mathematicization necessarily entailed analyzing Newtonian models of physical reality. Quite other mathematical methods might be and were developed for application to phenomena not reducible to the motions of material particles or bodies in space. The geometrization that Huygens applied to wave fronts, or later in the century Haüy to crystals, comes to mind, and also the analysis that Fourier invented for propagation of heat. Neither must it be supposed that the Newtonian inspiration to eighteenth-century methodology was confined to mathematicization. On the contrary, Newton was also, if not quite equally, an experimentalist. His Opticks had as powerful an influence on the tradition of experimental natural philosophy in the eighteenth century, in the persons of such notable investigators as Benjamin Franklin and the abbé Nollet, and of a host of lesser lights, as did Newton’s mathematical approach to the mechanization of astronomy and with it the world picture at large. In this connection the third, or methodological, meaning of Newtonianism at the turn of the nineteenth century overlaps to a considerable degree with the second, its role in physics. Experimental physicists generally, though over-simplistically, credited Newton with a uniquely corpuscular conception of the nature of light. Hence the primacy of optics in the notion of a Lapla-cean physics.

In other, and perhaps most, contexts a good deal of overlapping may be discerned between any two and often all three aspects of what Newtonianism meant to individual scientists. It will clarify interpretations, however, if the distinctions are kept in mind. The three meanings of Newtonianism did not entail one another and are not reducible one to the other in giving an account of eighteenth-century science. It was perfectly possible to adhere to Newtonianism in the first, astronomical, sense and not in the others. As we have already noticed, Delambre, the complete Newtonian astronomer, failed to perceive the prospect for Newtonianism in the second, mathematical sense, although it was right under his nose. Thinkers of a more general sort, for example Diderot, Buffon, and Lamarck, accepted and even celebrated the Newtonian theory of gravity, while disputing, each for a different reason, the applicability of mathematics to other areas of science, let alone to human concerns. As we shall soon see, Ampère considered himself a Newtonian in the third, methodological sense, but rejected the physical model of radial forces bearing on pointmasses, which for others of his generation was the essence of Newtonianism. It was also possible to consider that mathematics is the language of science, and yet not to accept either Newtonian gravitational theory (Leibniz and his followers did not) or New-tonian mechanics (Boskovic did not). Other permutations and combinations could be adduced, but these will suffice to suggest that Newtonianism was protean, but not all inclusive, inceptive, but not simple.

As for Laplace, there was somehow a latent physical component in his astronomy from the outset. He was a Newtonian in all three senses, but never a servile thinker except in politics. In the Principia the force of gravity is assumed to act instantaneously. An early memoir of Laplace tries out the conjecture that gravity, like light, is propagated in time. He posits a corpuscle to be the bearer of gravitational force and calculates that it must travel at a velocity 6. million times the speed of the corpuscles that constitute a light beam.

It is also assumed in the Principia that the attractive force of a body is the resultant of the attraction of each of its parts. Analysis of the shape of solids of revolution, such as the earth, might get a handle on that proposition and decide whether attraction acts, not just between centers of mass as in the theory of gravity, but among all particles at less than cosmic distances. Such was the motivation of Laplace’s entire series of researches on spheroidal attraction theory. It culminated in a memoir on the stability of Saturn’s rings. The reasoning is of a type characteristic of many a paper in mathematical physics in the centuries since, but not of prior thinking. There being no possibilty of measurement, Laplace invented a mathematical model. He imagines the ring covered with an infinitely thin layer of fluid at equilibrium under the influence of forces of inertia and gravity. Analysis of the equilibrium conditions then gives the shape. In the course of the reasoning, Laplace arrived at the basic equation governing the attraction that spheroidal bodies exert on an external point.

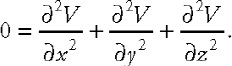
One does not need to be versed in mathematics to appreciate the elegance, simplicity, and symmetry of the expression that in Poisson’s hands became the potential function serving the nineteenth-century theory of electrostatics and magnetism.

Neither is there evidence of dogmatism, and scarcely of Newtonianism, in the earliest considerable physical investigation on which Laplace engaged, which was the collaboration with Lavoisier that issued in the famous Memoire sur la chaleur (1783). The idea of the experiments was Laplace’s. The execution was Lavoisier’s. So far as is known, Laplace never performed an experiment with his own hands. He had acute physical insight, however. On a number of occasions, and this was the first of which record remains, he suggested to associates the design of instruments that would elucidate the problem at hand. In this instance it was the ice calorimeter. The design bespeaks the mathematical modeling of physical reality. We are to imagine a hollow sphere of ice with a shell insulating it from the heat of the surroundings. The heat of a warm body introduced into the cavity would melt a portion of the inner surface until it had cooled down to zero, and the weight of water would be a measure of the heat required to produce the effect.⁵⁸

At about the same time, and quite independently of Laplace, new and important work appeared in exact physics. A reduction in the range of New-tonian forces, and application to phenomena other than gravity, are the central features of the seven memoirs that Charles-Augustin Coulomb read before the Academy between 1785 and 1791.59 He found, as everyone knows, that like electrostatic and magnetic forces repel each other, and conversely that unlike charges attract each other, with a force inversely proportional to the square of the distance between the charged bodies. He showed further, and this was more important for the mathematical analysis that Poisson later applied to his findings, that charge is spread evenly upon the surface of the bodies affected. He concluded, finally, that magnetism is molecular, and that magnetized bodies are composed of polarized particles.

All this was in the first instance experimental physics. Coulomb produced his results by means of an instrument he invented, the torsional balance. It measured the forces by the twist that their action imparted to the fine wire on which charged bodies, usually pith balls, were suspended. The investigation was experimental, but so exact as to verge on the mathematical. Coulomb was an engineer, a graduate of Mézières trained by Monge. His prescription in this work, and in complementary studies, was to mingle experiment with calculation. He did formulate his findings mathematically, but with a resort to mathematics very different from Laplace’s. His formulas are those of an engineer, empirical shorthands that he tests against the data and modifies accordingly. They are not abstracted from known or hypothetical physical laws in order to be subjected to an analysis that will, so to say, go off into the empyrean of calculation to confirm their validity, to account for anomaly, or to predict new effects, and only then, if indeed the equations can be solved, return to earth, or to the laboratory.

The electric current might have opened another field after Volta’s visit to Paris in 1800, but as we have seen his presentation was nothing mathematical—Delambre was right about that for the moment—and Biot’s application of analysis in his report aroused no interest. Isolated indications of another sort were mathematical, though no more Laplacian than Volta’s pile or Coulomb’s torsion balance. It is intriguing, for example, that as far back as the 1770s Cousin was giving courses at the Collège de France with the phrase “physique mathématique” in the title, and that in 1784–85 his subject was “Les progrès de l’analyse et en quoi ils peuvent servir aux progrès de la physique.” There is, alas, no way to know what was in those courses. Coming down another ten years, there are indications of what was to come in the early cahiers of the Journal de l’École Polytechnique. In the second (1796), Prony has a memoir, “Essai expérimental et analytique sur les lois de la dilatation des fluides élastiques, et sur celles de la force expansive de la vapeur de l’eau.” It consists of an analytical formulation and experimental compilation of tables for steam and other vapor pressures. The same cahier has a composite “Mémoire sur la détermination géométrique des teintes dans les desseins.” The purpose is dual: to find the law according to which apparent intensity of light varies on a surface, and to apply it in making a picture. The authors were students, chefs de brigade whose solutions to the problems were combined for publication.

A famous name makes its first appearance in print in the fifth cahier (1798). Fourier has a memoir, not on heat, but “Sur la statique, contenant la demonstration du principe des vitesses virtuelles.” The demonstration is a novel one in that it refers not alone to rational mechanics but to the theory of real machines. What it does, even like the Essai sur les machines en général (1783) of Lazare Carnot, whom he cites (and is one of the few to do so), is to transpose virtual velocity into virtual work. In the eleventh cahier (1802), Barruel has an “Extrait d’un mémoire sur l’élasticité,” which is geometric in form and physical in spirit. These inquiries, and a few others like them, were straws in search of a wind.

The wind, if one may judge from the contents of this journal, had come up by 1808. The fourteenth cahier, published in April of that year, contained two mathematical memoirs by Malus, out of which opened the debate on optics, and another by Poisson on theory of sound.

Meanwhile Laplace himself had turned his main attention to physics on completing the fourth volume of Mécanique céleste in 1805. Its concluding part, Book X, opens with an analysis of the effect of atmospheric refraction upon astronomical observation. That was the problem on which he sought data by encouraging Gay-Lussac’s and Biot’s balloon ascent and for which he designed the experimental determination of the refractive indices of various gases by Biot and Arago. They fitted a hollow prism, inside which gases could be sealed, to the lower scope of a Borda circle, and working from a window in the Luxembourg Palace, trained first it and then the upper scope on a lightning rod atop the Observatory. The difference in readings measured the refractive indices of the eight different gases tested. The results were as interesting to Berthollet as to Laplace.

The areas of physics in which Laplace intervened directly were the propagation of sound and the explanation of capillary action. Even like gravity, both topics were left imperfect by Newton while deriving from his physics. This is not the place to develop Laplace’s contributions in any detail. Suffice it to indicate their nature. With respect to sound, the problem was its velocity. Experiments dating from the 1730s showed that Newton’s value was too low. In 1802 Laplace suggested to Biot, barely out of school, that the discrepancy might result from Newton’s having ignored changes in temperature produced by alternate dilation and compression of air in transmitting the sound wave. Assuming that changes in temperature are proportional to changes in density, Biot calculated a correction factor bearing out Laplace’s idea, which has since been generally accepted. Laplace himself later showed that Biot’s factor is proportional to the ratio between specific heats at constant pressure and at constant volume.

Equally standard in the literature is Laplace’s account of capillary action. In the first of two supplements to Book X of Mécanique céleste, he obtains a differential equation for the curvature of the meniscus by analyzing the action of the force of attraction exerted by the inner surface of the tube on an infinitely thin canal of the liquid parallel to its axis. In the other, he analyzes the equilibrium in the tube by considering the action of the forces exerted on cylindrical layers of the liquid concentric with the circumference of the tube.

So much will serve as an account of French physics on the eve of the program of mathematicization emanating from the Society of Arcueil. Let us consider the fields one by one.

Optics

The displacement of the corpuscularian by the wave theory of light occurred in three stages in France. In the first, Malus discovered polarization. Ironies attend his reputation. A committed corpuscularian, he made the discovery that provided Fresnel with the phenomena that ultimately assured the victory of the wave theory. Though he was a favored Laplacian disciple, his analysis was preempted by his patron’s improvement on it while it also appeared to support the Huygens wave front construction for double refraction.

Malus entered the lists in support of neither model. His “Traité d’optique,” presented before the Institute on 20 April 1807, is a work of differential geometry in the style of Monge expressly abstracted from all considerations of the nature of light.⁶⁰ Its principal theorems define the loci of tangents to, and intersections of, the developable surfaces to which rays are normal before and after refraction. Laplace served as referee. Impressed, he drew Malus into the corpuscularian entourage. The discovery of polarization followed out of two papers in which Malus criticized the experiments of W. H. Wollaston in England on determination of the refractive index of a transparent substance as a function of the angle of incidence at which total reflection occurs. Holding a crystal of Iceland spar to his eye one evening, he observed the rays of the setting sun reflected in a window of the Luxembourg Palace and saw them, as he expected, refracted into two rays. On rotating the crystal he found the totally unexpected effect that the intensity of the two rays varied reciprocally. At a certain angle the extraordinary ray was totally extinguished while a further 90° rotation blanked out the ordinary ray. The reflecting window, in a word, acted on light precisely as if it were a second piece of Iceland spar.

Intrigued, the Institute on 4 January 1808 at Laplace’s instigation announced a prize for a mathematical account of double refraction. Malus, who was probably intended to win, prepared a paper in two parts. The first, experimental, assigned a rhomboidal shape with three orthogonal axes, A, B, and C, to each corpuscle of light. Malus assumed that the extraordinary refraction is caused by a repulsive force, the action of which is proportional to the sine of the angle between the axis of the crystal and the principal axis A of the corpuscle of light. All the molecules of which axis B is perpendicular to the repulsive force undergo ordinary refraction, and those of which axis C is perpendicular to the force undergo extraordinary refraction. Malus hastens to add that he intends this construction, not as an image of physical reality, but as a mathematical model permitting calculation of the relative intensity of the two rays as a trigonometric function of the angle between the planes of the refracting surfaces. The second part of Malus’s paper contains that analysis. It inadvertently lent some credence to the Huygens construction whereby a spherical wave front gives one ray and an ellipsoidal wave front the other. Laplace saw a first draft, and proceeded to compose and publish a simpler, more direct analysis before Malus could revise his paper for submission to the Institute.⁶¹ He won the prize anyway, shorn of its glory, and according to Arago never forgave his erstwhile mentor before an early death in 1812.⁶²

The second stage in the transformation of optics consists in the development of the phenomena of chromatic polarization both experimentally and mathematically, largely at the hands of Biot. Working at first with Arago, he began studying the production by means of polarized light of the colors, known as Newton’s rings, observed when rays of light pass through soap bubbles or very thin plates such as mica chips. Biot’s and Arago’s relations having come under strain in the course of extending the survey of the meridian to the Balearic Islands, they quarreled irreparably, but not before Arago had established that passage through mica chips appeared to depolarize the incident light. Faithful to the corpuscularian hypothesis, Biot managed to obtain a pair of (very complicated) equations for formulating these effects. More important, he proceeded to investigate the phenomenon of rotation of the plane of polarized light when passed through a plate of quartz. The resulting formula, under the name of Biot’s law of rotatory dispersion, has been part of working physics ever since, and also of chemistry. In 1815 Biot found that several transparent substances that had no effect on the passage of polarized light in their normal crystalline state did produce rotation when in solution. He determined further that other liquids, such as turpentine, cane sugar, beet sugar, oil of laurel, and oil of lemon, shared that property, some rotating a beam to the right, others to the left. He designed an instrument, the polariscope, to measure the degree of such rotation, which is an important indicator of the identity of the substance. The work, all on the corpuscular model, was thoroughly Laplacian. It was also good physics.⁶³

The third stage consists of the triumph of the wave theory. In 1818 the Institute, again at Laplace’s instance, set a prize for a mathematical treatment of the fringe effects of diffracted light, known since Newton, with the expectation that Biot would win it, even as Malus had done its predecessor on double refraction. Meanwhile, a young polytechnician, Augustin Fresnel, unknown to the scientific community, had been meditating the conviction he had reached in private that the propagation of light is an undulatory and not a corpuscular phenomenon. Isolated in the country, ignorant of English, Fresnel was unaware that Thomas Young in England had already designed and performed experiments on fringe effects, on the success of which he established just such a wave theory, but without formulating it mathematically. As early as 1814, Fresnel by contrast began with a mathematical analysis using the wave mechanics he had learned at the École Polytechnique in order to show that interference of crests and troughs in a diffracted ray would produce a pattern of fringes. He then designed experiments that confirmed his hypothesis. Encouraged by Arago, whose disaffection from Laplace, Biot, and Poisson was more personal than technical, Fresnel submitted a revision of his early memoir to the Institute, and won the prize.

Poisson thereupon derived a physical prediction from Fresnel’s theory, thinking to show its falsity. It followed from Fresnel’s equations, Poisson showed, that the shadow of a small diffracting disk placed in a beam of light would be illuminated as if the disk were not there. Arago tried the experiment. Poisson’s prediction was correct. It vindicated instead of refuted Fresnel’s theory. Laplace was duly impressed. Fresnel could not yet, however, account for polarization. Later in 1822 he substituted transversal for longitudinal vibrations, exhibited the non-interference of light beams polarized in orthogonal planes, and derived from his equations the Huygens predictions for the paths of the ordinary and extraordinary rays in double refraction. Laplace then acknowledged to Arago that he would place the results above everything the Academy had received in a very long time.⁶⁴

Acoustics

In 1807, the year when a collective Laplacian program may be said to have got under way, Poisson presented his first full-scale mathematical memoir to the First Class of the Institute. His subject was the theory of sound, which he purported to treat in complete generality. He considered an elastic fluid consisting of molecules subject to the action of any forces, and concentrated attention on the repulsive forces responsible for impressing on them vibrations transmitted through the fluid in the form of sound waves. Drawing on Lagrange’s treatment of compressible fluids, Poisson formulated a pair of basic equations for his model, and solved them for certain special cases: propagation in air at constant density and pressure, reflection from a surface, velocity of sound, propagation along an axis, and propagation in three dimensions. He proceeded to state theorems that he hoped would interest both physicists and mathematicians, such as that the speed of sound is independent of the vibrational frequency of the molecules in the air that transmit it and of the agent that causes it, that the velocity is the same in all directions so that the wave front is always spherical, and so on. The derivations are entirely mathematical, and the memoir has no significant physical content.

An experimental demonstration of the form of vibrations of the type that cause sound waves did reach Paris the next year, in 1808. The German physicist E. F. F. Chladni then visited the capital. His purpose was to exhibit effects of vibrating plates for which he had developed techniques that he had published in Germany some years previously. In the standard experiment he fastened a brass circular plate horizontally to a support at the center, scattered a layer of sand on the surface, and drew the bow of a violin rapidly up and down along the edge. The sand danced away from the os-cillating sectors and gathered at the nodes, where it was motionless, thus forming patterns that exhibited the mode of vibration of the surface.

The effect was graphic and dramatic. It appealed to the leadership of the Institute in the way that double refraction had done, and in 1811 the First Class set a prize for a mathematical theory of elastic surfaces confirmed by experiment. The definition was an invitation to Poisson. Only one paper came in, however. Although it was formally anonymous, the author was known to be Sophie Germain. No prize was then awarded, nor was it in the contest that was reopened in 1813, when her revised paper received an honorable mention. In 1816, finally, she received the prize in a third round, despite severe criticism by Poisson, who in 1814 had composed a paper considering the motion of elastic surfaces from the point of view of Laplacean theoretical molecular physics. Germain’s treatment, by contrast, was rather old-fashioned and geometric in spirit, harking back to the methods of Euler.

She obtained a fourth-order differential equation for the vibrating surface of any form, curved or flat, and explored the properties of curvature and their radii. Her methods have been criticized as fanciful, and it is agreed that her greatest strength was in number theory. Her early essays thereon had won her the esteem of Lagrange. Laplace never showed the slightest interest in that subject, and it was probably Lagrange’s support that led his colleagues to take her seriously. However gratifying her victory, her theory of elastic surfaces failed to enter in an important way into the development of acoustics, although it did contribute to the theory of elasticity, where Cauchy was the master presence.

Electricity and Magnetism

Here too, the story begins with Poisson, the complete Laplacian. The difference is that his work in this area, instead of being superseded as it was in acoustics, became the foundation of later development of the field, which transpired mostly outside of France. In 1812 Poisson presented the Institute his “Mémoire sur la distribution de l’électricité à la surface des corps conducteurs.” He had composed it for a prize competition set by the Institute, which it was undoubtedly intended he should win, but for which he became ineligible on election to the place left vacant by the death of Malus in that year. The physics in Poisson’s memoir is from Coulomb, the mathematics from Laplace. His merit was in bringing them together in a felicitous manner. The positive and negative electrical fluids are spread on the surface of conducting bodies without penetrating the interior. Forces of attraction and repulsion inversely as the square of the distance between the molecules are analyzed by means of Laplace’s theorem for the attraction of spheroids, to which Poisson added a term to take account of electrical density.

In a brief note in Bulletin de la Société Philomathique for 1801, Laplace himself had extended spheroidal attraction theory from the gravitational case to a thin layer of electrical fluid spread on a surface. Poisson fails to cite that source, but such is the model he analyzes. The excellence of the memoir resides in the mathematical virtuosity with which Poisson analyzes special cases of the distribution of electrical fluids, first on a nearby sphere, then on two spheres intersecting to varying degree and also in contact. Finally, Poisson compared the results of his calculations to Coulomb’s measurements. A second memoir generalizes the analysis beyond the specific form of Coulomb’s apparatus. The purpose is to obtain integrals that will determine the intensity of the charge, conceived as the thickness of the layer of electricity, at any point on the surfaces of two spheres at any distance. As usual with Poisson, the exercise is exclusively mathematical.

Only twelve years later did Poisson complete complementary studies of magnetism in a series of three memoirs presented in 1824 and 1825. Mean-while, in 1820 Oersted had discovered interaction between magnetic fields and electric currents; Ampère had begun investigating the electromagnetic effect; Fresnel had followed his papers on diffraction with his explanation of double refraction; Fourier had published his theory of heat. At the time of Poisson’s papers on electrostatics, Laplacean physics had been at the fore-front of research, at least in optics. His introductory review of his earlier work in “Mémoire sur la théorie du magnétisme” reads as if nothing had happened in the interval, except that he darkly denies any underlying identity of electrical and magnetic force. In this, as in the 1812 paper, the effects are those produced by forces of attraction and repulsion between particles affected at the molecular level by the distribution of two fluids, the boreal and austral. There are differences, however. The molecular fluids do not circulate except in the interior of each molecule of a magnetized body in which the sum of the magnetized elements is a function of its volume, a function that varies with the nature of the body and its temperature.

All this makes for greater analytical difficulties than in the electrostatic memoirs. With respect to application, Poisson limited himself to the case of a sphere, hollow or solid. What he had in mind was the earth. His analysis yielded numerical solutions for deviation of the compass needle, which he could compare to data assembled by the Royal Military College at Wool-wich. The correspondence was satisfactory. Poisson’s analysis of the action of magnets of other forms is purely hypothetical, as is the treatment in the two memoirs that followed, where he applies his formulas to magnets in a state of motion with respect to objects attracted or repelled.

The history of Poisson’s reputation is a curious one. The most promising mathematically of Laplace’s protégés in the Society of Arcueil, by the 1820s he was regarded as a diehard left behind by the progress of the science. That harsh verdict has never been reversed, or even appealed, in France, where tradition still ranks him something of a drudge and second-rater. Even now, no street in Paris bears his name. Abroad, however, Poisson has consistently been regarded as one of the cardinal figures of the first generation of mathematical physics. George Green, a self-taught English physicist, named Poisson’s adaptation of Laplace’s spheroidal attraction theory the Potential Function, and made it the point of departure for his Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism (1828). From there it became the basis of theoretical work in electrostatics and magnetism through the intermediary of William Thomson, later Lord Kelvin.

Electrodynamics

Ampère coined the very word. He did not thereby mean to connote the development of electricity as a source of power, which never occurred to him, but rather the study of forces operating between electrical currents. That currents in parallel conductors attract or repel each other according to whether they are flowing in opposite or the same directions is the essence of his discovery. In the concluding Mémoire sur la théorie mathématique des phénomènes électrodynamiques, uniquement déduites de l’expérience (1827), in which he formulated the laws, he presents the research as a model of New-tonian method.⁶⁵ He purports to join Fourier, “that great physicist,” in eschewing concern with causes and limiting the analysis to observable effects. First, he says, phenomena are gathered from experiment. The laws governing them are then deduced, formulated mathematically, and subjected to further experiment. It is true that in his formulation the force acting between two elements of current is inversely proportional to the square of the distance between the conductors. Apart from that, and more important apart from his mathematical virtuosity, it is very difficult to see how Ampère’s work was Newtonian, or how it could be fitted into any camp.

His career was sui generis. The physics for which he is famous occupied only seven years of his life, from 1820 until 1827. Except for that he would be remembered, if at all, as a middling mathematician, an unpopular and indifferent teacher, a second-rate chemist, an embarrassing philosopher, and the victim of dismaying misfortunes in his personal life, beginning with the loss of his father to the guillotine. What brought him to the fore was his reaction to Oersted’s discovery of the deflection of a magnetic needle by an electric current. The complexity of his research in the ensuing seven yearsdefies summary. Suffice it to say that he partook of all approaches to physics and denied himself none. Far from deducing mathematical laws from phenomena, he designed experiments to accord with the trigonometrical form of his expressions; far from acting radially, his forces made all sorts of angles with the directions of his currents; not really acting at a distance, they are transmitted through an aetherial medium, even like Fresnel’s light waves; far from its being experiment, it was his imagination running in circles that suggested to him how a helical current would act as a magnet; he refuted Biot’s orthodox construction of the interaction of currents and Poisson’s of magnetism, but made use of the former’s work and accepted the invitation to set up experiments in the latter’s home; though nothing could be less Laplacian than Ampère’s constructions, or his mathematics, Laplace suggested to him the making of an important experiment—on forces exerted by a current flowing in a very long wire; failing to convince Faraday at the outset, Ampère was stimulated by his criticism; anything but a positivist despite his admiration for Fourier, he reduced magnetism to electricity in motion and pictured it as the effect of elementary currents circling the molecules of a magnet. Of no scientist is it more important to follow what he does, as far as may be, rather than what he says about it in prefaces and obiter dicta.⁶⁶

Heat

Or rather propagation of heat: unlike Laplace and Lavoisier, indeed unlike everyone who had written on heat, Fourier is concerned in Théorie analyti-que de la chaleur (1822) not with the nature of heat, nor with its relation to bodies, nor with its repulsive force, nor with its chemical action, but uniquely and severely with its diffusion, which he saw as a phenomenon of exchanges between or within bodies. His goal was to determine the laws and in so doing abstract the study of heat from these unfruitful concerns and make of it a science in its own right, the peer of optics, of mechanics, and of electricity and magnetism. A delay of ten years intervened between completion of his theory and publication of the treatise. He developed it after returning from Egypt in the first decade of the century and submitted a memoir to the Institute in 1807, just the time when the program of the Society of Arcueil was taking form.

The problem was heat diffusion between separate bodies and in continuous bodies of specified form—a rectangle, a ring, a sphere, a cylinder, and so on—considered mathematically. Lagrange disliked the mathematics, mainly because of the use of trigonometric series, from which Fourier ultimately developed his method of analysis. Laplace was more receptive and favored publication, but did not prevail. In 1810 the Institute announced a competition for the subject, and Fourier submitted a revised version in the following year. Despite Lagrange’s reservations, it won the prize. The latter’s criticism so disaffected Fourier that he refrained from publishing. He was then prefect of the Isère and had worked out his theory in the isolation of Grenoble. When he did finally publish his book, in 1822, with the mathematical parts much developed, he was Permanent Secretary of the Academy of Science.

Half a generation older than Biot, Poisson, Arago, Malus, and Fresnel, Fourier developed the theory of heat neither as an instance of Laplacian physics nor in opposition to it, but independently and more or less simultaneously. Later in the 1820s his interests and Laplace’s tended to converge, more with respect to probability than physics, however. Apart from being mathematical, their physics had nothing in common, whether in the form of the mathematics or the mode of its application to physics. In Fourier’s thinking there is nothing comparable to Laplace’s mathematical models of physical phenomena, his electrical or other fluids on the surface of bodies, or his forces operating at ranges too short for observation but still finite. His physical facts are temperatures recorded by thermometers. Nor was Fourier content with the approximate solutions reached by conventional series expansion of the integrals. He expressed the variables for heat diffusion in continuous media by means of linear partial differential equations and formulated an integral theorem that permitted solving them at any value for time. His equations express physical reality for him, but were not themselves remarkable. It was the method of solving them that was the origin of Fourier analysis, which turned out to have great power in mathematics generally and also in engineering.

In his zeal to secure autonomy for the science of heat, Fourier laid down a limitation that can only be called legislative. The following passage appears in the Discours préliminaire. “But whatever the extent of mechanical theories, they do not at all apply to the effects of heat. These constitute a special order of phenomena which cannot be explained by principles of motion and equilibrium.” One may excuse Ampère’s ignoring the prospect for electric power in his preoccupation with forces generated by the passage of his currents. The dynamo had yet to be invented. Fourier’s restrictiveness is less easy to understand. The steam engine did exist, after all, and Sadi Carnot published Réflexions sur la puissance motrice du feu just two years after Théorie analytique de la chaleur. There is no hint in either book of the slightest awareness of the problems discussed in the other.⁶⁷

Thermodynamics

The word itself is an anachronism. It came into currency only a generation later among physicists developing the consequences of Sadi Carnot’s work. Nevertheless, the term is perfectly appropriate to what he set out to determine, which was (1) whether there is a limit to the motive power of heat; (2) what the optimal conditions are for the operation of a heat engine; (3) whether any agent would be preferable to steam as the means for realizing the potential of a heat engine. Sadi Carnot pictured heat as a fluid, caloric, flowing from bodies at higher to those at lower temperatures. It served his argument in much the way that mathematical fluids did for Laplace. Both adapted it from the subtle, imponderable fluids of eighteenth-century physical speculation, entities created in imagination as bearers of the effects of light, heat, electricity, magnetism, and perhaps life. Sadi Carnot’s argument is mathematical in its rigor, moreover, not in its form, which is verbal. The findings are (1) that there is indeed a limit, since otherwise perpetual motion would be possible; (2) that the condition of maximum efficiency in a heat engine is that no change in the temperature of the agent should occur that is not due to a change in volume; and (3) that the motive power of heat is independent of the agent put to work to realize it, its quantity being uniquely a function of the difference between the initial and final temperatures of the agent employed. The famous heat cycle that Sadi Carnot imagined and analyzed in order to establish these results has often been described, and this is not the place to do it again. Suffice it to inquire how it could have happened that these fundamental works in the physics of heat, Fourier’s and his, should have been ships that passed in the night.

The answer must be that the boundaries of disciplines, not of subject matter, impeded, not to say precluded, communication. Insofar as Sadi Car-not’s slim monograph was noticed at all upon publication, it was taken for a work of engineering, not of physics. His data on specific heats of gases came from chemists with close links to industry, such as Clément and Desormes.⁶⁸ His reasoning represents the application to heat engines that his father, Lazare, had developed for the mechanics of ordinary machines in Essai sur les machines en général in 1783 (also little noticed on its appearance). The basic principles are exclusion of perpetual motion, positing of reversible processes, and interconvertibility of the quantities later called work and energy.

Work and Energy

Coriolis, who also took his inspiration from Lazare Carnot, worked in comparable isolation from the physicists of his day. In Du calcul de l’effet des machines (1829), he defined the quantity work and for reasons of algebraic convenience equated it to what would later be called kinetic energy, one-half the quantity of the force traditionally called vis viva, the product of the mass of the moving body times its velocity squared. It is very curious that the dimensions of these, the basic quantities of what became the most fundamental topic of nineteenth-century science, the physics of energy, should thus have been defined by Frenchmen; further that its main tributary, thermodynamics, should have been started by a Frenchman; and, finally, that these signal accomplishments should have occurred quite apart from the movement for mathematicization of the fields then regarded as constituting the science, namely optics, acoustics, electricity, magnetism, and heat. Nor was it in France that physics was unified at mid-century around the conservation of energy and the first and second laws of thermodynamics. It was in Britain and Germany, at the hands of Mayer and Joule, of Helmholtz and Clausius.

What may be said of the physics the French did do? Each of the classic formulations, of Malus, of Biot, of Fresnel, of Sophie Germain, of Poisson, of Ampère, of Fourier, and in another vein of Sadi Carnot and Coriolis, was preceded by a dense set of technical exchanges among a number of participants. At a rough count the total volume of the literature comes to approximately two hundred memoirs and treatises composed by about thirty men and one woman in thirty years. There can be no doubt about the impetus given by Laplace, but it cannot be said that the creative strain was Laplacian or the contrary, or that the successful models were continuous or corpuscular in texture. Fourier’s initiative was quite independent of Laplace and altogether irrelevant to his program for short-range forces. The Coulomb and Chladni experiments were anterior to Laplacian physics. The Laplacian analysis that Poisson made of the one, far from being overturned by rebels of his generation, passed into later physics as the foundation of potential theory in electricity and magnetism. The Laplacian analysis that Poisson also attempted of the Chladni acoustical experiments had no success in the face of the more imaginative and geometric approach of Sophie Germain.

Opportunities were missed. Apart from Biot’s still-born attempt to mathematicize the phenomena of the battery, mathematicians ignored Volta for almost twenty years. When Ampère did take up electrical circuits—on learning of the quite fortuitous experiments of Oersted in Denmark—he claimed to be a Newtonian. He did analyze the action of inversesquare forces on elements of current, and might be thought Laplacian in that, except that Fresnel supported his work while Biot and Poisson criticized it because the configuration of his constructions was all circles and angles and the formulations were trigonometric. Fourier’s study of heat was an exercise in physics, where it proved of little practical or even theoretical value, whereas his analysis became of tremendous importance in mathematics and engineering. Already in the 1820s Navier was applying it to the design of suspension bridges (though—not for that reason—the first one he built collapsed into the Seine in the flood from a burst sewer main). Sadi Carnot’s analysis came out of engineering, not out of physics, and was later adopted as the foundation of thermodynamics.

The mathematical approaches to the many problems were very various, so much so that the remarkable work by Ivor Grattan-Guinness that analyzes them in three-volume detail has the title Convolutions in French Mathematics (1990). What selected one solution rather than others into the development of the science of physics was ultimately its technical value. The political influence and personal conduct of proponents and opponents were factors, but never the decisive factors. There was favoritism on all sides, but there is no evidence of significant contributions stifled for lack of favor. All concerned had the capacity, or felt the necessity, to accept occasional defeat, while the Institute knew how to recognize merit. Of the four famous prizes for mathematical theories of physical phenomena, three went to opponents of the establishment, or to outsiders, to Germain, Fourier, and Fresnel. The fourth—actually the first chronologically—went to Malus, but how Laplacian was a memoir on double refraction that ended by vindicating the Huygens construction, and the priority of which had been preempted prior to publication by the master himself?

5. CONCLUSION

In sum, it cannot be said of those physicists, anymore than it can of their contemporaries in zoology and physiology, that they formed a school. They admired and despised one another, praised and denigrated one another, and collaborated and competed with one another. All behaved as has many a company of scientists and scholars ever since. What mathematical physicists did constitute by the 1820s was a discipline, as did zoologists and experimental physiologists. The one thing that may be said of all the physics that mattered is that it was mathematical. The one thing that may be said of all comparative anatomy that mattered is that it was based on correlation of parts. The one thing that may be said of all experimental physiology that mattered is that it was based on vivisection. Agreement on theory was never prerequisite to the functioning of the new disciplines. Disagreement on theory motivated much research. Essential to formation of a discipline was agreement, not on theory, but on procedures and techniques, in a word on the practice of the science.

In all three emergent disciplines a decisive movement toward quantification and control marked the transition from the eighteenth to the nine-teenth century, from the encyclopedic enterprise of classifying things in a natural order to the positivist injunction to determine the facts and then to act upon them. The shift in spirit is from enlightenment to engineering, not so much hands-on as intellectual engineering, in established disciplines no less than new ones. One recalls Lavoisier and his parting summons to chemistry to become a mathematical science, only to be followed by Berthollet, Chaptal, Gay-Lussac and company, who turned it into a physical science strongly linked to industry. Even in so recondite an area as the foundations of the calculus, the new mathematics showed a displacement toward a rigor to be attained by manipulation and control of the situation. Lagrange’s theory of analytic functions belongs to the algebraic spirit of the eighteenth century. Lazare Carnot’s, and much more important Augustin Cauchy’s, justifications of the calculus are in the spirit of the nineteenth. In Carnot’s account, the procedures of the calculus compensate for errors entailed by the use of infinitesimal quantities that are introduced in order to achieve a solution, and do so by virtue of the calculator’s power to approach the quantities of an auxiliary system to those of the given system, not approximately, but as closely as he wishes. In Cauchy’s treatment, more satisfactory to mathematicians (though not to engineers), the reasoning turns on a more rigorous argument, one that proves the existence of a limit to which the calculator may in principle approach a quantity as closely (again) as he wills. Both Carnot and Cauchy were trained as engineers.

The shift in orientation is evident not only in science, however, and perhaps not first there. One thinks of the new precision brought to technology by the machine tools of Henry Maudslay and his like in England. One comes back to Laplace, with respect now to the application of probability to demography, to theory of error, to decision making, and to the analysis of electoral and judicial procedures started by Condorcet. One recalls the gathering of census data, most systematically by the Napoleonic administration. For there was indeed a complementarity between the science and the politics of the Revolutionary era. Both were progressive movements, future oriented and dismissive of the past. Both science and politics produced their protagonists out of their own internal dynamics. Of science, too, one sometimes wishes to say, not that scientists solve their problems, though they do so more often than do politicians, but that the problems find their scientists, even as the issues find their politicians. In both politics and science, the premium was upon effectiveness, on doing something rather than being someone. In both domains, the rules in principle depended upon the facts, and the point in determining the facts was to act upon them.

Since then politics and science have been, albeit in different ways, instruments of each other’s larger purposes throughout the course of modern history.

1 To name only foremost titles, for the exact sciences see Grattan-Guinness (1990); for zoology and comparative anatomy, Daudin (1926), Appel (1987), Laurent (1987); for medicine, Keel (2001); for experimental physiology, Lesch (1984). It is by no means clear that the authors would agree with the interpretation that follows. I have ventured several anticipatory essays, Gillispie (1991, 1994, 1997b), and have incorporated the gist of them in what follows.

2 For a discussion of professionalism in science, see Gillispie (1980), 84–91.

3 Cuvier (1809); Delambre (1809).

4 Cours de philosophie positive (1830–1842), 40^iéme leçon, 3, p. 269.

5 Histoire naturelle des animaux sans vertèbres, présentant les caractères généraux et particuliers de ces animaux, leur distribution, leurs classes, leurs familles, leurs genres, et la citation des principaux espèces qui s’y rapportent: précédée d’une introduction offrant la détermination des caractères essentielles de l’animal, sa distinction du végétal, et des autres corps naturels, enfin, l’exposition des principes fondamentaux de la zoologie), 7 vols. (1815–1822), 1, pp. 157–158.

6 Ibid., 1, p. 9.

7 Le Règne animal distribue d’après son organisation, pour servir de base à l’histoire naturelle des animaux et d’introduction à l’anatomie comparée (1817), 1, p. x.

8 Philosophie anatomique des organes respiratoires sous le rapport de l’identité de leurs pièces osseuses 1 (1818), p. 23.

9 Frédéric Cuvier and Étienne Geoffroy Saint-Hilaire, Histoire naturelle des mammifères, avec des figures originales enluminées, dessinées d’après des animaux vivants, 4 vols. (1824–1842).

10 On Savigny, see above, Chapter 8, section 2; and on classification in general, the classic and admirable work of Daudin (1926).

11 In their joint report to the Institute on Savigny, “Certains animaux confondus parmi les Alcyons,” PVIF 5 (8 May 1815), 496–500. See also the report of Cuvier, Lamarck, and Latreille on Savigny, “Organes de la bouche des Insectes sans ailes,” PVIF 5 (3 July 1815), pp. 521–526.

12 “Mémoire sur une nouvelle division des Mammifères et sur les principes qui doivent servir de base dans cette sorte de travail,” Magasin encylopédique 2 (1795), pp. 164–190.

13 Histoire naturelle des poissons, 27 vols. (1828–49).

14 Nouvelle dictionnaire d’histoire naturelle appliquée aux arts, à l’agriculture, à l’économie rurale et domestique, etc., called Dictionnaire de Déterville, 36 vols. (1816–19); Frédéric Cuvier, ed., Dictionnaire des sciences naturelles, called Dictionnaire de Levrault, 70 vols. plates (Strasbourg, 1816–30); Isidore Bourdon and Jean-Baptiste Bory de Saint-Vincent, eds., Dictionnaire classique d’histoire naturelle, 17 vols. (1822–31).

15 “Sur un nouveau rapprochement à établir entre les classes qui composent le règne animal,” Annales du Muséum 19 (1812), pp. 73–84.

16 Le Règne animal, ed. accompagnée de planches gravées par MM. Audouin, Blanchard, Deshayes, Alcide d’Orbigny, Doyère, Dugès, Duvernoy, Laurillard, Milne-Edwards, Roulin, et Valenciennes, 22 vols. (1836–49).

17 2nd ed. revue et augmentée par C.-P. Deshayes et H. Milne-Edwards, 11 vols. (1835–43).

18 Ibid., 1, p. 349.

19 Le Règne animal, 1, pp. 1–11.

20 Leçons d’anatomie comparée, 1, p. 47.

21 Ibid., p. 45.

22 Le Règne animal, 1, p. 6.

23 Système des animaux sans vertèbres, 1, pp. 14–15.

24 Philosophie anatomique, 1, p. 208.

25 There is a somewhat controversial literature on Bichat’s importance. The most recent biography is Dobo and Role (1989). Huneman (1998) discusses the philosophical and methodological aspects of his physiology. See also Albury (1977); Sutton (1984); Haigh (1984). Keel (2001) takes issue with the treatments of Foucault (1963), Ackerknecht (1967), and Lesch (1984).

26 Bichat, Recherches physiologiques Sur la vie et la mort, 3.

27 Quoted in Lesch (1984), p. 89.

28 Canguilhem (1955), pp. 125–126. On Legallois, see also Vladislav Kruta, DSB 8 (1973), pp. 132–135. Eugène Legallois collected his father’s works after his death, Oeuvres de J.C.C. Legallois avec des notes de M. Pariset, 2 vols. (1824).

29 Keel (2001), chapter 11, recapitulates successive criticisms of Bichat from his own time to Keel (1979).

30 Nosographie philosophique, 2nd ed. (2 vols.), 1, pp. xxiii–xiv; 2, pp. 9–10.

31 Die Welt als Wille und Vorstellung (1911 ed.), Zweites Band, chapter 20, p. 296.

32 Lesch (1984), pp. 84–85; Elliott (1987).

33 See the excellent article by Mirko D. Grmek, DSB 9 (1974), pp. 6–11. Olmsted (1944) remains the standard biography. The official éloge (Flourens [1858]) reflects the complexity of the author’s relations with Magendie. Lesch (1984) gives detailed examples of Magendie’s experimental practice in his chapters 5–8.

34 Poirier (1993), pp. 72–73.

35 Bulletin des sciences médicales 4 (1809), pp. 145–170.

36 Quoted in Grmek, “Magendie,” DSB 9 (1974), p. 7.

37 “Examen de l’action de quelques végétaux sur la moëlle épinière,” PVIF 4, p. 196.

38 PVIF (22 May 1809) 4, pp. 238–240. Magendie published the paper many years later in the first issue of Journal de physiologie expérimentale 1 (1821), pp. 18–32.

39 “Analyse de l’opoponax,” Annales de chimie 79 (1811), pp. 90–99; “Examen de quelques Gommes résines,” Annales de chimie 80 (1811), pp. 38–53. It is unclear whether Pelletier entered these papers in a prize competition set by the Société de Pharmacie in 1809. See Lesch (1984), p. 252, n. 46. On Pelletier more generally, see Alex Berman, DSB 10, pp.497–498.

40 For accounts of these experiments, see PVIF 5, pp. 205–208, 244–248, 447–449, 597–598; Olmsted (1944), pp. 51–55. A translation of the report on the first paper by Cuvier, Pinel, Humboldt, and Percy, “On Vomiting, being an Account of a Memoir of M. Magendie read to the Imperial Institute of France on the lst of March, 1813,” appeared in Annals of Philosophy 1 (1813), pp. 429–428.

41 PVIF 6, pp. 166–168, prepared jointly with Hallé.

42 For the Pelletier-Caventou collaboration, see Lesch (1984), 125–144.

43 Quoted in Grmek, “Magendie,” DSB 9 (1974), p. 8, from Bernard (1867), p. 7.

44 PVIF 5, pp. 174–79.

45 PVIF 5, pp. 447–449; 6, pp. 27–28.

46 “Mémoire sur les vaisseaux lymphatiques des oiseaux,” Journal de physiologie expérimenale 1 (1821), pp. 48–55, PVIF 6, pp. 436, 506.

47 “Mémoire sur l’action des artères dans la circulation,” Journal de physiologie expérimentale 1 (1821), pp. 102–115; PVIF 6, pp. 175–179.

48 “Recherches sur la force du coeur aortique,” Journal de physiologie expérimentale et physiologique 8 (1828), pp. 272–305; “Recherches sur l’action des artères, dans la circulation artérielle,” ibid., 9 (1829), pp. 44–52; “Recherches sur la force du coeur aortique,” ibid., 9 (1829), pp. 341–358.

49 Lesch (1984), pp. 127, 143, 248, n. 33.

50 “Mémoire sur le mécanisme de l’absorption chez les animaux à sang rouge et chaud,” Journal de physiologie expérimentale 1 (1821), pp. 1–18; PVIF 7 (11 December 1820), pp. 109–111.

51 Op.cit., above, n. 35, pp. 103–104.

52 Lesch (1984), pp. 118–121.

53 “Expériences sur les fonctions des racines des nerfs rachidiens,” Journal de physiologie expérimentale et pathologique 2 (1822), pp. 276–279; “Expériences sur les fonctions des nerfs qui naissent de la moëlle épinière,” ibid., pp. 366–371. Cranefield (1974) prints facsimile reproductions of these papers in a volume containing all the relevant publications and excerpts from the literature treating the controversy. There are fair accounts in Bernard (1867), pp. 154–158, and Olmsted (1944), pp. 93–122.

54 Above, n. 25; “Mémoire sur les fonctions de quelques parties du système nerveux,” Journal de physiologie expérimentale et pathologique 4 (1824), pp. 399–407; “Mémoire sur un liquide qui se trouve dans le crâne et le canal vertebral de l’homme et des animaux mammifères,” ibid., 5 (1825) pp. 27–37.

55 Phenomènes physiques de la vie, 4 vols. (1842).

56 Translation in Robinson (1978), p. 13.

57 Fox (1974a).

58 On Laplace’s early physical investigations, see Gillispie (1997), pp. 29–37.

59 On Coulomb, see Gillmor (1971).

60 PVIF 3, p. 516; Journal de l’École Polytdechnique 7, 14th cahier (1808), pp. 1–44, 84–129.

61 Théorie de la double réfraction dans les substances cristallisées (1810).

62 On Malus, see the too little known study by Chappert (1977).

63 On Biot and chromatic polarization, see Maurice Crosland, “Biot,” DSB 2 (1971), pp.133–140.

64 Fresnel’s papers are collected in Oeuvres complètes d’Augustin Fresnel, ed. Henri de Senarmont, Émile Verdet, and Léonor Fresnel, 2 vols. (1885–87). On the wave theory of light, see Buchwald (1989), and, on the principle of interference, the too little noticed Kipnis (1990).

65 Reprinted in 1958, with a foreword by Edmond Bauer. Ampère’s memoirs were gathered in Mémoires sur l’électrodynamique, 2 vols. (1885–87).

66 On Ampère, see Blondel (1982) and Hoffman (1995).

67 On Fourier, see Grattan-Guinness (1972).

68 Fox (1968, 1970).