11
Tile That Courtyard, Please
We shape our buildings; thereafter they shape us.
—Winston Churchill
Programming constructs and algorithmic paradigms covered in this puzzle: List comprehension basics. Recursive divide-and-conquer search.
Consider the following tiling problem. We have a courtyard with 2n × 2n squares and we need to tile it using L-shaped tiles, or trominoes. Each tromino consists of three square tiles attached to form an L shape, as shown below.

Can this be done without spilling over the boundaries, breaking a tromino, or having overlapping trominoes? The answer is no, simply because 2n × 2n = 22n is not divisible by 3, only by 2. The fundamental theorem in arithmetic, namely the unique prime factorization theorem, states that every integer greater than 1 either is prime itself or is the product of prime numbers, and that this product is unique up to the order of the factors. Since 2 is prime, the theorem implies that 22n can only be written as a product of 2n 2’s. Other primes, including 3, cannot be a factor of 22n. However, if there is one square that can be left untiled, then 22n − 1 is divisible by 3. Can you show this?1
We therefore have hope of properly tiling a 2n × 2n courtyard, leaving one square untiled because, for example, there is a statue of your favorite president on it. We’ll call this square the missing square.
Is there an algorithm that tiles any 2n × 2n courtyard with one missing square in an arbitrary location? As an example, below is a 23 × 23 courtyard where the missing square is marked Δ. Does the location of the missing square matter?
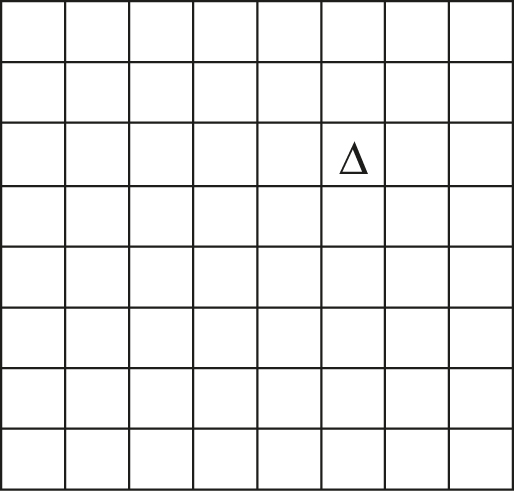
The answer is yes. We will describe and code a recursive divide-and-conquer algorithm that can tile a courtyard with 2n × 2n squares, with one missing square in an arbitrary location. To help you understand how recursive divide-and-conquer works, we will first describe how it is used in merge sort, a popular sorting algorithm.
Merge Sort
We can perform sorting using the elegant divide-and-conquer merge sort. Here’s how merge sort works.
Suppose we have a list, as shown here with symbolic values or variables, that needs to be sorted in ascending order:
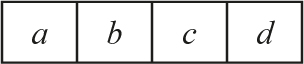
We divide it into two equal-sized2 sublists:

Then we sort the sublists recursively. At the base case of the recursion, if we see a list of size 2, we simply compare the two elements in the list and swap if necessary. Let’s say that a < b and c > d. Since we want to sort in ascending order, after the two recursive calls return we end up getting:
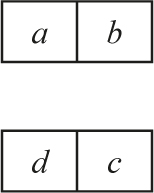
Now we come back to the first (or topmost) call to the sort function, and our task is to merge the two sorted sublists into one sorted list. We do this using a merge algorithm, which simply compares the first two elements of the two sublists, repeatedly. If a < d, it first puts a into the merged (output) list and effectively removes it from the sublist. It leaves d where it was. It then compares b with d. Let’s say d is smaller. Merge puts d into the output list next to a. Next, b and c are compared. If c is smaller, c is placed next into the output list, and finally b is placed. The output will be:

Here’s code for merge sort.
1. def mergeSort(L):
2. if len(L) == 2:
3. if L[0] <= L[1]:
4. return [L[0], L[1]]
5. else:
6. return [L[1], L[0]]
7. else:
8. middle = len(L)//2
9. left = mergeSort(L[:middle])
10. right = mergeSort(L[middle:])
11. return merge(left, right)
Lines 2–6 are the base case, where we have a list of two elements and we place them in the right order. If the list has more than two elements, we split the list in two (line 8) and make two recursive calls, one on each sublist (lines 9–10). We use list slicing; L[:middle] returns the part of the list L corresponding to L[0] through L[middle-1], and L[middle:] returns the part of the list corresponding to L[middle] to L[len(L)-1], so no elements are dropped. Finally, on line 11, we call merge on the two sorted sublists and return the result.
All that remains is the code for merge.
1. def merge(left, right):
2. result = []
3. i, j = 0, 0
4. while i < len(left) and j < len(right):
5. if left[i] < right[j]:
6. result.append(left[i])
7. i += 1
8 else:
9. result.append(right[j])
10. j += 1
11. while i < len(left):
12. result.append(left[i])
13. i += 1
14. while j < len(right):
15. result.append(right[j])
16. j += 1
17. return result
Initially, merge creates a new empty list result (line 2). There are three while loops in merge. The first one, which is the most interesting, corresponds to the general case when the two sublists are both nonempty. In this case, we compare the current first elements of each of the sublists (represented by counters i and j), pick the smaller one, and increment the counter for the sublist whose element we selected to place in result. The first while loop terminates when either of the sublists becomes empty.
When one of the sublists is empty, we simply append the remaining elements of the nonempty sublist to the result. The second and third while loops correspond to the left sublist being nonempty and the right one being nonempty, respectively.
Merge Sort Execution and Analysis
Suppose we have this input list for merge sort:
inp = [23, 3, 45, 7, 6, 11, 14, 12]
How does execution proceed? The list is split in two:
|
[23, 3, 45, 7] |
|
[6, 11, 14, 12] |
|
and the left list is sorted first, and the first step is to split it in two:
|
[23, 3] |
[45, 7] |
[6, 11, 14, 12] |
|
Each of these two-element lists is sorted in ascending order:
|
[3, 23] |
[7, 45] |
[6, 11, 14, 12] |
|
The sorted lists of two elements each are merged into a sorted result:
|
[3, 7, 23, 45] |
|
[6, 11, 14, 12] |
|
Next, the algorithm looks at the right list and splits it in two:
|
[3, 7, 23, 45] |
|
[6, 11] |
[14, 12] |
Each of the right sublists is sorted:
|
[3, 7, 23, 45] |
[6, 11] |
[12, 14] |
|
The sorted sublists of two elements each are merged into a sorted result:
|
[3, 7, 23, 45] |
|
[6, 11, 12, 14] |
|
And finally, the two sorted sublists of four elements each are merged:
[3, 6, 7, 11, 12, 14, 23, 45]
Merge sort is a more efficient sorting algorithm than the selection sort algorithm we described in puzzle 2. Selection sort had a doubly nested loop and therefore required, in the worst case, n2 comparisons and exchanges for a list of length n. In merge sort, we only perform n operations in each merge step of a list of length n. The top-level merge will require n operations, and the next level will run merge on two lists of length n/2, and will also require n operations. The next level after that will require n/4 operations on each of four lists, for a total of n operations. The number of levels is log2 n, so merge sort requires n log2 n operations.
As you can see, during the merge step we need to create a new list result (line 2) and return that. The amount of intermediate storage required for merge sort therefore grows with the length of the list to be sorted. This was not the case for selection sort. We will come back to this requirement in puzzle 13.
Now, let’s get back to courtyard tiling.
Base Case of a 2 × 2 Courtyard
Let’s start with n = 1, that is, a 2 × 2 courtyard with one missing square. The missing square can be in different locations, as shown below, where the Δ’s are in different locations. In all four of these cases, we can tile the remaining three squares with an L-shaped tile oriented appropriately.

This is an important step because we now have a base case for a recursive divide-and-conquer algorithm that we can apply. But how can we divide the 2n × 2n courtyard with one missing square, so that we get subproblems that are the same problem but smaller? If we divide the 2n × 2n courtyard into four 2n − 1 × 2n − 1 courtyards as shown below, we get one 2n − 1 × 2n − 1 courtyard with a missing square—the one on the top right—but the other three are full 2n − 1 × 2n − 1 courtyards.
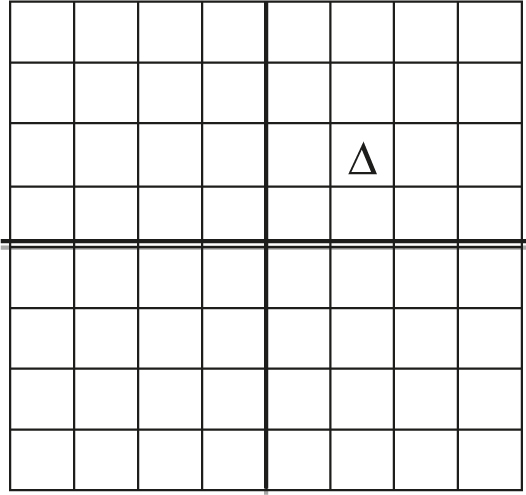
Recursive Step
In the above example, we recognize that the statue Δ is in the top right quadrant. Therefore we place a tromino strategically on the three “full” quadrants to create a set of four quadrants, each with one missing square that needs to be tiled (see the following example).

The top right quadrant is unchanged, but the other three have exactly one square tiled, so the remaining work is to tile four 2n − 1 × 2n − 1 courtyards with one missing square each. Sound familiar? Note that if the missing square were in the top left quadrant, we would rotate the tromino counterclockwise 90 degrees and obtain four smaller courtyards as before. Work out the rotations for the other two cases.
We do this recursively till we obtain 2 × 2 courtyards with one missing square. Each of these is trivially tiled with one tromino, as we showed earlier. We’re done.
Except not quite. You have a large 2n × 2n courtyard (with a statue) to tile, and working with L-shaped tiles is a complicated job. This means you have to be very specific to the flooring contractor about each tile that needs to be laid down. We need to write a program that will generate a “map” of all the tiles for this courtyard. (This is a book about programming—you didn’t think we’d stop with the algorithm, did you?)
We are going to number quadrants in a particular way, as shown in the code we write, below. Our courtyard will be represented as yard[r][c], where r is the row number and c is the column number. Row numbers increase from top to bottom, and column numbers increase from left to right, as shown below.

1. def recursiveTile(yard, size, originR, originC, rMiss,\
1a. cMiss, nextPiece):
2. quadMiss = 2*(rMiss >= size//2) + (cMiss >= size//2)
3. if size == 2:
4. piecePos = [(0,0), (0,1), (1,0), (1,1)]
5. piecePos.pop(quadMiss)
6. for (r, c) in piecePos:
7. yard[originR + r][originC + c] = nextPiece
8. nextPiece = nextPiece + 1
9. return nextPiece
10. for quad in range(4):
11. shiftR = size//2 * (quad >= 2)
12. shiftC = size//2 * (quad % 2 == 1)
13. if quad == quadMiss:
14. nextPiece = recursiveTile(yard, size//2,\ originR +\
14a. shiftR, originC + shiftC, rMiss\ - shiftR,\
14b. cMiss - shiftC, nextPiece)
15. else:
16. newrMiss = (size//2 - 1) * (quad < 2)
17. newcMiss = (size//2 - 1) * (quad % 2 == 0)
18. nextPiece = recursiveTile(yard, size//2,\ originR +\
18a. shiftR, originC + shiftC, newrMiss,\ newcMiss,\
18b. nextPiece)
19. centerPos = [(r + size//2 - 1, c + size//2 - 1)
19a. for (r,c) in [(0,0), (0,1), (1,0), (1,1)]]
20. centerPos.pop(quadMiss)
21. for (r,c) in centerPos:
22. yard[originR + r][originC + c] = nextPiece
23. nextPiece = nextPiece + 1
24. return nextPiece
The function recursiveTile takes as arguments a two-dimensional grid yard, the dimension of the current yard or quadrant being tiled (size), the row and column coordinates of the origin (originR, originC), and the location of the missing square (rMiss, cMiss) in relation to the origin. As a final argument, it also takes a helper variable, nextPiece, which is used to number tiles so we can print an easy-to-read map for the contractor. Assume for now that the origin is (0, 0).
The quadrant with the missing square is identified based on the location of the missing square on line 2, shown below:
quadMiss = 2*(rMiss >= size//2) + (cMiss >= size//2)
Rows are numbered from 0 at the top to size - 1 at the bottom. Columns are numbered 0 at the left to size - 1 on the right. As an example, if rMiss = 0, and cMiss = size - 1, we have the missing square in the top right quadrant, and quadMiss is computed as 2 * 0 + 1 = 1. For large rMiss and cMiss equal to or greater than size//2, we will get the lower right quadrant, numbered 3.
The base case is written first in recursiveTile, lines 3–9, and shows how nextPiece is used to mark the squares with the number of the tile that was used to cover the squares. The base case is for a 2 × 2 courtyard with one missing square in square quadMiss. We know we can tile the courtyard regardless of what quadMiss is, and we number the tile using nextPiece and fill in the courtyard yard. Since we do not want to tile the square quadMiss (it has either been tiled already or will have a statue on it), we remove it from the list of tuples piecePos using the pop function on the list. The pop function takes the index of the element in the list as an argument and removes that element from the list (line 5). Since the same data structure yard is filled in each recursive call, we need to use the origin coordinates to tile different, disjoint quadrants in each call (line 7). Once the 2 × 2 courtyard has been tiled, we increment nextPiece and return it (lines 8–9).
The overall recursion works as follows. Based on quadMiss, four recursive calls are made (lines 10–18). quadMiss is the location of the missing square in the yard, and the quadrant corresponding to quadMiss will have the missing square. However, in the three other quadrants, we will also have a missing square at one of the corners, since we will eventually place a tile at those corners. This center tile is placed after the recursive calls return (lines 19–23).
There is some computation to determine the arguments for the recursive calls. The size of the courtyard is size//2 and we pass nextPiece into the recursive calls. We also need to compute the origin coordinates for each of the four quadrants. The shifts required in the coordinates are computed in lines 11–12. Given our numbering of the quadrants, when we make the recursive calls, quadrants 0 and 1 will have the same origin row coordinates as in the parent procedure, and quadrants 2 and 3 will have their origin row coordinates shifted by size//2 in relation to the parent procedure (line 11). Quadrants 0 and 2 will have the same origin column coordinates as the parent procedure, and quadrants 1 and 3 will have origin column coordinates shifted by size//2 (line 12).
For the recursive call corresponding to the quadrant quadMiss, which has the square that was missing in the parent call, we simply compute the new rMiss and cMiss in relation to the shifted origin coordinates (line 14).
The computation of the rMiss and cMiss arguments is different for the other three recursive calls because the missing square will be at one of the corners and is unrelated to the values of rMiss and cMiss in the parent call. The computation is given in lines 16–17. For quadrant 0, the bottom right corner will be the missing square, and its coordinates in relation to the origin are rMiss, equaling size//2 - 1, and cMiss, equaling size//2 - 1. The other quadrants work similarly.
Finally, in lines 19–23, we place the center tile in the yard, again based on quadMiss, which points to the square on which the tile should not be placed. We could just as easily have placed the center tile before making the recursive calls. The only difference would be in the numbering of the tiles, not where the tiles are placed. Lines 19 and 19a show the creation of a list centerPos in Python list comprehension style—more on that below. This list initially contains the four middle squares in the courtyard being processed in this call, which are each corner squares of the four quadrants of the courtyard. Line 20 removes from centerPos the corner square that belongs to the quadrant containing quadMiss.
Let’s look at how to invoke recursiveTile.
1. EMPTYPIECE = -1
2. def tileMissingYard(n, rMiss, cMiss):
3. yard = [[EMPTYPIECE for i in range(2**n)]
3a. for j in range(2**n)]
4. recursiveTile(yard, 2**n, 0, 0, rMiss, cMiss, 0)
5. return yard
We will use -1 to signify an empty square in the yard (line 1). The function tileMissingYard is simply a wrapper for the function recursiveTile, which needs the arguments corresponding to the origin coordinates and nextPiece all initialized to 0. On lines 3 and 3a, we create a new two-dimensional list corresponding to a yard with each dimension equaling 2**n. We initialize it in Python list comprehension style, which is more compact than the standard nested for loops we would need to fill a two-dimensional list. It’s worth emphasizing that we allocate no memory for courtyards within the recursiveTile procedure—each recursive call fills in disjoint parts of the variable yard that is passed into the procedure.
The returned nextPiece value is ignored for the top-level call to recursiveTile, but is used in subsequent recursive calls.
List Comprehension Basics
List comprehensions can be used to create lists in a natural way. Suppose we want to produce the lists S and O, defined mathematically as:
S = {x3 : x in {0 … 9}}
O = {x | x in S and x odd}
Here’s how we can produce the lists using list comprehensions:
S = [x**3 for x in range(10)]
O = [x for x in S if x % 2 == 1]
The first expression in the list definition corresponds to an element of the list, and the rest generates list elements according to specified properties. We are including in S the cubes of all numbers from 0 to 9. We are including all odd numbers in S in the list O.
Here’s a more interesting example where we compute the list of prime numbers less than 50. First, we build a list of composite (non-prime) numbers, using a single list comprehension, and then we use another list comprehension to get the “inverse” of the list, which comprises the prime numbers.
cp = [j for i in range(2, 8) for j in range(i*2, 50, i)]
primes = [x for x in range(2, 50) if x not in cp]
The two loops in the definition of cp find all the multiples of numbers from 2 to 7 that are less than 50. The number 7 was chosen because 72 = 49, the highest number less than 50. Some composite numbers may be repeated in the cp list. The definition for primes simply walks through numbers from 2 to 49 and includes numbers that are not present in the cp list.
List comprehensions can produce very compact code, which is sometimes incomprehensible. Use them in moderation!
Pretty Printing
One reason for this coding exercise was to produce a contractor-friendly map, and here is the printing routine that does exactly that.
1. def printYard(yard):
2. for i in range(len(yard)):
3. row = ''
4. for j in range(len(yard[0])):
5. if yard[i][j] != EMPTYPIECE:
6. row += chr((yard[i][j] % 26) + ord('A'))
7. else:
8. row += ' '
9. print (row)
The procedure prints the two-dimensional yard on one line per row. It creates a row of characters corresponding to the tiles on that row, and prints the row. There is one missing square in the courtyard that is left empty by printing a space (line 8).
We could print the numbers, but we chose to replace them with letters A through Z.
The function chr takes a number and produces a letter associated with that number in ASCII format. The function ord is the inverse of chr—it takes a letter and produces its ASCII number. The tile with number 0 is assigned the letter A on line 5, and the tile with number 1 is assigned the letter B, and so on till number 26 gets Z. If the courtyard is 25 × 25 or larger, we will have more than 26 L-shaped tiles, and some tiles will get the same letter. (Of course, we could have printed these tiles’ unique numbers. One problem with printing numbers is that we would have to deal with single-digit and double-digit numbers during printing.)
Let’s run:
printYard(tileMissingYard(3, 4, 6))
to get:
AABBFFGG
AEEBFJJG
CEDDHHJI
CCDUUHII
KKLUPP Q
KOLLPTQQ
MOONRTTS
MMNNRRSS
This is descriptive enough for any contractor to tile the courtyard properly. You can see in what order the tiles are laid by recursiveTile. The recursive calls follow the order of the quadrants: 0, 1, 2, and 3 (line 12 of recursiveTile). The first tile laid is tile A, which corresponds to the top left quadrant. The center tile, U, is laid last since we chose to lay down the center tile after the recursive calls returned. If we had laid the center tile before making the recursive calls, the center tile would have been A.
Let’s do a runtime analysis of recursiveTile. It runs fairly fast on large yards. The key observation is that the yard size (i.e., the length and width of the courtyard) in each recursive call is half of the original. So if we start with a 2n × 2n courtyard, in n − 1 steps we will get to the base case: a 2 × 2 courtyard. Of course, at each step, we are making four recursive calls, giving us 4n − 1 calls, each of which tiles a 2 × 2 courtyard. The number of squares processed is exactly 2n × 2n, which is the number of squares in the initial courtyard. Of course, one of the squares is not tiled.
A Different Tiling Puzzle
The famous mutilated chessboard tiling puzzle goes as follows: Suppose a standard 8 × 8 chessboard has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2 × 1 so as to cover all these squares?
Exercises
Exercise 1: You are given a 2n × 2n courtyard to tile with L-shaped tiles with four tiles missing. There are (at least) two cases where this is possible:
- When the four missing tiles are in four different quadrants.
- When any three of the four tiles are such that you can tile them using a tromino.
Write a procedure that will determine whether you can tile the courtyard using recursiveTile by checking for the above two conditions. The procedure can just return True or False, given n and a four-element list of missing square coordinates.
Puzzle Exercise 2: Suppose you have a two-dimensional list or matrix T as shown below, where all rows and all columns are sorted. Devise and implement a binary search algorithm that works for lists such as T. You can assume that all elements are unique, as in the example below.
T = [[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]]
Here’s the strategy: Guess that the value is at position i, j and think of what it means if the value is less than T[i][j], or if the value is greater than T[i][j]. For example, if we are searching for 21 and we compare with T[2][2] = 9, we know that 21 cannot be in the T[<= 2][<= 2] upper left quadrant because all values in that quadrant are less than 9. However, 21 could be in any of the three other quadrants: the bottom left T[> 2][<= 2] quadrant, which it is in this example, or the top right T[<= 2][> 2] or bottom right T[> 2][> 2] quadrants, in different examples.
You can always eliminate one of the four quadrants in your two-dimensional binary search. You will have to make recursive calls on the other three quadrants.
Puzzle Exercise 3: It is natural to ask whether the two-dimensional binary search algorithm of exercise 2 is the best possible algorithm. Let’s look at T again:
T = [[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]]
Suppose we want to find out if element 13 exists in T. Here’s the strategy: Start with the top right element. If the element is smaller than 13, you can eliminate the entire first row and move one position down. If the element is larger, you can eliminate the entire last column and move one position left. Obviously, if the element is the top right element, you can stop.
The neat thing about this strategy is that it eliminates either a row or a column in each step. So you will find the element you are searching for in at most 2n steps for an n × n matrix, or you will determine that it does not exist. Code the above algorithm by making recursive calls on the appropriate submatrix (with one less row or one less column). In our example above, we will move from 15 to 11 to 12 to 16 to 9 to 14 to 13.