2
The Best Time to Party
No one looks back on their life and remembers the nights they got plenty of sleep.
—Author unknown
Programming constructs and algorithmic paradigms covered in this puzzle: Tuples, lists of tuples, nested for loops, and floating-point numbers. List slicing. Sorting.
There is a party to celebrate celebrities that you get to attend because you won a ticket at your office lottery. Because of the high demand for tickets, you only get to stay for one hour, but you get to pick which hour because you received a special ticket. You have a schedule that lists exactly when each celebrity is going to attend the party. You want to get as many pictures with celebrities as possible to improve your social standing. This means you wish to go for the hour when you get to hobnob with the maximum number of celebrities and get selfies with each of them.
We are given a list of intervals that correspond to when each celebrity comes and goes. Assume that these intervals are [i, j), where i and j correspond to hours. That is, the interval is closed on the left side and open on the right side. This means the celebrity will be partying on and through the ith hour, but will have left when the jth hour begins. So even if you arrive on the dot on the jth hour, you will miss this particular celebrity.
Here’s an example:
|
Celebrity |
Comes |
Goes |
|
Beyoncé |
6 |
7 |
|
Taylor |
7 |
9 |
|
Brad |
10 |
11 |
|
Katy |
10 |
12 |
|
Tom |
8 |
10 |
|
Drake |
9 |
11 |
|
Alicia |
6 |
8 |
When is the best time to attend the party? That is, which hour should you go?
By looking at each hour and counting celebrities, you probably figured out that going between the hours of 10 and 11 will get you selfies with Brad, Katy, and Drake. You can’t do better than three selfies.
Checking Time and Time Again
The straightforward algorithm looks at each hour and checks how many celebrities are available. A celebrity with [i, j) is available at hours i, i + 1, …, j − 1. The algorithm simply counts the number of celebrities at each hour and picks the maximum.
Here’s the code for this algorithm:
1. sched = [(6, 8), (6, 12), (6, 7), (7, 8),
(7, 10), (8, 9), (8, 10), (9, 12),
(9, 10), (10, 11), (10, 12), (11, 12)]
2. def bestTimeToParty(schedule):
3. start = schedule[0][0]
4. end = schedule[0][1]
5. for c in schedule:
6. start = min(c[0], start)
7. end = max(c[1], end)
8. count = celebrityDensity(schedule, start, end)
9. maxcount = 0
10. for i in range(start, end + 1):
11. if count[i] > maxcount:
12. maxcount = count[i]
13. time = i
14. print ('Best time to attend the party is at',
time, 'o\'clock', ':', maxcount,
'celebrities will be attending!')
The input to the algorithm is a schedule, which is a list of intervals. Each interval is a 2-tuple where both entries in each tuple are numbers. The first is the start time and the second is the end time. The algorithm can’t modify the intervals, and so we use a tuple to represent them.
Lines 3–7 determine the earliest time that any celebrity will be at the party, and the last time that any celebrity will be. Lines 3 and 4 assume that schedule has at least one tuple in it and initialize the start and end variables. We want start to be the earliest start time of any celebrity and end to be the latest end time of any celebrity. schedule[0] gives the first tuple in schedule. Accessing the two entries of the tuple is exactly the same as accessing a list. Since the tuple is schedule[0], we need another [0] for the first entry to the tuple (line 3) and [1] for the second entry (line 4).
In the for loop, we go over all the tuples, naming each one of them c. Note that if we tried to modify c[0] to be 10 (for example), the program would throw an error since c is a tuple. On the other hand, if we had declared sched = [[6, 8], [6, 12], …], we would be able to modify the 6 to 10 (for example), since each element of sched is a list.
Line 8 invokes a function that fills in a list count that will contain, for each time between start and end inclusive, the count of celebrities available at that time.
Lines 9–13 find the time with the maximum number of celebrities by looping through the various times from start to end and keeping track of the maximum celebrity count, namely, maxcount. These lines can be replaced by:
9a. maxcount = max(count[start:end + 1])
10a. time = count.index(maxcount)
Python provides a function max to find the maximum element of a list. In addition, we can use slicing to select a particular contiguous range of elements within the list. In line 9a, we find the maximum element between the indices start and end, inclusive. If we have b = a[0:3], this means that the first three elements of a, namely a[0], a[1], and a[2], are copied into list b, which will have length 3. Line 10a determines the index at which this maximum element is found.
Now for the core of the algorithm, implemented in the function celebrityDensity:
1. def celebrityDensity(sched, start, end):
2. count = [0] * (end + 1)
3. for i in range(start, end + 1):
4. count[i] = 0
5. for c in sched:
6. if c[0] <= i and c[1] > i:
7. count[i] += 1
8. return count
The function contains a doubly nested loop. The outer loop iterates through different times, incrementing the time i by 1 unit after each iteration, beginning with the time start as given by the first argument to range. For each time, the inner loop (lines 5–7) iterates through the celebrities, and line 6 checks if the celebrity is available at that time. As described earlier, the time needs to be greater than or equal to the celebrity’s start time and less than the celebrity’s end time.
If we run:
bestTimeToParty(sched)
the code will print:
Best time to attend the party is at 9 o'clock : 5 celebrities will be attending!
This algorithm seems reasonable but is unsatisfying for one primary reason. What is the unit of time? In our example, we could pretend that 6 stands for 6 p.m., 11 for 11 p.m., and 12 for 12 a.m. This means the unit of time is 1 hour. What if celebrities come and go at arbitrary times, as they are wont to do? For example, suppose Beyoncé comes at 6:31 and leaves at 6:42, and Taylor comes at 6:55 and leaves at 7:14. We could make the unit of time 1 minute as opposed to 1 hour. This means performing 60 times as many checks in the loop on line 16. And we would need to look at every second if Beyoncé chose to come at 6:31:15. Celebrities may want to time their entry and exit to the millisecond! (Okay, this is admittedly pretty hard to do even for Beyoncé.) Having to choose a unit of time is annoying.
Can you think of an algorithm that doesn’t depend on the granularity of time? The algorithm should use a number of operations that only depends on the number of celebrities and not their schedule.
Being Smart About Checking Times
Let’s pictorially represent all celebrities’ intervals, with time as the horizontal axis. Here’s a possible celebrity schedule:

This picture is evocative—it tells us that if we hold a “ruler” (as shown in dotted lines) at a particular time and count the celebrities whose intervals intersect the ruler, we will know how many we can meet at that time. But we already knew that and coded it in the straightforward algorithm. However, we can make two additional observations from this picture:
- We only need concern ourselves with the start and end points of celebrity intervals because those are the only times that the number of available celebrities changes. There is no reason to compute the number of celebrities available at the second dotted line’s time—it is the same as the first one because no new celebrity has come or gone between the first and second lines/times. (Remember that the fourth celebrity—fourth line from top—has already arrived at the time corresponding to the first dotted line.)
- We can move the ruler from left to right and find the time with the maximum number of celebrities through incremental computation, as we will elaborate below.
We keep a count of celebrities, initially zero. Every time we see the start time of a celebrity interval, we increment this count, and every time we see the end time of a celebrity interval, we decrement this count. We also keep track of the maximum celebrity count. While the count of celebrities changes at the start and end times of celebrity intervals, the maximum count only changes when we see the start point of a celebrity interval.
One crucial point—we have to perform this computation in increasing time to simulate the ruler moving left to right. This means that we have to sort the start times and end times of the celebrities. What we want in the picture above is to see the second-from-top celebrity’s start time, followed by the third-from-top celebrity’s start time, followed by the first-from-top celebrity’s start time, and so on. We’ll worry about how to sort these times a bit later, but we are now ready to look at code that corresponds to a more efficient and elegant way of discovering the best time to party.
1. sched2 = [(6.0, 8.0), (6.5, 12.0), (6.5, 7.0),
(7.0, 8.0), (7.5, 10.0), (8.0, 9.0),
(8.0, 10.0), (9.0, 12.0), (9.5, 10.0),
(10.0, 11.0), (10.0, 12.0), (11.0, 12.0)]
2. def bestTimeToPartySmart(schedule):
3. times = []
4. for c in schedule:
5. times.append((c[0], 'start'))
6. times.append((c[1], 'end'))
7. sortList(times)
8. maxcount, time = chooseTime(times)
9. print ('Best time to attend the party is at',
time, 'o\'clock', ':', maxcount,
'celebrities will be attending!')
Note that schedule and sched2 are lists of 2-tuples, as before, where the first number of each tuple is the start time, and the second number of each tuple is the end time. However, we are using floating-point numbers in sched2 as opposed to integers as in schedule to represent time. The numbers 6.0, 8.0, and so on are floating-point numbers. In this puzzle, we are only going to compare these numbers and won’t have to perform other arithmetic on them.
On the other hand, the list times, initialized to empty on line 3, is a list of 2-tuples where the first number of each tuple is a time, and the second item is a string label indicating whether the time is a start time or an end time.
Lines 3–6 collect all the start and end times for celebrities, labeling each time as such. This list is not sorted since we cannot assume that the argument schedule is sorted in any fashion.
Line 7 sorts the list times by invoking a sort procedure that we will describe later. Once the list has been sorted, line 8 invokes the critical procedure chooseTime, which performs the incremental computation of determining celebrity count (or density) at each time.
This code will print the same thing for the original schedule sched and will print for sched2:
Best time to attend the party is at 9.5 o'clock : 5 celebrities will be attending!
What about sorting the times? We have a list of intervals that we need to convert into times labeled with 'start' or 'end'. And then we just sort the times in ascending order, keeping the labels attached to the times. Here’s code that does that:
1. def sortList(tlist):
2. for ind in range(len(tlist)-1):
3. iSm = ind
4. for i in range(ind, len(tlist)):
5. if tlist[iSm][0] > tlist[i][0]:
6. iSm = i
7. tlist[ind], tlist[iSm] = tlist[iSm], tlist[ind]
How does this code work? It corresponds to the simplest possible sorting algorithm,1 called selection sort. The algorithm finds the minimum time and puts it at the front of the list after the first iteration of the outer for loop (lines 2–7). This search of the minimum needs to happen len(tlist)-1 times, not len(tlist) times—we don’t have to find the minimum when there is only one element left.
Finding the minimum element requires going through all the elements in the list, and this happens in the inner for loop (lines 4–6). Since there is already an element at the front of the list that needs to remain somewhere in the list, the algorithm swaps the two elements on line 7. Think of line 7 as two assignments that happen in parallel: tlist[ind] gets the old value of tlist[iSm], and tlist[iSm] gets the old value of tlist[ind].
In the second iteration of the outer for loop, the algorithm looks at the rest of the list (not including the first item), finds the minimum, and places it as the second item right next to the first, by swapping the element that was in the second position with the minimum in this iteration. Notice that line 4 has two arguments to range, to make sure that on each iteration of the outer loop, the inner loop starts at ind, where elements at indices less than ind are already positioned properly. This continues until the entire list is sorted. Since each element of the argument list is a 2-tuple, we have to use the time value in the comparison on line 5, which is the first item in the 2-tuple. This is the reason for the extra [0]’s on line 5. Of course, we are sorting the 2-tuples; the 2-tuples are being swapped on line 7, and the 'start' and 'end' labels remain attached to the same times.
Once the list has been sorted, procedure chooseTime (shown below) determines the best time and the celebrity count at that time by going through the list once.
1. def chooseTime(times):
2. rcount = 0
3. maxcount = time = 0
4. for t in times:
5. if t[1] == 'start':
6. rcount = rcount + 1
7. elif t[1] == 'end':
8. rcount = rcount - 1
9. if rcount > maxcount:
10. maxcount = rcount
11. time = t[0]
12. return maxcount, time
The number of iterations is twice the number of celebrities, because the list times has two entries (each of which is a 2-tuple) corresponding to the start and end times for each celebrity. Compare this to the doubly nested loop in the straightforward algorithm, which has a number of iterations equaling the number of celebrities times the number of hours (or minutes or seconds as the case may be).
Note that the best time to attend the party will always correspond to the start time of some celebrity. This is because rcount is incremented only at these start times, and therefore the peak is reached at one of these times. We’ll exploit this observation in exercise 2.
Sorted Representation
The technique of sorting a list of elements for more efficient processing is a fundamental one. Suppose you have two lists of words and you want to check whether the lists are equal or not. Let’s assume each of the lists has no repeated words and they are equal in size with n words each. The obvious way is to take each word in list 1 and check if it exists in list 2. We have to do n2 comparisons in the worst case, since the check for each word might take n comparisons before it succeeds or fails.
A better way is to sort each of the two lists in alphabetical order of words. Once they are sorted, we can simply check if the first word of sorted list 1 is equal to the first word of sorted list 2, the second word of sorted list 1 is equal to the second word of sorted list 2, and so on. This only requires n comparisons.
Wait, you say, what about the number of operations required for sorting? Doesn’t that selection sort procedure take n2 comparisons in the worst case? And we are sorting two lists. Stay tuned for better sorting algorithms that only require n log n comparisons in the worst case, which we will describe later in the book. For large n, n log n is way smaller than n2, making sorting prior to equality comparison very worthwhile.
Exercises
Exercise 1: Suppose you are yourself a busy celebrity and don’t have complete freedom in choosing when you can go to the party. Add arguments to the procedure and modify it so it determines the maximum number of celebrities you can see within a given time range between ystart and yend. As with celebrities, the interval is [ystart, yend), so you are available at all times t such that ystart <= t < yend.
Exercise 2: There is an alternative way of computing the best time to party that does not depend on the granularity of time. We choose each celebrity interval in turn, and determine how many other celebrity intervals contain the chosen celebrity’s start time. We pick the time to attend the party to be the start time of the celebrity whose start time is contained in the maximum number of other celebrity intervals. Code this algorithm and verify that it produces the same answer as the algorithm based on sorting.
Puzzle Exercise 3: Imagine that there is a weight associated with each celebrity dependent on how much you like that particular celebrity. This can be represented in the schedule as a 3-tuple, for example, (6.0, 8.0, 3). The start time is 6.0, the end time is 8.0, and the weight is 3. Modify the code so you find the time that the celebrities with maximum total weight are available. For example, given:
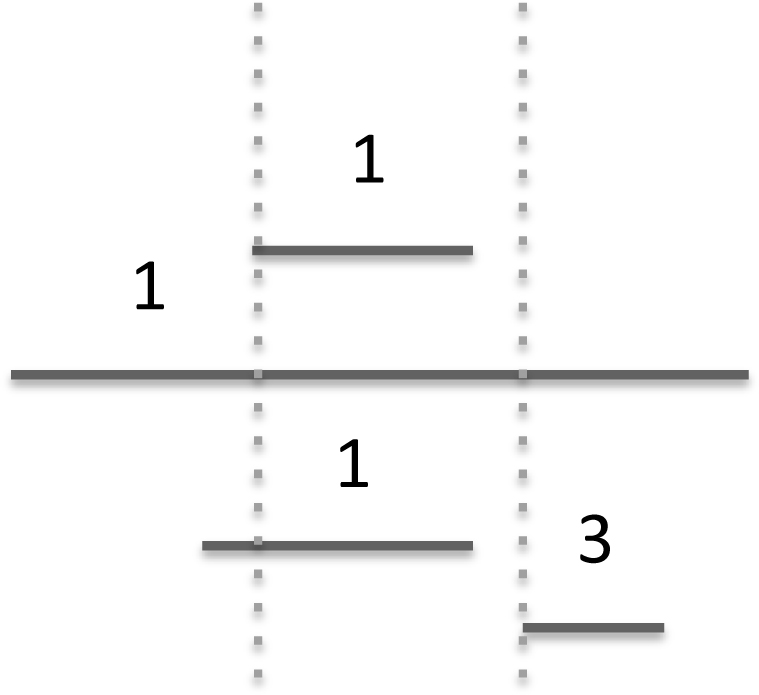
We want to return the time corresponding to the right dotted line even though there are only two celebrities available at that time. This is because the weight associated with those two celebrities is 4, which is greater than the total weight of 3 associated with the three celebrities available during the first dotted line.
Here’s a more complex example:
sched3 = [(6.0, 8.0, 2), (6.5, 12.0, 1), (6.5, 7.0, 2),
(7.0, 8.0, 2), (7.5, 10.0, 3), (8.0, 9.0, 2),
(8.0, 10.0, 1), (9.0, 12.0, 2),
(9.5, 10.0, 4), (10.0, 11.0, 2),
(10.0, 12.0, 3), (11.0, 12.0, 7)]
For this schedule of celebrities, you want to attend at 11.0 o'clock where the weight of attending celebrities is 13 and maximum.