21
Questions Have a Price
If you have to ask how much it costs, you can’t afford it.
—J. P. Morgan
Programming constructs and algorithmic paradigms covered in this puzzle: Object-oriented programming. Binary search trees.
We’ve all played the twenty questions game. Here’s one with a twist.
Your friend is going to think of a number from 1 to 7. Your job is to guess the number using the fewest number of guesses. Once you have guessed it correctly, it is your turn to think of a number and your friend’s turn to guess. The two of you have nothing better to do than play this game umpteen times, keeping track of all the guesses made by each person for each round, where in each round both of you have a chance to guess. Afterward, you’ll go to dinner, and the person with more guesses pays. So you are very motivated to win.
Now some details of how the game is played. We’ll call the person who thought of the number Thinker and the person who guesses Guesser. Thinker has to write the number down before Guesser starts guessing to ensure that Thinker does not cheat and change the number on the fly. When Guesser guesses a number, Thinker responds with Correct, Less, or More. These responses have the obvious meanings.
At this point, you are probably thinking binary search is going to be the best strategy. With numbers between 1 and 7 inclusive, you are going to need at most three guesses to find the number, since log2 7 is greater than 2 but less than 3. Here’s what the binary search tree (BST) looks like:
The BST above represents an execution of binary search. The root is the first guess, 4. You move to 2 with a Less response, move to 6 with a More response, and celebrate with a Correct response. If your friend thought 4, you use only one guess, and if your friend guessed 7, you will need three guesses: 4, 6, 7. The BST is a cool data structure and satisfies this invariant: All vertices to the left of a vertex will have numbers less than the vertex’s number, and all vertices to the right of a vertex will have numbers larger than the vertex’s number. This is true of every vertex in a BST—a recursive property. A vertex may have one, two, or no children.
Your friend knows about binary search and BSTs, so you figure it is going to be a toss-up who pays for dinner. But then you realize that your friend is constantly picking odd numbers because the odd numbers are at the bottom of the BST, and you need more guesses for these. In fact, you estimate that the probability of a number being chosen by your friend in each round is exactly as given below (and now listed on the BST figure below):
Pr(1) = 0.2 Pr(2) = 0.1 Pr(3) = 0.2 Pr(4) = 0
Pr(5) = 0.2 Pr(6) = 0.1 Pr(7) = 0.2
You reason that you can win this game by choosing a different BST, which needs fewer guesses for the odd numbers. You know your friend is stubborn and isn’t going to change the probabilities, so if you come up with a BST that requires, on average, fewer guesses, you are going to win.
Can you synthesize a different BST that minimizes the expected number of guesses you need to make, given the probabilities above? The following quantity should be minimized:
D(i) is the depth of the number i in your BST. For the conventional BST shown earlier, the above quantity is 0.2 · 3 + 0.1 · 2 + 0.2 · 3 + 0 · 1 + 0.2 · 3 + 0.1 · 2 + 0.2 · 3 = 2.8. For i = 1, the number 1 has probability 0.2 at depth 3, and for i = 2, the number 2 has probability 0.1 at depth 2. And so on.
You can do appreciably better with a different BST. A free dinner beckons.
Here’s the optimal BST for the given probabilities that minimizes the quantity:
The first thing to note is that it has vertices at greater depth, 4, than the “balanced” BST, which has a maximum depth of 3 and an average number of guesses of 2.8. The average number of guesses for the above BST, which is what we are calling the weight of the BST, is 0.2 · 2 + 0.1 · 3 + 0.2 · 1 + 0 · 3 + 0.2 · 2 + 0.1 · 4 + 0.2 · 3 = 2.3 < 2.8. This is the best you can do for the given probabilities.
Perhaps you came up with this BST through trial and error. Of course, the next time you play your friend or someone else, you might have to synthesize a different BST that optimizes a different set of probabilities. Not surprisingly, we want to write a program that automatically produces the optimal BST with minimum weight, given a vector of probabilities.
Binary Search Trees Using Dictionaries
We have already seen how we can represent graphs using dictionaries. A BST is a special kind of graph, so we can clearly use a dictionary representation.
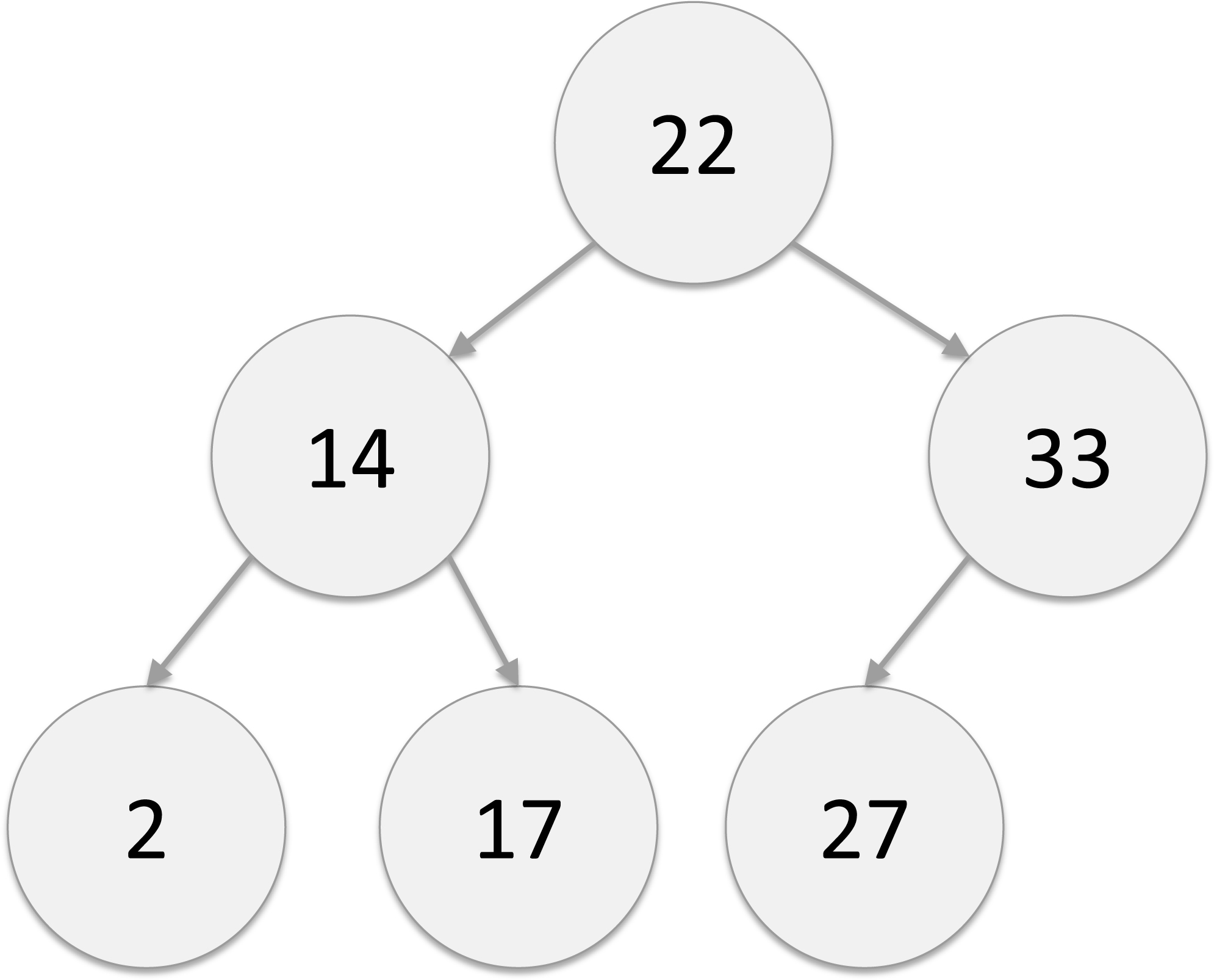
Here’s an example BST.
And here’s what the representation using a dictionary looks like.
BST = {‘root’: [22, ‘A’, ‘B’],
’A’: [14, ‘C’, ‘D’],
’B’: [33, ‘E’, ''],
’C’: [2, '', ''],
’D’: [17, '', ''],
’E’: [27, '', '']}
’root’ corresponds to the root vertex, with number 22, and BST[‘root’] gives us a value list (of length 3) that has the number associated with the root vertex, followed by the left child and then the right child. Therefore, BST[‘root’][1] gives us the left child, which is vertex ’A’. BST[BST[‘root’][1]] would give us the value list corresponding to vertex ’A’, namely, [14, ‘C’, ‘D’].
The empty string '' represents a child that does not exist. For example, the right child of the vertex named ’B’ with number 33 does not exist. Leaf vertices, such as vertex ’E’ with number 27, have no children.
Notice that our earlier BST picture examples did not have names for vertices. However, our BST dictionary representation does. We’ll assume that all numbers in a BST are unique, so numbers can uniquely identify vertices. It would be nice if we could simplify our representation and use the numbers directly as keys in our dictionary representation. We could try to do this:
BSTnoname = {22: [14, 33],
14: [2, 17],
33: [27, None],
2: [None, None],
17: [None, None],
27: [None, None]}
However, we have a problem here. How do we know which number corresponds to the root? Remember, we cannot depend on the order of keys in a dictionary. If we enumerate the keys in a dictionary and print them, we might get the order shown above or a different order with, say, 33 being the first key printed, which is not the root of our BST.
Of course, we could discover the root by going through the whole BST and determining that 22 does not appear as a number in any of the value lists in the dictionary—therefore, it has to be the root. But this involves significant computation that grows with the number of vertices—call it n—in the BST. Usually, we use BSTs so we can perform operations such as looking up a number using c log n operations, where c is a small constant. We have to have a way of marking the root. We could do this outside the dictionary structure using a list:
BSTwithroot = [22, BSTnoname]
Pretty cumbersome! So we will stick to the original representation and show you how we can create a BST, look up numbers in the BST, and more. And then we will dump the dictionary representation for an object-oriented programming representation!
Operations on BSTs under a Dictionary Representation
Let’s take a look at how we can use the dictionary representation for BSTs. We’ll look at code that checks if a number exists in the BST, code to insert a new number into the BST, and finally, code that produces all the numbers in the BST in sorted order. All these procedures will traverse the BST recursively from the root to the leaves. A leaf in the BST is a vertex without children. For instance, in our dictionary example, 2, 17, and 27 are leaves.
Here’s code to look up a number in a BST.
1. def lookup(bst, cVal):
2. return lookupHelper(bst, cVal, ‘root’)
3. def lookupHelpe (bst, cVal, current):
4. if current == '':
5. return False
6. elif bst[current][0] == cVal:
7. return True
8. elif (cVal < bst[current][0]):
9. return lookupHelper(bst, cVal, bst[current][1])
10. else:
11. return lookupHelper(bst, cVal, bst[current][2])
We look up a number starting with the root vertex, which we identify with the name ’root’ (line 2). If the current vertex we are looking at is empty (represented by the empty string ''), we return False (lines 4–5). If the current vertex’s value is equal to the value we are searching for, we return True (lines 6–7). Otherwise, if the value we are searching for is less than the current vertex’s value, we recursively search the left child of the current vertex (lines 8–9). The final case is that the value we are searching for is greater than the current vertex’s value, in which case we recursively search the right child of the current vertex (lines 10–11).
Next, let’s look at how we can modify the BST by inserting a new number into it. We have to insert it in such a way that the BST property is maintained. We pretend we are looking for this number in the BST and walk down from the root, going left or right based on the values encountered. When we reach a leaf and haven’t found the number, depending on whether the number is smaller or larger than the leaf, we create a left or right child of the leaf vertex, respectively, for the number to be inserted.
Suppose we have the BST shown to the left (in the diagram below) and we wish to insert 4 into it. The result is shown on the right.
We go right at 2 (since 4 > 2) to 3, right at 3 to 5 (4 > 3), and left at 5 (4 < 5) to create a new vertex corresponding to 4.
The insert algorithm code shown below assumes that the number (called val) does not exist in the BST—you can imagine that it is only called for the number if lookup produces False. It also assumes that there is already a vertex called ’root’. The root needs to have a number associated with it and initially has no children. Children are added using insert. Note also that unlike in our pictorial example above, we have to deal with the vertex names as well as vertex values in the code.
1. def insert(name, val, bst):
2. return insertHelper(name, val, ‘root’, bst)
3. def insertHelper(name, val, pred, bst):
4. predLeft = bst[pred][1]
5. predRight = bst[pred][2]
6. if ((predRight == '') and (predLeft == '')):
7. if val < bst[pred][0]:
8. bst[pred][1] = name
9. else:
10. bst[pred][2] = name
11. bst[name] = [val, '', '']
12. return bst
13. elif (val < bst[pred][0]):
14. if predLeft == '':
15. bst[pred][1] = name
16. bst[name] = [val, '', '']
17. return bst
18. else:
19. return insertHelper(name, val, bst[pred][1], bst)
20. else:
21. if predRight == '':
22. bst[pred][2] = name
23. bst[name] = [val, '', '']
24. return bst
25. else:
26. return insertHelper(name, val, bst[pred][2], bst)
The procedure insert simply calls insertHelper, with the root vertex assumed to have the name ’root’. Otherwise, we would have to store the name of the root somewhere and use it to begin the search.
In insertHelper we have several base cases strewn around the code. If we have a vertex with no children (the check is on line 6), we can insert the number as the left or right child of the current vertex (lines 7–12) and we are done. Otherwise, if the number to be inserted is less than the number of the vertex (line 13), we can insert the number as the left child, provided the left child does not already exist (lines 15–17), and stop. If the left child exists, we recursively call insertHelper with the left child. Lines 20–26 handle the case where the number to be inserted is greater than the number of the vertex, and mimic lines 13–19.
To create the BST corresponding to BST given earlier, we unfortunately can’t just use insert on an empty dictionary. We have to create an empty tree by creating an empty dictionary, then add the root vertex explicitly, and then add vertices with names and numbers as shown below:
BST = {}
BST[‘root’] = [22, '', '']
insert(‘A’, 14, BST)
insert(‘B’, 33, BST)
insert(‘C’, 2, BST)
insert(‘D’, 17, BST)
insert(‘E’, 27, BST)
The last insert returns:
{‘C’: [2, '', ''], ‘root’: [22, ‘A’, ‘B’], ‘E’: [27, '', ''],
‘A’: [14, ‘C’, ‘D’], ‘B’: [33, ‘E’, ''], ‘D’: [17, '', '']}
Having to do different things for the root and other vertices, and having to name vertices, is quite annoying. The former issue can be fixed with special case code in insert, but the latter is more fundamental to the dictionary representation, as discussed earlier.
Finally, let’s see how we can obtain the list of numbers stored in a BST in sorted (ascending) order. In-order traversal exploits the BST property to produce a sorted list, as shown in the following code.
1. def inOrder(bst):
2. outputList = []
3. inOrderHelper(bst, ‘root’, outputList)
4. return outputList
5. def inOrderHelper(bst, vertex, outputList):
6. if vertex == '':
7. return
8. inOrderHelper(bst, bst[vertex][1], outputList)
9. outputList.append(bst[vertex][0])
10. inOrderHelper(bst, bst[vertex][2], outputList)
The interesting code is in insertHelper. Lines 6–7 are the base case. In-order traversal means traversing the left child first (line 8), then appending the current vertex’s number to the in-order list (line 9), then traversing the right child (line 10).
This leads to yet another sorting algorithm: Given a set of numbers in arbitrary order, insert them into an initially empty BST one at a time. Then use inOrder to obtain a sorted list.
OOP-Style Binary Search Trees
We will reintroduce you to classes and object-oriented programming (OOP) and explain the basics. It’s “reintroduce” because we have already used built-in Python classes such as lists and dictionaries, and invoked methods on list and dictionary objects, the essence of OOP.
Here are a few examples. In puzzle 1, we wrote intervals.append(arg), which calls the append method on the list intervals and adds the argument arg to the list intervals. In puzzle 3 we used deck.index(arg) to find the index of the argument element arg in the list deck of cards. And in puzzle 14 we used vset.remove(arg) to remove the argument element arg from the set vset.
The big difference in this puzzle is that we will define our own Python classes. We’ll begin with defining a vertex class that will correspond to a vertex in a BST for our purposes, but could easily be used in graphs or other kinds of trees.
1. class BSTVertex:
2. def __init__(self, val, leftChild, rightChild):
3. self.val = val
4. self.leftChild = leftChild
5. self.rightChild = rightChild
6. def getVal(self):
7. return self.val
8. def getLeftChild(self):
9. return self.leftChild
10. def getRightChild(self):
11. return self.rightChild
12. def setVal(self, newVal):
13. self.val = newVal
14. def setLeftChild(self, newLeft):
15. self.leftChild = newLeft
16. def setRightChild(self, newRight):
17. self.rightChild = newRight
Line 1 defines the new class BSTVertex. Lines 2–5 define the class’s constructor, which needs to be named __init__. The constructor not only creates a new BSTVertex object and returns it (there is an implicit return) but also initializes the fields in BSTVertex. The fields themselves are defined through the initialization. Our BSTVertex has three fields: a value val, a left child leftChild, and a right child rightChild. We could easily have added a name field but chose not to, partly to contrast with the dictionary representation and partly to show that it is not required.
Here’s how we construct a BSTVertex object:
root = BSTVertex(22, None, None)
Note that we did not call __init__ but rather called the constructor by the name of the class BSTVertex, and we only specified three arguments, corresponding to the last three arguments of __init__. The argument self is just included so we can refer to the object inside the procedure. Otherwise, we would be writing leftChild = leftChild, which would be very confusing both to the reader and to Python! In the above constructor call we have created a vertex root (think of it as the root vertex of a BST that is yet to be created) that has a number/value 22 and no children.
In lines 6–17 we define methods to access and modify (or mutate) BSTVertex objects. Strictly speaking, these methods are not necessary, but they are good practice in OOP. It is certainly possible to access the value of a vertex bn simply by writing bn.val, rather than n.getVal(). Or to modify the value of the vertex by writing n.val = 10 as opposed to n.setVal(10). Note that we do not have to specify the argument self in the accessor and mutator methods, similar to how we did not specify it in the constructor method. Methods that read and return values of objects are called accessor methods and methods that modify or mutate values of objects are called mutator methods.
Let’s now look at the BST class. Here’s part of it:
1. class BSTree:
2. def __init__(self, root):
3. self.root = root
4. def lookup(self, cVal):
5. return self.__lookupHelper(cVal, self.root)
6. def __lookupHelper(self, cVal, cVertex):
7. if cVertex == None:
8. return False
9. elif cVal == cVertex.getVal():
10. return True
11. elif (cVal < cVertex.getVal()):
12. return self.__lookupHelper(cVal,\
12a. cVertex.getLeftChild())
13. else:
14. return self.__lookupHelper(cVal,\
14a. cVertex.getRightChild())
The constructor for the BST is very simple and is defined in lines 2–3. It creates a BST with a root vertex that is specified as an argument. The assumption is that we will use a BSTVertex object as a root, though that is not specified in the constructor. However, the lookup method specified in lines 4–14 makes this clear. The procedure lookup performs the search in the same way as the dictionary-based lookup we showed you earlier, but works on fields of objects rather than positions in lists or dictionaries. We are following Python convention in adding __ prefixes to the names of functions and procedures, such as lookupHelper, that are not called directly by the user of the class.
Here’s how we can create a BST and look up vertices.
root = BSTVertex(22, None, None)
tree = BSTree(root)
lookup(tree.lookup(22))
lookup(tree.lookup(14))
The first lookup returns True, and the second, False. This isn’t a particularly interesting BST, so let’s look at how we can insert vertices into the BST. Note that the code below is inside the BSTree class, so we continue the line numbering. The indentation of insert is at the same level as lookup.
15. def insert(self, val):
16. if self.root == None:
17. self.root = BSTVertex(val, None, None)
18. else:
19. self.__insertHelper(val, self.root)
20. def __insertHelper(self, val, pred):
21. predLeft = pred.getLeftChild()
22. predRight = pred.getRightChild()
23. if (predRight == None and predLeft == None):
24. if val < pred.getVal():
25. pred.setLeftChild((BSTVertex(val, None, None)))
26. else:
27. pred.setRightChild((BSTVertex(val, None, None)))
28. elif (val < pred.getVal()):
29. if predLeft == None:
30. pred.setLeftChild((BSTVertex(val, None, None)))
31. else:
32. self.__insertHelper(val, pred.getLeftChild())
33. else:
34. if predRight == None:
35. pred.setRightChild((BSTVertex(val, None, None)))
36. else:
37. self.__insertHelper(val, pred.getRightChild())
This code is much cleaner than the dictionary-based code. The procedure insert handles the case where the root of the tree does not exist. In fact, now that we have insert, we can do this:
tree = BSTree(None)
tree.insert(22)
This will create a BST with a root that has the number 22 and no children, and avoids having to create a BSTVertex object for the root before the BSTree object is created. And if you don’t feel like typing None when you create empty trees, you can modify the tree constructor to have a default parameter:
2. def __init__(self, root=None):
3. self.root = root
Finally, here’s a procedure that does in-order traversal of a tree. Again, it uses the exact same algorithm as the dictionary-based representation. This code, too, is inside the BSTree class.
38. def inOrder(self):
39. outputList = []
40. return self.__inOrderHelper(self.root, outputList)
41. def __inOrderHelper(self, vertex, outList):
42. if vertex == None:
43. return
44. self.__inOrderHelper(vertex.getLeftChild(), outList)
45. outputList.append(vertex.getVal())
46. self.__inOrderHelper(vertex.getRightChild(), outList)
47. return outList
The best part of this OOP-style code is that it is much more easily augmented. If we want to add a name to our BST vertices, we can easily do that by adding a field to BSTVertex. You will extend the BST data structure in exercises 1 and 2.
Back to Our Puzzle: Algorithm
Now that we have the data structure we need, let’s try a greedy algorithm to solve our problem. A greedy algorithm chooses as the root of the BST the number with the highest probability. The reasoning is that you want the smallest depth for the number with the highest probability. Once a root is chosen, we know what numbers need to be to the left of the root, and what numbers need to be to the right. We apply the greedy rule again to each of the sides. This seems like a fine algorithm that should work well. It does in many cases. Unfortunately, it does not produce the optimal BST in many others.1 An example where it fails is shown below.
Let’s assume the probability that Thinker chooses 1, 2, 3, or 4 is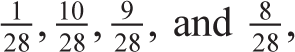 
respectively. The probability that Thinker chooses 2 is the highest, so a greedy algorithm would choose it as the root. This means that 1 needs to be to the left, and 3 and 4 need to be to the right of the root. Since choosing 3 has a higher probability than choosing 4, we choose 3 as the first vertex on the right side of the original root choice. This gives us the BST on the left (diagram above), which produces an average number of guesses or weight
equaling 
There is a better BST, that is, one with a
smaller weight, as shown on the right. This BST chooses 3 as the root and corresponds to
a weight of 
This means we have to try different possibilities for the root vertex and choose the best root to minimize the weight. Suppose e(0, n − 1) is the minimum weight, given numbers k(0), k(1), …, k(n − 1). Denote the probability of each k(i) as p(i). We will assume k(0) < k(1) … < k(n − 1). This means that if we choose k(i) as the root, k(0), … k(r − 1) will be to the left of this root, and k(r + 1), … k(n − 1) will be to the right, as shown in the picture below. Both of the subtrees (shown as triangles) are also BSTs and have minimum weights e(0, r − 1) and e(r + 1, n − 1).
The overall recursive decomposition is given by the two equations below, where i is the start index and j is the end index.
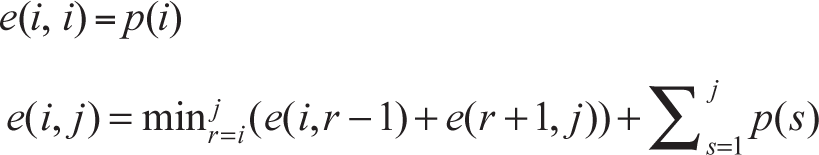
If there is a single number i, there is only one BST possible, and its minimum weight is p(i). This is the base case.
If we have a set of numbers k(i) through k(j), we have to choose every possible root and select the minimum weight corresponding
to the best root choice. There is an additional summation term in the second equation
that warrants explanation. This term accomplishes the multiplication of p(i) by (D(i) + 1) in our weight equation, 
For each vertex i, p(i) is added each time the vertex is not selected as a root, and added one last time
when the vertex is selected as a root, giving it a weight of (D(i) + 1). It’s worth emphasizing that once the vertex i is selected as a root, it does not belong to either subtree in the recursive decomposition,
so p(i) is not added again.
To see this clearly, consider three numbers k(0), k(1), and k(2) whose optimal BST is shown below.
The equations are:
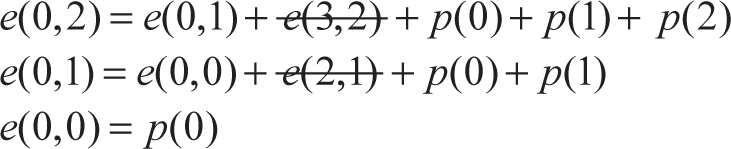
Substituting values produces:
e(0, 2) = 3 · p(0) + 2 · p(1) + p(2)
Exactly what we want.
Code to Solve Our Puzzle
First, we show the main procedure that provides the high-level structure for the code to solve the puzzle.
1. def optimalBST(keys, prob):
2. n = len(keys)
3. opt = [[0 for i in range(n)] for j in range(n)]
4. computeOptRecur(opt, 0, n-1, prob)
5. tree = createBSTRecur(None, opt, 0, n-1, keys)
6. print(‘Minimum average # guesses is’, opt[0][n-1][0])
7. printBST(tree.root)
Line 3 initializes the data structure opt that stores the minimum weights for the different subproblems associated with subtrees. We need a two-dimensional list since we have to store e(i, j) values. Each element of the opt list is a 2-tuple: The first element is the e(i, j) value and the second is the choice of root that produced this value. The index i of the number keys[i], corresponding to the chosen root, is stored as the second element.
The procedure computeOptRecur computes these optimal solutions and fills in the opt list (line 4). Then, we have to turn these values into the optimal BST (just like we had to trace back to find the coins in puzzle 18, our coin selection puzzle). This is done by procedure optimalBSTRecur (line 5).
Here’s how the computation of optimal weights is done recursively.
1. def computeOptRecur(opt, left, right, prob):
2. if left == right:
3. opt[left][left] = (prob[left], left)
4. return
5. for r in range(left, right + 1):
6. if left <= r - 1:
7. computeOptRecur(opt, left, r - 1, prob)
8. leftval = opt[left][r-1]
9. else:
10. leftval = (0, -1)
11. if r + 1 <= right:
12. computeOptRecur(opt, r + 1, right, prob)
13. rightval = opt[r + 1][right]
14. else:
15. rightval = (0, -1)
16. if r == left:
17. bestval = leftval[0] + rightval[0]
18. bestr = r
19. elif bestval > leftval[0] + rightval[0]:
20. bestr = r
21. bestval = leftval[0] + rightval[0]
22. weight = sum(prob[left:right+1])
23. opt[left][right] = (bestval + weight, bestr)
Lines 2–4 correspond to the base case of a single number. Lines 5–23 correspond to the recursive case, where we have to choose different numbers as roots and select the root that produces the minimum weight.
Lines 6–10 make a recursive call, provided the left subtree has at least two numbers for the choice of root. Similarly, lines 11–15 make a recursive call, provided the right subtree has at least two numbers.
Lines 16–23 find the minimum weight value. Lines 16–18 initialize bestval in the first iteration of the loop, and lines 19–21 update bestval if we have found a solution with smaller weight. Finally, lines 22–23 add in the
summation term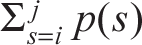 
and update the opt list.
You might have observed that the code for computeOptRecur is amenable to memoization, and you are right. You get to memoize this code in exercise 3.
Let’s now look at the procedure that creates the optimal BST once we know the optimal weights for all the subtrees.
1. def createBSTRecur(bst, opt, left, right, keys):
2. if left == right:
3. bst.insert(keys[left])
4. return bst
5. rindex = opt[left][right][1]
6. rnum = keys[rindex]
7. if bst == None:
8. bst = BSTree(None)
9. bst.insert(rnum)
10. if left <= rindex - 1:
11. bst = createBSTRecur(bst, opt, left, rindex - 1, keys)
12. if rindex + 1 <= right:
13. bst = createBSTRecur(bst, opt, rindex + 1, right, keys)
14. return bst
This procedure assumes that the given list of numbers in keys has length at least 2. The procedure looks at the choice of root for the current problem (line 5). It creates a BST with the chosen root (lines 7–9) and handles the case of when the BST does not exist. Recursive calls are made for the left (lines 10–11) and right (lines 12–13) subtrees, provided they are not empty.
Lines 2–4 are the base case where the BST has a single vertex. A base case is only encountered after the BST has been created, since we assume there are at least two numbers in the original BST. Therefore, we do not need to check whether the BST exists.
Let’s take a look at how we can print the BST in text form.
1. def printBST(vertex):
2. left = vertex.leftChild
3. right = vertex.rightChild
4. if left != None and right != None:
5. print(‘Value =‘, vertex.val, ‘Left =‘,
left.val, ‘Right =‘, right.val)
6. printBST(left)
7. printBST(right)
8. elif left != None and right == None:
9. print(‘Value =‘, vertex.val, ‘Left =‘,
left.val, ‘Right = None’)
10. printBST(left)
11. elif left == None and right != None:
12. print(‘Value =‘, vertex.val, ‘Left = None’,
‘Right =‘, right.val)
13. printBST(right)
14. else:
15. print(‘Value =‘, vertex.val,
’Left = None Right = None’)
Note that the procedure takes the root of the BST (i.e., a BSTVertex) as its argument. This way, it can simply call itself recursively on the left and right children of the root.
Let’s run the code on our original motivating example to see if it produces the right BSTs.
keys = [1, 2, 3, 4, 5, 6, 7]
pr = [0.2, 0.1, 0.2, 0.0, 0.2, 0.1, 0.2]
optimalBST(keys, pr)
This produces:
Minimum average # guesses is 2.3
Value = 3 Left = 1 Right = 5
Value = 1 Left = None Right = 2
Value = 2 Left = None Right = None
Value = 5 Left = 4 Right = 7
Value = 4 Left = None Right = None
Value = 7 Left = 6 Right = None
Value = 6 Left = None Right = None
Let’s next run the code on the example where the greedy algorithm fails.
keys2 = [1, 2, 3, 4]
pr2 = [1.0/28.0, 10.0/28.0, 9.0/28.0, 8.0/28.0]
optimalBST(keys2, pr2)
This produces:
Minimum average # guesses is 1.7142857142857142
Value = 3 Left = 2 Right = 4
Value = 2 Left = 1 Right = None
Value = 1 Left = None Right = None
Value = 4 Left = None Right = None
Comparing Data Structures
We have seen lists, dictionaries, and BSTs among the many data structures in this book. Lists are the simplest of the three, and require the least storage. If you have a collection of items, and all you want to do is store them and process them sequentially, the list is perfect for the job. However, lists can be inefficient for many tasks, such as checking for membership, where the required number of operations grows with the length of the list.
Dictionaries generalize lists in their ability to be indexed, but also provide an efficient means of querying membership. Using a hash table as the underlying data structure means that looking up an item requires only a few operations. On the other hand, range queries such as “Do I have a key between x and y?” require enumerating all the keys in the dictionary because dictionaries do not keep items in sorted order.
Looking up a key in a BST requires log n operations and is not as efficient as a dictionary, but is significantly more efficient than a list. Range queries on keys are conveniently implemented on BSTs since BSTs are a sorted representation—see exercise 4.
Choosing the right data structure for the task at hand often leads to interesting algorithmic puzzles!
Exercises
Exercise 1: Add a getVertex method to the BSTree class to return a BSTVertex, rather than True or False like lookup does. This is a modification of the BST data structure and has nothing to do with the puzzle per se.
Exercise 2: Add a size method mimicking inOrder that computes the size of the BST, which is defined as the number of vertices in the BST—another modification of the BST data structure.
Exercise 3: Memoize computeOptRecur, which does a huge amount of redundant work to create computeOptRecurMemoize. The memoized procedure should only compute each opt entry (i.e., e(i, j)) once.
Exercise 4: Implement a procedure rangeKeys(bst, k1, k2) that determines all keys k in the BST such that k1 <= k <= k2, and prints them out in increasing order. For the BST b below, rangeKeys(b, 10, 22) should print 14, 17, and 22.
