4
Keep Those Queens Apart
When the world says, “Give up,” Hope whispers, “Try it one more time.”
—Author unknown
Programming constructs and algorithmic paradigms covered in this puzzle: Two-dimensional lists, while loops, continue statements, and argument defaults in procedures. Exhaustive search via iteration. Conflict detection.
The eight-queens problem on a chessboard means finding a placement of eight queens such that no queen attacks any other queen. This means that:
- No two queens can be on the same column.
- No two queens can be on the same row.
- No two queens can be on the same diagonal.
Can you find a solution? (See the following board.)
If eight queens are too many to handle, try the five-queens problem below.
A solution to the eight-queens problem is shown in the following board. This is not the only solution.
And here’s a solution to the five-queens problem.
But how can we find the above solutions or different ones? Let’s simplify the problem first. Suppose we look at a smaller, 2 × 2 board (below). Can we place two queens so they don’t attack each other? The answer is no, since a queen on any square of a 2 × 2 board can attack every other square.
What about a 3 × 3 board? Here is an attempt:
For the first placement (above left), we can see that the queen attacks six other squares and occupies one. So seven squares are disallowed by the very first queen placement, leaving two squares available. When we put the second queen on one of those squares, there are no squares available. Of course, we could have tried putting the first queen in a different spot, but that won’t help. The first queen, regardless of where it is placed, will occupy and attack at least seven squares, leaving two. There is no solution for a 3 × 3 board.
Systematic Search
What about a 4 × 4 board? Let’s be systematic about searching for a solution. We will try to place queens column by column and change placements if we fail. We start by placing a queen in the top left corner in the first column as shown below (first picture). There are two choices in placing a queen on the second column, and we choose one, as shown in the second picture below. Now we are stuck! We can’t place a queen in the third column.
Note that when we tried to place the third queen in the third column above, we simply checked that the third queen didn’t conflict with the first and second. We do not need to check that the first two queens do not conflict with each other. This is because we did that check when we placed the second queen. This will be important to remember when we look at the code to check for conflicts.
Given that we failed at finding a solution, should we give up? No, because we could try a different positioning for the second queen. Here we go:
We went further, but are stuck again, this time on the fourth and last column. But we are not out of options. We arbitrarily chose the top corner for the first queen, and we could try a different position. (There are four options for the first queen.) Here we go:
Success! The four-queens problem has a solution.1
It will take a normal person quite a long time to use this strategy to find a solution to the eight-queens problem. But such an exhaustive brute-force strategy should work. And computers can do calculations billions of times faster than humans, so if we can code up our strategy, we will be able to run the program and find a solution in a matter of seconds.
The first step in writing code for eight-queens is to decide on a data structure for the problem: How are we going to represent the board and the positions of the queens?
Board as a 2-D List/Array
We have already seen 1-D lists/arrays in Python in puzzle 1, with the caps variable. Since a chessboard is a two-dimensional grid, a natural representation is a two-dimensional array:
B = [[0, 0, 1, 0],
[1, 0, 0, 0],
[0, 0, 0, 1],
[0, 1, 0, 0]]
Read the array just like you would look at the board, with the 0’s being blank squares and the 1’s being queens. B is an array of (single-dimensional) arrays: B[0] is the first row, B[1] is the second row, and so on. So B[0][0] = 0, B[0][1] = 0, B[0][2] = 1, and B[0][3] = 0. As a further example, B[2][3] = 1. This is the last 1 on the third row. The variable B above represents the solution that we came up with on the 4 × 4 board shown previously.
We will need to check that there is exactly one B[i][j] that is a 1 for each given i and varying j, and for each given j and varying i. We will also need to check for diagonal attacks. For example, B[0][0] = 1 and B[1][1] = 1 is an invalid configuration (not a solution).
Here’s code that checks whether a given 4 × 4 board with queens on it violates the rules. Note that this code does not check that there are four queens on the board. So an empty board will satisfy the checks. It is certainly possible that two queens by themselves will violate the checks. Remember, we want to follow the iterative strategy we showed earlier in placing one queen at a time on the board in a new column and checking for conflicts.
1. def noConflicts(board, current, qindex, n):
2. for j in range(current):
3. if board[qindex][j] == 1:
4. return False
5. k = 1
6. while qindex - k >= 0 and current - k >= 0:
7. if board[qindex - k][current - k] == 1:
8. return False
9. k += 1
10. k = 1
11. while qindex + k < n and current - k >= 0:
12. if board[qindex + k][current - k] == 1:
13. return False
14. k += 1
15. return True
Given an N × N board, any positioning of N queens on the board is called a configuration. If there are fewer than N queens, we will call it a partial configuration. Only if a configuration (with N queens) satisfies all three attack rules will we call it a solution.
The procedure noConflicts(board, current) checks a partial configuration to see if it violates the row and the diagonal rules. It takes as an argument qindex, which is the row index of the queen that has been placed on the column current. The procedure assumes that only one queen will be placed in any given column—our FourQueens iterative search procedure below has to guarantee that (and it does).
The value of current can be less than the size of the board; the columns after current are empty. The code checks whether the column numbered current has a queen conflicting with existing queens in columns with numbers less than current. This is all we want, since we want to mimic the manual iterative procedure we described earlier. When current = 3, for example, in a call to noConflicts, we are not checking that board[0][0] and board[0][1] are both 1’s (row attack across the first two columns) or that board[0][0] and board[1][1] are both 1’s (diagonal attack across the first two rows and columns). We can get away with this provided we call noConflicts each time we add to the partial configuration by positioning a new queen.
Lines 2–4 check that there is not already a queen in row qindex. Lines 5–9 and 10–14 check for the two forms of diagonal attacks. Lines 5–9 check
for 
attacks by decrementing qindex and current in proportion to an edge of the board. Lines 10–14 check for 
attacks by decrementing current and incrementing qindex in proportion till an edge of the board is reached. The board beyond the column current is assumed to be empty, so there is no need to increment current.
Now we are ready to invoke the checking-conflicts procedure while placing queens.
1. def FourQueens(n=4):
2. board = [[0,0,0,0], [0,0,0,0],
[0,0,0,0], [0,0,0,0]]
3. for i in range(n):
4. board[i][0] = 1
5. for j in range(n):
6. board[j][1] = 1
7. if noConflicts(board, 1, j, n):
8. for k in range(n):
9. board[k][2] = 1
10. if noConflicts(board, 2, k, n):
11. for m in range(n):
12. board[m][3] = 1
13. if noConflicts(board, 3, m, n):
14. print (board)
15. board[m][3] = 0
16. board[k][2] = 0
17. board[j][1] = 0
18. board[i][0] = 0
19. return
Thanks to lines 4 and 18, lines 6 and 17, lines 9 and 16, and lines 12 and 15, we are guaranteed that there is exactly one queen in each column—this is an invariant enforced by FourQueens. Initially the board B is empty and each pair of lines places one queen and removes it. This is why noConflicts does not need to check for column attacks, and only checks for row and diagonal attacks between the newly placed queen and existing queens.
Line 4 places the first queen on the board, and there cannot be any conflicts with only one queen, hence we do not have to call noConflicts after this placement. For the second and subsequent queen placements (lines 6, 9, and 12) we do have to check for conflicts.
While we have written noConflicts for general n, FourQueens assumes that n = 4, so we hardcoded the argument n = 4 when invoking it. We could easily have replaced all occurrences of n in FourQueens with the number 4, but we chose this description to emphasize that noConflicts is general enough to be invoked with arbitrary n, but FourQueens, as its name gives away, is not.
If you run FourQueens, you get:
[[0, 0, 1, 0],
[1, 0, 0, 0],
[0, 0, 0, 1],
[0, 1, 0, 0]]
[[0, 1, 0, 0],
[0, 0, 0, 1],
[1, 0, 0, 0],
[0, 0, 1, 0]]
Each row of the board is listed, from top to bottom. The code produces two solutions, each on four lines above, the first of which is the solution we manually discovered earlier. We stopped after we found the first solution, but if we had kept going, we would have discovered the second.
To code EightQueens we can simply add more loops to FourQueens. (As if four nested loops aren’t enough!) Before we do that, we will look at a better data structure for partial or full configurations that is not only more compact, but also makes the checks for the three rules above easier.
Board as a 1-D List/Array
The 2-D list representation of the board was natural and it clearly served our purpose. It turns out that, because we are only looking for solutions where there is a single queen on each column (or row, for that matter), we can get away with using a one-dimensional array where each index represents each column of the board and the entry represents the row on which the queen resides. Consider the array of size 4:
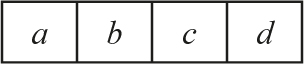
The values a, b, c, d can vary from −1 to 3. Here, −1 means there is no queen in the corresponding column, 0 means there is a queen in the first row of that column, and 3 means there is a queen in the last row. Here’s a general example that should make things clear:
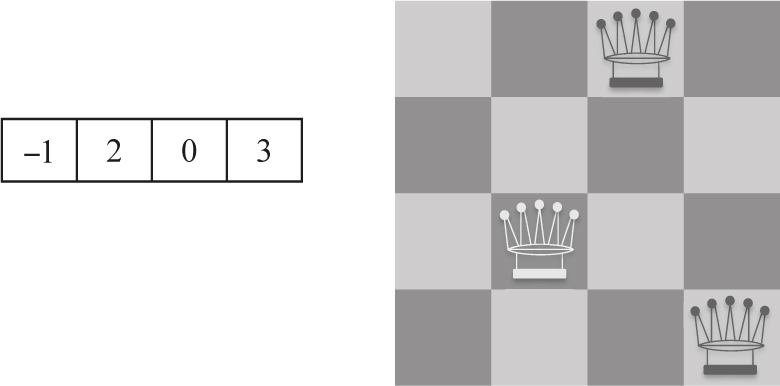
This data structure can represent partial configurations in the sense that there are only three queens on the 4 × 4 board above. This is important because we will want to build up a solution from an empty board as in our first algorithm. Of course, in our algorithm we placed queens in columns beginning from left to right, but that was an arbitrary choice.
We can now write code to check for the three rules, given our new representation. Notice that we get the first rule for free, in the sense that we cannot place two queens on the same column, since we can only have a single number between −1 and n − 1 as the value stored at each array index. Not only is the 1-D representation more compact, it also saves us from checking one of the rules. For the second rule, which checks that no row contains two or more queens, we just need to make sure that no number (other than −1) appears more than once in the array (lines 3–4 below). The third rule involves slightly more computation (lines 5–6 below).
1. def noConflicts(board, current):
2. for i in range(current):
3. if (board[i] == board[current]):
4. return False
5. if (current - i == abs(board[current] - board[i])):
6. return False
7. return True
Lines 3–4 check that there is no row attack. They assume that board[current] has a nonnegative value enforced by the calling procedure EightQueens. If that value equals the value in any preceding column, we have an invalid configuration.
Line 5 checks for diagonal attacks—this is much simpler to do in this representation.
Why the abs in line 5? We have to check for two diagonals corresponding to the and directions. Look at the example below:
The variable current = 4 and we are trying to place a queen in the column numbered 4. board[1] = 6 and board[4] = 3, so the diagonal check will fail for i = 1 on line 5.
{current = 4} - {i = 1} == abs({board[current] = 3} - {board[i] = 6})
Remember that we had to do the two diagonal checks in our old representation as well.
Here’s EightQueens using our new, compact representation.
1. def EightQueens(n=8):
2. board = [-1] * n
3. for i in range(n):
4. board[0] = i
5. for j in range(n):
6. board[1] = j
7. if not noConflicts(board, 1):
8. continue
9. for k in range(n):
10. board[2] = k
11. if not noConflicts(board, 2):
12. continue
13. for l in range(n):
14. board[3] = l
15. if not noConflicts(board, 3):
16. continue
17. for m in range(n):
18. board[4] = m
19. if not noConflicts(board, 4):
20. continue
21. for o in range(n):
22. board[5] = o
23. if not noConflicts(board, 5):
24. continue
25. for p in range(n):
26. board[6] = p
27. if not noConflicts(board, 6):
28. continue
29. for q in range(n):
30. board[7] = q
31. if noConflicts(board, 7):
32. print (board)
33. return
We place a queen simply by assigning a nonnegative number to the column that we are working on. There is no need to reset the value to 0 as we had to do in the old algorithm, because changing the number effectively removes a queen from the old position and moves it to a new one. That is, if board[0] = 1, and we change it to board[0] = 2, we just moved the queen. Again, the more compact representation saves us from writing code.
Remember that we have to check for conflicts each time we place a queen against the preceding columns. This is why we have a noConflicts call each time a queen is placed. To avoid having to indent the code even more than we already have to with eight loops, we employ the continue statement. If there is a conflict, that is, the if statement’s predicate returns False, we jump to the next loop iteration without executing any more statements.
5. for j in range(n):
6. board[1] = j
7. if not noConflicts(board, 1):
8. continue
9. for k in range(n):
If line 7 above produces False for the call to noConflicts, we will jump back to line 6 with an incremented value of j without bothering with line 9 or subsequent statements. This avoids having to enclose the for loop beginning on line 9 with the if statement of line 7 (without the not) as we did in the FourQueens code.
If we run the EightQueens code, it prints out different solutions. Here is a sample:
[0, 4, 7, 5, 2, 6, 1, 3]
[0, 5, 7, 2, 6, 3, 1, 4]
[0, 6, 3, 5, 7, 1, 4, 2]
[0, 6, 4, 7, 1, 3, 5, 2]
The last one is the solution we showed you at the beginning of this puzzle description. If you consider rotations and mirrored solutions as the same solution, there are twelve distinct solutions.
If we follow print (board) on line 32 with a return, we will only get the first solution:
29. for q in range(n):
30. board[7] = q
31. if noConflicts(board, 7):
32. print (board)
33. return
34. return
The eight-queens iterative code is the ugliest code in the entire book! Imagine what would happen if you wanted to solve the fifteen-queens problem. Fortunately, we’ll show you elegant recursive code that solves the N-queens problem for arbitrary N in puzzle 10.
Iterative Enumeration
The main algorithmic paradigm embodied by our N-queens code is that of iterative enumeration. We go column by column, and within each column, we go row by row. To ensure that we find a solution we need the enumeration to be exhaustive—if we skip placing a queen in a column or row, we may miss finding a solution. By numbering columns and rows and iterating through each of them, we ensure an exhaustive search.
The other algorithmic paradigm illustrated in the code is conflict detection during the iterative search. In the four-queens problem, for example, we could have placed four queens on the board, one in each column, and only then checked for conflicts. This is illustrated in the code below:
1. for i in range(n):
2. board[i][0] = 1
3. for j in range(n):
4. board[j][1] = 1
5. for k in range(n):
6. board[k][2] = 1
7. for m in range(n):
8. board[m][3] = 1
9. if noConflictsFull(board, n):
10. print (board)
11. board[m][3] = 0
12. board[k][2] = 0
13. board[j][1] = 0
14. board[i][0] = 0
15. return
This code is strictly worse than what we showed you in terms of performance and code complexity. It is worse in terms of performance because we will create configurations where there are three queens on the same row, for example. It is worse in terms of complexity because we need a more complex noConflictsFull check (line 9) rather than the incremental check we do in noConflicts where we simply check if the most recently placed queen conflicts with the already placed queens. In noConflictsFull, we have to check that each row has exactly one queen in it, and that each pair of queens does not have either type of diagonal conflict. There is repeated work done for configurations that are close to each other across the 44 calls to noConflictsFull.
We won’t bother with implementing noConflictsFull. The main purpose in showing you the above code is so you appreciate the FourQueens code a little more.
Exercises
Exercise 1: Modify the EightQueens code so it takes as an additional argument—the number of solutions you want to find—and prints that many, assuming that many exist. Note that default arguments have to be after non-default arguments, so the new argument has to be the first one, followed by the n=8 default argument.
Puzzle Exercise 2: Modify the EightQueens code so it looks for solutions with a queen already placed in a list of locations. You can use a 1-D list location as an argument that has nonnegative entries for certain columns that correspond to fixed queen positions. For example, location = [-1, 4, -1, -1, -1, -1, -1, 0] has two queens placed in the second and eighth columns. Your code should produce [2, 4, 1, 7, 5, 3, 6, 0] as a solution consistent with the prescribed queen locations.
Exercise 3: Reduce the level of indentation in the FourQueens code by using the continue statement. Both solutions should be printed. This is a little trickier than you might think!