9
America’s Got Talent
I have no particular talent. I am merely inquisitive.
—Albert Einstein
Programming constructs and algorithmic paradigms covered in this puzzle: Representing two-dimensional tables using lists.
You have decided to produce a television show titled “Who’s Got Talent?”1 Over spring break, you hold auditions for your show, after recruiting many candidates. Each candidate claims a certain set of talents (e.g., flower arranging, dancing, skateboarding), and you verify them during the audition. Most of the candidates don’t fulfill your expectations, but some do. Now you have a set of candidates who can each perform at least one talent.
In your show, you want to highlight a diverse set of talents. It won’t help ratings if you have different flower arrangements each week. You take your list of candidates and make a list of all their talents. Then you go to your producers for approval in including these talents on your show. Your producers whittle down the list (e.g., they don’t think regurgitation plays particularly well with audiences) and you settle on a final list. They also tell you to keep costs down.
You realize that the best way to keep costs down and ratings up is to contract out the fewest number of candidates while producing the most diverse show possible. You therefore want to select the fewest candidates who can perform all the talents on the final list you came up with.
Suppose you end up with the following candidates and talents.

In the above example, you could select Aly, Bob, Don, and Eve, and cover all the talents. Aly covers Flex and Code, Bob covers Dance and Magic, Don covers Dance and Sing, and Eve covers Dance, Act, and Code. Together, they have all six talents.
Can you cover all the talents with fewer people? More generally, how can you select the fewest candidates (rows) who cover all the talents (columns) in any given table? Another example is shown below.
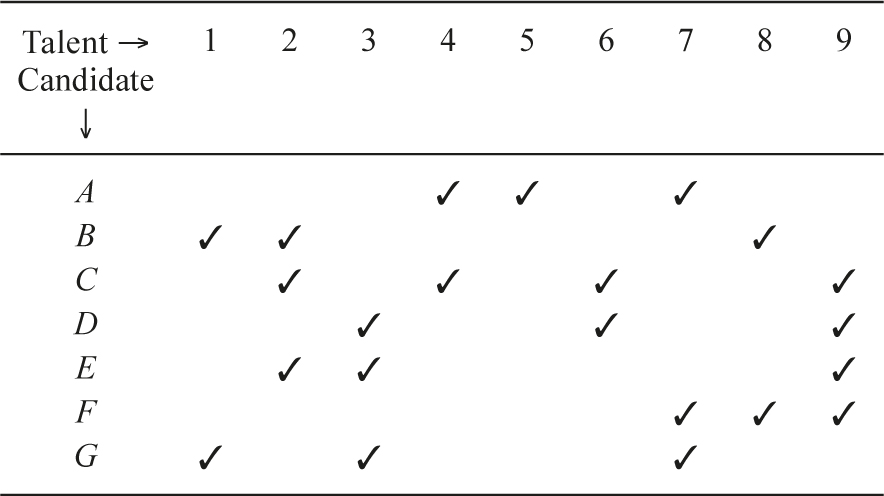
In our first example, you can do better than four candidates. You only need to hire Aly, Cal, and Eve. Aly covers Flex and Code, Cal covers Sing and Magic, and Eve covers Dance, Act, and Code. Together, they have all six talents.
We will follow the same strategy as we did for the dinner invitation problem (puzzle 8). The two problems are quite similar, even though in the dinner puzzle we wanted to maximize the number of people, and here we want to minimize the number of selected people. What they have in common is that we have to look at all possible combinations (i.e., subsets of candidates), eliminate subsets who do not collectively have all the talents, then choose the smallest subset. Another thing they have in common is that a greedy approach does not work.
The data structures of the two puzzles are different, since we need a table of information for our talent problem as opposed to a dislikes graph. Our example can be converted to data structures like this:
Talents = ['Sing', 'Dance', 'Magic', 'Act', 'Flex', 'Code']
Candidates = ['Aly', 'Bob', 'Cal', 'Don', 'Eve', 'Fay']
CandidateTalents = [['Flex', 'Code'], ['Dance', 'Magic'],
['Sing', 'Magic'], ['Sing', 'Dance'],
['Dance', 'Act', 'Code'], ['Act', 'Code']]
We have a list of talents (columns of the table) and a list of candidates (rows of the table). We need a list of lists, CandidateTalents, to represent the entries of the table. CandidateTalents has entries corresponding to rows of the table. The order of the entries is important because it reflects the order of the candidates in the list Candidates. Bob is the second candidate in Candidates and his talents correspond to the second list in CandidateTalents, namely, ['Dance', 'Magic'].
As you probably guessed, the code for the two puzzles is awfully similar. We’ll structure the code for this puzzle slightly differently, and we will base it on the optimized version in puzzle 8.
Generating and Testing One Combination at a Time
Here’s code for the top-level procedure, which generates each combination, tests whether it’s good, and picks the minimum-length good combination.
1. def Hire4Show(candList, candTalents, talentList):
2. n = len(candList)
3. hire = candList[:]
4. for i in range(2**n):
5. Combination = []
6. num = i
7. for j in range(n):
8. if (num % 2 == 1):
9. Combination = [candList[n-1-j]] + Combination
10. num = num // 2
11. if Good(Combination, candList, candTalents, talentList):
12. if len(hire) > len(Combination):
13. hire = Combination
14. print ('Optimum Solution:', hire)
Lines 4–10 generate the combination corresponding to value num = i. Line 11 invokes a function Good—to be described later—which checks whether the given combination of candidates covers all the talents. If it does, it is compared against the best combination of candidates seen thus far, and the best combination is updated if it has a greater number of candidates (lines 12–13).
Line 3 is different from the equivalent line in puzzle 8, which was invite = []. In the dinner invitation puzzle, we wanted to maximize the number of guests we could invite, so we started with the empty list as the initial best combination. Here, we want to minimize the number of candidates we hire, so we start with the entire candidate list as the initial best combination. We are assuming that the entire set of candidates does satisfy our requirement of covering all the talents. If they don’t, we can simply redefine our required talent list.
Determining Combinations That Lack a Talent
We invoked a function in Hire4Show that determines whether a given combination of candidates satisfies all the talents. The checks we need to make are quite different from those we applied in puzzle 8, as we will demonstrate below.
1. def Good(Comb, candList, candTalents, AllTalents):
2. for tal in AllTalents:
3. cover = False
4. for cand in Comb:
5. candTal = candTalents[candList.index(cand)]
6. if tal in candTal:
7. cover = True
8. if not cover:
9. return False
10. return True
The for loop (lines 2–9) iterates over each talent tal in the list of talents. For each candidate in the combination (inner for loop starting on line 4), we use the candidate’s index in the candidate list candList to index into the candidates-to-talents data structure (line 5).
We now have to check whether this candidate’s talents contain the talent tal we are looking for in this iteration of the for loop (that begins on line 2). This is done on line 6. If the candidate has the talent tal, we mark it so on line 7. However, if we complete the inner for loop and we have not found a candidate in the combination who covers talent tal, we know that this candidate combination needs to be discarded—one missing talent dooms a combination. Therefore, we need not bother checking for the other talents and we can simply return False (line 9).
If we get through all the talents without returning False in any of the iterations, it means that each talent is covered by this combination, and we can return True (line 10).
Let’s run this code on the example from the beginning. The table, converted to code, is:
Talents = ['Sing', 'Dance', 'Magic', 'Act', 'Flex', 'Code']
Candidates = ['Aly', 'Bob', 'Cal', 'Don', 'Eve', 'Fay']
CandidateTalents = [['Flex', 'Code'], ['Dance', 'Magic'],
['Sing', 'Magic'], ['Sing', 'Dance'],
['Dance', 'Act', 'Code'], ['Act', 'Code']]
If we run:
Hire4Show(Candidates, CandidateTalents, Talents)
It produces:
Optimum Solution: ['Aly', 'Cal', 'Eve']
Exactly what we want and expect.
If we run the code on the second, larger example:
ShowTalent2 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
CandidateList2 = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
CandToTalents2 = [[4, 5, 7], [1, 2, 8], [2, 4, 6, 9],
[3, 6, 9], [2, 3, 9], [7, 8, 9],
[1, 3, 7]]
Hire4Show(CandidateList2, CandToTalents2, ShowTalent2)
It produces:
Optimum Solution: ['A', 'B', 'D']
Applications
This puzzle is an instance of the set-covering problem, which has numerous applications. For example, a car company may wish to deal with the smallest set of vendors who can supply all the parts it needs to build its cars, minimizing the amount of vetting that the company needs to do. Or NASA wishes to minimize the total weight of the set of tools it sends into space, while ensuring that all maintenance tasks can be performed.
Set covering is a hard problem: Every known algorithm that guarantees the minimum cardinality of chosen candidates for all problem instances, including the algorithm we coded, can take time exponential in the number of candidates for some instances. In that sense, set covering is equivalent to our dinner puzzle (puzzle 8).
If we are not interested in the absolute minimum cardinality, we can use a greedy approach to solve our problem. It is guaranteed to be fast, that is, it will only require a few scans or passes over the table. A greedy algorithm for our puzzle would pick the candidate with the most talents. Once this candidate is picked, all talents covered by this candidate are eliminated from the table. The process continues until all talents are covered.
For our second, larger example with candidates A through G, we would first pick C, who covers four talents: 2, 4, 6, and 9. This results in the smaller table shown below.
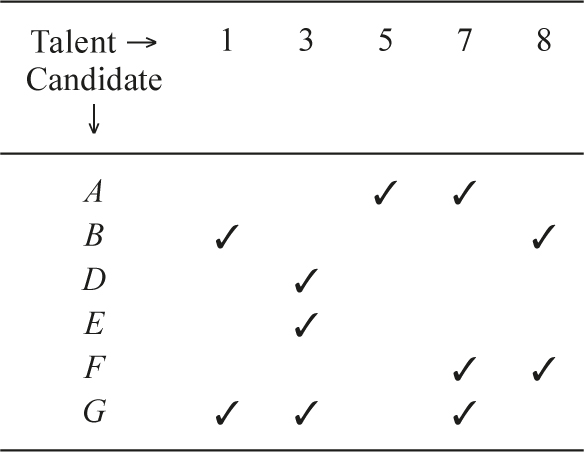
Here, candidate G covers three (additional) talents. G will be picked, since each of the others only covers two talents. After picking C and G, we obtain the table below.
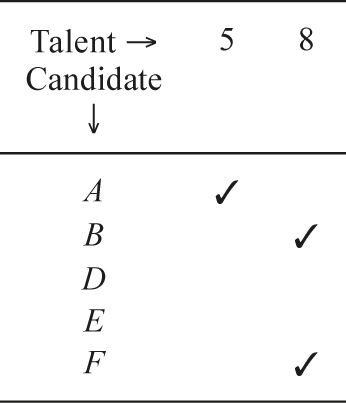
We still need to cover talent 5, which requires candidate A, and talent 8, which requires candidate B or F. That is a total of four candidates. We know this is not optimal; our code gave us a three-candidate result.
Exercises
Exercise 1: In our first example, Eve “dominates” Fay since she has all the talents that Fay has, and more besides. Modify the code so candidates who are dominated are removed from the table. This will make the generation of combinations more efficient.
Exercise 2: Aly has to be selected in our first example because she is the only one who can Flex. You can see this clearly in the table, since the column for Flex only has a single checkmark. Similarly, in our second example, D is the only candidate who covers talent 4, and F the only candidate who covers talent 7.
Modify the original code to (1) identify candidates who each have a unique talent, (2) shrink the table to remove all talents covered by such candidates, (3) find the optimum selection for the shrunken table, and (4) add in the candidates you identified in step 1.
Puzzle Exercise 3: You think that some of the candidates are full of themselves and will demand to be paid more than what they deserve. You therefore want a way of choosing candidates who will settle for what you pay them. You assign a weight to each candidate that reflects what you think they might cost. Change the code so it finds a set of candidates that covers all the talents as before, but with minimum weight.
Suppose you are given:
ShowTalentW = [1, 2, 3, 4, 5, 6, 7, 8, 9]
CandidateListW = [('A', 3), ('B', 2), ('C', 1), ('D', 4),
('E', 5), ('F', 2), ('G', 7)]
CandToTalentsW = [[1, 5], [1, 2, 8], [2, 3, 6, 9],
[4, 6, 8], [2, 3, 9], [7, 8, 9],
[1, 3, 5]]
where the numbers in the 2-tuples in CandidateListW correspond to how expensive each candidate is. Your code, which minimizes expense, should produce:
Optimum Solution: [('A', 3), ('C', 1), ('D', 4), ('F', 2)]
Weight is: 10
Note that the “domination” optimization is no longer valid, if Eve is going to be much more expensive than Fay! If Eve has the same weight as Fay or a smaller weight, only then is the optimization valid. So be careful if you are using code you wrote in exercise 1.
Exercise 4: Remember the optimization of essential candidates described in exercise 2? Add that to the code that solves the candidate selection problem for minimum weight, from puzzle exercise 3.