CHAPTER SIXTEEN
MEDIATION ANALYSIS IN SOCIAL EPIDEMIOLOGY
Arijit Nandi and Tyler J. VanderWeele
The inferential goal of mediation analysis is to assess the mechanisms that explain an observed relation between an exposure variable and an outcome, and how they relate to a third variable, the mediator (VanderWeele 2009a). Mediation analysis is fundamental to understanding how social factors contribute to population health. Given our emphasis on social (sometimes defined as non-biological) determinants, it is challenging to pose a hypothesis without distinguishing, or at least contemplating, the potential intervening pathways leading to the manifestation of disease. For example, questions concerning how social and racial inequalities are engendered have inspired some of the most trenchant discourse in the health sciences—is it genetic or biological, psychosocial, behavioral, socioeconomic, environmental, cultural, or other factors that explain observed disparities, or perhaps some combination of these mechanisms (Dressler, Oths, and Gravlee 2005; Braun 2002; Geronimus 1991; Kaufman and Hall 2003; Krieger 2006)? Similarly, when we consider our exposure to social factors over the life course, the question about whether there are critical periods during which exposures exert a “direct” influence on health in later life, exemplified by Barker's hypothesis about the fetal origins of coronary heart disease (Paneth and Susser 1995; Barker 1995, 2004), is one about mediation.
The relevance of mediation to the study of social determinants has not always been appreciated in epidemiology. For much of our history, we have considered biological and behavioral risk factors as autonomous. Just a couple of decades ago, there was a debate that was largely centered on what unit of analysis, whether the micro (genetic), the individual (behavioral), or the macro (social/environmental), is most relevant to the production of population health. Social epidemiology was criticized for being an overreaching “reincarnation of miasma theory” (Zeilhuis and Kiemeney 2001; Rothman, Adami, and Ttichopoulos 1998; Poole and Rothman 1998). In turn, social epidemiologists criticized microlevel and “black-box” epidemiology for being overly reductionist (Kaufman 2001). From this dialogue emerged the recognition that “we need to be equally concerned with causal pathways at the societal level and with pathogenesis and causality at the molecular level” (Susser and Susser 1996). A multilevel paradigm developed, and with it came a profusion of hierarchical conceptual frameworks characterized by “a multiplicity of pathways” (Glass and McAtee 2006; House 2002; Lynch 2000; Kaplan 2004). Common among them was the theory that factors ranging from genetic to social influence health over the life course from conception to older age. Consequently, investigation of mediation of social by proximal characteristics, as well as earlier by later exposures, has become a substantial area of research in social epidemiology.
In parallel to the development of theoretical frameworks has been the evolution of empirical methods for mediation analysis. Parametric methods for mediation analysis, commonly referred to as the product method, were popularized by the seminal work of Baron and Kenny (1986) and have been highly influential in psychology and the social sciences. The product method, which we will introduce in the following section, provides a simple approach to estimate and test for mediation. However, it provides valid results only under specific circumstances, including the absence of interactions, non-linearities, and unmeasured confounding. These assumptions, later articulated by Robins and Greenland (1992), Kaufman and colleagues (2004), Pearl (2001), and others may be violated when examining mediation in the social sciences in particular. Despite these critiques, the application of the product method has persisted largely unabatedly. Thousands of studies have attempted to “decompose” the effects of social factors on health using the approach outlined by Baron and Kenny, which had been cited more than 60 000 times in the 30 years since its publication, according to Google Scholar. The pervasiveness of the product method is likely attributable to its accessibility together with the lack of more sophisticated tools, lending support to the epigram “if all you have is a hammer, everything looks like a nail.” However, since the publication of the first edition of Methods in Social Epidemiology, there has been a “veritable explosion” of methodological developments for causal mediation analysis (Kaufman 2010a) and new alternatives are available. In particular, the counterfactual framework has been used to extend the product method in several ways and made explicit the necessary conditions for unbiased inference. Causal methods for mediation analysis have been described extensively, in epidemiology, psychology, and the social sciences (Ten Have and Joffe 2012, Imai, Keele, and Tingley 2012; Preacher 2015), and there is now a text devoted to this topic for epidemiologic audiences (VanderWeele 2015).
Our aim for this chapter is to introduce modern methods and approaches for mediation analysis. We begin by laying the necessary groundwork, including a recapitulation of the product method and an overview of the counterfactual approach to mediation analysis. Subsequently, we discuss recent developments and extensions that we consider most germane to the study of social determinants of health. This includes the decomposition of racial inequalities in health, which also applies to other social determinants that are not clearly codified as “causes” within the counterfactual framework. We describe the implications of exposure-induced mediator-outcome confounding, common when examining the effects of exposures at various stages in the life course, and review a method for estimating the controlled direct effect in this context. We introduce methods for mediation analysis with multiple mediators, which is relevant when our mediators are constructs represented by several indicators. Finally, we discuss simple methods for sensitivity analysis when the conditions necessary for a causal interpretation of mediated effects are violated.
The Product Method for Mediation Analysis
The product method presented a strategy for decomposing the total or overall effect of a change in exposure  on an outcome
on an outcome  into a direct effect that does not operate via the proposed mediator
into a direct effect that does not operate via the proposed mediator  and an indirect effect that does (Figure 16.1). With a continuous mediator and outcome, the direct and indirect effects can be estimated by fitting two regression models:
and an indirect effect that does (Figure 16.1). With a continuous mediator and outcome, the direct and indirect effects can be estimated by fitting two regression models:

FIGURE 16.1 MEDIATION MODEL IN BARON AND KENNY (1986)
Note: The figure shows the direct effect of the exposure A on the outcome Y, as well as the indirect effect through the mediator M.

and

Baron and Kenny proposed that the direct effect of the exposure on the outcome is given by estimating  in Model (2), the outcome regression model. In other words,
in Model (2), the outcome regression model. In other words,  estimates the effect of the treatment on the outcome at a fixed level of the mediator, with a significant effect often used as evidence that the treatment influences the outcome through mechanisms other than the mediator. The indirect effect, which implies mediation by the variable
estimates the effect of the treatment on the outcome at a fixed level of the mediator, with a significant effect often used as evidence that the treatment influences the outcome through mechanisms other than the mediator. The indirect effect, which implies mediation by the variable  , is given by
, is given by  , which represents the product of two effects: the effect of the treatment on the mediator,
, which represents the product of two effects: the effect of the treatment on the mediator,  , and the effect of the mediator on the outcome,
, and the effect of the mediator on the outcome,  . An important limitation of the product method is that it cannot be used to reliably estimate direct and indirect effects in models with interactions. Furthermore, indirect effects estimated via the product method will often be biased for outcomes analyzed with non-linear, including logistic regression, models (VanderWeele and Vansteelandt 2010).
. An important limitation of the product method is that it cannot be used to reliably estimate direct and indirect effects in models with interactions. Furthermore, indirect effects estimated via the product method will often be biased for outcomes analyzed with non-linear, including logistic regression, models (VanderWeele and Vansteelandt 2010).
Counterfactual Approach to Mediation Analysis
The counterfactual approach to mediation clarifies the assumptions needed for identifying direct and indirect effects. Moreover, the notions of direct and indirect effects, as defined in terms of potential outcomes, have been used to extend the product method to accommodate settings with an interaction between exposure and mediator (VanderWeele and Vansteelandt 2009; Valeri and VanderWeele 2013). Before outlining the methods for estimating total effects, controlled direct effects, and natural direct and indirect effects, we will briefly introduce the notation that we will use throughout the chapter.
For the sake of explanation, suppose that we are interested in assessing the mechanisms that explain the association between enrollment in a program that provides cash payments to low-income mothers below a certain poverty threshold (our exposure), which is a common social program in many lower-income countries (Owusu-Addo and Cross 2014), and their child's continuous height-for-age Z-score. As above, we will let  represent the exposure of interest, enrollment in the cash transfer program, and
represent the exposure of interest, enrollment in the cash transfer program, and  denote the outcome, children's height-for-age Z-score. Now suppose we would like to examine whether changing dietary patterns, measured by the child's average caloric intake and represented by the continuous variable
denote the outcome, children's height-for-age Z-score. Now suppose we would like to examine whether changing dietary patterns, measured by the child's average caloric intake and represented by the continuous variable  , mediate the effect of the program, under the hypothesis that the cash payments are used to purchase food. In terms of potential outcomes, the values
, mediate the effect of the program, under the hypothesis that the cash payments are used to purchase food. In terms of potential outcomes, the values  and
and  represent the values of the outcome and mediator, respectively, if the exposure
represent the values of the outcome and mediator, respectively, if the exposure 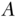 were set, potentially counter to the fact, to the level
were set, potentially counter to the fact, to the level  . Similarly,
. Similarly,  represents the value of the outcome that would have been observed had the exposure and mediator been set, potentially contrary to the fact, to the levels
represents the value of the outcome that would have been observed had the exposure and mediator been set, potentially contrary to the fact, to the levels  and
and  .
.
The Total Effect
When performing a mediation analysis, we typically start by estimating the total effect (TE) of an exposure variable,  , on an outcome,
, on an outcome, . The total effect comparing the outcome
. The total effect comparing the outcome  when we change the exposure from level
when we change the exposure from level 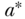 to
to  is given by
is given by  ; in terms of potential outcomes, this translates to the difference in children's mean height-for-age had all mothers been enrolled in the cash transfer program,
; in terms of potential outcomes, this translates to the difference in children's mean height-for-age had all mothers been enrolled in the cash transfer program, 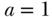 , compared to an alternative scenario where none of the participants were enrolled in the program,
, compared to an alternative scenario where none of the participants were enrolled in the program,  . In order for the total effect to have a causal interpretation, we must assume no unmeasured confounding of the relation between the treatment and outcome after accounting for potential confounding by covariates
. In order for the total effect to have a causal interpretation, we must assume no unmeasured confounding of the relation between the treatment and outcome after accounting for potential confounding by covariates  ; in formal notation this is
; in formal notation this is  , where the notation
, where the notation  is used to denote that
is used to denote that  is independent of
is independent of  conditional on
conditional on  . This would likely be the case if the cash transfer program was randomly allocated among eligible mothers (Leroy et al. 2008; Rivera et al. 2004); otherwise, we would have to assume no unmeasured confounding after accounting for the covariates predicting enrollment and children's height-for-age (e.g., sociodemographic characteristics). In this case, the total effect can be estimated by the following regression, where
. This would likely be the case if the cash transfer program was randomly allocated among eligible mothers (Leroy et al. 2008; Rivera et al. 2004); otherwise, we would have to assume no unmeasured confounding after accounting for the covariates predicting enrollment and children's height-for-age (e.g., sociodemographic characteristics). In this case, the total effect can be estimated by the following regression, where  represents a vector of potentially confounders of the total effect:
represents a vector of potentially confounders of the total effect:

The Controlled Direct Effect
After estimating the total effect, we might be interested in assessing the mechanisms that explain an observed association between the exposure and outcome. Suppose we observed a beneficial effect of the program on children's height-for-age and would now like to examine if changing dietary patterns mediate the effect of the program. We could start by estimating the controlled direct effect (CDE), which is defined as the effect of the treatment on outcome, through pathways other than the mediator  , had we intervened to set the mediator to some fixed level
, had we intervened to set the mediator to some fixed level  ,
,  .
.
In order to identify the CDE, we must assume no unmeasured confounding of the total effect,  (Condition 1, Figure 16.2A). Additionally, a second condition must hold. Specifically, we must assume that there is no unmeasured confounding of the relation between the mediator and the outcome conditional on covariates
(Condition 1, Figure 16.2A). Additionally, a second condition must hold. Specifically, we must assume that there is no unmeasured confounding of the relation between the mediator and the outcome conditional on covariates  , as well as variables
, as well as variables  , that do not confound the effect of the treatment on the outcome, but do confound the relation between the mediator and the outcome. In our example, this might include access to and use of child healthcare services, which might affect children's height-for-age by influencing dietary patterns, as well as through other mechanisms such as deworming and iron supplementation. Formally, this second condition requires that
, that do not confound the effect of the treatment on the outcome, but do confound the relation between the mediator and the outcome. In our example, this might include access to and use of child healthcare services, which might affect children's height-for-age by influencing dietary patterns, as well as through other mechanisms such as deworming and iron supplementation. Formally, this second condition requires that  (Condition 2, Figure 16.2B). Assuming that measured vectors
(Condition 2, Figure 16.2B). Assuming that measured vectors  and
and  suffice to control for confounding of the exposure-outcome and mediator-outcome effects, the CDE can be estimated by reformulating the outcome regression, Model (2), as follows:
suffice to control for confounding of the exposure-outcome and mediator-outcome effects, the CDE can be estimated by reformulating the outcome regression, Model (2), as follows:

FIGURE 16.2 CAUSAL DIAGRAMS SHOWING CONDITIONS NEEDED TO IDENTIFY TOTAL EFFECTS, CONTROLLED DIRECT EFFECTS, AND NATURAL DIRECT AND INDIRECT EFFECTS
(A) Condition (1) assumes no unmeasured confounding of the total effect conditional on covariates X.
(B) Condition (2) assumes no unmeasured confounding of the relation between the mediator and the outcome by the covariates W.
(C) Condition (3) assumes that, conditional on X, there can be no unmeasured confounding of the relation between the treatment and mediator.
(D) Condition (4) requires that there be no variable that is a consequence of treatment that confounds the relation between the mediator and outcome.

This model, which allows for interaction by including a cross-product term between the exposure and mediator, allows us to estimate the CDE:

If there were no interaction between the exposure and mediator (if  ), then the expression for the CDE reduces to the direct effect obtained using the Baron and Kenny approach multiplied by
), then the expression for the CDE reduces to the direct effect obtained using the Baron and Kenny approach multiplied by  . However, the absence of interaction, which suggests that the effect of exposure on the outcome is homogenous over levels of the mediator, may be less probable in the study of social determinants. For example, for our hypothetical mediation analysis of the cash transfer program, it would imply that the impact of the cash transfer program was equivalent for children with poorer and healthier dietary patterns.
. However, the absence of interaction, which suggests that the effect of exposure on the outcome is homogenous over levels of the mediator, may be less probable in the study of social determinants. For example, for our hypothetical mediation analysis of the cash transfer program, it would imply that the impact of the cash transfer program was equivalent for children with poorer and healthier dietary patterns.
Natural Direct and Indirect Effects
In contrast to the CDE, which estimates the treatment effect after setting the mediator to a fixed level for the entire population, the natural direct effect (NDE) sets the mediator for each individual to the level it would have been under some index level of the exposure, such as the presence or absence of the treatment, respectively  or
or  Formally, the NDE of a treatment
Formally, the NDE of a treatment  on outcome
on outcome  , setting the mediator to the value it would have been if
, setting the mediator to the value it would have been if  , is given by
, is given by  . In our example, this translates to the effect of the cash transfer program on height-for-age had we set each child's caloric intake to the value it would have been had their mother not been enrolled in the program. In terms of potential outcomes, it is a comparison of two quantities: (1) the average height-for-age for children had all mothers been enrolled in the program and their children assigned the caloric intake had their mothers not been enrolled and (2) the average height-for-age had all mothers not been enrolled and their children assigned the caloric intake had their mothers not been enrolled. Complementing the NDE is the natural indirect effect (NIE). Formally defined by
. In our example, this translates to the effect of the cash transfer program on height-for-age had we set each child's caloric intake to the value it would have been had their mother not been enrolled in the program. In terms of potential outcomes, it is a comparison of two quantities: (1) the average height-for-age for children had all mothers been enrolled in the program and their children assigned the caloric intake had their mothers not been enrolled and (2) the average height-for-age had all mothers not been enrolled and their children assigned the caloric intake had their mothers not been enrolled. Complementing the NDE is the natural indirect effect (NIE). Formally defined by  , the NIE answers the counterfactual question: if we were to hold the treatment constant (e.g.,
, the NIE answers the counterfactual question: if we were to hold the treatment constant (e.g.,  ), what would the effect on the outcome be if we intervened to change the mediator from the value realized under the control condition,
), what would the effect on the outcome be if we intervened to change the mediator from the value realized under the control condition,  , to the value realized under the treatment condition,
, to the value realized under the treatment condition,  ?
?
In addition to the assumptions necessary for identifying the CDE, specifically no unmeasured confounding of the exposure-outcome and mediator-outcome effects, two additional conditions must be satisfied for a causal interpretation of the NDE and NIE. Specifically, conditional on  , there can be no unmeasured confounding of the relation between the treatment and mediator,
, there can be no unmeasured confounding of the relation between the treatment and mediator,  (Condition 3, Figure 16.2C). Additionally, a fourth condition requires that there be no variable that is a consequence of treatment that confounds the relation between the mediator and outcome,
(Condition 3, Figure 16.2C). Additionally, a fourth condition requires that there be no variable that is a consequence of treatment that confounds the relation between the mediator and outcome,  (Condition 4, Figure 16.2D). If these conditions hold, we can calculate the natural direct and indirect effects for a change in the treatment from level
(Condition 4, Figure 16.2D). If these conditions hold, we can calculate the natural direct and indirect effects for a change in the treatment from level  to
to  . First we must reformulate the mediator regression, Model (1), so that it controls for confounding of the treatment-mediator relation by covariates
. First we must reformulate the mediator regression, Model (1), so that it controls for confounding of the treatment-mediator relation by covariates  :
:

Then, we can use Models (4) and (5) to calculate the natural direct and indirect effects as follows:

and

As these expressions imply, if there is no interaction between the exposure and mediator then Conditions (1) and (2) suffice to estimate the CDE and NDE, which can be shown to be equivalent (Robins and Greenland 1992; Robins 2003). Furthermore, in the absence of interaction, the NDE and CDE would coincide with the direct effect calculated using the Baron and Kenny approach multiplied by  , and the NIE would equal the indirect effect calculated using the product method times
, and the NIE would equal the indirect effect calculated using the product method times  . Standard errors for these direct and indirect effects can be calculated using the delta method or the bootstrap (VanderWeele and Vansteelandt 2009).
. Standard errors for these direct and indirect effects can be calculated using the delta method or the bootstrap (VanderWeele and Vansteelandt 2009).
Mediation Analysis for Dichotomous Outcomes
The counterfactual approach to mediation analysis with a binary outcome is analogous to the approach for continuous outcomes outlined above, albeit with a few additional caveats to consider (VanderWeele and Vansteelandt 2010; Valeri and VanderWeele 2013). With binary outcomes we can define direct and indirect effects on the odds and risk ratio scales. Suppose we now have a binary outcome  and wish to examine mediation by the continuous mediator
and wish to examine mediation by the continuous mediator  . Recall that our mediation analysis is based on the coefficients from two regression models, one for the mediator and the other for the outcome. For a continuous mediator, the mediator regression is given by Model (5). A common approach for estimating the model for the outcome would be to run a logistic regression:
. Recall that our mediation analysis is based on the coefficients from two regression models, one for the mediator and the other for the outcome. For a continuous mediator, the mediator regression is given by Model (5). A common approach for estimating the model for the outcome would be to run a logistic regression:
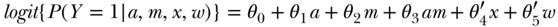
If the outcome is rare, the controlled direct effect and natural direct and indirect effects are given on the odds ratio scale by the following expressions:


and

where  is the variance of the error term in the regression for the mediator
is the variance of the error term in the regression for the mediator  . The approximations for the NDE and NIE hold to the extent that the outcome is rare; for relatively rare outcomes, the odds ratio approximates the risk ratio. Moreover, if the outcome is rare and there is no evidence of exposure–mediator interaction, then the expressions given above will coincide with the product method. However, as the outcome becomes more common, the odds ratio becomes a poorer approximation of the risk ratio and, because it is a “non-collapsible” measure of effect, cannot be used to obtain unbiased estimates of the NDE or NIE, which depend on the products of coefficients from two models that control for different covariates (VanderWeele and Vansteelandt 2010; Valeri and VanderWeele 2013). A practical, and highly recommended (Kaufman 2010a), alternative to odds ratios is to model the outcome regression on the risk ratio scale by running a generalized linear model with a binomial or Poisson distribution and log link. On the risk ratio scale, the expressions given above will not depend on the prevalence of the outcome and will hold exactly. For odds ratios (when the outcome is rare) and risk ratios, the total effect is equivalent to the product of the natural direct and indirect effects. Expressions for the CDE, NDE, and NIE when both the mediator and outcome are dichotomous are provided by Valeri and VanderWeele (2013).
. The approximations for the NDE and NIE hold to the extent that the outcome is rare; for relatively rare outcomes, the odds ratio approximates the risk ratio. Moreover, if the outcome is rare and there is no evidence of exposure–mediator interaction, then the expressions given above will coincide with the product method. However, as the outcome becomes more common, the odds ratio becomes a poorer approximation of the risk ratio and, because it is a “non-collapsible” measure of effect, cannot be used to obtain unbiased estimates of the NDE or NIE, which depend on the products of coefficients from two models that control for different covariates (VanderWeele and Vansteelandt 2010; Valeri and VanderWeele 2013). A practical, and highly recommended (Kaufman 2010a), alternative to odds ratios is to model the outcome regression on the risk ratio scale by running a generalized linear model with a binomial or Poisson distribution and log link. On the risk ratio scale, the expressions given above will not depend on the prevalence of the outcome and will hold exactly. For odds ratios (when the outcome is rare) and risk ratios, the total effect is equivalent to the product of the natural direct and indirect effects. Expressions for the CDE, NDE, and NIE when both the mediator and outcome are dichotomous are provided by Valeri and VanderWeele (2013).
Controlled or Natural Effects?
If there is an interaction between the treatment and mediator then the distinction between controlled and natural effects can become important because the CDE and NDE may differ. With interactions, the CDE will vary depending on the level of the mediator, whereas the NDE essentially averages over the various CDEs (Pearl 2001). Generally speaking, controlled direct effects are more relevant for policy purposes, whereas natural direct and indirect effects are more relevant to etiologic questions about the manner in which the treatment causes the outcome (Kaufman, MacLehose, and Kaufman 2004; Joffe, Small, and Hsu 2007; Hafeman and Schwartz 2009).
Natural direct and indirect effects are thought to be particularly relevant to etiologic questions because they have the attractive feature of summing to equal the total effect,  , even in settings with interactions between the treatment and mediator. In other words, we can “decompose” the total effect into the part that is explained by the mediator (the NIE) and the part that is due to other factors (the NDE), thereby giving insight into the role of various pathways. This, in general, is not true of CDEs (unless there is no interaction between the exposure and mediator) and the difference between the TE and CDE cannot be interpreted as an indirect effect and used to assess mediation (VanderWeele 2009; Robins and Greenland 1992; Robins 2003; Pearl 2001). The ability to decompose total effects allows calculation of the proportion mediated (PM). Calculated by taking the ratio of the natural indirect effect to the total effect,
, even in settings with interactions between the treatment and mediator. In other words, we can “decompose” the total effect into the part that is explained by the mediator (the NIE) and the part that is due to other factors (the NDE), thereby giving insight into the role of various pathways. This, in general, is not true of CDEs (unless there is no interaction between the exposure and mediator) and the difference between the TE and CDE cannot be interpreted as an indirect effect and used to assess mediation (VanderWeele 2009; Robins and Greenland 1992; Robins 2003; Pearl 2001). The ability to decompose total effects allows calculation of the proportion mediated (PM). Calculated by taking the ratio of the natural indirect effect to the total effect,  , the PM assesses what would happen to the effect of the exposure on the outcome if we were somehow able to disable the pathway from the exposure to the mediator (VanderWeele 2013). Quantifying the proportion of the total effect that is mediated by a specific intermediary can be informative, particularly in settings where there may not be a plausible intervention on the exposure and the goal is pure mechanistic inference. As we will discuss below, research that aims to explain racial inequalities in health is a prime example, although these effects do not correspond precisely to the NDE and NIE.
, the PM assesses what would happen to the effect of the exposure on the outcome if we were somehow able to disable the pathway from the exposure to the mediator (VanderWeele 2013). Quantifying the proportion of the total effect that is mediated by a specific intermediary can be informative, particularly in settings where there may not be a plausible intervention on the exposure and the goal is pure mechanistic inference. As we will discuss below, research that aims to explain racial inequalities in health is a prime example, although these effects do not correspond precisely to the NDE and NIE.
There are several reasons why the CDE may be of greater interest. Identification of the CDE requires fewer conditions, implying that it can be estimated in a broader range of situations. Moreover, CDEs are more policy relevant than natural direct effects. The contrast implied by the CDE, specifically the change in the outcome that would be achieved from intervening to set the mediator to the same value for the entire population (e.g., if all children had the same caloric intake), is clear and comprehensible. Conversely, the NDE, which sets the mediator to different values for individuals based on a potentially unobserved reference level for the exposure, is less transparent. It requires us to estimate the potential outcome with the exposure set to a particular value of  (e.g.,
(e.g.,  ) and the mediator set to what it would have been under a counterfactual and incompatible scenario (e.g.,
) and the mediator set to what it would have been under a counterfactual and incompatible scenario (e.g.,  ) (Robins and Greenland 1992). In our example of the cash transfer program, this would require defining an intervention that sets the caloric intake for a child whose mother was not enrolled in the program to the value it would have been had she been enrolled. Because we can never observe this quantity via any empirical study, observational or experimental, the NDE and NIE require what is sometimes called a “cross-world” independence assumption, which cannot be empirically verified or even checked in a randomized trial. Consequently, some have advocated for estimation of the CDE when the goal is to inform public health policy (Kaufman 2009; Naimi, Kaufman, and MacLehose 2014). Although the CDE cannot be used to estimate the PM in the presence of treatment–mediator interaction, it can be used to calculate the proportion of the total effect that could be eliminated, or proportion eliminated (PE), by intervening to set the mediator to a fixed value,
) (Robins and Greenland 1992). In our example of the cash transfer program, this would require defining an intervention that sets the caloric intake for a child whose mother was not enrolled in the program to the value it would have been had she been enrolled. Because we can never observe this quantity via any empirical study, observational or experimental, the NDE and NIE require what is sometimes called a “cross-world” independence assumption, which cannot be empirically verified or even checked in a randomized trial. Consequently, some have advocated for estimation of the CDE when the goal is to inform public health policy (Kaufman 2009; Naimi, Kaufman, and MacLehose 2014). Although the CDE cannot be used to estimate the PM in the presence of treatment–mediator interaction, it can be used to calculate the proportion of the total effect that could be eliminated, or proportion eliminated (PE), by intervening to set the mediator to a fixed value,  , for the population:
, for the population:  (VanderWeele 2013). As we noted earlier, the PE, which can also be calculated on the excess risk ratio scale (Suzuki et al. 2014), will coincide with the PM if there is no interaction between the treatment and mediator because, in this scenario, the CDE and NDE will be equivalent.
(VanderWeele 2013). As we noted earlier, the PE, which can also be calculated on the excess risk ratio scale (Suzuki et al. 2014), will coincide with the PM if there is no interaction between the treatment and mediator because, in this scenario, the CDE and NDE will be equivalent.
Decomposition of Racial Inequalities in Health
Reference to race in epidemiologic research has grown consistently since the 1970s, at least in the United States (Jones, LaVeist, and Lillie-Blanton 1991), sparking a discourse about the utility of studying race, if any, including how racial categories should be defined (Stolley 1999; Williams 1997; Cooper 1984) and treated in our analytical models (Kaufman and Cooper 2001). As consensus emerged that racial categorizations might reflect important social and class stratifications, interest in “explaining” racial inequalities in health grew. It became common practice to adjust for a hypothesized intermediate, usually an indicator of socioeconomic status (SES), and evaluate the statistical significance of the adjusted coefficient for race to determine if the factor accounted for, or mediated, observed racial inequalities in health (Smith et al. 1998; Galea et al. 2007; Hayward et al. 2000). This approach, as described earlier, can result in biased inference regarding the mechanisms that contribute to inequalities in health, unless specific conditions are satisfied (Kaufman and Cooper 2001).
Mediation analysis of racial inequalities presents some unique challenges. In particular, the total “effect” of race is ambiguous relative to many other exposures because it is not ostensibly mutable—the counterfactual question of what the outcome distribution for black participants would have been had they been white (or vice versa) is difficult to answer because there are no hypothetical interventions on race when race itself is the exposure (Kaufman and Cooper 1999). In other words, this contrast cannot be estimated using a randomized trial (though see below for exceptions). Attempting to estimate the effect of race in observational studies by conditioning on all of the differences that distinguish racial groups and may affect their health outcomes is an ambitious endeavor, to say the least, since race is inextricably intertwined with nearly all other social and behavioral characteristics (Kaufman 2008; Kaufman, Cooper, and McGee 1997). This has led some to reject outright the tenability of race as a potential cause in epidemiologic models (Kaufman and Cooper 1999, 2001; Holland 1986), unless observed racial inequalities are attributable to external characteristics. Estimating the causal effect of race is more conceivable if race represents the experience of discrimination based on a particular phenotype rather than innate biological or genetic characteristics. If we are interested in the effects of racial discrimination, for example, it may be possible to identify a credible counterfactual through the random assignment of self-reported race on employment applications (Bertrand and Mullainathan 2004). What are the implications for mediation analysis? Clearly, if the “causal effect” of race is not meaningful, then it is difficult to define the direct and indirect effects of race in terms of potential outcomes, as we did above for well-defined exposures. This limits the validity of mediation methods for separating direct (e.g., biological) and indirect (e.g., social determinants) effects of race on health in etiologic research (Kaufman and Cooper 2001). Fortunately, recent literature has revisited this issue and showed that it is possible to provide a causal interpretation of the race coefficient in a mediation model, albeit in a more nuanced manner that depends on the strength of the assumptions that we are disposed to making (VanderWeele and Robinson 2014).
Generally speaking, prior research attempting to decompose racial inequalities in health has adjusted for two sets of covariates: (1) potentially confounding variables  that are associated with race,
that are associated with race,  , and the health outcome of interest,
, and the health outcome of interest,  , assumed here to be continuous, but not affected by race, and (2) some measure of SES,
, assumed here to be continuous, but not affected by race, and (2) some measure of SES,  , that is hypothesized to mediate an observed racial health inequality. Following the illustration by VanderWeele and Robinson (2014), if, for example, family and neighborhood SES around the time of birth (
, that is hypothesized to mediate an observed racial health inequality. Following the illustration by VanderWeele and Robinson (2014), if, for example, family and neighborhood SES around the time of birth ( ) are related to race, then we can estimate the coefficient of race (e.g., where
) are related to race, then we can estimate the coefficient of race (e.g., where 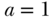 for participants who are black and
for participants who are black and  for white participants) by Model (3) above; if the effects of SES0, NSES0 are themselves unconfounded, then the race coefficient could be interpreted in a weaker manner as the residual racial inequality had the distributions of family and neighborhood SES for the black population been set to that of the white population. This interpretation requires milder assumptions than trying to attach a causal interpretation or intervene on race itself. In particular, it no longer assumes that race can be manipulated, but instead tells us what would happen to the observed racial inequality had we intervened on certain socioeconomic characteristics and set them to a potentially counterfactual value.
for white participants) by Model (3) above; if the effects of SES0, NSES0 are themselves unconfounded, then the race coefficient could be interpreted in a weaker manner as the residual racial inequality had the distributions of family and neighborhood SES for the black population been set to that of the white population. This interpretation requires milder assumptions than trying to attach a causal interpretation or intervene on race itself. In particular, it no longer assumes that race can be manipulated, but instead tells us what would happen to the observed racial inequality had we intervened on certain socioeconomic characteristics and set them to a potentially counterfactual value.
Suppose that we now want to decompose the relation between race and health into the indirect component “mediated” by differing SES levels in early adulthood,  , and the direct effect that is through other mechanisms. If there is no interaction between race and SES then we can fit a model regressing the health outcome on race as the exposure, SES as the mediator, exposure-outcome confounders
, and the direct effect that is through other mechanisms. If there is no interaction between race and SES then we can fit a model regressing the health outcome on race as the exposure, SES as the mediator, exposure-outcome confounders  , and mediator-outcome confounders
, and mediator-outcome confounders  :
:

If including  suffices to control for confounding of the association between SES and the outcome, then the race coefficient can be interpreted as the racial inequality in health remaining had the distribution of adult SES for the black population been set to equal that of the white population with the same values of potential confounders
suffices to control for confounding of the association between SES and the outcome, then the race coefficient can be interpreted as the racial inequality in health remaining had the distribution of adult SES for the black population been set to equal that of the white population with the same values of potential confounders  and
and  . We can also estimate the magnitude of the indirect effect through adult SES by comparing the racial inequality before and after controlling for adult SES and mediator-outcome confounders
. We can also estimate the magnitude of the indirect effect through adult SES by comparing the racial inequality before and after controlling for adult SES and mediator-outcome confounders  . The difference in the coefficients for race in these two models can be interpreted as the estimated change in health outcomes for the black population, with values for their potential confounders of
. The difference in the coefficients for race in these two models can be interpreted as the estimated change in health outcomes for the black population, with values for their potential confounders of  and
and  , if their adult SES distribution were set equal to that of the black population versus that of the white population.
, if their adult SES distribution were set equal to that of the black population versus that of the white population.
For binary outcomes, logistic (for rare outcomes) or log-linear (for common outcomes) regressions can be used to obtain direct and mediated inequality measures using the same procedures detailed above (VanderWeele and Robinson 2014). Moreover, if the effects of SES happened to differ by racial group so that there was interaction, the methods for estimating direct and indirect effects in the presence of exposure–mediator interactions, also described above, could still be used to decompose the overall racial inequality into direct versus mediated components. Furthermore, it is important to reiterate that, although estimated in a similar manner, the interpretations of the direct and mediated inequality measures are distinct from the interpretations of natural direct and indirect effects given earlier. In particular, the inequality measures do not manipulate the exposure or require the assumptions of no unmeasured exposure-outcome and exposure-mediator confounding needed for identifying natural direct and indirect effects. The expressions for the direct and mediated racial inequalities also do not depend on the “cross-world” independence assumption. They set the mediator to a randomly selected level from the distribution of the mediator among all of those with a particular exposure (given covariates), rather than fixing the mediator to the level it would have been under a particular exposure. Finally, other challenges for estimating and decomposing racial inequalities (e.g., structural confounding due to limited overlap of racial and socioeconomic groups) (Kaufman and Cooper 2001) still apply.
Exposure-Induced Mediator-Outcome Confounding
As we alluded to earlier, for some of the questions that we are interested in answering we may be unable to satisfy the conditions necessary for identifying natural direct and indirect effects. In particular, if there is a consequence of the treatment that confounds the relation between the mediator and outcome, then the fourth condition that we articulated is violated and the total effect cannot generally be decomposed into its direct and indirect components (unless there is no treatment–mediator interaction). Alternative methods are available for estimating direct and indirect effects when an exposure-induced mediator-outcome confounder is present; for example, as discussed in the following section, both the mediator and mediator-outcome confounding variable can be considered jointly as the mediator (VanderWeele, Vansteelandt, and Robins 2014).
The violation of the fourth condition of no exposure-induced mediator outcome confounding may be a concern in the study of social determinants of health. If we borrow Kaufman's (2009) metaphor of mediation analysis as a Rube Goldberg device, then the cascade of intermediate events between social exposures, intermediaries, and health outcomes is simply longer vis-à-vis biological exposures—the longer the potential chain of reactions between the exposure and mediator, the greater the opportunity for time-varying confounding (VanderWeele and Vansteelandt 2009). This is a particular challenge for examining the effects of social determinants over the life course. For example, if we would like to examine whether the effects of early-life circumstances on the development of chronic disease are mediated by experiences in early adulthood, we must be cognizant of the potential for consequences of early-life socioeconomic circumstances to then confound the effects of adult SES on the incidence of chronic disease (Nandi et al. 2012). Additionally, there is substantial interest in social epidemiology in “explaining” social inequalities in health and whether they are mediated by health behaviors, such as smoking, alcohol consumption, and physical activity (Stringhini et al. 2010–2012; Lantz et al. 1998, 2010); however, the potential for socially graded diseases (e.g., cardiovascular events) to predict changes in health behaviors and subsequent health events could introduce time-varying confounding (Nandi, Glymour, and Subramanian 2014). Similarly, if we would like to investigate whether socioeconomic inequalities in childhood mortality are mediated by vaccination coverage in a lower-income context, our analyses should account for the potential time-varying confounding by other factors, such as access to antenatal care, which may be influenced by household SES and also affect the probabilities of vaccination coverage and child mortality.
Although the NDE and NIE cannot be identified if there is exposure-induced mediator-outcome confounding, it is still possible to estimate the CDE. However, marginal structural models (MSMs) or structural mean models (SMMs), rather than the conventional regression approach for estimating the CDE illustrated by Model (4), should be used to appropriately account for time-varying confounding of the direct effect. These methods were originally developed by Robins for the context of time-varying treatments but have been adapted in the mediation setting for direct effects (VanderWeele 2009b; Vansteelandt 2009). The MSM methods were described by VanderWeele (2009b) and there are several recent applications of the MSM approach to mediation analysis (Nandi et al. 2012; Nandi, Glymour, and Subramanian 2014). We will illustrate this method using our hypothetical mediation analysis of the cash transfer program, dietary patterns, and children's height-for-age. Suppose, as in the case of many cash transfer programs, that receipt of benefits is contingent on compliance with certain conditions, including regular visits to the pediatrician; this makes receipt of child healthcare services a direct consequence of the treatment (represented by path 2 in Figure 16.3). A direct effect of enrollment on height-for-age (e.g., if all children were fixed to a “high” level of caloric intake) could be explained by changes in the utilization of child healthcare services (path 2*3), as well as other mechanisms (represented by path 1). Alternatively, enrollment in the program may influence nutritional status only through its influence on children's caloric intake (represented by paths 4*5 and 2*6*5). Of note, Figure 16.3 implies that use of child healthcare services has the potential to act simultaneously as a confounder of the mediator-outcome relation and mediator of the effect of enrollment on nutrition. If the assumptions made by the causal diagram are correct, then potential confounding by measured covariates cannot be handled by conditioning on these characteristics because regression adjustment might block pathways linking enrollment to child nutrition and underestimate the direct effect of the program on nutrition that is not transmitted via dietary patterns. Alternatively, omitting this time-varying covariate and conditioning on caloric intake may induce bias due to collider stratification. Therefore, our direct effect estimate will be biased whether we control for receipt of child healthcare services or not. By handling potential confounding through weighting rather than conditioning on covariates, MSMs allow for identification of the direct effect of enrollment on nutrition even in settings in which conventional approaches are biased, including when there are exposure-induced mediator-outcome confounders (VanderWeele 2009b; Robins, Hernán, and Brumback 2000).
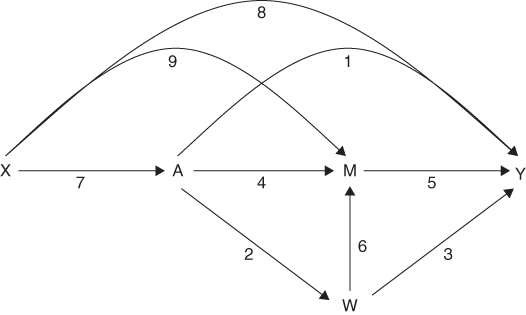
FIGURE 16.3 CAUSAL DIAGRAM OF THE EFFECTS OF A HYPOTHETICAL CONDITIONAL CASH TRANSFER PROGRAM ON CHILDREN'S HEIGHT-FOR-AGE
Note: W represents covariates measuring children's use of healthcare services that may operate as mediators of the effect of program enrollment on height-for-age and also as confounders of the relation between children's calorific intake and their height-for-age.Source: Adapted from Nandi et al. (2012).
If we again let  represent the binary exposure representing enrollment in the cash transfer program,
represent the binary exposure representing enrollment in the cash transfer program,  the mediator representing children's caloric intake,
the mediator representing children's caloric intake,  the outcome of height-for-age Z-score,
the outcome of height-for-age Z-score,  a vector of potential confounders of the treatment-outcome relation including sociodemographic characteristics, and
a vector of potential confounders of the treatment-outcome relation including sociodemographic characteristics, and  a vector of potential confounders of the mediator-outcome relation including use of child healthcare services, then the CDE of enrollment in the cash transfer program can be estimated using an inverse probability weighted MSM of the form
a vector of potential confounders of the mediator-outcome relation including use of child healthcare services, then the CDE of enrollment in the cash transfer program can be estimated using an inverse probability weighted MSM of the form

In contrast to Model (4), which accounted for potential confounding of the treatment-outcome and mediator-outcome effects by conditioning on these covariates, the MSM accounts for confounding with inverse probability weights of the form  , where
, where

and

There are several tutorials available for fitting inverse probability weighted MSMs (Robins, Hernán, and Brumback 2000; Hernán, Brumback, and Robins 2000, and Cole and Hernán 2008). In this context, the first weight,  , accounts for measured confounding of the total effect of enrollment on height-for-age and the second weight,
, accounts for measured confounding of the total effect of enrollment on height-for-age and the second weight,  , accounts for measured confounding of the mediator-outcome relation between caloric intake and the outcome. The denominators of the two weights are, respectively, the predicted probabilities of enrollment status and caloric intake in fact received, conditional on the sets of confounders. If caloric intake is measured categorically, the predicted probabilities can be obtained from the ordinal or multinomial logistic model; if it is continuous, the probabilities can be replaced by values from a probability density function (Robins, Hernán, and Brumback 2000). Stabilizing the weights by including probabilities in the numerator, that is,
, accounts for measured confounding of the mediator-outcome relation between caloric intake and the outcome. The denominators of the two weights are, respectively, the predicted probabilities of enrollment status and caloric intake in fact received, conditional on the sets of confounders. If caloric intake is measured categorically, the predicted probabilities can be obtained from the ordinal or multinomial logistic model; if it is continuous, the probabilities can be replaced by values from a probability density function (Robins, Hernán, and Brumback 2000). Stabilizing the weights by including probabilities in the numerator, that is,  for
for  and
and  for
for  , results in more efficient estimation (Robins, Hernán, and Brumback 2000). If the exposure and mediator are continuous rather than binary or categorical, it is often better to use a structural mean model approach to estimate the controlled direct effect, and further discussion can be found elsewhere (Vansteelandt 2009).
, results in more efficient estimation (Robins, Hernán, and Brumback 2000). If the exposure and mediator are continuous rather than binary or categorical, it is often better to use a structural mean model approach to estimate the controlled direct effect, and further discussion can be found elsewhere (Vansteelandt 2009).
Results from the marginal structural modeling approach for estimating the CDE may differ from the regression approach for a variety of reasons. First, as we noted earlier, the CDEs are in fact estimating different quantities—by accounting for potential mediator-outcome confounding through weighting rather than conditioning, the MSM allows for the effect of the treatment on the outcome to travel through the exposure-induced mediator-outcome confounder, whereas the regression adjustment approach blocks these pathways. Second, the regression adjustment approach may also induce bias by conditioning on colliders, if the mediators adjusted for in the vector  are affected by unmeasured characteristics
are affected by unmeasured characteristics  that also influence the outcome. We will discuss the implications of unmeasured confounding in further detail below. Additionally, depending on the particular measure of association, covariate conditional and marginal estimates may vary for reasons other than time-varying confounding (Kaufman 2010b).
that also influence the outcome. We will discuss the implications of unmeasured confounding in further detail below. Additionally, depending on the particular measure of association, covariate conditional and marginal estimates may vary for reasons other than time-varying confounding (Kaufman 2010b).
Mediation Analysis with Multiple Mediators
Until now we have described cases concerning a single mediator, as well as those with exposure-induced mediator-outcome confounding, which involves two mediators, but only one of primary interest. In many applications in social epidemiology we might, however, be interested in the contemporaneous role of multiple mediators. For example, quantifying the joint contribution of multiple health behaviors, including physical activity, alcohol consumption, smoking, and other behaviors to social inequalities in health has been an active research area (Stringhini et al. 2010–2012; Lantz et al. 1998, 2010; Nandi, Glymour, and Subramanian 2014). Similarly, we might be interested in examining mediation by constructs represented by several distinct but related indicators; this includes mediation of the effect of early-life SES by SES in adulthood (commonly measured by some combination of education, income, wealth, and occupational status) (Nandi et al. 2012; Pollitt, Rose, and Kaufman 2005; Galobardes, Smith, and Lynch 2006). Other work has explored whether psychosocial stress pathways, indicated by different biomarkers, explain social inequalities in health (Gebreab et al. 2012; McEwen 2012). Recent methodological developments provide guidance for mediation analysis when more than one mechanism is of interest (Avin, Shpitser, and Pearl 2005; Imai and Yamamoto 2013; Albert 2012; Zheng and van der Laan 2012). Here we introduce a simple extension of the parametric methods described earlier for estimating direct and indirect effects (VanderWeele and Vansteelandt 2013).
To begin, suppose that, instead of a single mediator, we are now interested in multiple mediators represented by the vector  . Our counterfactual definitions of direct and indirect effects are essentially unaltered, with the exception that
. Our counterfactual definitions of direct and indirect effects are essentially unaltered, with the exception that  now replaces the single mediator
now replaces the single mediator  . When the mediators in
. When the mediators in  affect one another, as illustrated by Figure 16.4 with only two mediators, treating them one-by-one in separate analyses and then summing their indirect effects to derive a joint effect will tend to overstate the true proportion mediated. Intuitively, this is because if
affect one another, as illustrated by Figure 16.4 with only two mediators, treating them one-by-one in separate analyses and then summing their indirect effects to derive a joint effect will tend to overstate the true proportion mediated. Intuitively, this is because if  influences
influences  then the path
then the path  would be included in the indirect effect for both
would be included in the indirect effect for both  and
and  ; this can result in estimates of the proportion mediated that exceed 100%. Even if they do not affect each other, interactions between the effects of multiple mediators on the outcome can cause the sum of mediated effects considered individually to differ from the joint mediated effect (VanderWeele and Vansteelandt 2013). Additionally, suppose that these direct and indirect effects are identified under the same set of Conditions (1) to (4) described previously, with the assumptions now applying to the entire vector of mediators
; this can result in estimates of the proportion mediated that exceed 100%. Even if they do not affect each other, interactions between the effects of multiple mediators on the outcome can cause the sum of mediated effects considered individually to differ from the joint mediated effect (VanderWeele and Vansteelandt 2013). Additionally, suppose that these direct and indirect effects are identified under the same set of Conditions (1) to (4) described previously, with the assumptions now applying to the entire vector of mediators  . These conditions underline additional challenges with attempting to estimate the joint effect of multiple mediators, and why summing their individual indirect effects will generally give us the wrong answer. It is clear from Figure 16.4 that estimation of the indirect effect through
. These conditions underline additional challenges with attempting to estimate the joint effect of multiple mediators, and why summing their individual indirect effects will generally give us the wrong answer. It is clear from Figure 16.4 that estimation of the indirect effect through  requires us to control for
requires us to control for  , since it is a confounder of the relation between
, since it is a confounder of the relation between  and
and  . However, including
. However, including  in the set of potentially confounding covariates
in the set of potentially confounding covariates  would not resolve this issue because
would not resolve this issue because  is affected by
is affected by  , making it an exposure-induced confounder of the mediator-outcome relation. Notably, Condition (4), which precludes such violations, can still be satisfied for the entire set of mediators
, making it an exposure-induced confounder of the mediator-outcome relation. Notably, Condition (4), which precludes such violations, can still be satisfied for the entire set of mediators  without holding for each individual mediator. Thus, exposure-induced confounders of any of the mediator-outcome relations should be included in the vector
without holding for each individual mediator. Thus, exposure-induced confounders of any of the mediator-outcome relations should be included in the vector  ; otherwise Condition (4) would be violated and natural direct and indirect effects generally unidentifiable.
; otherwise Condition (4) would be violated and natural direct and indirect effects generally unidentifiable.

FIGURE 16.4 CAUSAL DIAGRAM SHOWING THE MEDIATION MODEL WITH TWO MEDIATORS OF INTEREST
Source: Adapted from VanderWeele and Vansteelandt (2013).
Here we describe the regression-based approach for mediation analysis with multiple mediators introduced by VanderWeele and Vansteelandt (2013). Starting with the case of a continuous outcome and continuous mediators, we can fit one regression model for the outcome and separate models for each of the mediators:

and

In the absence of interactions, the controlled direct effect and natural direct and indirect effects are given by the following expressions:

and

This general approach can also accommodate exposure–mediator interactions. For example, if we wanted to account for the interaction between the exposure and a mediator  , then the cross-product representing the interaction between
, then the cross-product representing the interaction between  and
and  could be added to the outcome regression, Model (11):
could be added to the outcome regression, Model (11):

From Models (12) and (13), the expressions for the direct and indirect effects are then given by

and

Any number of additional exposure–mediator interactions, for example between the exposure and mediator  , could be accommodated by adding the term
, could be accommodated by adding the term  to the CDE,
to the CDE,  to the NDE, and
to the NDE, and  to the NIE. Expressions for direct and indirect effects can be adapted to allow for binary mediators, binary outcomes, and interactions, as explained in VanderWeele and Vansteelandt (2013).
to the NIE. Expressions for direct and indirect effects can be adapted to allow for binary mediators, binary outcomes, and interactions, as explained in VanderWeele and Vansteelandt (2013).
Sensitivity Analyses
As illustrated by the counterfactual approach to mediation, several conditions must be met for analyses to permit causal conclusions. In some cases these conditions can be empirically verified. For example, interactions between the exposure and mediator can be assessed and, if present, accommodated when estimating direct or indirect effects. By contrast, other conditions, notably the strong unmeasured confounding assumptions necessary for estimating direct and indirect effects, are unverifiable. This is of particular concern for social epidemiology because our studies are often observational and our exposures, including indicators of SES, non-randomized. Much attention has been given to study designs, statistical approaches, and sensitivity analyses to address confounding of total effects when we lack control over the assignment of our exposure. However, even if we were unworried about confounding of the total effect (e.g., through randomization of the exposure), mediation analyses may be biased by unmeasured common causes of the mediator and the outcome, among other sources. In addition to confounding bias, other biases common in epidemiologic studies, such as measurement error, also apply and threaten the validity of mediation analyses. In this section we introduce approaches to assess the sensitivity of our results to account for sources of bias common in mediation analysis, specifically: (1) confounding of the mediator-outcome relation and (2) error in the measurement of the mediator.
Sensitivity Analyses if There Is Unmeasured Mediator-Outcome Confounding
With social epidemiology making predominant use of observational data, unmeasured confounding is a ubiquitous problem. We have seen, through this volume for Methods in Social Epidemiology and elsewhere, how carefully designed studies that use randomized trials as a conceptual tool can be used to estimate the causal effects of social determinants (Kaufman, Kaufman, and Poole 2003). However, even if it were possible to prevent unmeasured exposure-outcome and exposure-mediator confounding, this does not imply that our mediation analyses will be unbiased. Identification of the controlled and natural direct and indirect effects, as described earlier, also requires the absence of mediator-outcome confounding, among other assumptions. This condition is often overlooked. For example, in our illustration, there could be unmeasured household and parental characteristics, such as the level of health literacy, that influence investments in child health and dietary patterns as well as health outcomes. Unmeasured confounding of the mediator-outcome relation can introduce bias due to collider-stratification, as illustrated by Glymour (see Chapter 19) and, importantly, randomizing the exposure does not prevent this bias (Robins and Greenland 1992; Pearl 2001; VanderWeele 2010). Fortunately, there are approaches available for assessing the sensitivity of direct and indirect effect estimates to unmeasured confounding by a characteristic  of the relation between the mediator and outcome (VanderWeele 2010; Hafeman 2011). We will focus on the methods described by VanderWeele (2010). We will adopt three simplifying assumptions, encoded by the causal diagram in Figure 16.5, that facilitate sensitivity analyses for direct and indirect effects; we refer the reader elsewhere for general formulas applicable if these assumptions are likely to be violated (VanderWeele 2010). The first condition assumes that the unmeasured confounder affects only the mediator and outcome, which would be violated if, for example,
of the relation between the mediator and outcome (VanderWeele 2010; Hafeman 2011). We will focus on the methods described by VanderWeele (2010). We will adopt three simplifying assumptions, encoded by the causal diagram in Figure 16.5, that facilitate sensitivity analyses for direct and indirect effects; we refer the reader elsewhere for general formulas applicable if these assumptions are likely to be violated (VanderWeele 2010). The first condition assumes that the unmeasured confounder affects only the mediator and outcome, which would be violated if, for example,  affected
affected  . Second, the effect of the unmeasured confounder on the outcome is assumed to be constant across strata of the exposure and measured covariates
. Second, the effect of the unmeasured confounder on the outcome is assumed to be constant across strata of the exposure and measured covariates  , which would be violated if there were interaction on the additive scale between
, which would be violated if there were interaction on the additive scale between  and
and  or
or  on
on  . Third, we assume that the unmeasured confounder is neither a cause or caused by the measured confounding variables.
. Third, we assume that the unmeasured confounder is neither a cause or caused by the measured confounding variables.
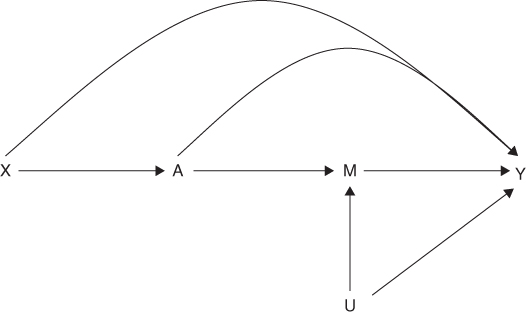
FIGURE 16.5 CAUSAL DIAGRAM SHOWING UNMEASURED CONFOUNDING OF THE MEADIATOR-OUTCOME RELATION BY THE CONFOUNDER U
For a binary unmeasured common cause  of the mediator and outcome, the bias in the estimated CDE (conditional on
of the mediator and outcome, the bias in the estimated CDE (conditional on  ) compared to the true CDE (conditional on
) compared to the true CDE (conditional on  and
and  ), estimated on the risk difference scale, is given by the product of two parameters: (1)
), estimated on the risk difference scale, is given by the product of two parameters: (1)  , which denotes the difference in the prevalence of
, which denotes the difference in the prevalence of  between individuals with exposure level
between individuals with exposure level  compared to
compared to  conditional on
conditional on  and
and  and (2)
and (2)  , which denotes the direct effect of
, which denotes the direct effect of  on
on  , measured by the risk difference, conditional on
, measured by the risk difference, conditional on  ,
,  , and
, and  :
:

The bias due to  can also be calculated on the risk ratio scale. If we let
can also be calculated on the risk ratio scale. If we let  denote the direct effect of
denote the direct effect of  on
on  , measured on the risk ratio scale, conditional on
, measured on the risk ratio scale, conditional on  ,
,  , and
, and  ;
;  represent the prevalence of
represent the prevalence of  among participants with exposure level
among participants with exposure level  ,
,  , and
, and  ; and
; and  represent the prevalence of
represent the prevalence of  among participants with exposure level
among participants with exposure level  ,
,  , and
, and  , then the bias is given by
, then the bias is given by

Once we compute the bias factor, we can assess the sensitivity of our estimates of the CDE. On the risk difference scale, we can vary values of  and
and  and subtract the bias from our regression estimate to obtain the corrected CDE had we been able to account for
and subtract the bias from our regression estimate to obtain the corrected CDE had we been able to account for  ; the lower and upper confidence limits for the CDE can also be corrected in this same manner. Similarly, on the risk ratio scale we can presuppose different values of
; the lower and upper confidence limits for the CDE can also be corrected in this same manner. Similarly, on the risk ratio scale we can presuppose different values of  ,
,  , and
, and  and divide the estimated risk ratio measuring the CDE, as well as its confidence limits, by the bias factor to obtain the true CDE had we hypothetically been able to account for
and divide the estimated risk ratio measuring the CDE, as well as its confidence limits, by the bias factor to obtain the true CDE had we hypothetically been able to account for  . It is also possible to vary values of
. It is also possible to vary values of  and
and  for different values of
for different values of  , since the CDE can vary across levels of the mediator.
, since the CDE can vary across levels of the mediator.
If there is no interaction between the exposure and mediator on the outcome, then the bias formula for the CDE will also apply to natural direct and indirect effects. In this instance, the NDE will equal the CDE and we could use the same strategy described above to obtain corrected values for the NDE had we been able to account for  . Because the bias of the NIE is the negation of the bias of the NDE, the same bias factor could be added (or multiplied if on the risk ratio scale) to the NIE and its confidence limits to obtain corrected estimates. However, in order to compute the bias factors for natural direct and indirect effects when interaction is present, one must specify the direct effect of
. Because the bias of the NIE is the negation of the bias of the NDE, the same bias factor could be added (or multiplied if on the risk ratio scale) to the NIE and its confidence limits to obtain corrected estimates. However, in order to compute the bias factors for natural direct and indirect effects when interaction is present, one must specify the direct effect of  on
on  , as well as the prevalence of the unmeasured confounder within each stratum of the mediator
, as well as the prevalence of the unmeasured confounder within each stratum of the mediator  . Specifically, the bias of the NDE and NIE, conditional on
. Specifically, the bias of the NDE and NIE, conditional on  , are given by
, are given by

and

where  again denotes the direct effect of
again denotes the direct effect of  on
on  conditional on
conditional on  ,
,  , and
, and  and
and  represents the difference in the prevalence of
represents the difference in the prevalence of  between exposed and unexposed individuals conditional on
between exposed and unexposed individuals conditional on  and
and  . See VanderWeele (2010) and Ding and VanderWeele (2016) for expressions in other scenarios as well.
. See VanderWeele (2010) and Ding and VanderWeele (2016) for expressions in other scenarios as well.
Ozer and colleagues (2011) used this framework in their analysis of Mexico's Oportunidades cash transfer program, including an examination of whether levels of perceived stress and control mediated the program's impact on mother's depressive symptoms. This study compared the number of depressive symptoms among 5050 women living in rural communities who participated in Oportunidades with 1293 women from matched communities who had received no exposure to the program at the time of the assessment, but were later enrolled. On average, women who were exposed to the program had 1.7 (95% CI = –2.46, –0.96) fewer symptoms of depression compared to women in the comparison group. The investigators posited that levels of perceived stress or control may have mediated the observed total effect, and furthermore that levels of social support may have confounded the effects of these mediators on the level of depressive symptomatology. There was not evidence for a significant interaction between the exposure and mediator on the outcome. After controlling for social support, in addition to measured confounders of the treatment-outcome relation (i.e., maternal age, education, head of household status, household ethnicity, crowding, dependency ratio, wealth index, head of household occupational indices, and state), the indirect effects of the program on depressive symptoms through perceived stress and control were –0.53 (95% CI = –0.82, –0.22) and –0.18 (95% CI = –0.39, 0.00), respectively. A bias analysis was then used to assess the implications of an unmeasured binary confounder of the mediator-outcome relation. Recall that if there is no interaction between the exposure and mediator then the bias of the indirect effect on the additive scale is given by  . The authors concluded that unmeasured mediator-outcome confounding was unlikely to explain the indirect effect of perceived stress because the confounder would have to be strongly associated with the outcome and substantially more common among the exposed relative to the comparison group. For example, if the prevalence difference
. The authors concluded that unmeasured mediator-outcome confounding was unlikely to explain the indirect effect of perceived stress because the confounder would have to be strongly associated with the outcome and substantially more common among the exposed relative to the comparison group. For example, if the prevalence difference  of
of  between the exposed and comparison groups were 30% then the direct effect
between the exposed and comparison groups were 30% then the direct effect  of
of  on the outcome would have to be 1.77 (implying that those with
on the outcome would have to be 1.77 (implying that those with  would report an average of 1.77 more symptoms of depression compared to those without
would report an average of 1.77 more symptoms of depression compared to those without  , conditional on other covariates) in order to fully explain the indirect effect of perceived stress. By contrast, the direct effect would only have to be 0.60 points to fully explain the indirect effect of perceived control, making unmeasured confounding a more likely explanation of this mechanism.
, conditional on other covariates) in order to fully explain the indirect effect of perceived stress. By contrast, the direct effect would only have to be 0.60 points to fully explain the indirect effect of perceived control, making unmeasured confounding a more likely explanation of this mechanism.
Measurement Error
Much of our discussion of threats to internal validity thus far has centered on confounding. However, measurement error, including error in the measurement of the mediator, can also bias a mediation analysis. The recent simulation study of Blakely and colleagues (2013) showed that even the slight misclassification of a binary mediator could lead us to markedly underestimate the proportion mediated (indirect effect). By contrast, misclassification of a binary exposure had only a modest effect on the proportion mediated. This led the authors to argue that “accurate classification of the mediator is essential and more important than accurate classification of the exposure” when the inferential goal of an analysis is to estimate the proportion mediated. Fortunately, methods have been developed for evaluating bias due to errors in the measurement of the mediator (VanderWeele, Valeri, and Ogburn 2012; le Cessie et al. 2012; Valeri, Lin, and VanderWeele 2014; Valeri and VanderWeele 2014).

FIGURE 16.6 CAUSAL DIAGRAM ILLUSTRATING A NON-DIFFERENTIAL ERROR IN THE MEASUREMENT OF THE MEDIATOR
M* is an imperfectly measured version of the true value of M, with the error term unaffected by the exposure or outcome.
In this section we present a simple strategy for assessing the sensitivity of direct and indirect effect estimates to non-differential error in the measurement of the mediator. This scenario is shown by Figure 16.6, where  is an imperfectly measured version of the true value of
is an imperfectly measured version of the true value of  , with the error term unaffected by the exposure or outcome. As implied by the causal diagram, proceeding with our mediation analysis using
, with the error term unaffected by the exposure or outcome. As implied by the causal diagram, proceeding with our mediation analysis using  instead of
instead of  would result in biased estimation because conditioning on
would result in biased estimation because conditioning on  instead of
instead of  will not completely block the path between
will not completely block the path between  and
and  . Intuitively, a classic non-differential measurement error thus generally biases mediated effects toward the null (VanderWeele, Valeri, and Ogburn 2012). In addition to assuming that the error is non-differential, we will also assume that there is no interaction between the exposure and mediator. Given these conditions, we can follow the procedures outlined by le Cessie and colleagues (2012) for correcting the direct effect, as well as the extension by VanderWeele and colleagues (2012) for indirect effects. First, we fit two models including the mismeasured mediator: (1) a model for the controlled direct effect that regresses the outcome on the exposure, mediator, and time-fixed covariates, shown here on the risk ratio scale for a binary outcome, and (2) a model regressing the mediator on the exposure and time-fixed covariates, shown here as a linear model for a continuous mediator:
. Intuitively, a classic non-differential measurement error thus generally biases mediated effects toward the null (VanderWeele, Valeri, and Ogburn 2012). In addition to assuming that the error is non-differential, we will also assume that there is no interaction between the exposure and mediator. Given these conditions, we can follow the procedures outlined by le Cessie and colleagues (2012) for correcting the direct effect, as well as the extension by VanderWeele and colleagues (2012) for indirect effects. First, we fit two models including the mismeasured mediator: (1) a model for the controlled direct effect that regresses the outcome on the exposure, mediator, and time-fixed covariates, shown here on the risk ratio scale for a binary outcome, and (2) a model regressing the mediator on the exposure and time-fixed covariates, shown here as a linear model for a continuous mediator:


These models are similar to the first models that we presented for estimating direct and indirect effects using the product method, with the exception that they account for baseline covariates  , which are assumed to control for confounding of the direct and indirect effects. As you recall, the coefficient for the exposure in a model that included the mediator was used to estimate the direct effect and the indirect effect was given by the product of two quantities: the effect of the treatment on the mediator and the effect of the mediator on the outcome. Second, we must presuppose the proportion of the variance in the mediator
, which are assumed to control for confounding of the direct and indirect effects. As you recall, the coefficient for the exposure in a model that included the mediator was used to estimate the direct effect and the indirect effect was given by the product of two quantities: the effect of the treatment on the mediator and the effect of the mediator on the outcome. Second, we must presuppose the proportion of the variance in the mediator  that is explained by the true value of
that is explained by the true value of  conditional on
conditional on  and
and  . This parameter,
. This parameter,  , commonly called the reliability ratio, can be varied in the sensitivity analysis to evaluate the impact of different magnitudes of measurement error. Third, we can calculate corrected coefficients for the parameters used to estimate controlled and natural direct effects using our specification of
, commonly called the reliability ratio, can be varied in the sensitivity analysis to evaluate the impact of different magnitudes of measurement error. Third, we can calculate corrected coefficients for the parameters used to estimate controlled and natural direct effects using our specification of  together with the estimates from Models (6) and (7):
together with the estimates from Models (6) and (7):

and

The controlled and natural direct effect risk ratios, assumed to be equivalent if there is no exposure–mediator interaction, are given by  . Under these conditions,
. Under these conditions,  and Models (6) and (7) can also be used to obtain the corrected NIE, which is given by
and Models (6) and (7) can also be used to obtain the corrected NIE, which is given by  . Although we presented a simplified scenario with a continuous mediator and no exposure–mediator interaction, the correction methods presented can be extended to accommodate misclassification of a binary mediator and addition of exposure–mediator interactions (Valeri, Lin, and VanderWeele 2014; Valeri and VanderWeele 2014).
. Although we presented a simplified scenario with a continuous mediator and no exposure–mediator interaction, the correction methods presented can be extended to accommodate misclassification of a binary mediator and addition of exposure–mediator interactions (Valeri, Lin, and VanderWeele 2014; Valeri and VanderWeele 2014).
This approach was illustrated by a recent study evaluating the extent to which health behaviors mediated the association between adult SES and all-cause mortality in the United States (Nandi, Glymour, and Subramanian 2014). Overall, analyses showed that smoking, alcohol consumption, and physical activity collectively explained more than two-thirds of the excess relative risk of mortality comparing the most-disadvantaged with the least-disadvantaged quartile of SES. However, the mediating health behaviors were measured based on self-report and subject to measurement error. Thus, the authors evaluated the sensitivity of results to non-differential error in the measurement of health behaviors, particularly physical activity, using the approach outlined above. Estimates of the observed CDE of adult SES not mediated by physical inactivity assuming no measurement error (reliability ratio of 1.0) were compared to corrected CDEs at various reliability ratios from 0.9 to 0.5. As expected, results showed that errors in the measurement of physical activity resulted in an overestimation of the CDE (and underestimation of the proportion of the total effect mediated). The sensitivity analyses demonstrated that the magnitude of the bias in the CDE was minimal for reliability ratios greater than 0.8; however, as the reliability ratio dropped below 0.8, the observed CDE assuming no measurement error became an increasingly greater overestimate of the corrected CDE.
Other work has considered the biases of direct and indirect effect estimators in the presence of non-differential measurement error of the exposure or the outcome. For non-differential measurement error of the outcome, both direct and indirect effects are unbiased for continuous outcomes, and both are biased toward the null for dichotomous outcomes (Jiang and VanderWeele 2015). Drawing intuitive conclusions about the direction of the bias of direct and indirect effects is thus relatively straightforward in the context of measurement error in the outcome. For nondifferential measurement error of the exposure, in the absence of exposure-mediator interaction, the natural direct effect is biased toward the null, but the indirect effect can be biased in either direction (Jiang and VanderWeele 2015). The intuition for the indirect effect is that measurement error of the exposure will tend to weaken the exposure–mediator association, but will strengthen the mediator-outcome association. Which of these two consequences is more substantial will determine whether the indirect effect is biased toward or away from the null. Correction methods for direct and indirect effect estimators in the presence of non-differential measurement error of the exposure and outcome are also available (Jiang and VanderWeele 2015).
Other Topics
Although we have considered a number of important topics here, a very large methodological literature has developed on mediation from a causal inference perspective. Methods are now available for time-to-event outcomes (Lang and Hansen 2011; VanderWeele 2011; Valeri and VanderWeele 2015), for time-varying exposures and mediators (VanderWeele and Tchetgen Tchetgen 2014), for sensitivity analysis using data from two trials (VanderWeele 2015), for path-specific effects (VanderWeele, Vansteelandt, and Robins 2014), and for decomposing a total effect into four components that simultaneously assess mediation and interaction specifically that due to just mediation, that due to just interaction, that due to both mediation and interaction, and that due to neither (VanderWeele 2014). We can of course not cover all of these topics here, and the interested reader is referred to the book-length coverage of mediation for further discussion of these topics (VanderWeele 2015).
Conclusions
There is a longstanding debate in social epidemiology about whether certain social factors, such as SES, represent “fundamental causes” with persistent effects on population health, in spite of changes in the mechanisms hypothesized to explain them (Link and Phelan 1995). In other words, if we intervened to set or change the distribution of a particular mediator linking SES to health, would we see an attendant change in the magnitude of the social inequality? Or, are the effects of fundamental causes inescapably reproduced over time? In many ways, this has been an intriguing theoretical debate. However, the application of contemporary mediation methods may also shed some empirical light on this topic as well. As we discussed, the counterfactual approach to mediation analysis has elucidated the conditions necessary for a causal interpretation of direct and indirect effects. It has also facilitated the estimation of direct and indirect effects even in setting with interactions and non-linearities. We have also outlined several extensions of these methods to address challenges common and salient to the study of social determinants of health, as well as sensitivity analyses for assessing the robustness of our conclusions. Through the thoughtful application of these methods we have the potential to promote a practicable and “consequentialist” social epidemiology (Nandi and Harper 2014) that, through the identification of relevant mechanisms, might create additional opportunities for improving health and reducing inequality.
References
- Albert, J.M. (2012) Mediation analysis for nonlinear models with confounding. Epidemiology (Cambridge, Mass.), 23 (6), 879.
- Avin, C., Shpitser, I., and Pearl, J. (2005) Identifiability of path-specific effects. Department of Statistics, UCLA, Los Angeles, CA.
- Barker, D.J. (1995) Fetal origins of coronary heart disease. BMJ: British Medical Journal, 311 (6998), 171.
- Barker, D.J. (2004) The developmental origins of well-being. Philosophical Transactions of the Royal Society of London, Series B, Biological Sciences, 1359–1366.
- Baron R.M. and Kenny D.A. (1986). The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51, 1173–1182.
- Bertrand, M. and Mullainathan, S. (2004) Are Emily and Greg more employable than Lakisha and Jamal? A field experiment on labor market discrimination. The American Economic Review, 94 (4), 991–1013.
- Blakely, T., McKenzie, S., and Carter, K. (2013) Misclassification of the mediator matters when estimating indirect effects. Journal of Epidemiology and Community Health, 67 (5), 458–466.
- Braun, L. (2002) Race, ethnicity, and health: can genetics explain disparities? Perspectives in Biology and Medicine, 45 (2),159–174.
- Cole, S.R. and Hernán, M.A. (2008) Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology, 168 (6), 656–664.
- Cooper, R. (1984) A note on the biologic concept of race and its application in epidemiologic research. American Heart Journal, 108 (3), 715–723.
- Ding, P. and VanderWeele, T.J. (2016) Sharp sensitivity bounds for mediation under unmeasured mediator-outcome confounding. Biometrika, 103 (2), 483–490.
- Dressler, W.W., Oths, K.S., and Gravlee, C.C. (2005) Race and ethnicity in public health research: models to explain health disparities. Annual Review of Anthropology, 34, 231–252.
- Galea, S., Blaney, S., Nandi, A., et al. (2007) Explaining racial disparities in incidence of and survival from out-of-hospital cardiac arrest. American Journal of Epidemiology, 166 (5), 534–543.
- Galobardes, B., Smith, G.D., and Lynch, J.W. (2006) Systematic review of the influence of childhood socioeconomic circumstances on risk for cardiovascular disease in adulthood. Annals of Epidemiology, 16 (2), 91–104.
- Gebreab, S.Y., Diez-Roux, A.V., Hickson, D.A., et al. (2012) The contribution of stress to the social patterning of clinical and subclinical CVD risk factors in African Americans: The Jackson Heart Study. Social Science and Medicine, 75 (9), 1697–1707.
- Geronimus, A.T. (1991) The weathering hypothesis and the health of African-American women and infants: evidence and speculations. Ethnology and Disease, 2 (3), 207–221.
- Glass, T.A. and McAtee, M.J. (2006) Behavioral science at the crossroads in public health: extending horizons, envisioning the future. Social Science and Medicine, 62 (7), 1650–1671.
- Hafeman, D.M. (2011) Confounding of indirect effects: a sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. American Journal of Epidemiology, 174 (6), 710–717.
- Hafeman, D.M. and Schwartz, S. (2009) Opening the black box: a motivation for the assessment of mediation. International Journal of Epidemiology, 38 (3), 838–845.
- Hayward, M.D., Miles, T.P., Crimmins, E.M., and Yang, Y. (2000) The significance of socioeconomic status in explaining the racial gap in chronic health conditions. American Sociology Review, 910–930.
- Hernán, M.A., Brumback, B., and Robins, J.M. (2000) Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology, 11 (5), 561–570.
- Holland, P.W. (1986) Statistics and causal inference. Journal of the American Statistical Association, 81 (396), 945–960.
- House, J.S. (2002) Understanding social factors and inequalities in health: 20th century progress and 21st century prospects. Journal of Health and Social Behavior, 43 (2), 125–142.
- Imai, K., Keele, L., and Tingley, D. (2010) A general approach to causal mediation analysis. Psychological Methods, 15 (4), 309.
- Imai, K. and Yamamoto, T. (2013) Identification and sensitivity analysis for multiple causal mechanisms: revisiting evidence from framing experiments. Political Analysis, 21 (2), 141–171.
- Jiang, Z. and VanderWeele, T.J. (2015) Causal mediation analysis in the presence of a mismeasured outcome. Epidemiology, 26 (1), e8–e9.
- Jiang, Z. and VanderWeele, T.J. (2015) Causal mediation analysis in the presence of a mismeasured outcome. Epidemiology, 26 (1), e8–e9.
- Joffe, M.M., Small, D., and Hsu, C.-Y. (2007) Defining and estimating intervention effects for groups that will develop an auxiliary outcome. Statistical Science, 22 (1), 74–97.
- Jones, C.P., LaVeist, T.A., and Lillie-Blanton, M. (1991) “Race” in the epidemiologic literature: an examination of the American Journal of Epidemiology, 1921–1991. American Journal of Epidemiology, 134 (10), 1079–1084.
- Kaplan, G.A. (2004) What's wrong with social epidemiology, and how can we make it better? Epidemiological Reviews, 26 (1), 124–135.
- Kaufman, J.S. (2001) Commentary: social epidemiology? Way! International Journal of Epidemiology, 30 (1), 48–49.
- Kaufman, J.S. (2008) Epidemiologic analysis of racial/ethnic disparities: some fundamental issues and a cautionary example. Society of Science and Medicine, 66 (8), 1659–1669.
- Kaufman, J.S. (2009) Commentary: gilding the black box. International Journal of Epidemiology, 38 (3), 845–847.
- Kaufman, J.S. (2010a) Invited commentary: decomposing with a lot of supposing. American Journal of Epidemiology, 172 (12), 1349–1351.
- Kaufman, J.S. (2010b) Marginalia: comparing adjusted effect measures. Epidemiology, 21 (4), 490–493.
- Kaufman, J.S., and Cooper, R.S. (1999) Seeking causal explanations in social epidemiology. American Journal of Epidemiology, 150 (2), 113–120.
- Kaufman, J.S. and Cooper, R.S. (2001) Commentary: considerations for use of racial/ethnic classification in etiologic research. American Journal of Epidemiology, 154 (4), 291–298.
- Kaufman, J.S., Cooper, R.S., and McGee, D.L. (1997) Socioeconomic status and health in blacks and whites: the problem of residual confounding and the resiliency of race. Epidemiology, 621–628.
- Kaufman, J.S. and Hall, S.A. (2003) The slavery hypertension hypothesis: dissemination and appeal of a modern race theory. Epidemiology, 14 (1), 111–118.
- Kaufman, J.S., Kaufman, S., and Poole, C. (2003) Causal inference from randomized trials in social epidemiology. Social Science and Medicine, 57 (12), 2397–2409.
- Kaufman, J.S., MacLehose, R.F., and Kaufman, S. (2004) A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation. Epidemiological Perspectives and Innovation, 1 (1), 4.
- Krieger, N. (2005) Stormy weather: race, gene expression, and the science of health disparities. American Journal of Public Health, 95 (12), 2155–2160.
- Lange, T. and Hansen, J.V. (2011) Direct and indirect effects in a survival context. Epidemiology, 22 (4), 575–581.
- Lantz, P.M., Golberstein, E., House, J.S., and Morenoff, J. (2010) Socioeconomic and behavioral risk factors for mortality in a national 19-year prospective study of U.S. adults. Social Science and Medicine, 70 (10), 1558–1566.
- Lantz, P.M., House, J.S., Lepkowski, J.M., et al. (1998) Socioeconomic factors, health behaviors, and mortality: results from a nationally representative prospective study of US adults. Journal of the American Medical Association, 279 (21), 1703–1708.
- le Cessie, S., Debeij, J., Rosendaal, F.R., et al. (2012) Quantification of bias in direct effects estimates due to different types of measurement error in the mediator. Epidemiology, 23 (4), 551–560.
- Leroy, J.L., García-Guerra, A., García, R., et al. (2008) The Oportunidades program increases the linear growth of children enrolled at young ages in urban Mexico. The Journal of Nutrition, 138 (4), 793–798.
- Link, B.G. and Phelan, J. (1995) Social conditions as fundamental causes of disease. Journal of Health and Social Behavior, 80–94.
- Lynch, J. (2000) Social epidemiology: some observations about the past, present and future. Australasian Epidemiologist, 7 (3), 7.
- McEwen, B.S. (2012) Brain on stress: how the social environment gets under the skin. Proceedings of the National Academy of Sciences, 109 (Suppl. 2), 17180–17185.
- Naimi, A.I., Kaufman, J.S., and MacLehose, R.F. (2014) Mediation misgivings: ambiguous clinical and public health interpretations of natural direct and indirect effects. International Journal of Epidemiology, 43 (5), 1656–1661.
- Nandi, A., Glymour, M.M., and Subramanian, S. (2014) Association among socioeconomic status, health behaviors, and all-cause mortality in the United States. Epidemiology, 25 (2), 170–177.
- Nandi, A., Glymour, M.M., Kawachi, I., and VanderWeele, T.J. (2012) Using marginal structural models to estimate the direct effect of adverse childhood social conditions on onset of heart disease, diabetes, and stroke. Epidemiology, 23 (2) 223–232.
- Nandi, A. and Harper, S. (2014) How consequential is social epidemiology? A review of recent evidence. Current Epidemiology Reports, 1–10.
- Owusu-Addo, E. and Cross, R. (2014) The impact of conditional cash transfers on child health in low- and middle-income countries: a systematic review. International Journal of Public Health, 1–10.
- Ozer, E.J., Fernald, L.C., Weber, A., et al. (2011) Does alleviating poverty affect mothers' depressive symptoms? A quasi-experimental investigation of Mexico's Oportunidades programme. International Journal of Epidemiology, 40 (6), 1565–1576.
- Paneth, N. and Susser, M. (1995) Early origin of coronary heart disease (the “Barker hypothesis”). BMJ: British Medical Journal, 310 (6977), 411.
- Pearl, J. (2001) Direct and indirect effects, in Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, Morgan Kaufmann Publishers Inc., San Francisco, CA, pp. 411–420.
- Pollitt, R.A., Rose, K.M., and Kaufman, J.S. (2005) Evaluating the evidence for models of life course socioeconomic factors and cardiovascular outcomes: a systematic review. BMC Public Health, 5, 7.
- Poole, C. and Rothman, K.J. (1998) Our conscientious objection to the epidemiology wars. Journal of Epidemiology and Community Health, 52 (10), 613.
- Preacher, K.J. (2015) Advances in mediation analysis: a survey and synthesis of new developments. Annual Review Psychology, 66, 825–852.
- Rivera, J.A., Sotres-Alvarez, D., Habicht, J.-P., et al. (2004) Impact of the Mexican program for education, health, and nutrition (Progresa) on rates of growth and anemia in infants and young children: a randomized effectiveness study. Journal of the American Medical Association, 291 (21), 2563–2570.
- Robins, J.M. (2003) Semantics of causal DAG models and the identification of direct and indirect effects, in Highly Structured Stochastic Systems (eds P. Green, N. I-ljort, and S. Richardson), Oxford University Press, New York, pp. 70–78.
- Robins, J.M. and Greenland, S. (1992) Identifiability and exchangeability for direct and indirect effects. Epidemiology, 3 (2), 143–155.
- Robins, J.M., Hernán, M.A., and Brumback, B. (2000) Marginal structural models and causal inference in epidemiology. Epidemiology, 11 (5), 550–560.
- Rothman, K.J., Adami, H.-O., and Ttichopoulos, D. (1998) Should the mission of epidemiology include the eradication of poverty? The Lancet, 352 (9130), 810–813.
- Smith, G.D., Neaton, J.D., Wentworth, D., et al. (1998) Mortality differences between black and white men in the USA: contribution of income and other risk factors among men screened for the MRFIT. The Lancet, 351 (9107), 934–939.
- Stolley, P.D. (1999) Race in epidemiology. International Journal of Health Service, 29 (4), 905–909.
- Stringhini, S., Dugravot, A., Shipley, M., et al. (2011) Health behaviours, socioeconomic status, and mortality: further analyses of the British Whitehall II and the French GAZEL prospective cohorts. PLoS Medicine, 8 (2), e1000419.
- Stringhini, S., Sabia, S., Shipley, M., et al. (2010) Association of socioeconomic position with health behaviors and mortality. Journal of the American Medical Association, 303 (12), 1159–1166.
- Stringhini, S., Tabak, A.G., Akbaraly, T.N., et al. (2012) Contribution of modifiable risk factors to social inequalities in type 2 diabetes: prospective Whitehall II cohort study. British Medical Journal, 345, e5452.
- Susser, M. and Susser, E. (1996) Choosing a future for epidemiology: I. Eras and paradigms. American Journal of Public Health, 86 (5), 668–673.
- Suzuki, E., Evans, D., Chaix, B., and VanderWeele, T.J. (2014) On the “proportion eliminated” for risk differences versus excess relative risks. Epidemiology, 25 (2), 309–310.
- Ten Have, T.R. and Joffe, M.M. (2012) A review of causal estimation of effects in mediation analyses. Statistical Methods in Medical Research, 21 (1), 77–107.
- Valeri, L., Lin, X., and VanderWeele, T.J. (2014) Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model. Statistics in Medicine, 33 (28), 4875–4890.
- Valeri, L. and VanderWeele, T.J. (2013) Mediation analysis allowing for exposure–mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychological Methods, 18 (2), 137.
- Valeri, L., and Vanderweele, T.J. (2014) The estimation of direct and indirect causal effects in the presence of misclassified binary mediator. Biostatistics, 15 (3), 498–512.
- Valeri, L. and VanderWeele, T.J. (2015) SAS macro for causal mediation analysis with survival data. Epidemiology, 26 (2), e23–e24.
- VanderWeele, T.J. (2009a) Mediation and mechanism. European Journal of Epidemiology, 24 (5), 217–224.
- VanderWeele, T.J. (2009b) Marginal structural models for the estimation of direct and indirect effects. Epidemiology, 20 (1), 18–26.
- VanderWeele, T.J. (2010) Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology (Cambridge, Mass.), 21 (4), 540.
- VanderWeele, T.J. (2011) Causal mediation analysis with survival data. Epidemiology (Cambridge, Mass.), 22 (4), 582.
- VanderWeele, T.J. (2013) Policy-relevant proportions for direct effects. Epidemiology, 24 (1), 175–176.
- VanderWeele, T.J. (2014) A unification of mediation and interaction: a 4-way decomposition. Epidemiology, 25 (5), 749–761.
- VanderWeele, T.J. (2015) Explanation in Causal Inference: Methods for Mediation and Interaction, Oxford University Press.
- VanderWeele, T.J. and Robinson, W.R. (2014) On the causal interpretation of race in regressions adjusting for confounding and mediating variables. Epidemiology, 25 (4), 473–484.
- VanderWeele, T.J. and Tchetgen Tchetgen, E. (2014) Mediation analysis with time-varying exposures and mediators. Harvard University Biostatistics Working Paper Series (Working Paper 168).
- VanderWeele, T.J., Valeri, L., and Ogburn, E.L. (2012) The role of measurement error and misclassification in mediation analysis: mediation and measurement error. Epidemiology, 23 (4), 561–564.
- VanderWeele, T.J. and Vansteelandt, S. (2009) Conceptual issues concerning mediation, interventions and composition. Statistics and Its Interface, 2, 457–468.
- VanderWeele, T.J. and Vansteelandt, S. (2010) Odds ratios for mediation analysis for a dichotomous outcome. American Journal of Epidemiology, 172 (12), 1339–1348.
- VanderWeele, T.J. and Vansteelandt, S. (2013) Mediation analysis with multiple mediators. Epidemiologic Methods, 2 (1), 95–115.
- VanderWeele, T.J., Vansteelandt, S., and Robins, J.M. (2014) Effect decomposition in the presence of an exposure-induced mediator-outcome confounder. Epidemiology (Cambridge, Mass.), 25 (2), 300.
- Vansteelandt, S. (2009) Estimating direct effects in cohort and case–control studies. Epidemiology, 20 (6), 851–860.
- Williams, D.R. (1997) Race and health: basic questions, emerging directions. Annals of Epidemiology, 7 (5), 322–333.
- Zheng, W. and van der Laan, M.J. (2012) Targeted maximum likelihood estimation of natural direct effects. The International Journal of Biostatistics, 8 (1), 1–40.
- Zielhuis, G.A. and Kiemeney, L. (2001) Social epidemiology? No way. International Journal of Epidemiology, 30 (1), 43.