CHAPTER NINETEEN
NATURAL EXPERIMENTS AND INSTRUMENTAL VARIABLES ANALYSES IN SOCIAL EPIDEMIOLOGY
M. Maria Glymour, Stefan Walter and Eric J. Tchetgen Tchetgen
“Alternatives to the experiment will always be needed, and a key issue is to identify which kinds of observational studies are most likely to generate unbiased results.”
Cook, Shadish, et al. (2008)
Social epidemiology is of little use if it cannot guide us in how to improve population health. Such guidance depends on understanding the causal structures that harm the health of people exposed to social disadvantage. Although evaluating the effects of social conditions on health is a central task in social epidemiology, the core analytic tools of our discipline are often insufficient; we may not be able to conclusively estimate the magnitude of health effects or even to determine whether important social exposures have any health effects at all. Social epidemiology largely inherited the methodological techniques of the parent discipline of epidemiology, and the usual approach to estimating treatment effects from observational data involves assessing the observed association between the exposure and outcome of interest, adjusting or stratifying to account for likely confounders.
Instrumental variables (IV) analyses provide an alternative to this approach when data from either researcher-randomized experiments or natural experiments are available. IV analyses depend strongly on the assumption that the data were generated by a valid experiment, that is, that subjects were effectively randomized, even if the randomization process was not initiated by the researcher and adherence to random assignment was low. For many of the exposures of interest in social epidemiology, opportunities to intentionally randomize are few and far between, but natural experiments may be more common. Social determinants of health, such as schooling, poverty, employment, and even marriage, fertility, and social connections, are influenced by administrative policies, state and local laws, and other forces external to the individual (Currie 1995; Angrist and Krueger 2001). These policies sometimes create natural or quasi-experiments in which an individual's probability of exposure to a particular social condition is influenced by a policy that is uncorrelated with the individual's personal characteristics or other factors that would affect the outcome of interest. Such natural experiments—in which a random process influences the probability of exposure but this random event is not instigated by researchers—provide a powerful approach to test causal claims.
We have organized this chapter to give a broad intuition first and provide greater detail in subsequent sections. The first section discusses the motivations for IV analyses. We then provide a brief introduction to the assumptions required to interpret IV estimates as causal parameters, and describe approaches to implementing IV analyses. The next section frames natural experiments and IV estimates in terms of the general problem of causal inference, and walks through a simple numerical example comparing the IV estimate to other parameters. We briefly introduce applications with binary and survival outcomes. We then discuss a few examples of specific instruments that seem especially clever or potentially relevant to social epidemiology. The concluding sections address common points of confusion regarding IV analyses and reiterate the limitations of IV. Much of the description below is informal, focusing on intuition. More formal introductions to IV are available in several excellent articles published elsewhere (Angrist et al. 1996; Greenland 2000; Angrist and Krueger 2001; Pearl 2009). IV is also discussed in standard econometrics textbooks (Kennedy 2008; Greene 2000; Wooldridge 2016).
Motivations for Using Instrumental Variables in Social Epidemiology Research
We recognize three related motivations for using IV approaches in social epidemiology. The first is to estimate the causal effect of treatment, rather than the intent to treat (ITT) effect (defined below). A second major motivation for IV analyses is to circumvent the problem of unmeasured confounders when it seems unlikely, or at least uncertain, that all of the confounding bias between the exposure and outcome can be addressed using regression adjustment or related methods. A third motivation for using IV analyses in social epidemiology is that the IV effect estimate may correspond to a parameter of substantive interest that cannot be directly estimated in conventional models, such as the effect of treatment differences induced by changes in the IV. IV analyses, although often used in natural or quasi-experimental settings, are also relevant in researcher randomized trials, such as the Moving To Opportunity (MTO) experiment (Ludwig et al. 2011).
Estimating the Effect of Being Treated Instead of the Effect of Being Randomized
Randomized trials are considered to provide the most convincing evidence for causal effects (Byar et al. 1976; Abel and Koch 1999; DeMets 2002). ITT analyses—in which the outcomes of those assigned to a treatment group are contrasted with the outcomes of those assigned to a comparison group—are the standard analytical method for data from randomized trials. Because of non-compliance, the ITT estimates do not estimate the effect of receiving the treatment (versus the comparison) on the outcome. Instead, ITT analysis estimates the effect of being assigned to receive the treatment on the subjects' health.
If the ITT effect estimate in a valid RCT is significantly positive (beneficial), this indicates that the treatment improves outcomes for at least some individuals in the population, but it does not reveal the magnitude of that relationship. It is often critical to learn whether the treatment effect is large or small. For example, the MTO trial randomized families residing in public housing developments to either receive a housing voucher to subsidize rental of a private market apartment or to receive no such voucher (and remain in public housing). Of those offered a voucher, only about half took advantage of the offer and moved to a private market rental. At 4–7 years after randomization, girls aged 12–17 in families who were randomized to receive a voucher were 12 percentage points less likely to meet criterion for psychological distress (measured with the Kessler 6 inventory). Accounting for non-adherence with an IV estimate indicated the impact of moving to a private market apartment for girls was a 23 percentage point reduction in the probability of psychological distress (Osypuk et al. 2012).
Several alternatives to the ITT effect estimate rely on defining the exposure variable in the analysis to be the treatment each participant received (regardless of their randomly assigned treatment). These approaches reintroduce confounding if there are common causes of treatment take-up and the outcome. For example, directly comparing the treated to the untreated (sometimes called as-treated analysis) or comparing compliers in the treatment arm to compliers in the control arm (per-protocol analysis) are well-known and long-rejected options (Hennekens and Buring 1987; Weiss 1998). IV analyses, however, can, under certain assumptions, provide an unconfounded estimate of the effect of treatment even if the association between treatment taken and the outcome is subject to unmeasured confounding. IV analyses do not directly compare treated to untreated people. IV analyses therefore avoid conditioning on post-randomization information to define the exposure variable. A caveat, explained in more detail below, is that if the effect of treatment is not the same for everyone in the population, IV analyses may not provide the average treatment effect for the whole population.
Avoiding Bias Due to Confounding in Observational Data Analyses
In the absence of randomized trial data, epidemiologists typically attempt to draw causal inferences from observational data by adjusting for common causes (confounders) of the exposure and the outcome. Such adjustment may take the form of regression adjustment (i.e., conditioning on the confounder in a regression model), standardization, stratification, restriction, or propensity score matching. These approaches have a common goal: identify an observed set of covariates such that, within strata of the covariates, the statistical association between treatment and outcome can be entirely attributed to the causal effect of the former on the latter (Greenland et al. 1999). The principal limitation of this approach is that such a set of covariates is rarely fully observed. Even if all common causes of the exposure and the outcome are known at a conceptual level, have they been well measured? Is the regression model incorporating such confounders correctly specified? If not, residual confounding could remain a threat to validity. Although recent meta-analyses suggest observational designs evaluating clinical interventions are not systematically biased compared to RCTs (Anglemyer et al. 2014), findings from observational studies often differ substantially from what is achieved with RCTs (McCarrey and Resnick 2015), and the problem may be especially acute in social epidemiology (Berkman 2009). With a valid instrument, IV analyses can sometimes be used to estimate the effect of the treatment even if important confounders of the treatment-outcome relation are not accounted for.
Estimating Complier-Specific Treatment Effects
The health effects of most exposures vary across individuals. Prior evidence suggests the effects of social or psychosocial interventions may differ by race, sex, or other background characteristics (Welch 1973; Link et al. 1976; Unger et al. 1999; Campbell et al. 2002; Kaufman et al. 2003; Liebman et al. 2004; Farmer and Ferraro 2005). When treatment effects are heterogeneous, the effect on a specific subgroup may be of greater interest than the average effect across the whole population. Consider a medical treatment, for example, hypertension medication. Patients with extremely high blood pressure probably stand the most to gain from medication, and they are thus the most likely to be treated. Patients with low blood pressure would not be treated. Those patients with borderline hypertension may or may not receive treatment, and it is the effect of medication on these “gray area” patients that would be the most useful for informing future medical practice. If some physicians tend to treat more aggressively than others, the prescribing patterns of the clinical provider might serve as an IV for the effect of treatment on these patients. The IV estimate then pertains specifically to that subgroup.
The fact that IV provides an estimate specific to a subgroup of the population can be an advantage or a disadvantage of IV analyses, but we suspect that it often is an advantage in analyses of social exposures. If we are analyzing the effects of incarceration on mental health, for example, the most relevant group is probably people who may or may not be incarcerated, that is, the individuals with moderate crimes or those who seem unlikely to reoffend. It is not as interesting to establish that incarceration harms the mental health of individuals whose crimes were so heinous that incarceration is inevitable. Evidence on the mental health effects among individuals with trivial infractions, who are unlikely to be incarcerated, is similarly irrelevant.
A closely related point is that under a certain monotonicity assumption described below, IV effect estimates pertain to the treatment as delivered to the compliers. In conventional observational analyses, many variations on the treatment may be analyzed as if they comprised a specific, well-defined treatment. For example, the effects of income may differ substantially based on how the extra money was delivered (e.g., via wages, tax credits, or lottery winnings). Compared to conventional observational studies, with IV analyses, we typically know much more about how the exposure in question was delivered, because this is implicit in the definition of the instrument. As a result of the specificity of the effect estimate, IV effect estimates will often be of greater substantive interest than typical observational effect estimates. For the same reason, the exposure evaluated by an IV analysis may be more likely to fulfill the consistency assumption (discussed later in the chapter).
Assumptions and Estimation in IV Analyses
To explain the assumptions necessary for IV analyses, it is helpful to distinguish between two goals: testing the null hypothesis that treatment has no effect on outcome, and estimating the magnitude of the effect of treatment on the outcome. The typical account of IV invokes assumptions so that the IV estimate can be interpreted as the average effect of receiving treatment on those individuals who received the treatment as a result of the value of the instrumental variable. This interpretation rests on the assumption that the instrument is valid and monotonically related to the treatment.1 However, if the goal of the analysis is merely to test the null hypothesis that treatment has no effect on the outcome, IV analyses require fewer assumptions.
Assumptions Necessary to Use the IV to Test the Null
The assumptions for a valid instrument can be concisely expressed using a causal directed acyclic graph (DAG) (Pearl 2009) (see Chapter 18 for an introduction to DAGs). Figure 19.1A shows the basic causal structure under which we would be interested in calculating an IV effect estimate. Because this is a causal DAG, all common prior causes of two or more variables in the DAG are also shown in the DAG (i.e., there are no sources of confounding that do not appear in the DAG). We are interested in the effect of X on Y, but the relation is confounded by an unmeasured common prior cause U. Z is a measured variable that affects X, but has no direct effect on Y (an assumption sometimes called the exclusion restriction) and no prior causes in common with Y. We can imagine the scenario in Figure 19.1A as a randomized controlled trial (RCT), in which Z is a random assignment to treatment, X represents receiving the treatment, and Y is the outcome of interest. In IV discussions, the variable X is often called the “endogenous variable”; we use “endogenous variable” and “treatment” or “exposure” interchangeably.
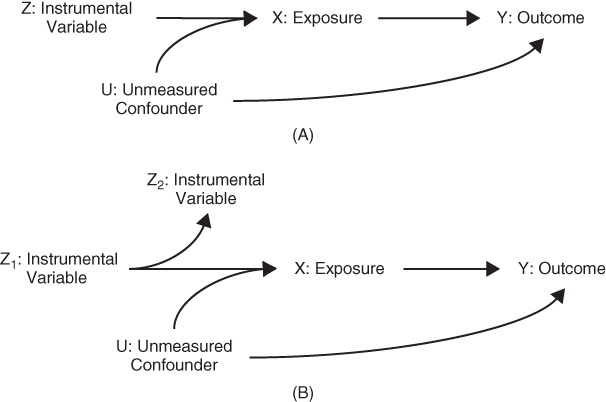
FIGURE 19.1 CAUSAL DIAGRAMS DEPICTING A VALID INSTRUMENT
A valid instrument must be associated with the predictor of interest and all unblocked paths between the instrumental variable and the outcome must pass through the exposure of interest (also called the endogenous variable). (A) The instrumental variable directly affects exposure but has no other effect on the outcome. (B) Both Z1 and Z2 are valid intrumental variables to estimate the effect of X on Y; Z2 is statistically associated with the exposure and all of the common causes of Z2 and the outcome operate via the exposure.
Under the assumptions shown in Figure 19.1A, if Z and Y are statistically related, it must be because Z affects X and X in turn affects Y (setting aside the possibility of chance). The traditional account of IV analysis defines the instrument as a variable that directly affects exposure. Recent applications of IV frequently use variables that do not directly affect exposure but are correlates of valid IVs that affect exposure, as in Figure 19.1B. This twist is best expressed by formalizing the assumptions for a valid IV based on paths in the causal DAG.
Given a causal DAG, we say Z is a valid IV for the effect of X on Y if Z and X are statistically dependent (associated) and if every unblocked path connecting Z and Y contains an arrow pointing into X.
In the following situations, Z would not be a valid instrument:
- If there were a path directly from Z to Y (Figure 19.2A).
- If there were a path directly from Z to U (Figure 19.2B).
- If there were a path from U to Z (Figure 19.2C).
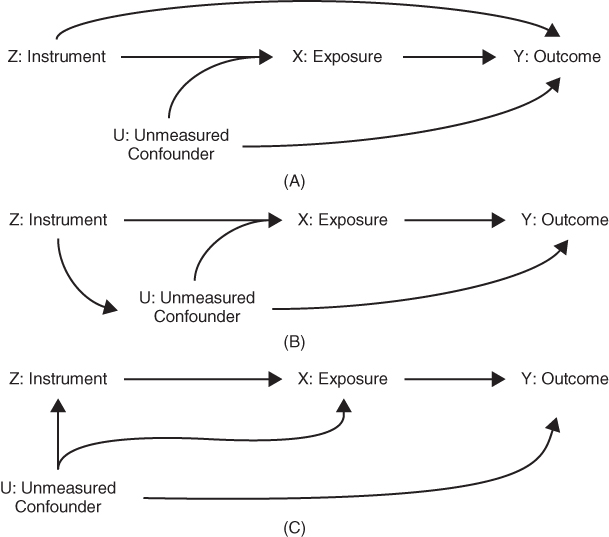
FIGURE 19.2 CAUSAL DIAGRAMS DEPICTING VARIABLES THAT ARE NOT VALID INSTRUMENTS
(A) If there is a direct path from Z to Y that does not pass through X, then Z is not a valid instrument for the effect of X on Y. (B) If there is a path from Z to a common prior cause of X and Y, then Z is not a valid instrument for the effect of X on Y. (C) If there is a prior cause of Z that directly affects Y (not exclusively mediated by X), then Z is not a valid instrument for the effect of X on Y.
Each of these scenarios (depicted graphically in Figures 19.2A, B, and C) would invalidate the instrument because the statistical relation between Z and Y would not arise exclusively due to the causal effect of X on Y. In some cases, the assumption for a valid instrument might be met only if we condition on (control for) some set of covariates. Such conditionally valid instruments are quite common but entail a few special considerations in the analysis. Note that a valid IV for the effect of X on Y is not a confounder of the relation between X and Y. If Z confounds the relation between X and Y, for example, because it is a common prior cause of X and Y, as in Figure 19.2A, then Z is not a valid instrument. Similarly, a variable that is itself affected by X is not a valid IV to estimate the effects of X.
Additional Assumptions to Estimate the Magnitude of the Effect of Treatment
To interpret IV effect estimates as causal parameters, rather than just tests of the null hypothesis that the exposure has no effect on the outcome, we need at least one additional assumption. The IV literature offers several options for this additional assumption, and these alternative assumptions can be invoked to support inferences about causal effects in slightly different subpopulations. We focus here on situations when the instrument and the exposure are binary, but these assumptions, or variations on these assumptions, are possible for continuous instruments and endogenous variables as well. We discuss four options for the additional assumption to link the IV estimate to a particular causal interpretation. The simplest assumption is that the effect of treatment is identical for all individuals in the population. With this assumption, we can interpret the IV estimate as the population average treatment effect. In many cases, it is difficult to believe that treatment would have an identical effect on anyone in the population, so typical IV interpretations are based on weaker assumptions that seem more plausible in the specific situation.
The most common additional assumption is “monotonicity,” which states that the direction, though not necessarily the magnitude, of the effect of Z on X must be the same for everyone in the sample. That is, if Z increases X for one person, it must either increase or not affect X for all other people as well. For example, in an RCT, the monotonicity assumption implies that there is no “defier” who would have refused the treatment if assigned to treatment but would have perversely sought out the treatment if assigned to control. This assumption is not encoded in the DAG. With this additional assumption, we can interpret the IV estimate as the effect of treatment on the individuals who received the treatment because of the value of the IV, also called the local average treatment effect (LATE) or complier average causal effect (CACE).
The LATE interpretation arose from a framework with a binary instrumental variable and a binary treatment. Each person was characterized based on whether he or she would take the treatment under either possible value of the IV (Figure 19.3). Individuals who would take the treatment for either value of the IV are described as “always-takers”; those who would not take the treatment regardless of the value of the IV are called “never-takers.” Those who take the treatment only for one value of the IV are referred to as “compliers” or “defiers” depending on whether they follow the treatment indicated by the IV or pursue the opposite treatment.
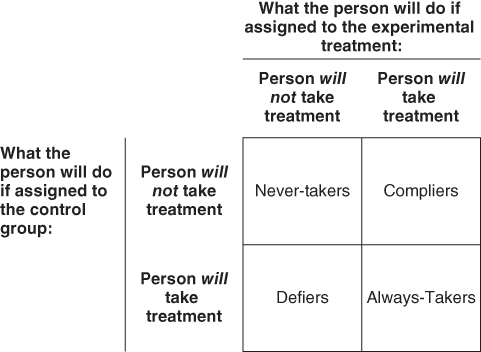
FIGURE 19.3 CHARACTERIZATION OF INDIVIDUALS BASED ON HOW THE INSTRUMENTAL VARIABLE OR RANDOM ASSIGNMENT AFFECTS THE EXPOSURE OR TREATMENT VARIABLE
Individuals who would not “take the treatment,” regardless of random assignment, are referred to as “Never-takers.” Individuals who would take the treatment, regardless of random assignment, are referred to as “Always-takers.” Random assignment influences the value of treatment only for individuals who are “Compliers” or “Defiers.” This conceptualization usually invokes the language of an experimental treatment versus a control treatment, as if treatment were a medication to be “taken,” but the categories can be applied with any type of exposure or in the context of quasi-experiments with pseudo-randomization.
Even with the monotonicity assumption that there are no defiers, we do not usually know which individuals are compliers; among those who take the treatment, some people will be compliers but some people may be always-takers. Thus, the complier average causal effect is not necessarily the same as the effect of treatment on people who were treated. Although we cannot identify individuals who are compliers, we can estimate the fraction of the population who are compliers, because this is simply the difference in the probability of receiving treatment for people assigned to treatment versus people assigned to control (Pr(X = 1|Z = 1) – Pr(X = 1|Z = 0)). In many cases, individuals with one value of the IV cannot access the treatment (e.g., the treatment is a drug only available through the experimental study). In analyses of MTO, it is often assumed that the housing voucher could only be accessed through the experimental treatment, because the wait list for individuals outside the trial was often years. When the exposure of interest cannot be accessed except through the randomization, the LATE equals the effect of treatment on the treated, because there are no “always-takers” in the population.
If we wish to estimate the effect of treatment on the treated (rather than just the effect on the compliers), then instead of the monotonicity assumption, we may assume that the effect of treatment on the outcome does not differ on a given scale, for example, additive or multiplicative, among the treated individuals with different values of the IV (Hernán and Robins 2006). This assumption essentially claims that the effect of treatment on the outcome is not modified by an unmeasured confounder of the exposure-outcome association. If this assumption holds, then the IV effect estimate can be interpreted as the effect of treatment on the treated.
If the above assumption does not necessarily seem plausible, an alternative assumption can be invoked to estimate the effect of treatment on the treated, based instead on assumptions about the determinants of the exposure. This assumption requires that there are no interactions (on the odds ratio scale) between the unmeasured confounder and the IV in a model for the exposure (Tchetgen Tchetgen and Vansteelandt 2013). Therefore, while the approach allows for latent heterogeneity in the treatment effect, it restricts the influence of the IV on the exposure to be independent of that of the unmeasured confounder on the odds ratio scale.
We emphasize that the above options are not alternative ways to estimate IV effects, but simply alternative assumptions to adopt when interpreting the IV effect estimate. We now turn to estimation.
Obtaining IV Estimates
There are several ways to calculate IV estimates. The intuition is best exemplified with the so-called Wald estimator. To calculate the Wald IV estimate, first calculate the relationship between the instrument and the outcome (Z and Y). If Z is treatment assignment in an RCT, this is the ITT estimate; it is also sometimes called the “reduced form” association. The relationship between Z and Y provides a test of the claim that X has a causal effect on Y: if X has no effect on Y then Z and Y should be independent. The effect of Z on Y is not, however, of the same magnitude as the effect of X on Y. To estimate the effect of X on Y, we must take into account the fact that Z does not perfectly determine X. This is the second step in calculating the Wald IV estimate: we scale up the effect of Z on Y by a factor proportional to the effect of Z on X. The IV estimate of the effect is simply the ratio of the difference in Y across different values of Z to the difference in X across different values of Z. Define Pr(Y = 1|Z = 1) as the probability of Y among subjects in the sample assigned to treatment Z = 1:
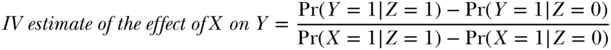
If everyone followed their assigned treatment, the denominator would be 1, since Pr(X = 1|Z = 1) = 1 and Pr(X = 1|Z = 0) = 0. Therefore, with perfect adherence, the IV effect estimate would equal the ITT effect estimate. As adherence declines, the denominator drops from 1 to 0; thus the IV estimate is calculated by inflating the ITT estimate in proportion to the severity of non-adherence in the trial.
The two-stage least squares estimator (2SLS) can be applied more generally for exposure and instruments with multiple values, including continuous variables. The 2SLS estimator also accommodates simultaneous adjustment for other covariates. A 2SLS estimate is derived by regressing measured X on Z (as in Equation (2) below) using ordinary least squares (OLS) estimation, calculating predicted values of X (denoted as 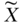 in the equation below) based on this regression, and using these predicted values of X as independent variables in a regression model of Y (as in Equation (3) below) using OLS estimation. The coefficient on the predicted value of X (β1 below) is then interpreted as the 2SLS IV estimate of the effect of X on Y. The estimated effect of the instrument on treatment, α1 in Equation (2) below, is sometimes called the first-stage coefficient:
in the equation below) based on this regression, and using these predicted values of X as independent variables in a regression model of Y (as in Equation (3) below) using OLS estimation. The coefficient on the predicted value of X (β1 below) is then interpreted as the 2SLS IV estimate of the effect of X on Y. The estimated effect of the instrument on treatment, α1 in Equation (2) below, is sometimes called the first-stage coefficient:
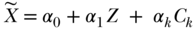
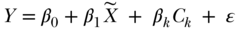
The same list of other covariates (Ck) should be included in both stages. The single instrumental variable Z in Equation (2) can easily be replaced by multiple instrumental variables, if additional credible instruments are available. Including additional instrumental variables will often improve statistical power, which is proportional to the fraction of variance in X that is explained by the instruments. Another advantage of multiple instrumental variables is that one can, in theory, simultaneously estimate the effects of multiple endogenous treatment variables (as many endogenous variables as there are instrumental variables). If Z is a continuous variable, it can be converted to multiple categorical variables to accomplish the goal of identifying multiple endogenous variables, although this does not in general enhance statistical power.
The 2SLS estimator provides the intuition behind an IV analysis, but an IV treatment effect estimate based on 2SLS is potentially biased toward the standard OLS treatment effect estimates in the event of a weak IV, that is, an IV that has hardly any effect on the exposure (Bound et al. 1995). This type of bias, traditionally called “weak instruments bias,” occurs because the first stage of the 2SLS models (the effect of the instrument on treatment) is generally not known with certainty. The first-stage parameters therefore must be evaluated empirically from the observed sample used to assess the effect of treatment on the outcome. The estimated coefficients for the first-stage regression may be unbiased, but they are based on a finite sample and will not be identical to the population causal coefficients, due to sampling variability. This chance deviation between the causal effects and the estimates in the first-stage sample will generally be in the direction that most improves the prediction of treatment in that sample. As a result, the estimated predicted value of the treatment will be correlated with unmeasured sources of variation in the treatment, including unmeasured common causes of the treatment and outcome variables. Typically this correlation is weak for a given IV but will generally increase with the number of weak instrumental variables.
To avoid weak instruments bias, particularly when there are multiple weak instruments, an alternative to the 2SLS IV estimator is preferred, such as limited information maximum likelihood (LIML), jackknife instrumental variables (JIVE) models, or separate-sample or split-sample IV estimators (Angrist et al. 1999; Angrist and Krueger 2001; Tchetgen Tchetgen et al. 2013). LIML estimates the first-stage coefficients while constraining the structural parameters to avoid the finite sample bias. JIVE models jackknife the estimated first-stage coefficients, so that for each observation the predicted value of the endogenous variable is estimated using coefficients calculated excluding that observation. Split-sample methods estimate the first stage on a different sample than the second stage. Any of these approaches avoids weak instruments bias.
Weak instruments bias, which can occur even when there is no violation of the IV assumptions, should be distinguished from structural bias that occurs, for example, if there is a direct path from the IV to the outcome. Weak instruments bias is resolved by using separate sample approaches and is a bias toward the conventional effect estimate, but structural bias in IVs cannot be reduced by using separate samples and is not necessarily toward the conventional estimate. These two sources of bias are often conflated, perhaps because as the association between the instrument and exposure is reduced, the plausible impact of structural bias becomes larger.
Another approach to deriving IV estimates is based on the “generalized method of moments” and simultaneously solves the equation for the exposure and the outcome, imposing the constraint that the residuals of these two models are uncorrelated. Finally, sometimes a control function approach—in which Y is regressed on X (as measured) and the residuals from Equation (2)—is used to derive IV estimates. Specifically, the control function approach replaces Equation (3) with
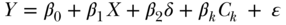
where 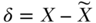 . With linear models, the control function approach is exactly equivalent to 2SLS, whereas the generalized method of moments is in principle more efficient than 2SLS in large samples.
. With linear models, the control function approach is exactly equivalent to 2SLS, whereas the generalized method of moments is in principle more efficient than 2SLS in large samples.
IV Effect Estimates for Binary and Survival Outcomes
Binary and survival outcomes are common in social epidemiology. Above, we considered how to use IV methods to estimate the risk difference for the effect of treatment on a binary outcome and how to estimate the effect of an exposure on average value of a continuous outcome. Here we extend to methods that may be more appealing for the discrete nature of a binary outcome and methods appropriate for a time to event/survival outcome that may be censored. In the case of a binary outcome, note that the standard IV estimand was given by Equation (1) for a binary outcome and described as the Wald estimator of the risk difference. This equation continues to apply even if one were to incorporate covariate adjustment by replacing each instance of Pr(Y = 1|X = x) with Pr(Y = 1|X = x, covariates) in the equation. These probabilities, incorporating covariate adjustment, might be estimated via standard binary regression analysis, say with a logit or probit link function. However, the resulting expression for the IV estimand upon making such a substitution is highly non-linear in X and covariates, and the effect estimate is not guaranteed to fall within the natural bounds of a causal effect for a binary outcome on the risk difference scale (i.e., between –1 and 1, the most extreme values possible for a risk difference). This drawback makes the approach unattractive and an alternative, more flexible, approach is preferable. Suppose that Y is a binary outcome such that, conditional on the endogenous exposure X and the unobserved confounder U, the following log-linear model is correctly specified:
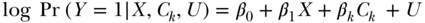
paired in the case of continuous exposure with a model for exposure:
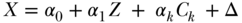
with error  independent of Z, such that U and
independent of Z, such that U and  are allowed to be dependent. Any association between U and Δ, that is, Cov(U,
are allowed to be dependent. Any association between U and Δ, that is, Cov(U,  ) ≠ 0, implies confounding of the X–Y association because there is an unmeasured cause of X that is correlated with an unmeasured cause of Y. The causal effect of interest is
) ≠ 0, implies confounding of the X–Y association because there is an unmeasured cause of X that is correlated with an unmeasured cause of Y. The causal effect of interest is 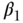 , which encodes the log of the relative risk corresponding to a unit increment of the exposure. Under the above pair of models, a simple two-stage regression approach parallel to the 2SLS described above for linear second-stage models would entail obtaining fitted values under the exposure model (2) via ordinary least-squares estimation. Estimation of
, which encodes the log of the relative risk corresponding to a unit increment of the exposure. Under the above pair of models, a simple two-stage regression approach parallel to the 2SLS described above for linear second-stage models would entail obtaining fitted values under the exposure model (2) via ordinary least-squares estimation. Estimation of 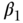 then follows by fitting a second-stage regression model for the outcome by replacing in Equation (5) the endogenous variable with its fitted value from the first stage (Mullahy 1997; Nagelkerke et al. 2000; Palmer et al. 2011):
then follows by fitting a second-stage regression model for the outcome by replacing in Equation (5) the endogenous variable with its fitted value from the first stage (Mullahy 1997; Nagelkerke et al. 2000; Palmer et al. 2011):
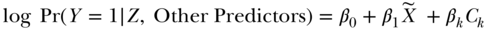
This model can be estimated via standard log-binomial regression or an alternative approach less susceptible to potential convergence issues (Wacholder 1986; Zou 2004); see also Tchetgen Tchetgen (2013) and accompanying citations. When the outcome is rare, a logit link may be substituted for the log link in the second stage, thus permitting the use of standard statistical software for logistic regression. In the case of a binary exposure, the first-stage linear regression is no longer appropriate and can be replaced with any standard binary regression model (e.g., logistic, probit), but a control function approach must then be used for the second stage, whereby one fits the model including the first-stage residuals (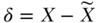 ):
):
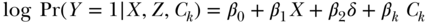
in order to obtain an estimate of 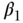 . Here again, in the event the outcome is rare, logistic regression may replace log-linear regression in the second stage (Tchetgen Tchetgen 2014).
. Here again, in the event the outcome is rare, logistic regression may replace log-linear regression in the second stage (Tchetgen Tchetgen 2014).
The above discussion assumes that the estimation is within a sample representative of the population, but IV methods can be applied when sampling was based on the outcome, that is, in case control studies. The appropriate estimator depends on whether the outcome is rare and options are available to derive correct estimates of the first-stage model (Bowden and Vansteelandt 2011; Tchetgen Tchetgen et al. 2013).
Regression methods analogous to the approaches described above have also developed in recent years in the context of hazard regression analysis for right censored time-to-event outcomes. For instance, following standard practice with survival outcomes, one may assume that the outcome T follows a Cox proportional hazards model:
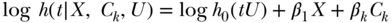
so that 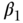 is the causal log-hazards ratio corresponding to a one-unit increment of the exposure and
is the causal log-hazards ratio corresponding to a one-unit increment of the exposure and 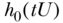 encodes the baseline hazard function within levels of the unobserved confounder U. Alternatively, one may assume additive hazards, such as
encodes the baseline hazard function within levels of the unobserved confounder U. Alternatively, one may assume additive hazards, such as
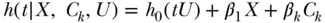
so that 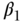 now encodes a hazard difference corresponding to a unit change of the exposure. Additive hazards models are of interest in epidemiology because they naturally correspond to a multiplicative model for the survival curves.2 Two-stage regression and the control function approaches can, under certain conditions, be used to estimate the above two hazard regression function models. Specifically, both two-stage and control function estimation approaches may be used in the context of Cox regression, provided that the outcome is cumulatively rare over the entire follow-up, which could occur if the follow-up is quite short and the censoring rate high, or if the cumulative incidence rate is low enough so that the survival curve barely departs from unity over the follow-up. Both estimation strategies can likewise be used to estimate the additive hazards model under straightforward conditions, even when the outcome is not rare over the follow-up study. See Tchetgen Tchetgen (2015) for a code to implement these methods.
now encodes a hazard difference corresponding to a unit change of the exposure. Additive hazards models are of interest in epidemiology because they naturally correspond to a multiplicative model for the survival curves.2 Two-stage regression and the control function approaches can, under certain conditions, be used to estimate the above two hazard regression function models. Specifically, both two-stage and control function estimation approaches may be used in the context of Cox regression, provided that the outcome is cumulatively rare over the entire follow-up, which could occur if the follow-up is quite short and the censoring rate high, or if the cumulative incidence rate is low enough so that the survival curve barely departs from unity over the follow-up. Both estimation strategies can likewise be used to estimate the additive hazards model under straightforward conditions, even when the outcome is not rare over the follow-up study. See Tchetgen Tchetgen (2015) for a code to implement these methods.
Framing Natural Experiments and IVs Causally
Framing IVs in terms of potential outcomes and counterfactuals helps clarify why they can be used to test causal hypotheses and how they relate to other methods of drawing causal inferences from observational data (Winship and Morgan 1999). We adopt here the “do” or “set” concept (Pearl 2009) and define Yx = 1 as the value Y would take if X were set to 1 and Yx = 0 as the value Y would take if X were set to 0. We assume that for each individual, there is a potential value for Y associated with each theoretically possible value of X. In the counterfactual framework, an individual level causal effect is given by the contrast Yx = 1 −Yx = 0. However, we cannot observe both of these potential outcomes for any single individual. Under an assumption known as consistency—an assumption so seemingly straightforward it sounds like a tautology—the observed outcome Y for a person who was treated, that is, a person with X = 1, coincides with the potential outcome Yx = 1 that person would have had if X were set to 1. In other words, if X = 1, then Yx = 1 = Y and E(Yx = 1|X = 1) = E(Y|X = 1).
Likewise, Yx=0 is observed and equal to the observed value of Y for persons with X = 0. However, for treated person with X = 1 we can never observe their potential outcome Yx=0 had treatment been withheld. In this framework, the values of both Yx=1 and Yx=0 are variables whose values are established before X is assigned. Assigning X simply determines which of the two potential outcomes of Y will be the actual outcome of Y. Because we cannot observe both Yx=1 and Yx=0 for the same individual, we cannot hope to identify causal effects for an individual.
Nonetheless, one may be able, under certain assumptions, to identify the average causal effect for the whole sample: E(Yx=1 – Yx=0). Such a counterfactual mean difference can be identified if one can identify3 the average counterfactuals E(Yx=1) and E(Yx=0). In randomized trials, X is essentially determined by a coin flip, in which case it is reasonable to assume that X is independent of all pre-treatment variables including potential outcomes Yx=0 and Yx=1. In this case, the average outcome of the group exposed to one treatment regimen represents, or is exchangeable with, the average outcome the comparison group would have had if they had been exposed to the same treatment regimen (Hernán 2004).Therefore under randomization, E(Yx=1|X=0) = E(Yx=1|X = 1) = E(Y|X = 1), where the second equality follows from the consistency assumption, and likewise E(Yx=0) = E(Y|X = 0). For example, suppose we are examining the health effects of attending an early education program versus no such program among children randomly assigned to either early education or to no extra services (controls); we typically assume that the health outcomes of children randomized to the early education program (treatment) represent the health the children randomized to control would have experienced, had they been assigned the early education program.
While randomization can sometimes be enforced by design, this is not the case for a number of interventions of potential interest in social epidemiology; thus observational studies are a primary source of inference. When treatment is not randomized, counterfactual outcome averages cannot be identified without an additional assumption, since E(Yx=1) ≠ E(Y|X = 1). This is because, due to confounding, it will generally not be the case that treatment assignment is independent of unobserved risk factors for the outcome, including the set of potential outcomes.
A way forward in such settings is possible if one has observed all common causes C of X and Y.4 We assume that within the strata of C, it is again as if X were assigned by a coin flip and therefore conditionally independent of the counterfactual values of Y (Yx=0, Yx=1) given C. Specifically, assuming no unmeasured confounding given C implies that we can validly estimate a counterfactual value using an actual value:
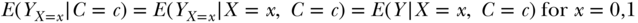
Based on this assumption, we can identify the causal effect of X on Y:
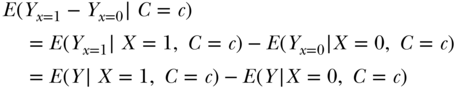
As mentioned above, when, as in observational studies, treatment is not randomly assigned, the assumption of exchangeability may not be plausible. If we were comparing health outcomes of children who attended an early education program to those of children who did not attend such a program in the absence of a randomized trial, we might suspect, for example, that individuals who attended the early education program had unobserved advantages or disadvantages compared to those who did not attend such a program. For example, such children might have had wealthier or more highly educated parents, and thus the early education attendees would have had better health even if they had skipped the early education program. Treatment received (early education program or no such program) is not independent of the outcomes the individual would have had under either treatment regime. This is equivalent to saying that there is a shared prior cause of whether someone attended the early education program and subsequent health, so the relationship is confounded.
Natural experiments mimic RCTs in that the mechanism determining each individual's exposure is independent of the individual's set of potential outcomes. The factor that determines the chance that an individual is exposed is an “instrument” for the effect of the exposure on the outcome (Angrist et al. 1996; Pearl 2009), in exactly the sense shown in Figure 19.1A. Treatment group assignment in a well-conducted RCT is an example of an ideal instrument. Suppose we assume that adherence to assigned treatment is imperfect because some people do not take the treatment to which they are assigned, as is typical in RCTs. The experiment can still be used to assess whether the treatment affects the outcome, provided we assume that nobody perversely seeks the treatment contrary to their assigned treatment (i.e., assuming monotonicity). Natural experiments created by circumstances outside of the control of the researchers or the individuals affected, for example, policy changes, weather events, or natural disasters, also provide plausible instruments.
The above discussion leads to the counterfactual definition of a valid instrument: Z is not independent of X, but Z is independent of Yx (the counterfactual value of Y for x = 0, 1) (Pearl 2009). Note how these counterfactual assumptions correspond to the assumptions we gave above when using the DAG to represent a valid IV. If there were either a direct effect of Z on Y or a confounder of Z and Y, Z would not be independent of Yx. The assumption that Z is independent of Yx cannot be empirically proven and it must be evaluated in part based on subject matter knowledge. Swanson and Hernán (2013) argue that it is easier to apply relevant subject matter knowledge to evaluate this assumption when it is restated as two separate claims: Yxz = Yx (no direct effect of Z on Y not mediated by X) and Yz independent of Z given covariates (no unmeasured confounding of Y and Z).
These assumptions for a valid IV correspond with assumptions for a well-conducted RCT. For example, the advantage of double blinding in an RCT is that it helps avoid violations of Yxz = Yx. Unblinding, such that either the participant or evaluator knows the treatment assignment, increases the chance that treatment assignment directly influences the outcome assessment via a mechanism unrelated to treatment received, such as differential measurement or compensatory behavior (Cook et al. 2006).
When considering natural experiments, the same assumptions as for an RCT are necessary, but must be evaluated with a more skeptical eye. For example, several papers have exploited changes in legally mandated years of compulsory schooling (CSLs) as natural experiments for the effect of schooling on health. Taking the United States as an example, although all states had compulsory schooling laws in place by 1918, states differed substantially with respect to the number of years required (i.e., the age of mandatory primary school enrollment and the age of permitted dropout). Over the course of the century, many states changed their schooling requirements, some more than once. As a result, some elderly US residents were born in states that required only a few years of school before a child could drop out, while others were born in places that required up to 12 years. Lleras-Muney demonstrated that CSLs influenced completed schooling for white children born in each state (Lleras-Muney 2002); individuals born in states with long CSL requirements completed more years of schooling, on average, than individuals born in states with short CSL requirements. This approach was subsequently used to estimate the effect of years of completed schooling on old-age cognitive scores and dementia risk (Glymour et al. 2008). The analysis treated year of birth and state of birth as “treatment assignments” that influenced, but did not perfectly determine, the amount of schooling children complete. Similar analyses have been conducted in several European countries, where changes in compulsory schooling typically occurred at a national (rather than regional or provincial) level and had larger effects on average schooling (Banks and Mazzonna 2012; Schneeweis et al. 2014).
In terms of hypothesized causal structure, natural experiments and RCTs ideally both follow the structure shown in Figure 19.1A, where Z represents treatment assignment. In a natural experiment, this might be an indicator for whether the observation was before or after a policy change. X represents the treatment received, for example, how much education the individual actually completed. The assumptions represented in this structure may of course be violated for either an RCT or for a natural experiment. An important difference between RCTs and natural experiments, however, is the extent to which we feel confident that this causal structure accurately describes the situation.
The ITT Estimate Versus the IV Estimate
The magnitude of the effect of the instrument on the exposure of interest is a second important difference between RCTs with non-compliance and typical natural experiments. In RCTs, this effect is referred to as adherence to assigned treatment. Imperfect adherence is the norm in RCTs, leading to extensive work on analyses of “broken experiments” (Barnard et al. 1998), but the level of “adherence” in natural experiments is often much lower than in RCTs. In fact, the effect of the instrument on exposure can be tiny in a natural experiment, either because the instrument has a large effect on only a small fraction of the population or because the instrument has only a small effect but has that effect for most people in the population. A crucial insight for using IVs is to understand that, although high adherence is preferable for many reasons, with a valid instrument it is possible to derive consistent estimates of the causal effect even if adherence is low. The ITT estimate can be calculated using data generated by either RCTs or natural experiments. In either case, the ITT estimate provides a consistent test of the sharp null hypothesis that treatment has no effect on the outcome for anyone (although this is not applicable for non-inferiority or equivalence trials comparing two alternative treatments, when the null is that the two alternatives have equivalent effects (Robins and Greenland 1996)). As adherence declines, however, the magnitude of the ITT estimate will usually be increasingly attenuated compared to the magnitude of the true causal effect of receiving the treatment (assuming this effect is non-zero). With declining adherence, the gap between the effect of being assigned to treatment and the effect of receiving treatment will grow.
IV analyses correctly account for this non-adherence. It is worth contrasting IV estimates with “as-treated” (Ellenberg 1996) analyses, in which the treated are compared to the non-treated or a “per-protocol” analysis (Montori and Guyatt 2001), in which compliers in the treated group (for whom Z=X=1) are compared to compliers in the control group (for whom Z=X=0). We will then explain why the IV estimate does not have the same problems as the other approaches. Consider the hypothetical example shown in Figure 19.4. There are three variables in addition to Y (the outcome of interest): Z (the instrument or treatment assignment), U1 (a three-level variable that affects both the treatment received, X, and the outcome, Y), and U2 (another cause of Y).
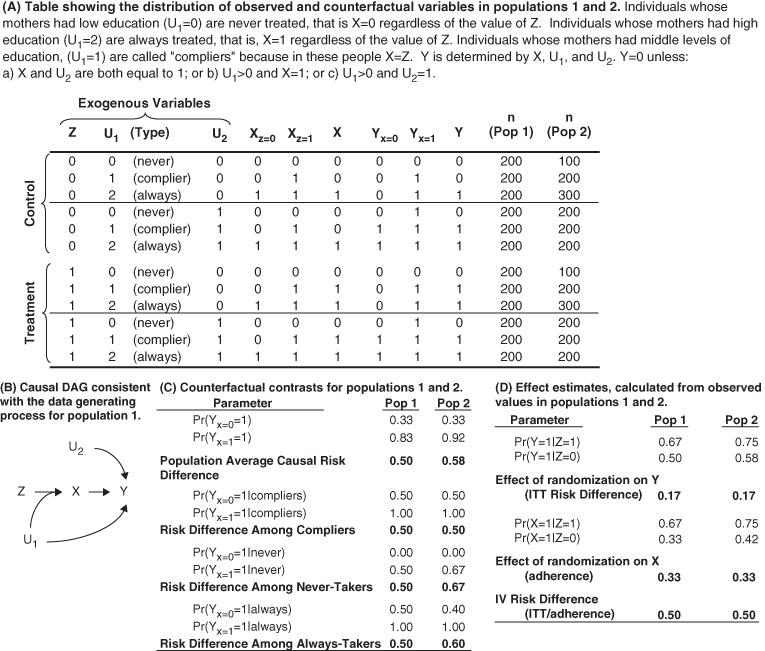
FIGURE 19.4 EXAMPLE CONTRASTING ITT, IV, AND POPULATION AVERAGE CAUSAL EFFECT IN TWO POPULATIONS
For example, let this represent an experiment in which participants are randomly assigned to receive a scholarship for college tuition (Z), with the goal of estimating the effect of completing college (X) on later health (Y). Let U1 represent the education of the participant's mother, classed into three levels, which affects both likelihood of completing college and the participant's later health. Let U2 represent a genetic determinant of health, which is independent of college completion and mother's education. Figure 19.4 contrasts outcomes for never-takers, always-takers, compliers, and defiers.
The data in Figure 19.4A were generated by assuming a population distribution (shown in column “n (Pop 1)”) for the three exogenous variables (Z, U1, and U2) and using the following two rules to determine the values of X and Y. The first rule specifies the value of college completion (X), given scholarship (Z), and mother's education (U1). The three values of U1 (0, 1, or 2) determine whether someone is an always-taker, never-taker, or a complier. We assume here that there are no defiers.
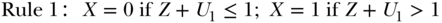
Rule 1 implies that, regardless of receipt of a scholarship, people with low maternal education do not complete college and people with higher maternal education do complete college. It is only for individuals whose mothers have the middle level of education that scholarship receipt determines college completion.
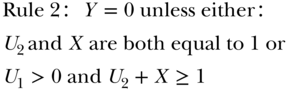
In other words, the person is healthy if he/she (a) both completes college and has a good genetic endowment or (b) his/her mother has one of the two higher values of education and he/she either completes college or has a good genetic endowment. These rules specify all counterfactual values of X and Y under all possible combinations of values for the exogenous variables, Z, U1, and U2. The data in Figure 19.4A show the actual value of education (X) and the counterfactual values of education (Xz=0, Xz=1) for alternative values of the scholarship (Z) and the actual value for health status (Y) and the counterfactual values of health status (Y, Yx=0, Yx=1), given alternative values of education (X). The counterfactual values in the two randomized groups are identical; the goal of randomization has been achieved. The actual values differ because randomized assignment affects the values of X (for people who follow their assigned treatment), which affects the value of Y. The causal risk difference for the effect of X on Y can be calculated as the weighted average of the difference in the counterfactuals:
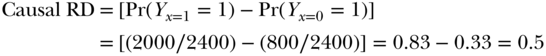
What is the RD estimated using an intent-to-treat analysis of the observed values of Z and Y?
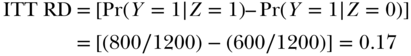
The ITT RD is much smaller than the causal RD because the randomized assignment only affected treatment in a third of the population (the compliers). We might also calculate the as-treated RD, comparing people who completed college to those who did not:
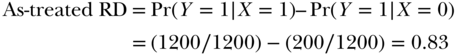
Finally, we could calculate the per-protocol RD by comparing individuals in the treatment group who completed college to individuals in the control group who did not complete college.
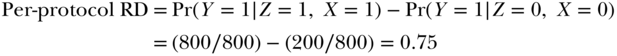
The as-treated RD and the per-protocol RD are both larger than the causal RD. This is because the relationship between college completion (X) and health is confounded by U1. By using treatment received instead of treatment assigned, we are throwing away the advantage of the randomized trial and are again vulnerable to all the confounding bias in any observational study.
Under our assumptions, the ITT underestimates the causal RD and both the per-protocol and as-treated RD overestimate the causal RD. The IV RD estimate uses the ITT RD and scales it up in inverse proportion to the level of adherence in the study. In this population, one-third of the people in the control group received the treatment and two-thirds of the people in the treatment group received the treatment. Thus, Pr(X = 1|Z = 1) – Pr(X = 1|Z = 0) = 0.33. The association between randomization and the outcome reflects the causal effect of X on Y in the third of the population whose treatment changed as a result of their randomized assignment, but it is diluted by a factor of 3 compared to the causal RD. The IV RD rescales the ITT RD based on the proportion of the population that adhered to their assigned treatment:
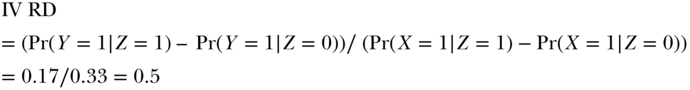
The above example obscures an important caveat in IV analyses. The setup, specifically the joint distribution of U1 and U2, implied that the effect of X on Y did not differ between never-takers, compliers, and always-takers. However, this need not be the case. To see this substantively, consider the example of college scholarships. Suppose that individuals whose mothers have the lowest education would benefit the most from a college degree, perhaps because the degree affords improved access to medical care, which is especially beneficial to people who had limited resources in childhood. We can demonstrate this in our numerical example by changing the sample size for each type of person (altering the number of people represented by each row in Figure 19.4). Imagine that the sample sizes were as described for population 2 (pop 2) in Figure 19.4, with only 100 people in rows 1 and 7, but 300 people in rows 3 and 9. This change does not violate the assumption of randomization (the distribution of covariates U1 and U2 is still identical between those with Z = 0 and those with Z = 1) but it implies that the variables U1 and U2, which were statistically independent in population 1, are statistically associated in population 2.
In this new population, the causal RD among compliers is 0.50, the causal RD among the always-takers is 0.60, and the causal RD among the never-takers is 0.67. The IV RD is 0.50, which is identical to the causal RD for compliers.
The above discussion is premised on the assumption that there is nobody in the population who will complete college if and only if assigned not to receive the scholarship. That is, although some respondents' behavior may not be affected by the treatment assignment, nobody will perversely pursue the opposite of his or her assigned treatment. If there are any such defiers in the population, the IV effect estimate does not converge to the causal effect among the compliers (Angrist et al. 1996). This assumption is often considered a limitation of IV analyses, but note that if we believe the population includes defiers, the ITT estimate is similarly hard to interpret and cannot be assumed to fall between the null and the population average causal effect of exposure on the outcome (the same is true for standard regression results obtained from observational studies). As discussed above, other causal parameters such as the effect of treatment on the treated may be estimated, or at least bounded, under alternative assumptions (Balke and Pearl 1997; Hernán and Robins 2006).
The potential discrepancy between the IV estimate and the average causal effect does not invalidate the IV effect estimate; it merely indicates that the effect of forcing the entire population to receive the treatment would not be accurately approximated by the IV estimate. In some cases, the IV estimate may be of greater interest than the population average treatment effect.
Evaluating IV Estimates
The first piece of evidence to consider in evaluating the credibility of an IV effect estimate is the association of the IV with the exposure of interest. An IV with only a weak effect on the exposure does not necessarily imply the IV effect is invalid, but it does imply that the estimate is susceptible to small biasing pathways and should therefore be viewed with more skepticism. This is important even if the IV passes the typical “weak instruments” test criterion (e.g., an F-statistic greater than 10 for the first stage association; Stock and Staiger 1997). In a sufficiently large sample, an IV with a much larger F-statistic may nonetheless explain only a tiny fraction of the variance in the exposure. Effectively, this tiny association will inflate any biasing pathway from the IV to the outcome.
Valid IVs must also fulfill the criterion that every unblocked path from Z to Y is mediated by X. This assumption cannot be proven, but it can sometimes be disproven. Because IV estimates can be substantially biased by small violations of the assumptions, it is important to deploy as many “falsification tests” as possible (Glymour et al. 2012; Swanson and Hernán 2013). Such tests often depend heavily on theoretical background or a combination of theoretical and statistical evidence. For example, Swanson and Hernán argue that if an IV is correlated with known, measured risk factors for Y, this suggests it may also be correlated with unmeasured risk factors for Y (Swanson and Hernán 2013).
IV estimates are often undertaken because conventional analyses are suspected of bias. If that bias is away from the null, we expect a valid IV to produce an effect estimate closer to the null. If the IV estimate is farther from the null than the conventional effect estimate, it suggests that either we were wrong about the direction of the bias in the conventional estimate or else our IV is biased. Another possible explanation is that conventional analyses underestimate the causal effect due to measurement error in the independent variable. As previously discussed, the IV effect may also differ from the population average effect because the compliers either benefit more or less from the treatment than others in the population.
Overidentification tests comparing IV effects from multiple different IVs provide another important approach to evaluating IV models. If two IVs, say Z1 and Z2, are used to estimate the same effect of X on Y, then the two IV effect estimates should be equal. If they differ, it suggests that at least one is biased. The caveat here, though, is that instruments may not affect the same mediator or affect it among the same people. Two IV estimates based on different instruments may each accurately estimate the causal effect of a slightly different exposure. For example, extending compulsory school by lowering the age for first enrollment may have different effects than extending compulsory school lengths by increasing the age for school dropout. The cognitive effect of a year of school in early childhood may differ from the effect of completing an additional year of schooling in adolescence (Mayer and Knutson 1999; Gorey 2001). A special case of an overidentification test is based on using variables that modify the effect of the instrument on exposure: such interactions effectively create multiple IVs, which can then be used in overidentification tests. This is often done informally, by identifying a population in which the IV should have no effect on the exposure and confirming that the IV is unrelated to the outcome in such a population. A related approach uses negative control outcomes, which are likely to be subject to the same confounding structure as the exposure-outcome of interest (Lipsitch et al. 2010). Recent innovations based on Egger regression are also powerful when multiple IVs are available (Bowden et al. 2015). In situations with a categorical exposure, certain inequality tests can be applied, although these are often unsatisfying because they may fail to detect even egregious violations of the IV assumptions (Balke and Pearl 1997; Glymour et al. 2012).
A Good Instrument Is Hard to Find
Thinking of good natural experiments for the exposure at hand requires a depth of understanding of the processes that lead individuals to be exposed:
Recognizing potential instruments requires substantive knowledge about the exposure of interest combined with a mental knack: a backwards leap of imagination from the exposure to the factors that determined that exposure. Finding testable implications of a particular story about why an instrument influences the exposure can buttress confidence in the instrument, and identifying such tests also requires substantive knowledge about the exposure and the instrument. Countless IV analyses have been published in the social science literature, some more compelling than others. IV methods are also gaining acceptance in health services research (Newhouse and McClellan 1998; McClellan and Newhouse 2000), and genetic IVs, popularly referred to as “Mendelian randomization” studies are increasingly influential (Davey Smith and Ebrahim 2003). A few specific examples, and some critiques of these examples, are reviewed below.
In an influential but controversial paper, Angrist and Krueger (1991) took advantage of a quirk in compulsory schooling laws (CSLs) to estimate the effect of educational attainment on earnings, using month of birth as an IV. Many states' CSLs effectively require less schooling for children born in January than for children born in December, because, for example, children must enter school in the fall of the calendar year in which they turn 6 but may quit school on their 16th birthday. On average, US children born in September, October, or December (who enter school right before their 6th birthday) complete slightly more school than children born in January, February, or March (who enter school several months after their 6th birthday). Because the effects of school may depend on the age at which a child is exposed, month of birth has even been used as an IV for the effect of age of entry to school, rather than duration of schooling per se (Angrist and Krueger 1992).
Others (Bound and Jaeger 1996) have argued that month of birth is not a valid IV for education on the grounds that season of birth is associated with personality characteristics (Chotai et al. 2001), shyness (Gortmaker et al. 1997), height (Weber et al. 1998), mortality (Gavrilov and Gavrilova 1999), schizophrenia risk (Mortensen et al. 1999), and family background (Buckles and Hungerman 2013). Any of these factors might affect health through mechanisms other than completed education. It is difficult to directly eliminate these alternative explanations. Angrist and Krueger bolstered their claim by pointing out that the alternatives implicate season of birth rather than the administrative concept of quarter of birth. Seasons do not have abrupt thresholds: with respect to weather, light, infectious agents, food availability, or other seasonal phenomena, December 31 is fairly similar to January 1. With respect to school age eligibility, these two dates are nearly a year apart. Angrist and Krueger show abrupt differences in education and income between December births and January births, suggesting that season-based explanations are not adequate. They also provided evidence that the differences in schooling emerge in middle and high school, as would be expected if they were due to CSLs.
Policy Changes as Instrumental Variables
Policy changes often provide useful IVs, and the conceptualization parallels regression discontinuity and difference-in-difference designs. Evans and Ringel (1999) used state cigarette taxes as an instrument for smoking during pregnancy because cigarette prices tend to affect smoking rates but would have no other obvious mechanism to influence birth outcomes. They found IV estimates of the causal effect of smoking on birth weight very similar to effect estimates derived from a randomized trial of a prenatal smoking cessation program (Permutt and Hebel 1989; Evans and Ringel 1999). Because state policies or state characteristics are ecological variables, using them as instruments invites criticism. Any one state policy is likely to correlate with numerous other state-level characteristics, potentially rendering the instrument invalid. Instrumenting based on changes in state policies over time may help alleviate this problem, especially if it is possible to combine geographic differences with temporal differences to define the instrument.
When policy changes are used as IVs, the model is sometimes described as a regression discontinuity (where the discontinuity occurs at the time of policy implementation) or difference-in-difference (DID) design (Banks and Mazzonna 2012). Angrist and Pischke (2009) describe fuzzy regression discontinuity designs, in which there are discontinuities in the probability of treatment, as IV models. The assumptions for these designs are closely linked with IVs, except that one conceptualizes the source of the IV as either an interaction term (for DID) or a discontinuity in an otherwise smooth function (for regression discontinuity). For example, Banks and Mazzonna (2012) leveraged the 1947 increase in English minimum school leaving age (from 14 to 15 years of age) to evaluate the effect of additional schooling on cognitive test performance in middle and old age. In a large sample of English adults born either shortly before or shortly after the policy change, they compared children born before or after the cut-off date for the new policy (i.e., born before 1933). Because of the close association between age of assessment and cognitive test scores in older adults, Banks and Mazzonna pooled multiple waves of data so they could assess the same respondents across multiple years and control for age at assessment. They then estimated a set of 2SLS models, with the first stage predicting years of education (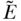 ), using as the instrument an indicator variable for whether the individual was born before or after the cut-off date for the policy mandating extra education (Z) and adjusting for a flexible function of the continuous birth cohort expressed in months (R) (omitting indexes for individual, birth cohort, and survey year):
), using as the instrument an indicator variable for whether the individual was born before or after the cut-off date for the policy mandating extra education (Z) and adjusting for a flexible function of the continuous birth cohort expressed in months (R) (omitting indexes for individual, birth cohort, and survey year):
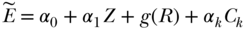
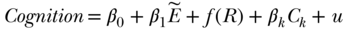
This model controls for the secular increases in educational attainment with successive birth cohorts—changes that are presumably unrelated to the policy change—and identifies the effect of the extra education induced by the policy change. In this case, identifying the effect of additional education relies on correctly specifying the functional form for birth cohort, a complex, continuous covariate. This type of covariate (such as a date or seasonal trend) is common with policy-change IVs and entails special methodological care (Barr et al. 2012).
Location, Timing, or Setting Characteristics as Instruments
Other notable IV applications in health research include estimating the impact of intensive treatment on outcome of acute myocardial infarction, using differential distance to alternative types of hospitals as an instrument (McClellan et al. 1994); the effect of length of post-partum hospital stay, instrumented using hour of delivery, on risk of newborn readmission (Malkin et al. 2000); the influence of prenatal care visits, instrumented using a bus drivers' strike, on birth outcomes (Evans and Lien 2005); and effects of physician advice on smoking cessation, instrumenting with physician advice on diet and physical activity (Bao et al. 2006). A general strategy, often appropriate when there is a clustering variable that influences exposure of several individuals, uses the average value of exposure for other people in the cluster as an instrument. For example, several applications have attempted to estimate the effect of a particular pharmaceutical treatment on various outcomes using the drug the physician chose for the patient prior to the index patient as an IV (Wang et al. 2005; Brookhart et al. 2010). These so-called “physician preference” instruments have been critiqued on grounds that the monotonicity assumption is unclear and unlikely to be strictly met (Swanson et al. 2015a). Perhaps more overtly, patients with the same physician are likely to share other, unobserved, characteristics, such as SES or place of residence or attitude about disease treatment. Such challenges might be overcome with larger datasets that allowed for identification based on changes over time in the physician's preferences (e.g., after a marketing campaign or an educational activity). In a similar effort to estimate the effect of physician's communication style on patient outcomes, Clever et al. (2008) used the communication style as described by other patients seen by the same physician as an IV.
Although many policies are implemented in a way that seems to intentionally preclude rigorous evaluation, lotteries are sometimes used to distribute policy-relevant resources. These studies have generated extraordinary evidence of immediate policy relevance. For example, a study of juvenile offenders evaluating the effects of parole versus incarceration on high school completion and recidivism used the judge assigned to the case as an IV. Some judges were systematically more lenient than others, and juveniles assigned to these lenient judges (for whom incarceration was less common) had better outcomes (Aizer and Doyle 2011) The impact of Social Security disability payments on labor market participation is an important policy question, but difficult to address with conventional analyses because the probability of receiving such payments is highly correlated with the extent of disability. A recent analysis used the fact that applications for such payments are adjudicated by arbitrarily assigned case reviewers, some of whom are more likely to decide favorably than others. Thus, the average approval rate of the assigned case reviewer can be used as an IV to estimate the effects of payments on long-term outcomes (Maestas et al. 2013). In both of these cases, the LATE could be of greater interest than the population average effect. The relevant policy question is not whether disability payments should be provided to the most profoundly disabled (they should be) or to individuals with no serious disability (they should not), but rather for “marginal” cases, about whose eligibility reasonable people might disagree. These people are precisely the group to whom the IV estimate based on differences in case reviewer approval rates refers under the monotonicity assumption. Similarly, the IV estimate based on differences in juvenile judges refers to effects on children about whom judges disagree. Preference-based instruments have been criticized because the monotonicity assumption seems unlikely to be strictly met (Imbens 2014). As discussed earlier, other assumptions can be adopted to estimate alternative causal parameters, such as the effect of treatment on the treated (Hernán and Robins 2006). These alternatives may be more appealing for preference-based instruments than the LATE interpretation.
Genetic Variants as Instrumental Variables
With the availability of genetic information on ever larger samples, the idea of exploiting genetic variations to draw inferences regarding the causal effects of modifiable risk factors (“Mendelian randomization studies”) is increasingly appealing (Davey Smith 2004). The essence of a Mendelian randomization design is to use information on genetic polymorphisms as IVs to estimate the health effects of a phenotype regulated by the genotypes (Davey Smith and Ebrahim 2004; Thomas and Conti 2004; Lawlor et al. 2008). Genetic information is largely established at conception, based on random allocation during meiosis. Post-meiotic changes in genetic loci are rare and in general genetic code cannot be influenced by the socioeconomic or behavioral characteristics that are commonly considered confounders in health research (Twfieg and Teare 2011).
Mendelian randomization is directly relevant for social epidemiology if we can identify genetic factors that are plausible instrumental variables for social determinants. There are two major challenges in using Mendelian randomization approaches to estimate health effects of social conditions: identifying genes that have any effects on social factors, and providing compelling evidence that the relevant genes operate only via the social factor in question. The field is changing rapidly, but, as of now, the former challenge is more salient. Few genes are established predictors of social conditions, and those that have been identified have tiny effects, and therefore have very limited statistical power as IVs.
Recent research identified genetic loci associated with educational attainment (Rietveld et al. 2013; Okbay et al. 2016), and anticipated larger meta-analyses may identify additional loci. Assuming that these genetic associations are replicated in other studies, these loci might be candidate instruments for estimating the causal effect of educational attainment on any disease or outcome of interest. The caveat is that if the genes operate via influencing cognitive skills (Rietveld et al. 2014), behavioral patterns, personality traits, or health conditions that influence educational attainment, these cognitive skills, behaviors, personality traits, or health conditions may have direct health effects not mediated by education, thus violating the IV assumptions (Nguyen et al. 2016).
The weak associations between genetic variants and phenotypes of interest is not unique to social epidemiology: single genetic loci often explain very little of the variation of complex phenotypes such as blood pressure, body fat, or heart disease. A notable exception to this is the impact of the ABO blood group locus on wait time for organ transplant. Because O blood type individuals have a much smaller pool of potential organ donors than AB blood type recipients, their wait time for a match is routinely longer. Blood type is therefore a popular IV to evaluate the impact of wait time on transplant-related outcomes (Howard 2000). This is rarely conceptualized as a Mendelian randomization design, presumably because blood type is not typically evaluated based on genotype. Regardless, the ABO gene is an exception and small effects of genetic variants are much more common in genetic IV studies.
Statistical power in genetic IV studies can be improved by increasing the sample size or combining multiple genetic polymorphisms into a more powerful IV. Larger sample sizes are certainly important, but the necessary sample sizes are often unrealistic. When combining multiple genetic loci to create a single IV, the strength of the first-stage association is substantially improved. Small improvements in the first-stage association can provide large statistical power improvements (Figure 19.5). Potential problems with weak instruments bias can be overcome by using separate sample IV, jackknifing, or combining multiple polymorphisms into a weighted count (Burgess and Thompson 2013; Freeman et al. 2013; Tchetgen Tchetgen et al. 2013). Polygenic scores calculated based on external weights—for example, weights derived from genome-wide association studies of the endogenous variable or phenotype—can also be used to test hypotheses about endogenous variables that have not even been assessed in the sample, but whose presence or absence is merely inferred from the genetic liability (Pierce and Burgess 2013). In this procedure, the first stage of the 2SLS is effectively borrowed from another study, the predicted exposure in the study population is calculated based on the other studies' genetic effect estimates, and the outcome of interest is regressed directly on this polygenic score. The caveat, as with any separate sample approach, is that we must assume that the effect of the IV on the endogenous variable is the same in both samples.
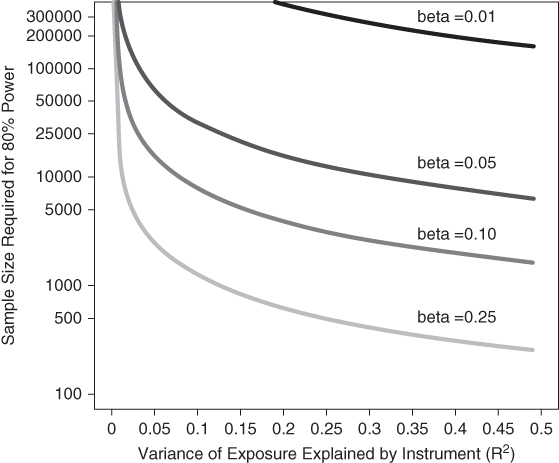
FIGURE 19.5 SAMPLE SIZE REQUIRED TO ACHIEVE 80% POWER AT α = 0.05 WITH IMPROVEMENTS IN THE FIRST-STAGE ASSOCIATION
This figure relies on the power calculation as described in Freeman et al. (2013). It assumes a linear probability model for the outcome of type 2 Diabetes and a single polygenic score or gene as the IV to estimate the effect of a unit change in BMI on the probability of type 2 diabetes, assuming a true risk difference of 0.1 per unit difference in BMI.
Using genetic variables as instruments requires attention to potential sources of statistical associations between genetic polymorphisms. Statistical correlations between polymorphisms (i.e., people who carry a minor allele for gene 1 are also likely to carry the minor allele for gene 2) emerge because some genetic loci are physically close to each other on the chromosome and therefore tend to be inherited together. Even if gene 1 influences our outcome of interest only via its effect on the phenotype of interest, if this gene is in linkage disequilibrium with another genetic variant that also influences the outcome, it is not a valid IV. Human mating patterns also produce statistical correlations between various polymorphisms. Mating in human populations is of course not random: parents tend to be correlated with respect to geographical region of origin, ethnic identity, religious traditions, socioeconomic status, and other factors that may affect health. These phenomena lead to shared ancestry and population stratification, for example, a similarity in the genetic profiles in specific subgroups, that can introduce confounding (Cardon and Palmer 2003). These challenges appear to be largely remediable with increasingly detailed genetic information, for example, allowing comprehensive ancestry characterizations, although this might depend on the strength of social stratification of the phenotypes under consideration.
Mendelian randomization studies are often criticized on the grounds that single genes may affect multiple phenotypes. This phenomenon is referred to as genetic pleiotropy and such a process could violate the exclusion restriction for a valid IV if the gene products independently affect the outcome under study. This is clearly a more serious concern in social epidemiology, because the “phenotypes” of greatest interest to us, although potentially partially influenced by genetics, are farther downstream from the genetic code. As we move our interest to more complex, downstream phenotypes, the potential for exclusion restriction violations increases. Such violations would typically lead to false positive associations, not false negatives, so it is less of a concern when the Mendelian randomization study provides null effect estimates. Regardless, the tools for evaluating the IV assumptions are just as relevant for genetic IVs as for policy or other types of IVs (Bowden et al. 2015; Glymour et al. 2012).
In the absence of convincing genetic IVs to estimate the health effects of social conditions, many research questions in social epidemiology may be indirectly addressed via Mendelian randomization designs. Such indirect applications include evaluating the effects of biological or health-related phenotypes on social outcomes, for example, evaluating the effects of obesity on educational attainment, experiences of discrimination, or marriage formation. The approach could help evaluate “reverse causation,” from health to SES, as a source of health inequalities. Important questions on how one person's health is affected by the health of his or her social network members may also be effectively addressed using Mendelian randomization. Finally, many of the most pressing questions in social epidemiology relate to mediators of social inequalities, but such mediators often appear hopelessly confounded. For example, efforts to evaluate the extent to which racial disparities in stroke are mediated by BMI may be stymied by numerous unmeasured potential common causes of BMI and stroke. Adopting genetic IVs for BMI could allow unbiased estimates of the effect of BMI on stroke among blacks and whites, and allow for the possibility of differential direct effects of race on stroke depending on BMI.
Natural Experiments When the Endogenous Variable Is Unmeasured
Some natural experiments may not be amenable to calculating a classic two-stage IV estimate, for example, because a direct measure of the treatment is not available. The number of days in the school term seems a promising instrument for estimating the effect of time in a school classroom on health: term length varied substantially between US states in 1900 and increased in most states between 1900 and 1950. An IV effect estimate cannot be directly calculated, however, because the amount of time in the classroom is not measured in epidemiology studies. Years of schooling is typically the most detailed available education measure, but years of schooling will have the same value for someone who completed 10 years of school in a 180-day term length school as for someone who completed 10 years of school in a 120-day term length school, although the former student would have spent 50% more time in the classroom. Assuming that longer term lengths increase the average amount of time a student spends in the classroom, even if actual classroom time is unknown, we can still use the reduced form coefficient (ITT estimate) to test the hypothesis that classroom time affects health. We cannot directly calculate the IV estimate without additional assumptions about the unobserved number of days in a classroom.
Just as in RCTs, there are some situations in which the ITT estimate rather than the IV estimate may be of primary substantive interest. If a natural experiment arises from a policy change, for example, the ITT estimate gives the estimated effect of the policy change on the health of the whole population. For example, if we are considering increasing compulsory schooling and wish to know the average population health impact of such a change, the ITT estimate might be most relevant. If, however, we are considering a range of possible policies to increase average schooling, and we wish to know what the effect of an additional year of schooling might be, we would be more interested in the IV estimate. For the IV estimate from such analyses to be useful, we must assume that the effects of a year of schooling elicited by a compulsory schooling law are equivalent to the effects of a year of schooling elicited by the other policy options.
Although natural experiments without measures of the primary exposure can be informative, a good natural experiment combined with solid measurement of the exposure variable is invaluable. During the Dutch Famine Winter of 1944, the Netherlands was occupied by German soldiers and food access for urban residents was restricted in retaliation for resistance activities. The calorie restrictions were very severe, and the timing of calorie restriction is fairly well documented. As a result, a host of studies have been generated focusing on infants conceived and born during the Famine Winter, and showing how calorie restriction at specific sensitive time points affects a number of health outcomes (Susser and Stein 1994; Susser et al. 1999). This approach is parallel to separate sample IV approaches, in that typically evidence on the impact of pregnancy timing on caloric intake is derived from historical data on food availability, and this information is linked to individual-level health outcomes (i.e., we never know the actual maternal caloric intake for any individual in the study).
Proxy Instruments, Conditional Instruments, and Unnecessary Instruments
A valid instrument need not directly affect the exposure of interest. A variable may be a valid instrument in some cases if it is merely statistically associated with this exposure. For example, if a variable Z2 shares a common cause with the exposure and that common cause is itself a valid instrument (i.e., Z1 in Figure 19.2), and no confounders influence both Z2 and the outcome, then Z2 is a valid instrument (Pearl 2009, p. 248). Such “proxy” instruments are essential in most implementations of Mendelian randomization studies, in which genetic variants are used as IVs, because the polymorphisms used as genetic IVs are rarely thought to be the causal loci. When using a proxy IV, the monotonicity assumption may not seem plausible. Various alternatives to the monotonicity assumption (discussed above) may be more appealing to support causal inferences based on a proxy IVs (Hernán and Robins 2006).
Some instruments may be valid only after conditioning on a measured covariate. A common prior cause of the instrument and the outcome renders the instrument invalid, unless that confounder can be measured and statistically controlled. Instruments with no such common prior cause are far more appealing than instruments that can be “fixed” by statistical adjustment.
An instrument Z may be valid for estimating the effect of X on Y but invalid for estimating the effect of X on some other outcome W. For example, there may be no common prior causes of Z and Y but several common prior causes of Z and W. In many cases, however, the substantive argument for the instrument validity for one exposure–outcome combination extends to other outcomes.
The 2SLS technique is sometimes confused with propensity score models, because the first step in both methods is to model the predicted value of the exposure of interest. The approaches have different goals and are technically distinct. The goal of propensity score modeling is to improve adjustment for measured confounders of the exposure–outcome association. The goal of IV analysis is to derive an unbiased effect estimate even when we have not measured all of the important confounders of the exposure outcome association. The second stage of a propensity score model would adjust for both observed exposure and the propensity score. The second stage of a 2SLS IV model regresses the outcome variable on all the covariates and the predicted value of the exposure (X), but excludes the actual value of exposure.
In some situations, IV models are not helpful. If the research question of interest is not about causal effects, IV analyses are unnecessary. For example, many models have a stated goal of predicting an outcome, such as a future major medical event (myocardial infarction, stroke, hospitalization), with the intent of prioritizing resources for some individuals, guiding treatment plans, motivating behavior change, or identifying potential study participants. In such predictive models, it does not matter whether the components of the model are causal or merely spuriously associated with the outcome; highly confounded exposures may even be desirable to improve predictive models. IV analyses are not necessary or useful in this context.
Limitations of IV Analyses
If conventional effect estimates, based on covariate adjustment or matching, are unbiased, these would typically be preferable to IV estimates. Conventional effect estimates are likely to be much more precisely estimated than IV estimates; informally, this is because the IV estimate is identified only on the individuals whose exposure was determined by the IV. Lack of precision poses an important challenge when evaluating IV models. A recent paper even noted that the imprecision of typical IV estimates is so severe that in many plausible epidemiology studies, the mean squared error (MSE) of an IV effect estimate would be worse than the MSE of a conventional estimate even if the conventional estimate were substantially confounded (Boef et al. 2014). IV estimates are often so imprecise as to be consistent with both the null hypothesis of no effect and a non-null conventional effect estimate. One response to such a pattern of findings is to conclude that the conventional estimate is unbiased (because it is not statistically distinguishable from the IV estimate) and conclude the non-null conventional effect estimate is valid. An alternative response is to conclude that there is no effect of exposure on outcome, given that the IV estimate is null, and disregard the conventional effect estimate. Both approaches depend on inappropriate interpretations of p-value thresholds and, to our knowledge, there is no a priori rule about which approach is preferable; the judgment depends on qualitative features of the results and strength of background assumptions. In general, if the confidence intervals for the IV effect estimate indicate that it is consistent with both the null and the observational effect estimates, there is no reason to always preference the null estimate. In Mendelian randomization studies, this challenge has been addressed by meta-analyzing IV effect estimates from multiple studies (C Reactive Protein Coronary Heart Disease Genetics Collaboration 2011).
The most devastating critique of an IV analysis is that the instrument is not valid because it either directly affects the outcome or it has a common prior cause with the outcome. If the instrument derives from an ecological variable, these concerns are especially pertinent. The weaker the instrument, that is, the worse the non-adherence, the greater is the dependence of the IV estimate on the assumption of a valid instrument. The adjustment for compliance in the IV estimator simultaneously inflates any bias in the ITT estimate. Even a small association between the instrument and the outcome that is not mediated by the exposure of interest can produce serious biases in IV effect estimates for the exposure. For this reason, criticisms of the validity of the instrument must be taken seriously, even if they hypothesize fairly small relationships.
A common error in IV analyses is to incorporate information on the endogenous variable incorrectly. Using the measured values of the endogenous variable, rather than the predicted values based on the IV, throws away the strengths of the IV, just as adopting an as-treated or per-protocol analysis in an RCT throws away the strengths of the RCT. Swanson et al. recently identified a more subtle problem that arises with endogenous variables with three or more possible values, if people with one or more of these values are excluded from analyses (Swanson et al. 2015b). For example, consider an evaluation of the effects of vocational education for high school graduates on long-term chronic disease risk, assuming that high school graduates may pursue vocational education, college education, or no further education. Although it may seem natural to use an IV analysis to contrast the effect of receiving vocational education to pursuing no further education, excluding any individuals who attended college, this is a form of conditioning on the endogenous variable and may induce important bias in the IV analysis. It is easy to see that if the IV influences probability of attending college, it will change the selection process for any analysis excluding the college graduates, thus potentially biasing analyses of the remaining sample.
A more prosaic challenge in interpreting IV estimates from natural experiments is fully understanding what the instrument influences, that is, the specific endogenous variable affected by the instrument and how this corresponds with the exposure as it is typically measured. For example, compulsory schooling laws affect the age children begin school, the age children leave school (and enter the labor market), the amount of time children spend in a classroom, the schooling credentials children receive, and whether or not they are exposed to occupational hazards at very young ages. It is possible to tell a story focusing on any of these phenomena as the crucial mediator between compulsory schooling laws and health. This is one reason it is extremely appealing to use multiple instruments to disentangle such correlated but conceptually distinct treatments.
Conclusion
Distinguishing between causal and non-causal explanations for the association between social risk factors (interpreted broadly) and health is crucial in order to identify potential interventions. Epidemiology, and social epidemiology in particular, is troubled by a fundamental dilemma. The RCT is often considered the “gold standard” for estimating causal effects (Byar et al. 1976; Abel and Koch 1999; DeMets 2002), but observational designs are essential for exposures that cannot be randomly assigned in a trial for practical or ethical reasons. Social gradients in health are extremely well documented, but the extent to which these gradients are “causal” is still hotly debated (Smith 1999; Glymour et al. 2014), in part because of the difficulties of randomizing the exposure. Insisting on RCTs as the only valid source of evidence rules out the pursuit of many critically important lines of research.
In the absence of RCTs, epidemiologists typically rely on covariate adjustment or stratification to estimate causal parameters from observational data. Researchers often reason that if several studies find similar results in various populations, this provides compelling evidence that the relationship is causal. Frequently, however, each study adjusts for a similar set of covariates, and is thus subject to a similar set of biases. Each study rests on the same assumptions and these assumptions are never directly tested. Repeating similar study designs in this context provides very little new information. Although some investigators have reported remarkable consistency between effect estimates from well-designed observational studies and randomized controlled trials (Benson and Hartz 2000; Concato et al. 2000; Anglemyer et al. 2014), troubling inconsistencies have also been documented (Omenn et al. 1996; Rossouw et al. 2002; Ioannidis 2005). Discrepancies between RCT results and observational studies of high-profile epidemiologic questions have reinvigorated the debate about the reliability of causal inferences in the absence of trial data.
Despite the difficulty of conducting full-scale randomized trials of social exposures, natural experiments occur with regularity. IV analyses, when applied to data from these natural experiments, offer useful causal tests because they are based on different, albeit strong, assumptions. The assumptions for a valid instrument are very strong, and small violations can lead to large biases (Bound et al. 1995). The core critique of any IV analysis is that the instrument influences the outcome in question through some pathway other than the exposure of interest. The major strength of the IV approach is that the assumptions for valid estimation are generally quite different from the assumptions for valid causal estimates from ordinary regressions. When regression models have repeatedly demonstrated an association, an additional regression estimate adds little new information because the analysis depends on the same assumptions. IV analyses of data from a natural or quasi-experiment, however, are generally premised on a different set of assumptions, which may (or may not) be more palatable. At a minimum, natural experiments and IV analyses provide a valuable complement to other analytic tools for examining causal relations in social epidemiology.
References
- Abel, U. and Koch, A. (1999) The role of randomization in clinical studies: myths and beliefs. Journal of Clinical Epidemiology, 52 (6), 487–497.
- Aizer, A. and Doyle, J.J., Jr (2011) Juvenile Incarceration and Adult Outcomes: Evidence from Randomly-Assigned Judges. NBER Working Paper.
- Anglemyer, A., Horvath, H.T., et al. (2014) Healthcare outcomes assessed with observational study designs compared with those assessed in randomized trials. The Cochrane Library.
- Angrist, J. and Pischke, J. (2009) Mostly Harmless Econometrics: An Empiricist's Companion, Princeton University Press, Princeton, NJ.
- Angrist, J.D., Imbens, G.W., et al. (1999) Jackknife instrumental variables estimation. Journal of Applied Econometrics, 14 (1), 57–67.
- Angrist, J.D., Imbens, G.W., et al. (1996) Identification of causal effects using instrumental variables. Journal of the American Statistical Association, 91 (434), 444–455.
- Angrist, J.D. and Krueger, A.B. (1991) Does compulsory school attendance affect schooling and earnings? The Quarterly Journal of Economics, 106 (4), 979–1014.
- Angrist, J.D. and Krueger, A.B. (1992) The effect of age at school entry on educational attainment: an application of instrumental variables with moments from two samples. Journal of the American Statistical Association, 87 (418), 328–336.
- Angrist, J.D. and Krueger, A.B. (2001) Instrumental variables and the search for identification: from supply and demand to natural experiments. Journal of Economic Perspectives, 15 (4), 69–85.
- Balke, A. and Pearl, J. (1997) Bounds on treatment effects from studies with imperfect compliance. Journal of the American Statistical Association, 92 (439), 1171–1176.
- Banks, J. and Mazzonna, F. (2012) The effect of education on old age cognitive abilities: evidence from a regression discontinuity design. The Economic Journal, 122, 418–448.
- Bao, Y., Duan, N., et al. (2006) Is some provider advice on smoking cessation better than no advice? An instrumental variable analysis of the 2001 National Health Interview Survey. Health Services Research, 41 (6), 2114–2135.
- Barnard, J., Du, J.T., et al. (1998) A broader template for analyzing broken randomized experiments. Sociological Methods and Research, 27 (2), 285–317.
- Barr, C.D., Diez, D.M., et al. (2012) Comprehensive smoking bans and acute myocardial infarction among Medicare enrollees in 387 US counties: 1999–2008. American Journal of Epidemiology, 176 (7), 642–648.
- Benson, K. and Hartz, A.J. (2000) A comparison of observational studies and randomized, controlled trials. New England Journal of Medicine, 342 (25), 1878–1886.
- Berkman, L.F. (2009) Social epidemiology: social determinants of health in the United States: Are ee losing ground? Annual Review of Public Health, 30 (1).
- Boef, A.G., Dekkers, O.M., et al. (2014) Sample size importantly limits the usefulness of instrumental variable methods, depending on instrument strength and level of confounding. Journal of Clinical Epidemiology 67 (11), 1258–1264.
- Bound, J. and Jaeger, D.A. (1996) On the Validity of Season of Birth as an Instrument in Wage Equations: A Comment on Angrist and Krueger's “Does compulsory school attendance affect schooling and earnings?” National Bureau of Economic Research. Working Paper 5835, p. 27.
- Bound, J., Jaeger, D.A., et al. (1995) Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. Journal of the American Statistical Association, 90 (430), 443–450.
- Bowden, J., Davey Smith, G., and Burgess, S. (2011) Mendelian randomization with invalid instruments: effect estimation and bias detection through Egger regression. International Journal of Epidemiology, 44 (2), 512–525.
- Bowden, J. and Vansteelandt, S. (2011) Mendelian randomization analysis of case-control data using structural mean models. Statistics in Medicine, 30 (6), 678–694.
- Brookhart, M.A., Rassen, J.A., et al. (2010) Instrumental variable methods in comparative safety and effectiveness research. Pharmacoepidemiology and Drug Safety, 19 (6), 537–554.
- Buckles, K.S. and Hungerman, D.M. (2013) Season of birth and later outcomes: old questions, new answers. Review of Economics and Statistics, 95 (3), 711–724.
- Burgess, S. and Thompson, S.G. (2013) Use of allele scores as instrumental variables for Mendelian randomization. International Journal of Epidemiology, 42 (4), 1134–1144.
- Byar, D.P., Simon, R.M., et al. (1976) Randomized clinical trials. Perspectives on some recent ideas. New England Journal of Medicine, 295 (2), 74–80.
- C Reactive Protein Coronary Heart Disease Genetics Collaboration (2011) Association between C reactive protein and coronary heart disease: Mendelian randomisation analysis based on individual participant data. British Medical Journal, 342.
- Campbell, F.A., Ramey, C.T., et al. (2002) Early childhood education: young adult outcomes from the Abecedarian Project. Applied Developmental Science, 6 (1), 42–57.
- Cardon, L.R. and Palmer, L.J. (2003) Population stratification and spurious allelic association. The Lancet, 361 (9357), 598–604.
- Chotai, J., Forsgren, T., et al. (2001) Season of birth variations in the temperament and character inventory of personality in a general population. Neuropsychobiology, 44 (1), 19–26.
- Clever, S.L., Jin, L., et al. (2008) Does doctor–patient communication affect patient satisfaction with hospital care? Results of an analysis with a novel instrumental variable. Health Services Research, 43 (5 Part1), 1505–1519.
- Concato, J., Shah, N., et al. (2000) Randomized, controlled trials, observational studies, and the hierarchy of research designs. New England Journal of Medicine, 342 (25), 1887–1892.
- Cook, T., Campbell, D., et al. (2006) Experimental and Quasi-experimental Designs for Generalized Causal Inference, Houghton Mifflin.
- Cook, T., Shadish, W., et al. (2008) Three conditions under which experiments and observational studies produce comparable causal estimates: new findings from within-study comparisons. Journal of Policy Analysis and Management, 27 (4), 724–750.
- Currie, J. (1995) Welfare and the Well-Being of Children, Harwood Academic Publishers, Chur, Switzerland.
- Davey Smith, G. (2004) Genetic epidemiology: an “enlightened narrative”? International Journal of Epidemiology, 33 (5), 923–924.
- Davey Smith, G. and Ebrahim, S. (2003) Mendelian randomization”: can genetic epidemiology contribute to understanding environmental determinants of disease? International Journal of Epidemiology, 32 (1), 1–22.
- Davey Smith, G. and Ebrahim, S. (2004) Mendelian randomization: prospects, potentials, and limitations. International Journal of Epidemiology, 33 (1), 30–42.
- DeMets, D.L. (2002) Clinical trials in the new millennium. Statistics in Medicine, 21 (19), 2779–2787.
- Ellenberg, J.H. (1996) Intent-to-treat analysis versus as-treated analysis. Drug Information Journal, 30, 535–544.
- Evans, W.N. and Lien, D.S. (2005) The benefits of prenatal care: evidence from the PAT bus strike. Journal of Econometrics, 125 (1–2), 207–239.
- Evans, W.N. and Ringel, J.S. (1999) Can higher cigarette taxes improve birth outcomes? Journal of Public Economics, 72 (1), 135–154.
- Farmer, M.M. and Ferraro, K.F. (2005) Are racial disparities in health conditional on socioeconomic status? Social Science and Medicine, 60 (1), 191–204.
- Frayling, T.M., Timpson, N.J., et al. (2007) A common variant in the FTO gene is associated with body mass index and predisposes to childhood and adult obesity. Science, 316 (5826), 889–894.
- Freeman, G., Cowling, B.J., et al. (2013) Power and sample size calculations for Mendelian randomization studies using one genetic instrument. International Journal of Epidemiology, 42 (4), 1157–1163.
- Gavrilov, L.A. and Gavrilova, N.S. (1999) Season of birth and human longevity. Journal of Anti-Aging Medicine, 2 (4), 365–366.
- Glymour, M.M., Avendano. M., Kawachi. I. (2014) Socioeconomic status and health, in Social Epidemiology, 2nd edition (eds. L.F. Berkman, I. Kawachi, and M.M. Glymour), Oxford University Press, New York, NY, pp. 17–63.
- Glymour, M.M., Kawachi, I., et al. (2008) Does childhood schooling affect old age memory or mental status? Using state schooling laws as natural experiments. Journal of Epidemiology and Community Health, 62 (6), 532–537.
- Glymour, M.M., Tchetgen Tchetgen, E., et al. (2012) Credible Mendelian randomization studies: approaches for evaluating the instrumental variable assumptions. American Journal of Epidemiology, 175 (4), 332–339.
- Gorey, K.M. (2001) Early childhood education: a meta-analytic affirmation of the short- and long-term benefits of educational opportunity. School Psychology Quarterly, 16 (1), 9–30.
- Gortmaker, S.L., Kagan, J., et al. (1997) Daylength during pregnancy and shyness in children: results from northern and southern hemispheres. Developmental Psychobiology, 31 (2), 107–114.
- Greene, W.H. (2000). Econometric Analysis, Prentice-Hall, Upper Saddle River, NJ.
- Greenland, S. (2000) An introduction to instrumental variables for epidemiologists. International Journal of Epidemiology, 29 (4), 722–729.
- Greenland, S., Pearl, J., et al. (1999) Causal diagrams for epidemiologic research. Epidemiology, 10 (1), 37–48.
- Hennekens, C.H. and Buring.J.E. (1987) Epidemiology in Medicine, Little, Brown and Company, Boston and Toronto.
- Hernán, M.A. (2004) A definition of causal effect for epidemiological research. Journal of Epidemiology and Community Health, 58 (4), 265–271.
- Hernán, M.A. and Robins, J.M. (2006) Instruments for causal inference—An epidemiologist's dream? Epidemiology, 17 (4):, 360–372.
- Howard, D. (2000) The impact of waiting time on liver transplant outcomes. Health Services Research, 35 (5 Part 2), 1117–1134.
- Imbens, G. (2014) Instrumental variables: an econometrician's perspective. Statistical Science, 29 (3), 323–358.
- Ioannidis, J.P. (2005) Contradicted and initially stronger effects in highly cited clinical research. Journal of the American Medical Association, 294 (2), 218–228.
- Kaufman, J.S., Kaufman, S., et al. (2003) Causal inference from randomized trials in social epidemiology. Social Science and Medicine, 57 (12), 2397–2409.
- Kennedy, P. (2008) A Guide to Econometrics, Sixth Edition. MIT Press, Cambridge, MA.
- Lawlor, D.A., Harbord, R.M., et al. (2008) Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Statistics in Medicine, 27 (8), 1133–1163.
- Liebman, J.B., Katz, L.F., et al. (2004) Beyond treatment effects: estimating the relationship between neighborhood poverty and individual outcomes in the MTO experiment. Princeton Industrial Relations Section, Princeton NJ, pp. 1–42.
- Link, C., Ratledge, E., et al. (1976) Black–white differences in returns to schooling—some new evidence. American Economic Review, 66 (1), 221–223.
- Lipsitch, M., Tchetgen Tchetgen, E., et al. (2010) Negative controls: a tool for detecting confounding and bias in observational studies. Epidemiology (Cambridge, Mass.), 21 (3), 383.
- Lleras-Muney, A. (2002) Were compulsory attendance and child labor laws effective? An analysis from 1915 to 1939. Journal of Law and Economics, 45 (2), 401–435.
- Locke, A.E., Kahali, B., et al. (2015) Genetic studies of body mass index yield new insights for obesity biology. Nature, 518 (7538), 197–206.
- Ludwig, J., Sanbonmatsu, L., et al. (2011) Neighborhoods, obesity, and diabetes—a randomized social experiment. New England Journal of Medicine, 365 (16), 1509–1519.
- Maestas, N., Mullen, K.J., et al. (2013) Does disability insurance receipt discourage work? Using examiner assignment to estimate causal effects of SSDI receipt. American Economic Review, 103 (5), 1797–1829.
- Malkin, J.D., Broder, M.S., et al. (2000) Do longer postpartum stays reduce newborn readmissions? Analysis using instrumental variables. Health Services Research, 35 (5 Part 2), 1071–1091.
- Mayer, S.E. and Knutson, D. (1999) Does the timing of school affect learning? in Earning and Learning: How Schools Matter (eds S.E. Mayer and P.E. Petterson), Brookings Institution Press, Washington, DC, pp. 79–102.
- McCarrey, A.C. and Resnick, S.M. (2015) Postmenopausal hormone therapy and cognition. Hormones and Behavior, 74, 167–172.
- McClellan, M.B. and Newhouse, J.P. (2000) Overview of the special supplement issue. Health Services Research, 35 (5 Part 2), 1061–1069.
- McClellan, M., McNeil, B.J., et al. (1994) Does more intensive treatment of acute myocardial infarction in the elderly reduce mortality? Analysis using instrumental variables. Journal of the American Medical Association, 272 (11), 859–866.
- Montori, V.M. and Guyatt, G.H. (2001) Intention-to-treat principle. Canadian Medical Association Journal, 165 (10), 1339–1341.
- Mortensen, P.B., Pedersen, C.B., et al. (1999) Effects of family history and place and season of birth on the risk of schizophrenia. New England Journal of Medicine, 340 (8), 603–608.
- Mullahy, J. (1997) Instrumental-variable estimation of count data models: applications to models of cigarette smoking behavior. Review of Economics and Statistics, 79 (4), 586–593.
- Nagelkerke, N., Fidler, V., et al. (2000) Estimating treatment effects in randomized clinical trials in the presence of non-compliance. Statistics in Medicine, 19 (14), 1849–1864.
- Newhouse, J.P. and McClellan, M. (1998) Econometrics in outcomes research: the use of instrumental variables. Annual Review of Public Health, 19, 17–34.
- Nguyen, T., Tchetgen Tchetgen, E., et al. (2016) Instrumental variable approaches to identifying the causal effect of educational attainment on dementia risk. Annals of Epidemiology, 26 (1), 71–76.
- Oakes, J. (2004) The (mis)estimation of neighborhood effects: causal inference for a practicable social epidemiology. Social Science and Medicine, 58 (10), 1929–1952.
- Okbay, A., Beauchamp, J.P., Fontana, M.A., et al. (2016) Genome-wide association study identifies 74 loci associated with educational attainment. Nature, 533 (7604), 539–542.
- Omenn, G.S., Goodman, G.E., et al. (1996) Risk factors for lung cancer and for intervention effects in CARET, the Beta-Carotene and Retinol Efficacy Trial. Journal of the National Cancer Institute, 88 (21), 1550–1559.
- Osypuk, T., Tchetgen Tchetgen, E.J., Acevedo-Garcia, D., et al. (2012) Differential mental health effects of neighborhood relocation among youth in vulnerable families: results from a randomized trial. Archives of General Psychiatry, 69 (12), 1284–1294.
- Palmer, T.M., Sterne, J.A., et al. (2011) Instrumental variable estimation of causal risk ratios and causal odds ratios in Mendelian randomization analyses. American Journal of Epidemiology, 173 (12), 1392–1403.
- Pearl, J. (2009) Causality: Models, Reasoning, and Inference, Cambridge University Press, Cambridge, UK.
- Permutt, T. and Hebel, J.R. (1989) Simultaneous-equation estimation in a clinical trial of the effect of smoking on birth weight. Biometrics, 45 (2), 619–622.
- Pierce, B.L. and Burgess, S. (2013) Efficient design for Mendelian randomization studies: subsample and 2-sample instrumental variable estimators. American Journal of Epidemiology, 178 (7), 1177–1184.
- Rietveld, C.A., Medland, S.E., et al. (2013) GWAS of 126,559 individuals identifies genetic variants associated with educational attainment. Science, 340 (6139), 1467–1471.
- Rietveld, C.A., T. Esko, T., et al. (2014) Common genetic variants associated with cognitive performance identified using the proxy-phenotype method. Proceedings of the National Academy of Sciences, 111 (38), 13790–13794.
- Robins, J.M. and Greenland, S. (1996) Identification of causal effects using instrumental variables—Comment. Journal of the American Statistical Association, 91 (434), 456–458.
- Rossouw, J.E., Anderson, G.L., et al. (2002) Risks and benefits of estrogen plus progestin in healthy postmenopausal women: principal results from the Women's Health Initiative randomized controlled trial. Journal of the American Medical Association, 288 (3), 321–333.
- Schneeweis, N., Skirbekk, V., et al. (2014) Does education improve cognitive performance four decades after school completion? Demography, 51 (2), 619–643.
- Smith, J.P. (1999) Healthy bodies and thick wallets: the dual relation between health and economic status. Journal of Economic Perspectives, 13 (2), 145–166.
- Sobel, M.E. (2006) What do randomized studies of housing mobility demonstrate? Causal inference in the face of interference. Journal of the American Statistical Association, 101 (476), 1398–1407.
- Speliotes, E.K., Willer, C.J., et al. (2010) Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nature Genetics, 42 (11), 937–948.
- Staiger, D., and Stock, J.H. (1997). Instrumental variables regression with weak instruments. Econometrica, 65 (3), 557–586.
- Susser, M. and Stein, Z. (1994) Timing in prenatal nutrition—a reprise of the Dutch Famine Study. Nutrition Reviews, 52 (3), 84–94.
- Susser, E.B., Brown, A., et al. (1999) Prenatal factors and adult mental and physical health. Canadian Journal of Psychiatry–Revue Canadienne De Psychiatrie, 44 (4), 326–334.
- Swanson, S.A. and Hernán, M.A. (2013) Commentary: how to report instrumental variable analyses (suggestions welcome). Epidemiology, 24 (3), 370–374.
- Swanson, S.A., Miller, M., et al. (2015a). Definition and evaluation of the monotonicity condition for preference-based instruments. Epidemiology, 26 (3), 414–420.
- Swanson, S.A., Robins, J.M., et al. (2015b). Selecting on treatment: a pervasive form of bias in instrumental variable analyses. American Journal of Epidemiology, 181 (3), 191–197.
- Tchetgen Tchetgen, E. (2013) Estimation of risk ratios in cohort studies with a common outcome: a simple and efficient two-stage approach. The International Journal of Biostatistics, 9 (2), 251–264.
- Tchetgen Tchetgen, E. (2014) A note on the control function approach with an instrumental variable and a binary outcome. Epidemiologic Methods, 3 (1), 107–112.
- Tchetgen Tchetgen, E.J. and Vansteelandt, S. (2013) Alternative Identification and Inference for the Effect of Treatment on the Treated with an Instrumental Variable. Harvard University Biostatistics Working Paper Series, Harvard School of Public Health, Boston, MA.
- Tchetgen Tchetgen, E.J., Walter, S., et al. (2013) Commentary: building an evidence base for Mendelian randomization studies: assessing the validity and strength of proposed genetic instrumental variables. International Journal of Epidemiology, 42 (1), 328–331.
- Thomas, D.C. and Conti, D.V. (2004) Commentary: the concept of “Mendelian randomization.” International Journal of Epidemiology, 33 (1), 21–25.
- Twfieg, M.E. and Teare, M.D. (2011) Molecular genetics and genetic variation. Methods in Molecular Biology, 713, 3–12.
- Unger, J.B., McAvay, G., et al. (1999) Variation in the impact of social network characteristics on physical functioning in elderly persons: MacArthur studies of successful aging. Journals of Gerontology Series B–Psychological Sciences and Social Sciences, 54 (5), S245–S251.
- VanderWeele, T.J., Tchetgen Tchetgen, E.J., et al. (2014) Interference and sensitivity analysis. Statistical Science: A Review Journal of the Institute of Mathematical Statistics, 29 (4), 687
- Wacholder, S. (1986) “Binomial regression in GLIM: estimating risk ratios and risk differences. American Journal of Epidemiology, 123 (1), 174–184.
- Wang, P.S., Schneeweiss, S., et al. (2005) Risk of death in elderly users of conventional vs. atypical antipsychotic medications. New England Journal of Medicine, 353 (22), 2335–2341.
- Weber, G.W., Prossinger, H., et al. (1998) Height depends on month of birth. Nature, 391 (6669), 754–755.
- Weiss, N.S. (1998) Clinical epidemiology, in Modern Epidemiology (eds K.J. Rothman and S. Greenland), Lippincott-Raven,Philadelphia, PA, pp. 519–528.
- Welch, F. (1973) Black–white differences in returns to schooling. American Economic Review, 63 (5), 893–907.
- Winship, C. and Morgan, S.L. (1999) The estimation of causal effects from observational data. Annual Review of Sociology, 25, 659–706.
- Wooldridge, J.M. (2002) Introductory Econometrics: A Modern Approach, Sixth Edition, Cengage Learning, Boston, MA.
- Zou, G. (2004) A modified Poisson regression approach to prospective studies with binary data. American Journal of Epidemiology, 159 (7), 702–706.