CHAPTER 4

NUMBER: THE FUNDAMENTAL CONCEPT

A marvelous neutrality have these things Mathematical, and also a strange participation between things supernatural, immortal, intellectual, simple, and indivisible, and things natural, mortal, sensible, compounded and divisible.

JOHN DEE (1527–1608)

4–1  INTRODUCTION

Just as we are inclined to accept the sun, moon, and stars as our birthright and do not appreciate the grandeur, the mystery, and the knowledge which can be gleaned from the contemplation of the heavens, so are we inclined to accept our number system. There is, however, this difference. Many of us would not claim the latter and would gladly sell it for a mess of pottage. Because we are forced to learn about numbers and operations with numbers while we are still too young to appreciate them—a preparation for life which hardly excites our interest in the future—we grow up believing that numbers are drab and uninteresting. But the number system warrants attention not only as the basis of mathematics, but because it contains weighty and beautiful ideas which lend themselves to powerful applications.

Among past civilizations, the Greeks best appreciated the wonder and power of the concept of number. They were, of course, a people with great intellectual perception, but perhaps because they viewed numbers abstractly, they saw more clearly their true nature. The very fact that one can abstract from many diverse collections of objects a property such as “fiveness” struck the Greeks as a marvelous discovery. If one may use the ridiculous to accentuate the sublime, one may say that the Greek delight in numbers was the rational counterpart of the hysteria which many young and old Americans experience when they encounter numbers in the form of baseball scores and batting averages.

4–2  WHOLE NUMBERS AND FRACTIONS

The first Greeks who, to our knowledge, expressed their satisfaction with numbers and propounded a philosophy based on numbers which is extremely alive and vital today were the Pythagoreans. This group was founded in the middle of the sixth century B.C. by Pythagoras. We know rather little that is certain about this man. However, it seems very likely that he was born in 569 B.C. in a Greek settlement on the island of Samos in the Aegean Sea. Like many other Greeks he traveled to Egypt and to the Near East to learn what these older civilizations had to offer, and then settled in Croton, another Greek city in southern Italy. Pythagoras and his followers were among the early founders of the great Greek civilization, and so it is not surprising to find that the rational attitude which characterizes the Greeks was still surrounded in his times with mystical and religious doctrines prevalent in Egypt and its eastern neighbors. In fact the Pythagoreans were a religious sect as well as students of philosophy and nature.

Membership in the group was restricted, and the members were pledged to secrecy. Among their religious doctrines was the belief that the soul was tainted by the body. To purify the soul they maintained celibacy; their religious practices were also supposed to be efficacious in purifying the soul. At death the soul was reincarnated in another human or an animal. Like most mystics they observed certain taboos. They would not touch a white cock, walk on the highways, use iron to stir a fire, or leave the marks of ashes on a pot.

The secrecy of the group, its aloofness, and an attempted interference in the political affairs of Croton finally aroused the people of this city to drive out the Pythagoreans. We do not know for certain what happened to Pythagoras. One story has it that he fled to Metapontum, another Greek city in southern Italy, and was murdered there. However, the Pythagoreans continued to be influential in Greek intellectual life. One of their notable members was the philosopher Plato.

The Pythagoreans were impressed with numbers and, because they were mystics, attached to the whole numbers meanings and significances which we now regard as childish. Thus, they considered the number “one” as the essence or very nature of reason, for reason could produce only one consistent body of doctrines. The number “two” was identified with opinion, clearly because the very meaning of opinion implies the possibility of an opposing opinion, and thus of at least two. “Four” was identified with justice because it is the first number which is the product of equals. Of course, one can also be thought of as 1 times 1, but to the Pythagoreans one was not a number in the full sense because it did not represent quantity. The Pythagoreans represented numbers as dots in sand or by pebbles, and for each number the dots or pebbles had a special arrangement. Thus the number “four” was pictured as four dots suggesting a square, and so the square and justice were also linked. Foursquare and square shooter still mean a person who acts justly. “Five” signified marriage because it was the union of the first masculine number, three, and the first feminine number, two. (Odd numbers were masculine and even numbers feminine.) The number “seven” represented health and “eight,” friendship or love.

We shall not pursue all the ideas which the Pythagoreans developed about numbers. What is significant about their work is that they were the first to study properties of whole numbers. As we shall see in a later chapter, they also possessed the vision of deep mystics and saw that numbers could be used to represent and even embody the essence of natural phenomena.

The speculations and results obtained by the Pythagoreans about whole numbers and ratios of whole numbers, or fractions as we prefer to call them, were the beginning of a long and involved development of arithmetic as a science as opposed to arithmetic as a tool for daily applications. During the 2500 years since the Pythagoreans first called attention to the importance of numbers, man has not only learned to better appreciate the idea but has invented excellent methods of writing quantity and of performing the four operations of arithmetic, i.e., ambition, distraction, uglification, and derision, as Lewis Carroll called them. While these methods of writing and operating with numbers are largely familiar, there are a few facts which are worthy of comment.

One of the most important members of our present number system is the mathematical representation of no quantity, that is, zero. We are accustomed to this number and yet usually fail to appreciate two facts about it. The first is that this member of our number system came rather late. The idea of using zero was conceived by the Hindus and, like other of their ideas, reached Europe through the Arabs. It had not occurred to earlier civilizations, even to the Greeks, that it would be useful to have a number which represents the absence of any objects. Connected with this late appearance of the number is the second significant fact, namely, that zero must be distinguished from nothing. Undoubtedly it was the inability of earlier peoples to perceive this distinction which accounts for their failure to introduce the zero. That zero must be distinguished from nothing is easily seen from several examples. A student’s grade in a course he never took is no grade or nothing. He may, however, have the grade of zero in a course he has taken. If a person has no account in a bank, his balance is nothing. If he has a bank account, he may very well have a balance of zero.

Because zero is a number, we may operate with it; for example, we may add zero to another number. Thus 5 + 0 = 5. By contrast 5 + nothing is meaningless or nothing. The only restriction on zero as a number is that one cannot divide by zero. Division by zero does, so to speak, produce nothing. Because so many false steps in mathematics result from division by zero, it is well to understand clearly why we cannot do this. The answer to a problem of division, say , is some number which when multiplied by the divisor yields the dividend. In our example, 3 is the answer because 3 · 2 = 6. Hence the answer to should be a number which when multiplied by 0 gives 5. However, any number multiplied by 0 gives 0 and not 5. Thus, there is no answer to the problem of . In the case of the answer should be some number which when multiplied by 0 yields the dividend 0. However, any number may then serve as a quotient because any number multiplied by 0 gives 0. But mathematics cannot tolerate such an ambiguous situation. If arises and any number may serve as an answer, we do not know what number to take and hence are not aided. It is as if we asked a person for directions to some place and he replied, Take any direction.

With the availability of zero, mathematicians were finally able to develop our present method of writing whole numbers. First of all we count in units and represent large quantities in tens, tens of tens, tens of tens of tens, etc. Thus we represent two hundred and fifty-two by 252. The left-hand 2 means, of course, two tens of tens; the 5 means 5 times 10; and the right-hand 2 means 2 units. The concept of zero makes such a system of writing quantities practical since it enables us to distinguish 22 and 202. Because ten plays such a fundamental role, our number system is called the decimal system, and ten is called the base. The use of ten resulted most likely from the fact that man counted on his fingers and, when he had used the fingers on his two hands, considered the number arrived at as a larger unit.

Because the position of an integer determines the quantity it represents, the principle involved is called positional notation. The decimal system of positional notation is due to the Hindus; however, the same scheme was used two millenniums earlier by the Babylonians, but with base 60 and in more limited form since they did not have zero.

The operations of arithmetic, addition, subtraction, multiplication, and division, are of course familiar to us, but it is perhaps not recognized that these operations are quite sophisticated and remarkably efficient. They date back to Greek times and gradually evolved, as improvements in the methods of writing numbers and the concept of zero were introduced. The Europeans picked up the methods from the Arabs. Previously the Europeans had used the Roman system of writing numbers, and the operations were based on that system. Partly because these latter methods were relatively cumbersome and partly because education was limited to a few people, those who acquired the art of calculation were regarded as skilled mathematicians. In fact the processes defied the average man so much that it seemed to him that those possessed of the ability must have magical powers. Good calculators were called practitioners of the “Black Art.”

To appreciate the efficiency of our present methods we would have to learn the older ones and even acquire some facility in them, to make the comparison a fair one. But we cannot spare the time and effort. Perhaps the one point we should emphasize is how much our methods of arithmetic depend upon positional notation. This can be seen even in a simple problem of addition. To add 387 and 359 say, the written work is

However, in performing this work, we think as follows. We add the units 7 and 9, the “tens” quantities 8 and 5, and the “hundreds” 3 and 3, separately. When we add the 7 and 9, we obtain 16. We recognize that 16 is 1 · 10 + 6, and so we add the 1 · 10 to the 13 · 10 already obtained from the 8 and 5. We say that we “carry” the 1 · 10 over, and instead of 13 · 10 we obtain 14 · 10. However, 14 · 10 is (10 + 4) · 10 or 1 · 10² + 4 · 10. Thus we write 4 in the tens’ column, add the 1 · 10² to the 6 · 10² already obtained from the 3 and 3, and arrive at 7 · 10². All these steps are usually executed rather mechanically by writing the appropriate numbers in the units’, tens’, and hundreds’ places and by using the process called carrying. Were we to analyze the processes of subtraction, multiplication, and division, we would again see how the steps which we learn mechanically in elementary school are just the skeletal processes of thinking suited to positional notation in base ten.

A word about fractions may also be in order. The natural method of writing fractions, for example, or , to express parts of a whole presents no difficulties of comprehension. However the operations with fractions do seem to be somewhat arbitrary and mysterious. To add and , say, we go through the following process:

What we have done is to express each fraction in an equivalent form such that the denominators are now alike, and then add the numerators. We are not required by law to add fractions in this manner. It would, of course, be much simpler if we agreed to add fractions by adding the numerators and adding the denominators so that

As a matter of fact, when we multiply two fractions, we do multiply the numerators and multiply the denominators so that it does seem as though the mathematicians prefer to be unnecessarily complicated about the addition of fractions.

The explanation of this seeming mathematical idiosyncrasy is simple: the operations with fractions are formulated to fit experience. When one has of a pie and of a pie, he has in all not but of a pie. In other words, if mathematical concepts and operations are to fit experience, the nature of the operations is forced upon us. In the case of multiplication of fractions it is correct that multiplying the numerators and multiplying the denominators will yield the fraction which represents the physical result. Thus suppose we had to find of , that is · . We think of as 2 · . Now

Then

The same result is obtained by multiplying the original numerators and multiplying the original denominators.

The operation of dividing one fraction by another presents a little more difficulty. To see how we arrive at the correct process let us start with some simple examples. Suppose we had to answer the question of how many one-thirds of a pie are in 2 pies. Mathematically this question is formulated as how much is

We should note that one bar is larger than the other and the longer bar separates the numerator, the 2, from the denominator . Now, we know on physical grounds that we can obtain 6 one-thirds from 2 pies. We can obtain this answer arithmetically by inverting the denominator and multiplying the inverse into the numerator 2. That is,

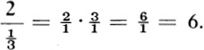
Now let us complicate the problem slightly. How many two-thirds of a pie are contained in 2 pies? Again this question is formulated mathematically as

We know on physical grounds that there are 3 two-thirds of a pie in 2 pies. We can obtain this answer arithmetically by inverting the denominator and multiplying this inverse fraction into the numerator. Thus,

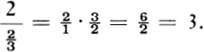
Now let us complicate the problem still more. We would certainly agree that 2 pies are the same as pies. If therefore we had to answer the question of how many two-thirds of a pie are contained in pies, we would know from the preceding example that the answer is 3. How could we obtain this answer directly? The question is, how much is

Let us invert the denominator and multiply the inverse into the numerator. Thus

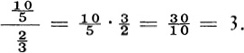
Again we see that the process of inverting the denominator and multiplying it into the numerator gives the result which we know on physical grounds is correct.

The significant point, then, is that the rule “to divide one fraction by another, invert the denominator and multiply this inverse into the numerator” is designed to make the mathematical operation give a result which fits experience. This is, of course, the same principle which applies to the other operations. Logically, we may say that we define the operations to be what we have just illustrated for addition, multiplication and division, and in our purely mathematical definitions we do not say anything about agreement with physical facts. But, of course, the definitions would be pointless if they did not give physically correct results.

Fractions, like the whole numbers, can be written in positional notation. Thus

If we now agree to suppress the powers of 10, that is 10, 100, and higher powers where they occur, then we can write . The decimal point reminds us that the first number is really , the second , and so forth. The Babylonians had employed positional notation for fractions, but they used base 60 rather than base 10, just as they had for whole numbers. The decimal base for fractions was introduced by sixteenth-century European algebraists. Of course, the operations with fractions can also be carried out in decimal form.

The disappointing feature of the decimal representation of fractions is that some simple fractions cannot be represented as decimals with a finite number of digits. Thus when we seek to express as a decimal, we find that neither 0.3, nor 0.33, nor 0.333, and so on, suffices. All one can say in this and similar cases is that by carrying more and more decimal digits one comes closer and closer to the fraction, but no finite number of digits will ever be the exact answer. This fact is expressed by the notation

where the dots indicate that we must keep on adding threes to approach the fraction more and more closely.

From the standpoint of applications the fact that some fractions cannot be expressed as decimals with a finite number of digits does not matter because we can always carry enough digits to obtain an answer as accurate as the application requires.

EXERCISES

1.  What is the principle of positional notation?

2.  Why is the number zero almost indispensable in the system of positional notation?

3.  What is the meaning of the statement that zero is a number?

4.  What two methods are there of representing fractions?

5.  What principle determines the definitions of the operations with fractions?

4–3  IRRATIONAL NUMBERS

The Pythagoreans, as we noted earlier, were the first to appreciate the very concept of number, and sought to employ numbers to describe the basic phenomena of the physical and social worlds. Numbers to the Pythagoreans were also interesting in and for themselves. Thus they liked square numbers, that is, numbers such as 4, 9, 16, 25, 36, and so on, and observed that the sums of certain pairs of square numbers, or perfect squares, are also square numbers. For example, 9 + 16 = 25, 25 + 144= 169, and 36 + 64= 100. These relationships can also be written as

3² + 4² = 5²,    5² + 12² = 13²,   and 6² + 8² = 10².

The three numbers whose squares furnish such equalities are today called Pythagorean triples. Thus 3, 4, 5 constitute a Pythagorean triple because 3² + 4² = 5².

Fig. 4–1

The Pythagoreans liked these triples so much because, among other features, they have an interesting geometrical interpretation. If the two smaller numbers are the lengths of the sides or arms of a right triangle, then the third one is the length of the hypotenuse (Fig. 4–1). Just how the Pythagoreans knew this geometrical fact is not clear, but assert it they did. They also claimed that in any right triangle, the square of the length of one arm added to the square of the length of the other gives the square of the length of the hypotenuse. This more general assertion is still called the Pythagorean theorem and a proof of it, such as we learn in high-school geometry, was given about 200 years later by Euclid. Pythagoras is said to have been so overjoyed with this theorem that he sacrificed an ox to celebrate its discovery.

This theorem proved to be the undoing of a central doctrine in the Pythagorean philosophy and caused woe and misery to many mathematicians. But before we pursue this story, we should look into a few simple properties of the whole numbers which are embodied in the following exercises.

EXERCISES

1.  Prove that the square of any even number is an even number. [Suggestion: By definition every even number contains 2 as a factor.]

2.  Prove that the square of any odd number is an odd number. [Suggestion: Every odd number ends in 1, 3, 5, 7, or 9.]

3.  Let a stand for a whole number. Prove that if a² is even, then a is even. [Suggestion: Use the result in Exercise 2.]

4.  Establish the truth or falsity of the assertion that the sum of any two square numbers is a square number.

There are tragedies in mathematics also, and one of these struck the very group of mathematicians who deserved a better fate. The Pythagoreans had constructed, at least to their own satisfaction, a philosophy which asserted that all natural phenomena and all social and ethical concepts were in essence just whole numbers or relationships among whole numbers. But one day it occurred to a member of the group to examine the seemingly simplest case of the Pythagorean theorem. Suppose each arm of a right triangle (Fig. 4–2) is 1 unit in length; how long, he asked, is the hypotenuse? The Pythagorean theorem says that the square of (the length of) the hypotenuse equals the sum of the squares of the arms. Hence if we call c the unknown length of the hypotenuse, then the theorem says that

c² = 1² + 1²

or

c² = 2.

Fig. 4–2

Now 2 is not a square number, that is, a perfect square, and so c is not a whole number. But it certainly seemed reasonable to this Pythagorean that c should be a fraction; that is, there should be a fraction whose square is 2. Even the simple fraction comes close to being the correct value because , and this is almost 2. However, simple trial does not easily yield a fraction whose square is 2. Hence this Pythagorean became worried, and he decided to investigate the question of whether there is a fraction whose square is 2. We shall examine his reasoning which, as far as we know, is the same as that given in Euclid’s famous work on geometry, the Elements.

The number c which we seek to determine is one whose square is 2. Let us denote it by . All we mean by this symbol is that it represents a number whose square is 2. And now let us suppose that is a fraction a/b, where a and b are whole numbers. Moreover, to make matters simpler, let us suppose that any factors common to a and b are cancelled. Thus if a/b were , for example, we would cancel the common factor 2 and write it as . Hence we have assumed so far that

and that a and b have no common factors.

If equation (1) is correct, then by squaring both sides, a step which utilizes the axiom that equals multiplied by equals give equals (because we multiply the left side by and the right side by a/b), we obtain

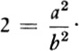
Again by employing the axiom that equals multiplied by equals yield equals, we may multiply both sides of this last equation by b² and write

The left side of this equation is an even number because it contains 2 as a factor. Hence the right side must also be an even number. But if a² is even, then, according to Exercise 3 above, a must be even. If a is even, it must contain 2 as a factor. That is, a = 2d, where d is some whole number. If we substitute this value of a in (2) we obtain

Since then

2b² = 4d²,

we may divide both sides of this equation by 2 and obtain

We now see that b² is an even number and so, by again appealing to the result in Exercise 3, we find that b is an even number.

What we have shown in the above argument is that if , then a and b must be even numbers. But at the very outset we had cancelled any common factors in a and b; yet we find that a and b still contain 2 as a common factor. This result contradicts the fact that a and b have no common factors.

Why do we arrive at a contradiction? Since our reasoning is correct, the only possibility is that the assumption that equals a fraction is not correct. In other words, cannot be a ratio of two whole numbers.

This proof is so neat that one can almost believe the legend that Pythagoras sacrificed an ox in honor of its creation. But there are at least two reasons for discrediting this tale. The first is that if all the legends telling of Pythagoras sacrificing an ox were true, he could not have had time for mathematics. The second reason is that the above proof was not a triumph for the Pythagoreans but a disaster. The symbol is a number because it represents the length of a line, namely the hypotenuse of the triangle in Fig. 4–2. But this number is not a whole number or a fraction. The Pythagoreans had, however, developed an embracing philosophy which asserted that everything in the universe reduced to whole numbers. Clearly, then, this philosophy was inadequate. Indeed the existence of numbers such as was such a serious threat to the Pythagorean philosophy that another legend, more credible, states that the Pythagoreans, who were at sea when the above discovery was made, threw overboard the member who made it, and pledged to keep the discovery secret.

But secrets will out, and later Greeks not only learned that is neither a whole number nor a fraction, but they discovered that there is an indefinitely large collection of other numbers which are not whole numbers or fractions. Thus , , , and, more generally, the square root of any number which is not a perfect square, the cube root of any number which is not a perfect cube, and so on, are numbers which are not whole numbers or fractions. The number π, which is the ratio of the circumference of any circle to its diameter, is also neither a whole number nor a fraction. All these new numbers are called irrational numbers, the word “irrational” now meaning that these numbers cannot be expressed as ratios of whole numbers, although in Pythagorean times it meant unmentionable or unknowable.

If these irrational numbers are really so common and represent lengths of sides of triangles and circumferences of circles in terms of the diameters, why weren’t they encountered before? Didn’t the Babylonians and Egyptians run across them? They did. But since they were concerned only with having numbers serve their practical purposes, they used convenient approximations. Thus, when they encountered a length such as , they were content to use a value such as 1.4 or 1.41. For π, as we noted in an earlier chapter, they used values even as crude as 3. Not only did these peoples use such approximations, but they never realized that the most complicated fraction or decimal could never represent an irrational number exactly. The Egyptians and Babylonians treated irrational numbers and their mathematics in general rather lightheart-edly. We may hail their blithe spirits, but mathematicians they never were.

The Greeks, as we know, were of a different intellectual breed and could not be content with approximations, but they also exhibited a weakness. Although they recognized that quantities exist which are neither whole numbers nor fractions, they were so convinced that the concept of number could not comprise anything else than whole numbers or fractions that they did not accept irrationals as numbers. Instead they thought of such quantities only as geometrical lengths or areas. Thus the Greeks never did develop an arithmetic of irrational numbers. In their astronomical work, for example, they used only whole numbers and fractions. The difficulty which the Greeks experienced also baffled all mathematicians up to modern times. The greatest mathematicians refused to accept irrationals as numbers and followed the Greek procedure of thinking about such quantities as lengths or areas. All these people wished that the Pythagoreans had thrown all irrational numbers overboard rather than the man who discovered them.

But the needs of society often oblige even mathematicians to face unpleasantnesses. In the seventeenth century, science began to develop at an amazing rate, and science needs quantitative results. It may be nice to know that is a certain length and that · is an area, but this knowledge does not suffice when one needs numerical results. And so finally mathematicians had to accept the fact that if they were to treat numerically all the quantities that arise in scientific work, they must handle irrational numbers as numbers. The mathematicians’ refusal over centuries to grant irrationals the status of numbers illustrates one of the surprising features of the history of mathematics. New ideas are often as unacceptable in this field as they are in politics, religion, and economics.

The situation, then, which must be faced squarely is that there are other numbers besides whole numbers and fractions. It is, of course, quite understandable that whole numbers and fractions should have been created and used first, for these numbers arise in the simplest physical situations man encounters. The irrational numbers on the other hand are not commonly encountered. Only the application of a theorem such as the Pythagorean theorem brings them to our attention, and even then one must go through a proof such as that examined above, to see that they are not whole numbers or fractions. But the fact that irrational numbers are late-comers does not mean that they are less acceptable or less genuine numbers. Just as we gradually add to our knowledge of the varieties of human beings and animals which exist in our physical world, so must we broaden our knowledge of the varieties of numbers and with true liberality accept these strangers on the same basis as the already familiar numbers.

However, if we are to use irrational numbers, we must know how to operate with them, that is, how to add, subtract, multiply, and divide them. We have already noted with whole numbers and fractions that if we wish the operations to fit experience, we must formulate the operations accordingly. So it is with the irrational numbers. We could define addition, multiplication, and the other operations as we please. But if we wish these operations to represent physical situations, we must define them properly. However, there is no real difficulty here. Since irrational numbers are quantities, as are whole numbers and fractions, we may use the latter as a guide to the proper operations with irrational numbers.

Let us consider a few examples which will be sufficient to indicate the general principles. Should we say that

To answer this question let us consider the analogous question: May we say that

It is clear in the latter case that 2 + 3 does not equal , for is certainly less than 4. Hence we should not add the radicands, that is, the 2 and the 3, in the preceding equation. One might then ask, How much is ? Since both summands are numbers, the sum is also a number, but it cannot be written more compactly than . This inability to combine the summands is not something new or troublesome. When we add 2 and , for example, the answer continues to be . We usually omit the plus sign and write , but the summands are really not combined.

Let us consider next whether

Here too we shall see what the analogous operation with whole numbers suggests. Is it true that

The answer is clearly yes, and so we shall agree that to multiply square roots we shall multiply the radicands. That is,

The definitions of the operations of subtraction and division are also readily determined. Thus yields a definite number, but the difference cannot be written any more compactly than .

For division, say , the procedure, as in the case of multiplication, is suggested by observing that

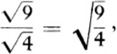
for this equation simply says that . Hence we shall agree that

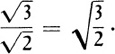
The general principle which these examples illustrate is that operations with irrational numbers are defined so as to agree with the same operations on whole numbers when the latter are expressed as roots. We could state our definitions in general form, but there is no need to do so.

In applications we often approximate irrational numbers by fractions or decimals because actual physical objects cannot be constructed exactly anyway. Thus if we had to construct a length which strictly should be , we would approximate . Since (1.4)² = 1.96 and 1.96 is nearly 2, we could approximate by 1.4. If we desired a more accurate approximation, we might determine to the nearest hundredth the number whose square approximates 2. Thus, since

(1.41)² = 1.988    and    (1.42)² = 2.016,

we see that 1.41 is a good two-decimal approximation of . We could, of course, improve still more on the accuracy of the approximation. We should, however, realize that no matter how many decimal places we employed, we would never obtain a number which is exactly because any decimal with a finite number of digits or a whole number plus such a decimal is just another way of writing a fraction, whereas , as the above proof showed, can never equal a quotient of two whole numbers.

The fact that we often approximate an irrational number when we wish to construct something raises a question which merits an answer. The question is, Why don’t we approximate irrational numbers wherever they arise and forget about operations with irrationals as such? For example, to calculate , we could approximate by, say 1.41, approximate by 1.73, and then multiply 1.41 by 1.73. The answer is 2.44, and since (2.44)² is 5.95, we see that we have a good approximation to . If we wanted a more accurate answer, we could approximate and more closely and then multiply. One reason we do not approximate in mathematics proper is that mathematics is an exact science. It insists on reasoning as rigorous as human beings can perform. We pay a price for this rigor by expending more thought and effort, but we shall see that mathematics has made its contributions just because it insists on exactness.

There is also a practical advantage in working with irrational numbers as such. Let us suppose that some problem required us to calculate , that is, . The person who insists on approximating would now approximate to some number of decimal places, for example, 1.732, and then calculate (1.732)⁴ While the practical person takes an hour to calculate and check his arithmetic, the mathematician would see at once that

and could spend the rest of the hour in refreshing sleep. Moreover, the mathematician’s answer is exact, whereas the practical man’s answer is not accurate even to the four demical places with which he started, because the product of two approximate numbers is less accurate than either factor. To achieve an answer accurate to four decimal places, the practical man would have to use an approximation of containing seven decimal places and then multiply.

The irrational number is the first of many sophisticated ideas which the mathematician has introduced to think about and cope with the real world. The mathematician creates these concepts, devises ways of working with them which fit real situations, and then uses his abstractions to think about the phenomena to which the ideas apply.

EXERCISES

1.  Express the answers to the following problems as compactly as you can:

    a)  

    b)  

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

    i)   

    j)   

    k)  

2.  Simplify the following:

    a)  

    b)  

    c)  

[Suggestion: ]

3.  Criticize the following argument: No irrational number can be expressed as a decimal with a finite number of decimal places. The number cannot be expressed as a decimal with a finite number of decimal places. Hence is an irrational number.

4–4  NEGATIVE NUMBERS

One more addition to the number system which has considerably extended the power of mathematics comes from far-off India. Numbers are commonly used to represent an amount of money, in particular the amount of money which a person owns. Perhaps because the Hindus were in debt more often than not, it occurred to them that it would also be useful to have numbers which represent the amount of money one owes. They therefore invented what are now called negative numbers, while the previously known numbers are called positive numbers. Thus numbers which we denote by −3, −, and − came into existence. Where necessary to distinguish clearly positive from negative numbers or to emphasize what is positive as opposed to what is negative, one writes +3 or + instead of 3 or .

It is not necessary, incidentally, to use such symbols as −3 to represent the negative counterpart to 3. Modern banks and large commercial corporations, which deal with negative numbers continually, often write these in red ink, whereas positive numbers are written in black ink. However, we shall find that placing the minus sign in front of a number to indicate a negative number is a convenience.

The use of positive and negative numbers is not limited to the representation of assets and debts. One represents temperatures below 0° as negative temperatures, while temperatures above 0° are positive. Likewise heights above and below sea level can be represented by positive and negative numbers, respectively. It is sometimes convenient to represent time after and before a specified event by positive and negative numbers. For example, using the birth of Christ as the event, the year 50 B.C. can just as well be described as the year −50.

To derive more use from the concept of negative numbers it must be possible to operate with them just as we operate with positive numbers. The operations with negative numbers and with negative and positive numbers together are easy to understand if one keeps in mind the physical significance of these operations. For example, suppose a man has assets of 3 dollars and debts of 8 dollars. What is his net wealth? Clearly the man is 5 dollars in debt. The same calculation is represented in terms of positive and negative numbers by stating that the amount 8 dollars must be taken from 3 dollars, that is, 3 − 8, or that a debt of 8 dollars must be added to assets of 3 dollars, that is, + 3 + (− 8). The answer is obtained by subtracting the smaller numerical value (that is, the smaller number without regard to sign) from the larger numerical value and giving the answer the sign attached to the larger numerical value. That is, we subtract 3 from 8 and call the answer negative because the larger numerical value, namely 8, has the minus sign attached to it.

Since negative numbers represent debts and subtraction usually has the physical meaning of “taking away” or “removing,” then the subtraction of a negative number means the removal of a debt. Thus, if a person has assets of, say 3 dollars, but this figure already takes into account a debt of 8 dollars, the removal or cancellation of the debt leaves the person with assets of 11 dollars. Mathematically we say +3 − (− 8) = + 11. In words, to subtract a negative number we add the corresponding positive number.

Suppose a man goes into debt at the rate of 5 dollars per day. Then in 3 days after a given date he will be 15 dollars in debt. If we denote a debt of 5 dollars as −5, then going into debt at the rate of 5 dollars per day for 3 days can be stated mathematically as 3 · (−5) = −15. That is, the multiplication of a positive and a negative number yields a negative number whose numerical value is the product of the two given numerical values.

In the very same situation in which a man goes into debt at the rate of 5 dollars per day, his assets three days before a given date are 15 dollars more than they are at the given date. If we represent time before the given or zero date by −3 and the loss per day as −5, then his relative financial position 3 days ago can be expressed as − 3 · (− 5) = + 15; that is, to consider his assets three days ago, we would multiply the debt per day by −3, whereas to calculate the financial status three days in the future, we multiply by +3. Hence the result is +15 in the former case compared to − 15 in the latter.

There is one more definition concerning negative numbers which is readily seen to be sensible. For the positive numbers and zero we say for obvious reasons that 3 is greater than 2, that 2 is greater than , and that any positive number is greater than zero. The negative numbers are said to be less than the positive numbers and zero. Moreover, we say that −5 is less than −3, or that − 3 is greater than −5. If one thinks of these various numbers as representing people’s wealth, then the agreement concerning their order fits our usual understanding of relative wealth. A person whose financial status is −3 is wealthier than one whose status is −5; one is better off to be 3 dollars than 5 dollars in debt. Incidentally, the symbol > is used to denote “greater than” as in 5 > 3, and the symbol < denotes “less than” as in −5 < −3.

The relative position of the various positive and negative numbers and zero is readily remembered if one visualizes these numbers as points on a line as shown in Fig. 4–3. The figure is really not different from that obtained by moving a thermometer scale into a horizontal position.

Fig. 4–3

The above situations, which illustrate how the definitions of the operations with positive and negative numbers were suggested, are of course by no means the only ones in which positive and negative numbers are employed. Indeed the usefulness of negative numbers would hardly be great were this the case. However, these simple financial transactions show not only how mathematicians arrived at the definitions, but that there is no more mystery about negative numbers than about positive ones. The definitions represent in abstract form what takes place physically, and, as with all numbers, we can think in terms of the abstractions to arrive at a knowledge of physical happenings.

It may be of some comfort to the reader to know that the concept of negative numbers, like the concept of irrational numbers, was resisted by mathematicians for several hundred years. The history of mathematics illustrates the rather significant observation that it is more difficult to get a truth accepted than to discover it. The mathematicians to whom “number” meant whole numbers and fractions found it hard to accept negative numbers as true numbers. They, too, failed to realize for centuries that mathematical concepts are man-made abstractions which can be introduced at will if they can serve useful purposes.

EXERCISES

1.  Suppose a man has $3 and incurs a debt of $5. What is his net worth?

2.  Suppose a man owes $5 and then incurs a new debt of $8. Use negative numbers to calculate his financial condition.

3.  Suppose a man owes $5 and earns $8. Use positive and negative numbers to calculate his net worth.

4.  Suppose a man owes $13, and a debt of $8 is cancelled. Use negative numbers to calculate his net worth.

5.  A man loses money in business at the rate of $100 per week. Let us denote this change in his assets by − 100 and let us denote time in the future by positive numbers and time in the past by negative numbers. How much will the man lose in 5 weeks? How much more was the man worth 5 weeks ago?

4–5  THE AXIOMS CONCERNING NUMBERS

In the preceding chapter we said that mathematics proceeds by deductive reasoning from explicitly stated axioms. Yet thus far in this chapter we have said nothing about axioms. The reason is simply that the axioms concerning numbers are such obvious properties that we use them automatically without realizing that we are doing so.

This situation may perhaps be better understood by means of an analogy. Whenever a child at play throws a ball up into the air, he expects that the ball will come down. He is really assuming that all balls thrown up will come down. Of course, this assumption is well founded in experience; nevertheless, the child’s expectation that the ball will come down is a deduction from the assumption just stated and the additional premise that he is throwing a ball up into the air. Recognition of the fact that he has made an assumption makes clear the reasoning, conscious or unconscious, behind the act.

To understand the deductive process in the mathematics of numbers, as well as in geometry, we must recognize the existence and use of the axioms. We do not hesitate to say that 275 + 384= 384 + 275. Surely we did not add 384 objects to 275, count the total, then add 275 objects to 384, count that total, and check that the two totals agree. Rather, whenever in our experience we combined two groups of objects, we found that we obtained the same total collection regardless of whether we put the first group with the second or the second with the first. Of course, our evidence to the effect that the order of addition is immaterial is limited to a small number of cases, whereas in practice we use this fact with all numbers. Hence, we are really making an assumption, namely, that for any two numbers a and b, integral, fractional, irrational, and negative, the order of addition will not affect the result. Thus our assumption also includes the affirmation that . It is important for another reason to recognize that this assumption is being made. Numbers are not apples or cows. They are abstractions from physical situations. Mathematics works with these abstractions in order to deduce information about physical situations. However, if the axioms are not well chosen, the deductions will not apply. Hence it is well to note what assumptions are being employed and to ascertain that they are well founded in experience.

Let us, therefore, note the axioms which we have been using and will continue to use. The first axiom is the one discussed in the preceding paragraph:

AXIOM 1. For any two numbers a and b,

a + b = b + a.

The axiom is called the commutative axiom of addition because it says that we can commute or interchange the order of the two numbers to be added. We note that subtraction is not commutative, that is, 3 − 5 does not equal 5 − 3.

If we had to calculate 3 + 4 + 5, we could first add 4 to 3 and then add 5 to this result, or we could add 5 to 4, and then add this result to 3. Of course, the result is the same in the two cases, and this is exactly what our second axiom says.

AXIOM 2. For any numbers a, b, and c,

(a + b) + c = a + (b + c).

This axiom is called the associative axiom of addition because we can associate the three numbers in two different ways in performing the addition.

The two axioms we have just discussed have their analogues for the operation of multiplication.

AXIOM 3. For any two numbers a and b,

a · b = b · a.

This axiom is called the commutative axiom of multiplication. Incidentally, the dot which is used to denote multiplication is omitted if there is no danger of misunderstanding. Thus, we could as well write ab = ba. The axiom is clearly a property of numbers; yet we sometimes fail to recognize that it is applicable. Many a student hesitates to write 5 · a instead of a · 5. But the commutative axiom says that the two expressions are equal. We might note in this context that the operation of division is not commutative, for 4 ÷ 2 does not equal 2 ÷ 4.

AXIOM 4. For any three numbers a, b, and c,

(ab)c = a(bc).

This axiom is called the associative axiom of multiplication. Thus (3·4)5 = 3(4·5).

We also find in our work with numbers that it is convenient to use the number 0. To recognize formally that there is such a number and that it has the properties which its physical meaning requires, we state another axiom.

AXIOM 5. There is a unique number 0 such that

    a)  0 + a = a for every number a,

    b)  0 · a = 0 for every number a,

    c)  if ab = 0 then either a = 0 or b = 0 or both are 0.

The number 1 is another whose properties are somewhat special. Again, we know from the physical meaning of 1 just what its properties are, but if one is to justify the operations with 1 by appealing to axioms rather than to physical meaning, there must be a statement which tells us just what these properties are. In the case of 1, it is sufficient to specify a sixth axiom.

AXIOM 6. There is a unique number 1 such that

1 · a = a

for every number a.

In addition to adding and multiplying any two numbers, we also have physical uses for the operations of subtraction and division. We know that given any two numbers a and b, there is a number c which results when b is subtracted from a. From a practical standpoint, it is helpful to recognize that subtraction is the inverse operation to addition. What this means is simply that if we have to find the answer to 5 − 3 we can and, in fact, do ask ourselves what number added to 3 gives 5. If we know addition, we can then answer the subtraction problem. Even if we obtain the answer by a special subtraction process, and we do in the case of large numbers, we check it by adding the result to what we subtracted to see if it gives the original number or minuend. Hence a subtraction problem such as 5 − 3 = x really asks for what number x added to 3 gives 5, that is, x + 3 = 5.

In our logical development of the number system we wish to affirm that we can subtract any number from any other number and we phrase this statement so that the meaning of subtraction is precisely what it is, the inverse of addition.

AXIOM 7. If a and b are any two numbers, there is a unique number x such that

a = b + x.

Of course, the quantity x is what we usually denote by a − b.

The relation of division to multiplication is also that of an inverse operation. When we seek the answer to we may happen to know directly from experience that the answer is 4. But if we don’t, we can reduce the division problem to a multiplication problem and ask what number, x, multiplied by 2 gives 8, and if we know multiplication we can find the answer. Here too, as in the case of subtraction, even if we use a special division process such as long division to find the answer, we check the answer by multiplying the divisor by the quotient to see if the product is the dividend. The reason for doing this is simply that the basic meaning of a/b is to find some number x such that bx = a.

In our logical development of the number system we affirm that we can divide any number by any other number (except 0) and we phrase the assertion so that the meaning of division is precisely what it actually is, the inverse of multiplication.

AXIOM 8. If a and b are any two numbers, except that b ≠ 0, then there is a unique number x such that

bx = a.

Of course x is the number usually denoted by a/b.

The next axiom is not quite so obvious. It says, for example, that 3·6 + 3·5 = 3(6 + 5). In this example we can perform the calculation to see that the left and right sides are equal, but this is really not necessary. Suppose we had 157 cows in one herd and 379 in another, and each herd increased sevenfold. The total number of cattle is then 7 · 157 + 7 · 379. But if the original two herds were one herd with 157 + 379 cows, and this single herd increased sevenfold, we would have 7(157 + 379) cows. It is physically clear that we have the same number of cows now as before, that is, that 7 · 157 + 7 · 379 = 7(157 + 379). Stated in general terms, the axiom is:

AXIOM 9. For any three numbers a, b, and c,

ab + ac = a(b + c).

This axiom, called the distributive axiom, is very useful. For example, to calculate 571 · 36 + 571 · 64 we can apply the axiom to state that this quantity is 571(36 + 64) or 571 · 100 or 57,100. We say often that we have factored the quantity 571 out of the sum 571 · 36 + 571 · 64.

We should note that from

ab + ac = a(b + c)

we can also state that

ba + ca = (b + c)a,

because in each term of the first equation we can apply the commutative axiom of multiplication to change the order of the factors.

We often use the second form of the distributive axiom. Thus, suppose a is some number and we wish to calculate 5a + 7a. We can replace this sum by (5 + 7) a, and obtain 12a.

The distributive axiom is also applicable in the following situation. Suppose we have to calculate

One might be tempted to cancel the two numbers 296. But this is incorrect. The given fraction means

and the distributive axiom tells us that we may write instead

In addition to the above axioms, we have the following evident properties of numbers:

AXIOM 10. Quantities equal to the same quantity are equal to each other.

AXIOM 11. If equal quantities are added to, subtracted from, multiplied with, or divided into equal quantities, the results are equal. However, division by zero is not permitted.

The set of axioms we have just given is not complete; that is, it does not form the logical basis for all of the properties of the positive and negative whole numbers, fractions, and irrational numbers. However, the set does provide the logical basis for what is usually done with numbers in ordinary algebra. Moreover, it does give some idea of what the axiomatic basis for mathematical work with numbers amounts to.

Now that we have the axioms, what do we do with them? We can prove theorems about numbers. Let us consider a few examples. Negative numbers were introduced to represent physical happenings such as debts or time before a given event. When we examined the physical situation in which we wished to use these numbers, we found that if the numbers are to be useful then we should agree that, for example,

– 2 · 3 = –6   and   –2 · (–3) = 6.

There we agreed to operate with positive and negative numbers so as to make the results fit the physical situation. In the deductive approach to numbers we prove on the basis of our axioms that certain theorems are correct. Let us prove that a positive number times a negative number is negative.

Let a and b be positive numbers. Then − b is a negative number; for example, −b = −5. We shall prove that a(− b) = −ab. We know by Axiom 7, wherein we let a be 0, that if b and 0 are given, then there is a number x such that b + x = 0. This number x is denoted by 0 − b or −b. Then

b + (–b) = 0.

Now we can multiply both sides of this equation by a, and since equals multiplied by equals give equals, we have

a[b + (–b)] = a · 0.

Now a · 0 = 0 · a by Axiom 3, and 0 · a = 0 by Axiom 5. By applying the distributive axiom, Axiom 9, to the left-hand side of our equation, we obtain

and now we see that a(– b) is the number which added to ab gives 0. But Axiom 7 says that given ab and 0 (these are the a and b of Axiom 7), there is a unique number x such that

This number x is denoted by 0 − ab or −ab. But equation (1) says that a(–b) is the number which added to ab gives 0. Since there is just one such number which when added to ab gives 0, and that number we know is –ab, it must be be that a(–b) = –ab.

The proof is now complete and yet may not be convincing. The reason is simply that we are so accustomed to operating with numbers on the basis of physical arguments and experience with them that we have not accustomed ourselves to reasoning with numbers on an axiomatic basis.

Let us consider another proof. In Section 4–2 we gave a physical argument to show that if we divide a/b by c/d then we can get the answer by inverting c/d to obtain d/c and then multiplying; that is,

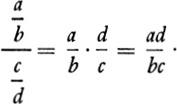
We can prove, on the basis of our axioms, that this rule of inverting the denominator and then multiplying is correct.

To divide a/b by c/d is to find a number x such that

Now Axiom 8 tells us that there is a unique number x which satisfies such an equation. We do know that

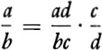
because if we cancel common factors in the numerator and denominator of the right side we obtain a/b. Hence one number which can serve as the x which satisfies equation (3) is ad/bc. But since the value of x is unique, x = ad/bc. Thus the result of dividing a/b by c/d is ad/bc. We note that the answer ad/bc is obtained by multiplying a/b by the inverse of c/d. Hence to divide one fraction by another, we invert the denominator and multiply.

This proof, like the preceding one, may not be convincing, and the reason is the same. We are not accustomed to reasoning about numbers on an axiomatic basis. Rather, we have relied upon the physical meaning of numbers and operations. Historically, the mathematicians did the same thing. They learned to operate with numbers by noting the uses to which numbers were put, and they constructed the axiomatic basis long afterward, just to satisfy themselves that deductive proofs of the properties of numbers could be made.

Since we, too, are accustomed to the properties and operations with numbers since childhood, and we are sure of these properties, we shall not often cite axioms to justify our steps. Thus if we write 3a in place of a · 3, we shall not cite the commutative axiom of multiplication as the justification for this step. In fact, it would be pedantic to do so. The axioms are useful, rather, in helping us to determine what is correct when our experience fails us or leaves us in doubt. However, we should not lose sight of the fact that the mathematics built upon the number system is a deductive system. This point needs emphasis because we begin to learn arithmetic at an early age by rote and thereafter we tend to operate with numbers mechanically without perceiving that we are constantly using axioms of numbers.

EXERCISES

1.  Do you believe that

256(437 + 729) = 256 · 437 + 256 · 729?

Why?

2.  Is it correct to assert that

a(b − c) = ab − ac?

[Suggestion: b − c = b + (−c).]

3. Perform the operations called for in the following examples:

    a)  3a + 9a

    b)  a · 3 + a · 9

    c)  

    d)  7a − 9a

    e)  3(2a + 4b)

    f)   (4a + 5b)7

    g)  a(a + b)

    h)  a(a − b)

    i)   2(8a)

    j)  a(ab)

4.  Carry out the multiplication:

(a + 3)(a + 2).

[Suggestion: Regard (a + 3) as a single quantity and apply the distributive axiom.]

5.  Calculate (n + 1)(n + 1).

6.  If 3x = 6, is x = 2? Why?

7.  If 3x + 2 = 7, is 3x = 5? Why?

8.  Is the equality x² + xy = x(x + y) correct?

9.  Is it correct to assert that

a + (bc) = (a + b)(a + c)?

4–6  APPLICATIONS OF THE NUMBER SYSTEM

Something of the power, methodology, and subtlety of mathematical reasoning can already be seen in the applications which have been made of the several types of number. Indeed, we shall see that these resulted in significant scientific discoveries.

Let us begin with some rather simple matters. Suppose a man drives a car for one mile at 60 miles per hour and for another mile at 120 miles per hour. What is his average speed? We tend to answer this question by applying the common procedure for finding an average. Thus, if a man buys one pair of shoes for $5 and another for $10, the average price is $5 + $10 divided by 2, or $7.50. Hence it would seem as though the average speed in the above problem should be 60 + 120 divided by 2, or 90 miles per hour. However, this answer is not correct. The number 90 is an average in the arithmetic sense, but it is not the average we seek. The average speed should be that speed which would enable the man to drive the two miles in the same time as it took him to drive that distance at the two different speeds. Now, it took the man 1 minute to drive the first mile and it took him minute to drive the second mile. Hence it took him 1 minutes to drive 2 miles. We now ask, what average speed maintained for 1 minutes would cover 2 miles? Since the average speed multiplied by the total time should give the total distance, the average speed is the total distance divided by the total time, that is,

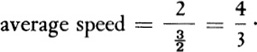
The average speed is then miles per minute or 80 miles per hour.

The point of this example, not a momentous one to be sure, is merely that the unthinking, blind application of arithmetic does not produce the correct result. The notion of average speed serves a physical purpose, and unless we are clear about what average speed is supposed to mean, we shall not profit by the use of arithmetic.

EXERCISES

1.  A man can row a boat in still water at 6 mi/hr. He plans to row upstream for 12 mi and then back in a river whose current flows at 2 mi/hr. Thus his speed upstream is 4 mi/hr and his speed downstream is 8mi/hr. He reasons that his average speed is 6 mi/hr and that the entire trip of 24 mi should therefore take 4 hr. Is this reasoning correct?

2.  Suppose that a merchant sells apples at a price of 2 for 5¢ and oranges at 3 for 5¢. To make his arithmetic simpler he decides to sell any 5 pieces of fruit for 10¢ or at the average price of 2¢ per piece. Thus, if he sells 2 apples and 3 oranges, he sells 5 pieces of fruit at 2¢ each and receives the same 10¢ as if he had sold them at the original separate prices. Is the merchant’s average price correct? [Suggestion: Consider what results if he sells 12 apples and 12 oranges.]

3.  Suppose the merchant wishes to sell a apples and b oranges to some customer at the prices given in Exercise 2. What should the average price be?

4.  Given the data of Exercise 2, is there an average price which would be correct no matter how many apples and how many oranges are sold?

5.  One man can dig a certain ditch in 2 days and another can dig the same ditch in 3 days. What is their average rate of ditch-digging per day?

Let us consider next an application of simple arithmetic to genetics. Suppose we have before us 2 red aces and 2 red kings from the usual deck of 52 cards. How many different pairs consisting of one ace and one king can be put together? Since each ace can be paired with either of 2 kings, there are 2 different pairs for any one ace. Since we have 2 aces, there are 2 · 2 or 4 different pairs.

Now let us suppose that we have 2 red aces, 2 red kings, and 2 red queens. How many different sets consisting of one ace, one king, and one queen can we form with the given cards? We saw above that there are 4 different pairs of aces and kings. With each of these 4 pairs we can place 2 different queens. Hence there are 4 · 2 or 8 different sets of 3 cards. We note that 4 · 2 = 2 · 2 · 2 = 2³.

If we have 2 red aces, 2 red kings, 2 red queens, and 2 red jacks, the number of different sets, each consisting of one ace, one king, one queen, and one jack, can also be readily calculated. Each of the 8 choices of ace, king, and queen can be paired with each of the 2 jacks. Hence there are 8 · 2 or 16 choices in all. Now,

8 · 2 = 4 · 2 · 2 = 2 · 2 · 2 · 2 = 2⁴.

Clearly, if we had 10 different pairs of cards and had to make all possible choices of 10 cards, one from each pair, the number of all possible sets of 10 cards would be

2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 2¹⁰ = 1024.

This simple reasoning about cards has an important application to genetics. The reproductive cells (as well as ordinary cells) of the human male contain 24 pairs of chromosomes. When a sperm cell is formed from the reproductive cell, it contains 24 chromosomes, each coming from one of the 24 pairs. Hence a sperm cell can be formed in 2²⁴ possible combinations. The reproductive cells of the human female also contain 24 pairs of chromosomes. An ovum formed from the female reproductive cell contains 24 chromosomes, each coming from one of the 24 pairs of the reproductive cell. Hence there are 2²⁴ possible ways in which an ovum can be formed. In conception, any one sperm joins, or fertilizes, any one ovum. Since there are 2²⁴ possible sperms and 2²⁴ possible ova, the number of possible chromosome combinations for the fertilized ovum is then

2²⁴ · 2²⁴ = 16,777,216 · 16,777,216 = 281,474,976,710,656.

This is the number of possible variations in the genetic make-up of any one child a man and wife may have. Actually, the number of variations is somewhat larger. Each chromosome contains genes, and these determine the hereditary qualities. Biologists have found that any two paired chromosomes in a reproductive cell may exchange some genes, and this exchange gives rise to new varieties of sperm cells and ova.

EXERCISES

1.  The usual deck of 52 cards contains 4 different aces and 4 different kings. How many different pairs of cards, each pair consisting of one ace and one king, can be formed from the aces and kings?

2.  A manufacturer offers his automobile in 3 different colors, with or without a heater, and with or without a radio. How many different choices can a purchaser make?

3.  A girl has 3 hats, 2 dresses, and 2 pairs of shoes. How many different costumes does she have?

4.  There are six numbers on a die (singular of dice). How many different pairs of numbers can show up on a throw of a pair of dice? The two dice are to be marked so that a throw of a 2 on one die (say A) and of a 5 on the other (say B) can be distinguished from the reverse arrangement (5 on A and 2 on B).

We have already discussed the fact that our method of writing quantities uses the idea of positional notation in base ten (see Section 4–2). However, some civilizations used other numbers as a base. For example, the Babylonians, for reasons that are obscure, selected 60. This system was taken over by the Greek astronomers and was used in Europe for many mathematical and all astronomical calculations as late as the seventeenth century. It still survives in our practice of dividing hours and angles into 60 minutes and 60 seconds. In adopting ten as a base, Europe followed the practice of the Hindus. Let us challenge history and see whether we can derive some advantage from a change to a new base.

We shall choose base six. The quantities from zero to five would be designated by the symbols 0, 1, 2, 3, 4, 5, as in base ten. The first essential difference comes up when we wish to denote six objects. Since six is to be the base, we would no longer use the special symbol 6, but place the 1 in a new position to denote 1 times the base, just as in base ten the 1 in 10 denotes one times the base, or the quantity ten. Hence, to write six in base six, we would write 10, but now the symbols 10 means 1 times six plus 0. Thus the symbols 10 can denote two different quantities, depending upon the base employed. Seven in base six would be written 11, because in base six these symbols mean 1 times six + 1, just as 11 in base ten means 1 times ten + 1. Again the symbols 11 represent different quantities, depending upon the base implied. As another example, to denote twenty-two in base six we write 34, because these symbols now mean 3 times six + 4.

In base ten, to write numbers larger than ninety-nine, we use a third position, the hundreds’ place, to indicate tens of tens. Similarly in base six, when we reach numbers larger than thirty-five, we use a third position to denote sixes of sixes. Thus thirty-eight would be written in base six as 102, wherein the one means 1 times six times six, the 0 means 0 times six, and the 2 denotes just 2 units. To express very large numbers we would use four-place numbers, five-place numbers, and so forth.

We can perform the usual arithmetic operations in base six. However, we would have to learn new addition and multiplication tables. For example, in base ten we write 5 + 3 = 8, whereas in base six, eight must be written 12. Hence our addition table would have to state that 5 + 3 = 12. Likewise, our new multiplication table would have to list 3 · 5 = 23, because fifteen is 2 · 6 + 3 or, in base six, 23. When we learned to use base ten, we had to memorize the result of adding each number from 0 to 9 to every number from 0 to 9, and the result of multiplying each number from 0 to 9 with every number from 0 to 9. For base six we would have to learn to add (and multiply) only numbers from 0 to 5 to (or with) the numbers of this set. Thus our addition and multiplication tables would be shorter, and we would learn arithmetic sooner as youngsters. We might even pass the hurdle of arithmetic so easily that we might get to like mathematics. The only disadvantage of base six would be that to represent large quantities we would have to use more digits. For example, the quantity fifty-four, written as 54 in base ten, must be written as 130 in base six, because fifty-four equals 1 · 6² + 3 · 6 + 0.

There are people who campaign for the adoption of base twelve, because it offers special advantages. For one thing, more fractions can be written as finite decimals in base twelve. Thus must be written as the unending decimal 0.333 . . . in base ten, but can be written as 0.4 in base twelve, since in this base 0.4 means . Also, since the English system of denoting length calls for 12 inches in one foot, we could, for example, express 3 feet and 6 inches as 36 inches in base twelve, whereas to express this number of inches in base ten, we must first calculate 3 · 12 + 6 and then write 42 in base ten. To a limited extent we could use base twelve in our method of recording time. In the United States the day has two sets of twelve hours, and in base twelve the hours of the day would run from 0 to 20. Whereas determining what 7 hours after 6 o’clock will be requires at present some computation, under the addition table for base twelve we would state at once that 7 + 6 = 11. However, base ten is now so widely used that a change to another base for ordinary daily use or commerce is hardly likely.

In the subject of bases we have an idea that was pursued for centuries, largely as an interesting and amusing speculation, but which suddenly became highly important in science and even in the commercial world. For several centuries mathematicians worked on the design of machines which would perform arithmetical computations quickly and thus remove a good deal of the drudgery of arithmetic. Although some types of computing machines were invented and used, mathematicians saw their golden opportunity in the electronic devices developed by modern radio engineers. The key is the radio vacuum tube, which can be made to pass current by applying a voltage to it or can be kept inactive. Two maneuvers are thus possible. In base two all numbers require only two symbols, the 0 and the 1. A typical number would be 1011, which means

1 · 2³ + 0 · 2² + 1 · 2 + 1.

This number can be recorded by the machine by employing four tubes, one for the units’ place, another for multiples of 2, a third for multiples of 2², and a fourth for multiples of 2³. To record 1011, the first, second, and fourth tubes can be activated, and the third, which records the third place in the number, kept inactive. The currents passed by the tubes which “fire” are recorded by the machine in special circuits. Another number can then be fed into the machine. Let us suppose that it is to be added to the first number. The result of having two l’s in the same place means, in base 2, that the sum is to be 0 and a 1 carried over to the next place. This operation is readily performed by the circuits. While this description of an electronic computer certainly doesn’t begin to present the ingenious ideas which engineers and mathematicians have incorporated, we may perhaps see that the workings of a vacuum tube are ideally suited to operations in base two.

To take advantage of the fact that computers can perform calculations in base two, the numbers to be worked on are converted beforehand from base ten to base two and then fed to the machine along with other instructions. The machine then operates in this latter base. The result is, of course, reconverted to base ten.

Because computers work with microsecond speed, they are exceedingly valuable in any commercial or industrial organization which must process a lot of numerical data. Calculations in banks, insurance companies, and in industry, which used to require an immense amount of human labor, are now performed by machines. Computers are the first in a new series of machines which keep track of great quantities of data, select information from millions of cards on which data are recorded, plan factory operations, direct machinery, and may soon provide translations of foreign-language publications.

Electronic computing machines are an enormous boon to science and mathematics also. The arithmetic required to extract concrete information from mathematical formulas is often so lengthy that it would take years to perform these calculations. Computing machines do such work in hours. Moreover, mathematicians no longer hesitate to work on problems which will lead to extensive computations, because they now know that their work will not be in vain.

Computing machines may help us to learn more about the action of the human brain. According to biologists, the nerve cells in the nerve chains and the cells in our brains respond to electrical impulses much as a vacuum tube does. Just as a tube will “fire” when it receives electrical current beyond a certain minimum value and remain inactive otherwise, so do the nerve cells in the nerve chains transmit an electrical impulse to whatever organ they may lead when this impulse exceeds a threshhold value; otherwise they are inactive. Computing machines also have a memory; that is, partial results of calculations are stored automatically in a special device, called the memory. When these results are needed, the memory device releases them. Thus the result of an addition process might be stored in the memory device until the result of some multiplication process is obtained and then, if so instructed, the machine will add these two results. The machine’s memory device, then, functions somewhat like the human memory. Hence, in two respects at least, electronic computing machines simulate the actions of human nerves and memory. Though machines are, in speed, accuracy, and endurance, superior to the human brain, one should not infer, as many popular writers are now suggesting, that machines will ultimately replace brains. Machines do not think. They perform the calculations which they are directed to perform by people who have the brains to know what calculations are wanted. Nevertheless, we undoubtedly have in the machine a useful model for the study of some functions of the human brain and nerves.

EXERCISES

1.  Construct an addition table for base six.

2.  Construct a multiplication table for base six.

3.  Construct an addition and multiplication table for base two.

4.  The following numbers are in base ten:

9, 10, 12, 36, 48, 100.

Write the respective quantities in base six.

5.  The following numbers are in base six:

5, 10, 12, 20, 100.

Write the respective quantities in base ten.

6.  Write the fraction as a decimal in base six.

7.  The quantity 0.2 is in base six. Write the corresponding quantity in base ten.

8.  The number 101 is written in some unknown base and equals ten. What is the base?

9.  Find the least number of weights needed to weigh, to the nearest pound, objects weighing from 0 to 63 lb. The scale to be used contains two pans and the weights are to be put in one pan. [Suggestion: Consider the problem of representing all numbers from 0 to 63 in base 2.]

Some of the most remarkable uses of numbers, which have led to profound discoveries, are found in the study of the structure of matter. During the early and middle part of the nineteenth century, certain basic experimental facts about the varieties of matter found in nature led, after some inevitable fumbling on the part of John Dalton, Amadeo Avogadro, and Stanislav Cannizzaro, to the theory that all matter is made up of atoms. Thus hydrogen, oxygen, chlorine, copper, aluminum, gold, silver, and all other varieties of matter are composed of atoms. Experimental techniques were developed to measure the relative weights of the atoms of different elements. The convenient unit of weight chosen was the weight of the oxygen atom, so that the weight of the atom of oxygen is 16. The weight of the hydrogen atom then proved to be 1.0080, that of copper 63.54, that of gold 197.0, and so on. By this time, too, a number of chemical properties of these various elements, such as their melting temperatures, boiling temperatures, and their ability to combine with other elements to form compounds, had been determined.

The question which had begun to stir the chemists was whether there existed any law or principle which utilized the atomic weights of these elements. The crowning discovery was made in 1869 by Dimitri Ivanovich Mendeléev (1834–1907). He found, as he began to arrange the elements in order of increasing atomic weight, that every eighth element, starting from a given one, had chemical properties similar to the first one. Thus, the gases fluorine and chlorine, the latter the eighth element starting from fluorine, both combine readily with metals. However, as he continued to place each of the 63 different elements known in his time in the eighth position after the one with similar chemical properties, he saw that he had to leave blank spaces. Mendeléev was so much impressed with the periodicity of chemical properties that he did not hesitate to leave the blank spaces and to affirm that there must be elements to fill these spaces. Since each of these missing elements should have chemical properties similar to those of the element found in the eighth position preceding or succeeding the missing element, he could even predict some of the properties of the unknown elements. Mendeléev described the properties of three of the missing elements, and his immediate successors discovered them. These are now called scandium, gallium, and germanium. Still later, others were found. The interesting fact about Mendeléev’s work from the mathematical standpoint is that he had no physical explanation of why elements eight positions removed from one another should have similar chemical properties. He knew only that the number eight was the key to the arrangement, and he followed this mathematical guide faithfully. Long after Mendeléev’s time, other elements, for example helium, were found, which do not fit into this arrangement, but his periodic table is still the basic one which all students of chemistry learn today.

Simple arithmetic continued to play a leading role in subsequent developments of atomic theory. The continuing study of the atomic weights of various elements and their chemical properties showed that elements formerly regarded as pure were really not so. Thus, there are two kinds of hydrogen. These have similar chemical properties, but different atomic weights; in fact, one is twice as heavy as the other. Since both were previously called hydrogen, and since they do, in any case, have similar chemical properties, these two forms of hydrogen are called isotopes of hydrogen. Likewise, there is not one substance, oxygen, but there are three, of atomic weights 16, 17, and 18. Uranium, a very important element today, has two isotopes of atomic weights 238 and 235.

The startling fact which emerged from the discovery of isotopes is that when all isotopes are distinguished and the relative weights of the distinct elements determined, the weight of any one element is within 1% of a whole number. Such a fact can hardly be accidental. The explanation would seem to be that all these elements are really multiples of a single element, namely the lighter isotope of hydrogen, which has the least weight of all elements. In other words, the various elements which previously appeared to be entirely different substances, now were seen to be just smaller or larger collections of the same element, but arranged in special ways peculiar to the substance. (Strictly speaking, the fundamental building block is not the lighter isotope of hydrogen, but what is now called the proton. The lighter hydrogen isotope also has an electron whose weight is insignificant by comparison.)

If all of the different elements are really just aggregates of the lighter hydrogen atom, it should be possible to remove some atoms and convert one substance into another. Thus, we should be able to convert mercury, which is the next heavier element after gold, into gold. And we can. What the medieval alchemists hoped to do on mystical and superficial grounds, we can now do on the basis of far better scientific knowledge. Unfortunately, the cost of converting mercury into gold is too great to make it worth while. But we do have uses for the transmutation of elements which are, in our age, more valued, and which we shall describe in a moment.

A scientist who has a theory cannot afford to overlook even one detail, trivial as it may seem, which does not square with his theory. If all elements are merely combinations of the lighter hydrogen atom, then their weights should be exact multiples of the weight of this atom instead of having values within 1% of such weights. (The electrons in the atoms do not account for the difference.) This discrepancy must be explained. The lightest isotope of oxygen had, somewhat arbitrarily, been given weight 16. With this rather arbitrary standard, the lighter hydrogen atom has weight 1.008 rather than exactly 1. But helium, which consists of 4 hydrogen atoms, proves to have weight 4.0028. However, if it consists of 4 hydrogen atoms, its atomic weight should be 4 times 1.008, or 4.032. The difference, 4.032 – 4.0028, or about 0.03, is the discrepancy which must be accounted for. Now it so happens that Einstein, working in an entirely different field, the theory of relativity, had already shown that mass can be converted into energy. Energy can take different forms. It can be the heat created by burning coal or wood, or it can be radiation such as comes to us from the sun. At the moment the precise form of it does not matter. What does matter is the thought which occurred to scientists that perhaps, when 4 hydrogen atoms are fused to form helium, the missing 0.03 of matter is converted into energy in the process. Hence the fusion of elements should release energy. And experiments showed that this is indeed what happens. The energy which is released is called the binding energy, and it is this energy which is released when a hydrogen bomb is exploded.

In this brief account of the role of arithmetic in chemistry and atomic theory, we have said almost nothing about the great thinking and brilliant experiments which physicists and chemists contributed. Our interest has been to show how the use of simple numbers supplies scientists with a powerful tool. Of course, the mathematics of numbers remains to be developed, and we shall learn how much more can be accomplished with slightly more advanced tools. But we can already see something of what the Pythagoreans envisioned when they spoke of numbers as the essence of reality.

REVIEW EXERCISES

1.  Calculate:

    a)  

    b)  

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

    i)   

    j)  

    k)  

2.  Calculate:

    a)  

    b)  

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

    i)   

    j)  

    k)  

    l)   

    m)  

    n)  

    o)  −8 ÷ −2

3.  Calculate:

    a)  (2 · 5) (2 · 7)

    b)  2a · 2b

    c)  2a · 3b

    d)  2x · 3y

    e)  2x · 3y · 4z

4.  Calculate:

    a)  

    b)  

    c)  

    d)  

    e)  

5.  Calculate:

    a)  

    b)  

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

6.  Simplify:

    a)  

    b)  

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

7.  Write as a fraction:

    a)  0.294

    b)  0.3742

    c)  0.08

    d)  0.003

8.  Approximate by a number which is correct to 1 decimal place:

    a)  

    b)  

    c)  

9.  Are the following equations true for all values of a and b? [Suggestion: If you wish to disprove a general statement, it is sufficient to show one instance where it does not hold.]

    a)  2(a + b) = 2a + 2b

    b)  2ab = 2a · 2b

    c)  

    d)  

    e)  

    f)   

    g)  

    h)  

    i)   

10.  Write the following numbers in positional notation but in base 2. The only digits one can use in base 2 are 0 and 1.

    a)  1

    b)  3

    c)  5

    d)  7

    e)  8

    f)   16

    g)  19

11.  The following numbers are in base 2. Write the corresponding quantities in base 10.

    a)  1

    b)  101

    c)  110

    d)  1101

    e)  1001

Topics for Further Investigation

1.  The Egyptian method of writing whole numbers and fractions.

2.  The Babylonian method of writing whole numbers and fractions.

3.  The Roman method of writing whole numbers and fractions.

4.  The fundamental arithmetical laws of atomic theory. (Use the references to Holton and Roller and to Bonner and Phillips).

5.  Pythagorean number theory.

Recommended Reading

BALL, W. W. ROUSE: A Short Account of the History of Mathematics, Chaps. 1 and 2, Dover Publications, Inc., New York, 1960.

BONNER, F. T. and M. PHILLIPS: Principles of Physical Science, Chap. 7, Addison-Wesley Publishing Co., Inc., Reading, Mass., 1957.

COLERUS, EGMONT: From Simple Numbers to the Calculus, Chaps. 1 through 8, Wm. Heineman Ltd., London, 1954.

DANTZIG, TOBIAS: Number, the Language of Science, 4th ed., Chaps. 1 through 6, The Macmillan Co., New York, 1954 (also in a paperback edition).

DAVIS, PHILIP J.: The Lore of Large Numbers, Random House, New York, 1961.

EVES, HOWARD: An Introduction to the History of Mathematics, Rev. ed., pp. 29–64, Holt, Rinehart and Winston, Inc., New York, 1964.

GAMOW, GEORGE: One Two Three . . . Infinity, Chap. 9, The New American Library, New York, 1953.

HOLTON, G. and D. H. D. ROLLER: Foundations of Modern Physical Science, Chaps. 22 and 23, Addison-Wesley Publishing Co., Inc., Reading, Mass., 1958.

JONES, BURTON W.: Elementary Concepts of Mathematics, Chaps. 2 and 3, The Macmillan Co., New York, 1947.

SMITH, DAVID EUGENE: History of Mathematics, Vol. I, pp. 1–75, Vol. II, Chaps. 1 through 4, Dover Publications, Inc., New York, 1953.

 

 

* Starred sections and chapters can be omitted without disrupting the mathematical continuity.