Algebra is the intellectual instrument which has been created for rendering clear the quantitative aspect of the world.
ALFRED NORTH WHITEHEAD
Mathematics is concerned with reasoning about certain special concepts, the concepts of number and the concepts of geometry. Reasoning about numbers—if one is to go beyond the simplest procedures of arithmetic—requires the mastery of two facilities, vocabulary and technique, or one might say, vocabulary and grammar. In addition, the entire language of mathematics is characterized by the extensive use of symbolism. In fact, it is the use of symbols and of reasoning in terms of symbols which is generally regarded as marking the transition from arithmetic to algebra, though there is no sharp dividing line.
The task of learning the vocabulary and techniques of algebra may be compared with that which faces the prospective musician. He must learn to read music and he must develop the technique for playing an instrument. Since our goal in mathematics is far more the acquisition of an understanding than the attainment of professional competence, the problem of learning the vocabulary and techniques will hardly be a severe one.
The nature and use of the language of algebra are readily illustrated, although the illustration is at the moment a trivial one. Most readers have encountered parlor number games, of which the following is an especially simple example. The leader of the game says to any member of the group: Take a number; add 10; multiply by 3; subtract 30; and give me your answer. And now, says the leader, I shall tell you the number you chose originally. To the amazement of the audience he does so immediately. The secret of his method is absurdly simple. Suppose the subject chooses the number a. Then adding 10 yields a + 10. Multiplication by 3 means 3(a + 10). By the distributive axiom, this quantity is 3a + 30. Subtraction of 30 yields 3a. The leader has only to divide by 3 the number given to him to tell the subject what his original choice was. If the leader wishes to be especially impressive, he can ask the subject to perform many more computations that will yield a simple and known multiple of the original number, and he can give the original number just as readily. By representing in the language of algebra the operations which he asks the subject to perform and by noting what the operations amount to, the leader can easily see how the final result is related to the original number chosen.
The language of algebra involves more than the use of a letter to represent a number or a class of numbers. The expression 3(a + 10) contains, in addition to the usual plus sign of arithmetic, the parentheses which denote that the 3 multiplies the entire quantity a + 10. The notation b2 is a shorthand expression for b · b and is read b-square. The word square enters here because b2 is the area of a square whose side is b. Likewise, the notation b3 means b · b · b and is read b-cube. The word cube is suggested by the fact that b3 is the volume of a cube whose side is b. The expression (a + b)2 means that the entire quantity a + b is to be multiplied by itself. An expression such as 3ab2 means 3 times some quantity a and that product multiplied by the quantity b2. In addition, the notation uses the convention that numbers and letters following one another with no symbol in between any two are to be multiplied together. Another important convention stipulates that if a letter is repeated in an expression, it stands for the same number throughout. For example, in a2 + ab the value of a must be the same in both terms. Thus algebra uses many symbols and conventions to represent quantities and operations with quantities.
Why do mathematicians bother with such special symbols and conventions? Why must they place hurdles in the way of would-be students of their subject? The answer is not that mathematicians are trying to introduce hurdles; nor are they seeking to impress people by making their subject look awesome. Rather the symbolism of algebra and the symbolism of mathematics in general are an unfortunate necessity. The most weighty reason is compre-hensibility. Symbolism enables the mathematician to write lengthy expressions in a compact form so that the eye can see quickly and the mind can retain what is being said. To describe in words even the simple expression 3ab2 + abc would require the phrase, “The product of 3 times a number multiplied by a second number which is multiplied into itself added to the product of the first number, the second number, and still a third number.” It is unfortunate that our eyes and minds are limited. The long and complicated sentences that would be required if ordinary language were used could not be remembered and, in fact, can be so involved as to be incomprehensible.
In addition to comprehensibility, there is the advantage of brevity. The expression in ordinary language of what is covered in typical texts on mathematics would require tomes of two to ten or fifteen times the customary size of such books.
Still another advantage is clarity. Ordinarily English or, for that matter, any other language is ambiguous. The statement, “I read the newspaper,” can mean that one reads newspapers regularly, once in a while, or often, or that one has read the newspaper, presumably the paper of the day. One must judge by the context just what this sentence means. Such ambiguity is intolerable in exact reasoning. By using symbols for specific ideas mathematics avoids ambiguity or, to put the matter positively, each symbol has its own precise meaning, and so the resulting expressions are clear.
Symbolism is one of the sources of the remarkable power of algebra. Suppose that one wished to discuss equations of the form 2x + 3 = 0, 3x + 7 = 0, 4x − 9 = 0, and the like. The particular numbers which appear in these equations do not happen to be important in the discussion; in fact, one wishes to include all equations in which the product of some number and x is added to some other number. The way to represent all possible equations of this form is
Here a stands for any number, and so does b. These numbers are known, but their precise value is not stated. The letter x stands for some unknown number. By reasoning about the general form (1) the mathematician covers the millions of separate cases which arise when a and b have specific values. Thus, by means of symbolism, algebra can handle a whole class of problems in one bit of reasoning.
Of course, it is unfortunate that one must learn the elements of a new language to master some mathematics. But one could with much justice complain that the French people insist on their language, the Germans on theirs, and so on. Obviously English is the best language, and the French and Germans are exhibiting provincialism by insisting on holding on to their respective languages. The language of mathematics has the additional merit of being universal.
There are justifiable criticisms of the symbolism of algebra, although they are hardly major ones. Mathematicians are greatly concerned about the accuracy of their reasoning, but pay little attention to the aesthetics or appropriateness of their symbolism. Very few symbols suggest their meaning. The signs +, −, =, 
are easy to write, but they are historical accidents. No mathematician has bothered to replace these by at least prettier ones, perhaps 
for plus. The seventeenth-century mathematician Gottfried Wilhelm Leibniz, who did spend days on the choice of symbols in an effort to make them suggestive, was an exception. There are even inconsistencies in symbolism which, once recognized, fortunately do not impair the clarity. For example, when two letters, such as ab, are written together with no symbol between them, then it is understood that multiplication is meant. However two numbers, such as 
, with no symbol between them, mean 
.
Symbolism entered algebra rather late. The Egyptians, Babylonians, Greeks, Hindus, and Arabs knew and applied a great deal of the algebra which we learn in high school. But they wrote out their work in words. Their algebraic style is in fact called rhetorical algebra because, except for a few symbols, they used ordinary rhetoric. It is significant that symbolism entered mathematics in the sixteenth and seventeenth centuries when pressure to improve the efficiency of mathematics was applied by science. The idea of using symbols was no longer new, but mathematicians were undoubtedly stimulated to extend the application of symbolism and to adopt it readily.
1. Why does mathematics use symbols?
2. Criticize the statement that all men are created equal.
3. In the following symbolic expressions the letters stand for numbers. Write out in words what the expressions state.
a) a + b
b) a(a + b)
c) a(a2 + ab)
d) 3x2y
e) (x + y)(x − y)
f) 
g) 
4. Does
[Suggestion: What do these symbolic expressions say in words?]
5. Write in symbols: (a) three times a number plus four; (b) three times the square of a number plus four.
One of the simplest examples of the convenience of algebraic symbolism or algebraic language is found in the use of exponents. We have already used frequently such expressions as 52. In this expression the number 2 is an exponent, and 5 is called the base. The exponent is placed above and to the right of the base to indicate that the quantity to which it applies, 5 in this example, is to be multiplied by itself, so that 52 = 5 · 5. Of course, there would be no great value in the use of exponents if their use were limited to such instances. Suppose, however, that we wished to indicate
5 · 5 · 5 · 5 · 5 · 5.
Here 5 occurs as a factor six times. We can indicate this quantity by means of exponents thus: 56. That is, when the exponent is a positive whole number it indicates how many times the quantity to which it is applied occurs as a factor in a product of this quantity and itself. In such instances as 56 the use of exponents saves a lot of writing and counting of factors.
Exponents are even more useful than we have thus far indicated. Suppose we wished to write
5 · 5 · 5 · 5 · 5 · 5 times 5 · 5 · 5 · 5.
With exponents we can write
56 · 54.
Moreover, the original product calls for 5 multiplied by itself to a total of 10 factors. This product can be written as 510. We see, however, that if we add the exponents in 56 · 54, we also get 510. That is, it is correct to write
56 · 54 = 56+4 = 510.
More generally, when m and n are positive whole numbers,
am · an = am + n.
This statement is really a theorem on exponents. Its proof is trivial. All that the theorem says is that if one quantity contains a as a factor m times, and another quantity contains a as a factor n times, the product of these two quantities contains a as a factor m + n times.
And now suppose we wished to write
With the use of exponents we can write
Moreover, if we were to calculate the value of the original quotient, we know that we could cancel 5’s in the numerator and denominator. We would be left with
We can obtain the same result if in 56/54 we subtract the 4 from the 6 and so arrive at 52. Here, too, as in the case of multiplication, the exponents keep track of the number of 5’s which occur in the numerator and denominator, and the subtraction of the 4 from the 6 tells us the net number of 5’s remaining as factors.
In more general language, we can say that if m and n are positive whole numbers, and if m is greater than n, then
This result, too, is a theorem on exponents, and the proof is again trivial because all the theorem states is that if we cancel the a’s common to numerator and denominator, we shall have m − n factors left over.
We might find that we have to deal with
In exponent form this quotient is
This time, if we cancel the 5’s common to the numerator and denominator, we are left with 5 occurring twice in the denominator; that is, we are left with
We can obtain this result at once by subtracting the exponent 4 in the numerator from the exponent 6 in the denominator. In general form we have the theorem: If m and n are positive whole numbers and if n is greater than m, then
There is the possibility of encountering
In exponent form this quotient is written
It would be nice to be able to simplify this expression, too, by using exponents. However, here, unlike the two previous cases, the two exponents are equal. If we were to, say, subtract the exponent 4 of the denominator from the exponent 4 of the numerator, we would have
Now 50 has no meaning. However we know that 54/54 has the value 1. If we agree to give a meaning to a zero exponent and, in fact, agree that a number to the 0 exponent is to be 1, then we can use the symbol 50. Further, with this meaning we can properly write
In general, if m is a positive whole number,
1. Simplify the following expressions by using the theorems on exponents:
a) 54 · 56
b) 63 · 67
c) 105 · 104
d) x2 · x3
e) 
f) 
g) 
h) 
i) 10 · 104
j) 
k) 
l) 
2. Could we apply the above theorems on exponents to negative numbers as bases? Then, is it true that (−3)5(−3)4 = (−3)9?
3. Which of the following equations are correct?
a) 32 + 34 = 36
b) 32 · 34 = 36
c) 32 + 34 = 66
d) 
e) 34 + 34 = 38
We can use exponents even more effectively than has thus far been indicated. Suppose that in the course of algebraic work, there occurred the expression
53 · 53 · 53 · 53.
Could we write this more briefly? By the very meaning of an exponent we certainly can write
53 · 53 · 53 · 53 = (53)4.
We can go further. The left-hand side of this equation contains 5 as a factor 12 times. We can recognize the same fact if we multiply the two exponents on the right-hand side. That is,
(53)4 = 512.
This example is the essence of another theorem on exponents, namely, if m and n are positive integers, then
(am)n = amn.
There is one more commonly useful theorem on exponents. Suppose we wished to denote
2 · 2 · 2 · 2 · 3 · 3 · 3 · 3
briefly, by taking advantage of exponents. We certainly could write this quantity as
24 · 34.
However, we know that the order in which we multiply numbers does not matter. Hence it is correct that
2 · 2 · 2 · 2 · 3 · 3 · 3 · 3 = 2 · 3 · 2 · 3 · 2 · 3 · 2 · 3,
and now if we use exponents, we can say that
24 · 34 = (2 · 3)4.
What this fact amounts to, in general terms, is that if m is a positive whole number, then
am · bm = (a · b)m.
1. Use the theorems on exponents to simplify the following expressions:
a) 34 · 34 · 34
b) (34)3
c) (54)2
d) 102 · 102 · 102
e) (104)3
f) 54 · 24
g) 37 · 33
h) 104 · 34
2. Calculate the values of the following quantities:
a) 25 · 55
b) 
c) 
d) 
e) 
3. Which of the following equations are correct?
a) (3 · 10)4 = 34 · 104
b) (3 · 102)3 = 33 · 106
c) (3 + 10)4 = 34 + 104
d) (32 · 53)4 = 38 · 512
e) (34)3 = 37
f) (32)3 = 39
All the above theorems deal with positive integral (whole-numbered) exponents or zero as an exponent. Though we shall not deal with other types of numbers as exponents, it is significant to know that the exponent notation can be more valuable than we have thus far indicated. Let us consider 
. We know that
Let us suppose that we would like to investigate whether the exponent notation could be used to simplify work with irrational numbers. (Of course, this is the kind of problem that one takes up when he has nothing better to do.) Now the right-hand side of the above equation can be written as 31. No matter what exponent notation we do adopt for , say 3a, the equation would have to read
3a · 3a = 31.
Moreover, we would like, if possible, to maintain the validity of our previous theorems on exponents. In the present case, we would like to be able to say that
3a · 3a = 3a + a = 32a,
and since 32a = 31, we would have to have 2a = 1 or a = 
. What these exploratory thoughts suggest is that if we denote
by 31/2,
then we would be able to use at least the first theorem on exponents to state that
31/2 · 31/2 = 31/2+1/2 = 31 = 3.
As a matter of fact, this example typifies what is done. Thus we use the notation
and so on.
Symbolism is a means to an end. The function of algebra is not to display symbols but to convert or transform expressions from one form to another which may be more useful for the problem in hand.
Let us consider an example. Suppose that in the course of some mathematical work we encounter the expression
The letter x in this expression may stand for some number whose value we do or do not happen to know, or it may stand for any one of some class of numbers. What matters is that x stands for a number. If x is a number, then x + 4 is a number. We may now apply the distributive axiom, which states that for any numbers a, b, and c,
If we compare (2) and (3) we see that (2) has the form of (3) if we think of x + 4 in (2) as the a of (3). Then by applying the distributive axiom to (2) we may assert that
We also know that there is another form of the distributive axiom, namely
(b + c)a = ba + ca.
If we apply this axiom to each of the terms on the right side of (4), we see that
(x + 4)x = x2 + 4x and (x + 4)3 = 3x + 12.
If we substitute these last two results on the right side of (4), we have
or
Before discussing what this example illustrates, let us note that we do not usually carry out the multiplication of (x + 4) by (x + 3) in this long and rather cumbersome fashion. Instead we write
The partial product 3x + 12 results from multiplying x + 4 by 3, and the partial product x2 + 4x results from multiplying x + 4 by x. The two partial products are then added. This manner of carrying out the multiplication is faster, but fails to indicate explicitly that we have used the distributive axiom several times.
The main point of the above example is that we have transformed the expression (x + 4)(x + 3) into the expression x2 + 7x + 12. We do not maintain that the latter expression is more attractive than the former, but it may be more useful in a particular mathematical application. On the other hand, we might, in some situation, find ourselves with the expression x2 + 7x + 12 and, by recognizing that it is equal to (x + 4)(x + 3), be able to make progress toward some significant conclusion. In this latter transformation we say that we have factored x2 + 7x + 12 into (x + 4)(x + 3). Which of the two forms is more useful depends upon the application in hand. At the moment we should merely see that algebra is concerned with the technique of such transformations, and that a skilled mathematician should be able to perform them rapidly. Since we shall not become too involved in complicated technical processes, we shall not spend much time in developing skills.
The problem of factoring to which we referred in the preceding paragraph does arise reasonably often. For example, one usually starts with an expression such as x2 + 6x + 8 and seeks to transform it into a product of factors of the form (x + a)(x + b). The original expression is said to be of second degree because it contains x2 but no higher power of x. The factors are first-degree expressions because each contains x but no higher power of x. The problem is to find the correct values of a and b so that the product (x + a) (x + b) will equal the original expression. We know from our work on multiplication [see equation (5)] that
x2 + (a + b)x + ab = (x + a)(x + b).
Hence to factor the second-degree expression, we should look for two numbers a and b whose sum is the coefficient of x and whose product is the constant. Thus to factor x2 + 6x + 8, we look for two numbers whose sum is 6 and whose product is 8. By mere trial of the possible factors of 8 we see that a = 4 and b = 2 will meet the requirement; that is:
x2 + 6x + 8 = (x + 4)(x + 2).
1. Transform to an equal expression:
a) 3x · 5x
b) (x + 4)(x + 5)
c) (3x + 4)(x + 5)
d) (x − 3)(x + 3)
e) 
f) 
2. Factor the following expressions. Experiment with numbers to find the correct factors.
a) x2 + 9x + 20
b) x2 + 5x + 6
c) x2 − 5x + 6
d) x2 − 9
e) x2 − 16
f) x2 + 7x − 18
3. Prove that x(x2 + 7x) = x3 + 7x2.
4. Can you think of a way of testing or verifying (not proving) that
x2 + 5xy + 6y2 = (x + 3y)(x + 2y)
for all values of x and y?
5. Write out in words the equivalent of
(x − 3)(x + 3) = x2 − 9.
6. A high school girl had to simplify (a2 − b2)/(a − b). She reasoned that a2 divided by a gives a. Minus divided by minus gives plus. And b2 divided by b gives b. Hence the answer is a + b. Is the answer correct? Is the argument correct?
7. There is a well known “proof” that 2 = 1. The proof runs as follows. Suppose a and b are two numbers such that
a = b.
We may multiply both sides of this equation by a and obtain
a2 = ab.
Now we may subtract b2 from both sides and obtain
a2 − b2 = ab − b2.
By factoring we may replace the left and right sides of this equation by
(a − b)(a + b) = b(a − b).
Division of both sides of this equation by a − b yields
a + b = b.
Since a = b, we may as well write
2b = b.
But now we can divide both sides of this last equation by b, and there results
2 = 1.
Find the flaw in this proof.
The study of algebraic transformations as such is not very interesting. It is much like the grammar of a language. The significant uses of these transformations occur in larger investigations which we shall undertake later. However, a direct use of the processes of algebra does arise in the problem of finding unknown quantities, a problem not without some interest in itself and one which also arises in the course of broader investigations.
A somewhat practical, though by no means vital, example is the following. The radiator of a car contains 10 gallons of liquid 20 per cent of which is alcohol. The owner wishes to draw off a quantity of liquid and replace it by pure alcohol so that the resulting mixture contains 50 per cent alcohol. How many gallons of liquid should he draw off?
Now the very practical person who refuses to use mathematics can handle this situation very readily. He can draw off 5 gallons of the mixture and replace it by 5 gallons of alcohol. Then the mixture will certainly contain at least 50 per cent alcohol because even the remaining 5 gallons contain some alcohol. However, if the final mixture need contain only 50 per cent alcohol, then the practical person has wasted alcohol and therefore money. If he draws off 4 gallons, 6 gallons will be left, and since 20 per cent of this is alcohol, the alcoholic content is 
gallons. If he now adds 4 gallons of alcohol he will have 
gallons of alcohol, or more than 50 per cent, in the 10 gallons. On the other hand, if he draws off only 3 gallons, 20 per cent of the remaining 7 gallons is 
gallons of alcohol, and the addition of 3 more will yield 
gallons of alcohol out of 10, or less than 50 per cent. The correct answer lies somewhere between 3 and 4, but where? Instead of continuing to guess let’s use a little algebra.
Let x be the number of gallons of the mixture to be drawn off and to be replaced by an equal amount of pure alcohol. Then the number of gallons remaining of the original mixture is 10 − x. Of this 20 per cent, or 
, is alcohol, so that of the 10 − x gallons, 
is alcohol. After the x gallons are replaced with pure alcohol, the amount of alcohol in the tank will be 
(10 − x) + x. We should like to fix x so that the amount of alcohol should be 50 per cent of 10 gallons, or 5 gallons. Hence we seek the value of x which satisfies the equation
Now we can apply the distributive axiom to start off our transformations and write
The terms 
or 
amount to 
. Hence (8) is equivalent to
If we now subtract 2 from both sides of this equation, the result will still be an equality because equals subtracted from equals give equals. Then
We now multiply both sides of this equation by 
, and since equals multiplied by equals give equals, we have
Hence the answer is that the owner of the car should draw off 
gallons of the original liquid. We knew before we applied algebra that the answer lies between 3 and 4, and we now know exactly where.
The more significant point made by this example, however, is that we started with equation (7) which expresses the condition to be satisfied by the unknown quantity x and that, by executing a series of almost mechanical steps justified by axioms about numbers, we arrived at a new equation, (10), which tells us what we wish to know. In other words, we performed a series of transformations which carried us from one equation to another and we profited thereby. The answer is not sensational, but we see how the manipulation of symbols gives us new information.
There is another point which the above example illustrates, at least in a minor way. Once we formulate equation (7) we forget all about the physical situation and concentrate solely on the equation. Nothing that is not relevant to the problem, i.e., to the problem of determining the number x, interferes with our thinking. Ernst Mach, a famous scientist of the late nineteenth century, said that mathematics is characterized by “a total disburdening of the mind,” and we can now see what he meant. The make of the car, the shape of the radiator, the fact that the owner may be concerned with protecting the liquid in the radiator from freezing, and any other facts which have nothing to do with determining x can be forgotten. We disburden our minds of everything but the quantitative facts expressed in equation (7), and proceed to handle quantitative relationships only.
Equation (7) is rather simple. It is called a linear or first-degree equation because the unknown x occurs to the first power only. Let us consider a second example which will again illustrate the transformation value of algebra, but which also has other interesting features. Suppose that one ship is at A (Fig. 5–1) and another is at B, exactly 10 miles north of A. The ship at B is steaming east at the rate of 2 miles per hour. The ship at A is capable of traveling at a speed of 5 miles per hour and wishes to intercept the other ship. To set his course properly the captain of the ship at A must know where the two will meet.
Let us suppose that C is the point where they will meet. If the captain can determine the distance BC, he will head along the hypotenuse of a right triangle whose arms are AB and BC. Let us therefore denote the distance BC by x. Now that we seem to have labeled all relevant quantities, we encounter the first puzzling aspect of this problem, namely, that we do not have any equation to find x. Without this, of course, we can only sit and do some wishful thinking. Yet we do have enough information to set up such an equation.
What we have overlooked is a physical fact which is implied by the given information: The time that the ship at B will take to travel to C must be the same as the time it will take the ship at A to reach C. Since the ship at B travels at 2 miles per hour, it will take x/2 hours to reach C. To calculate the time required by the ship at A to reach C, we need the distance AC. We do not know AC, but we can at least express its value by means of the Pythagorean theorem of geometry. This theorem says in the present instance that
AC2 = 100 + x2.
Then
Fig. 5–1
The time required for the ship at A to travel the distance AC at 5 miles per hour is
We next equate the time required for the ship at B to travel the distance BC and the time required for the ship at A to travel the distance AC. This equation is
We now have an equation to work with. Let us see whether we can transform it so that it will yield a value for x. Since the square root is annoying, let us square both sides, i.e., multiply the left side by itself and the right side by itself. Since the left side equals the right side we are in effect multiplying equals by equals, and so the step is justified. Squaring both sides, we obtain
Since fractions are also annoying, let us multiply both sides by 100. We choose 100 because both 25 and 4 divide evenly into 100. Thus
We may apply our operations with fractions to write
25x2 = 4(100 + x2).
Application of the distributive axiom yields
Now we subtract 4x2 from both sides, and because equals subtracted from equals yield equals, we obtain
Division of both sides by 21, which is a division of equals by equals, yields
Now we ask ourselves what number squared yields 400/21. Certainly 
is one possibility. But a negative number squared or multiplied by itself is also positive. Hence there are two possible answers:
Let us accept both of these for the moment and dispose first of a purely arithmetical question. How much is 
Well, we can divide 21 into 400 and obtain 19.05 to two decimal places. We must now find 
There is an arithmetic process for finding the square root of a number, but for our purposes it will be sufficient to estimate the answer. Clearly 4 is too small and 5 is too large. By sheer trial we find that (4.3)2 = 18.49 and (4.4)2 = 19.36. Hence the correct value lies between 4.3 and 4.4. If we wished to have a more accurate answer, we could now try 4.31, 4.32, and so on, until we found a result which came as close to 19.05 as possible, and so obtain an answer to the nearest hundredths’ place. We shall accept 4.4 as good enough for our purposes and thus we may say that
And now we have more than we want; we have two answers, whereas we sought only one. Of course, we wish to use the positive answer because the x we seek stands for a length which is positive. This is the value which has the proper physical meaning in our problem. But the question, How did the negative value of x get into the picture, remains open. The answer involves a rather important point about the nature of mathematics and its relation to the physical world. The mathematician starts with concepts and axioms which express some idealized facts about the world, and proceeds to apply these concepts and axioms to solve physical problems. In the present case the methods used lead to two solutions. Hence the methods may involve new elements which are not present in the physical world, even though the intent was to stay close to it. Thus, squaring both sides of equation (11), a justifiable mathematical step, introduced a new solution, for, if our original equation had been
we would have obtained the same equation, (12) and everything we did thereafter would have applied to (18) as well as (11). Hence, in this case, we can see specifically where mathematics departs from the physical situation.
The main point to be noted is then that, although mathematical concepts and operations are formulated to represent aspects of the physical world, mathematics is not to be identified with the physical world. However, it tells us a good deal about that world if we are careful to apply it and interpret it properly. We shall find that this point, which eluded the best thinkers until the late nineteenth century, will acquire increasing importance as we proceed.
There is another valuable lesson to be learned from the solution of the problem we have just examined. When we arrived at step (13), we combined terms in x2 and then proceeded to find x. The subsequent work led to a fair amount of arithmetic. An engineer working with the same problem and perhaps satisfied with an approximate answer might argue that the term 4x2 is small compared with the term 25x2 and so disregard it. Instead of our next equation, (14), his new equation would then read
25x2 = 400,
and by dividing both sides of this equation by 25, he would obtain
x2 = 16.
It now follows that
x = 4 and x = −4.
Thus 4 is an approximate answer. Engineers often are satisfied with such approximations because, in constructing actual objects of wood and steel, they cannot meet a specified value exactly. Not only can’t one measure exactly, but tools and machines also introduce errors. By neglecting 4x2 in (13) the engineer gained the advantage of finding the approximate answer much more readily than we were able to determine the correct answer even to one decimal place only.
In the present problem the saving is trivial, but approximation may make a lot of difference in more difficult problems. Whereas the mathematician, who seeks exact answers, will work months and years on a problem, the engineer will often settle for an approximate answer and obtain it far more easily. The point we are making is not that the engineer is smarter. To get on with his job the engineer must arrive at an answer quickly, whereas the mathematician’s job is to obtain a correct answer, no matter how long it takes. Both are true to the objectives and spirit of their own work. Moreover, in making approximations, the engineer raises a question which he may not be able to answer. How good is his approximation? After all, while physical constructions and measurements are not exact, beams must fit. Hence the engineer should really ascertain that the approximation is good enough for his purposes. If he can tolerate an error of only 0.1 of an inch, he must make sure that his approximations do not introduce a larger error.
In really difficult problems the engineer will make approximations and, usually with the aid of a mathematician, determine the error introduced. If he cannot do so, he will often overdesign; that is, if the approximate result shows that a beam supporting a building need be only one inch thick, he may make it two inches thick and thereby hope that he has more than allowed for the error. Is he certain even with this precaution that his beam will hold up? No. Big bridges have collapsed because such calculations and additional precautionary measures were not enough. A recent example was the Tacoma bridge in the State of Washington. The bridge did not withstand the force of the wind and collapsed.
1. The speed of sound in an iron rod is 16,850 ft/sec, and the speed in air is 1100 ft/sec. If a sound originating at one end of the rod is heard one second sooner through the rod than through the air, how long is the rod?
2. A bridge AB is 1 mi (5280 ft) long in winter and expands 2 ft in the summer. For simplicity suppose that the shape in summer is the triangle ACB shown in Fig. 5–2. How far does the center of the bridge drop in summer, that is, how long is CD? Before calculating the answer, estimate it. To calculate, use the Pythagorean theorem and estimate the square root to the nearest foot.
Fig. 5–2
3. An airplane which can fly at a speed of 200 mi/hr in still air flies a distance of 800 mi with the wind in the same time as it flies 640 mi against the wind. What is the speed of the wind? [Suggestion: If x is the speed of the wind, then the speed of the plane when flying with the wind is 200 + x; the speed of the plane when flying against the wind is 200 − x.]
4. The population of town A is 10,000 and is increasing by 600 each year. The population of town B is 20,000 and is increasing by 400 each year. After how many years will the two towns have the same population?
5. A rope hanging from the top of a flagstaff is 2 ft longer than the staff. When pulled out taut, it reaches a point on the ground 18 ft from the foot of the staff. How high is the staff?
6. A publisher finds that the cost of preparing a book for printing and of making the plates is $5000. Each set of 1000 printed copies costs $1000. He can sell the books at $5 per copy. How many copies must he sell to at least recover his costs?
7. We may certainly say that
We take the square root of both sides and obtain
What is wrong?
8. A glass which is half full certainly contains as much liquid as a glass which is half empty. Then
If we multiply both sides by 2 we obtain
1 full = 1 empty,
or a full glass contains as much as an empty glass. What is wrong?
Our discussion of the solution of equations in the preceding section dealt with two types of equations, first-degree equations illustrated by equation (7) and second-degree equations illustrated by equation (14). No difficulties can arise in the process of solving first-degree equations, i.e., equations which, by proper algebraic operations, can be expressed in the form
where a and b are definite numbers and x is the unknown. Equation (19) can readily be solved for x.
The case of second-degree equations is not so simple. We were fortunate that equation (14) led to (15), and that by taking the square root of both sides we obtained the two solutions, or roots as they are called. However we might have to solve an equation such as
This equation is more complicated than (14) because (20) also contains the first-degree term in x.
In solving equation (20), we still do not encounter much trouble. We know from our work on transforming algebraic expressions that the left-hand side of (20) can be factored; that is, the equation can be written as
We now see that when x = 2, the left side is zero because
(2 − 2) (2 − 4) = 0.
When x = 4, the left side is again zero because
(4 − 2) (4 − 4) = 0.
Hence the solutions or roots are
x = 2 and x = 4.
Now suppose we had to solve the second-degree equation
This time it is not possible to find simple factors of the left side. Equations such as (22) do arise in real problems. Hence the mathematician considers the question, Is there a method which will solve such second-degree equations? Naturally he studies those he can solve to see whether they furnish any clue to such a method.
Examination of equation (20) reveals an interesting fact. The roots are 2 and 4. The sum of these two numbers is 6, and the coefficient, or multiplier, of x is − 6. The product of 2 and 4 is 8, and 8 is the constant term, that is, the term free of x. These facts might be a coincidence, and so the mathematician would investigate whether they hold for other simple equations. Consider the very simple equation:
Here the roots are +2 and −2. Their sum is 0, and we note that the term in x is missing, which means it is 0 · x. The product of the roots is −4, precisely the constant term in (23). Presumably we have some facts about the roots, but how can we use them?
Equations of the form (23) are easy to solve, since one only has to take a square root. Perhaps the method we should seek is one which reduces all equations of the type (20) to the type (23). But how do we do this? The sum of the roots in (23) is zero. The sum of the roots in (20) is 6, and this is the negative of the coefficient of x. If we added to each root of (20) one-half the coefficient of x, that is, −3, the sum of the roots would be zero. What this suggests, then, is to form a new equation whose roots are the roots of the old one, each increased* by one-half the coefficient of x. Since the coefficient of x is −6, we let
y = x + (−3) = x − 3
or
If we substitute this value of x in (20), we obtain
(y + 3)2 − 6(y + 3) + 8 = 0.
We now calculate the square in the first term, carry out the multiplication in the second term, and find that
y2 + 6y + 9 − 6y − 18 + 8 = 0
or
y2 − 1 = 0.
Then
y2 = 1
and
y = 1 and y = − 1.
But from (24) we see that
x = 1 + 3 and x = − 1 + 3
or
x = 4 and x = 2.
Thus we obtain without factoring the very same roots of equation (20) that we found previously by factorization.
Now let us reconsider equation (22), namely
Since the roots cannot be obtained by any apparent method of factoring, let us see whether the idea just tried works here also; that is, let us form a new equation whose roots are the roots of (22) increased by one-half the coefficient of x. The roots of (22) are represented by x. Then we shall form a new equation whose roots y are:
From (25) we have
We substitute this value of x in (22) and obtain
(y − 5)2 + 10(y − 5) + 8 = 0.
We perform the indicated multiplications and obtain
y2 − 10y + 25 + 10y − 50 + 8 = 0.
By combining terms we find that
y2 − 17 = 0
or
y2 = 17.
Then
We now use (26) to state that
We have found the two roots of (22) without factoring.
1. Find the roots of the following equations by factoring the left-hand side:
a) x2 − 8x + 12 = 0
b) x2 + 7x − 18 = 0
2. Find the roots of each of the equations in Exercise 1 by forming a new equation whose roots are “larger” than those of the original equation by one-half the coefficient of x.
3. Solve the following equations by the method of forming a new equation whose roots are “larger” than those of the original equation by one-half the coefficient of x.
a) x2 + 12x + 9 = 0
b) x2 − 12x + 9 = 0
The method of solving second-degree equations by forming a new equation seems to work, but we have no proof that it will always work. To secure a general proof we shall use one of the basic devices of algebra; that is, instead of working with particular equations, we shall consider the general second-degree equation
Here p and q are letters, each of which can stand for any given real number. The use of the letters p and q must be distinguished from the use of x to stand for the specific unknown roots of the equation. Now we follow the method employed to solve equations (20) and (22); that is, we form a new equation whose roots are the roots of (28), each increased by one-half the coefficient of x. This means that we introduce the expression
Then
We substitute this value of x in (28) and obtain
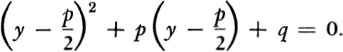
By squaring the first term and multiplying through by p in the second one, we obtain
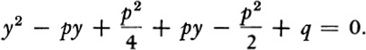
The terms involving py cancel. Moreover, p2/4 −p2/2 = − p2/4. Hence
By adding p2/4 to both sides and subtracting q from both sides, we obtain
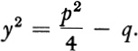
Hence
In this general case, we cannot determine the numerical value of the square root, but we can leave the result in this form. We now see from equation (29) that
This result is remarkable.* We have shown that the roots of any equation of the form (28) (that is, no matter what p and q are) are given by the expressions (30).
We really have accomplished more than we sought to accomplish. We sought a method of solving an equation such as (22). We not only have found such a method, but, since the result (30) holds for any such equation, we do not have to go through the entire process each time; we proceed by simply substituting the proper value of p and q in (30). Thus if we compare equations (22) and (28), we see that the p in (22) is 10 and q is 8. Hence let us substitute 10 for p and 8 for q in (30). We find
or
This is exactly the result obtained in (27).
By working with the general form x2 + px + q = 0 instead of equations with specific numbers as coefficients, we have shown how to solve any second-degree equation. This general result could never be derived from equations with numerical coefficients because there are infinitely many such equations, and one could not investigate them all. Thus the use of letters to represent any one of a class of numbers gives mathematics a power and generality which achieves what could not be accomplished in many lifetimes of effort with particular equations. Of course, to people who do not care to solve one quadratic the ability to solve all is no boon. But even these people have benefited indirectly. The preceding theory illustrates how the mathematician, when called upon to solve the same type of problem repeatedly, seeks a general method which will handle all of them.
The use of letters such as p and q, which has made an enormous difference in the effectiveness of mathematics, seems like a small idea once understood, and yet it is a rather recent development. From the time of the Babylonians and Egyptians to about 1550, all the equations solved had numerical coefficients. Although many algebraists realized that the method they used for one set of numerical coefficients would work for any other, they had no general proof. The idea of employing general coefficients in algebraic equations, an idea which, as we shall see, was taken over into other domains of mathematics, is due to François Vieta (1540–1603), a great French mathematician. The remarkable fact about Vieta is that he was a lawyer who worked for the kings of France. Mathematics was just a hobby to him, but one at which he “worked” extensively. Vieta was fully conscious of what he had done by introducing literal coefficients. He said that he was introducing a new kind of algebra which he called logistica speciosa, that is calculation with whole species, as opposed to the numerical work of his predecessors which he called logistica numerosa.
We could consider other examples of how the processes of algebra permit us to solve equations involving unknowns, but we shall not devote more time to the subject. What is important is the recognition that by means of algebra we can extract information from some given facts. It is also important to see how readily and mechanically the processes of solving equations yield the desired information. In fact, one of the curious things about mathematics that clearly emerges even from our brief work in algebra is that mathematics which is concerned with reasoning nevertheless creates processes which can be applied almost mechanically, that is, without reasoning. The thinking is, so to speak, mechanized and this mechanization enables us to solve complicated problems in no time. We think up processes so that we don’t have to think.
It may be necessary to caution the reader again that while the techniques of transformations are necessary to perform useful and interesting mathematical work, they are not the substance of mathematics. If all that one learns in mathematics is the ability to execute these techniques, however quickly and accurately, he will not see the real purpose, nature, and accomplishments of mathematics. To a large extent, techniques are a necessary evil, like practicing scales on a piano, in order to be able to play grand and beautiful compositions. Naturally those who wish to be professional mathematicians must learn as many of these techniques as possible.
1. Solve by means of (30) the following equations:
a) x2 − 8x + 10 = 0
b) x2 + 8x + 10 = 0
c) x2 − 6x − 9 = 0
d) 2x2 + 8x + 6 = 0
e) x2 − 8x + 16 = 0
5–7 THE HISTORY OF EQUATIONS OF HIGHER DEGREEThe search for generality in mathematics began in the sixteenth century. One type of generality became possible when Vieta showed how to treat a whole class of equations by means of literal coefficients. Another direction which the search for generality took was the investigation of equations of degree higher than the second.
The first of the notable mathematicians to pursue the mathematics of equations of higher degree and certainly the greatest combination of mathematician and rascal is Jerome Cardan. He was born in Pavia, Italy, in 1501 to somewhat disreputable parents, although his father was a lawyer, doctor, and minor mathematician. Cardan had no upbringing worth speaking about and was sickly during the first half of his life. Despite these handicaps, he studied medicine and became so celebrated a physician that he was invited to treat prominent people in many countries of Europe. At various times he was professor of medicine, and he also lectured on mathematics at several Italian universities.
He was aggressive, high-tempered, disagreeable, and even vindictive, as if anxious to make the world suffer for his early deprivations. Because illnesses continued to harass him and prevented him from enjoying life, he gambled daily for many years. This experience undoubtedly helped him to write a now famous book, On Games of Chance, which treats the probabilities in gambling. He even gives advice on how to cheat, which was also gleaned from experience.
A product of his age in many respects, Cardan collected and published prolifically legends, false philosophical and astrological doctrines, folk cures, methods of communion with spirits, and superstitions. Apparently he himself believed in spirits and in astrology. He cast horoscopes, many of which proved to be false. Toward the end of his life he was imprisoned for casting the horoscope of Christ, but was soon pardoned, pensioned by the Pope, and lived peacefully until his death in 1576. In his Book of My Life, an autobiography, he says that despite his years of trouble he has to be grateful, for he had acquired a grandson, wealth, fame, learning, friends, belief in God, and he still had fifteen teeth.
Part of Cardan’s rascality concerns our present subject. The mathematicians of the sixteenth century had undertaken to solve higher-degree equations, for example, equations of the third degree such as
x3 − 6x = 8.
Among them was another famous man, Nicolò of Brescia, better known as Tartaglia (1499–1557), whom we shall meet occasionally in other contexts. Tartaglia had discovered a method for solving third-degree equations, and Cardan wished to publish this method in a book he was writing on algebra, which later appeared under the title Ars Magna, the first major book on algebra in modern times. After refusing to divulge the method, Tartaglia finally acquiesced, but asked Cardan to keep it secret. However, Cardan wished his book to be as important as possible and so published the method, though acknowledging that it was Tartaglia’s. From this book, which appeared in 1545, the mathematical world learned how to solve third-degree equations. In this same book Cardan also published a method of solving fourth-degree equations discovered by one of his own pupils, Lodovico Ferrari (1522–1565). Although general coefficients were not in use as yet, it was clear that all third- and fourth-degree equations could be solved. In other words, the solutions could be expressed in terms of the coefficients by means of the ordinary operations of algebra, i.e., addition, subtraction, multiplication, division, and roots (though not necessarily square roots), in just about the manner in which (30) expresses the solutions of a second-degree equation in terms of the coefficients p and q.
And now the mathematicians’ interest in generality took over. Since the general equations of the first, second, third, and fourth degree could be solved, what about fifth-, sixth- and higher-degree equations? It seemed certain that these equations could also be solved. For three hundred years many mathematicians worked on this basic problem and made almost no progress. And then a young Norwegian mathematician, Niels Henrik Abel (1802–1829), showed at the age of 22 that fifth-degree equations could not be solved by the processes of algebra. Another youth, Évariste Galois (1811–1832), who failed twice to pass the entrance examinations for the École Polytechnique and spent just one year at the École Normale, demonstrated that all general equations of degree higher than the fourth cannot be solved by means of the operations of algebra. In a letter he wrote the night before he was killed in a duel, Galois explained his ideas and showed how a new and general theory of the solution of equations could be developed. Galois’ ideas gave algebra a totally new turn. Instead of being a tool, a series of techniques for the transformation of expressions into more useful ones, it became a beautiful body of knowledge which can be of interest in itself. Unfortunately we cannot undertake to study Galois’ ideas, or the Galois theory as it is called, because there are more basic things to be learned first.
This brief account of the search for generality in the solution of equations has been given here because it illustrates many important features of mathematics. One is the persistence, stubbornness if you will, of mathematicians over hundreds of years. Another is the experience that the search for generality leads to new and important developments, even though at the outset the generality is sought for its own sake. Today, the solution of higher-degree equations is a most practical matter, and we owe to Galois the most revealing insight into this subject. We also find in this history of the theory of equations a major example of how mathematicians find problems on which to work, problems of significance drawn from other problems which have humble and practical origins such as simple equations involving unknowns.
1. Carry out the indicated multiplication:
a) 3(2x + 6)
b) (x + 3)(x + 2)
c) (x + 7)(x − 2)
d) (x + 3)(x − 3)
e) 
f) (2x + 1)(x + 2)
g) (x + y)(x − y)
2. Factor the following expressions. You may have to experiment to find the correct factors.
a) x2 − 9
b) x2 − 16
c) x2 − a2
d) a2 − b2
e) x2 + 6x + 9
f) x2 + 7x + 6
g) x2 + 5x + 4
h) x2 − 6x + 9
i) x2 − 7x + 6
j) x2 − 5x + 4
k) x2 − 7x + 12
l) x2 + 6x − 16
m) x2 + 6x − 27
3. If 2x + 7 = 5, what does 2x equal, and what does x equal?
4. Solve the following equations. State what you do in each step.
a) 2x + 9 = 12
b) 2x + 12 = 9
c) 
d) 
e) 
f) 
g) 
h) ax + 2 = b
i) ax − b = c
5. A solution of acid and water contains 75% water. How many grams of acid would you add to 50 grams of the solution to make the percentage of water 60%?
6. A student has grades of 60 and 70 on two examinations. What grade must he earn on a third examination to attain an average of 75%?
7. Solve the following equations by factoring:
a) x2 − 6x + 5 = 0
b) x2 − 6x − 7 = 0
c) x2 − 7x + 6 = 0
d) x2 + 6x − 27 = 0
e) x2 − 7x + 12 = 0
f) x2 − 5x − 14 = 0
8. Solve the following equations by the method of forming a new equation whose roots are “larger” than those of the original equation by one-half the coefficient of x.
a) x2 + 10x + 9 = 0
b) x2 − 10x + 9 = 0
c) x2 + 10x + 6 = 0
e) x2 − 12x + 15 = 0
f) x2 + 12x + 15 = 0
9. Solve the following equations by applying formula (30) of the text:
a) x2 + 12x + 6 = 0
b) x2 − 12x + 6 = 0
c) x2 + 12x − 6 = 0
d) x2 − 12x − 6 = 0
e) 2x2 + 12x + 6 = 0
f) 3x2 + 27x + 15 = 0
g) t2 + 10t = 8
10. In Section 5–5 of the text, we solved a problem wherein one ship sets its course properly so as to overtake another ship. To set up the equation which solved the problem, equation (11), we started by letting x be the distance which the ship traveling east covers. Solve the same problem by letting t be the time that both ships travel until they meet. Then x = 2t. The algebra of this alternative solution is easier to handle. However it is not so obvious that we should let our unknown be the time of travel.
1. The rise of symbolism in algebra.
2. The history of the solution of equations.
BALL, W. W. ROUSE: A Short Account of the History of Mathematics, pp. 201–243, Dover Publications Inc., New York, 1960.
COLERUS, EGMONT: From Simple Numbers to the Calculus, Chaps. 9 through 13, Wm. Heinemann Ltd., London, 1954.
ORE, OYSTEIN: Cardano, The Gambling Scholar, Chaps. 1 through 5, Princeton University Press, Princeton, 1953.
SAWYER, W. W.: A Mathematician’s Delight, Chap. 7, Penguin Books Ltd., Harmondsworth, England, 1943.
SMITH, DAVID E.: History of Mathematics, Vol. II, pp. 378–470, Dover Publications Inc., New York, 1958.
WHITEHEAD, ALFRED N.: An Introduction to Mathematics, Chaps. V and VI, Holt, Rinehart and Winston, Inc., New York, 1939 (also in paperback).
* It is necessary to add that a must not be 0, because then the original quotient has no meaning.
* We use the term “increased” here, even though in the example we add a negative quantity to each root and really decrease the value of the roots.
* In many books a method is given for solving the general second-degree equation ax2 + bx + c = 0. If we divide this equation by a, we obtain x2 + (b/a)x + (c/a) = 0. This equation is now of the same form as (28), where p = b/a and q = c/a. If we enter these values of p and q in (30), we get the roots
