Trigonometry is the branch of mathematics concerned with the measurement of the parts, sides, and angles of a triangle. Plane trigonometry, which is the topic of this book, is restricted to triangles lying in a plane. Trigonometry is based on certain ratios, called trigonometric functions, to be defined in the next chapter. The early applications of the trigonometric functions were to surveying, navigation, and engineering. These functions also play an important role in the study of all sorts of vibratory phenomena—sound, light, electricity, etc. As a consequence, a considerable portion of the subject matter is concerned with a study of the properties of and relations among the trigonometric functions.
The plane angle XOP, Fig. 1.1, is formed by the two rays OX and OP. The point O is called the vertex and the half lines are called the sides of the angle.

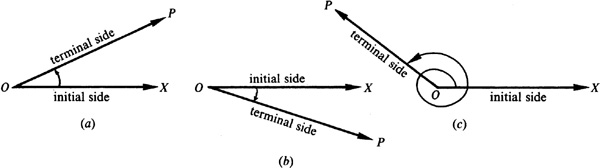
More often, a plane angle is thought of as being generated by revolving a ray (in a plane) from the initial position OX to a terminal position OP. Then O is again the vertex,  is called the initial side, and
is called the initial side, and  is called the terminal side of the angle.
is called the terminal side of the angle.
An angle generated in this manner is called positive if the direction of rotation (indicated by a curved arrow) is counterclockwise and negative if the direction of rotation is clockwise. The angle is positive in Fig. 1.2(a) and (c) and negative in Fig. 1.2(b).
When an arc of a circle is in the interior of an angle of the circle and the arc joins the points of intersection of the sides of the angle and the circle, the arc is said to subtend the angle.
A degree (°) is defined as the measure of the central angle subtended by an arc of a circle equal to 1/360 of the circumference of the circle.
A minute (′) is 1/60 of a degree; a second (″) is 1/60 of a minute, or 1/3600 of a degree.
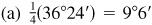
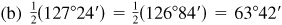
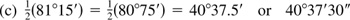
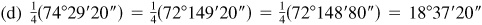
When changing angles in decimals to minutes and seconds, the general rule is that angles in tenths will be changed to the nearest minute and all other angles will be rounded to the nearest hundredth and then changed to the nearest second. When changing angles in minutes and seconds to decimals, the results in minutes are rounded to tenths and angles in seconds have the results rounded to hundredths.
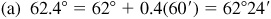
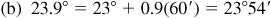
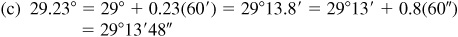
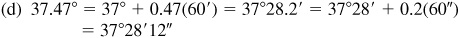
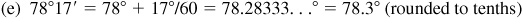
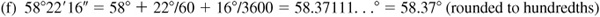
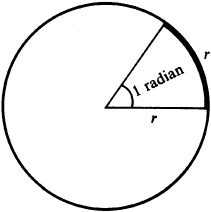
A radian (rad) is defined as the measure of the central angle subtended by an arc of a circle equal to the radius of the circle. (See Fig. 1.3.)
The circumference of a circle = 2π(radius) and subtends an angle of 360°. Then 2π radians = 360°; therefore
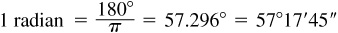
and
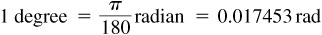
where 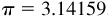 .
.
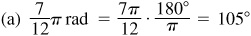
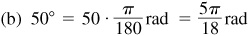
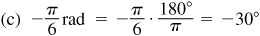
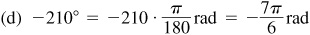
(See Probs. 1.1 and 1.2.)
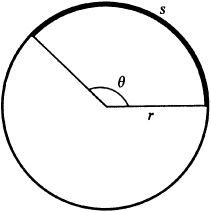
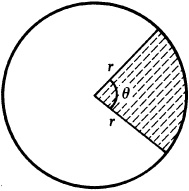
On a circle of radius r, a central angle of θ radians, Fig. 1.4, intercepts an arc of length
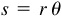
that is, arc length = radius × central angle in radians.
(NOTE: s and r may be measured in any convenient unit of length, but they must be expressed in the same unit.)
(a) On a circle of radius 30 in, the length of the arc intercepted by a central angle of 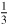 rad is
rad is
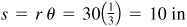
(b) On the same circle a central angle of 50° intercepts an arc of length
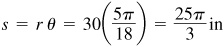
(c) On the same circle an arc of length 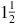 ft subtends a central angle
ft subtends a central angle
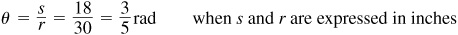
or
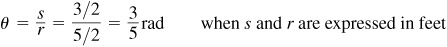
(See Probs. 1.3–1.8.)
The correspondence between points on a real number line and the points on a unit circle,  , with its center at the origin is shown in Fig. 1.5.
, with its center at the origin is shown in Fig. 1.5.
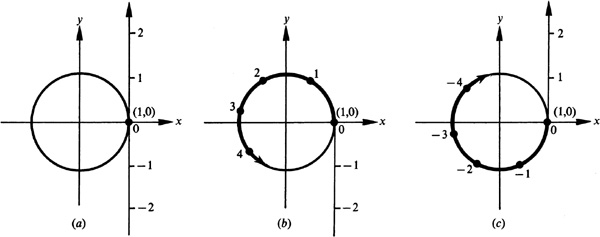
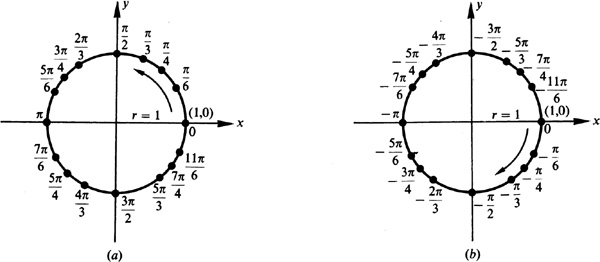
The zero (0) on the number line is matched with the point (1, 0) as shown in Fig. 1.5(a). The positive real numbers are wrapped around the circle in a counterclockwise direction, Fig. 1.5(b), and the negative real numbers are wrapped around the circle in a clockwise direction, Fig. 1.5(c). Every point on the unit circle is matched with many real numbers, both positive and negative.
The radius of a unit circle has length 1. Therefore, the circumference of the circle, given by 2πr, is 2π. The distance halfway around is π and the distance 1/4 the way around is π/2. Each positive number is paired with the length of an arc s, and since 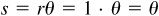 , each real number is paired with an angle θ in radian measure. Likewise, each negative real number is paired with the negative of the length of an arc and, therefore, with a negative angle in radian measure. Figure 1.6(a) shows points corresponding to positive angles, and Fig. 1.6(b) shows points corresponding to negative angles.
, each real number is paired with an angle θ in radian measure. Likewise, each negative real number is paired with the negative of the length of an arc and, therefore, with a negative angle in radian measure. Figure 1.6(a) shows points corresponding to positive angles, and Fig. 1.6(b) shows points corresponding to negative angles.
The area K of a sector of a circle (such as the shaded part of Fig. 1.7) with radius r and central angle θ radians is
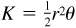
that is, the area of a sector = ½× the radius × the radius × the central angle in radians.
(NOTE: K will be measured in the square unit of area that corresponds to the length unit used to measure r.)
EXAMPLE 1.5 For a circle of radius 30 in, the area of a sector intercepted by a central angle of 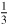 rad is
rad is

EXAMPLE 1.6 For a circle of radius 18 cm, the area of a sector intercepted by a central angle of 50° is
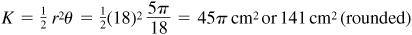
(NOTE: 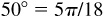 rad.)
rad.)
(See Probs. 1.9 and 1.10.)
Consider an object traveling at a constant velocity along a circular arc of radius r. Let s be the length of the arc traveled in time t. Let 2 be the angle (in radian measure) corresponding to arc length s.
Linear velocity measures how fast the object travels. The linear velocity, v, of an object is computed by 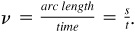
Angular velocity measures how fast the angle changes. The angular velocity, ω (the lower-case Greek letter omega) of the object, is computed by 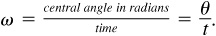
The relationship between the linear velocity v and the angular velocity ω for an object with radius r is
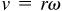
where ω is measured in radians per unit of time and v is distance per unit of time.
(NOTE: v and ω use the same unit of time and r and v use the same linear unit.)
EXAMPLE 1.7 A bicycle with 20-in wheels is traveling down a road at 15 mi/h. Find the angular velocity of the wheel in revolutions per minute.
Because the radius is 10 in and the angular velocity is to be in revolutions per minute (r/min), change the linear velocity 15 mi/h to units of in/min.
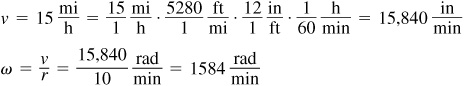
To change ω to r/min, we multiply by 1/2π revolution per radian (r/rad).
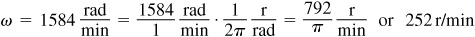
EXAMPLE 1.8 A wheel that is drawn by a belt is making 1 revolution per second (r/s). If the wheel is 18 cm in diameter, what is the linear velocity of the belt in cm/s?
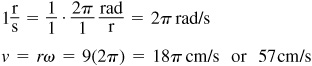
(See Probs. 1.11 to 1.15.)
SOLVED PROBLEMS
Use the directions for rounding stated on page 2.
1.1 Express each of the following angles in radian measure:
(a) 30°,
(b) 135°,
(c) 25°30′,
(d) 42°24′35″,
(e) 165.7°,
(f) –3.85°,
(g) –205°,
(h) –18°30″,
(i) –0.21°,
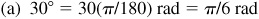 or 0.5236 rad
or 0.5236 rad
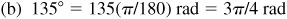 or 2.3562 rad
or 2.3562 rad
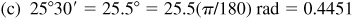 rad
rad
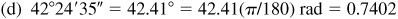 rad
rad
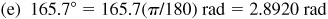
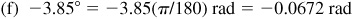
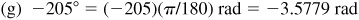
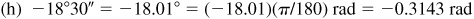
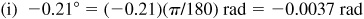
1.2 Express each of the following angles in degree measure:
(a) π/3 rad,
(b) 5π/9 rad,
(c) 2/5 rad,
(d) 4/3 rad,
(e) –π/8 rad,
(f) 2 rad,
(g) 1.53 rad,
(h) –3π/20 rad,
(i) –7π rad,
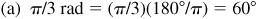
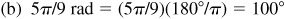
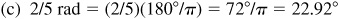 or 22°55.2′ or 22°55′12″
or 22°55.2′ or 22°55′12″
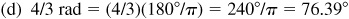 or 76°23.4′ or 76°23′24″
or 76°23.4′ or 76°23′24″
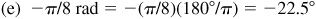 or 22°30′
or 22°30′
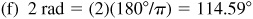 or 114°35.4′ or 114°35′24″
or 114°35.4′ or 114°35′24″
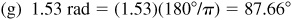 or 87°39.6′ or 87°39′36″
or 87°39.6′ or 87°39′36″
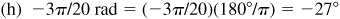
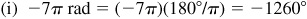
1.3 The minute hand of a clock is 12 cm long. How far does the tip of the hand move during 20 min?
During 20 min the hand moves through an angle 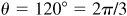 rad and the tip of the hand moves over a distance
rad and the tip of the hand moves over a distance 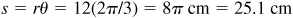 .
.
1.4 A central angle of a circle of radius 30 cm intercepts an arc of 6 cm. Express the central angle θ in radians and in degrees.
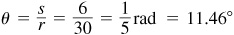
1.5 A railroad curve is to be laid out on a circle. What radius should be used if the track is to change direction by 25° in a distance of 120 m?
We are finding the radius of a circle on which a central angle 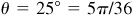 rad intercepts an arc of 120 m. Then
rad intercepts an arc of 120 m. Then
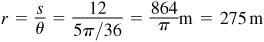
1.6 A train is moving at the rate of 8 mi/h along a piece of circular track of radius 2500 ft. Through what angle does it turn in 1 min?
Since 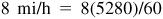 ft/min = 704 ft/min, the train passes over an arc of length
ft/min = 704 ft/min, the train passes over an arc of length 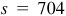 ft in 1 min. Then
ft in 1 min. Then 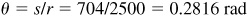 rad or 16.13°.
rad or 16.13°.
1.7 Assuming the earth to be a sphere of radius 3960 mi, find the distance of a point 36°N latitude from the equator.
Since 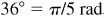 ,
, 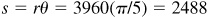 mi.
mi.
1.8 Two cities 270 mi apart lie on the same meridian. Find their difference in latitude.
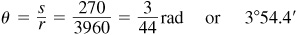
1.9 A sector of a circle has a central angle of 50° and an area of 605 cm2. Find the radius of the circle. 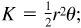 therefore
therefore 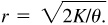
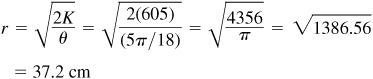
1.10 A sector of a circle has a central angle of 80° and a radius of 5 m. What is the area of the sector?
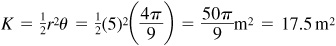
1.11 A wheel is turning at the rate of 48 r/min. Express this angular speed in (a) r/s, (b) rad/min, and (c) rad/s.
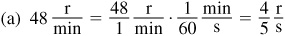
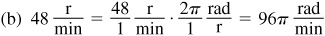 or
or 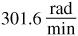
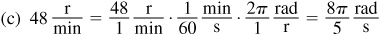 or
or 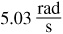
1.12 A wheel 4 ft in diameter is rotating at 80 r/min. Find the distance (in ft) traveled by a point on the rim in 1 s, that is, the linear velocity of the point (in ft/s).
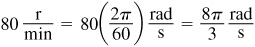
Then in 1 s the wheel turns through an angle 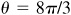 rad and a point on the wheel will travel a distance
rad and a point on the wheel will travel a distance 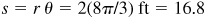 ft. The linear velocity is 16.8 ft/s.
ft. The linear velocity is 16.8 ft/s.
1.13 Find the diameter of a pulley which is driven at 360 r/min by a belt moving at 40 ft/s.
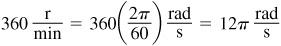
Then in 1 s the pulley turns through an angle 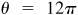 rad and a point on the rim travels a distance
rad and a point on the rim travels a distance 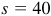 ft.
ft.
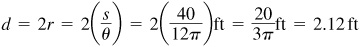
1.14 A point on the rim of a turbine wheel of diameter 10 ft moves with a linear speed of 45 ft/s. Find the rate at which the wheel turns (angular speed) in rad/s and in r/s.
In 1 s a point on the rim travels a distance 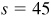 ft. Then in 1 s the wheel turns through an angle
ft. Then in 1 s the wheel turns through an angle 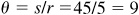 rad and its angular speed is 9 rad/s.
rad and its angular speed is 9 rad/s.
Since 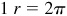 rad or
rad or 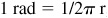 ,
, 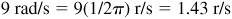 .
.
1.15 Determine the speed of the earth (in mi/s) in its course around the sun. Assume the earth’s orbit to be a circle of radius 93,000,000 mi and 1 year = 365 days.
In 365 days the earth travels a distance of 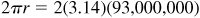 mi.
mi.
In 1 s it will travel a distance 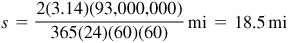 . Its speed is 18.5 mi/s.
. Its speed is 18.5 mi/s.
SUPPLEMENTARY PROBLEMS
Use the directions for rounding stated on page 2.
1.16 Express each of the following in radian measure:
(a) 25°,
(b) 160°,
(c) 75°30′,
(d) 112°40′,
(e) 12°12′20″,
(f) 18.34°
Ans.
(a) 5π/36 or 0.4363 rad
(b) 8π/9 or 2.7925 rad
(c) 151π/360 or 1.3177 rad
(d) 169π/270 or 1.9664 rad
(e) 0.2130 rad
(f) 0.3201 rad
1.17 Express each of the following in degree measure:
(a) π/4 rad,
(b) 7π/10 rad,
(c) 5π/6 rad,
(d) 1/4 rad,
(e) 7/5 rad
Ans.
(a) 45°,
(b) 126°,
(c) 150°,
(d) 14°19′12″ or 14.32°,
(e) 80°12′26″ or 80.21°
1.18 On a circle of radius 24 in, find the length of arc subtended by a central angle of (a) 2/3 rad, (b) 3π/5 rad, (c) 75°, (d) 130°.
Ans.
(a) 16 in,
(b) 14.4π or 45.2 in,
(c) 10π or 31.4 in,
(d) 52π/3 or 54.4 in
1.19 A circle has a radius of 30 in. How many radians are there in an angle at the center subtended by an arc of (a) 30 in, (b) 20 in, (c) 50 in?
Ans.
(a) 1 rad,
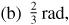
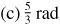
1.20 Find the radius of the circle for which an arc 15 in long subtends an angle of (a) 1 rad, 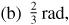 , (c) 3 rad, (d) 20°, (e) 50°.
, (c) 3 rad, (d) 20°, (e) 50°.
Ans.
(a) 15 in,
(b) 22.5 in,
(c) 5 in,
(d) 43.0 in,
(e) 17.2 in
1.21 The end of a 40-in pendulum describes an arc of 5 in. Through what angle does the pendulum swing?
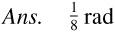 or 7°9′36″ or 7.16°
or 7°9′36″ or 7.16°
1.22 A train is traveling at the rate 12 mi/h on a curve of radius 3000 ft. Through what angle has it turned in 1 min?
Ans. 0.352 rad or 20°10′ or 20.17°
1.23 A curve on a railroad track consists of two circular arcs that make an S shape. The central angle of one is 20° with radius 2500 ft and the central angle of the other is 25° with radius 3000 ft. Find the total length of the two arcs.
Ans. 6250π/9 or 2182 ft
1.24 Find the area of the sector determined by a central angle of π/3 rad in a circle of diameter 32 mm.
Ans. 128π/3 or 134.04 mm2
1.25 Find the central angle necessary to form a sector of area 14.6 cm2 in a circle of radius 4.85 cm.
Ans. 1.24 rad or 71.05° or 71°3′
1.26 Find the area of the sector determined by a central angle of 100° in a circle with radius 12 cm.
Ans. 40π or 125.7 cm2
1.27 If the area of a sector of a circle is 248 m2 and the central angle is 135°, find the diameter of the circle.
Ans. diameter = 29.0 m
1.28 A flywheel of radius 10 cm is turning at the rate 900 r/min. How fast does a point on the rim travel in m/s?
Ans. 3π or 9.4 m/s
1.29 An automobile tire has a diameter of 30 in. How fast (r/min) does the wheel turn on the axle when the automobile maintains a speed of 45 mi/h?
Ans. 504 r/min
1.30 In grinding certain tools the linear velocity of the grinding surface should not exceed 6000 ft/s. Find the maximum number of revolutions per second of (a) a 12-in (diameter) emery wheel and (b) an 8-in wheel.
Ans. (a) 6000/π r/s or 1910 r/s, (b) 9000/π r/s or 2865 r/s
1.31 If an automobile wheel 78 cm in diameter rotates at 600 r/min, what is the speed of the car in km/h?
Ans. 88.2 km/h