For proofs of these formulas, see Prob. 10.1.
For proofs of these formulas, see Prob. 10.2.
SOLVED PROBLEMS
10.1 Derive the product formulas.
Since
Since
Since
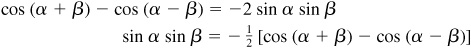
10.2 Derive the sum and difference formulas.
Let 
and 
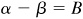so that 
and 
. Then (see Prob. 10.1)
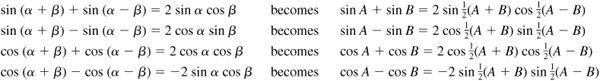
10.3 Express each of the following as a sum or difference.
(a) sin 40° cos 30°,
(b) cos 110° sin 55°,
(c) cos 50° cos 35°,
(d) sin 55° sin 40°
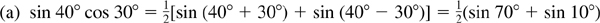
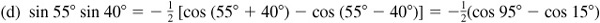
10.4 Express each of the following as a product.
(a) sin 50°+ sin 40°,
(b) sin 70°– sin 20°,
(c) cos 55°+ cos 25°,
(d) cos 35°– cos 75°
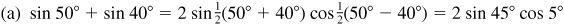
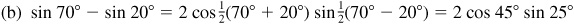
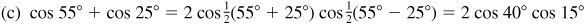
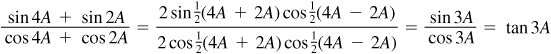
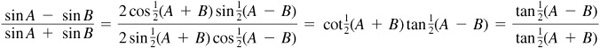
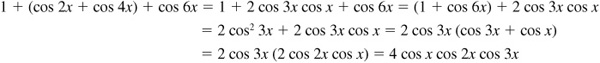
10.9 Transform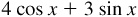 
into the form 
.
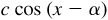Since 
, set 
and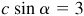 
.
Then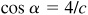 
and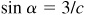 
. Since 
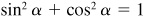, c = 5 and -5.
Using c = 5,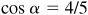 
, 
, and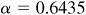 
rad. Thus,
Using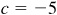 
, 
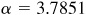rad and
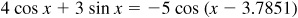
10.10 Find the maximum and minimum values of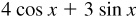 
on the interval 
.
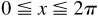From Prob. 10.9,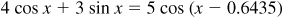 
.
On the prescribed interval, cos θ attains its maximum value 1 when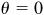 
and its minimum value –1 when 
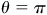. Thus, the maximum value of 
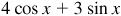is 5, which occurs when 
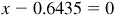or when 
, while the minimum value is –5, which occurs when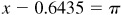 
or when 
.
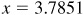SUPPLEMENTARY PROBLEMS
10.11 Express each of the following products as a sum or difference of sines or cosines.
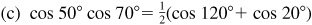
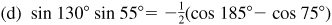
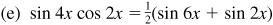
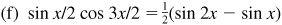
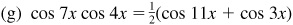
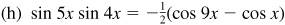
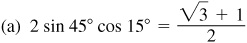and 
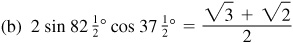
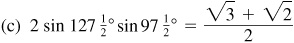
10.13 Express each of the following as a product.
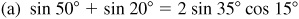
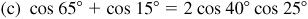
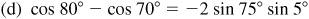
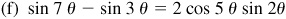
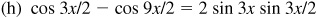
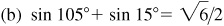
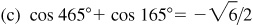
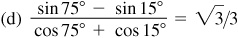
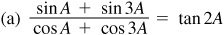
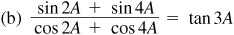
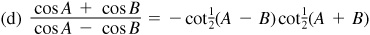
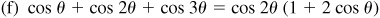
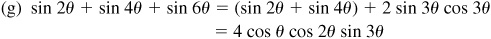
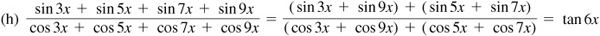
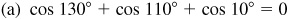
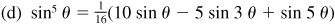
10.18 Transform (using radians):
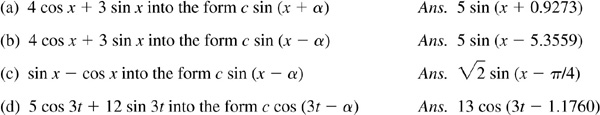
10.19 Find the maximum and minimum values of each sum of Prob. 10.18 and a value of x or t between 0 and 2π at which each occurs.
Ans. (a) Maximum = 5, when 
(i.e., when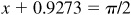 
); minimum = –5, when 
.
(b) Same as (a).
when 
; 
, when 
(d) Maximum = 13, when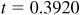 
; minimum = –13, when 
.
.
.