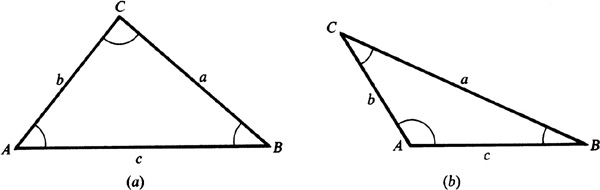
An oblique triangle is one which does not contain a right angle. Such a triangle contains either three acute angles or two acute angles and one obtuse angle.
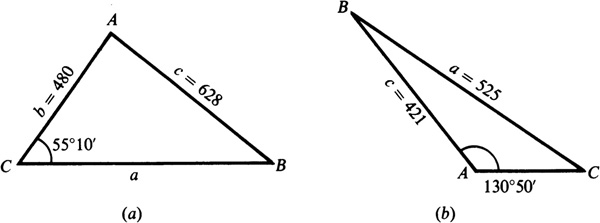
The convention of denoting the angles by A, B, and C and the lengths of the corresponding opposite sides by a, b, and c will be used here. (See Fig. 11.1.)
In any triangle ABC, the ratio of a side and the sine of the opposite angle is a constant; i.e.,
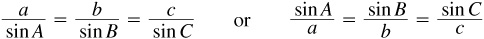
For a proof of the law of sines, see Prob. 11.1.
In any triangle ABC, the square of any side is equal to the sum of the squares of the other two sides diminished by twice the product of these sides and the cosine of the included angle; i.e.,
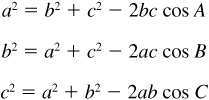
For a proof of the law of cosines, see Prob. 11.3.
When three parts of a triangle, not all angles, are known, the triangle is uniquely determined, except in one case noted below. The five cases of oblique triangles are
Case I: Given two angles and the side opposite one of them
Case II: Given two angles and the included side
Case III: Given two sides and the angle opposite one of them
Case IV: Given two sides and the included angle
Case V: Given the three sides
In Case III there is not always a unique solution. It is possible to have no solution for the angle, one solution for the angle, or two solutions—an angle and its supplement. See Example 11.3 and Prob. 11.2 for a complete discussion of this case.
Case I
Given two angles and the side opposite one of them
EXAMPLE 11.1 Suppose b, B, and C are given.
To find c, use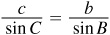 
, then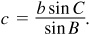 
To find A, use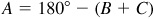 
.
To find a, use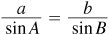 
then 
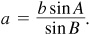
(See Prob. 11.4.)
Case II
Given two angles and the included side
EXAMPLE 11.2 Suppose a, B, and C are given.
To find A, use .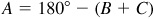
To find b, use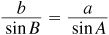 
; then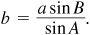 
To find c, use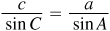 
; then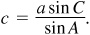 
(See Prob. 11.5.)
Case III
Given two sides and the angle opposite one of them
EXAMPLE 11.3 Suppose b, c, and B are given.
From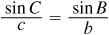 
, 
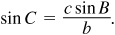
If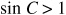 
, no angle C is determined.
If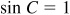 
, 
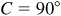and a right triangle is determined.
If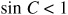 
, two angles are determined: an acute angle C and an obtuse angle 
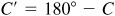. Thus, there may be one or two triangles determined. If 
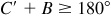, then the angle C’ is not a solution.
This case is discussed geometrically in Prob. 11.2. The results obtained may be summarized as follows:
When the given angle is acute, there will be
(a) One solution if the side opposite the given angle is equal to or greater than the other given side
(b) No solution, one solution (right triangle), or two solutions if the side opposite the given angle is less than the other given side
When the given angle is obtuse, there will be
(c) No solution when the side opposite the given angle is less than or equal to the other given side
(d) One solution if the side opposite the given angle is greater than the other given side
(1) When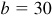 
, 
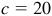, and 
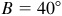, there is one solution since B is acute and b > c.
(2) When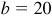 
, 
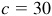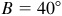, and , there is either no solution, one solution, or two solutions. The particular subcase is determined after computing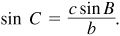 
(3) When 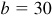, , 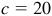and 
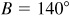, there is one solution.
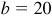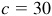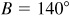(4) When , , and , there is no solution.
This, the so-called ambiguous case, is solved by the law of sines.
(See Probs. 11.9 to 11.11.)
Case IV
Given two sides and the included angle
EXAMPLE 11.5 Suppose a, b, and C are given.
To find c, use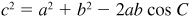 
.
To find A, use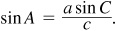 
To find B, use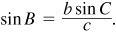 
To check, use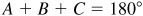 
.
(See Probs. 11.13 and 11.14.)
Case V
Given the three sides
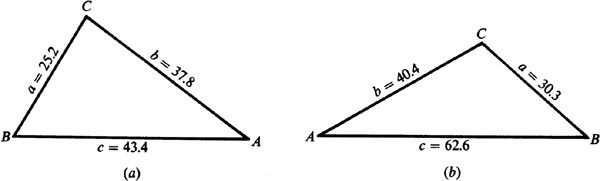
EXAMPLE 11.6 With a, b, and c given, solve the law of cosines for each of the angles.
To find the angles, use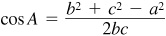 
, 
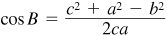, and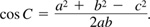 
To check, use A + B + C = 180°.
(See Probs. 11.17 and 11.18.)
Let ABC be any oblique triangle. In Fig. 11.2, angles A and B are acute, while in Fig. 11.3, angle B is obtuse. Draw CD perpendicular to AB or AB extended and denote its length by h.
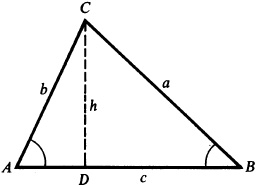
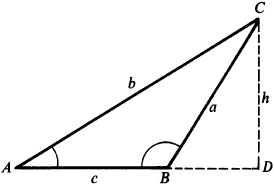
In the right triangle ACD of either figure,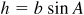 
, while in the right triangle BCD, 
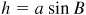since in Fig. 11.3, 
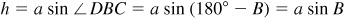. Thus,
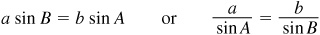
In a similar manner (by drawing a perpendicular from B to AC or a perpendicular from A to BC), we obtain
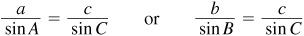
Thus, finally,
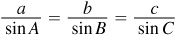
11.2 Discuss the several special cases when two sides and the angle opposite one of them are given.
Let b, c, and B be the given parts. Construct the given angle B and lay off the side 
. With A as center and radius equal to b (the side opposite the given angle), describe an arc. Fig. 11.4(a) to (e) illustrates the special cases which may occur when the given angle B is acute, while Fig. 11.4(f) and (g) illustrates the cases when B is obtuse.
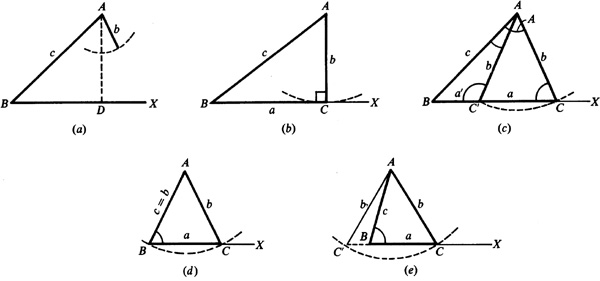
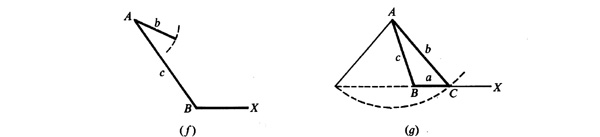
The given angle B is acute.
Fig. 11.4(a). When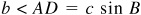 
, the arc does not meet BX and no triangle is determined.
Fig. 11.4(b). When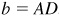 
, the arc is tangent to BX and one triangle—a right triangle with the right angle at C—is determined.
Fig. 11.4(c). When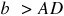 
and 
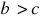, the arc meets BX in two points C and C’ on the same side of B. Two triangles—ABC, in which C is acute, and ABC ’, in which 
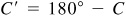is obtuse—are determined.
Fig. 11.4(d). When 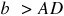and 
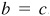, the arc meets BX in C and B. One triangle (isosceles) is determined.
Fig. 11.4(e). When 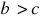, the arc meets BX in C and BX extended in C ’. Since the triangle ABC’ does not contain the given angle B, only one triangle ABC is determined.
The given angle is obtuse.
Fig. 11.4(f). When b <c or 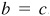, no triangle is formed.
Fig. 11.4(g). When 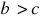, only one triangle is formed as in Fig. 11.4(e).
11.3 Derive the law of cosines.
In either right triangle ACD of Fig. 11.5,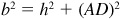 
.
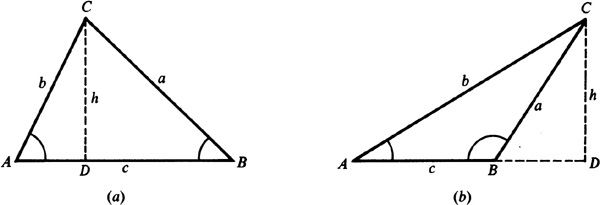
In the right triangle BCD of Fig. 11.5(a),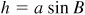 
and 
.
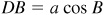Then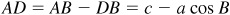 
and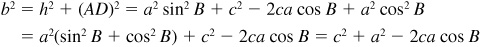 
In the right triangle BCD of Fig. 11.5(b),
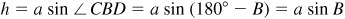
and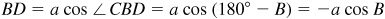 
Then 
The remaining equations may be obtained by cyclic changes of the letters.
11.4 Solve the triangle ABC, given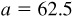 
, 
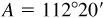, and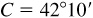 
. See Fig. 11.6.
The required parts are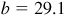 
, 
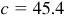, and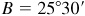 
.
Case II
11.5 Solve the triangle ABC, given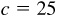 
, 
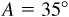, and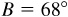 
. See Fig. 11.7.
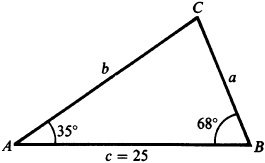
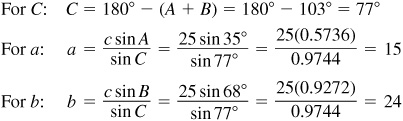
The required parts are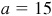 
, 
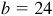, and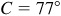 
.
11.6 A and B are two points on opposite banks of a river. From A, a line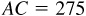 
m is laid off, and the angles 
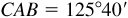and 
are measured. Find the length of AB.
In the triangle ABC of Fig. 11.8(a),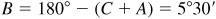 
and
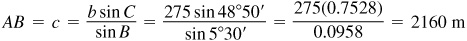
11.7 A ship is sailing due east when a light is observed bearing N62°10’E. After the ship has traveled 2250 m, the light bears N48°25’E. If the course is continued, how close will the ship approach the light? (See Prob. 5.5, Chap. 5.)
Refer to Fig. 11.8(b).
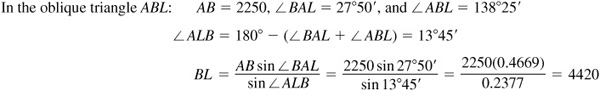
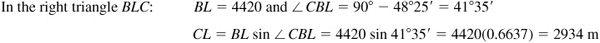
For an alternative solution, find AL in the oblique triangle ABL and then CL in the right triangle ALC.
11.8 A tower 125 ft high is on a cliff on the bank of a river. From the top of the tower, the angle of depression of a point on the opposite shore is 28°40’, and from the base of the tower, the angle of depression of the same point is 18°20’. Find the width of the river and the height of the cliff.
In Fig. 11.9, BC represents the tower, DB represents the cliff, and A is the point on the opposite shore.
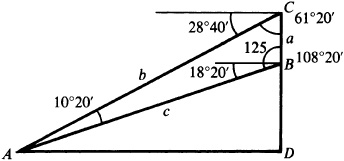
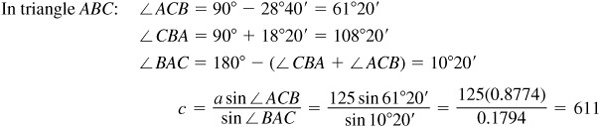
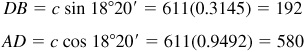
The river is 580 ft wide, and the cliff is 192 ft high.
Case III
11.9 Solve the triangle ABC, given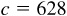 
, 
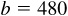, and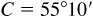 
. Refer to Fig. 11.10(a).
Since C is acute and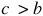 
, there is only one solution.
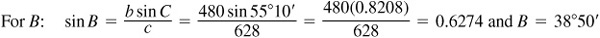
(NOTE: If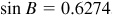 
, then 
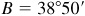or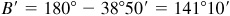 
and each could be an angle in a triangle. Since 
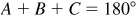, it follows that 
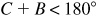; thus 
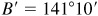is not a solution in this problem because 
.
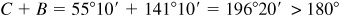Whenever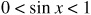 
, it is possible to find angles x in quadrants I and II that satisfy the value of sin x and could be angles in a triangle. The first-quadrant angle is always a solution but the second-quadrant angle is a solution only when its sum with the given angle is less than 180°.)
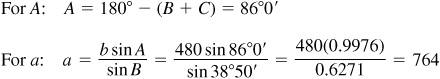
The required parts are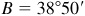 
, 
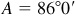, and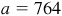 
.
11.10 Solve the triangle ABC, given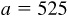 
, 
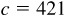, and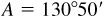 
. Refer to Fig. 11.10(b).
Since A is obtuse and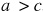 
, there is one solution.
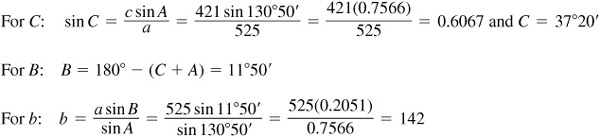
The required parts are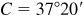 
, 
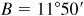, and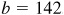 
.
11.11 Solve the triangle ABC, given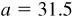 
, 
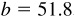, and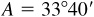 
. Refer to Fig. 11.11(a).
Since A is acute and a <b, there is the possibility of two solutions.
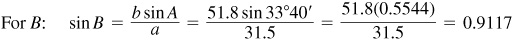
There are two solutions,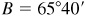 
and 
.
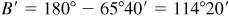The required parts are
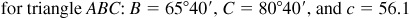
and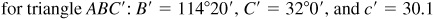 
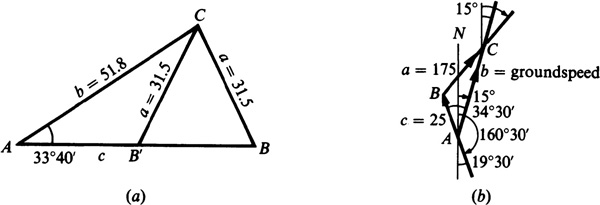
11.12 A pilot wishes a course 15°0’ against a wind of 25 mi/h from 160°30’. Find his required heading and the groundspeed when the airspeed is 175 mi/h. Refer to Fig. 11.11(b).
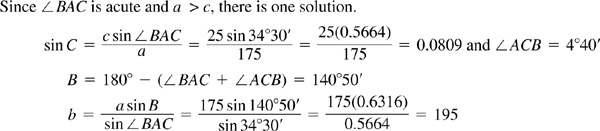
Case IV
11.13 Solve the triangle ABC, given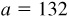 
, 
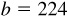, and 
. Refer to Fig. 11.12(a).
(Since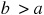 
, A is acute; since 
, 
.)
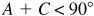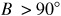Check: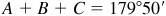 
. The required parts are 
, 
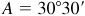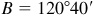, and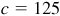 
.
11.14 Solve the triangle ABC, given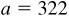 
, 
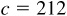, and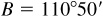 
. Refer to Fig. 11.12(b).
Check: A + B + C = 180°.
The required parts are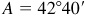 
, 
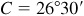, and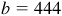 
.
11.15 Two forces of 17.5 and 22.5 lb act on a body. If their directions make an angle of 50°10’ with each other, find the magnitude of their resultant and the angle that it makes with the larger force.
Refer to Fig. 11.13(a).
In the parallelogram ABCD, 
and 
. In the triangle ABC,
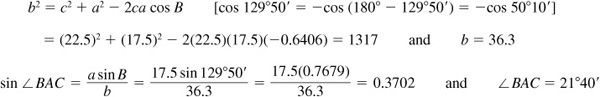
The resultant is a force of 36.3 lb and the required angle is 21°40’.
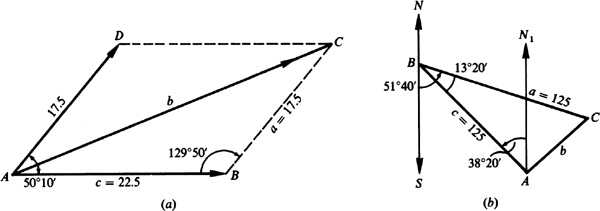
11.16 From A a pilot flies 125 km in the direction N38°20’W and turns back. Through an error, the pilot then flies 125 km in the direction S51°40’E. How far and in what direction must the pilot now fly to reach the intended destination A ?
Refer to Fig. 11.13(b).
Denote the turn-back point as B and the final position as C.
In the triangle ABC,
Since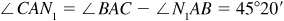 
, the pilot must fly a course = S45°20’W for 29.0 km in going from C to A.
Case V
11.17 Solve the triangle ABC, given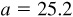 
, 
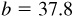, and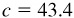 
. Refer to Fig. 11.14(a).
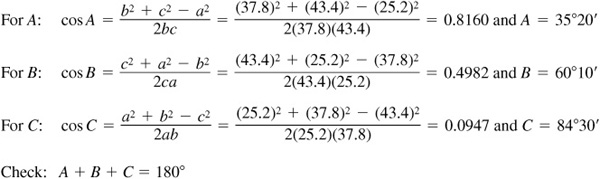
11.18 Solve the triangle ABC, given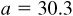 
, 
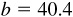, and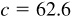 
. Refer to Fig. 11.14(b):
11.19 The distances of a point C from two points A and B, which cannot be measured directly, are required. The line CA is continued through A for a distance 175 m to D, the line CB is continued through B for 225 m to E, and the distances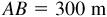 
, 
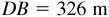, and 
are measured. Find AC and BC. See Fig. 11.15.
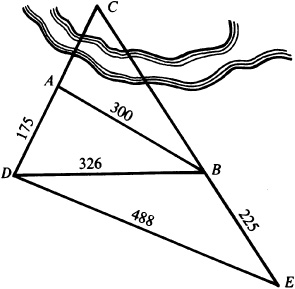
Triangle ABC may be solved for the required parts after the angles ∠BAC and ∠ABC have been found. The first angle is the supplement of ∠BAD and the second is the supplement of the sum of ∠ABD and ∠DBE.
In the triangle ABD whose sides are known,
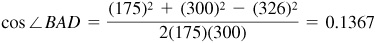
and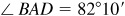 
and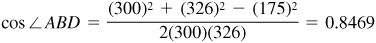 
and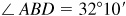 
In the triangle BDE whose sides are known,
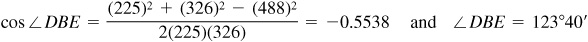
In the triangle ABC: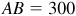 
, 
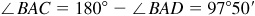
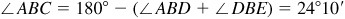
and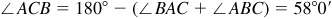 
Then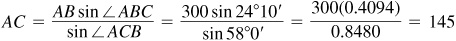 
and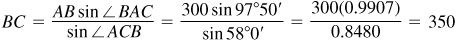 
The required distances are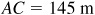 
and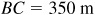 
.
11.20 Solve the triangle ABC, given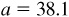 
, 
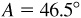, and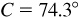 
. See Fig. 11.16.
.
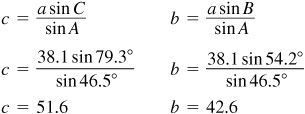
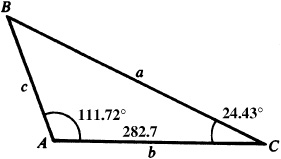
11.21 Solve the triangle ABC, given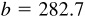 
, 
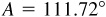, and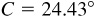 
. See Fig. 11.17.
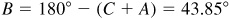
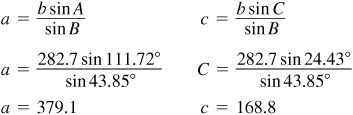
Case III
11.22 Solve the triangle ABC, given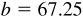 
, 
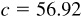, and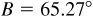 
. See Fig. 11.18.
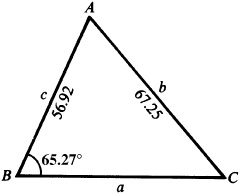
There could be two solutions in this case.
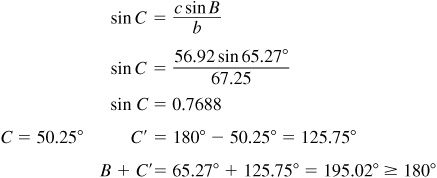
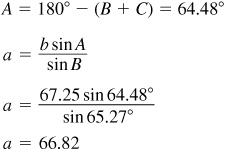
The required parts are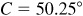 
, 
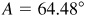, and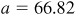 
.
11.23 Solve the triangle ABC, given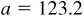 
, 
, 
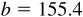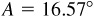. See Fig. 11.19.
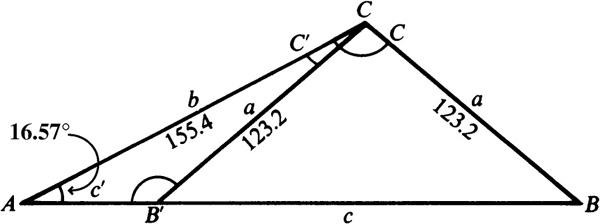
Since A is acute and a <b, there may be two solutions.
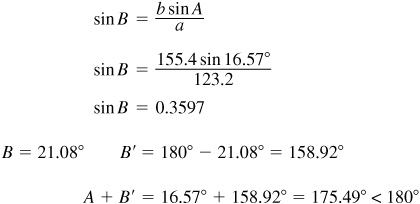
Therefore, B’ is a solution.
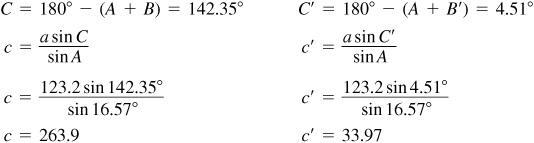
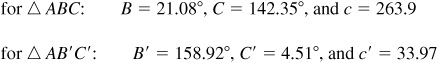
Case IV
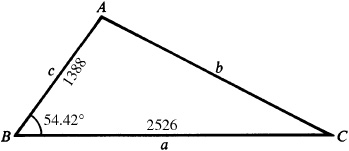
11.24 Solve the triangle ABC, given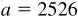 
, 
, 
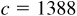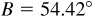. See Fig. 11.20.
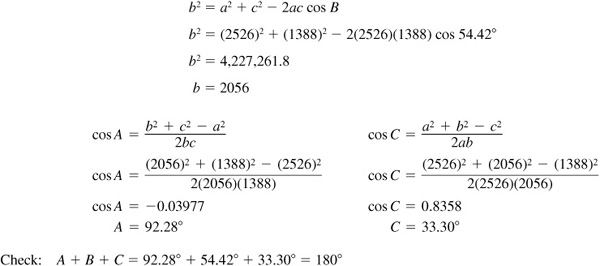
11.25 Solve the triangle ABC, given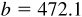 
, 
, , 
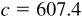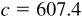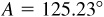. See Fig. 11.21.
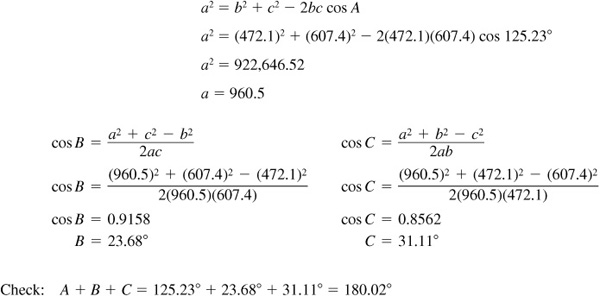
11.26 Two adjacent sides of a parallelogram are 3473 and 4822 ft, and the angle between them is 72.23°. Find the length of the longer diagonal. See Fig. 11.22.
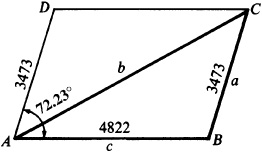
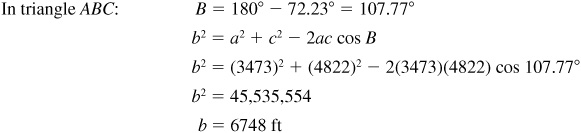
The longer diagonal is 6748 ft long.
Case V
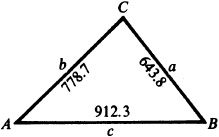
11.27 Solve the triangle ABC, given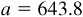 
, 
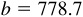, and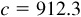 
. See Fig. 11.23.
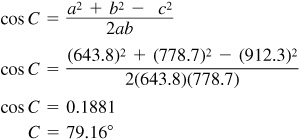
Check: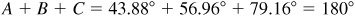 
11.28 Consider the given parts of triangle ABC. State whether the law of sines or cosines should be used to solve for the required part, and then find its value.
Solve each of the following oblique triangles ABC, given:
11.40 Two ships have radio equipment with a range of 200 km. One is 155 km N42°40′E and the other is 165 km N45°10′W of a shore station. Can the two ships communicate directly?
Ans. No; they are 222 km apart.
11.41 A ship sails 15.0 mi on a course S40°10′W and then 21.0 mi on a course N28°20′W. Find the distance and direction of the last position from the first.
Ans. 20.9 mi, N70°30′W
11.42 A lighthouse is 10 km northwest of a dock. A ship leaves the dock at 9 A.M. and steams west at 12 km/h. At what time will it be 8 km from the lighthouse?
Ans. 9:17 A.M. and 9:54 A.M.
11.43 Two forces of 115 and 215 lb acting on an object have a resultant of magnitude 275 lb. Find the angle between the directions in which the given forces act.
Ans. 70°50’
11.44 A tower 150 m high is situated at the top of a hill. At a point 650 m down the hill the angle between the surface of the hill and the line of sight to the top of the tower is 12°30’. Find the inclination of the hill to a horizontal plane.
Ans. 7°50’
11.45 Three circles of radii 115, 150, and 225 m are tangent to each other externally. Find the angles of the triangle formed by joining the centers of the circles.
Ans. 43°10’, 61°20’, 75°30’
Solve each of the oblique triangles ABC, given:
