
 and
and 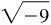 ) is called an imaginary number. Since by definition
) is called an imaginary number. Since by definition  and
and 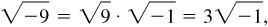 it is convenient to introduce the symbol
it is convenient to introduce the symbol  and to adopt
and to adopt  and
and  as the standard form for these numbers.
as the standard form for these numbers.The square root of a negative number (e.g., 
 and
and 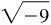 ) is called an imaginary number. Since by definition
) is called an imaginary number. Since by definition  and
and 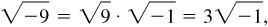 it is convenient to introduce the symbol
it is convenient to introduce the symbol  and to adopt
and to adopt  and
and  as the standard form for these numbers.
as the standard form for these numbers.
The symbol i has the property 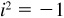 ; and for higher integral powers we have
; and for higher integral powers we have 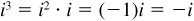 ,
,  ,
,  , etc.
, etc.
The use of the standard form simplifies the operations on imaginary numbers and eliminates the possibility of certain common errors. Thus  since
since  but
but  since
since 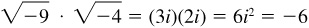 .
.
A number 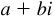 , where a and b are real numbers, is called a complex number. The first term a is called the real part of the complex number, and the second term bi is called the imaginary part.
, where a and b are real numbers, is called a complex number. The first term a is called the real part of the complex number, and the second term bi is called the imaginary part.
Complex numbers may be thought of as including all real numbers and all imaginary numbers. For example,  and
and  .
.
Two complex numbers 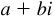 and
and  are said to be equal if and only if
are said to be equal if and only if  and
and  .
.
The conjugate of a complex number 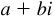 is the complex number
is the complex number  . Thus,
. Thus,  and
and  , and
, and  and
and  are pairs of conjugate complex numbers.
are pairs of conjugate complex numbers.
Addition
To add two complex numbers, add the real parts and the imaginary parts separately.
Subtraction
To subtract two complex numbers, subtract the real parts and the imaginary parts separately.
Multiplication
To multiply two complex numbers, carry out the multiplication as if the numbers were ordinary binomials and replace i 2 by –1.
To divide two complex numbers, multiply both numerator and denominator of the fraction by the conjugate of the denominator.
[Note the form of the result; it is neither  nor
nor  .]
.]
(See Probs. 15.1 to 15.9.)
The complex number  may be represented graphically by the point P [(see Fig. 15.1(a)] whose rectangular coordinates are (x, y).
may be represented graphically by the point P [(see Fig. 15.1(a)] whose rectangular coordinates are (x, y).
The point O having coordinates (0, 0) represents the complex number  . All points on the x axis have coordinates of the form (x, 0) and correspond to real numbers
. All points on the x axis have coordinates of the form (x, 0) and correspond to real numbers  . For this reason, the x axis is called the axis of reals. All points on the y axis have coordinates of the form (0, y) and correspond to imaginary numbers
. For this reason, the x axis is called the axis of reals. All points on the y axis have coordinates of the form (0, y) and correspond to imaginary numbers  . The y axis is called the axis of imaginaries. The plane on which the complex numbers are represented is called the complex plane.
. The y axis is called the axis of imaginaries. The plane on which the complex numbers are represented is called the complex plane.
In addition to representing a complex number by a point P in the complex plane, the number may be represented [see Fig. 15.1(b)] by the directed line segment or vector OP.

Let 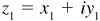 and
and 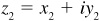 be two complex numbers. The vector representation of these numbers [Fig. 15.2(a)] suggests the familiar parallelogram law for determining graphically the sum
be two complex numbers. The vector representation of these numbers [Fig. 15.2(a)] suggests the familiar parallelogram law for determining graphically the sum  .
.
Since  , the difference
, the difference  of the two complex numbers may be obtained graphically by applying the parallelogram law to
of the two complex numbers may be obtained graphically by applying the parallelogram law to 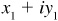 and
and  . [See Fig. 15.2(b).]
. [See Fig. 15.2(b).]
In Fig. 15.2(c) both the sum  and the difference
and the difference  are shown. Note that the segments OS and P2 P1 (the other diagonal of OP2 RP1) are equal.
are shown. Note that the segments OS and P2 P1 (the other diagonal of OP2 RP1) are equal.
(See Prob. 15.11.)
Let the complex number  be represented [Fig. 15.3(a)] by the vector OP. This vector (and hence the complex number) may be described in terms of the length r of the vector and any positive angle θ which the vector makes with the positive x axis (axis of positive reals). The number
be represented [Fig. 15.3(a)] by the vector OP. This vector (and hence the complex number) may be described in terms of the length r of the vector and any positive angle θ which the vector makes with the positive x axis (axis of positive reals). The number  is called the modulus or absolute value of the complex number. The angle θ, called the amplitude of the complex number, is usually chosen as the smallest positive angle for which tan θ = y/x, but at times it will be found more convenient to choose some other angle coterminal with it.
is called the modulus or absolute value of the complex number. The angle θ, called the amplitude of the complex number, is usually chosen as the smallest positive angle for which tan θ = y/x, but at times it will be found more convenient to choose some other angle coterminal with it.

From Fig. 15.3(a),  and
and  ; then
; then  . We call
. We call 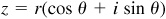 the polar or trigonometric form and
the polar or trigonometric form and  the rectangular form of the complex number z. An abbreviated notation is sometimes used and is written
the rectangular form of the complex number z. An abbreviated notation is sometimes used and is written  .
.
EXAMPLE 15.5 Express  in polar form. [See Fig. 15.3(b).]
in polar form. [See Fig. 15.3(b).]
The modulus is 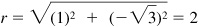 . Since
. Since  the amplitude θ is either 120° or 300°. Now we know that P lies in quadrant IV; hence,
the amplitude θ is either 120° or 300°. Now we know that P lies in quadrant IV; hence,  and the required polar form is
and the required polar form is  . Note that z may also be represented in polar form by
. Note that z may also be represented in polar form by  , where n is any integer.
, where n is any integer.
EXAMPLE 15.6 Express the complex number  in rectangular form.
in rectangular form.
Since  and
and  ,
,

is the required rectangular form.
(See Probs. 15.12 and 15.13.)
Multiplication
The modulus of the product of two complex numbers is the product of their moduli, and the amplitude of the product is the sum of their amplitudes.
Division
The modulus of the quotient of two complex numbers is the modulus of the dividend divided by the modulus of the divisor, and the amplitude of the quotient is the amplitude of the dividend minus the amplitude of the divisor. For a proof of these theorems, see Prob. 15.14.
EXAMPLE 15.7 Find (a) the product z1 z2, (b) the quotient z1/z2, and (c) the quotient z2/z1 where  and
and 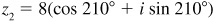 .
.
(a) The modulus of the product is  . The amplitude is
. The amplitude is  , but, following the convention, we shall use the smallest positive coterminal angle
, but, following the convention, we shall use the smallest positive coterminal angle  . Thus
. Thus  .
.
(b) The modulus of the quotient  and the amplitude is
and the amplitude is 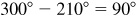 . Thus
. Thus  .
.
(c) The modulus of the quotient  . The amplitude is
. The amplitude is 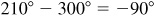 , but we shall use the smallest positive coterminal angle
, but we shall use the smallest positive coterminal angle  . Thus
. Thus

[NOTE: From Examples 15.5 and 15.6, the numbers are

in rectangular form. Then

as in (a), and

as in (c).]
(See Probs. 15.15 and 15.16.)
If n is any rational number,

A proof of this theorem is beyond the scope of this book; a verification for  and n = 3 is given in Prob. 15.17.
and n = 3 is given in Prob. 15.17.

(See Prob. 15.18.)
We state, without proof, the theorem: A complex number  has exactly n distinct nth roots.
has exactly n distinct nth roots.
The procedure for determining these roots is given in Example 15.9.
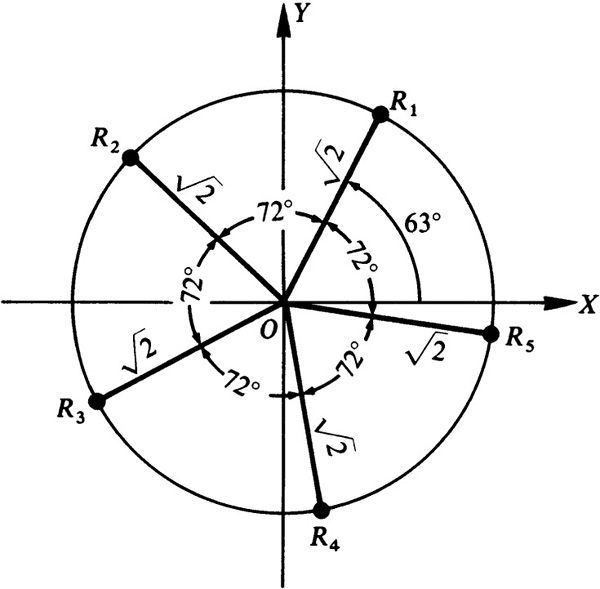
EXAMPLE 15.9 Find all fifth roots of  .
.
The usual polar form of  is
is  , but we shall need the more general form
, but we shall need the more general form

where k is any integer, including zero.
Using De Moivre’s theorem, a fifth root of  is given by
is given by

Assigning in turn the values 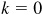 , 1, 2, …, we find
, 1, 2, …, we find

Thus, the five fifth roots are obtained by assigning the values 0, 1, 2, 3, 4 (i.e., 0, 1, 2, 3, …, n –1) to k.
(See also Prob. 15.19.)
The modulus of each of the roots is  hence these roots lie on a circle of radius
hence these roots lie on a circle of radius  with center at the origin. The difference in amplitude of two consecutive roots is 728; hence the roots are equally spaced on this circle, as shown in Fig. 15.4.
with center at the origin. The difference in amplitude of two consecutive roots is 728; hence the roots are equally spaced on this circle, as shown in Fig. 15.4.
In Probs. 15.1 to 15.6, perform the indicated operations, simplify, and write the result in the form a + bi.
Here 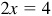 and
and 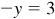 ; then
; then  and
and  .
.
15.8 Show that the conjugate complex numbers  and
and  are roots of the quadratic equation
are roots of the quadratic equation  .
.
For  :
:  .
.
For  :
:  .
.
Since each number satisfies the equation, it is a root of the equation.
15.9 Show that the conjugate of the sum of two complex numbers is equal to the sum of their conjugates.
Let the complex numbers be a + bi and c + di. Their sum is  and the conjugate of the sum is
and the conjugate of the sum is  .
.
The conjugates of the two given numbers are a – bi and  , and their sum is
, and their sum is
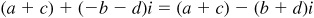
15.10 Represent graphically (as a vector) the following complex numbers:
 ,
,
 ,
,
 ,
,

We locate, in turn, the points whose coordinates are (3, 2), (2, –1), (–2, 1), (–1, –3) and join each to the origin O.
15.11 Perform graphically the following operations:
 ,
,
 ,
,
 ,
,

For (a) and (b), draw as in Fig. 15.5(a) and (b) the two vectors and apply the parallelogram law.
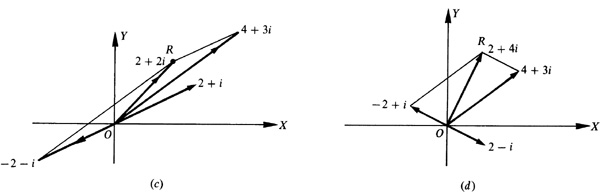
For (c), draw the vectors representing  and
and  and apply the parallelogram law as in Fig. 15.5(c).
and apply the parallelogram law as in Fig. 15.5(c).
For (d), draw the vectors representing  and
and  and apply the parallelogram law as in Fig. 15.5(d).
and apply the parallelogram law as in Fig. 15.5(d).
15.12 Express each of the following complex numbers z in polar form:
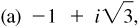 ,
,
 ,
,
 ,
,
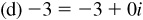 ,
,
 ,
,

(a) P lies in the second quadrant;  ;
;  and
and  .
.
Thus,  .
.
(b) P lies in the first quadrant; 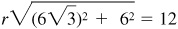 ;
;  and
and  .
.
Thus, 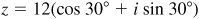 .
.
(c) P lies in the fourth quadrant;  ;
;  and
and  .
.
Thus,  .
.
(d) P lies on the negative x axis and  ;
; 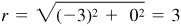 .
.
Thus,  .
.
(e) P lies on the positive y axis and  ;
; 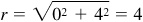 .
.
Thus, 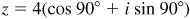 .
.
(f) P lies in the third quadrant;  ;
;  and
and  .
.
Thus,  . θ is not a special angle, so it must be approximated to get polar form.
. θ is not a special angle, so it must be approximated to get polar form.
15.13 Express each of the following complex numbers z in rectangular form:


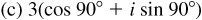
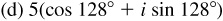 .
.



 . Since 128° is not a special angle, its function values are approximated.
. Since 128° is not a special angle, its function values are approximated.
(a) The modulus of the product of two complex numbers is the product of their moduli, and the amplitude of the product is the sum of their amplitudes.
(b) The modulus of the quotient of two complex numbers is the modulus of the dividend divided by the modulus of the divisor, and the amplitude of the quotient is the amplitude of the dividend minus the amplitude of the divisor.
Let  and
and  .
.

15.15 Perform the indicated operations, giving the result in both polar and rectangular form.

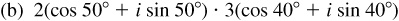

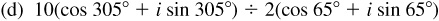
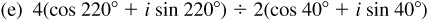

(a) The modulus of the product is  and the amplitude is
and the amplitude is 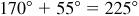 .
.
In polar form the product is  , and in rectangular form the product is
, and in rectangular form the product is  .
.
(b) The modulus of the product is  and the amplitude is
and the amplitude is  .
.
In polar form the product is 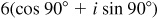 , and in rectangular form it is
, and in rectangular form it is  .
.
(c) The modulus of the product is 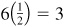 and the amplitude is
and the amplitude is  .
.
In polar form the product is  , and in rectangular form it is approximately
, and in rectangular form it is approximately  .
.
(d) The modulus of the quotient is 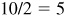 and the amplitude is
and the amplitude is  .
.
In polar form the product is  , and in rectangular form it is
, and in rectangular form it is  ,
,
(e) The modulus of the quotient is 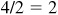 and the amplitude is
and the amplitude is  .
.
In polar form the quotient is 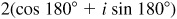 , and in rectangular form it is
, and in rectangular form it is  .
.
(f) The modulus of the quotient is  and the amplitude is
and the amplitude is  .
.
In polar form the quotient is  , and in rectangular form it is approximately
, and in rectangular form it is approximately 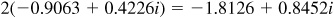 .
.
15.16 Express each of the numbers in polar form, perform the indicated operation, and give the result in rectangular form.

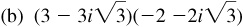



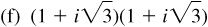



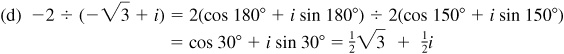
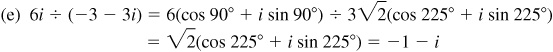
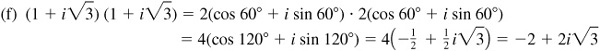
15.17 Verify De Moivre’s theorem for n = 2 and  .
.
Let  .
.

The theorem may be established for n a positive integer by mathematical induction.
15.18 Evaluate each of the following using De Moivre’s theorem and express each result in rectangular form:
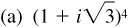 ,
,
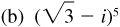 ,
,




15.19 Find the indicated roots in rectangular form, except when this would necessitate the use of tables or a calculator.
(a) Square roots of 
(b) Fourth roots of 
(c) Cube roots of 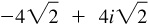
(d) Cube roots of 1
(e) Fourth roots of i
(f) Sixth roots of –1
(g) Fourth roots of –16i
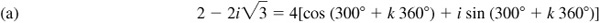
and

Putting 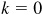 and 1, the required roots are
and 1, the required roots are


and

Putting 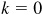 , 1, 2, and 3, the required roots are
, 1, 2, and 3, the required roots are


and

Putting 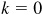 , 1, and 2, the required roots are
, 1, and 2, the required roots are

 and
and  .
.
Putting 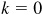 , 1, and 2, the required roots are
, 1, and 2, the required roots are


and

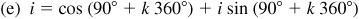 and
and  .
.
Thus, the required roots are

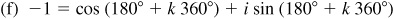 and
and 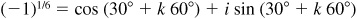 .
.
Thus, the required roots are

Note that  and thus R2 and R5 are the square roots of –1; that
and thus R2 and R5 are the square roots of –1; that  and thus R1, R3, and R5 are the cube roots of i; and that
and thus R1, R3, and R5 are the cube roots of i; and that  and thus
and thus  R2, R4, and R6 are the cube roots of –i.
R2, R4, and R6 are the cube roots of –i.

and

Thus, the required roots are

SUPPLEMENTARY PROBLEMS
15.20 Perform the indicated operations, writing the results in the form a + bi.

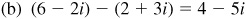



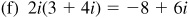


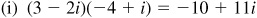


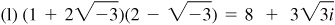




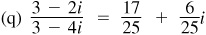

15.21 Show that  and
and 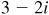 are roots of
are roots of 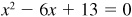 .
.
15.22 Perform graphically the following operations.




15.23 Express each of the following complex numbers in polar form.
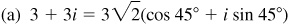


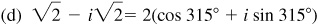



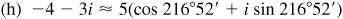
15.24 Perform the indicated operation and express the results in the form a + bi.

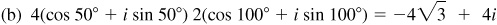


15.25 Use the polar form in finding each of the following products and quotients, and express each result in the form a + bi.

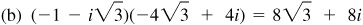

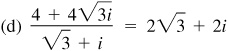
15.26 Use De Moivre’s theorem to evaluate each of the following and express each result in the form a + bi.





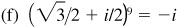

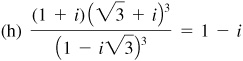
15.27 Find all the indicated roots, expressing the results in the form a + bi unless tables would be needed to do so.

15.28 Find the tenth roots of 1 and show that the product of any two of them is again one of the tenth roots of 1.
15.29 Show that the reciprocal of any one of the tenth roots of 1 is again a tenth root of 1.
15.30 Denote either of the complex cube roots of (Prob. 15.19d) by ω1 and the other by ω2. Show that  and
and 
15.32 Use the fact that the segments OS and P2 P1 in Fig. 15.2(c) are equal to devise a second procedure for constructing the difference 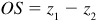 of two complex numbers z1 and z2.
of two complex numbers z1 and z2.