Appendix 1 is a summary of basic geometry definitions, relations, and theorems. The purpose of this material is to provide information useful in solving problems in trigonometry.
An angle is a figure determined by two rays having a common endpoint. An acute angle is an angle with a measure between 0 and 90°. A right angle is an angle with a measure of 90°, while an obtuse angle has a measure between 90 and 180°. When the sum of the measures of two angles is 90°, the angles are complementary. When the sum of the measures of two angles is 180°, the angles are supplementary. Two angles are equal when they have the same measure.
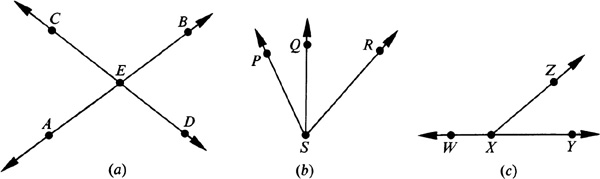
If two lines intersect, the opposite angles are vertical angles. In Fig. A1.1(a), ∠AED and ∠BEC are vertical angles and ∠CEA and ∠BED are also a pair of vertical angles. When two angles have a common vertex and a common side between them, the angles are adjacent angles. In Fig. A1.1(b), ∠PSQ and ∠QSR are a pair of adjacent angles. If the exterior sides of two adjacent angles form a straight line, the angles form a linear pair. In Fig. A1.1(c), ∠WXZ and ∠ZXY are a linear pair.
Fig. A1.1
Properties and Theorems
 The measures of vertical angles are equal.
The measures of vertical angles are equal.
 The angles in a linear pair are supplementary.
The angles in a linear pair are supplementary.
 If the angles in a linear pair are equal, the angles are right angles.
If the angles in a linear pair are equal, the angles are right angles.
 Angles complementary to the same or to equal angles are equal to each other.
Angles complementary to the same or to equal angles are equal to each other.
 Angles supplementary to the same or to equal angles are equal to each other.
Angles supplementary to the same or to equal angles are equal to each other.
Two lines in a plane either intersect or are parallel. If two lines intersect, they have exactly one point in common. Two lines in a plane are parallel if they have no common point.
When two lines intersect to form equal adjacent angles, the lines are perpendicular. Each of the angles formed by two perpendicular lines is a right angle. The sides of a right angle are perpendicular.
A transversal is a line that intersects two or more coplanar lines in distinct points. In Fig. A1.2, lines m and n are cut by transversal t. When two lines are cut by a transversal, the angles formed are classified by their location. The angles between the two lines are called interior angles and the angles not between the two lines are called exterior angles. Interior or exterior angles are said to alternate if the two angles have different vertices and lie on opposite sides of the transversal. A pair of corresponding angles are two angles, one an interior angle and one an exterior angle, that have different vertices and lie on the same side of the transversal. In Fig. A1.2, the interior angles are numbered 3, 4, 5, and 6 while the exterior angles are numbered 1, 2, 7, and 8. The angles numbered 3 and 6 and the angles numbered 4 and 5 are pairs of alternate interior angles. The angles numbered 1 and 8 and those numbered 2 and 7 are pairs of alternate exterior angles. The pairs of corresponding angles are numbered 1 and 5, 2 and 6, 3 and 7, and 4 and 8.
Fig. A1.2
Properties and Theorems
 In a plane, if two lines are perpendicular to the same line, then the lines are parallel.
In a plane, if two lines are perpendicular to the same line, then the lines are parallel.
 Two lines parallel to a third line are parallel to each other.
Two lines parallel to a third line are parallel to each other.
 If two parallel lines are cut by a transversal, then the alternate interior angles are equal.
If two parallel lines are cut by a transversal, then the alternate interior angles are equal.
 If two parallel lines are cut by a transversal, then the alternate exterior angles are equal.
If two parallel lines are cut by a transversal, then the alternate exterior angles are equal.
 If two parallel lines are cut by a transversal, then the corresponding angles are equal.
If two parallel lines are cut by a transversal, then the corresponding angles are equal.
 If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary.
If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary.
 Any pair of horizontal lines are parallel.
Any pair of horizontal lines are parallel.
 Any pair of vertical lines are parallel.
Any pair of vertical lines are parallel.
 Any vertical line is perpendicular to any horizontal line.
Any vertical line is perpendicular to any horizontal line.
 If two angles have their sides parallel, right side to right side and left side to left side, then the angles are equal.
If two angles have their sides parallel, right side to right side and left side to left side, then the angles are equal.
 If two angles have their sides perpendicular, right side to right side and left side to left side, then the angles are equal.
If two angles have their sides perpendicular, right side to right side and left side to left side, then the angles are equal.
 If two lines are cut by a transversal so that the alternate interior angles formed are equal, then the lines are parallel.
If two lines are cut by a transversal so that the alternate interior angles formed are equal, then the lines are parallel.
 If two lines are cut by a transversal so that the alternate exterior angles formed are equal, then the lines are parallel.
If two lines are cut by a transversal so that the alternate exterior angles formed are equal, then the lines are parallel.
 If two lines are cut by a transversal so that the corresponding angles formed are equal, then the lines are parallel.
If two lines are cut by a transversal so that the corresponding angles formed are equal, then the lines are parallel.
 If two lines are cut by a transversal so that the interior angles on the same side of the transversal are supplementary, then the lines are parallel.
If two lines are cut by a transversal so that the interior angles on the same side of the transversal are supplementary, then the lines are parallel.
 If a transversal is perpendicular to one of two parallel lines, it is perpendicular to the other one as well.
If a transversal is perpendicular to one of two parallel lines, it is perpendicular to the other one as well.
 Through a point not on a line there is exactly one line parallel to a given line.
Through a point not on a line there is exactly one line parallel to a given line.
 Through a point not on a line there is exactly one line perpendicular to a given line.
Through a point not on a line there is exactly one line perpendicular to a given line.
 In a plane, there is exactly one line perpendicular to a given line at any point on the line.
In a plane, there is exactly one line perpendicular to a given line at any point on the line.
A triangle is a plane closed figure formed by three line segments that intersect each other at their endpoints. Triangles that have no two sides with the same length are called scalene triangles, those with at least two sides having the same length are called isosceles triangles, and those with all three sides having the same length are called equilateral triangles. If a triangle contains a right angle, it is a right triangle. A triangle that does not contain a right angle is called an oblique triangle.
Two triangles are said to be congruent when they have the same size and the same shape. When two triangles are congruent, the pairs of corresponding sides have the same length and the pairs of corresponding angles are equal. Triangles that have the same shape are said to be similar. Similar triangles have corresponding sides that are proportional in length and corresponding angles that are equal.
A median of a triangle is a line segment from a vertex to the midpoint of the opposite side. An altitude of a triangle is a line segment from one vertex perpendicular to the opposite side.
Properties and Theorems
 If three sides of one triangle are equal to the three sides of another triangle, the triangles are congruent.
If three sides of one triangle are equal to the three sides of another triangle, the triangles are congruent.
 If two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, the triangles are congruent.
If two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, the triangles are congruent.
 If two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, the triangles are congruent.
If two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, the triangles are congruent.
 If two angles and a nonincluded side of one triangle are equal to the corresponding two angles and nonincluded side of another triangle, the triangles are congruent.
If two angles and a nonincluded side of one triangle are equal to the corresponding two angles and nonincluded side of another triangle, the triangles are congruent.
 If the hypotenuse and leg of one right triangle are equal to the corresponding sides of another right triangle, then the two right triangles are congruent.
If the hypotenuse and leg of one right triangle are equal to the corresponding sides of another right triangle, then the two right triangles are congruent.
 If two angles of one triangle are equal to the corresponding two angles of another triangle, the triangles are similar.
If two angles of one triangle are equal to the corresponding two angles of another triangle, the triangles are similar.
 The sum of the measures of the angles of a triangle is 180°.
The sum of the measures of the angles of a triangle is 180°.
 An exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles of the triangle.
An exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles of the triangle.
 The acute angles of a right triangle are complementary.
The acute angles of a right triangle are complementary.
 The measure of each angle of an equiangular triangle is 60°.
The measure of each angle of an equiangular triangle is 60°.
 If two sides of a triangle are equal, then the angles opposite these sides are equal.
If two sides of a triangle are equal, then the angles opposite these sides are equal.
 If a triangle is equilateral, then it is also equiangular.
If a triangle is equilateral, then it is also equiangular.
 If two angles of a triangle are equal, then the sides opposite these angles are equal.
If two angles of a triangle are equal, then the sides opposite these angles are equal.
 If a triangle is equiangular, then it is also equilateral.
If a triangle is equiangular, then it is also equilateral.
 The altitude to the base of an isosceles triangle bisects the base and the vertex angle.
The altitude to the base of an isosceles triangle bisects the base and the vertex angle.
 The median to the base of an isosceles triangle bisects the vertex angle and is perpendicular to the base.
The median to the base of an isosceles triangle bisects the vertex angle and is perpendicular to the base.
 The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base.
The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base.
 In a right triangle, the square of the length of the hypotenuse c is equal to the sum of the squares of the lengths of the two legs a and b; i.e.,
In a right triangle, the square of the length of the hypotenuse c is equal to the sum of the squares of the lengths of the two legs a and b; i.e., 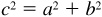 (Pythagorean theorem).
(Pythagorean theorem).
 In a 45°–45° right triangle, the length of the hypotenuse c is equal to
In a 45°–45° right triangle, the length of the hypotenuse c is equal to 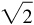 times the length of a leg a; i.e.,
times the length of a leg a; i.e., 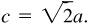
 In a 30°–60° right triangle, the length of the hypotenuse c is equal to 2 times the length of the leg a opposite the 30° angle; i.e.,
In a 30°–60° right triangle, the length of the hypotenuse c is equal to 2 times the length of the leg a opposite the 30° angle; i.e.,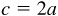 . Also, the length of the leg b opposite the 60° angle is equal to
. Also, the length of the leg b opposite the 60° angle is equal to 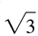 times the length of the leg a opposite the 30° angle; i.e.,
times the length of the leg a opposite the 30° angle; i.e., .
.
 The midpoint of the hypotenuse of a right triangle is equidistant from all three vertices of the triangle.
The midpoint of the hypotenuse of a right triangle is equidistant from all three vertices of the triangle.
 If the square of the length of one side c of a triangle is equal to the sum of the squares of the lengths of the other two sides a and b of the triangle, i.e.,
If the square of the length of one side c of a triangle is equal to the sum of the squares of the lengths of the other two sides a and b of the triangle, i.e.,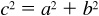 , then the triangle is a right triangle.
, then the triangle is a right triangle.
 The area K of a triangle is one-half the product of its altitude a and base b; i.e.,
The area K of a triangle is one-half the product of its altitude a and base b; i.e., 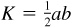 .
.
 The area of an equilateral triangle is equal to one-fourth of the square of a side s times
The area of an equilateral triangle is equal to one-fourth of the square of a side s times 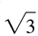 ; i.e.,
; i.e., 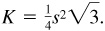
A polygon is a plane closed figure whose sides are line segments that are noncollinear and each side intersects exactly two other line segments at their endpoints. A quadrilateral is a polygon having four sides. A regular polygon is a polygon that is both equilateral and equiangular. A diagonal of a polygon is a line segment that joins two nonadjacent vertices of the polygon.
A parallelogram is a quadrilateral with opposite sides parallel. A rectangle is a parallelogram with one right angle. A rhombus is a parallelogram with two adjacent sides equal. A square is a rectangle with two adjacent sides equal.
A trapezoid is a quadrilateral with exactly one pair of parallel sides. An isosceles trapezoid is a trapezoid with the nonparallel sides having equal lengths.
Properties and Theorems
 The opposite angles of a parallelogram are equal.
The opposite angles of a parallelogram are equal.
 The opposite sides of a parallelogram are equal.
The opposite sides of a parallelogram are equal.
 The diagonals of a parallelogram bisect each other.
The diagonals of a parallelogram bisect each other.
 The consecutive interior angles of a parallelogram are supplementary.
The consecutive interior angles of a parallelogram are supplementary.
 The sum of the interior angles of a quadrilateral is 360°.
The sum of the interior angles of a quadrilateral is 360°.
 If both pairs of opposite angles of a quadrilateral are equal, the quadrilateral is a parallelogram.
If both pairs of opposite angles of a quadrilateral are equal, the quadrilateral is a parallelogram.
 If both pairs of opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram.
If both pairs of opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram.
 If the diagonals of a quadrilateral bisect each other, the quadrilateral is a parallelogram.
If the diagonals of a quadrilateral bisect each other, the quadrilateral is a parallelogram.
 A rectangle is an equiangular parallelogram.
A rectangle is an equiangular parallelogram.
 A rhombus is an equilateral parallelogram.
A rhombus is an equilateral parallelogram.
 The diagonals of a rectangle are equal.
The diagonals of a rectangle are equal.
 The diagonals of a rhombus are perpendicular.
The diagonals of a rhombus are perpendicular.
 If the diagonals of a parallelogram are equal, the parallelogram is a rectangle.
If the diagonals of a parallelogram are equal, the parallelogram is a rectangle.
 If the diagonals of a parallelogram are perpendicular, the parallelogram is a rhombus.
If the diagonals of a parallelogram are perpendicular, the parallelogram is a rhombus.
 The diagonals of a square are the perpendicular bisectors of each other.
The diagonals of a square are the perpendicular bisectors of each other.
 A rhombus with a right angle is a square.
A rhombus with a right angle is a square.
 A square is a regular polygon.
A square is a regular polygon.
 The diagonals of an isosceles trapezoid are equal.
The diagonals of an isosceles trapezoid are equal.
 The area K of a parallelogram is equal to the product of its altitude a and base b; i.e.,
The area K of a parallelogram is equal to the product of its altitude a and base b; i.e., 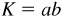 .
.
 The area K of a rectangle is equal to the product of its length l and width w; i.e.,
The area K of a rectangle is equal to the product of its length l and width w; i.e., 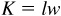 .
.
 The area K of a rhombus is equal to one-half the product of its diagonals d and d ’; i.e.,
The area K of a rhombus is equal to one-half the product of its diagonals d and d ’; i.e., 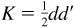 .
.
 The area K of a square is equal to the square of its side s; i.e.,
The area K of a square is equal to the square of its side s; i.e.,  .
.
 The area K of a square is equal to one-half the square of its diagonal d; i.e.,
The area K of a square is equal to one-half the square of its diagonal d; i.e., 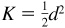 .
.
 The area K of a trapezoid is equal to one-half the product of the altitude h and the sum of the bases b and b ’; i.e.,
The area K of a trapezoid is equal to one-half the product of the altitude h and the sum of the bases b and b ’; i.e., 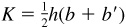 .
.
A circle is the set of all points in a plane that are at a given distance from a given point. Any line segment which has its endpoints on a circle is a chord of the circle. If a chord of a circle passes through the center of the circle, then it is a diameter. A radius is a line segment from the center of a circle to a point on the circle. A secant is a line that intersects a circle in two points. A tangent is a line that intersects a circle in one point.
An arc of a circle is a part of the circle from one point on the circle to another. A semicircle is an arc of a circle joining the endpoints of a diameter of the circle. An inscribed angle is an angle with sides that are chords of a circle. A central angle is an angle with sides that are radii of the circle.
Properties and Theorems
 A circle contains 360°.
A circle contains 360°.
 A semicircle contains 180°.
A semicircle contains 180°.
 A central angle is equal in degrees to its intercepted arc.
A central angle is equal in degrees to its intercepted arc.
 An inscribed angle is equal in degrees to one-half its intercepted arc.
An inscribed angle is equal in degrees to one-half its intercepted arc.
 An angle inscribed in a semicircle is a right angle.
An angle inscribed in a semicircle is a right angle.
 In a circle, if a diameter is perpendicular to a chord, it bisects the chord and its arc.
In a circle, if a diameter is perpendicular to a chord, it bisects the chord and its arc.
 In a circle, two chords that are equal are equidistant from the center of the circle.
In a circle, two chords that are equal are equidistant from the center of the circle.
 In a circle, two chords that are equidistant from the center of the circle are equal.
In a circle, two chords that are equidistant from the center of the circle are equal.
 A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
 If a triangle is inscribed in a semicircle, then the triangle is a right triangle.
If a triangle is inscribed in a semicircle, then the triangle is a right triangle.
 In a plane, if a line is perpendicular to a radius of a circle at its endpoint on the circle, then the line is tangent to the circle.
In a plane, if a line is perpendicular to a radius of a circle at its endpoint on the circle, then the line is tangent to the circle.
 The line segment joining an external point to the center of a circle bisects the angle formed by the two tangents to the circle from that point.
The line segment joining an external point to the center of a circle bisects the angle formed by the two tangents to the circle from that point.
 The lengths of the two tangent segments from an external point to a circle are equal.
The lengths of the two tangent segments from an external point to a circle are equal.
 If two secants intersect in the interior of a circle, then the angle formed is equal in degrees to one-half the sum of the arcs intercepted by it and its vertical angle.
If two secants intersect in the interior of a circle, then the angle formed is equal in degrees to one-half the sum of the arcs intercepted by it and its vertical angle.
 If a line through the center of a circle bisects a chord that is not a diameter, then it is perpendicular to the chord.
If a line through the center of a circle bisects a chord that is not a diameter, then it is perpendicular to the chord.
 The circumference C of a circle is equal to π times the diameter d; i.e.,
The circumference C of a circle is equal to π times the diameter d; i.e., 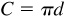 .
.
 The radius r of a circle is equal to one-half the diameter d; i.e.,
The radius r of a circle is equal to one-half the diameter d; i.e., 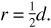
 The area K of a circle is equal to π times the radius r squared; i.e.,
The area K of a circle is equal to π times the radius r squared; i.e., 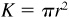 .
.