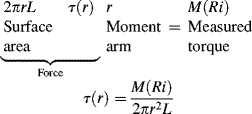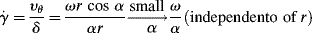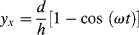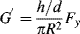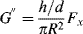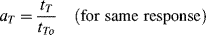Chapter 16
Polymer Mechanical Properties
16.1 Introduction
This chapter covers some of the methods and instruments used to determine the mechanical properties of polymers. Examples of instrument designs and typical data generated in these measurements will be introduced. In particular, automated axial tensiometers (to find elastic modulus, yield stress, and ultimate stress), dynamic mechanical analyzers (to determine storage and loss moduli), and rheometers (to measure flow viscosity) will be introduced. This chapter considers the principles behind the devices used to establish and measure the properties of viscometric flows. One of the common techniques used to determine viscous flow properties, Poisueille (laminar) flow in cylindrical tubes, is also important in technical applications, as polymer melts and solutions are often transported and processed in this manner. The time–temperature superposition principle is also covered as a way to predict polymer behavior over long timescales by testing materials across a range of temperatures.
16.2 Mechanical Properties of Polymers
A number of physical parameters can be measured as a way to characterize polymers. The specific tests that are done are normally dictated by the end use of a particular part. We have defined many of these parameters in the previous few chapters, such as elastic (or Young's) modulus, E, shear (or Hooke's) modulus, G, storage modulus (E' or G'), loss modulus (E” or G”), tan δ, which all apply to solids, as well as the viscosity used for polymer melts (and solutions) as described with polymer rheology. In addition to these terms, you may also run across hardness (how resistant the polymer is to penetration by a needle), toughness (measures the total amount of energy that can be absorbed by a polymer before it fails or breaks), impact resistance (ability not to shatter upon sudden application of force), fatigue (ability to withstand cyclic forces and maintain mechanical integrity), and wear (how the surface of a polymer may be degraded or worn by friction).
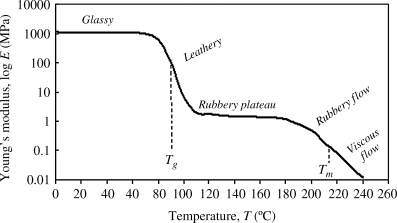
While any individual polymer will have unique properties (due to sample geometry, polymer molecular weight, presence of crystals or crosslinks, etc.), some generalized characterizations can be made. We are well aware that temperature plays a large role in the state and behavior of polymers. Many mechanical properties follow a similar trend to that observed in Figure 16.1 for elastic modulus versus temperature. There are five general regions that describe the polymer depicted in this graph. At low temperatures (below Tg), the polymer is considered glassy. Closer to the Tg, the feel of the polymer softens slightly, and thus is referred to as leathery; above the Tg, the polymer reaches a rubbery plateau, where it is pliable and flexible. Nearing Tm, the polymer starts to melt and reaches a rubbery flow region, where the flow may be somewhat reversible if a force is removed. At the highest temperatures (assuming the polymer is not degraded), we have viscous flow, which is covered by the discussion on rheology in Chapter 14. While the absolute numbers on the y-axis will not be true for all polymers, it does show that temperature has a large effect on mechanical properties of the polymer.
Figure 16.1 The effects of temperature on Young's Modulus.
16.3 Axial Tensiometers
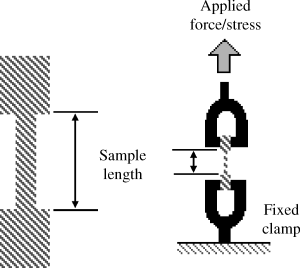
In many common applications of polymers, they are exposed to a uniaxial stress, by which they can stretch and rebound (if purely elastic) or stretch and deform with a smaller degree of rebound (for true viscoelastic materials). The equipment used for testing polymer mechanics are largely the same as those used for metals or ceramics, but the amount of force required to stretch a polymer will be (considerably) smaller. Automated materials testing apparatus (such as the one shown in Figure 16.2) have a range of designs, from the most common stretching, done by placing flat dogbone-shaped samples between clamps and measuring the force required to stretch, to instruments that can measure the force and deformation on samples subjected to compression or three-point bending and even instruments that can model human joints or test materials that are submerged in water.
Figure 16.2 An automated materials testing apparatus typically applies a known stress on a dogbone-shaped sample and measures the resulting stretch (strain). A fixed or linear strain can also be programmed with the required force (or stress) measured as the sample is stretched.
For such axial tension experiments, the results are normally plotted as stress–strain curves. If the rate of strain is fixed and constant, the x-axis (independent variable) can be either strain or time. The y-axis normally represents the stress on the given sample that is calculated by dividing the forces measured during the stretching experiment by the initial cross-sectional area of the sample, to give the typical pressure units of stress (Pa, or more commonly MPa or GPa).
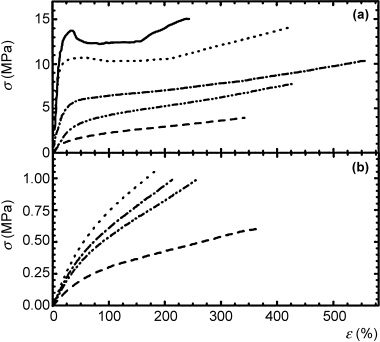
A set of stress–strain curves are shown in Figure 16.3. At the lower temperature (the upper plot), the slopes of the linear portion of each plot are higher, as would be expected for glassy polymers (compared to rubbery polymers at the higher temperature). The modulus of elasticity is easily found from the slope in the linear portion of the curve.
(16.1) 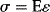
The higher the slope, the higher the modulus, indicating that the material resists stretching with greater force. For most polymers, there exists a yield stress, σy, below which the deformation is elastic, as the material can snap back to its original conformation upon release of the force. The yield stress is most easily seen in Figure 16.3a, which marks the transition from linearity to uneven stretching. Beyond this yield stress, the material begins to deform permanently. As the force continues to stretch the sample, polymer chains physically move and rearrange the macromolecular structure. This causes necking and narrowing of the sample width and thickness. Because the polymer chains are slipping over each other above the yield stress, the sample is likely to “give” much easier, resulting in what can be significant, stretching without any additional force. This is the behavior that is described by the dashpot in viscoelastic models, but just because chains are able to slip over each other and rearrange does not mean that the material has failed . . . just that it cannot snap back to its original configuration. By continuing to stretch the polymer, it may actually toughen a bit (often because the rearrangement of chains leads to an increase in crystallinity) before reaching the ultimate stress, σu, where the sample breaks. In Figure 16.3, the ultimate stress for each of the samples is the highest stress each sample can withstand, which is at the right end of each curve, just prior to the sample breaking (and the measured stress dropping to zero).
Figure 16.3 Stress–strain curves for different samples of block copolymers of caprolactone with n-butyl acrylate tested at (a) room temperature and (b) 70 °C. Polymer compositions were 0, 20, 39, 50 and 71 wt% n-butyl acrylate from top to bottom in (a). Reprinted with permission from Referenece 1. Copyright 2001 National Academy of Sciences, USA.
These experiments are great at picking out mechanical properties of materials subjected to single axial stresses. To study the effect of cyclic stresses, a dynamic mechanical analyzer (DMA) is recommended (next section).
16.4 Viscosity Measurement
As noted in Chapter 5, viscometry can be used to estimate polymer molecular weight,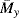 , but those solutions were required to be dilute. For polymer melts and more concentrated solutions, viscosity measurements require viscometers configured somewhat differently from the capillary viscometers introduced in Chapter 5. Details of such instruments and procedures have been reviewed [2, 3].
, but those solutions were required to be dilute. For polymer melts and more concentrated solutions, viscosity measurements require viscometers configured somewhat differently from the capillary viscometers introduced in Chapter 5. Details of such instruments and procedures have been reviewed [2, 3].
16.4.1 The Couette Viscometer
One common device for measuring viscous properties is the cup-and-bob or Couette viscometer (Figure 16.4). The fluid is confined in the gap between two concentric cylinders, one of which rotates relative to the other at a known angular velocity while the torque on one is measured. This is a classic example of viscometric flow. In cylindrical coordinates, we assume only a tangential velocity component, so the 1 coordinate is the tangential or θ direction and the 2 coordinate is the radial direction.
Figure 16.4 Schematic of Couette (cup-and-bob) viscometer.

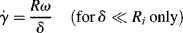
Where the geometric approximations in the example above are not applicable,a more sophisticated analysis has been developed by Kreiger and Maron [5]. Another challenge to analyzing the Couette viscometer is accounting for the area below the bob at the bottom of the viscometer. This is best accounted for by making measurements with two fluid depths, the lower being well above the bottom of the bob, and using the differences between torques and depths in Equation (16.2), thereby subtracting out the effects of non-Couette flow at the bottom of the viscometer. Another approach is illustrated later in Example 16.3.
16.4.2 The Cone-and-Plate Viscometer
The cone-and-plate viscometer is another type of rotational viscometer. Here, the sample is sheared between a flat plate and a broad cone whose apex contacts the plate (Figure 16.5). For small cone-plate angles α, this approximates a viscometric flow with (in spherical coordinates) flow in the tangential θ or 1 direction and the gradient in the azimuthal ϕ or 2 direction. Here, the radial direction is the neutral or 3 coordinate.1 It turns out that true viscometric flow of this type is inconsistent with the equations of motion if the inertial terms are included. (Formal flow solutions for rotational viscometers normally neglect the inertial terms in the equations of motion, as we tacitly do here.) There must, therefore, be radial and azimuthal velocity components. These are minimized in practice by keeping α quite small, often less than 1°. The great advantage of this type of device is that (for small α) the shear rate, and hence the shear stress, is uniform throughout the material.
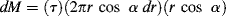
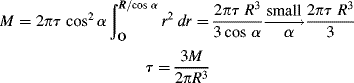
Figure 16.5 Schematic of cone-and-plate viscometer.
Cone-and-plate viscometers of the type shown here are usually limited to fairly low shear rates. At higher shear rates, solutions tend to be flung from the gap by centrifugal force, and melts tend to “ball up” (like rubbing a finger over dry rubber cement). These problems can be overcome by enclosing the fluid around a biconical rotor, giving, in effect, two cone-and-plate viscometers back-to-back [6]. The flow curves earlier in this chapter were obtained with such a device.
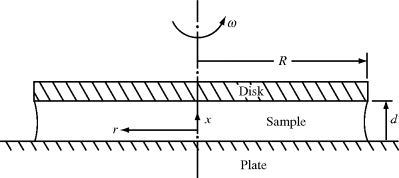
16.4.3 The Disk-and-Plate Viscometer
Another type of viscometer that finds occasional use is the disk-and-plate viscometer (Figure 16.6). A disk of radius R rotates with an angular velocity of ω relative to a parallel plate. The disk-and-plate are separated by a distance d (d « R), with the test fluid in between. The torque M on either the disk or the plate is measured. This is known as torsional (twisting) flow, and is another example of a viscometric flow.
 . Why is the cone-and-plate geometry usually preferred?
. Why is the cone-and-plate geometry usually preferred?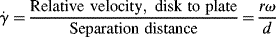
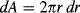
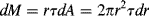
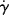 n = K(rω/d)n,
n = K(rω/d)n,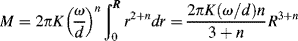
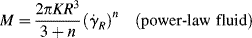
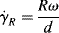
Figure 16.6 Schematic of disk-and-plate viscometer.
16.5 Dynamic Mechanical Analysis: Techniques
Basically, three methods are available for determining dynamic properties: free oscillation, forced oscillation, and steady-state rotation. Experimental and analytical details for the first two are reviewed extensively by Ferry [7].
16.5.1 Free Oscillation
16.5.1.1 Torsion Pendulum
Free-oscillation measurements are made with a torsion pendulum (Figure 16.7). The sample is given an initial torsional displacement, and the frequency and amplitude decay of the oscillations are observed on release. G′ is determined from the sample geometry, moment of inertia of the oscillating mechanism, and the observed period of oscillation. For example, with a cylindrical specimen of length L and radius R,
vFigure 16.7 Torsion pendulum with its output [8].
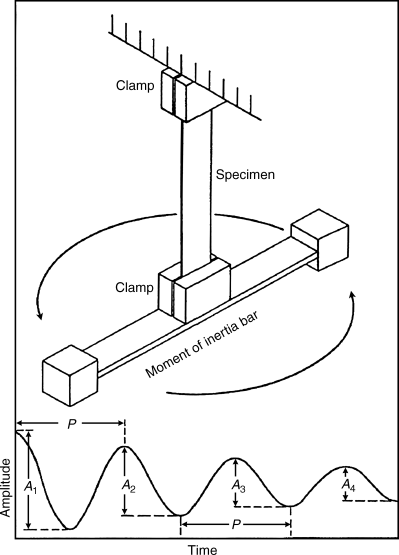
(16.9) 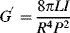
where I is the moment of inertia of the oscillating mechanism and P is the observed period of oscillation (P = 2π/ω). The damping or logarithmic decrement Δ is calculated from the amplitude decay of the oscillations (with a perfectly elastic material, there would be no damping of the oscillations):
(16.10) 
and for Δ < 1:
(16.11) 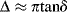
Expressions for other specimen geometries and higher damping are reviewed by Nielson [9]. Solid or rubbery samples are twisted as illustrated in the form of rods, tubes, strips, etc. Liquids or soft solids may be contained in one of the geometries described for rotational viscometry earlier (Couette, cone-and-plate, etc.).
16.5.1.2 Torsional Braid Analysis
In torsional braid analysis [10], a flexible, braided fiber, usually glass, is impregnated with the material to be studied. The impregnated fiber then becomes the torsion member in the pendulum. This type of device is useful for following the cure of a material that starts out as a liquid and cures to a solid (e.g., an epoxy). In analyzing the data from such a device, care must be exercised in separating interactions between the sample and the supporting fiber.
Although the frequency can be varied somewhat by changing the moment of inertia of the oscillating portion of the mechanism, torsion pendulums are usually intended to study only the temperature dependence of dynamic properties at a constant, relatively low frequency (≈ 1 cycle/s). On the other hand, they are inexpensive and rather simple to construct.
16.5.2 Forced Oscillation Devices
16.5.2.1 Dynamic Mechanical Analyzers
DMAs are forced-oscillation devices (“jiggle machines”) that apply a sinusoidal stress or strain of known amplitude and frequency and measure the resulting strain or stress. The dynamic properties are calculated from the relation between the two. Solid materials are clamped into a DMA (Figure 16.8), where the cyclic load (stress or strain) can be applied, with the resulting strain or stress measured. For liquid samples, the geometries discussed in conjunction with rotational viscometry are often used with the drive system modified to produce sinusoidal rather than steady rotational deformation. Flexible samples such as fibers, films, and rubber are preloaded in tension and oscillated about a positive tensile strain so that they do not go slack at the “bottom” of the sine wave. Such tests give dynamic tensile properties, E′, E″, etc., which are related to the corresponding shear properties by
Figure 16.8 Dynamic mechanical analysis testing clamps (used with permission from TA Instruments, New Castle, DE). Different clamp setups can be used for tension, compression, three-point bending, and shear tests. The application of stress (or strain) is sinusoidal.

(16.12) 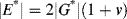
where ν is Poisson's ratio (ν = 1/2 for an incompressible material). Another type of forced-oscillation device applies a sinusoidal shear or compression wave to one end of a sample and monitors the attenuation of the wave as it progresses through the sample.
Forced-oscillation devices are generally intended to study dynamic properties as a function of frequency as well as temperature. Drive and detection systems for such devices may be strictly mechanical, but more sophisticated ones make use of piezoelectric crystals and, inorganic crystals (e.g., barium titanate) that change dimension in proportion to an applied voltage and, conversely, generate an output voltage proportional to an imposed deformation. Thus, the amplitude and, especially, the frequency of the applied strain can be conveniently controlled over a wide range in the form of electrical signals (the response of the crystals extends to very high frequencies, and electrons have very little inertia, unlike mechanical linkages). Input and output signals may be fed to a computer for online control and computations.
16.5.3 Steady Rotation Methods
The expense and complexity of oscillating devices and associated detection systems has led to the increased popularity of instruments that determine dynamic properties, but are driven in steady rotation and detect steady (nonoscillating) forces. This sounds like a contradiction in terms, but they really do work! We will attempt to describe the operation of one of the more popular of them. Mathematical details are provided in elegant fashion by Walters [11].
16.5.3.1 Orthogonal Rheometry
In the Maxwell orthogonal rheometer [12] (Figure 16.9), material is sheared between two parallel disks of radius R, separated from one another by a distance h, each rotating at the same steady angular frequency ω, but with their axes of rotation displaced by a distance d. Transducers are set up to measure three steady, orthogonal force components (hence, the name) on one of the disks, Fx, Fy, and Fz.
Figure 16.9 Orthogonal rheometer.
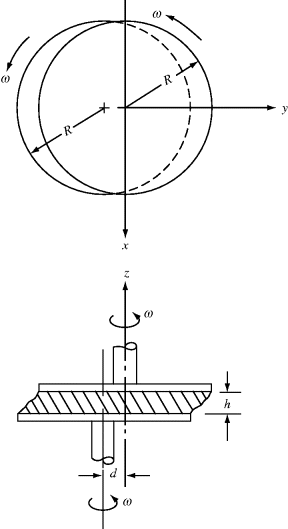
How, you ask, does this result in oscillating deformation? Well, the easiest way to see is to follow the motion of a point on the upper disk (point 2), relative to one on the lower disk (point 1) as the disks rotate. Here, we choose point 1 on the axis of rotation (center) of the lower disk and point 2 directly above it at the start of the analysis, ωt = 0. This is the simplest choice, because point 1 remains stationary, but the same result will be obtained for any pair of points initially at the same values of x and y (you can prove this with a compass, ruler, and protractor). Figure 16.10a shows the relative displacement vector in the xy plane, l, and how it varies with the angle of rotation ωt. From Figure 16.10b, the magnitude of the relative displacement is then:
Figure 16.10 Analysis of the orthogonal rheometer: (a) relative displacement vector between point 1 on the center of the lower disk and point 2 immediately above it at ωt = 0; (b) geometry of the displacement vector and its components.

(16.13) 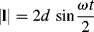
and its x and y components are
(16.14) 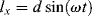
and
(16.15) 
If we assume that the strain is simply the relative displacement divided by the disk separation h, the x and y components of strain are3
(16.16) 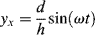
Thus, both components of strain undergo simple harmonic oscillation as a result of the steady angular rotation.
It is important to note that the x component of strain is symmetrical about 0, while the y component is not (it varies between 0 and + 2d/h). For linear materials, because stress is directly proportional to strain, any shear stresses and, therefore, forces parallel to the xy plane produced by γx's in the region 0 < ωt < π will be cancelled by those arising from the equal-and-opposite x-component strains in the region (π < ωt < 2π). As a result, the measured forces Fx and Fy can depend only on γy.
Looking at it another way, consider a purely elastic material in the rheometer to be represented by rubber bands stretched between points 1 and 2. Viewed from above, the rubber bands coincide with 1. It is obvious that the x components of the tug of the rubber bands will cancel, leaving only a net force (and, therefore, only a stress component τzy) in the y direction. Thus, the purely elastic stress is in phase with γy, so Equation (16.17) represents the variation of γ′ with location in a disk as constant z, that is,
(16.18) 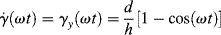
and
(16.19) 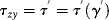
Any measured value of Fx, therefore, must arise from a viscous component, whose stress τzx will be 90° out of phase with γy, that is,
(16.20) 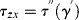
To determine the total force component on a disk, the stress-area product must be integrated over the surface of the disk:
(16.21) 
From Equation 15.37, τ′=G′ γ′ and, in polar coordinates, dA = r d(ωt) dr, so that
(16.22) 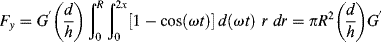
or
Similarly,
(16.24) 
and since τ″ = G″ γ′ (Eq. 15.38), it follows that
Equations(16.23) and (16.25) show how dynamic properties can be obtained from a device in steady rotation by measuring steady forces, which mechanically and analytically represents a great simplification over forced-oscillation techniques. It must be pointed out that there have been some questions as to whether a nonviscometric flow such as this can be used to determine quantities such as G′, G″, η′, η″, which are really defined in terms of viscometric deformations, but it is now pretty generally agreed that the technique is valid, at least in the limit of small strains, d/h [13, 14].
Also, analyses are based on the assumption that both disks rotate at the same angular velocity, ω. In the usual instrument, one disk is driven and the other goes along for the ride; so with bearing friction and hydrodynamic effects, the assumption might not be strictly true. An analysis by Davis and Macosko [15] shows it to be a pretty good assumption under most conditions of interest.
16.5.3.2 Other Steady Rotation Devices
Other devices have been developed that operate along similar lines. The so-called balance rheometer confines a test fluid between two concentric hemispheres that rotate at the same rate but whose axes of rotation are at an angle to one another. Similarly, cone-and-plate geometry, in which the axis of the cone is not perpendicular to the plate, and Couette (cup-and-bob) geometry, with the bob not centered on the cup, can also be used to obtain dynamic data [11]. Dynamic tensile properties can be obtained for relatively rigid materials by subjecting a rotating cylindrical rod to a cantilever deflection [16].
Many of these dynamic tests can also be used to determine the thermal behavior of polymers. Figure 16.11 illustrates G′ and damping ≈ π tan δ versus. T for poly(methyl methacrylate), an amorphous, linear polymer. The data were obtained with a torsion pendulum at about 1 cycle/s. At low temperatures, the typical glassy modulus 1–10 GPa is observed. In the vicinity of 110–130 °C, G′ drops precipitously, ultimately reaching a plateau of 0.1–1 MPa, the typical rubbery modulus. Also, a sharp peak in the damping is observed in this region. Although the temperature at which this peak and drop are observed is frequency dependent, at low frequencies (such as obtained with the usual torsion pendulum), they are identified with the material's glass transition temperature, and the drop in G′ is indicative of the decrease in “stiffness” at Tg, going from the straining of bond angles and lengths to coiling and uncoiling as the dominant response mechanism. The damping peak represents the onset of cooperative motion of 40–50 main-chain carbon atoms at Tg (Chapter 6).
Figure 16.11 Dynamic mechanical properties of poly(methyl methacrylate) [8]. The data were obtained with a torsion pendulum at about 1 cycle/s.
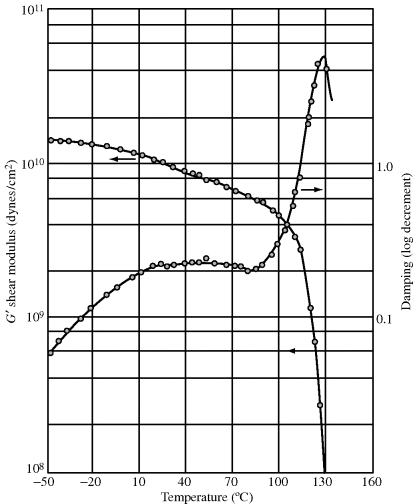
In terms of the four-parameter model for viscoelasticity, below Tg, only spring 1 is operative, and the material is almost completely elastic (low damping). In the vicinity of Tg, the viscosity of dashpot 2 drops to the point where it can deform and dissipate energy, giving the damping peak. At higher temperatures, its viscosity drops to the point where it dissipates little energy, and the material is again highly elastic, mainly through spring 2. At still higher temperatures, the modulus drops off rapidly due to viscous flow, dashpot 1. The broad damping “hill” centered at about 40 °C (and the accompanying gradual drop in G′) in Figure 16.11 has been shown to arise from the motion of the -CO-O-CH3 side groups on the PMMA molecules.
Note that the dimensions of the angular frequency ω are per time. The angular frequency thus corresponds to a reciprocal timescale. For dynamic (oscillating) deformations, then, the Deborah number is
(16.26) 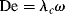
In dynamic tests, a viscoelastic material becomes more like solid as the frequency is increased and the time-dependent response mechanisms (coiling and uncoiling, slip) are less able to follow the rapidly reversing stress. In the limit of very high frequencies, the straining of bond angles and lengths will be the only operative response mechanism and the polymer will exhibit the typical glassy modulus even though it may be well above its glass transition temperature.
16.6 Time–Temperature Superposition
One of the big challenges in developing materials that are expected to have a lifetime of years is developing laboratory tests to prove that the materials will last. One way to accelerate aging is to conduct tests at higher temperatures. Anyone who has ever wrestled with a cheap garden hose in cold weather appreciates the fact that polymers become stiffer and more rigid at lower temperatures, while at high temperatures they are softer and more flexible. In preceding examples, we have seen that the timescale (or frequency) of the application of stress has a similar influence on mechanical properties, short times (or high frequencies) corresponding to low temperatures and long times (low frequencies) corresponding to high temperatures. The quantitative application of this idea, time–temperature superposition, is one of the most important principles in polymer physics. It is based on the fact that the Deborah number determines quantitatively just how a viscoelastic material will behave mechanically. Changing either ts (or ω) or λc can change De. The nature of the applied deformation determines ts (or ω), while a polymer's characteristic time is a function of temperature. The higher the temperature, the more thermal energy the chain segments possess and the more rapidly they are able to respond, lowering λc. Thus, e.g., De can be doubled by halving ts (or doubling ω in a dynamic test) or by lowering the temperature enough to double λc. The change in mechanical response will be the same either way, according to the time–temperature superposition principle.
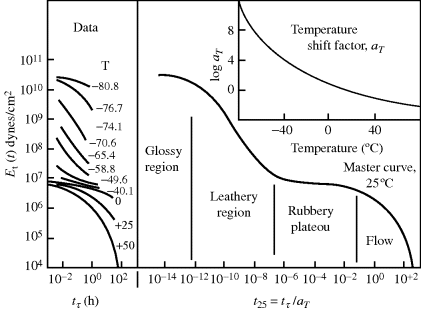
Although time–temperature superposition is applicable to any viscoelastic response test (creep, dynamic, etc.), here, we will focus on its application to stress relaxation. Figure 16.12 shows tensile stress relaxation data at various temperatures for polyisobutylene, plotted in the form of a time-dependent tensile (Young's) modulus Er(t) versus. time on a log–log scale:
Figure 16.12 Time–temperature superposition for NBS polyisobutylene. Adapted from Tobolsky and Catsiff [17].
(16.27) 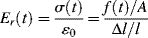
where f(t) is the measured tensile force in the sample held at a constant strain εo = Δl/l and A is its cross-sectional area. The technique is, of course, equally applicable to shear deformation. In stress relaxation, the lower measurement time limit is set by the assumption that the constant strain is applied instantaneously. In practice, inertia and other mechanical limitations make this impossible, so data are valid only at times an order of magnitude or so longer than it actually takes to apply the constant strain. The upper limit is set by the dedication (and patience) of the experimenter and the long-term stability of the sample and equipment. These data were obtained over a range of seconds to a couple of days. As might be expected, the modulus drops with time at a given temperature, and at a given time, it drops with increasing temperature.
Staring at the curves for a while indicates that they appear to be sections of one continuous curve, chopped up, with the sections displaced along the log-time axis. That this is indeed so is shown in Figure 16.12. Here, 25 °C has arbitrarily been chosen as a reference temperature To and the curves for other temperatures have been shifted along the log time axis to line up with it. The data below 25 °C are shifted to the left (shorter times) and those above 25 °C are shifted to the right (longer times), giving a master curve at 25 °C.
Sometimes, the relaxation moduli at each temperature T are corrected to the reference temperature To by multiplying be the ratio To/T before superimposing. This correction is based on the theory of ideal rubber elasticity (Chapter 13), which states that the modulus is proportional to the absolute temperature. This procedure is, however, open to question. Although ideal rubber elasticity might be a reasonable approximation when the major response mechanism is chain coiling and uncoiling, it certainly is not where response is dominated by straining of bond angles and lengths (glassy region) or molecular slippage (viscous flow region). In any event, such corrections are of minor practical significance.
Shifting a constant-temperature curve along the log-time axis corresponds to dividing every value of its abscissa by a constant factor (it is immaterial what kind of scale is used for the ordinate). This constant factor, which brings a curve at a particular temperature T into alignment with the one at the reference temperature To, is known as the temperature shift factor aT:
where tT is the time required to reach a particular response (Er in this case) at temperature T and tTo is the time required to reach the same response at the reference temperature To. The time value for each relaxation datum on the abscissa of the master curve is from Equation (16.28) or tTo = tT/aT.
For temperatures above the reference temperature, it takes less time to reach a particular response (the material responds faster, i.e., has a shorter relaxation time), so aT is less than one, and vice versa for temperatures below the reference temperature. The logarithm of the experimentally determined temperature shift factor is plotted as a function of temperature in the inset graph of Figure 16.12.
The master curve now represents stress relaxation at 25 °C over 17 decades of time. Since tTo = tT/aT, multiplication by the appropriate value of aT (shifting along the log-time axis) establishes the master curve at any other temperature T, and can thus be used to predict material responses at that temperature over 17 decades of time.
Two additional aspects enhance the utility of the time–temperature superposition concept. First, the same temperature shift factors apply to a particular polymer regardless of the nature of the mechanical response, that is, the shift factors as determined in stress relaxation are applicable to the prediction of the time–temperature behavior in creep or dynamic testing. Second, if the polymer's glass transition temperature is chosen as the reference temperature, the shift factors are given by the Williams–Landel–Ferry (WLF) equation in the range Tg < T < (Tg + 100 K):
(16.29) 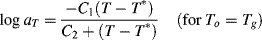
With T* = Tg, the “universal” constants C1 = 17.44 and C2 = 51.6 (with T's in K) give a rough fit for a wide variety of polymers. The WLF equation is most useful in this form because Tg is extensively tabulated [18]. Better fits can be obtained by using constants C1, C2, and T* specific to the polymer, but these constants are not readily available. It has also been suggested that the fit can be improved by using C1 = 8.86 and C2 = 101.6, with T* adjusted to fit specific data, if available. When this is done, T* generally turns out to be Tg + (50 ± 5) K [19].
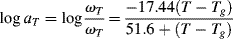
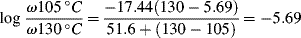
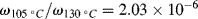
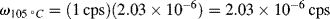
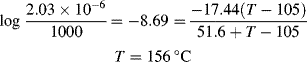
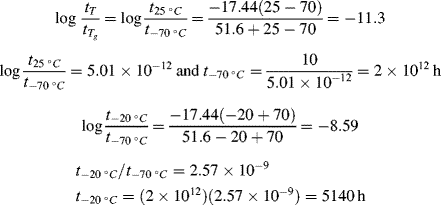
Let us take a closer look at the stress–relaxation master curve. The one shown in Figure 16.12 is typical of linear, amorphous polymers, and illustrates the five regions of viscoelastic behavior [20]. At low temperatures, or short times (large De), only bond angles and lengths can respond, and so the typical glassy modulus of 1010–1011 dyn/cm2 (1–10 GPa) is observed. This is the so-called glassy region. At longer times or higher temperatures, the relaxation response is governed by the uncoiling of the chains, with the characteristic modulus 106–107 dyn/cm2 (0.1–1 MPa) in the rubbery plateau. The intermediate region, where the modulus drops because of glassy to rubbery, is sometimes known as the leathery region because of the leather-like feel of materials with moduli in this range. At still longer times or higher temperatures (low De), the modulus drops from the rubbery plateau into the rubbery-flow region, where the material is still quite elastic but has a significant flow component and then falls off rapidly as a result of molecular slippage in the viscous-flow region (this last distinction is somewhat artificial; usually by this time (or temperature), the polymer is significantly deformed and for many polymers (and all thermosets) degradation begins before the polymer can flow).
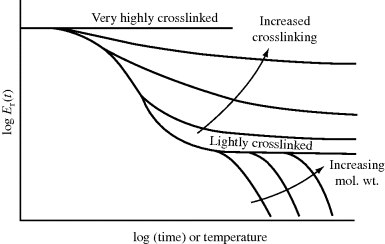
Figure 16.13 illustrates the effects of molecular weight and crosslinking on the stress–relaxation master curve. Molecular weight should have no significant influence on straining of bond angles and lengths or on uncoiling, so the glassy and rubbery moduli are unchanged for these regions. Flow, however, is severely retarded by increasing molecular weight, which extends the rubbery plateau. For very low molecular weight polymers, the rubbery plateau is not even seen (they are liquids at room temperature). In the limit of infinite molecular weight (light crosslinking), flow is entirely eliminated and the curve levels off with the rubbery modulus. Higher degrees of crosslinking restrict uncoiling, ultimately leading to a material that responds only by straining of bond angles and lengths.
Figure 16.13 The effects of molecular weight and crosslinking on stress–relaxation master curves.
The effects of crystallinity on properties are similar to those of crosslinking. However, the applicability of time–temperature superposition in and across the region of Tm is open to question. In this region, the degree of crystallinity and crystalline morphology may change, and one would be, in effect, superimposing data for different materials. A second, vertical shift has been suggested to help superimpose data for crystalline polymers.
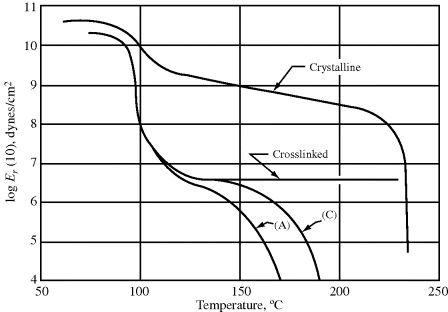
To illustrate the effect of temperature on mechanical properties, it is sometimes preferable to plot the property versus temperature for constant values of time. For example, data of the type shown in Figure 16.12 may be cross-plotted as Er [10] (the 10-s relaxation modulus) versus T. Such a plot is given in Figure 16.14 for several polystyrene samples [20]. The five regions of viscoelastic behavior are evident in the linear, amorphous (atactic) samples (A) and (C) along with the effect of molecular weight in the flow region. The drop in modulus in the vicinity of Tg (100 °C) is clearly seen. The crystalline (isotactic) sample maintains a fairly high modulus all the way up to Tm (~235 °C). Given values of aT, one can convert data in the form Er versus. t at constant T (a master curve) to Er versus T at constant t and vice versa.
Figure 16.14 The 10-s tensile relaxation modulus Er [10] versus temperature for several polystyrenes [20]. Samples (A) and (C) are linear, amorphous (atactic) materials with narrow molecular weight distributions. 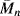 (A) = 140,000;
(A) = 140,000; 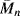 (C) = 217,000. The crosslinked sample is also amorphous. The crystalline material is isotactic.
(C) = 217,000. The crosslinked sample is also amorphous. The crystalline material is isotactic.
16.7 Summary
Material testing for polymers can be rather complex. Thus, a number of different methods is required for determining the mechanical properties of polymers when subjected to deformations, either glassy, rubbery, or solid (or even during a temperature ramp). A number of viscometers can be used to accurately determine the behavior of polymer solutions and melts, while dynamic mechanical analysis is used to determine the behavior of polymers to cyclic stresses, with the moduli separated into storage (or elastic) moduli and loss (or viscous) moduli. The time–temperature superposition principle is a valuable technique to take measurements for polymers at higher temperatures to estimate the behavior of a polymer sample at lower temperatures over long periods of time. The modern polymer characterization laboratory has rheometers, viscometers, dynamic mechanical analyzers, and techniques mentioned in earlier chapters such as differential scanning calorimeters and gel permeation chromatographs (or other equipment to measure molecular weights).
Notes
1. At first glance, it might seem that there is a gradient component in the r direction because the tangential velocity increases with r. However, material points in a cone at constant ϕ do not move relative to one another, that is, they undergo rigid-body rotation, so there is no shearing in the r direction.
2. See the previous footnote. Here, points at constant z undergo rigid-body rotation like a phonograph record.
3. This requires that each fluid element move at fixed z in a circle that is centered on a line connecting the centers of the disks. There has been some controversy about this, but it is probably at least a good approximation for d/h < 0.5.
Problems
| Sample Length, cm | Force, N |
| 5.00 | 0.0 |
| 5.03 | 6.8 |
| 5.08 | 14.3 |
| 5.12 | 22.0 |
| 5.23 | 41.0 |
| 5.25 | 38.0 |
| 5.29 | 39.5 |
| 5.33 | 41.5 |
| 5.36 | 42.5 |
| 5.39 | 44.9 |
| Q, in3/s | ΔPtotal psi | ΔPent psi |
| 2.10 | 1.898 | 0.036 |
| 3.11 | 2.510 | 0.039 |
| 3.49 | 2.732 | 0.081 |
| 4.48 | 2.947 | 0.082 |
| 5.04 | 3.330 | 0.123 |
| 6.16 | 3.599 | 0.132 |
| 7.87 | 4.238 | 0.211 |
| 10.74 | 4.965 | 0.341 |
| 14.31 | 6.046 | 0.620 |
| 15.49 | 6.249 | 0.675 |
| 15.85 | 6.451 | 0.726 |
| 20.13 | 7.597 | 1.183 |
| 23.35 | 8.670 | 1.607 |
| 29.09 | 10.130 | 2.335 |
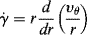

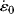 = 1's The initial slope (Young's modulus) is 5000 psi. At a temperature of 30 °C, what would
= 1's The initial slope (Young's modulus) is 5000 psi. At a temperature of 30 °C, what would  have to be to give again an initial modulus of 5000 psi?
have to be to give again an initial modulus of 5000 psi?1. Lendlein, A., A.M. Schmidt, and R. Langer, PNAS 98 (3), 842 (2001).
2. Collyer, A.A. and D.W. Clegg (eds), Rheological Measurement, Elsevier, New York, 1988.
3. Dealy, J.M., Rheometers for Molten Plastics, Van Nostrand Reinhold, New York, 1982.
4. Bird, R.B., W.E. Stewart, and E.N. Lightfoot, Transport Phenomena, Wiley, New York, 1960, p. 94, Example 3.5-1.
5. Krieger, I.M. and S.H. Maron, J. Appl. Phys. 25, 72 (1954).
6. Best, D.M. and S.L. Rosen, Polym. Eng. Sci. 8 (2), 116 (1968).
7. Ferry, J.D., Viscoelastic Properties of Polymers, 3rd ed., Wiley, New York, 1980.
8. Nielsen, L.E., SPE J. 16, 525 (1960).
9. Nielsen, L.E., Mechanical Properties of Polymers and Composites, Vol. 1, Dekker, New York, 1974.
10. Gillham, J.K., Am. Inst. Chem. Eng. J. 20, 1066 (1974).
11. Walters, K., Rheometry, Halsted, New York, 1975.
12. Maxwell, B. and R.P. Chartoff, Trans. Soc. Rheol., 9, 41 (1965).
13. Bird, R.B. and E.K. Harris, Am. Inst. Chem. Eng. J. 14, 758 (1968).
14. Macosko, C.W. and W.M. Davis, Rheol. Acta 13, 814 (1974).
15. Davis, W.M. and C.W. Macosko, Am. Inst. Chem. Eng. J. 20, 600 (1974).
16. Maxwell, B., J. Polym. Sci. 20, 551 (1956).
17. Tobolsky, A.V. and E. Catsiff, J. Polym. Sci. 19, 111 (1956).
18. Brandrup, J. and E.H. Immergut (eds), Polymer Handbook, 3rd ed., Wiley-Interscience, New York, 1989.
19. Bird, R.B., R.C. Armstrong, and O.A. Hassager, Dynamics of Polymeric Liquids, Vol. 1, Fluid Mechanics, Wiley, New York, 1977.
20. Tobolsky, A.V., Properties and Structure of Polymers, Wiley, New York, 1960.