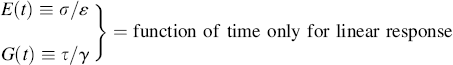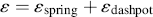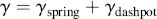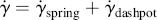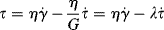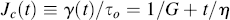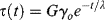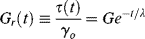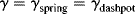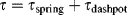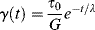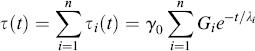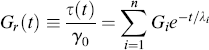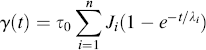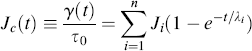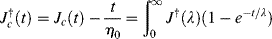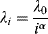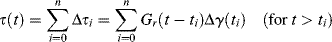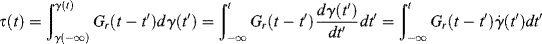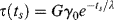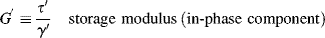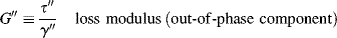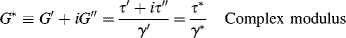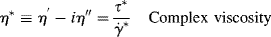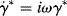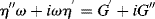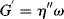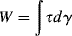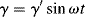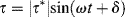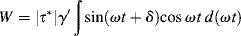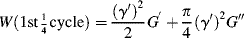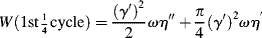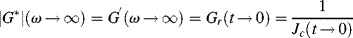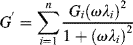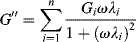Chapter 15
Linear Viscoelasticity
15.1 Introduction
In a traditional sense, engineers typically deal with elastic solids and viscous fluids as two separate and distinct classes of materials. Design procedures based on these concepts have worked pretty well because most traditional materials (water, air, steel, concrete), at least to a good approximation, fit into one of these categories. The realization has grown, however, that these categories represent only the extremes of a broad spectrum of material response. Polymer systems fall somewhere in between (thus, the use of the term “viscoelastic”), giving rise to some of the unusual properties of melts and solutions described previously. Other examples are important in the structural applications of polymers. In a common engineering stress–strain test, a sample is strained (stretched, bent, or compressed) at an approximately constant rate and the stress is measured as a function of strain. With traditional solids, the stress–strain curve is pretty much independent of the rate at which the material is strained. However, the stress–strain properties of many polymers are markedly rate dependent. Similarly, polymers often exhibit pronounced creep and stress relaxation behavior (to be defined shortly). While such behavior is exhibited by other materials (e.g., metals near their melting points), at normal temperatures it is negligible and is not usually included in design calculations. If the time-dependent behavior of polymers is ignored, the results can sometimes be disastrous.
15.2 Mechanical Models for Linear Viscoelastic Response
An as aid in visualizing viscoelastic response, we introduce two linear mechanical models to represent the extremes of the mechanical response spectrum. The spring in Figure 15.1a represents a linear elastic or Hookean solid that can be used to describe the response to a shear force, whose constitutive equation (relation of stress to strain and time) is simply τ = Gγ, where G is a (constant) shear modulus of the material (or if subjected to a stretching force, σ = Eε, where E is the elastic modulus). Similarly, a linear viscous or Newtonian fluid is represented by a dashpot (a sort-of piston moving in a cylinder of Newtonian fluid) whose constitutive equation is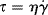 
, where η is a (constant) viscosity. In contrast to the spring, which snaps back to its original length after the strain is removed, a dashpot continues to expand as long as a force is applied, and when that force (strain) is removed, the dashpot remains at its stretched position. In the model, the strain is represented by the extension (stretching) of spring and/or dashpot.
Figure 15.1 Linear viscoelastic models: (a) linear elastic; (b) linear viscous; (c) Maxwell element; (d) Voigt–Kelvin element; (e) three-parameter; (f) four-parameter.
The models developed here are visualized in tension, with tensile stress σ, tensile strain ε, and Young's modulus E. However, the same theory holds true for pure shear (viscometric) deformation, where a shear stress τ results in a shear strain γ with proportionality constant G (Hooke's modulus). η represents the Newtonian (shear) viscosity, while the elongational (Trouton) viscosity is given by ηe.
Some authorities strongly object the use of mechanical models to represent materials. They point out that real materials are not made of springs and dashpots. This is true, but they are not made of equations either, and it is much easier for most people to visualize the deformation of springs and dashpots than the solutions to equations.
A word is needed for the meaning of the term linear. For the present, a linear response will be defined as one in which the ratio of overall stress to overall strain, the overall modulus, E(t) or G(t), is a function of time only, not of the magnitudes of stress or strain:
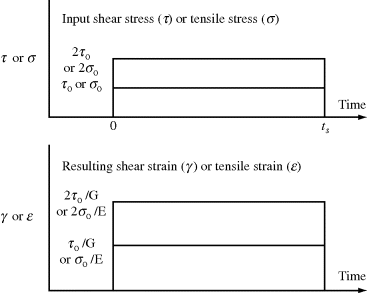
The Hookean spring responds instantaneously to reach an equilibrium strain (ε or γ) upon application of a constant stress (σo or τo), and the strain remains constant as long as the stress is maintained constant. Sudden removal of the stress results in instantaneous recovery of the strain (Figure 15.2). Doubling the stress on the spring simply doubles the resulting strain, so the spring is linear, with E(t) = E or G(t) = G, with E or G as constants, according to Equations (15.1a) and 15.1b. (In assuming that the spring instantaneously reaches an equilibrium strain under the action of a suddenly applied constant stress, we have neglected inertial effects. Although it is not necessary to do so, including them would contribute little to the present discussion.)
Figure 15.2 Response of spring (purely elastic component) to shear stress or tensile stress applied from time 0 to time ts. The spring snaps back to its original position immediately after the stress is removed. Also note that the magnitude of the strain is directly proportional to the applied stress.
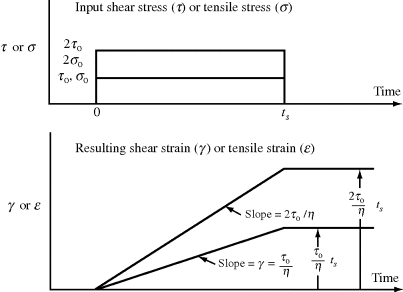
If a constant stress (σo or τo) is suddenly applied to the dashpot, the strain increases with time according to σ = (ε/ηe)t or γ = (τo/η)t (considering the strain to be zero when the stress is initially applied), Figure 15.3. Doubling the stress doubles the slope of the strain-time line, and at any time, the modulus E(t) ≡ σ/ε = ηe/t = E or G(t) ≡ τ/γ = η/t = G, where E or G are functions of time only. So the dashpot is also linear.
Figure 15.3 Response of a dashpot (purely viscous component) to shear stress or tensile stress applied from time 0 to time ts. The dashpot is permanently deformed from its original position. Also note that the slope of the strain versus time curve is proportional to the applied stress. Not shown on the figure: for the tensile strain, the slope would be σo/ηe or 2σo/ηe, respectively, for the two input stresses, with the permanent deformation being ε = (σo/ηe) ts for the input strain of σo or (2σo/ηe) ts for the input strain of 2σo.
It may be shown that any combination of linear elements must be linear, so any models based on these linear elements, no matter how complex, can represent only linear responses. Just how realistic is a linear response? Its most conspicuous shortcoming is that it permits only Newtonian behavior (constant viscosity) in equilibrium viscous flow. For most polymers at strains greater than a few percent or so (or rates of strain greater than 0.1/s), a linear response is not a good quantitative description. Moreover, even within the limit of linear viscoelasticity, a fairly large number of linear elements (springs and dashpots) are usually needed to provide an accurate quantitative description of the material's response. Hence, the quantitative applicability of simple linear models (those with a few springs and dashpots) is limited, but the models are extremely valuable in visualizing viscoelastic response and in understanding how and why variations in molecular structure influence that response.
15.2.1 The Maxwell Element
James Clerk Maxwell realized that neither a linear viscous element (dashpot) nor a linear elastic element (spring) was sufficient to describe his experiments on the deformation of asphalts, so he proposed a simple series combination of the two, the Maxwell element (Figure 15.1c). In a Maxwell element, the spring and dashpot support the same stress so
(15.2a)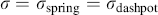 
(15.2b)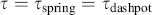 
Furthermore, the total strain (extension) of the element is additive (i.e., the sum of the strains in the spring and dashpot):
Differentiating Equations (15.3a) and (15.3b) with respect to time gives
(15.4a)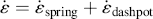 
Considering the shear strain in Equation (15.4b), and realizing that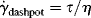 
and 
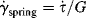, plugging in and rearranging gives the differential equation for the Maxwell element:
The quantity λ = η/G has the dimension of time and is known as a relaxation time. Its physical significance will be apparent shortly.
15.2.1.1 Creep Testing
Let us examine the response of the Maxwell element in two mechanical tests commonly applied to polymers. First consider a creep test, in which a constant shear stress is instantaneously (or at least very rapidly) applied to the material and the resulting strain is followed as a function of time. Deformation after removal of the stress is known as creep recovery.
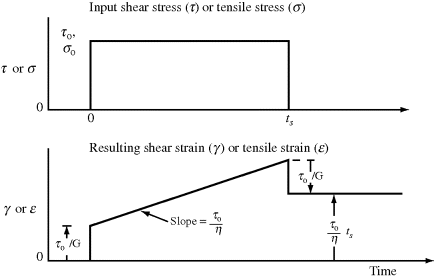
As shown in Figure 15.4, the sudden application of stress to a Maxwell element causes an instantaneous stretching of the spring to an equilibrium value of τo/G (or σo/E if a tensile stress is applied), where τo is the constant applied shear stress (or σo is the constant applied extensional stress). The dashpot extends linearly with time with a slope of τo/η (or σo/ηe for tensile experiments), and will continue to do so as long as the stress is maintained. Thus, the Maxwell element is a fluid, because it will continue to deform as long as it is stressed. The creep response of a Maxwell element is therefore
(15.6a)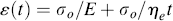 
(15.6b)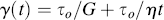 
or, in terms of compliance (for an applied tensile stress), where J ≡ ε(t)/σo, or a creep compliance (for an applied shear stress), where Jc(t) ≡ γ(t)/τo,
(15.7a)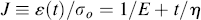 
The creep compliance Jc(t), being independent of the applied stress τo (for a linear material), is a more general way to represent the creep response. When the stress is removed at time ts, the spring immediately contracts by an amount equal to its original extension, a process known as elastic recovery. The dashpot, of course, does not recover, leaving a permanent set of (τo/η)ts, or σo/ηets (for a tensile stress), representing the amount the dashpot has extended during the application of stress. Although real materials never show sharp breaks in a creep test as does the Maxwell element, the Maxwell element does exhibit the phenomena of elastic strain, creep recovery, and permanent set, which are often observed with real materials.
Figure 15.4 Creep response of a Maxwell element to an applied stress. The bottom figure shows the shear response, but a similar figure would also show the initial stretching of the spring due to a tensile stress (σo/E), and slope of the deformation due to the dashpot (σo/ηe), with the recoil of the spring being −σo/E and the permanent deformation being σo/ηe * ts.
Creep testing also demonstrates another term commonly used in material testing, that is, deformation. There are two types of deformation that may arise after a stress is applied to a material: elastic deformation and plastic deformation. Elastic deformation refers to materials whose shape changes temporarily, and once the force is removed, the material resumes its original shape; this is equivalent to the spring representation in viscoelasticity models. Plastic deformation refers to nonreversible changes in shape, represented by the dashpot here. It is interesting to note that even for metals, the term plastic deformation is used to indicate that a material has been deformed in a way that cannot be recovered.
15.2.1.2 Stress Relaxation
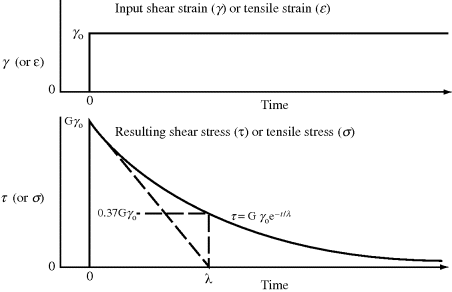
Another important test used to study viscoelastic responses is stress relaxation. A stress-elaxation test consists of suddenly applying a strain to the sample, and following the stress as a function of time as the strain is held constant. When the Maxwell element is strained instantaneously, only the spring can respond initially (for an infinite rate of strain, the resisting force in the dashpot is infinite) to a shear stress of Gγo, where γo is the constant applied shear strain (or similarly for a tensile stress of Eεo, where εo is the constant applied tensile strain). The extended spring then begins to contract, but the contraction is resisted by the dashpot. The more the spring retracts, the smaller is its restoring force, and, correspondingly, the rate of retraction drops. Solution of the differential equation for shear relaxation with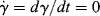 
and the initial condition τ = Gγo at t = 0 shows that the stress undergoes a first-order exponential decay:
or, in terms of a relaxation modulus,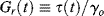 
,
Again, the relaxation modulus, Gr(t), is a more general means of representing a stress-relaxation response because it is independent of the applied strain for linear materials.
From Equations (15.8b), we see that the relaxation time λ is the time constant for the exponential decay, that is, the time required for the stress to decay to a factor of 1/e or 37% of its initial value. The stress asymptotically drops to zero as the spring approaches complete retraction (Figure 15.5).
Figure 15.5 Shear stress relaxation of a Maxwell element to a constant applied shear strain.
Stress-relaxation data for linear polymers actually look like the curve for the Maxwell element. Unfortunately, they cannot often be fitted quantitatively with a single value of G and a single value of λ, that is, the decay is not really first order.
.
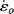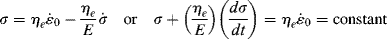
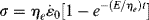
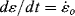is constant and we can assume that ε = 0 when t = 0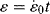
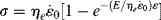
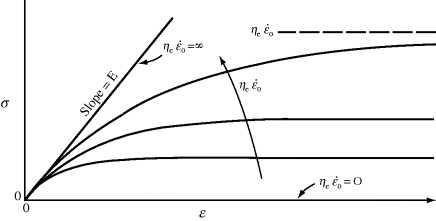
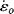, that is, the material appears “stiffer” (has a higher modulus). As crude as this model might prove to be in fitting experimental data, it does account, at least qualitatively, for some of the observed properties of linear polymers in engineering stress–strain tests.Figure 15.6 Response of a Maxwell element under constant rate of tensile strain (Example 15.1).
15.2.2 The Voigt–Kelvin Element
If a series combination of a spring and dashpot has its drawbacks, the next logical thing to try is a parallel combination, a Voigt or Voigt–Kelvin element (Figure 15.1d). Here, it is assumed that the crossbars supporting the spring and the dashpot always remain parallel, so that the strain is the same in the spring and in the dashpot at all times:
The stress supported by the element is then the sum of the stresses in the spring and in the dashpot:
Combination of Equations (15.9) and (15.10) with the equations for the deformation of the spring and the dashpot gives the differential equation for the Voigt–Kelvin element:
(15.11)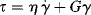 
When the stress is suddenly applied in a creep test, only the dashpot offers an initial resistance to deformation, so the initial slope of the strain versus time curve is τo/η. As the element is extended, the spring provides an increasingly greater resistance to further extension, so the rate of creep decreases. Eventually, the system comes to equilibrium with the spring alone supporting the stress (with the rate of strain zero, the resistance of the dashpot is zero). The equilibrium strain is simply τo/G. Quantitatively, the response is an exponential rise,
(15.12a)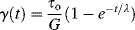 
or, in terms of the creep compliance:
(15.12b)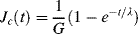 
If the stress is removed after equilibrium has been reached, the strain decays exponentially,
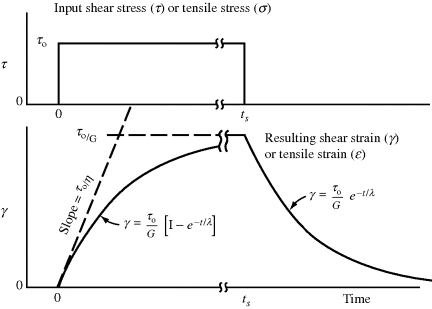
Note that the Voigt–Kelvin element does not continue to deform as long as stress is applied, and it does not exhibit any permanent set (see Figure 15.7). It therefore represents a viscoelastic solid, and gives a fair qualitative picture of the creep response of some crosslinked polymers.
Figure 15.7 Creep response of a Voigt–Kelvin element to an applied shear stress.
The Voigt–Kelvin element is not suited for representing stress relaxation. The instantaneous application of strain would be met by an infinite resistance in the dashpot, and so would require the application of an infinite stress, which is obviously unrealistic.
15.2.3 The Three-Parameter Model
The next step in the development of linear viscoelastic models is the so-called three-parameter model (Figure 15.1e). By adding a dashpot in series with the Voigt–Kelvin element, we get a liquid. The differential equation for this model may be written in operator form as
(15.14)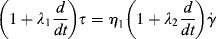 
where λ1 = (η1 + η2)/G and λ2 = η2/G. Further, the form of Equation (15.13) suggests modification by adding higher order derivatives and more constants:
(15.15)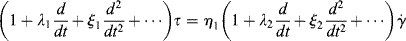 
This, of course, will fit data to any desired degree of accuracy if enough terms are used.
15.3 The Four-Parameter Model and Molecular Response
The four-parameter model (Figure 15.1f) is a series combination of a Maxwell element with a Voigt–Kelvin element. Its differential equation is
(15.16)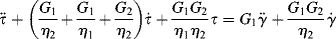 
Its creep response is the sum of the creep responses of the Maxwell and Voigt–Kelvin elements:
(15.17a)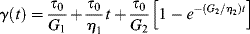 
or, in terms of creep compliance:
(15.17b)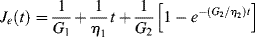 
This is summarized in Figure 15.8.
Figure 15.8 Creep response of a four-parameter model for an input shear stress. Note that the model also works for tensile stress, σ, with its corresponding tensile strain, ε.
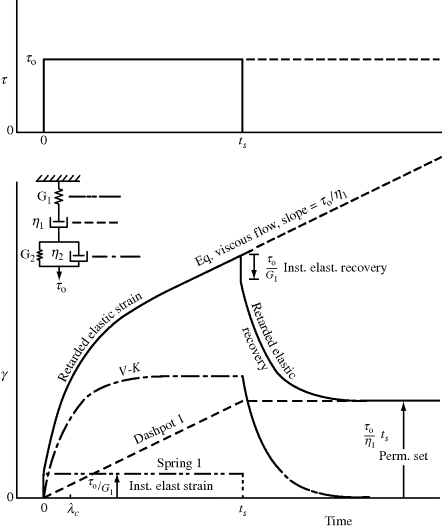
The four-parameter model provides at least a qualitative representation of all the phenomena generally observed in the creep of viscoelastic materials: instantaneous elastic strain, retarded elastic strain, steady-state viscous flow, instantaneous elastic recovery, retarded elastic recovery, and permanent set. It also describes at least qualitatively the behavior of viscoelastic materials in other types of deformation. Of equal importance is the fact that the model parameters can be identified with the various molecular response mechanisms in polymers, and can, therefore, be used to predict the influences that changes in molecular structure will have on mechanical response. The following analogies may be drawn.
The magnitude of the timescale shown in Figure 15.8 will of course depend on the values of the model parameters. The two viscosities, in particular, depend strongly on temperature. Well below Tg, for example, where η1 and η2 are very large, ts needs to be on the order of days or weeks to observe appreciable retarded elasticity and flow. Well above Tg, ts might be only seconds or less to permit the deformation shown. An important thing to keep in mind is that designs based on short-term property measurements will be inadequate if the object supports a stress for longer periods of time.
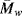. Thus, the slope in the steady-state flow region τo/η1 is greatly decreased as the molecular weight increases, and the permanent set (τo/η1)ts is reduced correspondingly (Figure 15.9).Figure 15.9 The effects of molecular weight and crosslinking on the creep response to application of a shear stress on an amorphous polymer. A similar response would be observed for elongational strain, ε, upon application of a fixed tensile stress, σ.
The four-parameter model nicely accounts for the interesting examples of viscoelastic response mentioned earlier. For example, dashpot 1 allows viscous flow, while the elastic restoring forces of springs 1 and 2 provide the “rubber band” elasticity responsible for the Weissenberg effect, which is when a polymer solution is drawn up around a mixing rod rather than being flung outward. In engineering stress–strain tests, the moduli of polymers are observed to increase with the applied rate of strain. At high rates of strain, spring 1 provides the major response mechanism. As the rate of strain is lowered, dashpot 1 and the Voigt–Kelvin element contribute more and more to the overall deformation, giving a greater strain at any stress, that is, a lower modulus. When Silly Putty is bounced (stress applied rapidly for a short period of time), spring 1 again provides the major response mechanism. There is not time for appreciable flow according to dashpots 1 and 2, so not much of the initial potential energy is converted to heat through the molecular friction involved in slippage and uncoiling, and the material behaves in an almost perfectly elastic fashion. When it is stuck on the wall, the stress (in this case due to its own weight) is applied for a long period of time, and it flows downward as a result of the molecular slip represented by dashpot 1.
15.4 Viscous or Elastic Response? The Deborah Number [1]
As discussed above, whether a viscoelastic fluid behaves as an elastic solid or a viscous liquid depends on the relation between the timescale of the deformation to which it is subjected and the time required for the material's time-dependent mechanisms to respond. Strictly speaking, the concept of a single relaxation time applies only to a first-order response, and thus is not applicable to real materials, in general. Nevertheless, a characteristic relaxation time λc for any material can always be defined as, for example, the time required for the material to reach 1 − 1/e or 63.2% of its ultimate retarded elastic response to a step change. A precise value is rarely necessary. The characteristic time is simply a means of characterizing the rate of a material's time-dependent elastic response, short λc's indicating rapid response and large λc's indicating sluggish response. The ratio of this characteristic material time to the timescale of the deformation is the Deborah number:
(15.18)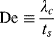 
Response will appear elastic at high Deborah numbers (De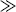 
1) and viscous at low Deborah numbers (De → 0).
Consider, for example, the creep response of the four-parameter model (Figure 15.8). For this model, a logical choice for λc would be the time constant for its Voigt–Kelvin component, η2/G2. For De 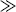1 (ts 
λc), the Voigt–Kelvin element and dashpot 1 will be essentially immobile, and the response will be due almost entirely to spring 1, that is, almost purely elastic. For De → 0 (ts 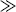λc), the instantaneous and retarded elastic response mechanisms have already reached equilibrium, so the only remaining response will be the purely viscous flow of dashpot 1, and the deformation due to viscous flow will completely overshadow that due to the elastic response mechanisms (imagine the creep curve of Figure 15.8 extended a meter or so beyond the page). Under conditions where De → 0, materials can be treated by the techniques outlined in Chapter 14 for purely viscous fluids.
Modifications of the devices described in Chapter 14 can also be used to obtain information on the material's elastic response. For example, if the stress is suddenly removed from a rotational viscometer, the creep recovery or elastic recoil of the material can be followed. This provides a value of λc for the material.
0) jog to get around it. The retarded elastic response mechanisms simply cannot respond fast enough in the immediate vicinity of the probe, which for all practical purposes behaves as if it were covered with a solid plug. What is measured, therefore, is not characteristic of the fluid in an unobstructed stream.15.5 Quantitative Approaches to Model Viscoelasticity [2–5]
Although the four-parameter model is useful from a conceptual standpoint, it does not often provide an accurate fit of experimental data and therefore cannot be used to make quantitative predictions of material response. To do so, and to infer some detailed information about molecular response, more general models have been developed. The generalized Maxwell model (Figure 15.10) is used to describe stress-relaxation experiments. The stress relaxation of an individual Maxwell element is given by
(15.19)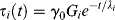 
where λi = ηi/Gi. The relaxation of the generalized model, in which the individual elements are all subjected to the same constant strain γo is then:
Expressed in terms of the time-dependent relaxation modulus Gr(t), the response is
Now, if n is large, the summation in Equation (15.20a) may be approximated by the integral over a continuous distribution of relaxation times G(λ):
(15.21)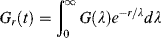 
Note that while the Gi's have modulus units (e.g., dyn/cm2 or MPa), G(λ) is in modulus/time units. Also note that if the generalized Maxwell model is to represent a viscoelastic solid such as a crosslinked polymer, at least one of the viscosities has to be infinite.
Figure 15.10 Generalized Maxwell model for material response to shear. Note that the model can also be used to show the response to extensional stress, σ.
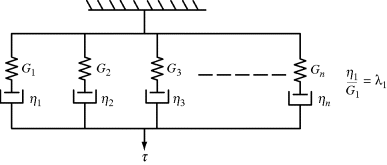
For creep tests, a generalized Voigt–Kelvin model is used (Figure 15.11). The creep response of an individual Voigt–Kelvin element is given by
(15.22)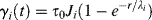 
where Ji = 1/Gi is the individual spring compliance. The response of the array, in which each element is subjected to the same constant applied stress τo, is then
or, in terms of the overall creep compliance, Jc(t):
Again, for large n, the discrete summation above may be approximated by
(15.24)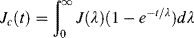 
where J(λ) is the continuous distribution of retardation times (1/modulus·time).
Figure 15.11 Generalized Voigt–Kelvin model for an input shear stress, τ. This model could also be used for modeling tensile stress, σ, with the corresponding moduli Ei.
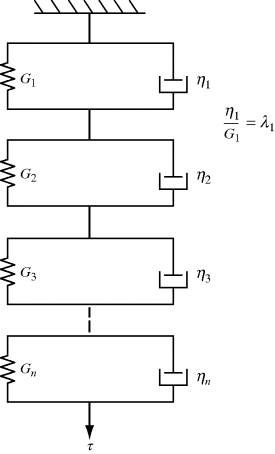
If the generalized Voigt–Kelvin model is to represent a viscoelastic liquid such as a linear polymer, the modulus of one of the springs must be zero (infinite compliance), leaving a simple dashpot in series with all the other Voigt–Kelvin elements. Sometimes, the steady-flow response of this lone dashpot, γdashpot = (τo/ηo)t, is subtracted from the overall response, leaving the compliances to represent only the elastic contributions to the overall response:
(15.25a)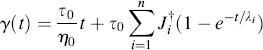 
(15.25b)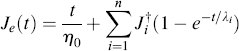 
(15.26)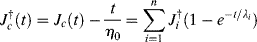 
Here, ηo is the steady-state (Newtonian) viscosity. The daggers indicate that the steady-state viscous flow has been removed and is treated separately.
Application of the discrete Equations (15.20b) and (15.23b) often involves a fairly large n to describe data accurately, thus requiring an impractically large number of parameters λi and Gi = 1/Ji. It has been suggested, however, that the individual parameters are related by [6]
Equations (15.27) and (15.28) require that the Gi all be the same and that ηo = Σηi (with ηi = λiGi). They reduce the number of necessary parameters to three: ηo, the steady-state zero-shear viscosity; λo, a maximum relaxation time; and α, an empirical constant. The Rouse theory [7] for dilute polymer solutions predicts α = 2, but for concentrated solutions and melts, better fits are obtained with α's between 2 and 4 [6].
Often, enough discrete parameters to provide reasonable response models can be extracted from experimental creep or stress-relaxation data using Tobolsky's “Procedure X” [4]. This procedure will be illustrated for stress-relaxation data in the form of the relaxation modulus Gr(t). According to Equation (15.20b),
(15.20b)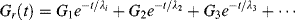 
The procedure is based on two assumptions. First, the Gi's do not differ much in magnitude. This often turns out to be the case. As noted in Equation (15.29), theory suggests that the Gi should be identical. Second, there are a few discrete λi, with λ1 > λ2 > λ3 > ..., and they differ enough so that at long times, the second-, third-, and higher-order terms approach zero, leaving only the first term to determine Gr(t). These assumptions are easily tested. If a plot of ln Gr(t) versus t becomes linear at large t, the assumptions are valid. If that turns out to be the case, the slope of the linear region at long times is −1/λ1 and its t = 0 intercept is ln G1. The known response of the first Maxwell element can then be subtracted from the overall response:
(15.30)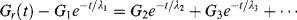 
and 
is plotted versus t. Again, if a linear region is reached at long times, the slope of that region is −1/λ2 and its intercept is ln G2, and so on.
In principle, this procedure can be repeated indefinitely. In practice, the precision and timescale of typical single-temperature experimental data rarely justify going beyond i = 3. Even so, the resulting three-element generalized Maxwell model can often give a good fit to the data used to establish it. More importantly, the model can then be used to predict material response in other types of deformation, at least over similar timescales. The time–temperature superposition principle, which is discussed below, can extend timescales to the point where the parameters may be established to i = 6 or 7 or so.
Using the method developed here, a creep response can be predicted from stress-relaxation measurements, and vice versa. This interconvertability also applies to a variety of linear mechanical responses in addition to the two types discussed here, as is illustrated in the next section. The interconversion procedures have been discussed in detail by Schwarzl [8,9]. Furthermore, the shape of the distributions G(λ) or J(λ) provides the polymer scientist with information on molecular response mechanisms within the polymer. For example, peaks in a certain region of λ might imply motion of side chains on the molecules. This type of information can lead to the “design” of polymers with the type of side chains needed to provide particular mechanical properties.
15.6 The Boltzmann Superposition Principle
Suppose a material initially free of stress is subjected to a test in which a strain γ(to) is suddenly imposed at t = 0 and maintained constant for a while. This is classical stress relaxation, and the stress will decay according to the material's time-dependent relaxation modulus Gr(t), that is, τ(t) = Gr(t)γ(to). Now, however, at time t1, the strain is suddenly changed to a new level γ(t1), held there for a while, then at t2 changed to γ(t2), and so on, as sketched in Figure 15.12a. What happens to the stress as a result of this strain history? Well, way back in 1876, Boltzmann suggested that the stresses resulting from each individual strain increment should be linearly additive, that is,
where
(15.32a)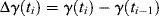 
and
(15.32b)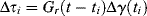 
Here Δτi is the stress increment that results from the strain increment Δγi. The argument t − ti is the time after the application of a particular strain increment Δγi. This behavior is sketched in Figure 15.12b.
Figure 15.12 Boltzmann superposition principle: (a) applied strain history; (b) resulting stress history. The experiment can also be reversed, with an applied stress history causing a strain history. The shear stresses and strains shown can also be replaced with tensile stresses and strains.
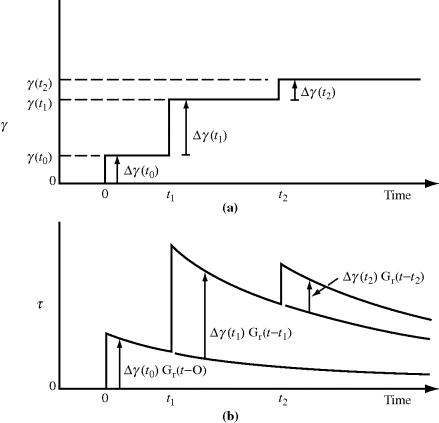
According to Boltzmann, the stress in the material at any time t depends on its entire past strain history, although since Gr(t) is a decreasing function of time, the further back a Δγ(ti) has occurred, the smaller will be its influence in the present. This leads to the anthropomorphic concept of viscoelastic materials having a fading memory (like an aging professor), with Gr(t) sometimes known as the memory function. (The concept, of course, is valid even in the absence of linear additivity—it is just much more difficult to quantify.)1
Figure 15.13 Stress response of a Maxwell element to a changing shear strain (Example 15.5).
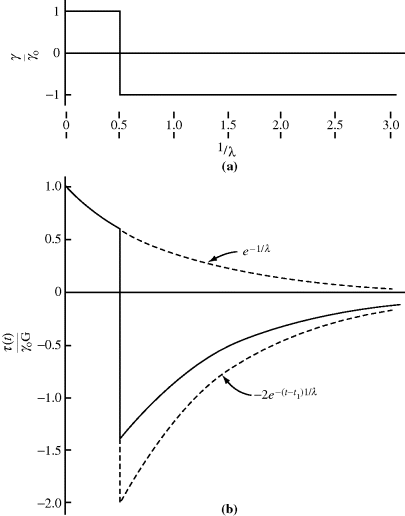
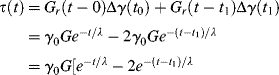
Of course, not all strain histories consist of a nice series of finite step changes. No matter how an applied strain varies with time, however, it can always be approximated by a series of differential step changes, for which Equation (15.31) becomes
where t = present time and t′ = past time. A word is needed about the somewhat bizarre (but fairly standard) notation in Equation (15.33). The implication is that to evaluate the stress at the present time t, we must integrate over the entire past strain history of the sample; hence, the lower limit of t′ = −∞. In some (but not all) cases, it is convenient to assume that τ = γ = 0 for t′ < 0, in which case the lower limit on the integrals becomes zero.
Equation (15.33) allows calculation of τ(t) from stress-relaxation data Gr(t) for any applied strain history as long as the response is linear. Furthermore, by inversion of Equation (15.31), it is possible (at least in principle) to obtain Gr(t) from any test in which both τ(t) and γ(t) are measured. When the independent variable is τ(t) and you wish to calculate γ(t), analogs of Equations (15.31) and (15.33) may be written in terms of the creep compliance Jc(t):
(15.34)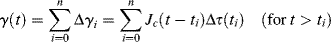 
(15.35) 
When all is said and done, probably the best definition of a linear material is simply one that follows Boltzmann's principle. Thus, spring–dashpot models, which are linear, automatically follow Boltzmann's principle. However, it is important not to infer a dependence of the Boltzmann principle on spring–dashpot models. The Boltzmann principle applies to a linear response regardless of whether it can be described with a spring–dashpot model. All that is needed are experimental Gr(t) or Jc(t) data. Models are used here simply as a matter of convenience to illustrate application of the principle.
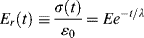
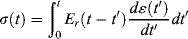
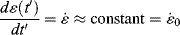
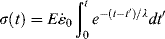
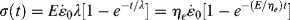
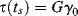
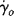= γo/ts. By analogy to the solution of Example 15.6 above:
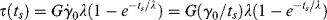
15.7 Dynamic Mechanical Testing
Creep and stress-relaxation measurements correspond to the use of step-response techniques to analyze the dynamics of electrical and process systems. Those familiar with these areas know that frequency-response analysis is perhaps a more versatile tool for investigating system dynamics. An analogous procedure, dynamic mechanical testing, is applied to the mechanical behavior of viscoelastic materials. It is based on the fundamentally different response of viscous and elastic elements to a sinusoidally varying stress or strain.
If a sinusoidal strain, γ = γ′ sin ωt (where ω is the angular frequency in radian/s) is applied to a linear spring, since τ = Gγ, the resulting stress τ = Gγ′ sin ωt is in phase with the strain. For a linear dashpot, however, because the stress is proportional to the rate of strain rather than the strain,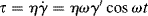 
, the stress is 90° out of phase with the strain. These relations are sketched in Figure 15.14.
Figure 15.14 Stress in a linear spring and in a linear dashpot in response to a sinusoidal applied strain.
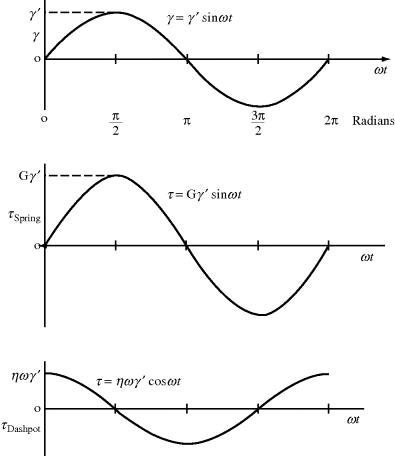
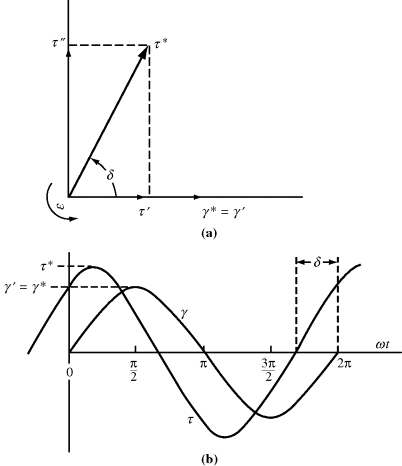
As might be expected, viscoelastic materials exhibit some sort of intermediate response, which might look like Figure 15.15b. This can be thought of as being a projection of two vectors, τ* and γ*, rotating in a complex plane (Figure 15.15a). The angle between these vectors is the phase angle δ (δ = 0 for a purely elastic material and 90° for a purely viscous material). It is customary to resolve the vector representing the dependent variable into components in phase (designated by a prime) and 90° out of phase (designated by a double prime) with the independent variable. In this example, the applied strain is the independent variable, so the stress vector (τ*) is resolved into its in-phase (τ′) and out-of-phase (τ″) components, |γ*| = γ′ and γ″ = 0. In complex notation,
(15.36)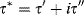 
where i is the out-of-phase unit vector.
An in-phase or storage modulus is defined by
and an out-of-phase or loss modulus is defined by
Both of these moduli have important physical significance to the design of materials. A material with a high storage modulus and low loss modulus will be springy—it can be used over and over again with little deformation. A material with a high loss modulus and low storage modulus will favor the dashpot, resulting in an easily deformed material (which is particularly useful in absorbing energy in a car collision).
The complex modulus G* is the vector sum of the in-phase and out-of-phase moduli:
Additionally, a complex viscosity, η*, may be defined as
Also [10],
By combining Equations (15.39)–(15.41) (and recalling that i2 = −1), we get
Comparison of the real (in-phase) and imaginary (out-of-phase) parts of Equation 18.40 gives
and
(15.44)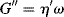 
Furthermore, combination of Equations (15.40)–(15.43) and (15.43) reveals that
(15.45)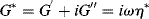 
From the geometry of Figure 15.15 and the relations above, the loss tangent, tan δ, is
(15.46)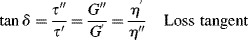 
Figure 15.15 Quantities in dynamic testing: (a) rotating vector diagram; (b) stress and strain.
The physical significance of the quantities just defined can best be appreciated by considering what happens to the energy applied to a sample undergoing cyclic deformation. From Equation 13.3, the work done on a unit volume of material undergoing a pure shear deformation is
From Figure 15.15,
and
Differentiating Equation (15.48) with respect to (ωt) gives
Inserting Equations (15.49) and (15.50) into Equation (15.47) gives
Let us first consider the work done on the first quarter-cycle of the applied strain, that is, integrate Equation (15.51) between 0 and π/2. Using appropriate trigonometric identities and a good set of integral tables gives
(15.52)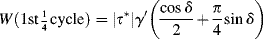 
Putting in terms of moduli or viscosities, using the trigonometry of Figure 15.15 and Equations (15.41) and (15.42), we find:
The first term on the right side of Equation (15.53a) is simply the work done in straining a linear spring of modulus G′ an amount γ′ (the area under the spring's stress–strain curve). It, therefore, represents the energy stored elastically in the material during its straining in the first-quarter cycle. Hence, G′ is the storage modulus. If the applied mechanical energy (work) is not stored elastically, it must be “lost,” converted to heat through molecular friction, that is, viscous dissipation, within the material. This is precisely what the second term on the right represents, so G″ is known as the loss modulus. Likewise, from Equation (15.53b), stored energy is proportional to η″ and the dissipated energy is proportional to η′.
Considering the second quarter of the cycle, integrating Equation (15.51) from π/2 to π gives results identical to Equation (15.53a) except that the sign on the first (storage) term is negative. This simply means that the energy stored elastically in straining the material from 0 to γ′ is recovered when it returns from γ′ to 0. Thus, over a half cycle (0 to π or 180°) or a full cycle (0 to 2π), there is no net work done or energy lost by the elastic component. The sign of the second term, however, is positive for any quarter cycle, so the net energy loss (converted to heat within the material) for a full cycle (also obtainable by integrating Eq. (15.51) between 0 and 2π) is simply
(15.54)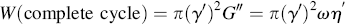 
The average power dissipated as heat within the material 
is obtained by dividing the energy dissipated per cycle by the period (time) of a cycle, 2π/ω:
(15.55)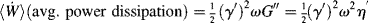 
These results are of direct importance in the design of polymeric objects that are subjected to cyclic deformation. In a tire, for example, high temperatures contribute to rapid degradation and wear. A rubber compound with a low G″ (or η′) therefore helps to minimize the energy dissipation and the resultant heat buildup. Moreover, dissipated energy wastes gasoline, therefore such a compound also contributes to better gas mileage. In the design of an engine mount, however, the goal is usually to prevent vibrations being transmitted from the engine. Here, a material with a large G″ (or η′) would dissipate considerable vibrational energy as heat rather than transmit it to the passengers.
Dynamic mechanical analyses are also done to estimate a material's fatigue. The fatigue lifetime for a polymer is defined as the number of cyclic loading and unloading it can stand for a given stress before it fails. The higher the applied stress, the lower the fatigue lifetime.
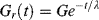
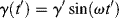
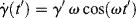
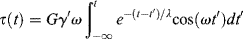
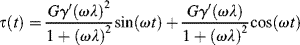
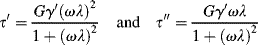
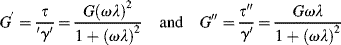
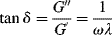
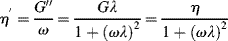
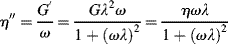
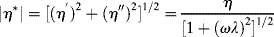
Figure 15.16 (a) Dynamic moduli of a Maxwell element (Example 15.8). (b) Dynamic viscosities of a Maxwell element (Example 15.8).
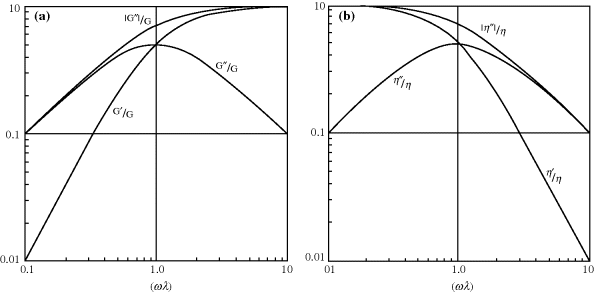
As when applied to other types of mechanical tests, the Maxwell element will not win any prizes for quantitatively fitting dynamic data for real materials. Nevertheless, Example 15.8 does serve to illustrate the frequency dependence of dynamic mechanical properties, and Figures 15.16a and 15.16b do in some ways that resemble the variation in isothermal dynamic data with frequency for real materials. In particular, the apparent “stiffness” |G*| increases to a limiting value with frequency. In the model, the dashpot simply cannot keep up with high frequencies, leaving only the spring to respond. Also, the maximum in G″ is usually observed at frequencies in the range where G′ and |G*| are falling from their high-frequency limit. In the model, at low frequencies, the dashpot offers little resistance to motion and so dissipates little energy. At high frequencies, its high resistance prevents its motion, limiting response to the spring, and energy dissipation again falls off.
With real materials, the high-frequency limit of |G*| and G′ corresponds quantitatively to the moduli obtained in the limit of short times in stress-relaxation and creep measurements, that is,
Furthermore, the measured low-frequency limit of |η*| and η′ agrees with the zero-shear-rate steady-flow viscosity ηo:
(15.57)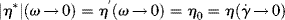 
The viscosity analogy has been pushed a bit further. The drop in |η*| with frequency resembles the variation in steady-flow viscosity η with shear rate. On a purely empirical basis, Cox and Merz [11] suggested that |η*| and η are the same when compared at equal values of frequency and shear rate:
(15.58)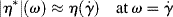 
Although not exact, Equation (15.56) appears to be at least a reasonable approximation.
For a generalized Maxwell model consisting of n elements (Figure 15.10), the results obtained for a single Maxwell element in Example 15.8 are readily generalized to
and
(the other dynamic properties may be obtained from the two above, as in Example 15.8). Presumably, the Gi and λi determined from, for example, stress-relaxation data can be used in Equations (15.59) and (15.60) to predict dynamic response, and vice versa. Equations (15.28) and (15.29) should be equally applicable to both. Also, the continuous distributions G(λ) and J(λ) as obtained from stress-relaxation and creep measurements are at least approximately interconvertible with G′(ω) and G″(ω) [2, 4, 8, 9].
Techniques used to determine the complex behavior of real viscoelastic materials are covered in Chapter 16.
15.8 Summary
This chapter described spring and dashpot models for the viscoelastic behavior of polymers. While a truly elastic material will stretch and contract back to its original form, most polymers will deform to an extent dependent on the magnitude and duration of an applied stress (shear or elongational). The ability of these materials to resist stretching or shearing is measured through the elastic or shear moduli (E or G). Dynamic mechanical testing breaks down these moduli into two components: a storage modulus that represents elastic behavior and a loss modulus that represents viscous flow or deformation. These moduli change with temperature, representing the material behavior below Tg (glassy), between Tg and Tm (rubbery) and above Tm (flow). Finally, time–temperature superposition was shown to be a useful tool by which the long-time behavior of a polymer can be predicted through measurements covering a range of temperatures.
Problems
| G1 = 109 Pa | η1 = 106 P |
| G2 = 105 Pa | η2 = 106, 108, ∞ P |
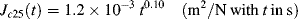
| t < 0 s | τ = 0 Pa |
| 0 ≤ t < 1000 s | τ = 1000 Pa |
| 1000 ≤ t < 2000 s | τ = 1500 Pa |
| 2000 ≤ t s | τ = 0 Pa |
| t < 0 | τ = 0 |
| 0 ≤ t < ts | τ = −τo |
| ts ≤ t < 2ts | τ = +2τo |
| 2ts ≤ t | τ = 0 |
constant), what is the limiting high strain rate (
) modulus.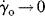
) modulus.Notes
1. Note that this analysis is also applicable to material behavior when subjected to a tensile strain ε(to), with tensile stress σ(t) and relaxation modulus Er(t) or vice versa when an applied tensile stress results in material strain.
1. Reiner, M., Phys. Today, Jan. 1964, p. 62.
2. Ferry, J.D., Viscoelastic Properties of Polymers, 3rd ed., Wiley, New York, 1980.
3. Eirich, F.R. (ed.), Rheology, Vols. 1–4, Academic, New York, 1956–1964.
4. Tobolsky, A.V., Properties and Structure of Polymers, Wiley, New York, 1960.
5. Nielsen, L.E., Mechanical Properties of Polymers and Composites, Vol. 1, Dekker, New York, 1974.
6. Spriggs, T.W., Chem. Eng. Sci., 20, 931 (1965).
7. Rouse, P.E., Jr., J. Chem. Phys. 24, 269 (1956).
8. Schwarzl, F.R., Pure and Appl. Chem. 23, 219 (1970).
9. Schwarzl, F.R., Rheol. Acta, 8, 6 (1969);9, 382 (1970);10, 166 (1971);14, 581 (1975).
10. McKelvey, J.M., Polymer Processing, Wiley, New York, 1962.
11. Cox, W.P. and Merz, E.H., J. Polym. Sci. 28, 619 (1958).