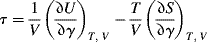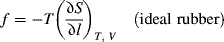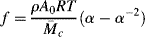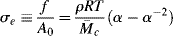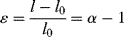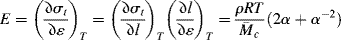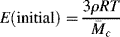Chapter 13
Rubber Elasticity
13.1 Introduction
Natural and synthetic rubbers possess some interesting, unique, and useful mechanical properties. No other materials are capable of reversible extension of 600–700%. No other materials exhibit an increase in strength (elastic modulus) with increasing temperature. It was recognized long ago that vulcanization (crosslinking with sulfur) was necessary for rubber deformation to be completely reversible. We now know that this is a result of the crosslinks that prevent the bulk slippage of the polymer chains past one another, eliminating flow (irrecoverable deformation). More recently, this function of the covalent crosslinks has been achieved using physical (instead of chemical) means and using rigid domains (either glassy or crystalline) within some linear polymers, such as poly(vinyl alcohol). Thus, when a stress is applied to a sample of crosslinked rubber, equilibrium is fairly rapidly established. Once at equilibrium, the properties of the rubber can be described by thermodynamics.
13.2 Thermodynamics of Elasticity
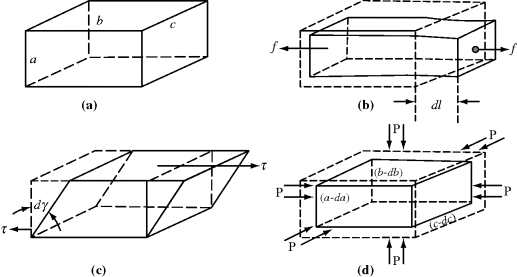
Consider an element of material with dimensions a × b × c, as sketched in Figure 13.1.
Figure 13.1 Types of mechanical deformation: (a) unstressed (b) uniaxial tension (c) pure shear, and (d) isotropic compression.
Applying the first law of thermodynamics to this system yields:
(13.1)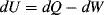 
where dU is the change in the system's internal energy, and dQ and dW are the heat and work exchanged between the system and its surroundings as the system undergoes a differential change. (We have adopted the convention here that work done by the system on the surroundings is positive.)
We will consider three types of mechanical work.
(13.2)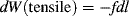 
(13.4)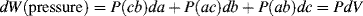 
If the deformation process is assumed to occur reversibly (in a thermodynamic sense), then:
(13.5) 
where S is the system's entropy.
Combining the preceding five equations gives a general relation for the change of internal energy of an element of material undergoing a differential deformation:
Now, let us consider three individual types of deformation.
It is very difficult to carry out tensile experiments at constant volume to obtain the partial derivatives in Equation (13.7). Most experimental tests are carried out at constant pressure (atmospheric), and in general, there is a change in volume with tensile straining. Fortunately, Poisson's ratio is approximately 0.5 for rubbers, so this change in volume is small, and also Equation (13.7) is approximately valid for tensile deformation at constant pressure. For precise work, the hydrostatic pressure must be varied to maintain V constant or theoretical corrections applied to the constant-pressure data to obtain the constant-volume coefficients [1, 2]. In pure shear experiments, V should be constant and Equation (13.8) should be valid.
13.2.1 Types of Elasticity
Equations (13.7)–(13.9) reveal that there are energy (the first term on the right) and entropy (the second term on the right) contributions to the tensile force, shear stress, or isotropic pressure. In polymers, energy elasticity represents the storage of energy resulting from the rotation of bonds (Figure 6.4) and the straining of bond angles and lengths from their equilibrium values. Compare this behavior with other inelastic solids (metals, ceramics); because polymers deform, they are able to store energy temporarily due to any of the three cases above. Interestingly, energy elasticity is almost entirely intramolecular (within single polymer chains) in origin, that is, there is no change in the energy interaction between different polymer chains with deformation [2].
Entropy elasticity is caused due to decrease in entropy upon straining. This can be visualized by considering a single polymer molecule subjected to a tensile stress. In an unstressed state, the molecule is free to adopt an extremely large number of random, “balled-up” configurations (Figure 13.2a) switching from one to another through rotation about the bonds. Now imagine the molecule to be stretched out under the application of a tensile force (Figure 13.2b). It is obvious that there are far fewer configurational possibilities, and the more it is stretched, the fewer there are. Now, S = k ln Ω, where k is the Boltzmann's constant and Ω is the number of configurational possibilities, so stretching decreases the entropy (increases the molecular order). Raising the temperature has precisely the opposite effect. The added thermal energy of the chain segments increases the intensity of their lateral vibrations, favoring a return to the more random or higher entropy state. This tends to pull the extended chain ends together, giving rise to a retractive force.
Figure 13.2 The effects of stress and temperature on chain configurations.
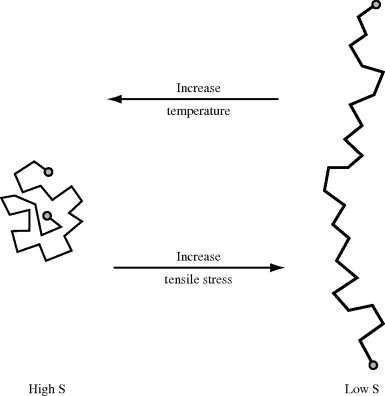
It should be obvious from the discussion above that to exhibit significant entropy elasticity, the material must be above its glass transition temperature and cannot have appreciable amounts of crystallinity.
13.2.2 The “Ideal” Rubber
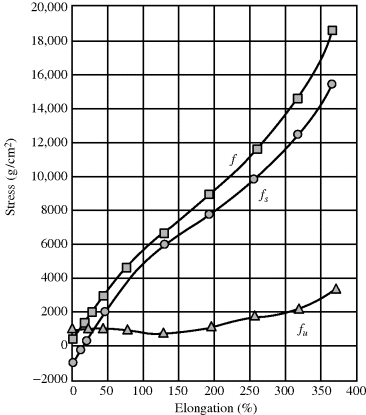
To demonstrate the “ideal” rubber, let us start with a gas subjected to an isotropic pressure, where the energy term in Equation (13.9) arises from the change in the intermolecular forces with volume and the entropy term arises from the increased space (and therefore greater “disorder”) the molecules gain with increased volume. In an ideal gas, there are no intermolecular forces, (∂U/∂V)T = 0. By analogy, in an ideal rubber, (∂U/∂l)T,V = (∂U/∂γ)T,V = 0 and elasticity arises only from entropy effects. For many gases around room temperature and above, and around atmospheric pressure and below, (∂U/∂V)T < T (∂S/∂V)T, the ideal gas law is a good approximation. Similarly, as illustrated in Figure 13.3 [3], under some circumstances, (∂U/∂l)T,V < T(∂S/∂l)T,V for rubbers and they behave just as ideal rubbers.
Figure 13.3 Energy (fV) and entropy (fS) contributions to tensile stress in natural rubber at 20 °C. Reprinted from Anthony et al. [3] Copyright 1942 by the American Chemical Society. Reprinted by permission of the copyright owner.
13.2.3 Effects of Temperature at Constant Force
Now let us consider what happens to the length of a piece of rubber when its temperature is changed while a weight is suspended from it, that is, when it is maintained at a constant tensile force, assuming constant volume (an approximation, in the usual constant-pressure experiment), dU = TdS + f dl. Solving for dl, dividing by dT, and restricting to constant f as well as V gives
(13.10) 
As before, the first term on the right represents energy elasticity and the second represents entropy elasticity. Since internal energy increases with temperature, the partial derivative in the energy term is positive, as is f. The energy term, therefore, causes an increase in length with temperature (positive contribution to (∂l/∂T)f,V). This is the normal thermal expansion observed in all materials (ceramics, metals, glasses, etc.), reflecting the increase in the average distance between atomic centers with temperature. All factors in the entropy term are positive, however, and since it is preceded by a negative sign, it gives rise to a decrease in length with increasing temperature. In rubbers, where the entropy effect overwhelms the normal thermal expansion, this is what is actually observed. In all other materials, where the structural units are confined to a single arrangement (e.g., the atoms in a crystal lattice cannot readily interchange), the entropy term is small. To visualize this, consider Figure 13.2 and the large amount of entropy gained by balling up a polymer chain.
The magnitude of the entropy contraction in rubbers is typically much greater than the thermal expansion of other materials. An ordinary rubber band will contract an inch or so when heated to 300 °F under stress, while the expansion of a piece of metal of similar length over a similar temperature range would not be noticeable without a microscope. According to a well-known metallurgist [4], “Polymers are all entropy.”
13.2.4 Effects of Temperature at Constant Length
It is interesting to consider what happens to the force in a piece of rubber when it is heated while stretched to a constant length. The exact thermodynamic Maxwell relation
can be used to describe approximately the usual experiment conducted at constant pressure. A better approximation to the constant pressure experiment is
where α = l/lo is the extension ratio, the ratio of stretched to unstretched length at a particular temperature. Combining Equations (13.11a) and (13.7) gives
Now, both f and T are positive, so the first term on the right causes the force to increase with temperature, a result of the greater thermal agitation (tendency toward higher entropy) of the extended chains. The partial derivative in the second term is usually (but not always!) positive, as energy is stored like a spring when it is extended. With the negative sign in front, this term predicts a relaxation of the tensile force with increasing temperature. Again, the second term reflects the ordinary thermal expansion obtained with all materials, but in rubbers, at reasonably large values of f, it is overshadowed by the first (entropy) term and the force increases with temperature. For an ideal rubber, (∂U/∂l)T,V = 0, and integration of Equation (13.12) at constant volume yields
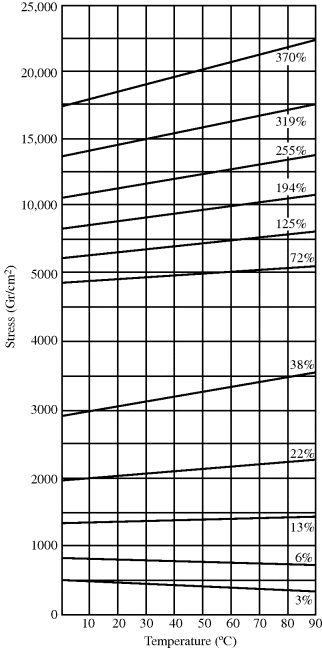
This is analogous to the linearity between P and T in an ideal gas at constant V. These observations are confirmed in Figure 13.4. When the polymer is not stretched much (e.g., the 3% elongation line), the polymer softens as the temperature is raised. This negative slope at low elongations arises from the predominance of thermal expansion when elongation, and hence f, is low. Note that there is an intermediate elongation, the thermoelastic inversion point (at approximately 13% elongation in Figure 13.4), at which force is essentially independent of temperature, where thermal expansion and entropy contraction balance. In the upper portions of the graph, the highly elongated samples require more stress to maintain greater elongation ratios, and the stress goes up appreciably with temperature, as the entropic terms dominate over thermal expansion, causing an even greater force of the polymer trying to coil back from its extended state.
Figure 13.4 Force versus temperature in natural rubber maintained at constant extension (% relative to length at 20 °C) [3]. Copyright 1942 by the American Chemical Society. Reprinted by permission of the copyright owner.
13.3 Statistics of Ideal Rubber Elasticity [1,2,5]
A typical rubber consists of long chains connected by short crosslinks every few hundred carbon atoms. The chain segments between crosslinks are known as network chains. (These segments are characterized by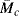 
, the molecular weight between crosslinks.) The change in entropy upon stretching a sample containing N moles of network chains is
(13.14)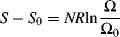 
where the subscript 0 refers to the unstretched state, Ω is the number of configurations available to the N moles of network chains, and R is the gas constant. By statistically evaluating the Ω's, it is possible to show that for constant-volume stretching,
where α = l/lo is the extension ratio. (Newer theories give somewhat different results [2], but this is adequate for our purposes.)
For an ideal rubber, in which the tensile force is given by
differentiation of Equation (13.15) and insertion into Equation (13.16) yields
(13.17)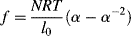 
Also,
(13.18) 
where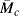 
is the number-average molecular weight of the chain segments between consecutive crosslinks, ρ is the density, and A is the cross-sectional area of the sample (since the volume change in stretching a piece of rubber is negligible, Aolo = Al). Therefore,
The engineering tensile stress, σe, is defined as the tensile force divided by the initial cross-sectional area of the sample Ao and is, therefore,
and the true tensile stress σt, the tensile force over the actual area A at length l, is
Since the tensile strain ε is
the slope of the true stress–strain curve (which gives the tangent Young's modulus) is
and the initial modulus (as α → 1) for an ideal rubber becomes
The modulus is representative of the strength of a material (or how much resistance the material will give) when a force (axial tension, shear stress) is applied.
Equations (13.19)–(13.24) point out two important concepts: (1) the force (or modulus) in an ideal rubber sample held at a particular strain increases in proportion to the absolute temperature (in agreement with Eq. (13.13)), and (2) the force is inversely proportional to the molecular weight of the chain segments between crosslinks. Thus, increased crosslinking, which reduces 
, is an effective means of stiffening a rubber. Equation (13.24) is often used to obtain 
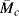from mechanical tests and thereby evaluate the efficiency of various crosslinking procedures.
Even noncrosslinked polymers exhibit rubbery behavior above their Tg values for limited periods of time. This is due to mechanical (physical) entanglements acting as temporary crosslinks; 
then represents the average length of the chain segments between those entanglements.
When compared with experimental data, Equation (13.19) does a reasonably good job in compression but begins to fail at extension ratios a greater than about 1.5, where the experimental force becomes greater than predicted. There are a number of reasons for this. First, Equation (13.15) is based on the assumption of a Gaussian distribution of network chains. This assumption fails at high elongations, and it is also in error if crosslinks are formed when chains are in a strained configuration. Second, it does not take into account the presence of chain end segments, which do not contribute to the support of stress. Third, some rubbers (natural, in particular) begin to crystallize as a result of chain orientation at high elongations. (Orientation reduces ΔSm and raises Tm above the test temperature. See Example 6.6.) This causes the stress–strain curve to shoot up markedly. Some theoretical modifications to the theory are available that improve on the accuracy of these equations, for example, Mark and Erman [2] address the issues of non-Gaussian distribution of chain length and factor at the chain ends.
It is also important to keep in mind that in practice, rubbers are rarely used in the form of pure polymer. They are almost always reinforced with carbon black, and often contain other fillers, plasticizing, and extending oils, etc., all of which influence the stress–strain properties, and are not considered in the theories discussed here.
13.4 Summary
Rubbery materials are a class of crosslinked polymers that are characterized by their response to mechanical stimuli (stretching, compression, etc.). This chapter explained the unusual behavior of polymers through the (often) competing combination of internal energy and entropic energy. The thermodynamic analysis used in this chapter served to develop equations to quantifiably predict the behavior of rubbers in stress environments and even use rubber elasticity experiments to estimate 
. This chapter served as an introduction to the thermodynamic basis for rubber elasticity; the practical implications of this behavior will be discussed in detail in the beginning of Chapter 15. While this chapter introduced the behavior of purely elastic materials, the next chapter covers the opposite extreme of viscous polymer melts (and solutions). These two concepts will be brought together in Chapter 15 on viscoelastic materials, which have features of both elastic solid rubbers and viscous liquid melts. Other texts are available for more in-depth study of rubber elasticity [1, 2].
Problems
| f, lb | l, cm |
| 0 | 2.42 |
| 0.33 | 2.80 |
| 0.54 | 3.08 |
| 0.79 | 3.58 |
| 1.10 | 3.97 |
| 1.36 | 4.70 |
| 1.66 | 5.60 |
| 1.89 | 6.42 |
| 2.20 | 7.28 |
| 2.68 | 8.45 |
| 3.07 | 9.30 |
. How well does Equation (13.19) fit these data? Estimate the average number of repeating units between crosslinks, 
and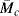 
.
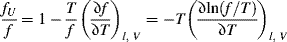
1. Flory, P.J., Principles of Polymer Chemistry, Cornell UP, Ithaca, NY, 1953, Chapter 11.
2. Mark, J.E. and Erman, B. Rubberlike Elasticity: A Molecular Primer, Wiley, New York, 1988.
3. Anthony, R.L., R.H. Caston, and E. Guth, J. Phys. Chem. 46, 826 (1942).
4. Paxton, H.W., personal communication.
5. Tobolsky, A.V., Properties and Structure of Polymers, Wiley, New York, 1960, Chapter 2.