2 Nature: or growth of living matter
Perhaps the most remarkable attribute of natural growth is how much diversity is contained within the inevitable commonality dictated by fundamental genetic makeup, metabolic processes, and limits imposed by combinations of environmental factors. Trajectories of all organismic growth must assume the form of a confined curve. As already noted, many substantial variations within this broad category have led to the formulation of different growth functions devised in order to find the closest possible fits for specific families, genera or species of microbes, plants or animals or for individual species. S-shaped curves are common, but so are those conforming to confined exponential growth, and there are (both expected and surprising) differences between the growth of individuals (and their constituent parts, from cells to organs) and the growth of entire populations.
Decades-long neglect of Verhulst’s pioneering growth studies postponed quantitative analyses of organismic growth until the early 20th century. Most notably, in his revolutionary book Darwin did not deal with growth in any systematic manner and did not present any growth histories of specific organisms. But he noted the importance of growth correlation—“when slight variations in any one part occur, and are accumulated through natural selection, other parts become modified” (Darwin 1861, 130)—and, quoting Goethe (“in order to spend on one side, nature is forced to economise on the other side”), he stressed a general growth principle, namely that “natural selection will always succeed in the long run in reducing and saving every part of the organization, as soon as it is rendered superfluous, without by any means causing some other part to be largely developed in a corresponding degree” (Darwin 1861, 135).
This chapter deals with the growth of organisms, with the focus on those living forms that make the greatest difference for the functioning of the biosphere and for the survival of humanity. This means that I will look at cell growth only when dealing with unicellular organisms, archaea and bacteria—but will not offer any surveys of the genetic, biochemical and bioenergetic foundations of the process (both in its normal and aberrative forms) in higher organisms. Information on such cell growth—on its genetics, controls, promoters, inhibitors, and termination—is available in many survey volumes, including those by Studzinski (2000), Hall et al. (2004), Morgan (2007), Verbelen and Vissenberg (2007), Unsicker and Krieglstein (2008) and Golitsin and Krylov (2010).
The biosphere’s most numerous, oldest and simplest organisms are archaea and bacteria. These are prokaryotic organisms without a cell nucleus and without such specialized membrane-enclosed organelles as mitochondria. Most of them are microscopic but many species have much larger cells and some can form astonishingly large assemblages. Depending on the species involved and on the setting, the rapid growth of single-celled organisms may be highly desirable (a healthy human microbiome is as essential for our survival as any key body organ) or lethal. Risks arise from such diverse phenomena as the eruptions and diffusion of pathogens—be they infectious diseases affecting humans or animals, or viral, bacterial and fungal infestations of plants—or from runaway growth of marine algae. These algal blooms can kill other biota by releasing toxins, or when their eventual decay deprives shallow waters of their normal oxygen content and when anaerobic bacteria thriving in such waters release high concentrations of hydrogen sulfide (UNESCO 2016).
The second subject of this chapter, trees and forests—plant communities, ecosystems and biomes that are dominated by trees but that could not be perpetuated without many symbioses with other organisms—contain most of the world’s standing biomass as well as most of its diversity. The obvious importance of forests for the functioning of the biosphere and their enormous (albeit still inadequately appreciated and hugely undervalued) contribution to economic growth and to human well-being has led to many examinations of tree growth and forest productivity. We now have a fairly good understanding of the overall dynamics and specific requirements of those growth phenomena and we can also identify many factors that interfere with them or modify their rates.
The third focus of this chapter will be on crops, plants that have been greatly modified by domestication. Their beginnings go back to 8,500 BCE in the Middle East, with the earliest domesticates being einkorn and emmer wheat, barley, lentils, peas, and chickpeas. Chinese millet and rice were first cultivated between 7,000 and 6,000 BCE and the New World’s squash was grown as early as 8,000 BCE (Zohary et al. 2012). Subsequent millennia of traditional selection brought incremental yield gains, but only modern crop breeding (hybrids, short-stalked cultivars), in combination with improved agronomic methods, adequate fertilization, and where needed also irrigation and protection against pests and weeds, has multiplied the traditional crop yields. Further advances will follow from the future deployment of genetically engineered plants.
In the section on animal growth I will look first at the individual development and population dynamics of several important wild species but most of it will be devoted to the growth of domestic animals. Domestication has changed the natural growth rates of all animals reared for meat, milk, eggs, and wool. Some of these changes have resulted in much accelerated maturation, others have also led to commercially desirable but questionable body malformations. The first instance is illustrated with pigs, the most numerous large meat animals. In traditional Asian settings, animals were usually left alone to fend for themselves, rooting out and scavenging anything edible (pigs are true omnivores). As a result, it may have taken more than two years for them to reach slaughter weight of at least 75–80 kg. In contrast, modern meat breeds kept in confinement and fed a highly nutritious diet will reach slaughter weight of 100 kg in just 24 weeks after the piglets are weaned (Smil 2013c). Heavy broiler chickens, with their massive breast muscles, are the best example of commercially-driven body malformations (Zuidhof et al. 2014).
The chapter will close with the examination of human growth and some of its notable malfunctions. I will first outline the typical progress of individual growth patterns of height and body mass from birth to the end of adolescence and the factors that promote or interfere with the expected performance. Although the global extent of malnutrition has been greatly reduced, shortages of food in general or specific nutrients in particular still affect too many children, preventing their normal physical and mental development. On the opposite end of the human growth spectrum is the worrisome extent of obesity, now increasingly developing in childhood. But before turning to more detailed inquiries into the growth of major groups of organisms, I must introduce the metabolic theory of ecology. This theory outlines the general approach linking the growth of all plants and all animals to their metabolism, and it has been seen by some as one of the greatest generalizing advances in biology while others have questioned its grand explanatory powers (West et al. 1997; Brown et al. 2004; Price et al. 2012). Its formulation arises from the fact that many variables are related to body mass according to the equation y = aM b where y is the variable that is predicted to change with body mass M, a is a scaling coefficient and b is the slope of allometric exponent. The relationship becomes linear when double-logged: log y = log a + b log M.
The relationship of body size to metabolic characteristics has long been a focus of animal studies, but only when metabolic scaling was extended to plants did it become possible to argue that the rates of biomass production and growth of all kinds of organisms, ranging from unicellular algae to the most massive vertebrates and trees, are proportional to metabolic rate, which scales as the ¾ power of body mass M (Damuth 2001). Metabolic scaling theory for plants, introduced by West et al. (1997), assumes that the gross photosynthetic (metabolic) rate is determined by potential rates of resource uptake and subsequent distribution of resources within the plant through branching networks of self-similar (fractal) structure.
The original model was to predict not only the structural and functional properties of the vertebrate cardiovascular and respiratory system, but also those of insect tracheal tubes and plant vascular system. Relying on these assumptions, Enquist et al. (1999) found that annual growth rates for 45 species of tropical forest trees (expressed in kg of dry matter) scale as M3/4 (that is, with the same exponent as the metabolism of many animals) and hence the growth rates of diameter D scale as D1/3. Subsequently, Niklas and Enquist (2001) confirmed that a single allometric pattern extends to autotrophic organisms whose body mass ranged over 20 orders of magnitude and whose lengths (either cell diameter or plant height) spanned over 22 orders of magnitude, from unicellular algae to herbs and to monocotyledonous, dicotyledonous, and conifers trees (figure 2.1).

Allometric pattern of autotrophic mass and growth rate. Based on Niklas and Enquist (2001).
And a few years later Enquist et al. (2007) derived a generalized trait-based model of plant growth. The ¾ scaling also applies to light-harvesting capacity measured either as the pigment content of algal cells or as foliage phytomass of plants. As a result, the relative growth rate of plants decreases with increasing plant size as M−1/4, and primary productivity is little affected by species composition: an identical density of plants with similar overall mass will fix roughly the same amount of carbon. The uniform scaling also means that the relative growth rate decreases with increasing plant size as M−1/4. Light-harvesting capacity (chlorophyll content of algal cells or foliage in higher plants) also scales as M3/4, while plant length scales as M1/4.
Niklas and Enquist (2001) had also concluded that plants—unlike animals that have similar allometric exponents but different normalization constants (different intercepts on a growth graph)—fit into a single allometric pattern across the entire range of their body masses. This functional unity is explained by the reliance on fractal-like distribution networks required to translocate photosynthate and transpire water: their evolution (hierarchical branching and shared hydro- and biomechanics) had maximized metabolic capacity and efficiency by maximizing exchange surfaces and throughputs while minimizing transport distances and transfer rates (West et al. 1999).
But almost immediately ecologists began to question the universality of the metabolic scaling theory in general, and the remarkable invariance of exponents across a wide range of species and habitats in particular. Based on some 500 observations of 43 perennials species whose sizes spanned five of the 12 orders of magnitude of size in vascular plants, Reich et al. (2006) found no support for ¾-power scaling of plant nighttime respiration, and hence its overall metabolism. Their findings supported near-isometric scaling, that is exponent ~ 1, eliminated the need for fractal explanations of the ¾-power scaling and made a single size-dependent law of metabolism for plants and animals unlikely.
Similarly, Li et al. (2005), using a forest phytomass dataset for more than 1,200 plots representing 17 main forest types across China, found scaling exponents ranging from about 0.4 (for boreal pine stands) to 1.1 (for evergreen oaks), with only a few sites conforming to the ¾ rule, and hence no convincing evidence for a single constant scaling exponent for the phytomass-metabolism relationship in forests. And Muller-Landau et al. (2006) examined an even large data set from ten old-growth tropical forests (encompassing more than 1.7 million trees) to show that the scaling of growth was clearly inconsistent with the predictions based on the metabolic theory, with only one of the ten sites (a montane forest at high elevation) coming close to the expected value.
Their results were consistent with an alternative model that also considered competition for light, the key photosynthetic resource whose availability commonly limits tropical tree growth. Scaling of plant growth that depends only on the potential for capturing and redistributing resources is wrong, and there are no universal scaling relationships of growth (as well as of tree mortality) in tropical forests. Coomes and Allen (2009) confirmed these conclusions by demonstrating how Enquist et al. (1999), by failing to consider asymmetric competition for light, underestimated the mean scaling exponent for tree diameter growth: rather than 0.33, its average across the studied Costa Rican forest species should be 0.44.
Rather than testing the metabolic theory’s predictions, Price at al. (2012, 1472) looked at its physical and chemical foundations and at its simplifying assumptions and concluded that there is still no “complete, universal and causal theory that builds from network geometry and energy minimization to individual, species, community, ecosystem and global level patterns.” They noted that the properties of distribution model are mostly specific to the cardiovascular system of vertebrates, and that empirical data offer only limited support for the model, and cited Dodds et al. (2001), who argued that ¾ scaling could not be derived from hydraulic optimization assumed by West et al. (1997). Consequently, these might be the best conclusions regarding the metabolic scaling theory: it provides only coarse-grained insight by describing the central tendency across many orders of magnitude; its key tenet of ¾ scaling is not universally valid as it does not apply to all mammals, insects or plants; and it is only a step toward a truly complete causal theory that, as yet, does not exist. Not surprisingly, the growth of organisms and their metabolic intensity are far too complex to be expressed by a single, narrowly bound, formula.
Microorganisms and Viruses
If the invisibility without a microscope were the only classification criterion then all viruses would be microorganisms—but because these simple bundles of protein-coated nucleic acids (DNA and RNA) are acellular and are unable to live outside suitable host organisms they must be classified separately. There are some multicellular microorganisms, but most microbes—including all archaea and bacteria—are unicellular. These single-celled organisms are the simplest, the oldest, and by far the most abundant forms of life—but their classification is anything but simple. The two main divisions concern their structure and their metabolism. Prokaryotic cells do not have either a nucleus or any other internal organelles; eukaryotic cells have these membrane-encased organelles.
Archaea and Bacteria are the two prokaryotic domains. This division is relatively recent: Woese et al. (1990) assigned all organisms to three primary domains (superkingdom categories) of Archaea, Bacteria, and Eucarya, and the division relies on sequencing base pairs in a universal ribosomal gene that codes for the cellular machinery assembling proteins (Woese and Fox 1977). Only a tiny share of eukaryotes, including protozoa and some algae and fungi, are unicellular. The basic trophic division is between chemoautotrophs (able to secure carbon from CO2) and chemoheterotrophs, organisms that secure their carbon by breaking down organic molecules. The first group includes all unicellular algae and many photosynthesizing bacteria, the other metabolic pathway is common among archaea, and, of course, all fungi and animals are chemoheterotrophs.
Further divisions are based on a variety of environmental tolerances. Oxygen is imperative for growth of all unicellular algae and many bacteria, including such common genera as Bacillus and Pseudomonas. Facultative anaerobes can grow with or without the element and include such commonly occurring bacterial genera as Escherichia, Streptococcus and Staphylococcus, as well as Saccharomyces cerevisiae, fungus responsible for alcoholic fermentation and raised dough. Anaerobes (all methanogenic archaea and many bacterial species) do not tolerate oxygen’s presence. Tolerances of ambient temperature divide unicellular organisms among psychrophilic species able to survive at low (even subzero) temperatures, mesophilic species that do best within a moderate range, and thermophiles that can grow and reproduce at temperatures above 40°C.
Psychrophiles include bacteria causing food spoilage in refrigerators: Pseudomonas growing on meat, Lactobacillus growing on both meat and dairy products, and Listeria growing on meat, seafood, and vegetables at just 1–4°C. Some species metabolize even in subzero temperatures, either in supercooled cloud droplets, in brine solutions or ice-laden Antarctic waters whose temperature is just below the freezing point (Psenner and Sattler 1998). Before the 1960s no bacterium was considered more heat-tolerant than Bacillus stearothermophilus, able to grow in waters of 37–65°C; it was the most heat-tolerant known bacterium before the discoveries of hyperthermophilic varieties of Bacillus and Sulfolobus raised the maximum to 85°C during the 1960s and then to 95–105°C for Pyrolobus fumarii, an archaeon found in the walls of deep-sea vent chimneys spewing hot water; moreover, Pyrolobus stops growing in waters below 90°C (Herbert and Sharp 1992; Blöchl et al. 1997; Clarke 2014).
Extremophilic bacteria and archaea have an even larger tolerance range for highly acidic environments. While most species grow best in neutral (pH 7.0) conditions, Picrophilus oshimae has optimal growth at pH 0.7 (more than million times more acid than the neutral environment), a feat even more astonishing given the necessity to maintain internal (cytoplasmic) pH of all bacteria close to 6.0. Bacteria living in acidic environments are relatively common at geothermal sites and in acid soils containing pyrites or metallic sulfides and their growth is exploited commercially to extract copper from crushed low-grade ores sprinkled with acidified water.
In contrast, alkaliphilic bacteria cannot tolerate even neutral environments and grow only when pH is between 9 and 10 (Horikoshi and Grant1998). Such environments are common in soda lakes in arid regions of the Americas, Asia, and Africa, including Mono and Owens lakes in California. Halobacterium is an extreme alkaliphile that can tolerate pH as high as 11 and thrives in extremely salty shallow waters. One of the best displays of these algal blooms, with characteristic red and purple shades due to bacteriorhodopsin, can be seen in dike-enclosed polders in the southern end of San Francisco Bay from airplanes approaching the city’s airport.
And there are also polyextremophilic bacteria able to tolerate several extreme conditions. Perhaps the best example in this category is Deinococcus radiodurans, commonly found in soils, animal feces and sewage: it survives extreme doses of radiation, ultraviolet radiation, desiccation and freeze-drying thanks to its extraordinary capacity to repair damaged DNA (White et al. 1999; Cox and Battista 2005). At the same time, for some bacterial growth even small temperature differences matter: Mycobacterium leprae prefers to invade first those body parts that are slightly cooler and that is why leprotic lesions often show up first in the extremities as well as ears. Not surprisingly, optimum growth conditions for common bacterial pathogens coincide with the temperature of the human body: Staphylococcus aureus responsible for skin and upper respiratory infections prefers 37°C as does Clostridium botulinum (producing dangerous toxin) and Mycobacterium tuberculosis. But Escherichia coli, the species most often responsible for the outbreaks of diarrhea and for urinary tract infections, has optimum growth at 40°C.
Microbial Growth
Microbial growth requires essential macro- and micronutrients, including nitrogen (indispensable constituent of amino acids and nucleic acids), phosphorus (for the synthesis of nucleic acids, ADP and ATP), potassium, calcium, magnesium, and sulfur (essential for S-containing amino acids). Many species also need metallic trace elements, above all copper, iron, molybdenum, and zinc, and must also obtain such growth factors as vitamins of the B group from their environment. Bacterial growth can be monitored best by inoculating solid (agar, derived from a polysaccharide in some algal cell walls) or liquid (nutrient broth) media (Pepper et al. 2011).
Monod (1949) outlined the succession of phases in the growth of bacterial cultures: initial lag phase (no growth), acceleration phase (growth rate increasing), exponential phase (growth rate constant), retardation phase (growth rate slowing down), and stationary phase (once again, no growth, in this case as a result of nutrient depletion or presence of inhibitory products) followed by the death phase. This generalized sequence has many variations, as one or several phases may be either absent or last so briefly as to be almost imperceptible; at the same time, trajectories may be more complex than the idealized basic outline. Because the average size of growing cells may vary significantly during different phases of their growth, cell concentration and bacterial density are not equivalent measures but in most cases the latter variable is of the greater importance.
The basic growth trajectory of cultured bacterial cell density is obviously sigmoidal: figure 2.2 shows the growth of Escherichia coli O157:H7, a commonly occurring serotype that contaminates raw food and milk and produces Shiga toxin causing foodborne colonic escherichiosis. Microbiologists and mathematicians have applied many standard models charting sigmoidal growth—including autocatalytic, logistic and Gompertz equations—and developed new models in order to find the best fits for observed growth trajectories and to predict the three key parameters of bacterial growth, the duration of the lag phase, the maximum specific growth rate, and the doubling time (Casciato et al. 1975; Baranyi 2010; Huang 2013; Peleg and Corradini 2011).

Logistic growth of Escherichia coli O157:H7. Plotted from data in Buchanan et al. (1997).
Differences in overall fit among commonly used logistic-type models are often minimal. Peleg and Corradini (2011) showed that despite their different mathematical structure (and also despite having no mechanistic interpretation), Gompertz, logistic, shifted logistic and power growth models had excellent fit and could be used interchangeably when tracing experimental isothermal growth of bacteria. Moreover, Buchanan et al. (1997) found that capturing the growth trajectory of Escherichia coli does not require curve functions and can be done equally well by a simple three-phase linear model. A logical conclusion is that the simplest and the most convenient model should be chosen to quantify common bacterial growth.
Under optimal laboratory conditions, the ubiquitous Escherichia coli has generation time (the interval between successive divisions) of just 15–20 minutes, its synchronous succinate-grown cultures showed generation time averaging close to 40 minutes (Plank and Harvey 1979)—but its doubling takes 12–24 hours in the intestinal tract. Experiments by Maitra and Dill (2015) show that at its replication speed limit (fast-growth mode when plentiful nutrition is present) Escherichia duplicates all of its proteins quickly by producing proportionately more ribosomes—protein complexes that a cell makes to synthesize all of the cell’s proteins—than other proteins. Consequently, it appears that energy efficiency of cells under fast growth conditions is the cell’s primary fitness function.
Streptococcus pneumoniae, responsible for sinusitis, otitis media, osteomyelitis, septic arthritis, endocarditis, and peritonitis, has generation time of 20–30 minutes. Lactobacillus acidophilus—common in the human and animal gastrointestinal tract and present (together with other species of the same genus, Lactobacillus bulgaricus, bifidus, casei) in yoghurt and buttermilk—has generation time of roughly 70–90 minutes. Rhizobium japonicum, nitrogen-fixing symbiont supplying the nutrient to leguminous crops, divides slowly, taking up to eight hours for a new generation. In sourdough fermentation, industrial strains of Lactobacillus used in commercial baking reach their peak growth between 10–15 hours after inoculation and cease growing 20–30 hours later (Mihhalevski et al. 2010), and generation time for Mycobacterium tuberculosis averages about 12 hours.
Given the enormous variety of biospheric niches inhabited by microorganisms, it comes as no surprise that the growth of archaea, bacteria, and unicellular fungi in natural environments—where they coexist and compete in complex assemblages—can diverge greatly from the trajectories of laboratory cultures, and that the rates of cellular division can range across many orders of magnitude. The lag phases can be considerably extended when requisite nutrients are absent or available only in marginal amounts, or because they lack the capacity to degrade a new substrate. The existing bacterial population may have to undergo the requisite mutations or a gene transfer to allow further growth.
Measurements of bacterial growth in natural environments are nearly always complicated by the fact that most species live in larger communities consisting of other microbes, fungi, protozoa, and multicellular organisms. Their growth does not take place in monospecific isolation and it is characterized by complex population dynamics, making it very difficult to disentangle specific generation times not only in situ but also under controlled conditions. Thanks to DNA extraction and analysis, we came to realize that there are entire bacterial phyla (including Acidobacteria, Verrucomicrobia, and Chloroflexi in soils) prospering in nature but difficult or impossible to grow in laboratory cultures.
Experiments with even just two species (Curvibacter and Duganella) grown in co-culture indicate that their interactions go beyond the simple case of direct competition or pairwise games (Li et al. 2015). There are also varied species-specific responses to pulsed resource renewal: for example, coevolution with Serratia marcescens (an Enterobacter often responsible for hospital-acquired infections) caused Novosphingobium capsulatum clones (able to degrade aromatic compounds) to grow faster, while the evolved clones of Serratia marcescens had a higher survival and slower growth rate than their ancestor (Pekkonen et al. 2013).
Decomposition rates of litterfall (leaves, needles, fruits, nuts, cones, bark, branches) in forests provide a revealing indirect measure of different rates of microbial growth in nature. The process recycles macro- and micronutrients. Above all, it controls carbon and nitrogen dynamics in soil, and bacteria and fungi are its dominant agents on land as well as in aquatic ecosystems (Romaní et al. 2006; Hobara et al. 2014). Their degradative enzymes can eventually dismantle any kind of organic matter, and the two groups of microorganisms act in both synergistic and antagonistic ways. Bacteria can decompose an enormous variety of organic substrates but fungi are superior, and in many instances, the only possible decomposers of lignin, cellulose, and hemicellulose, plant polymers making up woody tissues and cell walls.
Decomposition of forest litter requires the sequential breakdown of different substrates (including waxes, phenolics, cellulose, and lignin) that must be attacked by a variety of metallomic enzymes, but microbial decomposers live in the world of multiple nutrient limitations (Kaspari et al. 2008). Worldwide comparison, using data from 110 sites, confirmed the expected positive correlation of litter decomposition with decreasing latitude and lignin content and with increasing mean annual temperature, precipitation, and nutrient concentration (Zhang et al. 2008). While no single factor was responsible for a high degree of explanation, the combination of total nutrients and carbon: nitrogen ratio explained about 70% of the variation in the litter decomposition rates. In relative terms, decomposition rates in a tropical rain forest were nearly twice as high as in a temperate broadleaved forest and more than three times as fast as in a coniferous forest. Litter quality, that is the suitability of the substrate for common microbial metabolism, is clearly the key direct regulator of litter decomposition at the global scale.
Not surprisingly, natural growth rates of some extremophilic microbes can be extraordinarily slow, with generation times orders of magnitude longer than is typical for common soil or aquatic bacteria. Yayanos et al. (1981) reported that an obligate barophilic (pressure-tolerant) isolate, retrieved from a dead amphipod Hirondella gigas captured at the depth of 10,476 meters in Mariana Trench (the world’s deepest ocean bottom), had the optimal generation times of about 33 hours at 2°C under 103.5 MPa prevailing at its origin. Similarly, Pseudomonas bathycetes, the first species isolated from a sediment sample taken from the trench, has generation time of 33 days (Kato et al. 1998). In contrast, generation times of thermophilic and piezophilic (pressure-tolerant) microbes in South Africa’s deep gold mines (more than 2 km) are estimated to be on the order of 1,000 years (Horikoshi 2016).
And then there are microbes buried deep in the mud under the floor of the deepest ocean trenches that can grow even at gravity more than 400,000 times greater than at the Earth’s surface but “we cannot estimate the generation times of [these] extremophiles … They have individual biological clocks, so the scale of their time axis will be different” (Horikoshi 2016, 151). But even the span between 20 minutes for average generation time of common gut and soil bacteria and 1,000 years of generation time for barophilic extremophiles amounts to the difference of seven orders of magnitude, and it is not improbable that the difference may be up to ten orders of magnitude for as yet undocumented extremophilic microbes.
Finally, a brief look at recurrent marine microbial growths that are so extensive that they can be seen on satellite images. Several organisms—including bacteria, unicellular algae and eukaryotic dinoflagellates and coccolithophores—can multiply rapidly and produce aquatic blooms (Smayda 1997; Granéli and Turner 2006). Their extent may be limited to a lake, a bay, or to coastal waters but often they cover areas large enough to be easily identified on satellite images (figure 2.3). Moreover, many of these blooms are toxic, presenting risks to fish and marine invertebrates. One of the most common blooms is produced by species of Trichodesmium, cyanobacteria growing in nutrient-poor tropical and subtropical oceans whose single cells with gas vacuoles form macroscopic filaments and filament clusters of straw-like color but turning red in higher concentrations.

Algal bloom in the western part of the Lake Erie on July 28, 2015. NASA satellite image is available at https://
The pigmentation of large blooms of Trichodesmium erythraeum has given the Red Sea its name, and recurrent red blooms have a relatively unique spectral signature (including high backscatter caused by the presence of gas vesicles and the absorption of its pigment phycoerythrin) that makes them detectable by satellites (Subramaniam et al. 2002). Trichodesmium also has an uncommon ability to fix nitrogen, that is to convert inert atmospheric dinitrogen into ammonia that can be used for its own metabolism and to support growth of other marine organisms: it may generate as much as half of all organic nitrogen present in the ocean, but because nitrogen fixation cannot proceed in aerobic conditions it is done inside the cyanobacteria’s special heterocysts (Bergman et al. 2012). Trichodesmium blooms produce phytomass strata that often support complex communities of other marine microorganisms, including other bacteria, dinoflagellates, protozoa, and copepods.
Walsh et al. (2006) outlined a sequence taking place in the Gulf of Mexico whereby a phosphorus-rich runoff initiates a planktonic succession once the nutrient-poor subtropical waters receive periodic depositions of iron-rich Saharan dust. The availability of these nutrients allows Trichodesmium to be also a precursor bloom for Karenia brevis, a unicellular dinoflagellate infamous for causing toxic red tides. This remarkable sequence, an excellent example of complex preconditions required to produce high rates of bacterial growth, is repeated in other warm waters receiving more phosphorus-rich runoff from fertilized cropland and periodic long-range inputs of iron-rich dust transported from African and Asian deserts. As a result, the frequency and extent of red tides have become more common during the 20th century. They are now found in waters ranging from the Gulf of Mexico to Japan, New Zealand, and South Africa.
Pathogens
Three categories of microbial growth have particularly damaging consequences: common pathogens that infect crops and reduce their harvests; a wide variety of microbes that increase human morbidity and mortality; and microorganisms and viruses responsible for population-wide infections (epidemics) and even global impacts (pandemics). A few exceptions aside, the names of bacterial and fungal plant pathogens are not recognized outside expert circles. The most important plant pathogenic bacteria are Pseudomonas syringae with its many pathovars epiphytically growing on many crops, and Ralstonia solanacearum responsible for bacterial wilts (Mansfield et al. 2012). The most devastating fungal pathogens are Magnaporthe oryzae (rice blast fungus) and Botrytis cinerea, a necrophytic grey mold fungus attacking more than 200 plant species but best known for its rare beneficial role (producing noble rot, pourriture noble) indispensable in the making of such sweet (botrytic) wines as Sauternes and Tokaj (Dean et al. 2012).
Although many broad-spectrum and targeted antibiotics have been available for more than half a century, many bacterial diseases still cause considerable mortality, particularly Mycobacterium tuberculosis in Africa, and Streptococcus pneumococcus, the leading cause of bacterial pneumonia among older people. Salmonella is responsible for frequent cases of food contamination, Escherichia coli is the leading cause of diarrhea, and both are ubiquitous causes of morbidity. But widespread use of antibacterial drugs has shortened the span of common infections, accelerated recovery, prevented early deaths, and extended modern lifespans.
The obverse of these desirable outcomes has been the spread of antibiotic-resistant strains that began just a few years after the introduction of new antimicrobials in the early 1940s (Smith and Coast 2002). Penicillin-resistant Staphylococcus aureus was found already in 1947. The first methicillin-resistant strains of Staphylococcus aureus (MRSA, causing bacteremia, pneumonia, and surgical wound infections) emerged in 1961, have spread globally and now account for more than half of all infection acquired during intensive hospital therapy (Walsh and Howe 2002). Vancomycin became the drug of last resort after many bacteria acquired resistance to most of the commonly prescribed antibiotics but the first vancomycin-resistant staphylococci appeared in 1997 in Japan and in 2002 in the US (Chang et al. 2003).
The latest global appraisal of the state of antibiotics indicates the continuation of an overall decline in the total stock of antibiotic effectiveness, as the resistance to all first-line and last-resort antibiotics is rising (Gelband et al. 2015). In the US, antibiotic resistance causes more than 2 million infections and 23,000 deaths every year and results in a direct cost of $20 billion and productivity losses of $35 billion (CDC 2013). While there have been some significant declines in MRSA in North America and Europe, the incidence in sub-Saharan Africa, Latin America, and Australia is still rising, Escherichia coli and related bacteria are now resistant to the third-generation cephalosporins, and carbapenem-resistant Enterobacteriaceae have become resistant even to the last-resort carbapenems.
The conquest of pathogenic bacterial growth made possible by antibiotics is being undone by their inappropriate and excessive use (unnecessary self-medication in countries where the drugs are available without prescription and overprescribing in affluent countries) as well as by poor sanitation in hospitals and by massive use of prophylactic antibiotics in animal husbandry. Preventing the emergence of antibiotic-resistant mutations was never an option but minimizing the problem has received too little attention for far too long. As a result, antibiotic-resistance is now also common among both domestic and wild animals that were never exposed directly to antibiotics (Gilliver et al. 1999).
The quest to regain a measure of control appears to be even more urgent as there is now growing evidence that many soil bacteria have a naturally occurring resistance against, or ability to degrade, antibiotics. Moreover, Zhang and Dick (2014) isolated from soils bacterial strains that were not only antibiotic-resistant but that could use the antibiotics as their sources of energy and nutrients although they were not previously exposed to any antibiotics: they found 19 bacteria (mainly belonging to Proteobacteria and Bacteriodetes) that could grow on penicillin and neomycin as their sole carbon sources up to concentrations of 1 g/L.
The availability of antibiotics (and better preventive measures) have also minimized the much larger, population-wide threat posed by bacteria able to cause large-scale epidemics and even pandemics, most notably Yersinia pestis, a rod-shaped anaerobic coccobacillus responsible for plague. The bacterium causing plague was identified, and cultured, in 1894 by Alexandre Yersin in Hong Kong in 1894, and soon afterwards Jean-Paul Simond discovered the transmission of bacteria from rodents by flea bites (Butler 2014). Vaccine development followed in 1897, and eventually streptomycin (starting in 1947) became the most effective treatment (Prentice and Rahalison 2007).
The Justinian plague of 541–542 and the medieval Black Death are the two best known historic epidemics (not pandemics, as they did not reach the Americas and Australia) due to their exceptionally high mortality. The Justinian plague swept the Byzantine (Eastern Roman) and Sassanid empires and the entire Mediterranean littoral, with uncertain death estimates as high as 25 million (Rosen 2007). A similarly virulent infestation returned to Europe eight centuries later as the Black Death, the description referring to dying black skin and flesh. In the spring of 1346, plague, endemic in the steppe region of southern Russia, reached the shores of the Black Sea, and then it was carried by maritime trade routes via Constantinople to Sicily by October 1346 and then to the western Mediterranean, reaching Marseilles and Genoa by the end of 1347 (Kelly 2006).
Flea-infested rats on trade ships carried the plague to coastal cities, where it was transmitted to local rat populations but subsequent continental diffusion was mainly by direct pneumonic transmission. By 1350 plague had spread across western and central Europe, by 1351 it reached northwestern Russia, and by 1853 its easternmost wave was reconnected to the original Caspian reservoir (Gaudart et al. 2010). Overall European mortality was at least 25 million people, and before it spread to Europe plague killed many people in China and in Central Asia. Between 1347 and 1351 it also spread from Alexandria to the Middle East, all the way to Yemen.
Aggregate mortality has been put as high as 100 million people but even a considerably smaller total would have brought significant depopulation to many regions and its demographic and economic effects lasted for generations. Controversies regarding the Black Death’s etiology were definitely settled only in 2010 by identification of DNA and protein signatures specific for Yersinia pestis in material removed from mass graves in Europe (Haensch et al. 2010). The study has also identified two previously unknown but related Yersinia clades associated with mass graves, suggesting that 14th century plague reached Europe on at least two occasions by distinct routes.
Gómez and Verdú (2017) reconstructed the network connecting the 14th-century European and Asian cities through pilgrimage and trade and found, as expected, that the cities with higher transitivity (a node’s connection to two other nodes that are also directly connected) and centrality (the number and intensity of connections with the other nodes in the network), were more severely affected by the plague as they experienced more exogenous reinfections. But available information does not allow us to reconstruct reliably the epidemic trajectories of the Black Death as it spread across Europe in the late 1340s.
Later, much less virulent, outbreaks of the disease reoccurred in Europe until the 18th century and mortality records for some cities make it possible to analyze the growth of the infection process. Monecke et al. (2009) found high-quality data for Freiburg (in Saxony) during its plague epidemics between May 1613 and February 1614 when more than 10% of the town’s population died. Their models of the epidemic’s progress resulted in close fits to the historical record. The number of plague victims shows a nearly normal (Gaussian) distribution, with the peak at about 100 days after the first deaths and a return to normal after about 230 days.
Perhaps the most interesting findings of their modeling was that introducing even a small number of immune rats into an otherwise unchanged setting aborts the outbreak and results in very few deaths. They concluded that the diffusion of Rattus norvegicus (brown or sewer rats, which may develop partial herd immunity by exposure to Yersinia because of its preference for wet habitats) accelerated the retreat of the 17th-century European plague. Many epidemics of plague persisted during the 19th century and localized plague outbreaks during the 20th century included those in India (1903), San Francisco (1900–1904), China (1910–1912) and India (Surat) in 1994. During the last two generations, more than 90% of all localized plague cases have been in African countries, with the remainder in Asia (most notably in Vietnam, India, and China) and in Peru (Raoult et al. 2013).
Formerly devastating bacterial epidemics have become only a matter of historic interest as we have taken preventive measures (suppressing rodent reservoirs and fleas when dealing with plague) and deployed early detection and immediate treatment of emerging cases. Viral infections pose a greater challenge. A rapid diffusion of smallpox, caused by variola virus, was responsible for well-known reductions of aboriginal American populations that lacked any immunity before their contact with European conquerors. Vaccination eventually eradicated this infection: the last natural outbreak in the US was in 1949, and in 1980 the World Health Organization declared smallpox eliminated on the global scale. But there is no prospect for an early elimination of viral influenza, returning annually in the form of seasonal epidemics and unpredictably as recurrent pandemics.
Seasonal outbreaks are related to latitude (Brazil and Argentina have infection peaks between April and September), they affect between 10% and 50% of the population and result in widespread morbidity and significant mortality among elderly. Annual US means amount to some 65 million illnesses, 30 million medical visits, 200,000 hospitalizations, 25,000 (10,000–40,000) deaths, and up to $5 billion in economic losses (Steinhoff 2007). As with all airborne viruses, influenza is readily transmitted as droplets and aerosols by respiration and hence its spatial diffusion is aided by higher population densities and by travel, as well as by the short incubation period, typically just 24–72 hours. Epidemics can take place at any time during the year, but in temperate latitudes they occur with a much higher frequency during winter. Dry air and more time spent indoors are the two leading promoters.
Epidemics of viral influenza bring high morbidity but in recent decades they have caused relatively low overall mortality, with both rates being the highest among the elderly. Understanding of key factors behind seasonal variations remains limited but absolute humidity might be the predominant determinant of influenza seasonality in temperate climates (Shaman et al. 2010). Recurrent epidemics require the continuous presence of a sufficient number of susceptible individuals, and while infected people recover with immunity, they become again vulnerable to rapidly mutating viruses as the process of antigenic drift creates a new supply of susceptible individuals (Axelsen et al. 2014). That is why epidemics persist even with mass-scale annual vaccination campaigns and with the availability of antiviral drugs. Because of the recurrence and costs of influenza epidemics, considerable effort has gone into understanding and modeling their spread and eventual attenuation and termination (Axelsen et al. 2014; Guo et al. 2015).
The growth trajectories of seasonal influenza episodes form complete epidemic curves whose shape conforms most often to a normal (Gaussian) distribution or to a negative binomial function whose course shows a steeper rise of new infections and a more gradual decline from the infection peak (Nsoesie et al. 2014). More virulent infections follow a rather compressed (peaky) normal curve, with the entire event limited to no more than 100–120 days; in comparison, milder infections may end up with only a small fraction of infected counts but their complete course may extend to 250 days. Some events will have a normal distribution with a notable plateau or with a bimodal progression (Goldstein et al. 2011; Guo et al. 2015).
But the epidemic curve may follow the opposite trajectory, as shown by the diffusion of influenza at local level. This progression was studied in a great detail during the course of the diffusion of the H1N1 virus in 2009. Between May and September 2009, Hong Kong had a total of 24,415 cases and the epidemic growth curve, reconstructed by Lee and Wong (2010), had a small initial peak between the 55th and 60th day after its onset, then a brief nadir followed by rapid ascent to the ultimate short-lived plateau on day 135 and a relatively rapid decline: the event was over six months after it began (figure 2.4). The progress of seasonal influenza can be significantly modified by vaccination, notably in such crowded settings as universities, and by timely isolation of susceptible groups (closing schools). Nichol et al. (2010) showed that the total attack rate of 69% in the absence of vaccination was reduced to 45% with a preseason vaccination rate of just 20%, to less than 1% with preseason vaccination at 60%, and the rate was cut even when vaccinations were given 30 days after the outbreak onset.

Progression of the Hong Kong influenza epidemic between May and September 2009. Based on Lee and Wong (2010).
We can now get remarkably reliable information on an epidemic’s progress in near real-time, up to two weeks before it becomes available from traditional surveillance systems: McIver and Brownstein (2014) found that monitoring the frequency of daily searches for certain influenza- or health-related Wikipedia articles provided an excellent match (difference of less than 0.3% over a period of nearly 300 weeks) with data on the actual prevalence of influenza-like illness obtained later from the Centers for Disease Control. Wikipedia searches also accurately estimated the week of the peak of illness occurrence, and their trajectories conformed to the negative binomial curve of actual infections.
Seasonal influenza epidemics cannot be prevented and their eventual intensity and human and economic toll cannot be predicted—and these conclusions apply equally well to the recurrence of a worldwide diffusion of influenza viruses causing pandemics and concurrent infestation of the world’s inhabited regions. These concerns have been with us ever since we understood the process of virulent epidemics, and it only got more complicated with the emergence of the H5N1 virus (bird flu) in 1997 and with a brief but worrisome episode of severe acute respiratory syndrome (SARS). In addition, judging by the historical recurrence of influenza pandemics, we might be overdue for another major episode.
We can identify at least four viral pandemics during the 18th century, in 1729–1730, 1732–1733, 1781–1782, and 1788–1789, and there have been six documented influenza pandemics during the last two centuries (Gust et al. 2001). In 1830–1833 and 1836–1837, the pandemic was caused by an unknown subtype originating in Russia. In 1889–1890, it was traced to subtypes H2 and H3, most likely coming again from Russia. In 1918–1919, it was an H1 subtype with unclear origins, either in the US or in China. In 1957–1958, it was subtype H2N2 from south China, and in 1968–1969 subtype H3N2 from Hong Kong. We have highly reliable mortality estimates only for the last two events, but there is no doubt that the 1918–1919 pandemic was by far the most virulent (Reid et al. 1999; Taubenberger and Morens 2006).
The origins of the 1918–1919 pandemic have been contested. Jordan (1927) identified the British military camps in the United Kingdom (UK) and France, Kansas, and China as the three possible sites of its origin. China in the winter of 1917–1918 now seems the most likely region of origin and the infection spread as previously isolated populations came into contact with one another on the battlefields of WWI (Humphries 2013). By May 1918 the virus was present in eastern China, Japan, North Africa, and Western Europe, and it spread across entire US. By August 1918 it had reached India, Latin America, and Australia (Killingray and Phillips 2003; Barry 2005). The second, more virulent, wave took place between September and December 1918; the third one, between February and April 1919, was, again, more moderate.
Data from the US and Europe make it clear that the pandemic had an unusual mortality pattern. Annual influenza epidemics have a typical U-shaped age-specific mortality (with young children and people over 70 being most vulnerable), but age-specific mortality during the 1918–1919 pandemic peaked between the ages of 15 and 35 years (the mean age for the US was 27.2 years) and virtually all deaths (many due to viral pneumonia) were in people younger than 65 (Morens and Fauci 2007). But there is no consensus about the total global toll: minimum estimates are around 20 million, the World Health Organization put it at upward of 40 million people, and Johnson and Mueller (2002) estimated it at 50 million. The highest total would be far higher than the global mortality caused by the plague in 1347–1351. Assuming that the official US death toll of 675,000 people (Crosby 1989) is fairly accurate, it surpassed all combat deaths of US troops in all of the wars of the 20th century.
Pandemics have been also drivers of human genetic diversity and natural selection and some genetic differences have emerged to regulate infectious disease susceptibility and severity (Pittman et al. 2016). Quantitative reconstruction of their growth is impossible for events before the 20th century but good quality data on new infections and mortality make it possible to reconstruct epidemic curves of the great 1918–1919 pandemic and of all the subsequent pandemics. As expected, they conform closely to a normal distribution or to a negative binomial regardless of affected populations, regions, or localities. British data for combined influenza and pneumonia mortality weekly between June 1918 and May 1919 show three pandemic waves. The smallest, almost symmetric and peaking at just five deaths/1,000, was in July 1918. The highest, a negative binomial peaking at nearly 25 deaths/1,000 in October, and an intermediate wave (again a negative binomial peaking at just above 10 deaths/1,000) in late February of 1919 (Jordan 1927).
Perhaps the most detailed reconstruction of epidemic waves traces not only transmission dynamics and mortality but also age-specific timing of deaths for New York City (Yang et al. 2014). Between February 1918 and April 1920, the city was struck by four pandemic waves (also by a heat wave). Teenagers had the highest mortality during the first wave, and the peak then shifted to young adults, with total excess mortality for all four waves peaking at the age of 28 years. Each wave was spread with a comparable early growth rate but the subsequent attenuations varied. The virulence of the pandemic is shown by daily mortality time series for the city’s entire population: the second wave’s peak reached 1,000 deaths per day compared to the baseline of 150–300 deaths (figure 2.5). When compared by using the fractional mortality increase (ratio of excess mortality to baseline mortality), the trajectories of the second and the third wave came closest to a negative binomial distribution, with the fourth wave displaying a very irregular pattern.

Daily influenza mortality time series in New York between February 1918 and April 1920 compared to baseline (1915–1917 and 1921–1923). Simplified from Yang et al. (2014).
Very similar patterns were demonstrated by analyses of many smaller populations. For example, a model fitted to reliable weekly records of incidences of influenza reported from Royal Air Force camps in the UK shows two negative binomial curves, the first one peaking about 5 weeks and the other one about 22 weeks after the infection outbreak (Mathews et al. 2007). The epidemic curve for the deaths of soldiers in the city of Hamilton (Ontario, Canada) between September and December 2018 shows a perfectly symmetrical principal wave peaking in the second week of October and a much smaller secondary wave peaking three weeks later (Mayer and Mayer 2006).
Subsequent 20th-century pandemics were much less virulent. The death toll for the 1957–1958 outbreak was about 2 million, and low mortality (about 1 million people) during the 1968–1969 event is attributed to protection conferred on many people by the 1957 infection. None of the epidemics during the remainder of the 20th century grew into a pandemic (Kilbourne 2006). But new concerns arose due to the emergence of new avian influenza viruses that could be transmitted to people. By May 1997 a subtype of H5N1 virus mutated in Hong Kong’s poultry markets to a highly pathogenic form (able to kill virtually all affected birds within two days) that claimed its first human victim, a three-year-old boy (Sims et al. 2002). The virus eventually infected at least 18 people, causing six deaths and slaughter of 1.6 million birds, but it did not spread beyond South China (Snacken et al. 1999).
WHO divides the progression of a pandemic into six phases (Rubin 2011). First, an animal influenza virus circulating among birds or mammals has not infected humans. Second, the infection occurs, creating a specific potential pandemic threat. Third, sporadic cases or small clusters of disease exist but there are no community-wide outbreaks. Such outbreaks mark the fourth phase. In the next phase, community-level outbreaks affect two or more countries in a region, and in the sixth phase outbreaks spread to at least one other region. Eventually the infections subside and influenza activity returns to levels seen commonly during seasonal outbreaks. Clearly, the first phase has been a recurrent reality, and the second and third phases have taken place repeatedly since 1997. But in April 2009, triple viral reassortment between two influenza lineages (that had been present in pigs for years) led to the emergence of swine flu (H1N1) in Mexico (Saunders-Hastings and Krewski 2016).
The infection progressed rapidly to the fourth and fifth stage and by June 11, 2009, when WHO announced the start of an influenza pandemic, there were nearly 30,000 confirmed cases in 74 countries (Chan 2009). By the end of 2009, there were 18,500 laboratory-confirmed deaths worldwide but models suggest that the actual excess mortality attributable to the pandemics was between 151,700 and 575,400 cases (Simonsen et al. 2013). The disease progressed everywhere in typical waves, but their number, timing, and duration differed: there were three waves (spring, summer, fall) in Mexico, two waves (spring-summer and fall) in the US and Canada, three waves (September and December 2009, and August 2010) in India.
There is no doubt that improved preparedness (due to the previous concerns about H5N1 avian flu in Asia and the SARS outbreak in 2002)—a combination of school closures, antiviral treatment, and mass-scale prophylactic vaccination—reduced the overall impact of this pandemic. The overall mortality remained small (only about 2% of infected people developed a severe illness) but the new H1N1 virus was preferentially infecting younger people under the age of 25 years, while the majority of severe and fatal infections was in adults aged 30–50 years (in the US the average age of laboratory confirmed deaths was just 37 years). As a result, in terms of years of life lost (a metric taking into account the age of the deceased), the maximum estimate of 1.973 million years was comparable to the mortality during the 1968 pandemic.
Simulations of an influenza pandemic in Italy by Rizzo et al. (2008) provide a good example of the possible impact of the two key control measures, antiviral prophylaxis and social distancing. In their absence, the epidemic on the peninsula would follow a Gaussian curve, peaking about four months after the identification of the first cases at more than 50 cases per 1,000 inhabitants, and it would last about seven months. Antivirals for eight weeks would reduce the peak infection rate by about 25%, and social distancing starting at the pandemic’s second week would cut the spread by two-thirds. Economic consequences of social distancing (lost school and work days, delayed travel) are much more difficult to model.
As expected, the diffusion of influenza virus is closely associated with population structure and mobility, and superspreaders, including health-care workers, students, and flight attendants, play a major role in disseminating the virus locally, regionally, and internationally (Lloyd-Smith et al. 2005). The critical role played by schoolchildren in the spatial spread of pandemic influenza was confirmed by Gog et al. (2014). They found that the protracted spread of American influenza in fall 2009 was dominated by short-distance diffusion (that was partially promoted by school openings) rather than (as is usually the case with seasonal influenza) long-distance transmission.
Modern transportation is, obviously, the key superspreading conduit. Scales range from local (subways, buses) and regional (trains, domestic flights, especially high-volume connections such as those between Tokyo and Sapporo, Beijing and Shanghai, or New York and Los Angeles that carry millions of passengers a year) to intercontinental flights that enable rapid global propagation (Yoneyama and Krishnamoorthy 2012). In 1918, the Atlantic crossing took six days on a liner able to carry mostly between 2,000 and 3,000 passengers and crew; now it takes six to seven hours on a jetliner carrying 250–450 people, and more than 3 million passengers now travel annually just between London’s Heathrow and New York’s JFK airport. The combination of flight frequency, speed, and volume makes it impractical to prevent the spread by quarantine measures: in order to succeed they would have to be instantaneous and enforced without exception.
And the unpredictability of this airborne diffusion of contagious diseases was best illustrated by the transmission of the SARS virus from China to Canada, where its establishment among vulnerable hospital populations led to a second unexpected outbreak (PHAC 2004; Abraham 2005; CEHA 2016). A Chinese doctor infected with severe acute respiratory syndrome (caused by a coronavirus) after treating a patient in Guangdong travelled to Hong Kong, where he stayed on the same hotel floor as an elderly Chinese Canadian woman who got infected and brought the disease to Toronto on February 23, 2003.
As a result, while none of other large North American cities with daily flights to Hong Kong (Vancouver, San Francisco, Los Angeles, New York) was affected, Toronto experienced a taxing wave of infections, with some hospitals closed to visitors. Transmission within Toronto peaked during the week of March 16–23, 2003 and the number of cases was down to one by the third week of April; a month later, the WHO declared Toronto SARS-free—but that was a premature announcement because then came the second, quite unexpected wave, whose contagion rate matched the March peak by the last week of May before it rapidly subsided.
Trees and Forests
Now to the opposite end of the size spectrum: some tree species are the biosphere’s largest organisms. Trees are woody perennials with a more or less complex branching of stems and with secondary growth of their trunks and branches (Owens and Lund 2009). Their growth is a marvel of great complexity, unusual persistence, and necessary discontinuity, and its results encompass about 100,000 species, including an extreme variety of forms, from dwarf trees of the Arctic to giants of California, and from tall straight stems with minimal branching to almost perfectly spherical plants with omnidirectional growth. But the underlying mechanisms of their growth are identical: apical meristems, tissues able to produce a variety of organs and found at the tips of shoots and roots, are responsible for the primary growth, for trees growing up (trunks) and sideways and down (branches). Thickening, the secondary growth, produces tissues necessary to support the elongating and branching plant.
As Corner (1964, 141) succinctly put it,
The tree is organized by the direction of its growing tips, the lignification [i.e. wood production] of the inner tissues, the upward flow of water in the lignified xylem, the downward passage of food in the phloem, and the continued growth of the cambium. It is kept alive, in spite of its increasing load of dead wood, by the activity of the skin of living cells.
The vascular cambium, the layer of dividing cells and hence the generator of tree growth that is sandwiched between xylem and phloem (the living tissue right beneath the bark that transports leaf photosynthate), is a special meristem that produces both new phloem and xylem cells.
New xylem tissue formed in the spring has lighter color than the tissue laid down in summer in smaller cells, and these layers form distinct rings that make it easy to count a tree’s age without resorting to isotopic analysis of wood. The radial extent of the cambium is not easy to delimit because of the gradual transition between phloem and xylem, and because some parenchymal cells may remain alive for long periods of time, even for decades. Leaves and needles are the key tissues producing photosynthate and enabling tree growth and their formation, durability, and demise are sensitive to a multitude of environmental factors. Tree stems have been studied most closely because they provide fuelwood and commercial timber and because their cellulose is by far the most important material for producing pulp and paper.
Roots are the least known part of trees: the largest ones are difficult to study without excavating the entire root system, the hair-like ones that do most nutrient absorption are ephemeral. In contrast, crown forms are easiest to observe and to classify as they vary not only among species but also among numerous varieties. The basic division is between excurrent and decurrent forms; the latter form, characteristic of temperate hardwoods, has lateral branches growing as long or even longer than the stem as they form broad crowns, the former shape, typical in conifers, has the stem whose length greatly surpasses the subtending laterals.
Massed trees form forests: the densest have completely closed canopies, while the sparsest are better classified as woodland, with canopies covering only a small fraction of the ground. Forests store nearly 90% of the biosphere’s phytomass and a similarly skewed distribution applies on other scales: most of the forest phytomass (about three-quarters) is in tropical forests and most of that phytomass (about three-fifths) is in the equatorial rain forests where most of it is stored in massive trunks (often buttressed) of trees that form the forest’s closed canopy and in a smaller number of emergent trees whose crowns rise above the canopy level. And when we look at an individual tree we find most of its living phytomass locked in xylem (sapwood) and a conservative estimate put its share at no more than 15% of the total (largely dead) phytomass.
Given the substantial differences in water content of plant tissues (in fresh tissues water almost always dominates), the only way to assure data comparability across a tree’s lifespan and among different species is to express the annual growth rates in mass units of dry matter or carbon per unit area. In ecological studies, this is done in grams per square meter (g/m2), t/ha or in tonnes of carbon per hectare (t C/ha). These studies focus on different levels of productivity, be it for an entire plant, a community, an ecosystem, or the entire biosphere. Gross primary productivity (GPP) comes first as we move from the most general to the most restrictive productivity measure; this variable captures all photosynthetic activity during a given period of time.
Primary Productivity
Total forest GPP is about half of the global GPP assumed to be 120 Gt C/year (Cuntz 2011). New findings have changed both the global total and the forest share. Ma et al. (2015) believe that forest GPP has been overestimated (mainly due to exaggerated forest area) and that the real annual total is about 54 Gt C or nearly 10% lower than previous calculations. At the same time, Welp et al. (2011) concluded that the global GPP total should be raised to the range of 150–175 Gt C/year, and Campbell et al. (2017) supported that finding: their analysis of atmospheric carbonyl sulfide records suggests a large historical growth of total GPP during the 20th century, with the overall gain of 31% and the new total above 150 Gt C.
A large part of this newly formed photosynthate does not end up as new tree tissue but it is rapidly reoxidized inside the plant: this continuous autotrophic respiration (RA) energizes the synthesis of plant biopolymers from monomers fixed by photosynthesis, it transports photosynthates within the plant and it is channeled into repair of diseased or damaged tissues. Autotrophic respiration is thus best seen as the key metabolic pathway between photosynthesis and a plant’s structure and function (Amthor and Baldocchi 2001; Trumbore 2006). Its intensity (RA/GPP) is primarily the function of location, climate (above all of temperature), and plant age, and it varies widely both within and among species as well as among ecosystems and biomes.
A common assumption is that RA consumes about half of the carbon fixed in photosynthesis (Litton et al. 2007). Waring et al. (1998) supported this conclusion by studying the annual carbon budgets of diverse coniferous and deciduous communities in the US, Australia, and New Zealand. Their net primary productivity (NPP)/GPP ratio was 0.47 ± 0.04. But the rate is less constant when looking at individual trees and at a wider range of plant communities: RA at 50% (or less) is typical of herbaceous plants, and the actual rates for mature trees are higher, up to 60% of GPP in temperate forests and about 70% for a boreal tree (black spruce, Picea mariana) as well as for primary tropical rain forest trees (Ryan et al. 1996; Luyssaert et al. 2007).
In pure tree stands, RA rises from 15–30% of GPP during the juvenile stage to 50% in early mature growth, and it can reach more than 90% of GPP in old-growth forests and in some years high respiration can turn the ecosystem into a weak to moderate carbon source (Falk et al. 2008). Temperature-dependent respiration losses are higher in the tropics but due to higher GPP the shares of RA are similar to those in temperate trees. Above-ground autotrophic respiration has two major components, stem and foliar efflux. The former accounts for 11–23% of all assimilated carbon in temperate forests and 40–70% in tropical forests’ ecosystems, respectively (Ryan et al. 1996; Chambers et al. 2004). The latter can vary more within a species than among species, and small-diameter wood, including lianas, accounts for most the efflux (Asao et al. 2015; Cavaleri et al. 2006).
The respiration of woody tissues is between 25% and 50% of the total above-ground RA and it matters not only because of the mass involved but also because it proceeds while the living cells are dormant (Edwards and Hanson 2003). Because the autotrophic respiration is more sensitive to increases in temperature than is photosynthesis, many models have predicted that global warming would produce faster increases in RA than in overall photosynthesis, resulting in declining NPP (Ryan et al. 1996). But acclimation may negate such a trend: experiments found that black spruce may not have significant respiratory or photosynthetic changes in a warmer climate (Bronson and Gower 2010).
Net primary productivity cannot be measured directly and it is calculated by subtracting autotrophic respiration from gross primary productivity (NPP = GPP − RA): it is the total amount of phytomass that becomes available either for deposition as new plant tissues or for consumption by heterotrophs. Species-dependent annual forest NPP peaks early: in US forests at 14 t C/ha at about 30 years for Douglas fir, followed by a rapid decline, while in forests dominated by maple beech, oak, hickory, or cypress it grows to only 5–6 t C/ha after 10 years, when it levels off (He et al. 2012). As a result, at 100 years of age the annual NPP of American forests ranges mostly between 5 and 7 t C/ha (figure 2.6). Michaletz et al. (2014) tested the common assumption that NPP varies with climate due to a direct influence of temperature and precipitation but found instead that age and stand biomass explained most of the variation, while temperature and precipitation explained almost none. This means that climate influences NPP indirectly by means of plant age, standing phytomass, length of the growing season, and through a variety of local adaptations.

Bounds of age-related NPP for 18 major forest type groups in the US: the most common annual productivities are between 5 and 7 t C/ha. Modified from He et al. (2012).
Heterotrophic respiration (RH, the consumption of fixed photosynthate by organisms ranging from bacteria and insects to grazing ungulates) is minimal in croplands or in plantations of rapidly growing young trees protected by pesticides but considerable in mature forests. In many forests, heterotrophic respiration spikes during the episodes of massive insect invasions that can destroy or heavily damage most of the standing trees, sometimes across vast areas. Net ecosystem productivity (NEP) accounts for the photosynthate that remains after all respiratory losses and that enlarges the existing stores of phytomass (NEP = NPP-RH), and post-1960 ecosystemic studies have given us reliable insights into the limits of tree and forest growth.
The richest tropical rain forests store 150–180 t C/ha above ground (or twice as much in terms of absolutely dry phytomass), and their total phytomass (including dead tissues and underground growth) is often as much as 200–250 t C/ha (Keith et al. 2009). In contrast, boreal forests usually store no more than 60–90 t C/ha, with above-ground living tissues of just 25–60 t C/ha (Kurz and Apps 1994; Potter et al. 2008). No ecosystem stores as much phytomass as the old-growth forests of western North America. Mature stands of Douglas fir (Pseudotsuga menziesii) and noble fir (Abies procera) store more than 800 t C/ha, and the maxima for the above-ground phytomass of Pacific coastal redwoods (Sequoia sempervirens) are around 1,700 t C/ha (Edmonds 1982). Another instance of very high storage was described by Keith et al. (2009) in an Australian evergreen temperate forest in Victoria dominated by Eucalyptus regnans older than 100 years: its maximum density was 1,819 t C/ha in living above-ground phytomass and 2,844 t C/ha for the total biomass.
Not surprisingly, the world’s heaviest and tallest trees are also found in these ecosystems. Giant sequoias (Sequoiadendron giganteum) with phytomass in excess of 3,000 t in a single tree (and lifespan of more than 3,000 years) are the world’s most massive organisms, dwarfing blue whales (figure 2.7). But the comparison with large cetaceans is actually misleading because, as with every large tree, most of the giant sequoia phytomass is dead wood, not living tissue. Record tree heights are between 110 m for Douglas firs and 125 m for Eucalyptus regnans (Carder 1995).

Group of giant sequoia (Sequoiadendron giganteum) trees, the most massive terrestrial organisms, in Sequoia National Park. National Park Service image is available at https://
Net ecosystem productivity is a much broader growth concept than the yield used in forestry studies: it refers to the entire tree phytomass, including the steam, branches, leaves, and roots, while the traditional commercial tree harvest is limited to stems (roundwood), with stumps left in the ground and all branches and tree tops cut off before a tree is removed from the forest. New ways of whole-tree harvesting have changed and entire trees can be uprooted and chipped but the roundwood harvests still dominate and statistical sources use them as the basic wood production metric. After more than a century of modern forestry studies we have accumulated a great deal of quantitative information on wood growth in both pure and mixed, and natural and planted, stands (Assmann l970; Pretzsch 2009; Weiskittel et al. 2011).
There are many species-specific differences in the allocation of above-ground phytomass. In spruces, about 55% of it is in stem and bark, 24% in branches, and 11% in needles, with stumps containing about 20% of all above-ground mass, while in pines 67% of phytomass is in stem and bark, and the share is as high as 78% in deciduous trees. This means that the stem (trunk) phytomass of commercial interest (often called merchantable bole) may amount to only about half of all above-ground phytomass, resulting in a substantial difference between forest growth as defined by ecologists and wood increment of interest to foresters.
Patterns of the growth of trees over their entire lifespans depend on the measured variable. There are many species-specific variations but two patterns are universal. First, the rapid height growth of young trees is followed by declining increments as the annual growth tends to zero. Second, there is a fairly steady increase of tree diameter during a tree’s entire life and initially small increments of basal area and volume increase until senescence. Drivers of tree growth are difficult to quantify statistically due to covarying effects of size- and age-related changes and of natural and anthropogenic environmental impacts ranging from variability of precipitation and temperature to effects of nitrogen deposition and rising atmospheric CO2 levels (Bowman et al. 2013).
Tree Growth
Height and trunk diameter are the two variables that are most commonly used to measure actual tree growth. Diameter, normally gauged at breast height (1.3 m above ground) is easy to measure with a caliper, and both of these variables correlate strongly with the growth of wood volume and total tree phytomass, a variable that cannot be measured directly but that is of primary interest to ecologists. In contrast, foresters are interested in annual stem-wood increments, with merchantable wood growth restricted to trunks of at least 7 cm at the smaller end. Unlike in ecological studies, where mass or energy units per unit area are the norm, foresters use volumetric units, cubic meters per tree or per hectare, and as they are interested in the total life spans of trees or tree stands, they measure the increments at intervals of five or ten years.
The US Forest Service (2018) limits the growing stock volume to solid wood in stems “greater than or equal to 5.0 inches in diameter at breast height from a one-foot high stump to a minimum 4.0-inch top diameter outside bark on the central stem. Volume of solid wood in primary forks from the point of occurrence to a minimum 4-inch top diameter outside bark is included.” In addition, it also excludes small trees that are sound but have a poor form (those add up to about 5% of the total living tree volume). For comparison, the United Nations definition of growing stock includes the above-stump volume of all living trees of any diameter at breast height of 1.3 m (UN 2000). Pretzsch (2009) gave a relative comparison of the ecological and forestry metrics for a European beech stand growing on a mediocre site for 100 years: with GPP at 100, NPP will be 50, net tree growth total 25, and the net stem growth harvested only 10. In mass units, harvestable annual net stem growth of 3 t/ha corresponds to GPP of 30 t/ha.
Productivity is considerably higher for fast-growing species planted to produce timber or pulp, harvested in short rotations, and receiving adequate fertilization and sometimes also supplementary irrigation (Mead 2005; Dickmann 2006). Acacias, pines, poplars, and willows grown in temperate climates yield 5–15 t/ha, while subtropical and tropical plantings of acacias, eucalypts, leucaenas, and pines will produce up to 20–25 t/ha (ITTO 2009; CNI 2012). Plantation trees grow rapidly during the first four to six years: eucalypts add up to 1.5–2 m/year, and in Brazil—the country with their most extensive plantations, mostly in the state of Minas Gerais, to produce charcoal—they are now harvested every 5–6 years in 15-year to 18-year rotations (Peláez-Samaniegoa 2008).
The difference between gross and net growth (the latter is reduced by losses and tree mortality) is particularly large in forests with turnover of high whole trees due to their advanced age. Foresters have studied long-term growth of commercially important species both as individual trees and as their pure or mixed stands and express them in terms of current annual increment (CAI) in diameter, height, and stem volume (Pretzsch 2009). The expansion of tree diameter at breast height is the most commonly monitored dimension of tree growth: not only is it easily measured but it also strongly correlates with the tree’s total phytomass and with its wood volume.
Annual additions are commonly just 2–3 mm for trees in boreal forests and 4–6 mm for leafy trees in temperate forests, but slow-growing oaks add just 1 mm, while some coniferous species and poplars can grow by up to 7–10 mm (Teck and Hilt 1991; Pretzsch 2009). Annual diameter additions of tropical trees are strongly influenced by their growth stage, site, and access to light. Small, shade-tolerant species in a secondary forest can add less than 2 mm/year and annual growth of just 2–3 mm is common for tropical mangrove formations, while annual increments in rich natural forests range mostly between 10 and 25 mm (Clark and Clark 1999; Menzes et al. 2003; Adame et al. 2014).
Young poplars in temperate-climate plantations add more than 20 mm/year (International Poplar Commission 2016), and some species of commonly planted city trees also grow fast: urban plane trees (Acer platanoides) in Italy average about 12 mm/year up to 15 years after planting and about 15 mm/year during the next 10 years (Semenzato et al. 2011). For most trees, annual increments peak at a time when the trunks reach about 50 cm of breast-height diameter and decline by 40–50% by the time the trees measure 1 meter across. In terms of age, stem diameter CAI reach maxima mostly between 10 and 20 years and brief peaks are followed by exponential declines. But stem diameter can keep on expanding, albeit at much slower rates, as long as a tree is alive, and many mature trees continue to add phytomass for their entire life spans.
Excellent examples of this lifelong growth were provided by Sillett et al. (2010). His team climbed and measured crown structures and growth rates of 43 trees of the biosphere’s two tallest species, Eucalyptus regnans and Sequoia sempervirens, spanning a range of sizes and ages. Measurements at ground level found expected declines in annual growth of diameters and ring width—but wood production of both the main stem and of the entire crown kept on increasing even in the largest and oldest studied trees. As expected, the two species have divergent growth dynamics: eucalyptus trees die at a relatively young age because of their susceptibility to fire and fungi, while sequoias attain a similar size more slowly and live much longer not only because they are more fire resistant but also because they channel more of their photosynthate into decay-resistant hardwood. Remarkably, not just individual old trees but even some old-growth forests continue to accumulate phytomass (Luyssaert et al. 2008).
Increases in tree height do not follow the indeterminate growth of tree mass: even where soil moisture is abundant, taller trees experience increasing leaf water stress due to gravity and greater path length resistance that eventually limit leaf expansion and photosynthesis for further height growth. Young conifers reach maxima of height CAI rate of growth (60–90 cm) mostly between 10 and 20 years; some slower growing deciduous trees (maxima of 30–70 cm) can reach maximum height rate of growth only decades later, followed (as in the case of diameter expansion) by exponential declines. Koch et al. (2004) climbed the tallest surviving northern California redwoods (Sequoia sempervirens, including the tallest tree on Earth, 112.7 m) and found that leaf length as well as the angle between the long axis of the leaf and the supporting stem segment decrease with height, with leaf length more than 10 cm at 2 m but less than 3 cm at 100 m. Their analysis of height gradients in leaf functional characteristics put the maximum tree height (in the absence of any mechanical damage) at 122–130 m, the range confirmed by the tallest recorded trees in the past.
Lianas, common in tropical rain forests and, to a lesser extent, in many temperate biomes, should grow faster than the host trees because they reduce biomass investment in support tissues and can channel more of their photosynthate in leaves and stem extension. Ichihashi and Tateno (2015) tested this obvious hypothesis for nine deciduous liana species in Japan and found they had 3–5 times greater leaf and current-year stem mass for a given above-ground mass and that they reached the canopy at the same time as the co-occurring trees but needed only 1/10 of the phytomass to do so. But this growth strategy exacts a high cost as the lianas lost about 75% of stem length during their climb to the canopy.
The addition of annual increments over the entire tree life span produces yield curves which are missing the earliest years of tree growth because foresters begin to measure annual increments only after a tree reaches a specified minimal diameter at breast height. Growth curves for both tree heights and stem diameters are available in forestry literature for many species from ages of five or ten to 30–50 years and for some long-lived species for a century or more, and they follow confined exponential trajectories with a species-specific onset of declining growth. All of the nonlinear growth models commonly used in the studies of other organisms or other growth processes have been used in forestry studies (Fekedulegn et al. 1999; Pretzsch 2009). In addition, several growth functions rarely encountered elsewhere (Hossfeld, Levakovic, Korf) were found to provide good fits when charting the growth of heights and volumes.
Confined exponential curves characterize the growth of such different trees as the tallest Douglas firs east of the Cascades in the Pacific Northwest between the ages of 10 and 100 years (Cochran 1979) and fast-growing poplars grown in plantations 10–25 years old on Swedish agricultural land (Hjelm et al. 2015). Growth equations are used to construct simple yield tables or to offer more detailed specific information, including mean diameter, height and maximum mean annual increment of tree stands, their culmination age, and the volume yield by species to several diameter limits. For example, natural stands of Douglas fir in British Columbia will reach their maximum volume (800–1200 m3/ha depending on the degree of crown closure) after about 140 years of growth (Martin 1991; figure 2.8). The maximum mean annual increment of planted Douglas fir stands is reached (depending on the site) after 50–100 years of growth, but the merchantable volume of such stands keeps increasing even after 150 years of growth before it eventually saturates, or is reduced to marginal rates, at ages of 200–300 years.

Age-related and site-dependent growth of merchantable volume for coastal Douglas fir in British Columbia. Based on Martin (1991).
But, as already noted, this well-documented growth decline of even-aged (nearly coeval) forest stands is not, contrary to commonly held assumption, applicable to individual healthy aged trees. Despite their declining growth efficiency (expressed as phytomass growth per unit mass of photosynthesizing tissues), annual growth increments of aging trees can increase until the tree dies due to external forces (ranging from drought to lightning). This continuing accumulation of carbon at increasing rates—a type of accelerating indeterminate mass growth—is well documented by studies of exceptionally large trees. For example, until it was killed by fire in 2003, an enormous 480-year-old Eucalyptus regnans tree in Tasmania had above-ground phytomass of about 270 t and an estimated annual growth increment of 1 t (Sillett et al. 2015).
A global analysis of 403 tropical and temperate tree species showed the widespread occurrence of the increasing annual additions of old tree phytomass (Stephenson et al. 2014). Such trees are not senescent reservoirs of phytomass but continue to fix large amounts of carbon when compared to smaller trees. The total annual phytomass addition of trees with 100 cm in trunk diameter is typically nearly three times the rate for trees of the same species with a diameter of 50 cm, and this rapid growth of old trees is the global norm rather than being limited to a few unusual species. At the extreme, a single old massive tree can add annually the same amount of carbon as is stored in an entire mid-sized tree, even as stand-level productivity is declining.
Stephenson et al. (2014) explain this apparent paradox by increases in a tree’s total leaf area that are able to outpace decreasing productivity per unit of leaf area and by reductions in age-related population density. The younger trees grow faster in relative terms, older trees, having more leaves and more surface across which new wood gets deposited, grow faster in absolute terms. But to say that “tree growth never slows” (Tollefson 2014) is to leave out the critical qualifier: absolute growth (mass addition per year) may not slow but relative growth does as no group of organisms can keep on growing exponentially.
But some studies have questioned the validity of traditional asymptotic-size models. Bontemps et al. (2012) published an original non-asymptotic growth model formulated as a first-order four-parameter differential equation. They tested the resulting sigmoid curve on 349 old growth series of top height in seven temperate tree species growing in pure and even-aged stands, and it produced a better fit than asymptotic growth equations and hence it may have general relevance to tree growth modelling. The growth of individual trees—much like the growth of some animals and unlike the growth of annual crops and other herbaceous plants—will be indeterminate but the age-related decline in forest productivity is primarily a size-related decline as populations of trees, much like all the assemblages of all organisms, must follow sigmoidal growth curves (Weiner et al. 2001).
As a result, continuing growth of individual trees can be achieved only by reducing the number of stems per unit area: sooner or later, resources (nutrients, water) become insufficient to support all growing trees and self-thinning (plant mortality due to competition in crowded even-aged plant communities) begins to regulate the growth of tree stands. Many trees have to stop growing and have to die in order to make room for other, incessantly growing, survivors. The process lowers the stem density (ρ, numbers/m2) and it limits the average mass per plant in a highly predictable way captured by the allometric relationship M = k.ρ−a with the exponent between −1.3 and −1.8 and an ideal value of −1.5 and with k at between 3.5 and 5.0 (Reineke 1933; Yoda et al. 1963; Enquist et al. 1998).
As growth gets concentrated in fewer trees, those larger-size trees require larger, long-lasting structures (heavy stems and branches) and effective protection (barks or defensive chemicals). The self-thinning rule means that time can be ignored (mortality depends only on phytomass accumulation) and that thinning proceeds more slowly under poor growing conditions. In terms of actual tree growth, it means (to give a specific example for a commonly planted tree) that in an even-aged monospecific stand of North American balsam fir (Abies balsamea) containing 100,000 stems/ha, the mass of an average sapling will be no more than 100 g and their total mass will add up to only about 10 t, while the same lot containing 10,000 (1/10 as many) stems will have trees averaging 10 kg and will hold the total of 100 t of phytomass (Mohler et al. 1978).
Much like in the case of metabolic scaling theory, the universality of the self-thinning rule exponent has been questioned. Lonsdale (1990) argued that it does not approximate to the −1.5 rule and that the straight lines delimiting maximum phytomass are exceptional. Hamilton et al. (1995) concluded that there is no theoretical or empirical evidence for a −1.5 slope. Competition for light is far from being the only cause of self-thinning stem mortality, the maximum supportable phytomass depends on the site quality, and thinning trajectories can be more or less steep than −1.5. Pretzsch (2006) confirmed this absence of narrow clustering as he tested both Reineke’s 1.605 and Yoda’s 1.5 rule against 120 years of growth in unthinned, even-age stands of deciduous trees spread across southern part of Germany. He found species-specific exponents ranging from −1.4 for common beech to −1.8 for common oak. There were also many nonlinear trajectories caused by storm damage and ice breakage.
Tree growth is strongly affected by the growing conditions, above all the quality of soils and climatic variables. That is why foresters almost invariably use the species-specific site index that measures potential site productivity and that is defined as the average height reached by freely growing (undamaged, unsuppressed) dominant (top height) trees in 50 years of growth above their breast height (Ministry of Forestry 1999). For example, British Columbia’s Douglas fir with site index 40 (dominant trees at 40 m) and breast-height diameter of 12.5 cm will have a maximum annual increment of about 15 m3, while the same species with site index 25 (and the same diameter) will add only 6.3 m3.
This also means that tree growth can respond rapidly to changed conditions. Large interannual differences in growth rates are common and widely documented. To cite just one recent example, in English temperate broadleaf trees the growth rate was 40% lower in 2010 compared to 2011 and 2012, mostly because low temperature delayed the start of the growing season (Butt et al. 2014). Height increment is often the most sensitive variable affected by drought and annual mass growth can be affected by environmental variables ranging from nutrient shortages to fire damage. Tree rings provide convenient records of these growth fluctuations and their study (dendrochronology) has evolved into a sophisticated discipline (Vaganov et al. 2006; Speer 2011).
Forests can also experience vigorous regrowth and expansion following both natural and anthropogenic disruptions. For example, pollen analysis from the southeastern Netherlands enabled a clear reconstruction of the extent and timing of significant agricultural regression caused by population decline following the Black Death and notable forest regrowth in its aftermath between 1350 and 1440 (van Hoof et al. 2006). Preindustrial deforestation in Massachusetts reduced the state’s extent of forest cover from about 85% in 1700 to only about 30% by 1870, but by the year 2000 tree cover had returned to about 70% of the state (Foster and Aber 2004).
And New England’s forests, subject to recurrent (infrequent but enormously devastating) super-hurricanes, are also a perfect reminder of the fact that in some regions most trees are not able to live their maximum natural life span. The cyclone of 1938 downed about 70% of all timber in Harvard Forest in central Massachusetts (Spurr 1956). Regrowth has largely healed those losses (Weishampel et al. 2007), but one of the region’s dominant trees is now on the verge of extinction. Before 2030, the eastern hemlock (Tsuga canadensis) might join the American chestnut as yet another species that has succumbed to a pest, in this case to the woolly adelgid (Adelges tsugae), a small aphid-like insect from East Asia that has been killing hemlock trees since the 1960s with no known defense against its depredations (Foster 2014).
Reforestation has been particularly impressive in Europe. First, the transition from wood to coal stopped large-scale forest cutting for fuel during the first half of the 20th century. Post-1950 gains came from a combination of natural reforestation of marginal farmland (made redundant by rising agricultural productivity) and extensive replanting. Between 1900 and 2005, Europe gained almost 13 Mha of forests (approximately the area of Greece), and the gains during the second half of the 20th century were in the order of 20% in Italy and 30% in both France and Germany, and they were even higher in terms of the growing stock (Gold 2003).
Extensive reforestation tied to the abandonment of marginal farmland has also taken place in eastern and southern parts of the US, but no other nation has supported such massive afforestation campaigns as modern China. Unfortunately, most of the Mao-era plantings have failed and only the post-1979 campaigns have been relatively successful (Liu et al. 2005). When using the definition of the Food and Agriculture Organization (FAO) of the United Nations, forests now cover up to 22% of the nation’s territory (FAO 2015a), but most of these gains have been in monocultural plantings of fast-growing pines and poplars rather than in mixed stands that would at least somewhat resemble natural growth.
But deforestation continues to be a serious problem in Southeast and South Asia, throughout Africa, and in Latin America, with the largest absolute losses in the Amazon Basin: between 1990 and 2015, the lost forest area of 129 Mha has been almost equal to the territory of South Africa (FAO 2015a). Relative estimates of global deforestation depend on the definition of forests. There is, obviously, a large difference between defining forests only as closed-canopy growth (the ground 100% covered by tree crowns in perpendicular view) or allowing, as FAO does, as little as 10% canopy cover to qualify as a forest. As a result, different estimates imply losses of 15–25% of pre-agricultural (or potential) forest cover (Ramankutty and Foley 1999; Williams 2006), and Mather (2005) emphasized that it is impossible to compile reliable historical series of forested areas even for the 20th century.
Global deforestation estimates have become more reliable only with regular satellite monitoring (the first LANDSAT was launched in 1972). The best estimates see worldwide deforestation rising from 12 Mha/year between 1950 and 1980 to 15 Mha/year during the 1980s, to about 16 Mha/year during the 1990s, and then declining to about 13 Mha/year during the first decade of the 21st century. As already noted, the latest FAO account put the global loss at 129 Mha between 1990 and 2015 but during the same period the rate of net global deforestation had slowed down by more than 50% (FAO 2015a). This slowdown was helped by increasing protection of forests in national parks and other reservations. The beginnings of protected areas go to the closing decade of the 19th century (Yellowstone National Park was set up in 1891) but the process accelerated with the diffusion of environmental consciousness that started in the 1960s. In 2015 about 16% of the world’s forested area was under some kind of protection (FAO 2015a).
No simple generalizations can capture the prospects of forest in the coming warmer biosphere with higher concentrations of atmospheric CO2 (Bonan 2008; Freer-Smith et al. 2009; IPCC 2014). Currently there is no doubt that forests are a major net carbon sink on the global scale, sequestering annually on the order of 4 Gt C, but because of continuing deforestation, particularly in the tropics, the net storage is only about 1 Gt C/year (Canadell et al. 2007; Le Quéré et al. 2013). As with all plants, forest productivity (everything else being equal) should benefit from higher levels of atmospheric CO2. Experience from greenhouses and a number of recent field tests have shown that higher levels of atmospheric CO2 result in higher water use efficiency, particularly for C3 plants (wheat, rice).
This response would be welcome in all those regions where global warming will reduce average precipitation or change its annual distribution. Moreover, Lloyd and Farquhar (2008) found no evidence that tropical forests (by far the most import contributors to annual phytomass growth) are already dangerously close to their optimum temperature range and concluded that enhanced photosynthetic rates associated with higher atmospheric CO2 levels should more than offset any decline in photosynthetic productivity due to higher leaf-to-air water pressure deficits and leaf temperatures or due to ensuing increased autotrophic respiration rates.
Perhaps the most convincing evidence of positive consequences of higher CO2 and higher temperatures for forest growth was provided by McMahon et al. (2010). They analyzed 22 years of data from 55 temperate forest plots with stands ranging from 5–250 years and found that the observed growth was significantly higher than the expected increase. Besides increased temperature (and hence an extended growing season) and higher atmospheric CO2 levels, their explanation has also included nutrient fertilization (via atmospheric nitrogen deposition) and community composition (with some pioneering species growing faster than late-succession trees).
In contrast, an analysis of all major forest biome types (at 47 sites from boreal to tropical environments) showed that while the post-1960s increase of over 50 ppm CO2 did result in 20.5% improvement of intrinsic water use efficiency (with no significant difference among biomes), the growth of mature trees has not increased as expected as the sites were evenly split between positive and negative trends and showed no significant trend within or among biomes (Peñuelas et al. 2011). Obviously, other factors (most likely periods of drought, nutrient shortages, and acclimation difficulties) negated a significantly positive improvement. In addition, several studies suggest (albeit with low confidence) that in many regions this stimulatory effect may have already peaked (Silva and Anand 2013).
Many forests will adapt to higher temperatures by migrating northward or to higher altitudes but the pace of these displacements will be highly specific to species, region, and site. Net assessments of coming productivity changes remain highly uncertain even for well-studied forests of Europe and North America as faster growth may be largely or entirely negated by a higher frequency of fires, cyclones, and pest damage (Shugart et al. 2003; Greenpeace Canada 2008). And Europe’s managed forests have actually contributed to global warming during the past two centuries, not only because of the release of carbon that would have remained stored in litter, dead wood, and soil, but because the conversion of broadleaved forests to economically more valuable conifers increased the albedo and hence evapotranspiration, both leading to warming (Naudts et al. 2016).
Crops
In the preceding section, I explained the relationships between gross and net plant productivity and autotrophic and heterotrophic respiration. Using those variables, it is obvious that agriculture—cultivation of domesticated plants for food, feed, and raw materials—can be best defined as a set of activities to maximize NEP, the goal that is achieved by maximizing GPP while minimizing RA and, above all, by reducing RH. Maximized photosynthetic conversion and minimized autotrophic respiration are achieved largely through breeding; by supplying adequate plant nutrients and, where needed, water; by minimizing competition due to weed growth by applying herbicides; by limiting heterotrophic respiration of crops by a variety of defensive measures, now most prominently by applying insecticides and fungicides; and by timely harvesting and waste-reducing storage.
Although several species of mushrooms and of freshwater and marine algae are cultivated for food or medicinal uses, most crops are domesticated species of annual or perennial plants whose structure, nutritional value, and yield have been substantially modified by long periods of selective breeding and recently also by the creation of transgenic forms. Hundreds of plants have been cultivated to supply food, feed, fuel, raw materials, medicines, and flowers, with most species contributed by fruits and vegetables. Some of them include numerous cultivars, none more so than Brassica oleracea including various cabbages, collard greens, kales, broccoli, cauliflowers, brussels sprouts, and kohlrabi.
But the range of staples was always much smaller and it has been further reduced in modern mass-scale agriculture, with only a few cultivars providing most of the nutrition, be it in terms of overall energy, or as sources of the three macronutrients. This small group of staples is dominated by cereals. In the order of global harvest in 2015, they are corn (although in affluent countries it is used overwhelmingly not as food but as animal feed), wheat, and rice. These three crops account for more than 85% of the global cereal harvest (just over 2.5 Gt in 2015), the remainder being mostly coarse grains (millets, sorghum) and barley, oats, and rye.
The other indispensable categories of major crops are tubers (white and sweet potatoes, yams, cassava, all almost pure carbohydrates with hardly any protein), leguminous grains (now dominated by soybeans and including various beans, peas, and lentils, all high in protein), oil seeds (the principal sources of plant lipids, ranging from tiny rapeseed to sunflower seeds, with soybeans and oil palm being now major contributors) and the two largest sugar sources, cane and beets (but high-fructose syrup derived from corn has become a major sweetener in the US). Vegetables and fruits, rich in vitamins and minerals, are consumed mainly for these micronutrients, while nuts combine high protein and high lipid content. Major nonfood crops include natural fibers (with cotton far ahead of jute, flax, hemp, and sisal) and a wide variety of feed crops (most grains are also fed to animals, while ruminants require roughages, including alfalfa and varieties of hay and straw).
Our species has relied on domesticated plants for only about one-tenth of its evolutionary span (distinct Homo sapiens can be traced since about 200,000 years ago). The earliest dates (years before the present) for well-attested cultivation are as follows: 11,500–10,000 years for emmer (Triticum dicoccum), einkorn wheat (Triticum monococcum) and barley (Hordeum vulgare) in the Middle East, most notably in the upper reaches of the Tigris and Euphrates rivers (Zeder 2008); 10,000 years for millets (Setaria italica) in China and squash (Cucurbita species) in Mexico; 9,000 years for corn (Zea mays) in Central America; 7,000 for rice (Oryza sativa) in China and potatoes (Solanum tuberosum in the Andes (Price and Bar-Yosef 2011).
Tracing the growth of major crops can be done in several revealing ways. Their planted areas have been expanding or shrinking as new crops have been introduced and old ones have fallen out of favor and as new tastes and preferences have displaced old dietary patterns. The most notable example in the first category has been the diffusion of corn, potatoes, tomatoes, and peppers. Unknown outside Central and South America before 1492, these crops eventually became worldwide favorites of enormous economic and dietary importance. The most common example in the second category has been the declining consumption of legumes and rising intake of processed cereals. As modern societies have become more affluent, eating of leguminous grains (nutritious but often difficult to digest) has receded (with more affordable meat supplying high-quality protein), while intakes of white rice and white flour (increasingly in the form of convenience foods, including baked goods and noodles) have reached new highs.
Two variables have driven the increases in total crop harvests: growing populations that have required larger harvests for direct food consumption, and dietary transitions that have resulted in higher consumption of animal foodstuffs (meat, dairy foods, eggs) whose production has required greatly expanded cultivation of feed crops. As a result, in affluent countries crop production is not destined primarily for direct food consumption (wheat flour, whole grains, potatoes, vegetables, fruits) or for processing to produce sugar and alcoholic beverages, but for feeding meat and dairy mammals and meat and egg-laying birds (and in the US about 40% of all corn is now diverted to produce automotive ethanol).
But no growth indicator of crop cultivation has been more revealing than the increase in average yields. Given the finite amount of good-quality farmland, modern societies would not provide adequate diets to greatly expanded populations without rising yields. In turn, these rising yields have been made possible by the development of improved cultivars and by rising materials and energy inputs, most notably by more widespread irrigation, mass-scale fertilization by synthetic and inorganic compounds, and now nearly universal mechanization of field tasks enabled by growing consumption of liquid fuels and electricity.
Crop Yields
All crop yields have their productivity limits set by the efficiency of photosynthesis. Its maximum limit of converting light energy to chemical energy in new phytomass is almost 27% but as only 43% of the incoming radiation is photosynthetically active (blue and red parts of the spectrum), that rate is reduced to about 12%. Reflection of the light and its transmission through leaves make a minor difference, taking the overall rate down to about 11%. This means that an ideal crop, with leaves positioned at 90° angle to direct sunlight, would fix daily 1.7 t/ha of new phytomass or 620 t/ha if the growth continued throughout the year.
But inherently large losses accompany the rapid rates of photosynthetic conversion. Plant enzymes cannot keep up with the incoming radiation, and because chlorophyll cannot store this influx the incoming energy is partially reradiated, lowering the performance to roughly 8–9%. Autotrophic respiration (typically at 40–50% of NPP) lowers the best achievable plant growth efficiencies to around 5%—and the highest recorded short-term rates of net photosynthesis under optimum conditions are indeed that high. But most crops will not perform that well during the entire growing season because their performance will be limited by various environmental factors.
In addition, there are important interspecific differences. The photosynthetic pathway used by most plants, a multistep process of O2 and CO2 exchange energized by red and blue light, was first traced by Melvin Calvin and Andrew Benson during the early 1950s (Bassham and Calvin 1957; Calvin 1989). Because the first stable carbon compound produced by this process is phosphoglyceric acid containing three carbons plants deploying this carboxylation, reduction and regeneration sequences are known as C3 plants and they include most of the staple grain, legume, and potato crops, as well all common vegetables and fruits. Their principal downside is photorespiration, daytime oxygenation that wastes part of the newly produced photosynthates.
Some plants avoid this loss by producing first four-carbon acids (Hatch 1992). Most of these C4 plants are also structurally different from C3 species, as their vascular conducting tissue is surrounded by a bundle sheath of large cells filled with chloroplasts. Corn, sugar cane, sorghum, and millets are the most important C4 crops. Unfortunately, some of the most persistent weeds—including crab grass (Digitaria sanguinalis), barnyard grass (Echinochloa crus-galli), and pigweed (Amaranthus retroflexus)—are also C4 species, presenting an unwelcome competition for C3 crops. Although the C4 sequence needs more energy than the Calvin-Benson cycle, the absence of photorespiration more than makes up for that and C4 species are inherently better overall converters of sunlight into phytomass. Differences are around 40% when comparing the maximum daily growth rates, but daily maxima integrated and averaged over an entire growing season are up to 70% higher.
Moreover, photosynthesis in C4 species proceeds without any light saturation, while C3 plants reach their peak at irradiances around 300 W/m2. And while C3 crops do best in a temperature between 15° and 25°C, photosynthetic optima for C4 crops are 30°–45°C, making then much better adapted for sunny, hot, and arid climates. Everything else being equal, typical yields of corn and sugar cane are thus well ahead of average yields of wheat and sugar beets, the two common C3 species that have a similar nutritional composition. Peak daily growth rates actually measured in fields are more than 50 g/m2 for corn, but less than 20 g/m2 for wheat. Means for the entire growing season are obviously much lower: in 2015, a very good corn harvest of 10 t/ha corresponded (assuming total growth period of 150 days) to average daily growth of less than 10 g/m2.
There can be no reliable reconstruction of prehistoric crop yields, only isolated approximations are available to quantify the harvests in antiquity, and even the reconstructions of medieval yield trajectories remain elusive. But if such data were available, they would not reveal any surprises because indirect agronomic and population evidence attests to low, barely changing and highly fluctuating staple grain yields. And the history of English wheat yields—a rare instance where we have nearly a millennium of evidence of reports, estimates and eventually of actual measurements that allows us to reconstruct the growth trajectory—illustrates how uncertain our conclusions are even regarding the early part of the early modern era.
There are two major reasons for these uncertainties. European yields were traditionally expressed in relative terms, as returns of planted seed, and poor harvests yielded barely enough to produce sufficient seed for the next year’s planting. Up to 30% of all seed from below-average harvests had to be diverted to seed and only with higher yields during the early modern era did that share gradually decline to less than 10% by the mid-18th century. In addition, the original medieval measures (bushels) were volumetric rather than in mass units, and because premodern seeds were smaller than our high-yielding cultivars their conversions to mass equivalents cannot be highly accurate. And even some of the best (usually monastic) records have many gaps, and yields were also subject to considerable annual fluctuations caused by inclement weather, epidemics, and warfare, making even very accurate rates for one or two years hard to interpret.
Earlier studies of English wheat yields assumed typical wheat seed returns of between three and four during the 13th century, implying very low harvests of just above 500 kg/ha, with reported maxima close to 1 t/ha (Bennett 1935; Stanhill 1976; Clark 1991). Amthor’s (1998) compilation of yields based on a wide range of manorial, parish, and country records show values ranging mostly between 280 and 570 kg/ha for the 13th to 15th centuries (with exceptional maxima of 820–1130 kg/ha) and 550–950 kg/ha for the subsequent two centuries. A permanent doubling of low medieval wheat yields took about 500 years, and discernible takeoff began only after 1600. But uncertainties mark even the 18th century: depending on the sources used, wheat yields did not grow at all—or as much as doubled by 1800 (Overton 1984).
More recent assessments produce a different trajectory. Campbell (2000) derived his average wheat yield for the year 1300—0.78 t/ha—from the assessments of demesne (land attached to manors) harvests and assumed the seeding rate of almost 0.2 t/ha. But in the early 14th century the demesnes accounted only about 25% of the cultivated land and assumptions must be made about the average output from peasant fields, with arguments made for both higher or lower outputs (and a compromise assumption of equal yields). Allen (2005) adjusted his 1300 mean to 0.72 t/ha and put the 1500 average about a third higher at 0.94 t/ha. There is little doubt that by 1700 the yields were much higher, close to 1.3 t/ha, but according to Brunt (2015), English wheat yields of the 1690s were depressed by unusually poor weather while those of the late 1850s were inflated by exceptionally good weather, and this combination led to overestimating the period’s growth of yields by as much as 50%.
After a pause during the 18th century, the yields rose to about 1.9 t/ha by 1850, with the general adoption of regular rotations with legumes and improved seed selection accounting for most of the gain. According to Allen (2005), average English wheat yields thus increased almost threefold between 1300 and 1850. Subsequent yield rise was credited by Chorley (1981) primarily to the general adoption of rotations including legume cover crops, as in the common four-year succession of wheat, turnips, barley, and clover in Norfolk. These practices had at least tripled the rate of symbiotic nitrogen fixation (Campbell and Overton 1993), and Chorley (1981) concluded that the importance of this neglected innovation was comparable to the effects of concurrent industrialization.
Other measures that boosted English wheat yields included extensive land drainage, higher rates of manuring, and better cultivars. By 1850 many counties had harvests of 2 t/ha (Stanhill 1976), and by 1900 average British wheat yields had surpassed 2 t/ha. Dutch wheat yields showed a similar rate of improvement but average French yields did not surpass 1.3 t/ha by 1900. Even when opting for Allen’s (2005) reconstruction (an almost threefold rise between 1300 and 1850), average annual linear growth would have been just 0.3% and the mean rate during the second half of the 19th century would have been just above 0.2%/year.
The long-term trajectory of English wheat yields is the first instance of a very common growth sequence that will be pointed out many times in the coming chapters of this book dealing with technical advances. Centuries, even millennia, of no growth or marginal improvements preceded an eventual takeoff that was followed by a period of impressive gains that began in a few instances already during the 18th century, but much more commonly during the 19th and 20th centuries. While some of these exponential trajectories continue (albeit at often attenuated rates), recent decades have seen many of these growth phenomena approaching unmistakable plateaus, some even entering a period of (temporary or longer-lasting) decline.
And wheat yields also represent one of those relatively rare phenomena where the US has not only not led the world in their modern growth but was a belated follower. This is due to the extensive nature of US wheat farming, dominated by vast areas of the Great Plains where the climate is much harsher than in Atlantic Europe. Recurrent shortages of precipitation preclude heavy fertilizer applications, and low temperatures limit the cultivation of winter wheat and reduce the average yield. Records from Kansas, the heart of the Great Plains wheat region, show nearly a century of stagnating (and highly fluctuating) harvests. Average yields (calculated as the mean of the previous five years) was 1 t/ha in 1870 as well as in 1900 and 1950 (1.04, 0.98 and 1.06, to be exact), and they rose above 2 t/ha only by 1970 (USDA 2016a). Nationwide wheat yield rose only marginally during the second half of the 19th century from 0.74 t/ha in 1866 to 0.82 t/ha in 1900, and it was still only 1.11 t/ha by 1950.
During the first half of the 20th century, plant breeders aimed at introducing new cultivars that would be more resistant to wheat diseases and whose shorter and stiffer stalks would reduce the lodging (falling over) of maturing crops and the resulting yield loss. Traditional cereal cultivars had a very low harvest index expressed as the ratio of grain yield and the total above-ground phytomass including inedible straw (stalks and leaves). This quotient, often called the grain-to-straw ratio, was as low as 0.2–0.3 for wheat (harvests produced three to five times as much straw as grain) and no higher than 0.36 for rice (Donald and Hamblin 1976; Smil 1999).
Short-stalked wheat varieties may have originated in Korea in the third or fourth century. They reached Japan by the 16th century and by the early 20th century the Japanese variety Akakomugi was brought to Italy for crossing. In 1917 Daruma, another Japanese short-straw variety, was crossed with American Fultz; in 1924 that cultivar was crossed with Turkey Red; and in 1935 Gonjiro Inazuka released the final selection of that cross as Norin 10, just 55 cm tall (Reitz and Salmon 1968; Lumpkin 2015). Two key genes produced semidwarf plants and allowed better nitrogen uptake and heavier grain heads without becoming top-heavy and lodging. Samples of Norin 10 were brought to the US by an American breeder visiting Japan after World War II, and Orville Vogel used the cultivar to produce Gaines, the first semidwarf winter wheat suitable for commercial production, released in 1961 (Vogel 1977). Vogel also provided Norin 10 to Norman Borlaug, who led Mexico’s antilodging, yield-raising breeding program that has operated since 1966 as CIMMYT, the International Maize and Wheat Improvement Center.
CIMMYT released the first two high-yielding semidwarf commercial Norin 10 derivatives (Pitic 62 and Penjamo) in 1962 (Lumpkin 2015). These cultivars and their successors enabled the sudden yield growth that became known as the Green Revolution and resulted in a Nobel Prize for Norman Borlaug (Borlaug 1970). Their harvest indices were around 0.5, yielding as much edible grain as inedible straw, and their worldwide diffusion changed the yield prospects. Berry et al. (2015) offered a closer look at the long-term impact of short-stalked wheat by analyzing the height of UK winter wheat using data from national variety testing trials between 1977 and 2013. Overall average height reduction was 22 cm (from 110 to 88 cm) and annual yield increases attributable to new varieties were 61 kg/ha between 1948 and 1981 and 74 kg/ha between 1982 and 2007, amounting to a total genetic improvement of about 3 t/ha between 1970 and 2007.
Until the 1960s, wheat was the world’s leading grain crop, but Asia’s growing populations and high demand for meat pushed both rice and corn ahead of wheat. Corn has become the most important grain (with an annual global harvest just above 1 Gt), followed by rice, with wheat closely behind. China, India, US, Russia, and France are the world’s largest wheat producers, Canada, US, Australia, France, and Russia are the crop’s leading exporters. Wheat’s global yield (depressed by crops grown in a semi-arid environment without adequate irrigation and fertilization) rose from 1.2 t/ha in 1965 to 1.85 t/ha in 1980, a gain of nearly 55% in just 15 years, and in the next 15 years it increased by another 35%. The response was no less impressive in the most productive European agricultures where the yields of 3–4 t/ha reached during the early 1960s marked the limit of improved traditional cultivars grown under near-optimal environmental conditions with plenty of fertilizers. Western European wheat yields more than doubled from 3 t/ha during the early 1960s to 6.5 t/ha during the early 1990s (FAO 2018).
After the yields began to rise during the 1960s, progress remained linear but average growth rates were substantially higher (in some places up to an order of magnitude) than during the previous decades of marginal gains. Global wheat yields rose from the average of just 1.17 t/ha (mean of 1961–1965) to 3.15 t/ha (mean of 2010–2014), an annual gain of 3.2% or about 40 kg/year per hectare (FAO 2018). During the same period, the British harvest grew by 1.7% a year, the French by 3.2%, and growth rates reached 5% in India and 7% in China. The yield trajectories of other major wheat-producing countries show decades of stagnating low productivity pre-1960 followed by more than half a century of linear growth, including in Mexico (showing a fairly steep improvement), Russia, and Spain (Calderini and Slafer 1998).
Nationwide means of US wheat yields have been available annually since 1866 (USDA 2017a) and their trajectory closely fits a logistic curve with obvious plateauing since the 1980s and with the prospect for 2050 no higher than the record harvests of the early 2010s (figure 2.9). Will the stagnation persist this time? The introduction of modern cultivars raised the nationwide average yield from 1.76 t/ha in 1960 to 2.93 t/ha in 2015, a growth rate of 1.2% a year. A closer look reveals the continuation of substantial annual deviation from the long-term trends, with both above- and below-average yields fluctuating by more than 10% for winter wheat, and much larger departures (up to about 40%) for Western Canadian spring wheat (Graf 2013).

Logistic growth (inflection point in 1970, asymptote at 46.5 bushels/acre) of average American wheat yields, 1866–2015. Data from USDA (2017a).
And there are also clear regional differences. Harvests in the eastern (rainier) states grew a bit faster than those in the central (more arid) states, and western yields rose from just over 2 t/ha to nearly 4.5 t/ha by the early 1990s (an average annual growth rate of nearly 4%) before their linear growth reached a distinct plateau from 1993. Unfortunately, the western US is not the only region that has seen the arrival of wheat yield plateaus. Statistical testing by Lin and Huybers (2012) confirmed that average wheat yields have also leveled off not only in the high-yielding countries of the European Union—in Italy (since 1995), in France (since 1996), in the UK (since 1997)—but also in Turkey (since 2000), India (since 2001), Egypt (since 2004), Pakistan (since 2007), and most notably, since 2009 in China. In total, nearly half of the 47 regions they tested had transitioned from linear growth to level trajectories. Most of these yield plateaus are in affluent countries with large food surpluses where agricultural policies discourage further yield increases.
Brissona et al. (2010) took a closer look at the French decline and stagnation in the growth trend of wheat yields that has been evident in most of the country’s regions mainly since 1996–1998. They concluded that this was not due to genetic causes, but that the continuing breeding progress was partially negated by a changing climate, mainly due to heat stress during grain filling and drought during stem elongation. Agronomic changes guided by economic considerations (decline of legumes in cereal rotations, expanded rapeseed cultivation, reduced nitrogen fertilization) had also contributed to the new trend since the year 2000. In any case, even a prolonged yield plateau would have no effect on domestic supply and a minor effect on exports, but the presence of China (with nearly stabilized population but rising meat demand) and India and Pakistan (with their still expanding populations) among the countries with wheat yield stagnation is worrisome.
Chinese crop yield stagnation has not been limited only to wheat. Between 1980 and 2005, when wheat yields increased on about 58% of the total harvest area but stagnated on about 16% of the area, rice and corn yields stagnated, respectively, on 50% and 54% of their total harvested areas (Li et al. 2016). Areas particularly prone to yield stagnation have included regions planted to lowland rice, upland intensive subtropical plantings with wheat, and regions growing corn in the temperate mixed system. The extent of these yield stagnations is high enough to raise questions about the country’s long-term staple food self-sufficiency: unlike Japan or South Korea, China is too large to secure most of its grain by imports.
But not all major wheat-growing countries show the dominant trajectory of flat yield followed by rising (or rising and leveling-off) trajectories. The Australian experience has been perhaps the most idiosyncratic (Angus 2011). Yields fell from around 1 t/ha in 1860 to less than 0.5 t/ha by 1900 due to soil nutrient exhaustion, and although they recovered somewhat due to superphosphate fertilization, new cultivars, and fallowing, they remained below 1 t/ha until the early 1940s. Legume rotations boosted the yield above 1 t/ha after 1950, but the period of rapid yield increases brought by semidwarf cultivars after 1980 was relatively short as a millennium drought caused great fluctuations and depressed yields in the new century.
Global rice production is larger than the worldwide wheat harvest when measured in unmilled grain (paddy rice), smaller when compared after milling (extraction rates are about 85% for wheat but just 67% for white rice, with the voluminous milling residues use for feed, specialty foods, and for various industrial products). Average per capita rice consumption has been declining in all affluent countries where rice was the traditional staple (Japan, South Korea, Taiwan) and recently also in China. Global output is still rising to meet the demand in Southeast Asia and Africa. The long-term trajectory of rice yield has been very similar to changes in wheat productivity: centuries of stagnation or marginal gains followed by impressive post-1960 growth due to the introduction of short-stalked, high-yielding cultivars.
The best long-term record of rice yields is available for Japan (Miyamoto 2004; Bassino 2006). Average yields were above 1 t/ha already during the early Tokugawa period (1603–1867) period and by the end of the 19th century they rose to about 2.25 t/ha (as milled, 25% higher as unmilled paddy rice). Long-term linear growth during the 300 years from 1600 was thus less than 0.4%/year, similar to contemporary European rates for wheat harvests. But Japanese rice harvests (much like the English wheat yields) were exceptional: even during the 1950s, typical yields in India, Indonesia, and China were no higher than, respectively, 1.5, 1.7, and 2 t/ha (FAO 2018).
The development of short-stalked rice cultivars (crossing the short japonica variety with the taller indica) was begun by FAO in 1949 in India but the main work proceeded (concurrently with the breeding of high-yielding wheats) at the International Rice Research Institute (IRRI) at Los Baños in the Philippines, established in 1960. The first high-yielding semidwarf cultivar released by the IRRI was IR8, whose yields in field trials in 1966 averaged 9.4 t/ha and, unlike with other tested cultivars, actually rose with higher nitrogen fertilization (IRRI 1982; Hargrove and Coffman 2006). But IR8 also had undesirable properties: its chalky grain had a high breakage rate during milling and its high amylose content made it harden after cooling.
But the cultivar launched Asia’s Green Revolution in rice and it was followed by better semidwarf varieties that were also more resistant to major pests and diseases. IR36 in 1976 was the first rapidly maturing cultivar (in just 105 days compared to 130 days for IR8) producing preferred slender grain, and it was followed by other releases developed at the IRRI by teams led by Gurdev Singh Khush (IRRI 1982). The adoption of new cultivars has diffused rapidly from Southeastern Asia to the rest of the continent as well as to Latin America and Africa (Dalrymple 1986). Productivity results have been impressive: between 1965 and 2015, average rice yields in China rose 2.3 times to 6.8 t/ha (figure 2.10). Yields in India and Indonesia increased 2.8 times (to 3.6 and 5.1 t/ha, respectively), implying annual linear growth rates of 2.7–3.7%, while the mean global yield had improved from 2 to 4.6 t/ha (2.6%/year).

Longsheng Rice Terraces in Guangxi province in China: even these small fields now have high yields thanks to intensive fertilization. Photo available at wikimedia.
Corn, the dominant feed grain in affluent countries and an important staple food in Latin America and Africa, was the first crop whose yields benefited from hybridization. In 1908 George Harrison Shull was the first breeder to report on inbred corn lines showing deterioration of vigor and yield that were completely recovered in hybrids between two inbred (homozygous) lines (Crow 1998). After years of experiments, American breeders developed crosses that produced consistently higher yields and introduced them commercially starting in the late 1920s. The subsequent diffusion of hybrid corn in the US was extraordinarily rapid, from less than 10% of all plantings in 1935 to more than 90% just four years later (Hoegemeyer 2014). New hybrids also produced more uniform plants (better for machine harvesting) and proved considerably more drought-tolerant, a more important consideration during the exceptional Great Plains drought of the 1930s than their higher yield under optimal conditions.
Yields of traditional pre-1930 open-pollinated corn varieties stayed mostly between 1.3 and 1.8 t/ha: in 1866 (the first recorded year), the US mean was 1.5 t/ha, in 1900 it was 1.8 and in 1930 just 1.3 t/ha, and while there were expected annual weather-induced fluctuations the yield trajectory remained essentially flat (USDA 2017a). Between 1930 and 1960, the adoption of new commercial double crosses improved the average yield from 1.3 t/ha to about 3.4 t/ha corresponding to an average yield gain of 70 kg/year and mean annual linear growth of 5.4%. Subsequent adoption of single-cross varieties (they became dominant by 1970) produced even higher gains, about 130 kg/year, from 3.4 t/ha in 1965 to 8.6 t/ha by the year 2000, implying an average linear growth rate of 3.8%/year (Crow 1998; figure 2.11).
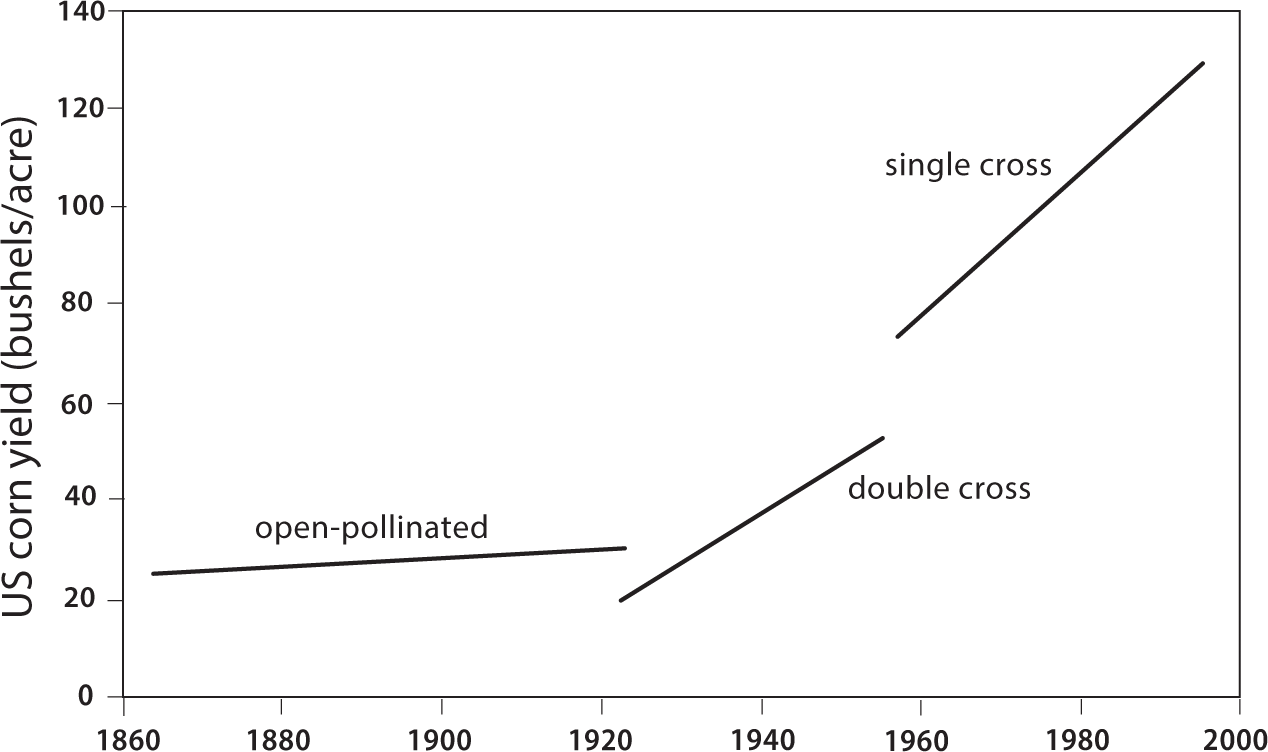
Trends of distinct stages of stagnation and growth of average American grain corn yields, 1866–1997. Based on Crow (1998).
And the growth continued in the early 21st century, with the 2015 crop setting a new record of 10.6 t/ha and linear growth rate of about 1.6% during the 15 years. But it would be wrong to credit that impressive yield growth (nearly an order of magnitude gain, from 1.3 t/ha in 1930 to 10.6 t/ha in 2015) solely to hybrid seeds. High yields would have been impossible without greatly expanded applications of nitrogenous fertilizers which allowed a far greater density of planting, widespread use of herbicides and insecticides, and complete mechanization of planting and harvesting that minimized the time needed for field operations and reduced grain losses (Crow 1998). The complete trajectory of average US corn yields (1866–2015) fits almost perfectly a logistic curve that would plateau around 2050 at about 12 t/ha (figure 2.12). That would be a challenging, but not an impossible achievement given that Iowa’s record 2016 yield (in the state with the best growing conditions) was 12.7 t/ha.

Logistic growth trajectory (inflection point in 1988, asymptote at 194.1 bushels/acre) of average American grain corn yields, 1866–2015. Data from USDA (2017a).
Higher planting densities were made possible by hybrid improvements in stress tolerance but higher yields could not be achieved without requisite increases in fertilizer applications. During the past 30 years, average North American corn seeding rates have increased at a linear rate by about 750 seeds/ha every year; in 2015 they averaged about 78,000 seeds/ha and in that year almost 10% of the total corn area in the US and Canada was planted with more than 89,000 seeds/ha (Pioneer 2017). Nitrogen applications in US corn production nearly quadrupled between 1960 and 2015, while phosphate applications about doubled and potassium use more than doubled.
America’s corn yields remain exceptionally high and they have kept on growing, from a higher base, more impressively than the global mean. Six decades after the widespread adoption of hybrids, American farmers were the first producers to grow transgenic corn. The first genetically modified variety was commercialized in 1996 by Monsanto as “Roundup Ready Corn”: it incorporated genes from Bacillus thuringiensis that make corn plants tolerant to high levels of herbicide applications (initially to glyphosate, a broad-spectrum herbicide) (Gewin 2003). Bacillus thuringiensis transfers expressing toxins can be also used to combat insect infestations. Genetically modified cultivars should have increased yields by preventing the losses that would have taken place in the absence of insect and herbicide tolerance, and the actual gains depend on the efficacy of insect and weed control before the introduction of transgenic plants.
Transgenic corn conquered US production quite rapidly: starting from zero in 1996, the area planted to new cultivars rose to 25% in the year 2000, and in 2016 89% of all corn plantings had herbicide tolerance, 79% had insect tolerance, and 76% were stacked varieties, containing both traits (USDA 2016b). Genetically modified soybeans, rapeseed (and cotton) had followed soon afterward, but the adoption of transgenic crops has encountered a great deal of consumer as well as regulatory resistance (particularly in the EU). As a result, there is still no large-scale cultivation of transgenic wheat or rice. But the opposition is not based on solid scientific foundations. Klümper and Qaim (2014) examined all principal factors that influence outcomes of genetically modified cropping and their meta-analysis provided robust evidence of benefits for producers in both affluent and low-income countries. On average, the adoption of transgenic crops has reduced pesticide use by 37% while it increased crop yields by 22% and profits by 68%, and yield gains were larger for insect-resistant than for herbicide-tolerant crops, and they have been higher in low-income countries.
But there has been one worrisome trend. Lobell et al. (2014) analyzed corn yields in the most productive Corn Belt states (Iowa, Illinois, and Indiana) and found that between 1995 and 2012 agronomic changes translated into improved drought tolerance of plants but that corn yields remain sensitive to water vapor pressure deficit (VPD), a variable that was not included in the previous analyses of yields and climate change. Because VPD is expected to increase from 2.2 kPa in 2014 to 2.65 kPa by 2050, the unchanged annual rainfall across the study area (940 mm) would support an average yield about 10% lower, making production more vulnerable to even moderate droughts (Ort and Long 2014).
But neither short-stalked cultivars nor genetically modified plants have changed the fundamental nature of crop yield trajectories: linear growth has been the dominant long-term trend in increasing average global productivity of staple grains since the beginning of the green revolution of the 1960s. Exponential increase in crop yields is possible during relatively short time periods (10–20 years) but not over the long term because it must eventually approach a yield potential ceiling determined by biophysical limits: that is why projections assuming that future crop yields will increase at exponential rates have absolutely no justification in past experience (Grassini et al. 2013). Such a growth pattern would require unprecedented departures from the prevailing ways of crop breeding and from the best agronomic procedures. And while some astonishing advances in designing synthetic crops de novo cannot be absolutely excluded, such designs remain in the realm of science fiction and cannot be seen as plausible contributions to feeding the world in the coming few decades.
Moreover, it is important to reiterate that a wide variety of annual crop yield gains have begun to deviate from decades of linear growth. This has ranged from declines in the annual rate of yield gain (some fairly abrupt, others showing a gradual transition to reduced rates) to the establishment of clear yield plateaus. Grassini et al. (2013) showed that since the beginning of the Green Revolution of the 1960s the first pattern, linear piecewise growth with a decreasing growth rate, has applied to such crops as Indonesian rice and Chinese corn, while the second pattern (linear growth with upper plateau) is much more common, evident for Chinese, Korean, and Californian rice, wheat in northwestern Europe and India, and corn in Italy. Although these slowdowns and plateaus have not been worldwide phenomena extending to all major crops, some of these shifts have been worrisome because they have affected some key crops in major cropping regions.
Looking ahead, a warmer world with higher atmospheric CO2 levels will have complex impacts on future crop productivity. Net outcome will depend on species- and environment-specific responses not only to higher average temperatures but also to changes in growing season and temperatures (and water availability) during critical phases of plant development. Even one of the least controversial expectations—that C3 plants should benefit more from increasing concentrations of atmospheric CO2 than C4 species, mainly because of promoting stomatal closure and saving water (Bazzaz and Sombroek 1996; Körner et al. 2007)—will be greatly affected by nutrient availability and higher temperatures.
The extent of what has become known (inaccurately) as the CO2 fertilization effect has been put at a 20–60% increase of gross primary productivity for land photosynthesis at large. Wenzel et al. (2016) constrained that uncertainty (by looking at annual amplitude of the CO2 seasonal cycle) to 37 ± 9% for high-latitude ecosystems and 32% or extratropical ecosystems under a doubling of CO2 concentrations. But such findings cannot be extrapolated to specific crops, net gains could be much lower, and some crops may see substantial yield declines. Most notably, an assessment based on 30 different wheat crop models concluded that warming is already slowing yield gains in most wheat-growing locations, with wheat yield declines with rising temperature likely to be larger than previously expected (falling by 6% for every degree of temperature increase) and becoming more variable (Asseng et al. 2014).
Moreover, even an unchanged trajectory or a clear new trend may be accompanied by greater yield variability and increased unpredictability of harvests. Analysis of changes in yield variability of major crops during the last two decades of the 20th century showed a decrease in 33% of the global harvested area for corn, in 21% of areas for wheat, and 19% of areas for rice, while significant variability increases were found in 11%, 22%, and 16% of the respective areas (Iizumi and Ramankutty 2016). Major agricultural regions with higher variability included Indonesia and South China for rice and Australia, France, and Ukraine for wheat.
Assessments of future crop harvests are on a safer ground when examining yield potential and quantifying the yield gap for specific crops in specific locations. Yield potential refers to a crop whose harvest is limited by the plant’s genetic makeup, received solar radiation, temperature during the growing season, and atmospheric CO2 concentration, and not by shortages of nutrients and water or by pests and weeds. The yield gap is the difference between yield potential (with different values for fully irrigated, partially irrigated, and rainfed crops) and actual yield. Record yields achieved during contests designed to maximize productivity realize 70–85% of the potential, and the difference between 85% of potential yields and actual prevailing crop yields is the exploitable yield gap (FAO 2015c). This value is perhaps the most revealing information about the prospects of long-term crop yield growth and ensuing food security in all regions where nutritional supply remains barely adequate or inadequate.
The best way to determine the yield potential is to use a variety of crop growth models primed with appropriate natural parameters. Global Yield Gap and Water Productivity Atlas uses them to provide what it terms “robust estimates of untapped crop production potential on existing farmland based on current climate and available soil and water resources” (GYGA 2017). In 2017 the atlas covered, respectively, 60%, 58%, and 35% of the world’s rice, corn, and wheat production and it identifies the regions with the greatest potential for yield growth, allowing an appraisal of the likelihood of food self-sufficiency or the extent of future imports.
Average absolute nationwide yield gaps (all in t/ha) in the US are 2–3 for both rainfed and irrigated corn and 3–4 for irrigated rice (wheat coverage is not yet available), 1.6–2.4 for rainfed and 3.2–4 for irrigated wheat in India, and 2–3 for irrigated rice in China. As expected, absolute gaps are much larger in sub-Saharan Africa where inadequate nutrient supply and poor agronomic practices have kept yields far below their potential. For example, water-limited yields for corn are 12–13 t/ha in Ethiopia and 10–11 t/ha in Nigeria, and with actual harvest being, respectively, just 2–3 and 1–2 t/ha this creates huge yield gaps between 9 and 11 t/ha. This means that even with modest agronomic improvements crop yields in the sub-Saharan Africa could see the fastest growth rates during the coming decades. Yield gaps, quantified and mapped on large scales, are useful guides for assessing the extent of future crop yield growth.
In contrast, world record harvests achieved on small plots under optimal growing conditions should not be taken as indicators of the potential growth of national or regional yields but as demonstrations of how close some of these performances have come to achievable photosynthetic maxima. Remarkably, the US record corn yield rose from 23.5 t/ha in 1985 to 33.3 t/ha in 2015, which means that its average annual gain of 327 kg/ha was three times higher than the corresponding value for the nationwide mean (averages of 7.4 and 10.6 t/ha, that is annual yield gain of 107 kg/ha during those 30 years). Three decades before a Virginia farmer set the record corn harvest of just over 33 t/ha, Tollenaar (1985) calculated that the maximum theoretical yield with existing cultivars should be about 32 t/ha, but that plausible future changes in the plant’s energy conversion and photosynthate partitioning might raise the theoretical level to just over 83 t/ha.
And 2015 saw new world records also for winter wheat and rice. Wheat yield of 16.52 t/ha harvested in Lincolnshire in eastern England was nearly twice the national mean of 8.8 t/ha and five time the global mean of 3.3 t/ha (AHDB 2015; FAO 2018). The record for rice of 22.4 t/ha, by a farmer in Nalanda district of India’s Bihar state, was nearly five times the global mean of 4.6 t/ha and more than six times the Indian mean of 3.5 t/ha. For comparison, the yield potential of temperate direct-seeded high-yielding rice grown in a southern US state and in California (which now yields between 8.3 (long-grain) and 9.1 (medium-grain) t/ha) has been set at 14.5 t/ha, with actual top yields falling within 85% of the calculated value (Espe et al. 2016).
The best available long-term records for major crops other than staple grain follow the same general pattern of very long premodern yield stagnation followed by decades of linear growth made possible by better cultivars, adequate fertilization, use of pesticides and herbicides, mechanized harvesting and, in many cases, also by supplementary irrigation. In 2015 soybeans were the leading US crop by planted area (usually they are second only to corn) but their cultivation took off only during the 1930s. Yields rose from just 875 kg/ha in 1930 to 1.46 t/ha by 1950, 2.56 t/ha by the year 2000, and 3.2 t/ha in 2015 (USDA 2017a), a linear growth adding annually about 27 kg/ha.
Assessments of future global supply focus on staple crops and typically give little attention to fruits and vegetables. Harvests of these crops have also benefited from the combination of better cultivars, better agronomic practices, and enhanced protection against diseases and pests. During the 50 years between the early 1960s and the early 2010s, the American fruit crop had averaged an annual linear harvest increment of about 150 kg/ha (but apples did much better at 500 kg/ha and are now at about 40 t/ha) and during the same period the average annual gain for all vegetables (excluding melons) was nearly 400 kg/ha (FAO 2018).
But the gains in low-income countries have been much smaller, with annual fruit gains of less than 100 kg/ha. This lag matters, because low intakes of fruit and vegetables are a leading risk factor for chronic disease, and Siegel et al. (2014) showed that in most countries their supply falls below recommended levels. In 2009 the global shortfall was 22%, with median supply/need ratios being just 0.42 in low-income and 1.02 in affluent countries. This inadequacy could be eliminated only by a combination of rising yields and reduced food waste, but improving fruit and vegetable yields is often highly resource-intensive as many of these crops need high nitrogen fertilizer inputs and supplementary irrigation.
Animals
Animal growth has always fascinated many scientific observers, and modern contributions to its understanding have come both from theoretical biology studies and careful field observations, and from disciplines ranging from genetics and biochemistry to ecology and animal husbandry. Thompson (1942) and Brody (1945) remain the classic book-length treatments and they have been followed by volumes dealing with animal growth in general (McMahon and Bonner 1983; Gerrard and Grant 2007), as well as by volumes on growth and its regulation in farm animals (Campion et al. 1989; Scanes 2003; Hossner 2005; Lawrence et al. 2013).
Animal growth begins with sexual reproduction, and embryonic growth in birds and mammals (much less studied than postnatal development) is well described by the Gompertz function (Ricklefs 2010). As expected, embryonic growth rates decline with neonate size as the −¼ power. Growth rates of neonates weighing 100 g (a typical kitten) are nearly an order of magnitude faster than those of neonates weighing 10 kg (red deer is a good example). The postnatal growth rate scales linearly with embryonic growth rates but it is, on the average, nearly five times more rapid in birds than in mammals.
Growth Imperatives
Extremes of animal growth are dictated by energetic and mechanical imperatives. The temperature limits of animal life are much narrower than those for unicellular organisms (Clarke 2014). Rare marine invertebrates associated with ocean hydrothermal vents can function in temperatures of 60–80°C and few terrestrial invertebrates can survive temperatures of up to about 60°C. Even the most resilient ectothermic vertebrates (cold-blooded organisms that regulate their body temperature by relying on external energy inputs) can manage only up to 46°C, and the cellular temperature of endothermic vertebrates ranges between 30° and 45°C.
Ectotherms can be microscopic (smaller than 50 μm) or, as is the case with hundreds of thousands of insect species, have body mass less than 1 milligram. Even beetles (Coleoptera) and butterflies (Lepidoptera) rarely go above 0.2 g (Dillon and Frazier 2013). In contrast, endotherms, warm-blooded organisms that maintain a steady body temperature, have minimum weights determined by the ratio of body area to body volume. Obviously, for any increase in size (height, length), body area goes up by the square of that increase and body volume by its cube. An endothermic shrew sized as a tiny insect would have too much body surface in relation to its body volume and its radiative heat loss (particularly during cooler nights) would be so high that it would have to eat constantly but that would require spending more energy on incessant searching for food. That is why we have no smaller mammal than the Etruscan pygmy shrew (Suncus etruscus) with average body mass of 1.8 (1.5–2.5) g and 3.5 cm long without its tail.
The same imperative limits the minimum bird size: there is no smaller bird that than the bee hummingbird (Mellisuga helenae)—endemic to Cuba and now near threatened (IUCN 2017b)—with average body mass of 1.8 (1.6–2.0) g and length of 5–6 cm. At the other extreme, the growth of endotherms reduces the ratio of their surface area to their body volume (this would eventually lead to overheating), and massive animals would also encounter mechanical limits. Their volume and body mass will grow with the third power of their linear dimensions while the feet area needed to support that growing mass will scale up only with the second power, putting an extraordinary load on leg bones.
Other mechanical challenges can be alleviated by a better design, but still only within limits. For example, very long dinosaur necks reduced the need for moving around as they grazed the treetops within their reach, and hollow vertebrae (weighing only about a third of solid bones) made it possible to support very long necks as well as tails (Heeren 2011). The largest sauropods also had additional sacral vertebrae connecting their pelvis and backbone and interlocking bones in forelimbs to enhance their stability. Calculating body masses of the largest known dinosaurs might not seem to be so difficult given the preservation of complete, or nearly complete, skeletons and given the well-established ways of relating skeletal mass to body mass.
That is particularly true with birds providing the clear evolutionary link to dinosaurs—and measurements of skeletal mass and total body mass of 487 extant birds belonging to 79 species have confirmed that the two variables are accurate proxies for estimating one another (Martin-Silverstone et al. 2015). But there are large variabilities of both variables within a single species, and with phylogeny being the key controlling variable it may not be appropriate to use this relationship for estimating total body masses of extinct non-avian dinosaurs. Conceptual and methodological uncertainties in reconstructing dinosaur body masses are reviewed by Myhrvold (2013), who examined published estimates of dinosaur growth rates and reanalyzed them by improved statistical techniques.
The corrections have ranged from relatively small differences (the highest growth rate for Albertosaurus at about 155 kg/year compared to the published value of 122 kg/year) to very large discrepancies (the highest growth rate for Tyrannosaurus at 365 kg/year compared to the published value that was more than twice as large). As for the total body mass, the weight of the largest known dinosaur, a Mesozoic Argentinosaurus huinculensis was estimated, on the basis of a preserved femur (using regression relationship between humeral and femoral circumferences) to be 90 t, with 95% prediction interval between 67.4 and 124 t (Benson et al. 2014). Other most likely totals for the animal have been given as 73, 83, 90, and 100 t (Burness et al. 2001; Sellers et al. 2013; Vermeij 2016).
For comparison, African male elephants grow to as much as 6 t. But all extraordinarily large mass estimates for extinct animals remain questionable. Bates et al. (2015) found that the value obtained for a newly discovered titanosaurian Dreadnoughtus by using a scaling equation (59.3 t) is highly implausible because masses above 40 t require high body densities and expansions of soft tissue volume outside the skeleton that are both several times greater than found in living quadrupedal mammals. On the other hand, reconstructions of total weights for Tyrannosaurus rex (6–8 t, with the largest preserved animal up to 9.5 t) are based on multiple specimens of well-preserved complete skeletons and hence have smaller margins of error (Hutchinson et al. 2011).
In addition, the decades-long debate about thermal regulation in dinosaurs remains unresolved. Benton (1979) argued that dinosaurian ectothermy would have been both distinctly disadvantageous and unnecessary, but ectothermic dinosaurs could have achieved endothermy inertially, simply by being large. Grady et al. (2014) believes that the animals were mesothermic, having a metabolic rate intermediate between endothermy and ectothermy, but Myhrvold (2015) questioned their analysis. Perhaps the best conclusion is that “the commonly asked question whether dinosaurs were ectotherms or endotherms is inappropriate, and it is more constructive to ask which dinosaurs were likely to have been endothermic and which ones ectothermic” (Seebacher 2003, 105). The biomechanics of running indicates that endothermy was likely widespread in at least larger non-avian dinosaurs (Pontzer et al. 2009).
Erickson et al. (2004) concluded that a Tyrannosaurus rex whose mature mass was 5 t had a maximal growth rate of 2.1 kg/day. This rate was only between a third and one half of the rates expected for non-avian dinosaurs of similar size—but a new peak growth rate resulting from a computational analysis by Hutchinson et al. (2011) largely erases that difference. In any case, it appears that the maximum growth rates of the largest dinosaurs were comparable to those of today’s fastest growing animal, the blue whale (Balaenoptera musculus), whose reported gains are up to 90 kg/day. We may never know either the fastest growth rate or the greatest body mass of the largest dinosaur with a great degree of certainty, but there is no doubt that the body mass evolution spanning 170 million years produced many successful adaptations, including 10,000 species of extant birds (Benson et al. 2014).
Inevitably, animal growth will result in higher absolute metabolic rates but there is no simple general rule for this relationship. Allometric scaling has been used to quantify the link between body mass and metabolism across the entire range of heterotrophic organisms (McMahon and Bonner 1983; Schmidt-Nielsen 1984; Brown and West 2000). Because animal body mass is proportional to the cube and body area to the square of a linear dimension (M∝L3 and A∝L2), area relates to mass as A∝M2/3. Because of the heat loss through the body surface, it is then logical to expect that animal metabolism will scale as M2/3. Rubner (1883) confirmed this expectation by relying on just seven measurements of canine metabolism and (as already noted in the introductory chapter) his surface law remained unchallenged for half a century until Kleiber (1932) introduced his ¾ law. His original exponent was actually 0.74 but later he chose to round it to 0.75 and the actual basal metabolic rates can be calculated as 70M0.75 in kcal/day or as 3.4M0.75 in watts (Kleiber 1961).
Biologists have not been able to agree on the best explanation. The simplest suggestion is to see it as a compromise between the surface-related (0.67) and the mass-related (1.0, required to overcome gravity) exponents. McMahon (1973) ascribed the 0.75 exponent to elastic criteria of limbs. West et al. (1997), whose work has already been noted in the section on plant growth, applied their explanation of allometric scaling—based on the structure and function of a network of tubes required to distribute resources and remove metabolites—also to animals. Terminal branches of these networks must be identically sized in order to supply individual cells. Indeed, mammalian capillaries have an identical radius and the animals have an identical number of heartbeats per lifetime although their sizes span eight orders of magnitude, from shrews to whales (Marquet et al. 2005). The entire system must be optimized to reduce resistance, and a complex mathematical derivation indicates that the animal metabolism must scale with the ¾ power of body mass.
Other explanations of the ¾ law have been offered (Kooijman 2000), and Maino et al. (2014) attempted to reconcile different theories of metabolic scaling. In retrospect, it seems futile to focus on a single number because several comprehensive reexaminations of animal metabolic rates ended up with slightly to substantially different exponents. White and Seymour’s (2003) data set included 619 mammalian species (whose mass spanned five orders of magnitude) and they found that animal basal metabolic rate scales as M0.686 and that the exponent is 0.675 (very close to Rubner’s exponent) for the temperature-normalized rate. The inclusion of nonbasal metabolic rates and of too many ruminant species in older analyses were seen as the key misleading factor.
Among the major orders, Kozłowski and Konarzewski (2004) found the exponents close to 0.75 for carnivores (0.784) and for primates (0.772) but as low as 0.457 for insectivores and intermediate (0.629) for lagomorphs. The resting metabolic rate for mammals changes from around 0.66 to 0.75 as their body size increases (Banavar et al. 2010), while analysis of the best available avian metabolic data yielded 0.669, confirming Rubner’s exponent (McKechnie and Wolf 2004). Bokma (2004) concluded that it is more revealing to focus on intraspecific variability and after analyzing 113 species of fish he found no support for any universal exponent for metabolic scaling.
Glazier (2006) supported that conclusion by finding that the metabolic rate of pelagic animals (living in open water) scales isometrically (1:1, for pelagic chordata actually 1:1.1) with their body mass during their development. The most obvious explanations are high energy costs of the continual swimming required to stay afloat and rapid rates of growth and reproduction due to high levels of mortality (predation). Ectothermic exponents vary widely, 0.57–1 in lizards, 0.65–1.3 in jellyfish and comb jellies, and as much as 0.18–0.83 in benthic cnidarians. Killen et al. (2010) found the full range of intraspecific allometries in teleost fishes between 0.38 and 1.29. Boukal et al. (2014) confirmed a wide variability of the exponent within various taxa.
Additional meta-analyses will confirm the findings just cited, but at least ever since White et al. (2007) published a meta-analysis of 127 interspecific allometric exponents there should have been no doubts about the absence of any universal metabolic allometry. The effect of body mass on metabolic rate is significantly heterogeneous and in general it is stronger for endotherms than for ectotherms, with observed mean exponents of 0.804 for ectotherms and 0.704 for endotherms. A range of exponents, rather than a single value, is thus the most satisfactory answer, and Shestopaloff (2016) developed a metabolic allometric scaling model that considers both cellular transportation costs and heat dissipation constraints and that is valid across the entire range, from torpid and hibernating animals to the species with the highest levels of metabolic activity.
The model does not explicitly incorporate the ¾ value, but considers it as a possible compromise when a body mass grows both through cell enlargement (exponent 0.667) and increase in cell number (isometric scaling, with the allometric exponent of 1). Alternatively, Glazier (2010) concluded that the unifying explanation for diverse metabolic scaling that varies between 2/3 and 1 will emerge from focusing on variation between extreme boundary limits (rather than from explaining average tendencies), on how the slope and elevation (metabolic level) are interrelated, and on a more balanced consideration of internal and external (ecosystemic) factors.
Growth Trajectories
Of the two possible growth trajectories—determinate growth ceasing at maturity and indeterminate growth continuing throughout life—the first one is the norm among the endotherms. The outermost cortex of their long bones has a microstructure (an external fundamental system) showing that they have reached skeletal maturity and hence the end of any significant growth in bone circumference or girth. Continued weight gain after maturity is not uncommon among mammals but that is different from continued skeletal growth. For example, most male Asian elephants (Elephas maximus) complete their growth by the age of 21 years but then they continue to gain weight (at reduced rates) for decades, reaching 95% of asymptotic mass by about 50 years of age (Mumby et al. 2015).
Indeterminate growers can accomplish most of their growth either before or after maturation. Kozłowski and Teriokhin (1999) originally concluded that in seasonal environments most of the growth should take place before maturation where winter survival is high and mainly after maturation (displaying highly indeterminate growth) where winter survival is low. But a model that incorporates the decrease in the value of newborns (devaluation of reproduction) with the approach of the end of the favorable season changes the outcome: the relative contribution of growth before and after maturation becomes almost independent of winter survival, and most of the growth comes only after maturation, conforming to a highly indeterminate pattern (Ejsmond et al. 2010). Indeterminate growth has been described in all major ectothermic taxa (Karkach 2006).
Among invertebrates, indeterminate growth is the norm for many benthic marine organisms, freshwater bivalves, clams and mussels and for sea urchins. Insects with indeterminate growth include species with no terminal mold and no fixed number of instars (apterygota: jumping bristletails, silverfish). Indeterminately growing crustaceans include tiny cladocerans (Daphnia) as well as shrimp, crayfish, and large crabs and lobsters. Short-lived fishes in warmer regions have determinate growth, long-lived species in colder waters—commercially important salmonids (Atlantic salmon, trout) and perch as well as sharks and rays—continue growing after maturity. As already noted, the growth of fish has been most often modeled with von Bertalanffy’s function, but this choice has been problematic (Quince et al. 2008; Enberg et al. 2008; Pardo et al. 2013). The function fits better with growth after maturation but it does not do so well for the immature phase. Alternative models distinguish between the juvenile growth phase (often approaching linearity) and mature growth, where energy is diverted into reproduction (Quince et al. 2008; Enberg et al. 2008).
Evidence of indeterminate growth in reptiles has been equivocal and it is based on inadequate data (Congdon et al. 2013). Recent studies have questioned the existence, or at least the importance, of that growth pattern. The American alligator (Alligator mississippiensis) has parallel-fibered tissue that ends periosteally in an external fundamental system, confirming it as another instance of reptilian determinate growth (Woodward et al. 2011). Desert tortoises continue to grow past sexual maturity and into adulthood but their growth ends later in life (Nafus 2015). And while Congdon et al. (2013) concluded that indeterminate growth is a common feature among long-lived freshwater turtles, they found that nearly 20% of all adults of both sexes stopped growing for a decade or more and that the results of indeterminate growth are not a major factor in the evolution and longevity of those species. Indeterminate growth is uncommon among mammals, with examples including males of some kangaroo and deer species, of American bison, and of both African and Asian elephants.
Compensatory growth describes a spell of faster than usual growth rate that follows a period of reduced or arrested growth caused by inadequate nutrition (often precipitated by an extreme environmental event). Because of their determinate growth, birds and mammals invest more resources in such accelerated growth required to achieve their final size, while ectotherms with indeterminate growth remain relatively unaffected by periods of restricted nutrition (Hector and Nakagawa 2012). Fish in particular show little change in their growth rates because their lower metabolism makes them more resistant to short spells of starvation and depletion of their fat stores.
Animal growth spans a continuum of strategies delimited by a single reproductive bout (semelparity) at one end, and repeated successive breeding (iteroparity) at the other. The first extreme produces a large, in some cases truly prodigious, number of offspring; the second one results in single births or, at most, a few offspring spaced far apart. Iteroparity is favored in all cases where the juvenile survival rate varies more than an adult survival rate that is relatively high (Murphy 1968). Katsukawa et al. (2002) related these reproduction strategies to the two growth modes. Their model demonstrated that iteroparity with indeterminate growth is the best choice either when there is a nonlinear relationship between weight and energy production, or in fluctuating environments even with a linear relationship between weight and energy production. The optimal strategy in such environments is to maximize the long-term population growth rate, a goal that does not correspond with maximizing total fecundity.
Zoologists and ecologists now commonly call semelparity r selection (or strategy) and iteroparity K selection, the terms chosen first by MacArthur and Wilson (1967) and borrowed from growth-curve terminology (r being the rate of increase, K the maximum asymptotic size). Each strategy has its advantages and drawbacks. R-selected species (which include most insects) are opportunists par excellence, taking advantage of conditions that may be temporarily favorable for rapid growth. These include numerous water puddles after heavy rains to shelter mosquito larvae, trees damaged by fire presenting seemingly endless munching ground for wood-boring beetles, or a carcass of a large animal providing breeding ground for flesh flies. R-selected species produce large numbers of small offspring that mature rapidly and usually without any parental care. Such a strategy assures that more than a few will always survive, and it presents opportunities for rapid colonization of new (usually nearby but sometimes quite distant) habitats and creates problems with what are often bothersome and sometime destructive pests.
For obnoxious species that can spread rapidly over short distances, think of mosquitoes, bedbugs, or black flies; for the destructive ones traveling afar, think of migrating locusts (Schistocerca gregaria), whose largest swarms may contain billions of individuals and travel thousands of kilometers as they devour crops, tree leaves, and grasses. If environmental conditions are right, a few successive reproduction bouts can result in exponential increases that may cause a great deal of distress or harm. But because the r-selection parents must channel such large shares of their metabolism into reproduction, their life spans, and hence their reproductive chances, are limited and once the conditions enabling their exponential growth end, their numbers may crash.
They live long only if they have an assured steady supply of nutrients, as is the case with parasites, especially with some intestinal species. Pork tapeworm (Taenia solium), the most common tapeworm parasite in humans, can produce up to 100,000 eggs per worm and it can live for as long as 25 years. Parasites and insects are not the only r-selected forms of life: there are plenty of r-selected small mammals whose litters, while considerably smaller, can still translate into overwhelming growth rates. Brown rats (Rattus norvegicus) mature in just five weeks, their gestation period is just three weeks, and with at least six to seven newborns in a typical litter the number of females can increase by an order of magnitude in just 10 weeks. If all offspring were to survive, the increase would be about 2,000-fold in a year (Perry 1945).
K-selected species have adapted to a specific range of more permanent resources and maintain their overall numbers fairly close to the carrying capacity of their environment. They reproduce slowly, they have a single offspring that requires prolonged maternal care (direct feeding of regurgitated biomass for birds, suckling by mammals), take long to mature, and have long life expectancy. African elephants (Loxodonta africana) and the smaller, and now more endangered, Asian Elephas maximus are perfect examples of that reproductive strategy: African elephants start reproducing only at 10–12 years of age, pregnancy lasts 22 months, a newborn is cared for by females of an extended family, and they can live for 70 years. All of the largest terrestrial mammals, as well as whales and dolphins, reproduce in the extreme K-selected mode (twin births are rare, one in 200 births for cattle) but there are also many smaller mammals with a single offspring.
Sibly and Brown (2009) concluded that mammal reproductive strategies are driven primarily by offspring mortality/size relationships (preweaning vulnerability to predation). In order to minimize the chances of predation, animals which give birth in the open on land or in the sea produce one, or just a few precocial offspring (born relatively mature and instantly mobile) at widely separated intervals. These mammals include artiodactyls (even-toed ungulates including cattle, pigs, goats, sheep, camels, hippos, and antelopes), perissodactyls (odd-toed ungulates, including horses, zebras, tapirs, and rhinos), cetaceans (baleen and toothed whales), and pinnipeds (seals, sea lions). And those mammals which carry the young until weaning—including primates, bats, and sloths—must also have a single (or just two) offspring. In contrast, those mammals whose offspring are protected in burrows or nests—insectivores (hedgehogs, shrews, moles), lagomorphs (rabbits, hares), and rodents—produce large litters of small, altricial (born in an undeveloped state) newborns.
Efficiency of animal growth is a function of feed quality, metabolic functions, and thermoregulation (Calow 1977; Gerrard and Grant 2007). Assimilation efficiency (the share of consumed energy that is actually digested) depends on feed quality. Carnivores can extract 90% or more of available energy from their protein- and lipid-rich diets, digestibility rates are between 70–80% for insectivores and for seed-eating animals, but only 30–40% for grazers, some of which can (thanks to symbiotic protozoa in their gut) digest cellulose that remains indigestible for all other mammals.
Net production efficiency (the share of assimilated energy diverted into growth and reproduction) is highly correlated with thermoregulation. Endotherms keep diverting large shares of digested energy for thermoregulation and have low net production efficiencies: just 1–2% for birds (whose internal temperature is higher than in mammals) and for small mammals (whose large surface/volume ratio cause faster heat loss) and less than 5% for larger mammals (Humphreys 1979). In contrast, ectotherms can divert much larger shares of assimilated energy into growth and reproduction. The rates are more than 40% for nonsocial insects, more than 30% for some aquatic invertebrates, and 20–30% for terrestrial invertebrates but (due to their much higher respiration rates) only about 10% for social insects (ants, bees). The earliest growth is often linear, with the published examples including such different species as young Angus bulls and heifers in Iowa (Hassen et al. 2004) and New Zealand sea lion pups (Chilvers et al. 2007).
Growth Curves
As expected, studies of many terrestrial and aquatic species have shown that their growth was best described by one of the confined-growth functions. The Gompertz function represents well the growth of the broiler chicken (Duan-yai et al. 1999) as well as of the domestic pigeon (Gao et al. 2016) and goose (Knizetova et al. 1995). The logistic function describes very accurately the growth of a traditional Chinese small-sized Liangshan pig breed (Luo et al. 2015) as well as of modern commercial pigs, including those reared to heavy weights (Vincek et al. 2012; Shull 2013).
The von Bertalanffy equation has been used to express the growth of many aquatic species, including aquacultured Nile tilapia (de Graaf and Prein 2005) and the shortfin mako shark in the North Atlantic (Natanson et al. 2006). It also captured well the central growth tendency of polar bears collared in the Canadian Arctic—but this study also illustrated significant variance among wild animals which tends to increase with age. Weights of five-year-old bears clustered tightly; for ten-year-old bears averaging about 400 kg, the extremes were between just over 200 kg and more than 500 kg (Kingsley 1979).
Fitting sigmoidal growth curves to 331 species of 19 mammalian orders has shown that the Gompertz equation was superior to von Bertalanffy and logistic function for capturing the complete growth history of mammals (Zullinger et al. 1984). This large-scale analysis also confirmed numerous deviations from expected trajectories. Notable departures include ground squirrels (having faster-than-expected growth rates) and seals (growing slower than expected by the Gompertz function). Chimpanzee (Pan troglodytes) growth displayed both negative and positive deviation from the expected growth both in infancy and near maturity; for comparison, human growth appears faster than expected in both of these cases. In contrast, Shi et al. (2014) concluded that the logistic equation, rather than a modified von Bertalanffy equation with a scaling exponent of ¾, is still the best model for describing the ontogenetic growth of animals.
West and his colleagues introduced a general growth equation (universal growth curve) that is applicable to all multicellular animals. The equation is based on the observation that all life depends on hierarchical branching networks (circulatory systems) which have invariant terminal units, fill available space, and have been optimized by evolution (West and Brown 2005). As organisms grow, the number of cells that have to be supplied with energy grows faster than the capacity of branching networks required to supply them and, inevitably, this translates into S-shaped growth curves. When growth data for invertebrates (represented by shrimp), fish (cod, guppy, salmon), birds (hen, heron, robin) and mammals (cow, guinea pig, pig, shrew, rabbit, rat) are plotted as dimensionless mass ratio (m/M)1/4 against a dimensionless time variable, they form a confined growth curve with rapid gains followed by a relatively prolonged asymptotic approach (figure 2.13).

Universal growth curve, a plot of the dimensionless mass ratio and the dimensionless time variable. Based on West et al. (2001).
Early growth gains are often linear and their daily maxima can be expressed as power functions of adult mass (in grams per day it is 0.0326M0.75 for placental mammals). The two animal groups that depart from this general rule are primates with their much slower growth, and pinniped carnivores with their very fast growth. Maximum vertebrate growth scales with mass as about 0.75: larger species acquire their mass by proportional acceleration of their maximum growth rate but there are important differences among thermoregulatory guilds and major taxa (Grady et al. 2014; Werner and Griebeler 2014). As expected, endotherms grow faster than ectotherms. Lines of the best fit show an order of magnitude difference between mammals and reptiles, and two orders of magnitude difference between fishes and altricial birds.
Actual maximum gains (all in g/day, rounded) for a few common species with similar final body mass (all about 1 kg) are as follows: rock cod 0.2; cottontail rabbit 8; black grouse (a precocial bird) 14; common raven (an altricial bird) 50. Pinnipeds (walruses and seals) have the highest daily growth rates, with the largest animals (large male walrus, Odobenus rosmarus weighing 1–1.5 t) adding maxima of well over 1 kilogram a day (Noren et al. 2014). Growth rates increase with the rate of metabolism, but there are exceptions to this rule. Juvenile altricial birds, brooded by their parents, have lower metabolic rates but higher growth rates than thermoregulating, juvenile precocial birds (McNab 2009). Actual maxima for terrestrial animals range from nearly 2 kg/day for rhinoceros and more than 700 g/day for horse to about 1 g/day for small possums and 0.01 g/day for the smallest skinks and geckos. The African elephant manages only less than 400 g/day, chimpanzees add up to 14 g/day, gorillas about twice as much (human maxima are 15–20 g/day).
One of the most remarkable cases of avian growth is that of the wandering albatross (Diomedea exulans), and not only because this bird has the largest wingspan (2.5–3.5 m) as well as the longest postnatal growth period: it also loses up to almost 20% of its body mass before fledging (Teixeira et al. 2014; figure 2.14). The wandering albatross needs 280–290 days to grow from hatchling to fledgling, and then 6–15 years before it becomes sexually mature. After 80 days of incubation, single hatchlings are brooded by adults for just 21–43 days and then they are left alone, with a parent returning at progressively longer intervals for brief periods of feeding. This results in a declining amount of food a chick receives during its growing season, and after its body mass peaks in August (at about 1.5 times the adult weight) the chick loses about half of the weight difference from adults before it fledges in November or December, when it still weighs more than the adult.

Wandering albatross (Diomedea exulans) in flight. Photo available at wikimedia.
Finally, a brief clarification of a supposed evolutionary trend in animal growth. According to Cope’s rule, animal lineages should evolve toward larger body size over time. Increased body mass has been seen to offer several competitive advantages (increased defense against predation, more successful inter- and intraspecific competition, higher longevity, and more generalized diet) that should outweigh inevitable downsides, above all lower fecundity, longer gestation and development, and higher food and water needs (Schmidt-Nielsen 1984; Hone and Benton 2005). Although he researched evolutionary trends, Edward D. Cope, a much-published 19th-century American paleontologist, never made such a claim. Charles Depéret, a French geologist, favored the notion in his book about the transformations of the animal world (Depéret 1907) but the rule got its name only after WWII (Polly and Alroy 1998) and its thorough examinations began only during the closing decades of the 20th century.
The verdict has been mixed. Alroy’s (1998) analysis of Cenozoic mammalian fossils found that the descendant species were, on the average, about 9% larger than their ancestors. Kingsolver and Pfennig (2004) concluded that such key attributes as survival, fecundity, and mating success were positively correlated with larger body size not only in animals but also in insects and plants. Perhaps most impressively, Heim et al. (2015) tested the hypothesis across all marine animals by compiling data on body sizes of 17,208 genera since the Cambrian period (that is during the past 542 million years) and found the minimum biovolume declining by less than a factor of 10 but the maximum biovolume growing by more than a factor of 100,000, a pattern that cannot be explained by neutral evolutionary drift and that has resulted from differential diversification of large-bodies classes.
Another seemingly convincing confirmation came from Bokma et al. (2016). They found no tendency for body size increase when using data from more than 3,000 extant mammalian species, but when they added 553 fossil lineages they found decisive evidence for Depéret’s rule. Naturally, they stressed the importance of a long-term perspective, and their findings also indicated that the tendency toward larger body size is not due to gradual increase over time in established species, but that it is associated with the formation of new groups of organisms by evolutionary divergence from their ancestral forms.
In contrast, reconstruction of the evolution of different carnivore families (using both fossil and living species) found that some have acquired larger body sizes while others have become smaller (Finarelli and Flynn 2006). Such a mixed finding was also the result of Laurin’s (2004) study of more than 100 early amniote species, and he suggested that the rule’s applicability depends largely on the data analyzed and on the analytical method. The most convincing refutation of Cope’s rule has come from Monroe and Bokma (2010), who tested its validity by Bayesian analyses of average body masses of 3,253 living mammal species on a dated phylogenetic tree. Difference in natural log-transformed body masses implied that descendant species tend to be larger than their parents, but the bias is negligible, averaging only 0.4% compared to 1% when assuming that the evolution is a purely gradual process.
Smith et al. (2016) offered the most comprehensive review of body size evolution for the three domains of life across the entire Geozoic (3.6 billion years) as organisms had diversified from exclusively single-celled microbes to large multicellular forms. Two major jumps in body sizes (the first in the mid-Paleoproterozoic about 1.9 billion years ago, the second during the late Neoproterozoic to early Paleozoic 600–450 million years ago) produced the variation seen in extant animals. The maximum length of bodies increased from 200 nm (Mycoplasma genitalium) to 31 m (blue whale, Balaenoptera musculus), that is eight orders of magnitude, while the maximum biovolume (for the same two species) grew from 8 × 10–12 mm3 to 1.9 × 1011 mm3, an evolutionary increase of about 22 orders of magnitude. There has been an obvious increase in typical body size from Archaea and Bacteria to Protozoa and Metazoa, but average biovolumes of most of the extinct and extant multicellular animals have not shown similar evolutionary growth.
Average biovolumes of marine animals (Mollusca, Echinodermata, Brachiopoda) have fluctuated mostly within the same order of magnitude, and only marine Chordata have shown a large increase (on the order of seven magnitudes). Average biovolumes of Dinosauria declined during the early Cretaceous period but at the time of their extinction they were nearly identical to the early Triassic sizes. Average biovolumes of arthropods have shown no clear growth trend for half a billion years, while the average biovolumes of Mammalia grew by about three orders of magnitude during the past 150 million years (figure 2.15). Several animal groups (including marine animals, terrestrial mammals, and non-avian dinosaurs) show size increase over their evolution (confirming Cope’s rule) but statistical analyses make it clear that unbiased random walk is the best evolutionary trend for five animal phyla (Brachipoda, Chordata, Echinodermata, Foraminifera, Mollusca), while stasis captures best the evolution of arthropod sizes.

Evolutionary trends of biovolumes for Dinosauria and Mammalia. Simplified from Smith et al. (2016).
Growth of Domesticated Animals
By far the greatest changes of animal growth have resulted from domestication, whose origins go back more than 10 millennia. Archaeological evidence allows reliable dating of animal domestication: first goats and sheep (about 11,000 years ago), then pigs and cattle (10,500–10,000 years ago), all in the Middle Eastern region where today’s Turkey, Iraq, and Iran meet (Zeder 2008). Domestication of horses on the Eurasian steppes came much later, about 2,500 BCE (Jansen et al. 2002). These five species (and dogs) eventually achieved a global distribution, while an additional eight species of domesticated mammals—water buffaloes, yaks, dromedary and Bactrian camels, donkeys, alpacas, rabbits, and guinea pigs—remain spatially restricted. Why just these species, why have we not domesticated dozens of other mammals?
Proclivity to taming, ability to reproduce in captivity, low or no aggressiveness and, with large species, easy herding were obvious selection criteria for domestication (Russell 2002). The growth cycle (time to reach sexual maturity), the rate of reproduction, the length of pregnancy and lactation, and the time to reach the slaughter weight were other key considerations. Extremes were excluded. Small mammals with a high rate of metabolism grow fast but yield very little: this puts 1–2 kg rabbits and guinea pigs at the bottom of domesticates. Very large mammals grow too slowly and require large amounts of feed. As McCullough (1973) observed, animals raised for meat can be thus seen as compromise mammals, combining relatively fast growth with the capacity to accumulate mass, and that limits their body weights mostly to 40–400 kg. Not surprisingly, the largest domesticates are ruminants that can (because of the protozoa in their gut) digest roughages indigestible by other mammals and can survive only by grazing.
Most birds are far too small (and hence their basal metabolism is far too high) to be rewardingly domesticated for meat or egg production and the body weight of wild species that were eventually adopted ranges from less than 500 g for pigeons to about 10 kg for wild turkeys. Southeast Asia’s wild fowl were domesticated already some 8,000 years ago and chickens have become by far the most important domesticated birds. Domesticated turkeys (in Mesoamerica) date back to about 7,000 years ago, ducks (in China) to about 6,000 years ago (in China), and geese were domesticated about a millennium later, most likely in Egypt.
Both the pace of maturation and the final slaughter weights were elevated to unprecedented levels by the combination of modern breeding (genetic selection), better feeding in confinement, and the use of prophylactic medications. This combination has worked particularly well for pigs and broilers (Whittemore and Kyriazakis 2006; Boyd 2003; Havenstein 2006; Zuidhof et al. 2014; NCC 2018). Extensive studies of nutritional requirements for cattle, pigs, and poultry have established optimum ratios of macronutrients and supplements for different stages of growth, and periodic updates of guidelines prepared by expert committees of the US National Research Council offer their best summaries (NRC 1994, 1998, 1999, 2000b). Modern practices have also relied on growth enhancers, on widespread preventive use of antibiotics, and on extreme confinement of animals, practices seen by the meat-producing industries as economically imperative but judged from other perspectives, regarded as definitely undesirable (Smil 2013c).
No domesticated mammal can produce meat as efficiently as a pig, not because of its omnivory but because its basal metabolism is almost 40% lower than would be expected for its adult body weight. During the fastest phase of its growth, a healthy pig converts almost two-thirds of all metabolized energy in feed to grow new tissues, a performance more than 40% better than in cattle and even slightly ahead of chickens. Pig growth is also exceptionally rapid and starts from an unusually low birth weight. Human newborns (average 3.6 kg) weigh about 5% of the adult mass, pigs less than 2% (birth weight about 1.5 kg, slaughter weight of 90–130 kg). Piglets grow linearly after birth, doubling their weight during the first week and more than quintupling it by the end of the third week (Chiba 2010). Piglets are weaned in just 25 days (compared to 56 days 50 years ago) and receive supplementary (creep) feeding before weaning. Faster weaning makes it possible to raise the number of piglets per sow from 20 to 25 a year.
Wild pigs, who have to spend a great deal of energy on searching for food and on rooting, reach their maximum adult weight only after three years for males and two years for females (they live 8–15 years). The postweaning growth of domesticated pigs has been compressed into a fraction of that span due to a combination of better feeding in confinement. Landless “confined animal feeding operations” have become the norm in modern meat production and the limits for pigs, normally widely roaming animals, are particularly severe. In the EU they are confined within 0.93 m2, in Canada the minimum allotment is just 0.72 m2, both for a mature 100-kg animal on a slatted floor (Smil 2013c).
While the proportions of human and pig bodies differ, adult masses are similar, and for Western men (whose normal body masses range mostly between 65 and 85 kg, in the same range as maturing pigs) it might be an instructive exercise trying to spend a day confined even to 2 m2, to say nothing about a third of that space! Usually more than 1,000 pigs are now kept under one roof in small stalls and pig production is highly concentrated. Iowa, North Carolina, and Minnesota now produce nearly 60% of all marketed animals (USDA 2015). The growth of confined animal feeding operations has thus created unprecedented concentrations of organic waste.
Newborn piglets grow by about 200 g/day, young pigs add 500 g/day, and mature pigs approaching slaughter weight gain 800 g/day. Modern breeds reach slaughter weight just 100–160 days after weaning, or less than half a year after birth. As always, growth efficiency declines with age, from 1.25 units of feed per unit of gain for young piglets to as many as four units for heavy mature animals (NRC 1998). The US has a unique long-term record of nationwide feeding efficiencies thanks to the calculations regularly published by the Department of Agriculture (USDA 2017c). Data for pigs and beef cattle start in 1910, for chickens 25 years later, and they include all feedstuffs (grain, legumes, crop residues, forages) converted to corn feeding units (containing15.3 MJ/kg).
In 1910 the average feed/live weight efficiency of American pigs was 6.7; it declined only marginally during the 20th century (fluctuating between 5.9 and 6.2 during the 1990s) but since 2009 it has been just below 5.0 (USDA 2017c). There is a simple explanation for this relatively limited progress: modern pigs have been bred to meet the demand for leaner meat and the animals are significantly less fatty than their predecessors of three or four generations ago and hence less efficient in converting feed to added body mass. For fat the conversion can exceed 70%, for protein (lean muscle) it does not go above 45% (Smil 2013c).
Modern breeding and feeding in confinement has also compressed the growth of domesticated birds, and altered their body size (largest male turkeys now weight more than 20 kg, double the mass of their wild ancestors), composition, and proportions. South Asian red jungle fowl (Gallus gallus), the wild ancestor of modern chickens, took up to six months to reach its maximum weight. Traditional free-running chicken breeds (mostly fending for themselves and only occasionally receiving some grain feed) were slaughtered when four to five months old while today’s free-range chicken (fed high-quality commercial feed mixtures) are slaughtered in 14 weeks (about 100 days).
In 1925 American broilers commercially produced in confined spaces were marketed after 112 days and their live weight was just 1.1 kg. By 1960, when broiler production began to take off, the market age was 63 days and weight rose to 1.5 kg. By the century’s end, the age declined to 48 days (just short of seven weeks) and the weight rose to 2.3 kg; by 2017, the marketing age had not changed, but the weight was just over 2.8 kg (Rinehart 1996; NCC 2018). In 90 years, the feeding span was thus reduced by 57%, the final weight had risen 2.5-fold, and the number of days required to add 500 g of weight was cut from 49 to 8.5. And while during the 1920s it was no more efficient to feed a chicken than to feed a pig, with feed/live weight gain close to five, subsequent improvements lowered the ratio to three by 1950, to two by 1985 and 1.83 by 2017 (NCC 2018), and the USDA series gives even slightly lower values with a minimum at 1.53 in 2012 (USDA 2017c).
Consequently, no terrestrial animal can now grow meat as efficiently as chickens, while ducks need about 50% more feed per unit weight gain, and the recent ratios for American turkeys have been between 2.5 and 2.7. This reality explains the extraordinary rise of chicken production from a relatively minor share of total meat output right after WWII to its recent dominance in many markets. The US output of chicken meat has risen more than 20-fold since 1950, from 1.1 to 23.3 Mt in 2015, and the worldwide growth has been even more impressive, from less than 4 Mt in 1950 to just over 100 Mt in 2015 (FAO 2018). But this growth has subjected modern broilers to a great deal of stress, even to outright suffering.
Increasing growth through confinement has led to such restrictions on bird movement (both for broilers and egg-laying hens) that detestable would be the right adjective to label this practice. There are no legally binding density restrictions for American broilers but guidelines by the National Chicken Council specify just 560–650 cm2 per bird. The smaller area is easy to visualize, it is smaller than the standard A4 paper sheet, which measures 602 cm2, or a square with sides just short of 25 cm. Canada’s national regulations are only relatively more generous: 1,670 cm2 on slat or wire flooring is a square of 41 cm (CARC 2003). And turkeys, much larger birds, get no more than 2,800 cm2 (53 cm square) for lighter individuals.
This crowding is also a perfect illustration of how maximization of profit drives growth even as that growth is not optimal. Studies have shown that broilers convert feed more efficiently, grow heavier, and have lower mortality when given more space (Thaxton et al. 2006), but as Fairchild (2005) noted broiler farmers cannot afford low densities because they would not achieve a satisfactory return. Similarly, feeding efficiency and daily weight gain of pigs improve with lower stocking density, but the overall return (total meat sold) is marginally higher with the highest density.
American broiler houses are large rectangles (typically 12 × 150 m) that house more than 10,000 birds at a time and produce up to 135,000 birds a year, with some large growers operating as many as 18 houses and marketing about 2 million birds from a single operation. Waste disposal of chicken waste is not helped by the extraordinary concentration of broiler operations. Georgia, Arkansas, and Alabama produce nearly 40% of birds, and Delaware, Maryland, and Virginia (Delmarva) Peninsula have the highest US concentrations of broiler chickens per unit of farmland (Ringbauer et al. 2006). Inside the houses, broilers spend their short lives not only in extreme crowding but also in near darkness.
Hart et al. (1920) discovered that the addition of vitamin D (dispensed in cod liver oil) prevents leg weakness caused by the absence of outdoor ultraviolet light and this made it possible to grow the birds indoors under artificial lighting and in increasingly smaller spaces. Light intensity up to seven days of age is 30–40 lux but afterwards the prescribed broiler house lighting delivers just 5–10 lux (Aviagen 2014). For comparison, 10 lux is an equivalent of twilight and illuminance on a very dark overcast day is about 100 lux. Not surprisingly, this practice affects the bird’s normal circadian rhythm, dampens behavioral rhythms, and has possible health effects (Blatchford et al. 2012).
Selection for excessively enlarged breast has been particularly painful as it shifts the bird’s center of gravity forward, impairing its natural movement and stressing its legs and heart (Turner et al. 2005). This, in sum, is the growth of modern broilers: abbreviated lives with malformed bodies in dark crowded places that preclude normal activity of what are, after all, social birds, forced to live on a layer of excrement that damages feet and burns skin. Of course, this unprecedented growth causing a great deal of suffering has its ultimate commercial reward, inexpensive lean meat. And there is yet another common feeding practice that carries the risks of white meat production beyond the broiler house.
Soon after the discovery that antibiotics boost broiler weight gain by at least 10%, the US Food and Drug Administration allowed the use of penicillin and chlortetracycline as commercial feed additives in 1951. The two compounds, and oxytetracycline added in 1953, became common growth enhancers in the broiler industry. Half a century later, American poultry producers were feeding more antibiotics than were pig or cattle farmers, a practice that has undoubtedly contributed to the spread of antibiotic-resistant bacterial strains in the modern world (NRC 1994; UCS 2001; Sapkota et al. 2007). Of course, many people have argued that without antibiotics the modern meat industry would collapse, but the recent Danish experience with a more than halving of the use of antibiotics in livestock demonstrates otherwise (Aarestrup 2012).
Unlike in the case of broilers and pigs, the natural cattle cycle leaves much less room for accelerating the growth of animals reared for beef. Heifers, the young females before their first pregnancy, become sexually mature at 15 months of age, are inseminated when two years old, and after nine months of pregnancy a calf stays with the mother for 6–8 months. After weaning, most male calves are castrated and the steers (castrated males) and heifers (except for small numbers set aside to maintain the herd) are fed to market weight. After 6–10 months of stocker phase (summer pasture or roughage), they are moved for the finishing to feedlots where they spend usually three to six months (NCBA 2016).
During the finishing period, American beef animals are fed rations composed of optimized carbohydrate-protein and roughage mixtures (70–90% grain) and nutritional supplements and they gain 1.1–2 kg of live weight a day, with a dry feed-to-liveweight ratio between 6:1 to 8:1. Finishing periods, rations, and maximum gains are similar in two major beef-producing countries, in Canada and Australia. In Canada, finishing animals average 200 days on feed and gain about 1.6 kg/day, in Australia the average weight gain for both the domestic and Japanese market is 1.4 kg/day (BCRC 2016; Future Beef 2016).
For more than 50 years, America’s cattlemen have been accelerating this growth by using steroid hormones implanted under the skin on the back of an ear. They dissolve in 100–120 days and promote the growth in finishing beef lots (NCBA 2016). Four out of five of beef animals in US feedlots receive the treatment, and three naturally occurring hormones (estradiol, progesterone, and testosterone) and three synthetic compounds (Zeranol, Trenbolone, and Melengestrol) are approved for use. Depending on the implant used and on the age and sex of the animal, the growth rate will increase by 10–120%, reducing production costs by 5–10%, but the implants do not change the need to reach a certain degree of fatness before the meat marbles and can be awarded a higher quality grade.
Growth hormones used in cattle have been approved as safe not only by the US regulatory bodies but also by the World Health Organization and Food and Agriculture Organization. Beef produced with growth promotants has minuscule amounts of estrogen residue compared to many natural foods and faster growth also translates into reduced demand for feed and hence to reduced greenhouse gas emissions (Thomsen 2011). Nevertheless, the use of hormones in meat production has been prohibited in the European Union since 1981 and the ban survived a US and Canadian challenge (European Commission 2016).
Cattle crowding in large feedlots is, necessarily, less extreme than with smaller animals. American minima are just 10–14 m2 in unpaved lots and the Canadian allotment is just 8 m2 on unpaved lots and only 4.5 m2 on paved ground in a shed (Hurnik et al. 1991). And large beef feedlots are also the extreme illustrations of how the unprecedented agglomerations of animals create inevitable environmental problems, with objectionable odors, waste removal, and water contamination. The country’s largest beef cattle feedlots used to finish the animals contain more than 50,000 heads, with the record operations confining 75,000 animals (Cactus Feeders 2017; JBS Five Rivers Cattle Feeding 2017) or a total living zoomass on the order of 30 Mt.
While all those widely cited USDA feed/live weight gain ratios are good indicators of overall growth, they cannot provide comparable data for assessing the energy and protein costs of actually consumed meat. That is why I have recalculated all feeding ratios in terms of feed to edible product (Smil 2013c). This adjustment is particularly important for proteins because collagen (protein present mostly in bones, tendons, ligaments, skin, and connective tissues) accounts for about a third of all protein in mature animals. That is, as Blaxter (1986, 6) put it, “a sobering thought in view of its abysmal nutritive value as food. It is indeed disturbing to think that animal scientists spend so much time and treasure in producing animal protein when a third of it has been recognized since the times of the Paris soup kitchens to be of very poor nutritive worth.”
The protein digestibility corrected amino acid score (PDCAAS) is the best way to evaluate protein quality and while in lean meat (be it red meat, poultry, or fish) it ranges between 0.8 and 0.92 (and it is a perfect 1.0 in ovalbumin in eggs or in milk protein), PDCAAS for pure collagen is zero. While only feathers, beak, and bones (all high collagen tissues) may remain uneaten after cooking a chicken in some traditional Asian cuisines, less than 40% of live weight in heavy beef cattle may be edible even when most organ meats have been consumed (in protein terms, the rest is again largely collagen in heavy bones, ligaments, and skin). That is why I have not only recalculated all feeding ratios in terms of feed to edible product but also calculated separate conversion rates for energy (using gross feed input and average energy content of edible tissues) and protein (as direct ratios of feed protein units needed to produce a unit of edible protein as well as in terms of gross feed energy per unit of food protein).
These adjustments show that in mass terms (kg of feed/kg of edible meat and associated fat), the recent American feeding efficiency ratios have averaged about 25 for beef (but it must be remembered that most of it is phytomass indigestible by nonruminants), nine for pork and more than three for chicken, implying respective energy conversion efficiencies of less than 4%, nearly 10% and 15%, and protein conversion efficiencies of 4%, 10% and 30%, while about 25 MJ of feed energy are needed to produce a gram of beef protein and the rates are about10 MJ/g for pork and 2.5 MJ/g for chicken (Smil 2013c). These comparisons show (even more convincingly than the feed/live weight ratios) that chicken growth produces meat protein with by far the highest efficiency and hence with relatively the lowest environmental impact, and the combination explains why chicken became the modern world’s most popular meat.
Humans
Long periods of gestation and of helpless infancy, growth during childhood and subsequent spurt during adolescence have been always matters of keen human interest and endless wonder, and eventually subjects of detailed inquiry by a number of scientific disciplines and interdisciplinary studies (Ulijaszek et al. 1998; Bogin 1999; Hoppa and Fitzgerald 1999; Roche and Sun 2003; Hauspie et al. 2004; Karkach 2006; Tanner 2010; Cameron and Bogin 2012). Those inquiries have focused on the one hand on normal, healthy development—whose outward manifestation, besides height and weight, are all those notable and timely developmental milestones: first smile, first words, first walk, naming things, counting (CDC 2016). Extensive research has also looked at retarded and stunted growth, at the failure to thrive caused by malnutrition and poor sanitation, and at the long-term consequences of such deprivations (Jamison et al. 2006; WaterAid 2015). I will review the progress of normal growth, and its secular changes (for both height and body mass) and note the extent of two opposite undesirable conditions, stunting and excessive weight.
Growth in stature is a complex trait involving the interaction of many genes—which are moderately to strongly determinative with overall heritability of 0.5–0.8 (Visscher 2008)—with available nutrition, disease, and other exogenous factors. In its entirety the process is distinctly nonlinear, biophysically driven by selective hormonal stimulation of bone epiphyses. The most important factor is human growth hormone, whose secretion by the adenophysis (pituitary gland) is controlled by the hypothalamus (the brain section governing the production of many hormones) via various stimulating mediators (Bengtsson and Johansson 2000). Sex hormones (above all estrogens) stimulate secretion of growth hormone and insulin-like growth factor.
The growth curves of humans differ substantially from the pattern shared by other placental mammals regardless of their size, a fact first recognized by Brody (1945) and confirmed by von Bertalanffy (1960) and Tanner (1962). Bogin (1999) identified five ways in which human growth differs from that of all other placental mammals. First, human growth velocity, both in mass and length, peaks during gestation and postnatal growth decelerates during infancy, while other placental mammals, be they mice or cattle, have the highest growth velocities during their infancy. Second, sexual maturation of mammals occurs soon after their weaning, but in humans there is, on average, a delay for more than a decade between gestation and puberty.
Third, puberty in mammals occurs while their growth rates are in decline but still close to maxima, while in humans it takes place while growth in both height and mass are at their lowest postnatal points. Fourth, human puberty is marked by an adolescent growth spurt, while mammalian growth rates continue to decline: this growth spurt in stature and skeletal maturation is uniquely human, absent even in the closest primate species. Lastly, other mammals begin to reproduce soon after puberty but humans delay their reproduction. Moreover, this postponement of reproduction has recently lengthened in virtually all affluent societies, as marriage age has risen above 25 in some countries and as first births to older women, including those above 35 years of age, continue to rise (Mathews and Hamilton 2014).
Embryonic growth (up to eight weeks after conception) and fetal development usually end in term delivery (38 weeks from conception, with a range of 37–42 weeks). Survival of prematurely born babies (gestation shorter than 37 weeks, now comprising more than 10% of all American births) has been improving even in the case of very (29–34 weeks) and extremely (24–28 weeks) premature deliveries—but significant shares of surviving infants pay a high price for that survival. About 10% of all premature babies develop a permanent disability, but half of those born before the 26th weeks are disabled in some way, and at six years of age roughly one of every five prematurely born children remains severely affected (Behrman and Butler 2007).
The growth of our brain is a key consideration for the length of pregnancy (longer than in other primates, both in absolute and relative terms) and the need for intensive postnatal feeding and care. The brain of a mature chimpanzee (Pan troglodytes) averages less than 400 cm3, Australopithecus afarensis (3 million years ago) had brains of less than 500 cm3, Homo erectus (1.5 million years ago) averaged less than 900 cm3—while modern adult brains average close to 1,300 cm3 (Leonard et al. 2007). The human encephalization quotient (the ratio of actual to expected brain mass for a given body weight) is thus as much as 7.8 compared to 2.2–2.5 in chimpanzees and 5.3 in dolphins (Foley and Lee 1991; Lefebvre 2012).
Humans are born with less-developed brains than chimpanzees but at the time of delivery human brain size is a larger percentage of maternal body mass than for primates (Dunsworth et al. 2012). This means that the baby’s head size is more likely limited by the mother’s metabolic cost of carrying a large fetus rather than (as believed previously) by the width of the birth canal. The subsequent growth of the human brain is rapid, reaching 80% of adult size by age four and nearly 100% by age seven, while the body continues to grow for at least another decade (Bogin 1999). Moreover, the combination of a large active brain (and its need for further substantial growth) and an inept body requires a prolonged period of feeding and maternal care (Shipman 2013).
How we could afford such large brains was a puzzle as long as it was believed that our metabolic rate was very similar to that of other large primates. The best explanation of that paradox was the expensive-tissue hypothesis (Aiello and Wheeler 1995): it posits the need for a tradeoff, a reduction in the mass of another metabolic organ. That would be difficult with heart, liver, and kidneys but it has been accomplished with the human gastrointestinal tract thanks to an improved quality of diet (Fish and Lockwood 2003). Unlike in nonhuman primates that have nearly half of their gut mass in the colon and 14–29% in the small intestine, the reverse is true in humans, with the small intestine accounting for nearly 60% and the colon for 17–25%. In turn, this shift was obviously related to eating more foods of better quality and higher energy-density, including the meat, nutrient-rich innards and fat that began to enter hominin diets with higher frequency in contrast to grasses, leaves, fruits, and tubers that dominate simian diets. Improved walking efficiency was another explanatory ingredient.
But a new study of total energy expenditure in humans and large primates—using the doubly labelled (with isotopes of hydrogen and oxygen) water method (Lifson and McClintock 1966; Speakman 1997)—shows that the key to our high encephalization has been metabolic acceleration. The total energy expenditure of humans exceeds that of chimpanzees (and bonobos), gorillas, and orangutans by, respectively, about 400, 635, and 820 kcal/day, and this difference (averaging 27% more energy per day than chimpanzees) readily accommodates the cost of growth and maintenance of our greater brain and reproductive output (Pontzer et al. 2016). High encephalization is thus supported by hypermetabolic existence.
Height and Mass
Human height is a highly heritable but also a highly polygenic trait: by 2017 researchers had identified 697 independent variants located within 423 loci but even those explain only about 20% of the heritability of height (Wood et al. 2014). As with so many quantitative inquiries, the first systematic monitoring of human growth was done in prerevolutionary France, between 1759 and 1777, by Philibert Guéneau de Montbeillard, who measured his son every six months from birth to his 18th birthday, and the Comte de Buffon published the table of the boy’s measurements in the supplement to his famous Histoire naturelle (de Buffon 1753).
De Montbeillard’s height chart shows a slightly undulating curve, while the plot of annual height increments displays a rapidly declining rate of growth until the fourth year of age followed by the slower decline that precedes the pubertal growth spurt (figure 2.16). These spells of accelerated growth are not unique to our species: sub-adult growth spurts are the norm in both New World and Old World anthropoid primates, more commonly in males (Leigh 1996). This saltatory growth often takes place during small intervals of time and because it is detectable only by appropriately detailed sampling and it easily missed by infrequent measurements of large populations (Lampl et al. 1992; Lampl 2009; Gliozzi et al. 2012).

Growing height and height gain (cm/year) of de Montbeillard’s son. Height data from de Buffon (1753).
Montbeillard’s pioneering observations of a single boy were revealing but they did not, by chance, catch the process close to its statistical mean. As I will show shortly, his son was tall even by the standards of the early 21st century: as a young adult he matched today’s average young Dutchman, who belongs to the world’s tallest national male group. In 1835 Edouard Mallet applied the concept of normal distribution (for its origins see chapter 1) to his pioneering study of heights of Genevan conscripts (Staub et al. 2011). But the most famous contribution to early studies of human stature was published by Adolphe Quetelet, who related weight and height (body mass index) and, inspired by work linking poverty and the height of French recruits (Villermé 1829) and his own surveys of child growth (in 1831 and 1832), prepared growth tables (for both height and weight of children and adolescents (Quetelet 1835; figure 2.17). After Francis Galton introduced percentile grading (Galton 1876), everything was in place to produce the first charts of human growth (Davenport 1926; Tanner 2010; Cole 2012).

Quetelet’s loi de le croissance de la femme (law of women’s growth) shows a final average height of 1.58 m. Reproduced from Quetelet (1835), 27.
Bowditch (1891) pioneered the practice based on the growth of Massachusetts children, and during the 20th century this was followed by a number of national and international standard curves based on large-scale monitoring of birth weights and heights and of subsequent infant, child, and adolescent growth. We now have many detailed weight-for-age, height-for-age, weight-for-height standards, as well as velocity charts assessing changes in the rate of growth with age. In the US, recommendations are to use the WHO growth charts to monitor growth for infants and children up to two years of age and CDC growth charts for children older than two years (WHO 2006; CDC 2010).
These charts confirm that human ontogeny (the pattern of growth and development) differs substantially not only from that of other similarly massive mammals (pigs are one of the closest examples) but also from other primate species, including chimpanzees, our genetically closest animal predecessors. Growth curves are complex for both body mass and stature (containing sinuous as well as linear intervals); there are dramatic changes of many proportions between infancy and adolescence, and high levels of parental care and a long time between birth and maturation are ontogenetic traits as distinctive among human attributes as a large brain and language (Leigh 2001).
Early linear growth is due to endochondrial ossification taking place at the end of long bones and subject to complex regulation by endocrine, nutritional, paracrine, and inflammatory factors and also by other cellular mechanisms (Millward 2017). This growth proceeds most rapidly during the first 1,000 days after conception, and in malnourished children it can be postponed until they are better fed and catch-up growth takes place. And when Lampl et al. (1992) measured (semiweekly and daily) 31 infants aged 3 days to 21 months they found that 90–95% of the normal development during infancy is growth-free and that the body length accretion is a distinctly saltatory process as brief incremental bursts punctuate much longer periods of stasis. These saltations get less frequent as children age and are governed by maternal and environmental factors.
WHO standards start with average birth weights of 3.4 kg for boys (98th and 2nd percentiles at, respectively, 4.5 and 2.5 kg) and 3.2 for girls (the same percentiles at 4.4 and 2.4 kg). They show, for both sexes, a brief span of linear growth during the first two months (by that time male infants add about 2 kg and female infants about 1.8 kg), followed by accelerated growth until six or seven months of age, and then slightly declining growth rates until the first year of age when boys reach about 9.6 kg and girls about 9 kg (WHO 2006). Afterwards comes a period of an almost perfectly linear growth until 21–22 months of age, then a longer period of accelerating childhood growth until the age of 14–15 years when American boys add 5 kg and girls about 3 kg a year, and finally an asymptotic approach to the mature weight (figure 2.18).

Expected weight-for-age growth of American boys and girls. Based on Kuczmarski et al. (2002).
The growth curves of body mass charted by these standards approximate Gompertz or logistic functions, but even an early study noted that it might be better analyzed as a combination of curves (Davenport 1926). The growth, in terms of both height and mass, is best seen as a growth curve divided into three separate, additive, and partially overlapping components expressed by three separate growth curves, and, inevitably, modeling the velocity curve of human growth also requires three mathematical functions (Laird 1967). The stature growth curve in infancy is an exponential function that lasts for a year and it fades away during the next two years. The childhood curve slows down gradually; it includes a period of near-linear growth between the ages of four and nine (when American boys add 6–7 cm every year), and its best fit is a second-degree polynomial. Pubertal growth is a hormonally induced acceleration that slows down when reaching genetic limits and that is well described by a logistic growth function: annual additions peak at 8–9 cm between the ages of 13 and 14 and slow down to 1 cm between 17 and 18. Each of these curves is determined by the three parameters of the dynamic phenotype: initial length at birth, genetic limits of body length, and maximum velocity of length growth.
Not surprisingly, examinations of specific populations show nonnegligible deviations from WHO’s global growth standards. A recent study in the world’s most populous nation—based on the growth of nearly 95,000 Chinese urban children and young adults (0–20 years of age)—showed that all measured variables differed from those standards at nearly all ages, with the most notable differences in height and body mass index (BMI) (Zong and Li 2013). Chinese boys aged 6–10 years are strikingly heavier than the WHO standard, those younger than 15 years (and girls younger than 13 years) are taller, but both genders are significantly shorter when older. BMI is higher for boys of 6–16 years but appreciably lower for girls of 3–18 years. The authors proposed to base a new Chinese growth standard on these findings but inclusion of nonurban children would certainly shift the outcomes: China’s population, unlike in the overwhelmingly urban EU or North America, is still about 45% rural.
And we now have a worldwide examination (albeit with inadequate number of observations for Africa) of these departures from WHO standards. When Natale and Rajagopalan (2014) compared them with the worldwide variation in human growth, they concluded that both height and weight curves are not optimal fits in all cases. Height variations were generally within 0.5 of a standard deviation of WHO’s means, weights varied more than heights, and for the mean head circumference many groups had means consistently between 0.5 and 1 standard deviation above the WHO standard. Using WHO charts would thus put many children at risk for misdiagnosis of macrocephaly or microcephaly. That is why in the future we may rely on more specific curves not only for different populations but also for various stages of childhood (Ferreira 2012).
Growth (formation of new body tissues and their energy content) requires major shares of total energy expenditure in infants and children: approximately 40% in a newborn, with 35% the mean for the first three months of life. Exponential decline halves it during the next three months, and the share is just 3% at the end of the first year. Subsequent growth claims only 1–2% of total energy expenditure until the end of adolescence. And the share in all individuals who maintain steady body mass is only a small fraction of 1% afterwards, used for the renewal and replacement of short-lived tissues (intestinal lining, epidermis, nails, hair).
But the share of energy intakes claimed by growth has been obviously slightly higher for many adults in modern societies whose body mass keeps on increasing throughout their entire life. The first study that followed a small number of Americans from birth to 76 years of age for weight and stature showed a small decline in height starting in late middle age but continuous (albeit fluctuating) increase in body weight into old age (Chumlea et al. 2009). By age 70, the studied men gained about 20 kg compared to their weight at age 20, while women had a slightly smaller increase. As a result, the BMI (defined as the quotient of weight in kilograms and height in meters squared, kg/m2) of these individuals rose from desirable levels below 25 to overweight level (25–30).
Adequate energy intake is only a part of human growth requirements. Infants and children could have a surfeit of energy supplied as carbohydrates and lipids and would fail to thrive because humans cannot synthesize nine essential amino acids, required to build body tissues (muscles, internal organs, bones) and to maintain the necessary levels of metabolic and control compounds (enzymes, hormones, neurotransmitters, antibodies), and must digest them preformed in plant and animal proteins. Moreover, these amino acids must be present in adequate proportions: while all common plant foods have incomplete proteins, all animal proteins have the desirable amino acid ratios and are also almost completely digestible (digestibility of legume proteins is less than 80%).
That is why milk and egg proteins are used as the standards to which the quality of all dietary protein is compared, and why the growth of stunted children and acutely malnourished children is best promoted by dairy protein (Manary et al. 2016). Stunting—poor (linear) growth that produces a low height for age in young children—remains common in many low-income countries and it has a number of causes ranging from antenatal and intra-uterine development to postnatal malnutrition. For example, stunting from birth to 10 years of age in a rural district in Bangladesh (with 50% of children affected at age two, 29% at age 10) was independently correlated with maternal height, maternal educational level, and season of conception; the highest probability of stunting was for children born to short, uneducated mothers who were conceived in the pre-monsoon season (Svefors et al. 2016). In more pronounced cases, stunting is linked to such long-lasting consequences as poor cognition, low educational performance, low adult wages, and lost productivity.
De Onis et al. (2011) analyzed nearly 600 representative national surveys in nearly 150 countries and estimated that in 2010 stunting (defined as height less than two standard deviations below the WHO growth targets) affected 171 million children (167 million in low-income countries). The good news was that the global prevalence of stunting had declined from about 40% in 1990 to about 27% in 2010 and was expected to fall to about 22% by 2020, largely due to impressive improvements in Asia (mostly in China). Unfortunately, the share of African stunting has stagnated during the past generation, and if the current trends remain, it would increase by 2025 (Lartey 2015). Improved eating can eliminate stunting fairly rapidly through the process of catch-up growth.
One of the most impressive illustrations of this phenomenon is the growth history of American slave children documented by measurements during the early part of the 19th century in the country’s cotton states (Steckel 2007). The growth of those children who received inadequate nutrition was depressed to such an extraordinary degree that even by ages 14 or 15 their height was less than the fifth percentile of modern height standards—but the adult heights of American slaves were comparable to those of the contemporary European nobility, only 1.25 cm shorter than the Union Army soldiers, and less than 5 cm below the modern height standard.
Social inequality, manifested through inferior nutrition, has been a common cause of stunting in societies ranging from relatively rich 19th-century Switzerland (Schoch et al. 2012) to China of the early 21st century, where even the rapid pace of modernization had still left many children behind. Data extracted from the China National Nutrition and Health Survey in 2002 showed that, according to China’s growth reference charts, 17.2% of children were stunted and 6.7% severely so, both shares being significantly higher than when using the WHO growth standards (Yang et al. 2015). And in 2010 a survey by the Chinese Center for Disease Control and Prevention found that 9.9% of children younger than five years were stunted (Yuan and Wang 2012).
Advances in economic development can erase such growth differences quite rapidly: stunting is much less common in China’s richest coastal cities than in the country’s poorest interior provinces, and the growth of children born and growing outside the countries of their parents’ birth can become rapidly indistinguishable from the new normal. For example, there is now a sizable Chinese immigrant population in Italy, and a study of Chinese children born and living in Bologna showed that their body length was greater than that of children born and living in China and that their weight and height were higher than those of Italian children during the first year of life and comparable afterwards (Toselli et al. 2005).
Because human height is easy to measure, it has become widely accepted as a simple but revealing marker of human welfare that is linked to health status, wages, and income and gender inequality (Steckel 2008, 2009). Modern societies, whose improved nutrition resulted in a steady increase in average heights, see normal stature as highly desirable and above-normal height as welcome, if not preferable: there is no widespread yearning for growing up short and correlations confirm why. Sohn (2015, 110) summed it well: “It has long been understood that tall people generally exhibit a variety of positive attributes: they are healthier, stronger, smarter, more educated, more sociable, more liked, and more confident than short people. Hence, it is not surprising that they are richer, more influential, more fertile, happier, and longer-lived than short people.”
These conclusions now rest on a multitude of quantitative confirmations. Continuation of robust childhood growth into adulthood has been associated with better cognitive function, better mental health, and better conduct of daily activities (Case and Paxson 2008). Being taller correlates with a surprisingly large number of other positives, including such critical physical factors as higher life expectancy, lower risk of cardiovascular and respiratory diseases, and lower risk of adverse pregnancy outcomes, and such socioeconomic benefits as higher cognitive ability, higher probability of getting married, higher education, higher lifetime earnings, and higher social status. The correlation between height and earnings has been known for a century (Gowin 1915) and it has been demonstrated for both physical and intellectual occupations. Choosing just a few of many studies, taller men earn more as coalminers in India (Dinda et al. 2006), as farmers in Ethiopia (Croppenstedt and Muller 2000), and in all categories of occupation in the US, UK, and Sweden (Case and Paxson 2008; Lundborg et al. 2014).
Perhaps the most comprehensive study of this link, a comparative examination by Adams et al. (2016) of 28,000 Swedish men who acted as CEOs between 1951 and 1978, showed not only that they were taller than the population mean but that their height increased in firms with larger assets. CEOs managing companies worth more than 10 billion Swedish kronor average 183.5 cm compared to 180.3 cm for those running companies worth less than 100 million Swedish kronor. And in Western societies, taller bodies win even female beauty contests: the preferred height range of female fashion models (172–183 cm) is significantly above their cohort average of 162 cm (CDC 2012). Top of the female range is thus 13% higher than the mean, while for the men the difference (188 vs. 176 cm) is only about 7%.
Excessive height is a different matter. A reasonably nimble man can leverage his 2 meter height as a basketball star. In 2015 the average height of players in the top teams of the National Basketball Association was exactly 200 cm, with the two tallest players ever measuring 231 cm (NBA 2015). Otherwise there is not much value in exceptional height, and runaway growth that characterizes gigantism, acromegaly, and Marfan syndrome often carries other serious health risks. Pituitary malfunction in children, taking place before the fusion of the epiphyseal growth plates, leads to gigantism that makes young bodies exceptionally large for their age (heights in excess of 2.1 m) and produces extremely tall adults (Eugster 2015). Excessive production of growth hormone by the pituitary gland in middle age, after complete epiphyseal fusion, does not increase stature but it causes acromegaly, abnormal enlargement of bones, especially evident in larger-than-usual sizes of hands, feet, and face. Fortunately, both of these conditions are rather rare. Gigantism is extremely rare and acromegaly affects one out of every 6,250 people.
Marfan syndrome is a slightly more common instance of excessive growth, affecting roughly one out of every 5,000 people. In this genetic disorder a mutation affects the gene controlling the production of fibrillin-1, a connective tissue protein, and results in an excess of another protein, transforming growth factor beta (Marfan Foundation 2017). The resulting features, individually quite different, include generally taller bodies, curved spine, long arms, fingers and legs, malformed chest, and flexible joints—but the heart (aortic enlargement), blood vessels, and eyes may be also affected. Abraham Lincoln is the most famous American who lived with the syndrome, but it is much less known that the mutation affected two virtuoso players and composers of classical music, Niccolò Paganini and Sergei Rachmaninov. Heart complications are relatively common.
Because human height is easy to measure, we can use skeletal remains (femur length has the best correlations with body height) and data from diverse historical sources to trace long-term trends in human growth (Floud et al. 2011; Fogel 2012). Steckel’s (2004) millennial perspective used data on more than 6,000 Europeans from the northern part of the continent (ranging from Icelanders in the 9th–11th centuries to 19th-century Britons) and it indicated a significant decline of average heights from about 173.4 cm in the early Middle Ages to about 167 cm during the 17th and 18th centuries, and a return to the previous highs only during the early 20th century.
Both the high early level and a broadly U-shaped time trend are remarkable. The early highs could be explained by a warmer climate during those centuries, and subsequent declines by a cooler climate and medieval warfare and epidemics, while the post-1700 recovery was driven by improved farming methods, new crops, and food imports from the colonies (Fogel 2004). But another long-term European study, extending over two millennia, did not replicate the decline. Koepke and Baten (2005) assembled measurements of 9,477 adults who lived in all major areas of Europe between the 1st and the 18th centuries, and their most surprising finding was one of stagnant heights and no progress even during the early modern centuries (1500–1800) when economic activity was increasing (Komlos 1995) or during Roman times. The latter conclusion contradicts the common view of improving living standards due to the effects of the pax Romana: according to Kron (2005), the average male height during the Roman period equaled that of the mid 20th-century European man.
Weighted averages for European males fluctuated narrowly between 169 and 171 cm, with only two significant departures, one of a slight increase above 171 cm during the 5th and 6th centuries, and one of a slight dip below 169 cm during the 18th century. Moreover, average heights were very similar in central, western and southern Europe, and climate and social and gender inequality were also of marginal significance. Clark’s (2008) much smaller pre-1867 global data set (with nearly 2,000 skeletons from Norway, and about 1,500 from locations ranging from Mesolithic Europe to Edo Japan) spans heights from 166 to 174 cm with an average of 167, very similar to Koepke and Baten’s (2005) mean. Evidence becomes much more abundant for the 19th and 20th centuries and Baten and Blum’s (2012) anthropometric set includes 156 countries between 1810 and 1989; it is now also readily accessible in a graphic form (Roser 2017). The authors also published an informative summary of worldwide height trends between 1820 and the 1980s (Baten and Blum 2014).
By far the best analysis of heights for the 20th century was published by the NCD Risk Factor Collaboration (2016) that reanalyzed 1,472 population-based studies, with height data on more than 18.6 million people born between 1896 and 1996 in 200 countries. These analyses documented post-1850 growth throughout Europe, and widespread, but not universal, gain in adult height during the 20th century. Onsets of European growth cluster between the 1830s for the Netherlands—until that time the Dutch, now the world’s tallest population, were not exceptionally tall (de Beer 2004)—and the 1870s for Spain, and for men the process resulted in increases of 12–17 cm before the end of the 20th century.
The average gain in adult height for cohorts born between 1896 and 1996 was 8.3 ± 3.6 cm for women and 8.8 ± 3.5 cm for men. When plotted for all studied countries, these increases were largely linear until the 1950s, but afterwards there has been clear plateauing in the tallest populations among both men and women in high-income countries, and Marck et al. (2017) point to this trend as another example of reaching the limits of Homo sapiens. This conclusion is strengthened by the fact that the mid 20th-century height plateau is found in all major US sports which select for tall individuals. The average National Football League player gained 8.1 cm between 1920 and 2010, but his height has remained constant at 187 cm since 1980 (Sedeaud et al. 2014).
The largest 20th-cenury increases were in South Korean women (they gained 20.2 cm on average) and Iranian men (average increase of 16.5 cm). Every population in Europe has grown taller, and perhaps the best long-term record of height increases is available for Japan where the government has been recording the height of both sexes at 5, 6, 8, 10, 12, 14, 15, 16, 18, 20, 22, and 24 years of age since 1900 (SB 2006). The trajectory for 18-year-old males shows an average gain of 11.7 cm and, a brief post–WWII period aside, a good logistic fit with inflection point in 1961 and only marginal gains ahead (figure 2.19). Data for females and for other ages show generally similar trajectories with steadily rising trends interrupted during WWII and a few hungry postwar years, renewed growth at faster rates afterwards, and peak heights reached during the 1990s followed by two decades of stagnation (SB 2017a). The overall 1900–2015 gain was 13 cm for young men and 11 cm for young women.

Average height of 18-year-old Japanese males, 1900–2020. Plotted from data in SB (1996). Logistic curve has R2 of 0.98, inflection point in 1961, and asymptote height is 172.8 cm.
The gains have been much smaller in the US and Australia. Even during the colonial times (thanks to an abundance of good farmland and low population density) Americans were taller than any contemporary population whose average heights are known, but there was actually a slight dip in average male height between 1830 and 1890, followed by a more than 10 cm gain by the year 2000 (Komlos 2001; Chanda et al. 2008). Australia has closely matched that rise. And a study of 620 infants born in Ohio between 1930 and 2008 (the Fels Longitudinal Study) showed that the most pronounced differences in growth occurred in the first year of life (Johnson et al. 2012). Boys and girls born after 1970 were 1.4 cm longer, and about 450 g heavier but during their first year of life their growth was slower than that of infants born before 1970 (“catch-down growth”).
Chinese gains were briefly interrupted by the world’s largest famine (1959–1961) but growth of the country’s youth in 16 major cities over the period of half a century between the 1950s and 2005 shows that the average height at 18 years of age increased from 166.6 to 173.4 cm for males and from 155.8 to 161.2 cm for females, gains of 1.3 and 1.1 cm/decade (Ji and Chen 2008). And there was no, or very little change, in adult height in some sub-Saharan countries as well as in South Asia: minimal gains in India and Nigeria, no gain in Ethiopia, slight decrease in Bangladesh, but Indonesia has managed a 6 cm gain for its males since the 1870s.
The five nations with the tallest males are now the Netherlands, Belgium, Estonia, Latvia, and Denmark, the female ranking is led by Latvia, Netherlands, Estonia, Czech Republic, and Serbia, and the tallest cohort ever born (average surpassing 182.5 cm) are the Dutch men of the last quarter of the 20th century. The height differential between the tallest and shortest populations was 19–20 cm in 1900 and despite substantial changes in the ranking of countries it has remained the same a century later for women and it increased for men. The lowest average male height is now in Timor-Leste, Yemen (both less than 160 cm), Laos, Madagascar, and Malawi, while the list of shortest adult women is headed by Guatemala (less than 150 cm), Philippines, Bangladesh, Nepal, and Timor-Leste (NCD Risk Factor Collaboration 2016).
Rates of average consumption of high-quality animal proteins are the best explanation of significant height differences through history. The smaller statures of Mediterranean populations during the Roman era reflected limited intakes of meat and fresh dairy products that were consumed often only by high-income groups (Koepke and Baten 2005). Extensive cattle grazing was only a limited option in seasonally arid Mediterranean environments and in all traditional agricultures whose low (and highly fluctuating) cereal and legume yields made it impossible to divert a significant share of grains to animal feeding (available feed went primarily to draft animals). As a result, cow milk—one of the best sources of protein for human growth and a staple food among many northern European populations—was consumed much less in the Mediterranean countries.
Koepke and Baten (2008) investigated the link between height and availability of protein-rich milk and beef by analyzing a data set of more than 2 million animal bones in central-western, northeastern and Mediterranean Europe. Their indices of agricultural specialization for these three regions during the first and the second millennia of the common era confirm that the share of cattle bones was a very important determinant of human stature. The Germanic, Celtic, and Slavic populations of northern and eastern Europe were not taller than the Mediterranean populations for genetic reasons but because of their higher, and more egalitarian intakes of high-protein foodstuffs (milk, unlike meat, could not be traded easily and was consumed locally).
Improved nutrition—above all the increased supply of high-quality animal protein in general and of dairy products in particular—and a reduced burden of childhood and adolescent diseases have clearly been the two key drivers of the modern growth of average stature. The effect of dairy products on stature is evident from national comparisons and it has been quantified by meta-analysis of modern controlled trials (de Beer 2012). The most likely result of dairy product supplementation is 0.4 cm of additional growth per year per 245 mL (US cup is about 237 mL) of daily intake. The nationwide effect is clearly seen by diverging US and Dutch height trends. American milk consumption was stable during the first half of the 20th century and steadily declined afterwards, while Dutch consumption was increasing until the 1960s and, despite its subsequent decline, is still above the US level; Dutch males, smaller than Americans before WWII, surpassed their American peers after 1950.
There may be other important explanatory variables. Perhaps most intriguingly, Beard and Blaser (2002) have suggested that the human microbial environment played a substantial role in determining the increase of average human height during the 20th century. Its change has included both exogenous and indigenous biota (now the much-researched human microbiome), and particularly microbial transmission of Helicobacter pylori in childhood. The recent slowdown of this secular increase (especially among better-off population groups) indicates that we have become increasingly specific pathogen-free.
We do not have as much historical information on changing body weights as we do on growth in height. Skeletal studies of hominins and early humans yielded two general, and opposite, trends, while the modern, and virtually universal, body mass trend is obvious even without any studies. Archaeological evidence (derived from regressions on femoral head size) shows a marked increase of body size with the appearance of genus Homo some 2 million years ago (reaching between 55 and 70 kg), and in higher latitudes this was followed about half a million years ago by a further increase of hominin body masses (Ruff 2002). The body masses of Pleistocene Homo specimens (reaching up to 90 kg) were, on average, about 10% larger than the averages for humans now living in the same latitudes. The decline of average body masses began about 50,000 years ago and continued during the Neolithic period, undoubtedly associated with the declining selective advantage of larger body weights.
Obesity
The obvious modern trend has been “from growth in height to growth in breadth” (Staub and Rühli 2013, 9). There are sufficient long-term data to show that entire populations as well as such specific groups as Swiss conscripts, US major league baseball players, or Chinese girls (Staub and Rühli 2013; Onge et al. 2008; O’Dea and Eriksen 2010) have been getting heavier, and that this process has accelerated since the 1960s to such an extent that large shares of them are now overweight and obese. These undesirable trends are best measured not in terms of absolute mass gains but as changes of BMI, and this quotient has been used to gauge relative adiposity among all ages. WHO categorization puts people with BMI above 25 kg/m2 into the overweight category and those with BMI>30 are classified as obese (WHO 2000)—but these cutoffs may not be the best choice for every adult population and for children and adolescents (Pietrobelli et al. 1998). These are important concerns because obesity, traditionally a condition of mature and old age, has become a major adolescent and even childhood problem.
US data make it clear that large-scale obesity is not a new type of disease but a consequence of overeating and insufficient activity. Until the late 1970s, the two excesses were holding steady, with about a third of Americans being overweight and about 13% obese. By the year 2000, the share of overweight people remained steady but the prevalence of obesity among adults older than 20 years had more than doubled and by 2010 it reached 35.7%, and the share of extremely obese adults has surpassed 5% of the total (Ogden et al. 2012). This means that by 2010 three in four American men (74% to be exact) were either overweight or obese. Among American children and adolescents, almost as many as among adults (one in three) were overweight and 18.2% were obese, with the latter share rising to nearly 23% among Hispanic and 26% among black youth.
Disaggregated statistics show that since 1990 adult obesity has increased in every state. Weight gains have been highest among adults with less than completed high school education but they have affected all socioeconomic groups. Progression of the prevalence was linear between 1990 and 2010 (with frequency gain averaging 0.8%/year and the range mostly 0.65–0.95%/year) and the growth rate has slowed down since 2010. S-shaped trajectories are tending to very different asymptotic prevalence levels: in Mississippi to around 35–36%, in Colorado, the least obese state, to just 20%. A longer nationwide data series (1960–2015) supports that conclusion, with its logistic curve saturating at about 37.5% (figure 2.20). Unfortunately, by 2015 the adult obesity prevalence in Louisiana, now number one at just over 36%, was still increasing (The State of Obesity 2017).
Growing prevalence of obesity in the US. Data from Ogden et al. (2012) and The State of Obesity (2017). The logistic curve had its inflection point in 1993 and its asymptote is at 37.5% of the total population.
British growth has been nearly as bad. Between 1993 and 2013, the percentage of obese males doubled and that of obese women rose by nearly half, and in 2013 67.1% of British men, and 57.2% of women, were overweight or obese, rates only slightly lower than in the US (HSCIC 2015). And China’s rapid post-1980 economic advances—making the country the world’s largest economy (in terms of purchasing power parity) and lifting its average daily per capita food availability above that in Japan (FAO 2018)—have resulted in notable increases of childhood and adolescent overweight and obesity, from just 4.4% for the cohort born in 1965 to 9.7% by 1985 and 15.9% in the year 2000 (Fu and Land 2015).
The first global analysis of trends in BMI looked at 28 years of data (1980 to 2008) for adults 20 years of age and older in 199 countries, and it found an increase in male BMI in all but eight countries, with the global mean rising by 0.4 kg/m2/decade, and female BMI rising slightly faster at 0.5 kg/m2/decade (Finucane et al. 2011). The globally standardized mean reached 23.8 kg/m2 for males and 24.1 kg/m2 for women, with the highest rates in the Pacific islands (Nauru, Tonga, Samoa, Palau) in excess of 30 kg/m2, and the worldwide prevalence of obesity (9.8%) being more than twice the 1980 rate. As a result, an estimated 205 million men (highest share in North America) and 297 million women (highest share in Southern Africa) were obese. Japanese women have been the only notable exception to the global trend of rising BMI and spreading obesity (Maruyama and Nakamura 2015). Not only is their BMI significantly lower than in other affluent countries, but for women at age 25 it decreased from 21.8 in 1948 to 20.4 kg/m2 in 2010, while the BMI of Japanese men had increased concurrently from 21.4 to 22.3 kg/m2.
The most worrisome component of this global epidemics is the early onset of the condition because childhood obesity tends to persists into adult age. As a result, we are now seeing an increasing frequency of individuals spending nearly entire life spans as overweight or obese. Khodaee and Saeidi (2016) estimated that in 2013 the worldwide total of overweight children under the age of five years had surpassed 42 million. According to WHO, the total of obese children and adolescents has increased tenfold in four decades and by 2016 there were about 124 million (7%) obese youngsters, with another 213 million overweight (WHO 2017). And WHO predicted that the number of obese children will surpass the total of undernourished ones as soon as 2022. The most comprehensive nationwide US study showed that between 2011and 2014 the obesity rate among children and adolescents aged 2–19 years was 17% (nearly 6% extremely obese), and that among children aged 2 to 5 years it was nearly 10% (Ogden et al. 2016). The only hopeful sign is that the obesity of young children (2–5 years) increased until 2003–2004 and then it began to decline slowly.
Recent trends in human growth are marked by a great contradiction. On one hand, there is excessive growth that actually worsens the quality of life and reduces longevity, on the other hand there is insufficient growth that weakens proper development during childhood and reduces the likelihood of realizing life’s full physical and mental potential. The first failure is entirely preventable by a combination of moderate eating (and there is a surfeit of information about how to manage that) and active lifestyle (and that does not require any strenuous exercises, just frequent quotidian activity). A few most impoverished African countries aside (where a foreign intervention would be required), the problem of childhood stunting and malnutrition can be effectively addressed by national resources: it is not the food supply that falls short but adequate access to food that could be much improved by limited redistribution and supplementary feeding, steps that get repaid manifold by avoiding, or minimizing, physical and mental disabilities stemming from inadequate nutrition in the early years of life.
This concludes my surveys of natural growth on the organismic level and the next two chapters will be devoted to the growth of inanimate objects. Chapter 3 deals with the long-term advances in the capabilities and efficiencies of energy converters (whose deployment is an indispensable precondition of any complex human activities), while chapter 4 surveys the growth of artifacts, man-made objects ranging from the simplest tools (levers, wheels) to complex machines, structures, and infrastructures. As in nature, the ultimate patterns of these classes of growth conform to various confined growth functions, but the qualitative growth of artifacts (their increased durability, reliability, safety) has been no less important than many quantitative gains marking their rising capacities and performance.