6 Everyone—The Malthusian Threat
6.1 Introduction
In this chapter, we cross a dividing line. Until now we have been discussing concerns about life extension that I consider unproblematic, insignificant, or clearly outweighed by the upside of longer life. Those concerns are interesting and worth discussing, but my judgment is that they are not good reasons to oppose life extension. From this chapter through chapter 11, we will be considering concerns about life extension that I consider very significant. I still think the reasons in favor of developing life extension and making it available outweigh these more significant reasons against doing so, but this is a closer call.
In this chapter, I’ll discuss one of the most common worries about life extension: If people live far longer, the earth will become overpopulated, partly because people fail to die on schedule and hang around a lot longer and partly because they have more time to have children. I call this the Malthusian threat. I will argue that this is a serious threat and that life extension should be made available only on the condition that those who extend their lives restrict their reproduction enough to avoid a Malthusian crisis. I propose a reproductive policy I call Forced Choice to achieve this, and I try to show that it is feasible and just.
Before I begin, I want to express my gratitude and acknowledge a significant debt to Shahin Davoudpour, a doctoral candidate in the school of social sciences at the University of California, Irvine. Mr. Davoudpour is a demographer. He performed all the calculations in this chapter, developed the tables and graphs for the population projections I will discuss, and double-checked my work from a demographer’s standpoint. He is effectively the coauthor of this chapter, and I could not possibly have written this without his generous help. Those who are interested in the formula he developed for his calculations will find a detailed explanation of it in section 6.8.
6.2 Will life extension cause a Malthusian crisis?
As we saw in section 1.9, surveys indicate that the Malthusian threat is a major concern for members of the general public. It’s also a major concern for ethicists. Peter Singer, for example, asks us to “imagine that we develop and release [a] drug which will slow aging. . . . since people are living twice as long, there will soon be more people than the world can support.”1 Scientists who conduct life extension research run into this concern quite often. According to pathologist Richard Miller, “No one who speaks in public about longevity research goes very far before encountering the widespread belief that research on extending the life span is unethical, because it will create a world with too many old people and not enough room for young folks.”2 Judith Campisi, of the Berkeley National Laboratory, says that after giving a public lecture on aging, “a number of people came up to me and said: ‘How dare you do this research? The earth is already being raped by too many people, there is so much garbage, so much pollution.’ I was really quite taken aback.”3
There is reason for serious concern. According to the United Nations Population Division, the world’s population was approximately 7.349 billion in 2015, and according to “medium variant” projections (in other words, the middle of a range of projections), it will reach approximately 8.5 billion in 2030, 9.7 billion in 2050, and 11.2 billion in 2100.4 (According to these projections, most of the growth will occur in less developed countries, particularly in Africa.) Small differences in the fertility rate (the average number of children the average woman has during her life) can pull the projections up or down; in a high-variant projection, the world’s population would be 10.9 billion in 2050.
Both because the world’s population is so large and because economic development is happening all over the world, we are putting more and more pressure on the world’s resources and ecosystem. According to an estimate from the Global Footprint Network, the world is now consuming the equivalent of one and a half earths.5 In other words, to provide the resources and absorb the waste we are already consuming and producing, without depleting the earth’s resources and overloading the planet’s capacity to absorb waste, would take a planet half again as big as the earth itself. According to the Network, by the 2030s (less than 15 years from now), we will need two earths. Moreover, roughly 80 percent of the world’s population lives on less than $3,650 a year,6 but we can expect incomes to rise around the world, putting further pressure on the environment. If this continues, two earths won’t be enough.
So we may be facing a Malthusian crisis even without life extension. How much worse will this become if life extension becomes widely available? There are two ways to try to answer that question. First, we can try to predict what will happen. This requires estimating when life extension will become widely available, how large the world’s population will be at that point, what percentage of the human race will have access to life extension, how long people with life extension will live, and how many children they are likely to have. However, any estimates of these factors would be almost pure speculation.
There is a better way to approach this. Instead of asking what these demographic trends will be, we can ask what they should be. In other words, we can ask how much a population would increase given various combinations of life expectancies and fertility rates, look over the projections, and then pick the fertility rate for a given life expectancy that will avoid a Malthusian crisis. This is a matter of simple mathematics and doesn’t require trying to predict the future; all we have to do is run some numbers. Think of this as prescriptive demography rather than predictive demography.
Let’s start with what it takes to keep the current population steady—neither increasing nor decreasing. This is called the replacement fertility level, and for a population with a normal life expectancy, the figure is an average of 2.1 children per woman (the 0.1 is for infant mortality).7 What would happen if people who had life extension reproduced at this rate?
To answer this, consider a hypothetical population of one billion people. Everyone in that population uses life extension and lives an extended life. That one billion may be part of a much larger population, most of whom do not use life extension, but right now we’re interested in the part of the human race that does, so we’ll focus on just that one billion.
I’ll make four artificial assumptions about that population: (a) the percentage of women will be 50 percent at all times, (b) no women will experience menopause, (c) infant mortality is zero, and (d) women will have children at average ages specified for each projection (they will have children at various ages of childbirth that will average out to the particular numbers specified). With the possible exception of menopause, these assumptions are almost certainly false. In reality, infant mortality is never zero, the percentage of women in a population is rarely (if ever) a precise 50 percent at any given time, and women will not choose to have children at, for example, precisely ages 25 and 75. However, we don’t have the information we need to avoid making assumptions about these matters. When the time comes to limit reproduction, demographers with more information than we have now can work out the details.
To keep this discussion manageable, I’ll work with two possible life expectancies: 150 years and 1,000 years. The 150-year life expectancy is chosen because some reputable scientists have suggested that slowing aging enough to produce a 150-year life span is not implausible. The 1,000-year life expectancy is chosen because that’s the life expectancy people would have if aging were halted completely and people died only from causes of death that are not related to aging—the far end of what’s possible. I will then run projections for each of these life expectancies with various numbers of children ranging from 0.5 children per woman to 3.0 children per mother, at various average ages of childbirth. I focus on the number of children per woman not because women should bear the entire brunt of any reproductive policy but simply because they’re the childbearers and this is the clearest way to talk about how many children people will have. I will discuss how those limits apply to men when I propose a reproductive policy in the next section.
150-year life expectancy, 2 children per woman at average ages 25 and 75
In the first scenario, the life span is roughly twice as long but the fertility rate is more or less the same as it is now. We will suppose that the average mother’s age at the time of the first birth is 25, and her average age at the time of the second birth is 75. These average ages are somewhat arbitrary. I picked the ages of 25 and 75 simply because 25 is close to when many people have their first child now, and 75 is the midpoint of a 150-year life span.
Of course, some people will die sooner than 150 years and some will live longer. Some women may have more than two children, some may have one child, and some may have none. Some will have a child at 18, some at 25, some at 37, some at 59, and so on—the ages of 25 and 75 are merely averages. The total population figures in our projection will not be affected by the fact that these figures are averages. For example, a woman who has her first child at 18 and a woman who has her first child at 32 offset each other, so we can represent both of them as having their first child at 25 for purposes of calculating the population at a given time. The same thing is true of life span and number of children per woman. (It does, however, matter what the mother’s average age at childbirth is. When births are spaced earlier in a woman’s life, the population will increase faster, and when they are spaced later in a woman’s life, the population will increase more slowly. We’ll say more about this later.)
When we run the numbers, it turns out that if people live an average of 150 years and women have an average of one child at an average age of 25 and an average of one child at an average age of 75, the original population of 1 billion will triple and then stabilize! Here is the relevant graph (this graph appears again in appendix C as graph 1). The vertical numbers on the left represent the total population in millions, and the horizontal numbers at the bottom represent the generations:
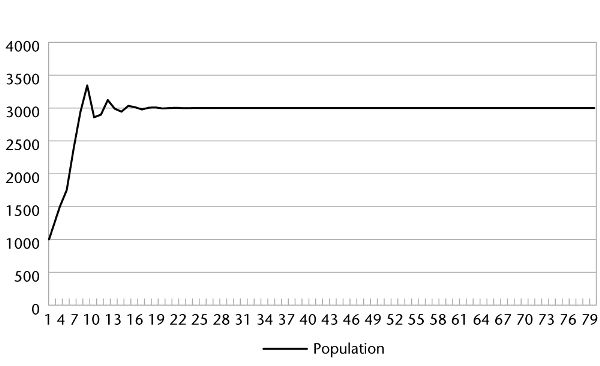
Life extension of 150 years, 1.0 child at age 25 and 1.0 child at age 75
This is a surprising result. People are living only a few decades longer and having roughly as many children as they do in many countries now, yet the population triples.
If you want to understand how we got to that conclusion, then we need to start with table 6.1, which illustrates what happens to this population over time. (A longer version of this table appears as table 1 in appendix C. That version carries the calculations out to 80 generations, but this version will stop at 20. There are similar tables in appendix C for all the projections.) The numbers are in millions (1,000 = 1 billion).
150-year life expectancy, 1 child at average age 25, 1 child at average age 75
| Generation | Year | Birth at 25 | Birth at 75 | Population |
|---|---|---|---|---|
|
0 |
0 |
0 |
0 |
1000 |
|
1 |
25 |
500 |
0 |
1500 |
|
2 |
50 |
250 |
0 |
1750 |
|
3 |
75 |
125 |
500 |
2375 |
|
4 |
100 |
312.5 |
250 |
2937.5 |
|
5 |
125 |
281.25 |
125 |
3343.75 |
|
6 |
150 |
203.125 |
312.5 |
2859.375 |
|
7 |
175 |
257.8125 |
281.25 |
2898.4375 |
|
8 |
200 |
269.5313 |
203.125 |
3121.0938 |
|
9 |
225 |
236.3281 |
257.8125 |
2990.2344 |
|
10 |
250 |
247.0703 |
269.53125 |
2944.3359 |
|
11 |
275 |
258.3008 |
236.328125 |
3032.7148 |
|
12 |
300 |
247.3145 |
247.0703125 |
3011.4746 |
|
13 |
325 |
247.1924 |
258.3007813 |
2977.9053 |
|
14 |
350 |
252.7466 |
247.3144531 |
3005.3101 |
|
15 |
375 |
250.0305 |
247.1923828 |
3008.3923 |
|
16 |
400 |
248.6115 |
252.746582 |
2993.1488 |
|
17 |
425 |
250.679 |
250.0305176 |
2999.2294 |
|
18 |
450 |
250.3548 |
248.6114502 |
3003.8109 |
|
19 |
475 |
249.4831 |
250.6790161 |
2998.4798 |
|
20 |
500 |
250.0811 |
250.3547668 |
2998.8546 |
Now let’s see how table 6.1 was calculated. The other tables in appendix C all work the same way, though with different life expectancies, different fertility rates, and different birth spacings. Some readers will find this tedious, so if you trust my arithmetic, you can skip this discussion
There are five columns from left to right. The column titled “Generation” indicates the generation that comes into existence at that time, starting with our initial generation: generation 0. (Generation 1 is the first generation born to that group, not the first group who has life extension. They are the first people generated—produced, as it were—by the first group to receive life extension.) “Year” indicates the number of years from the birth of the initial generation (generation 0); we can also use this as the number of years from the advent of life extension in this group. “Birth at 25” indicates the number of people born when the previous generation in the table (the one in the line above) turns 25, and the column titled “Birth at 75” indicates the number of people born when that generation has reached age 75. In table 6.1, the generation that has children at 75 will be three lines above the line where those children appear. For example, the line for generation 3 indicates that 500 million children are born that year—that group of children is born to the women in generation 0, which appears three lines above, for generation 0 has now turned 75.
The column on the far right, titled “Population,” indicates the total population—all generations alive by the end of that year. That figure results from adding the previous population figure from the line above to the generation born that year. The generation born that year is the sum of the number under “Birth at 25” and the number under “Birth at 75.” For example, the line for generation 3 in table 6.1 includes those born to women who turn 25 that year (125 million children) and those born to women who turn 75 that year (500 million), so generation 3 includes 625 million children.
When a generation dies, that generation is subtracted, of course. For example, in the line for generation 6 in table 6.1, generation 0 has died off, so that one billion people is subtracted from the population to produce the population total for that year.
Now let’s walk through the first few lines of table 6.1. We will focus on the total population for each year and see how that yearly population figure is generated, line by line. We will refer to each line by the figure for the “Year” column, using that to indicate the number of years since the birth of generation 0. Generation 0 is the first generation to have a life expectancy of 150 years:
Year 0 population: 1 billion
Half of generation 0 are women. They each have one child when they reach age 25, adding half a billion children (generation 1) to the population:
Year 25 population: 1.5 billion
Generation 1, the first generation born to the original group of people living extended lives, contains 500 million people. In year 50, the women in generation 1 have one child each when they turn 25. This adds 250 million more people (generation 2) to the population:
Year 50 Population: 1.75 billion
In year 75, the women in generation 2 turn 25 and have one child each, adding 125 million people to the population. The women in generation 0 turn 75 and have a second child, adding 500 million children. This produces a total of 625 million people in generation 3. We add that sum to the total population from the previous line:
Year 75 Population: 2.375 billion
In year 100, the women in generation 3 turn 25 and have one child each, adding 312.5 million people to the population, while the women in generation 1 turn 75 and have one child each, adding 250 million people to the population, for a total of 562.5 million people in generation 4:
Year 100 Population: 2.93 billion
In year 125, the women in generation 4 turn 25 and have one child each, adding 281.25 million people to the population, while the women in generation 2 turn 75 and have one child each, adding 125 million people to the population, for a total of 406.25 million people in generation 5:
Year 125 Population: 3.34 billion
This is the year the population peaks. Let’s follow this for one more generation.
In year 150, the women in generation 5 turn 25 and have one child each, adding 203.125 million people to the population, while the women in generation 3 turn 75 and each have a second child, adding 312.5 million people to the population, for a total of 515.625 million people in generation 6. That same year, generation 0 reaches the age of 150 and dies off, removing 1 billion people from the population:
Year 150 Population: 2.859375 billion
Table 6.1 carries this projection out for many generations more, but you can see the trend: the population stabilizes at around 3 billion.
The lingering guest problem
The forgoing discussion is meant to show how the population triples even though these people live only roughly 70 years longer than people in developed countries do now and have no more children than the current replacement level. However, this does not quite explain why it triples. The answer lies in what I call the lingering guest problem.
Imagine that you’re holding an open house party for your neighbors. The party begins at 10 o’clock in the morning and continues until 10 o’clock at night—12 hours. Your house can comfortably hold 30 people at any given time. Suppose that each guest stays for an average of one hour and then leaves. Suppose further that they arrive randomly during the day, so the total number of guests is distributed evenly over the 12 hours of your open house party (one-twelfth of them arrive each hour, on average). At any given time, your house will have roughly 30 people in it, and there will be room enough for everyone.
Now suppose your party is more successful than you expected and that all of your guests linger. They arrive randomly during the day (another one-twelfth arriving every hour, on average), but they all stay until the party is over. The house will gradually fill up and up and up, and after a few hours, you’ll have several times as many guests as your house can comfortably contain. It will stay that way for the rest of the day.
That is what happens when we live longer. Even if our population of one billion people with 150-year life expectancies has only two children per woman, they are still alive—lingering in the population—several decades longer than people live now. So are their children, who also enjoy 150-year life expectancies, and so are their children, and so on. Thus, the generations pile up and hang around instead of clearing out after seven or eight decades, and the population will increase, eventually stabilizing at a much higher level as people finally start leaving the party.
This also explains why the birth spacing—the average ages at which women have children—is important. If women have children earlier in their lives, the population will increase faster, just as your house will get more crowded if all your guests arrive before noon instead of arriving every hour all day. Similarly, if women have children later in their lives or space later births further out (the second child at age 125, for example), then the population will increase more slowly, just as your house will remain uncrowded longer if most guests wait until late afternoon to show up.
Is this a Malthusian crisis?
So the population in this scenario will triple and then stabilize. Is this a Malthusian crisis, or is it something we can live with? That depends on how large a population we are tripling. Initially only some people will have access to life extension, but it would not be safe to assume that life extension will always be unavailable to most people. Suppose that a combination of falling cost and economic growth around the world make it available to anyone who wants it and that most of them choose to get it. The United Nations Population Division medium variant project tells us that the world’s population will be approximately 11.2 billion in 2100.8 If 90 percent of that population chooses extended life, then sometime after 2100, the earth will be carrying more than 33 billion people.
Supporting 30 billion people at a first-world income level would require finding a sustainable and nonpolluting source of energy, solutions to climate change, radical increases in agricultural efficiency, far more complete recycling than we have now, far tighter controls on pollution and refuse dumping in the oceans, an end to overfishing, and so on. Of course, we need to do these things even if the world’s population never rises above its present 7.5 billion. If we can do these things at all, perhaps we can do them in a world with a much larger population.
Still, running the risk of increasing the world’s population to 30 billion in hopes that technological breakthroughs will arrive in time is one hell of a science experiment to run on the only planet we have, and common sense suggests that the task of saving the world’s environment will only be harder if we are coping with population growth at the same time. Moreover, even if we can support 30 billion people, such a world would be unpleasantly crowded.
Perhaps things will not get that bad. Perhaps life extension will always be too expensive for most people (though that raises a serious concern about the justice of a world where most people must watch the lucky minority live far longer than anyone else). Perhaps most people will not want it. Perhaps they will have far fewer children.
Perhaps the world’s population will be much less than 11.2 billion by the time life extension becomes widely available. Fertility levels are dropping below the replacement level nearly everywhere except in sub-Saharan Africa, and they are falling there too. About 46 percent of the world’s population lives in countries with fertility levels below the replacement level, including all of Europe, China, Brazil, Russia, Japan, Vietnam, Iran, Thailand, and the United States, and the worldwide fertility level is expected to drop to or below replacement level by 2095. The International Institute for Applied Systems Analysis (IIASA) in Austria concluded that if the world stabilizes at a fertility level of 1.5—where Europe is right now—the world’s population will drop by half by the year 2200, to roughly 3.5 billion. By 2300, according to their projections, it will drop to 1 billion and continue dropping from there.9
Let us hope so. However, this period of decline will not happen immediately; the world’s population is still increasing right now. Moreover, it’s not likely that life extension will be unavailable until 2200—nearly two centuries from now. We are already suffering the beginnings of catastrophic climate change, overfishing, soil depletion, water shortages, and many other Malthusian problems at the current population of just over 7 billion people, and most of those 7 billion are not living at a first-world level. If life extension arrives well before 2200, then all this will be that much worse.
And all of this assumes that women have an average of only two children each, despite living many decades longer. If people have an average life expectancy of 150 years and women have an average of three children per woman at average ages of 25, 50, and 75, the initial population of one billion grows to nearly seven times its original size in 200 years and grows indefinitely thereafter, reaching a titanic 25 million times its original size 2,000 years after the advent of life extension! (See table 2 and graph 2 in appendix C.) That third child makes the difference between a population that stabilizes at three times its original size and a population that never stops increasing.
150-year life expectancy with other numbers of children
What if women have only one and a half children each at average ages of 25 and 75 (every other woman has one child at 75)? In that scenario the population increases from 1 billion to 2.656 billion in year 125 but then declines steadily and indefinitely thereafter. By year 250, the total population drops below the original 1 billion; by year 600, it drops below 100 million people; by year 950, it drops below 10 million; and by year 1300, it drops below 1 million—and continues to drop indefinitely. (Table 3 and graph 3, appendix C.)
This is much better than stabilizing at 3.0 times the original population, but it still increases the original population by more than 2.5 times for at least a generation, and it takes 100 years to drift back down to 1.18 billion (roughly the original population), declining further from there. If increasing the world’s population to 2.6 times its original size is a Malthusian crisis (and I believe it is), then we would have a temporary Malthusian crisis for the better part of a century.
If women have an average of only one child each at an average age of 25, the population roughly doubles in a little over a century, peaking at 1.968 billion in year 125, and then rapidly drops to below the original 1 billion in the year 150. (It declines by half in a mere 25 years.) It continues to drop thereafter. (Table 4 and graph 4, appendix C.) However, even temporarily doubling the world’s population is at least a Malthusian threat, even if it does not quite rise to a crisis. We get a similar result if women wait until an average age of 50 to have one child; the population rises to 1.75 times its original size by year 100, drops to less than a quarter of that by year 200, and continues to drop thereafter. (Table 5 and graph 5, appendix C.)
Let’s consider an even lower fertility rate: half a child per woman at an average age of 25. Here is the graph (see also table 6 and graph 6, appendix C):

Life extension of 150 years, 0.5 child at age 25
Now the population increases by slightly more than 30 percent in 50 years, then levels off, peaking at 1.333 billion in the year 125. A generation later, in the year 150, the population has plummeted to 333 million and declines dramatically from there on—to less than 1 million by year 275. It then fluctuates indefinitely between a few million and a few hundred thousand but never reaches even 20 million from then on. Obviously, we would need to raise the rate of reproduction soon after the population peaks, but to achieve this result, the initial limit must be 0.5 children for 125 years. (We get a similar result if women wait until an average age of 50 to have 0.5 children each, so delaying the age of childbirth won’t make much difference. See table 7 and graph 7, appendix C.)
Would allowing the world’s population to increase by one-third for 125 years be an intolerable Malthusian crisis? My personal judgment—for whatever that’s worth—is that this is a tolerable increase, particularly since it lasts for only a century.
Bear in mind that the 0.5-child limit applies only to those who extend their lives. Moreover, this limit applies only for 125 years; after that, everyone can have up to 2.1 children per woman (or whatever the replacement level must be for the entire population to stabilize). The downside, of course, is that every other woman in the population of people living extended lives will not have a child at all. (This limit applies to men as well. I’ll explain how that works in section 6.3.)
I conclude that a 0.5-child limit for 125 years is a plausible initial target birthrate if life extension provides a life expectancy of 150 years and everyone in the world has access to life extension. This may not be the actual limit when the time comes, of course. If the life expectancy is less or not everyone has access, the limit could be correspondingly higher. We can’t pin down exactly what the target fertility level should be without knowing more about the extended life expectancy and the number of people who would have access to life extension, but we do know that if life extension gives us at least several extra decades and becomes widely available, then we must temporarily limit reproduction to significantly less than two children per woman for those who use life extension.
1,000-year life expectancy
Of course, it’s not safe to assume that we’ll never be able to extend the human life expectancy past 150 years. If it’s possible to slow aging, it may be possible to slow it to a halt. As I explained in section 1.7, if we halted aging and the current rate of accidents and violence were unchanged, our life expectancy would be around 1,000 years. Some people would live much longer, some would die much sooner, but the various life spans would average out to approximately 1,000 years. What must our reproductive policy be like in order to keep life extension from making our Malthusian problems worse in that world?
Once again, let’s start by supposing that each woman has two children—the reproductive limit necessary to prevent excessive population growth in the absence of life extension. Suppose further that each woman has one child at age 25 and one child at age 500. Specifying age 500 as the age for having a second child is arbitrary; I chose it simply because it’s the midway point. Bear in mind that if births occur earlier in life, the population grows much larger and faster and that if they occur later in life, the population will grow more slowly and less.
Here is the relevant graph (this graph appears as graph 8 in appendix C; see also table 8, appendix C):
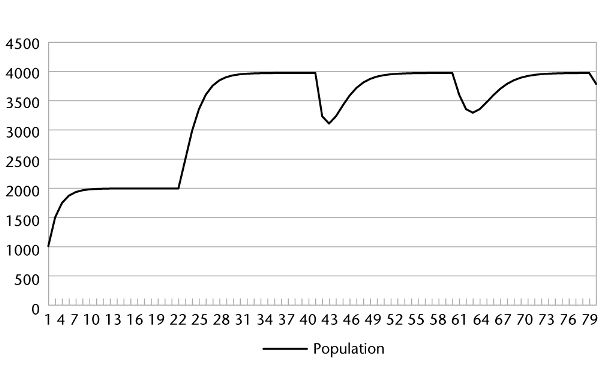
Life extension of 1000 years, 1.0 child at age 25 and 1.0 child at age 500
This population increases from 1 billion to nearly 2 billion very quickly—in just 75 years. The population then levels off at roughly 2 billion for the next 400 years. From year 475 to year 600, it increases to nearly 4 billion, stays at roughly that level until year 975, and then fluctuates between 3 and 4 billion for centuries, eventually stabilizing at around 4 billion. Notice that this is only 1 billion more than the eventual population in the scenario where the life expectancy is only 150 years, even though people are living several times longer in this scenario. The Malthusian threat posed by radical, 1,000-year life extension may not be much worse than the one posed by moderate, 150-year life extension!
Still, we had serious concerns about whether increasing the population threefold is tolerable, and those concerns are even more serious when we consider increasing the population fourfold. And that’s just for starters. If this population has three children per woman (at average mother’s ages of 25, 50, and 500), the population reaches nearly seven times its original size by year 225 and continues increasing thereafter, reaching a staggering 1,700 times its original size by year 2,000. (Table 9 and graph 9, appendix C.)10
What if women have an average of one and a half children at average ages of 25 and 500 (half the women have a second child at 500)? As we can see from table 10 and graph 10 in appendix C, the population roughly doubles by year 100, rises to 3 billion around year 700, then declines to around 2 billion around year 1,000 and then slowly declines for many centuries thereafter. However, the population still triples for most of a thousand years. This too is a Malthusian crisis.
If women have an average of only one child at an average age of 25, the population roughly doubles in the first 100 years and then remains at that level for another 875 years. It then declines over a period of many centuries. (Table 11 and graph 11, appendix C.) I don’t know about you, but doubling the world’s population for 875 years sounds like a Malthusian crisis to me.
Now consider what happens if women have an average of half a child each at an average age of 25 (half the women never have a child at all, and the other half have no additional children for a thousand years). Here is the relevant graph (see also table 12 in appendix C, where this graph appears again as graph 12):

Life extension of 1000 years, 1.0 child at age 50
In this scenario, the population rises to 1.250 billion in year 25, 1.312 billion in year 50, and peaks at 1.333 billion in year 125. The population then stabilizes at 1.333 for 850 years (to year 975) and then starts dropping sharply and continuously from then on. If women postpone that half of a child until age 50, we get a similar result: the population rises to 1.250 billion in year 50, 1.312 billion in year 100, and 1.333 billion in year 250. (See table 13 and graph 13, appendix C.) That population levels off until year 950 and then begins to decline continuously and sharply.
Is increasing that world’s population by one-third for several centuries a tolerable increase? Let’s put this in perspective. If the growth estimates we considered earlier are correct, by 2100, the current world population of roughly 7.5 billion will increase by approximately 45 percent according to the United Nations Population Division and approximately 25 percent according to the Institute for Applied Systems Analysis (IIASA) in Austria. We are likely to see the world’s current population increase by one-third even in the absence of life extension, and the spread in estimates is fairly large: 1.9 billion (9 billion according to the Austrians, 10.9 according to the UN).
My judgment is that if these increases are tolerable, then a one-third increase on top of that is not intolerable. If we can find renewable sources of energy, more efficient ways to produce food, better ways to dispose of waste, and solutions to climate change for a population numbering in the billions, then we should be able to find those things for a population one-third larger than that. (Of course, this assumes we can achieve all those things. If we can’t, then we may be doomed in any event.)
So I reach the same conclusion: if life extension halts aging completely and the entire world gets a life expectancy of 1,000 years, a plausible target fertility level is 0.5 children per woman at an average age of 25 or above—at least for 1,000 years or so. Of course, that 0.5 figure is only one of many plausible estimates, and it might go up if childbirth is delayed. My main point is to demonstrate that a population with life extension reproducing at anything close to current fertility levels poses a very serious Malthusian risk.
6.3 A policy to prevent a Malthusian crisis: Forced Choice
Suppose we want to design a policy that enforces a target birthrate of 0.5 children per woman. (I pick that target just for illustration; what I say in this section doesn’t turn on that particular target.) I’ll call this policy “Forced Choice,” for it forces people to choose between extended life and having more children than the target birthrate—those who choose to have more children are denied life extension.
Here is one way Forced Choice could work. We are supposing that those who extend their lives can have an average of only 0.5 children per woman at an average age of 25 at childbirth. In effect, half of all couples have one child, and half have none. This policy is imposed on men too. (To be clear, it is applied on an individual basis, not on couples as units.) So divide one child among four people (one child for every two couples): each person gets a 25 percent chance of having a child. That is, one person out of every four gets a chance to reproduce. To decide who gets that chance, those who wish to extend their lives must enter a reproductive lottery (or be denied access to life extension). The lottery applies to both men and women and any other genders, and it applies in the same way to all of them. If you win the right to reproduce, anyone you reproduce with can do so as well, even if they lost the lottery. In other words, if you win the lottery, you don’t have to look around for another lottery winner in order to exercise your right. You can share your good fortune with a partner who lost the lottery but won you.
If you have had no children yet and you enter the lottery, you have a 25 percent chance of winning the right to reproduce. If you have already had one child and you then enter the lottery, the trade-off is reversed, in a way: you enter the lottery with a 25 percent chance of winning the right to extend your life. Thus, having one child reduces your chances of being allowed to extend your life from 100 percent to 25 percent. You’ll want to consider that first child very carefully; it could be a fatal choice.
If you have had two children already, then you are forbidden to have life extension: your odds of extended life are now zero.
The limit of 0.5 children per woman was based on the expectation that people who have a child would do so at age 25. However, if they wait until a later age, then the lingering guest phenomenon is lessened, and we could keep the population within a tolerable limit with a higher reproductive limit. Of course, Forced Choice is not meant to tell anyone they must have a child by a particular age, and this opens up another possibility. Delaying the average age of childbirth slows the population increase to some extent, so your odds of winning the right to reproduce could be correspondingly higher the longer you wait to enter the lottery (linked to whatever higher rate of childbirth at that average age of childbirth will produce the same population increase). And here is another possibility: if you lose the lottery when seeking to reproduce at age 25, you might subtract your odds at age 25 (25 percent from your higher odds at some later age) and enter the lottery again at that later age with a percentile chance of reproducing equivalent to the difference between 25 percent and whatever higher odds you would have had if you had waited until that later age to enter the lottery the first time. We can even imagine repeating this several times in a lifetime with various odds of success, though the more often one does this, the lower the odds would be each time one enters the lottery.11
Those who extend their lives may, of course, have children with people who do not extend their lives. However, the reproductive limits still apply to the person who lives an extended life. For example, if you have extended your life and you want to have a child with someone who has not done so, your partner is not limited, but you are, and the two of you can have a child only if you can have a child. If your partner can but you can’t, then your partner can have a child only with someone else who has the right to reproduce. (You might, presumably, be able to adopt the child of that union.) Otherwise, the limit on reproduction would be ineffective, for anyone living an extended life would merely need to reproduce with someone who is not. To see this, suppose our entire population of one billion people living extended lives had children with a billion other people whose lives are not extended: the result is a billion children when the target calls for 250 million children (0.25 children per person).
These limits do not apply to adoption, except insofar as the child comes from parents living extended lives.
If you are living an extended life and your child dies, Forced Choice allows you to have another child to replace the one who died. The reproductive limit is based on the number of children, not the number of childbirths.
This works for same-sex couples too. Each adult gets a 25 percent chance regardless of gender identity or sexual orientation. If you’re gay and you win the right to reproduce, you and your same-sex partner can have a child, just as a heterosexual couple would. This also works for people who are infertile: each adult gets a 0.25 chance even if they are biologically unable to reproduce for some reason. An infertile person who wins the lottery can then use assisted reproductive technology and egg and/or sperm donors (or even cloning) to exercise that right and have a child. If that person is unable to reproduce even with the help of such technology, then they might be allowed to sell or give that right to someone else who can use it, somewhat like a carbon credit. We might allow this also for those who win the lottery and decide not to use their right to reproduce—that way it won’t go to waste.
If you’ve already extended your life and you then have a child without having won the reproductive right to do so, your life-extending treatments are terminated and you resume aging at a normal pace. (Remember that life-extending treatments are likely to require periodic or ongoing interventions of some kind, such as drugs or stem cell treatments. This is not likely to be akin to a vaccine you take only once in your life. Thus, it won’t be hard to cut people off.) Your reproduction is now no longer limited (assuming your society has not imposed some other limit on reproduction that applies to everyone), but you will resume aging.
In other words, your decision to extend your life and limit your reproduction is reversible. If you extend your life and you later wish you had reproduced instead (or wish you had more children than you were allowed to), you simply reverse that decision and revert to normal aging, just as if you had never extended your life in the first place. You can then have more children. Of course, a decision to have two children and then extend your life is not reversible.
You can make these choices at any time during your life. You reduce your choice only if you have one child before you request life extension, and you lose it only if you have two or more children before you request life extension. The timing of that request is up to you.
What if lots of people extend their lives and then, after many decades or centuries, they decide to discontinue their life-extending treatments and then have an extra child? In that event the population of those who live extended lives might get too large due to the lingering guest problem (having one child and living 280 years will create more population pressure than having one child and living 80 years). In that event, the target birthrate might have to be lowered to compensate for this.
Note that this is not a complete population policy, for I’ve said nothing about limiting the reproductive choices of those who cannot or choose not to get life extension. Thus, Forced Choice may not prevent a population crisis; we might overpopulate the earth even without life extension. We may need other policies to prevent that. Forced Choice is meant merely to ensure that life extension does not make that crisis worse.
6.4 Practical problems with Forced Choice
How do we know when people have had life extension but exceeded their reproductive limit? In many cases, this is straightforward. Societies around the world would have to keep track of birth records to see who has had children and how many children each person has had. Life extension clinics would have to be licensed and supervised, and each person who comes in would have to be identified (perhaps with a pinprick blood sample and a DNA chip12) and their reproductive records called up. If that person has exceeded his or her reproductive limit, then the penalties kick in.
Of course, some people will try to hide their children and keep society from finding out about their children’s birth and parentage. However, it should not be difficult to use genetic testing (again, with a pinprick of blood and a DNA chip) to read every child’s genome. That genome can then be compared with all others in the system and the biological parents (or at least sperm or egg donors) identified. There would be no penalty for the child, obviously, but if a child is traced to a parent who has exceeded his or her reproductive limit, then the parent is penalized. If both parents have exceeded their limits, then both parents are penalized. One would have to hide a child from the public schools, the healthcare system, and all other authorities indefinitely to do this, and while that’s possible, it’s sufficiently difficult that few people will succeed indefinitely.
Some people might seek to avoid Forced Choice in another way. Instead of hiding their children, they might try to hide the fact that they are getting life extension. For example, they might fly to some overseas clinic operating beyond the reach of the authorities or have a back-alley operation at home and get their life-extending treatments from a source that doesn’t care about their reproductive history.
There are a couple of ways to deal with this. One way is to try to find and shut down any illicit operations. Another way is to police the user. We could take a pin-prick blood sample and a genetic reading with a DNA chip, check that against the birth records, and thereby see how old someone is. Anyone above a certain age is obviously using life extension. That genome can then be compared with the genetic records for all children, and if any of the children turn out to be a match with that adult, then we know how many children that person has had.
These methods of enforcement are not airtight (law enforcement never is), but they don’t have to be. Forced Choice does not have to be enforced in absolutely all cases in order to be effective. It can be effective at staving off a Malthusian crisis provided it’s enforced in the great majority of cases. Moreover, Forced Choice need not be entirely effective at first. All of these details can be adjusted and revised as needed for some decades, for a Malthusian crisis would develop slowly enough for us to watch trends and see what works.
It may be cumbersome and difficult to develop this system and enforce it. Is there a better alternative? We could simply let people reproduce at will and see what happens (a policy of Free Choice), but that may turn out badly for the human race. We could also try to ban life extension altogether (a policy of Prohibition concerning access). However, banning life extension may be just as difficult as controlling the reproduction of those who extend their lives and require nearly as much record-keeping, for we would still have to keep track of birth records and run genetic tests on anyone who has lived past a certain age. Moreover, banning life extension altogether may be politically more controversial and unpopular than controlling the reproduction of those who extend their lives. Prohibiting life extension denies decades or centuries of life to people who want it, while Forced Choice merely limits how many children they have.
There really is no better alternative to limiting the reproduction of those who extend their lives, at least for a few generations.
6.5 Reproductive ethics and Forced Choice
Forced Choice raises some difficult issues concerning the ethics of individual reproductive choice. I will offer some fairly brief responses to these issues. We may not be able to analyze them fully until after Forced Choice is implemented, when such cases arise in practice.
To begin with, Forced Choice assumes that people choose between extended life and having more children, but what about those who don’t reproduce voluntarily? There are many versions of this case, including people who are raped, people who have sex with someone who is too young or otherwise not competent to make that choice, people who use forms of birth control that fail for some reason (especially if they have moral objections to abortion—the birth control of last resort), and people who had good reason to believe they were not at risk of becoming a mother or father (perhaps due to infertility) but became one anyway (again, especially if they have moral objections to abortion).
Each of these cases concerns whether or not someone voluntarily became a parent. Implementing Forced Choice will require carefully thinking through such cases and deciding when someone’s reproductive choice was truly voluntary, competent, informed, and so on. For example, a clear case of rape is a clear case where the victim should be treated as if her child had never come into existence so far as access to life extension is concerned. A more subtle, ambiguous case involving, for example, someone of dubious competence, might be harder to analyze. However each case is decided, we can say this much: if we decide that the mother or father did voluntarily reproduce, then that birth counts under Forced Choice, and if we decide that she or he did not, then that birth does not. Many of these cases might have to be settled by the courts.
What if you lose the reproductive lottery and you don’t want to forgo extended life? Presumably you’re free to try to find a mate who won the lottery. However, this might make it much harder to create and sustain a committed relationship and give a huge advantage to the winners of the reproductive lottery. As I mentioned earlier, some winners in the reproductive lottery might choose not to exercise their right, instead selling or giving it to someone else, like carbon credits. To that extent, reproduction would be yet another privilege of the rich. If that concerns us, we might ban selling reproductive rights to prevent such inequality, just as we ban the sale of organs. My judgment is that these problems are just part of the price we would have to pay to live in a world with life extension and avoid a Malthusian crisis, but they are unquestionably a downside to that world.
Of course, adoption is still possible under Forced Choice. Presumably the great majority of children available for adoption would come from people who are not extending their lives. Does this create an incentive for Have-nots to produce babies for the adoption market? If so, society might have to ban any form of compensation to those who produce such children, or impose limits on such adoptions, or lower the target birthrate to compensate for increased reproduction by Have-nots.
What about those who had good reason to believe they would never have access to life extension (they were born poor), so they went ahead and had children, but later found that they could have life extension after all, perhaps because they suddenly came into money? Their choice to reproduce was made under conditions where they had reason to believe extended life was not an option. Is it fair to deny them life extension later on just because they didn’t know they would have access one day?
Frankly, I’m not sure how to handle such cases. We could simply take a hard line and say that people must weigh those odds when they choose to have children and take their chances. We could also say that being denied extended life because you are poor is no worse than being denied extended life because you mistakenly thought you would always be poor and you had children.
A better approach might be this: those who came into money later in life could be allowed to appeal the denial of extended life and try to prove to some tribunal that they had good reason to believe they would never be able to pay for life extension. People who won millions of dollars in a monetary lottery would be able to meet that standard quite easily, while those who simply succeeded in business (due to the foreseeable effects of hard work) might have a more difficult time meeting it.
In the end, it’s impossible to entirely avoid inequity in the details of a reproductive policy like Forced Choice. The price of making life extension available and avoiding a Malthusian crisis may simply be to tolerate the partial injustice of any real world version of Forced Choice.
6.6 Is Forced Choice an oppressive government intrusion into private reproductive choices?
Forced Choice may sound a lot like China’s one-child policy, and it might trigger an objection sometimes leveled at that policy. You might object that this is an unacceptable intrusion into the personal affairs of citizens and that governments should not tell people how many children to have. However, that objection is not valid when applied to Forced Choice. Forced Choice is very different from China’s one-child policy.
First, Forced Choice doesn’t set limits on how many children people can have when they don’t extend their lives. (We may want to limit reproduction within that period for reasons having nothing to do with life extension, but that’s another matter.) Second, Forced Choice doesn’t apply to everyone, aside from taking genetic samples for record-keeping. The limits it imposes apply only to those who choose extended life, and by choosing extended life, they can be said to have consented to certain limits on their behavior. Third, Forced Choice is meant to prevent harm to people who don’t want life extension (the Will-nots) or can’t get it (the Have-nots). If there is a right of reproductive freedom (as an instance of the right to self-determination in general), that right—like the right to self-determination generally—is subject to the harm principle. It’s generally recognized that you have a right to determine your own life (including your reproductive life) but that you may not do so in ways that harm other people. Fourth, if there is something biologically unnatural about living without aging (and by “unnatural” I don’t mean “therefore bad”), then we should accept that such a life might be bound by biologically unnatural limits on reproductive behavior. A new life may require new ways of living, and seen from that perspective, Forced Choice should not seem unduly restrictive or intrusive.
6.7 What if some countries impose Forced Choice and others do not?
What if not all countries impose Forced Choice? Suppose country A makes life extension widely available but imposes no limits on reproduction. We live in country B, and we’re deciding whether to impose Forced Choice. We see what’s happening over in country A, and many of our citizens complain at living under constraints that aren’t applied to the citizens of country A.
Does the fact that we (in country B) see country A behaving recklessly in its population policy give us a reason to be reckless too? Surely not. The fact that someone else is contributing to a problem is not a reason for you to make things worse too. It may seem like it is if everyone else is ignoring the problem and you are the only one doing something about it, just as you might give up trying to recycle your trash if everyone around you fails to recycle, but that’s not how we usually think about moral duties. We tend to think that our moral duties are not contingent on everyone else performing that duty too, even if we must all perform that duty in order to avoid some widespread harm.
To see why, consider another response to country A: we might decide that A’s failure is a reason for us to control our own population even more severely to offset the harm A is doing. In other words, instead of instituting Forced Choice, which allows limited reproduction, we might institute Prohibition either for reproduction or for access to life extension, or both.
Do we have a duty to do this? We don’t generally think so in other situations. We don’t, for example, think that you have a duty to do more than your share to clean up the local environment just because others do less than their share. Your duty is to do your share—period. You cannot have a duty to do more than your share, for that amounts to a duty to do more than your duty. Imposing a harsher duty penalizes those who do their share, and that seems unreasonable. Similarly, country B has no duty to inhibit or prohibit access to life extension or impose more draconian limits on population than Forced Choice calls for just because there are other countries that don’t do enough. Forced Choice is enough, regardless of what other countries may be doing.
If your share is not increased by someone else’s dereliction, then your share is also not decreased by someone else’s dereliction. Whether someone else performs their duty is morally irrelevant here. Therefore, the fact that country A does not impose Forced Choice on its citizens is not a reason for country B to allow those living extended lives to reproduce without limit.
I’m not dismissing concerns about whether an individual’s moral duty is sometimes contingent on others performing their duty. A duty to obey the law, for example, might be permissibly ignored in a society where everyone else ignores the law, especially when obeying the law imposes some cost on those who obey it. However, we’re not talking about an individual’s duty to limit his or her reproduction. (In this discussion I’m neither claiming nor denying that such a duty exists.) We’re talking about whether an entire country has such a duty. When an entire country fails to limit its population, especially if the country is large, that dereliction has consequences that are significantly harmful for the entire world in the long run. (Similarly, an individual may have a duty to obey the law in a very small society where everyone else ignores the law if that individual’s disobedience imposes significant harm on everyone else.) I’m not suggesting that potential harm is the only source of a duty, but it can override other reasons to suppose a duty has been suspended.
Of course, getting every country (or at least most of them) to institute a responsible reproductive policy for those citizens who extend their lives will be necessary to avoiding a Malthusian crisis, and that may be very difficult. However, that’s a problem in enforcing our duty to control reproduction, not a reason to think we have no such duty.
That said, there is some reason for guarded optimism that all or most countries will eventually impose some reasonable limits on population, for the world is starting to do something like that concerning climate change. By 2016, 195 countries had signed a pact popularly known as the Paris Climate Agreement, promising to do what is necessary to keep the average global temperature from rising more than 2° Celsius over preindustrial levels, provided that enough of the countries signing that pact ratified the agreement. In 2017, Donald Trump declared that the US would not abide by it, yet several American states and more than three hundred American cities have declared that they will, so not all hope is lost. Perhaps we can achieve something similar for limiting reproduction worldwide. In fact, it may be even easier to limit reproduction worldwide, for unlike preventing climate change, Forced Choice doesn’t require technologies that have not been developed, radical changes in our economy, or reducing our material consumption. Moreover, the population trends that make Forced Choice necessary will unfold slowly, generation by generation, while the world’s climate may suffer serious deterioration as soon as a century from now. Therefore, we have more time to institute Forced Choice than we have to prevent climate change.
6.8 The demographic formula used in this chapter
The formula for the calculations behind the tables and graphs in this chapter and in appendix C was developed by Shahin Davoudpour, who also co-authored this section. For ease of exposition we did not go into the formula earlier, but for those who are interested, here it is:

We want to know what happens to a given population over a span of time ending at time t. Pt is the total population at time t. Pt-1 is the initial population at an earlier time. Φg is the gender ratio of a particular generation g (for simplicity we set the ratio at 50/50 in all our calculations). βg is the number of children allowed per woman in generation g at time t. θg is the number of deaths for generation g at time t. Finally, we must calculate for all generations during the span of time we considering. Hence, Σ indicates that the sum of the multiplication of the three variables in the parentheses for each generation of women having children at that time, which are between 1 and n (1,n), must be added to the sum for every other generation of women having children at that time. (In other words, more than one generation of women may be having babies at that time; we must run the numbers for all generations having babies at that time and add them up.)
Suppose, for example, that we want to know how much an initial population of one billion will grow by the birth of the third generation, fifty years after that one billion begins using life extension, where people have an average life expectancy of 150 years, the gender ratio is 50/50, and women have an average of one child at age 25 and .5 children at age 50. P0 (Pt-1, t is 1, hence P0) is the initial population. Variable g is 1 since it is the first generation, Φ1 is .5 (the percentage of women in that population of 1 billion [P1] is 50%), and β1 is 1 child per woman for the generation of women who have their first child in that year (in other words, those who just turned 25 years of age). We get a total of 500 million children. Now the population of the world is 1.5 billion.
Twenty-five years later, the women in g1 turn 50; they are now entitled to have an additional .5 children each. We run the numbers again (except that this time β1 is .5 children per woman) and get another 250 million children. At the same time, 500 million people turn 25 (g2), and the women in that group have an average of 1 child each. We run the numbers again with β2 of 1, and get an additional 250 million births. Finally, we add the initial 1.5 billion to 250 million (those who are 50 years old) and 250 million (those who are 25 years old), for a total of 2 billion people at time t, 50 years after life extension became available to this population.
6.9 Conclusion
- M. There is good reason to believe that making life extension widely available will pose a serious risk of a Malthusian crisis of overpopulation, pollution, and resource shortages. To avoid this, it is very likely that we will have to significantly limit the reproduction of those who extend their lives. (Section 6.2)
- N. A policy of Forced Choice, which requires people to choose between extending their lives and having as many children as they wish, is feasible and just. (Sections 6.3, 6.4, 6.5, 6.6, and 6.7)