Between the 1930s and the 1970s economics became mathematized in the sense that it became the normal practice for economists to develop their arguments and to present their results, at least to each other, using mathematics. This usually involved geometry (particularly important in teaching) and algebra (particularly differential calculus and matrix algebra). In the 1930s only a small minority of articles published in the leading academic journals used mathematics, whereas by the 1970s it was unusual to find influential articles that did not. Though the speed of the change varied from one field to another, it affected the whole of the discipline – theoretical as well as applied work.
Mathematics is used in two ways in economics. One is as a tool of theoretical research. Algebra, geometry and even numerical examples enable economists to deduce conclusions that they might otherwise not see, and to do so with greater rigour than if they had used only verbal reasoning. This use of mathematics has a long history. Quesnay and Ricardo had made such extensive use of numerical examples in developing their theories that they were criticized in much the same way that the use of mathematics in present-day economics is criticized critics argued that mathematics rendered their arguments incomprehensible to outsiders. Marx also made extensive use of numerical examples. The use of algebra goes back at least to the beginning of the nineteenth century, though in retrospect the most significant development was the use of differential calculus by Thünen (1826) and Cournot (1838). With the work of Jevons, Walras and their turn-of-the-century followers notably Fisher the use of mathematics, in particular calculus and simultaneous equations, was clearly established as an important method of theoretical inquiry.
The second use of mathematics is as a tool in empirical research – to generalize from observations (induction) and to test economic theories using evidence (usually statistical data) about the real world. Given that calculating averages or ratios is a mathematical technique, this has a very long history. A precondition for the use of such methods is the availability of statistical data. This has meant that the scope for such work increased dramatically with the extensive collection of such data early in the nineteenth century by economists and statisticians such as McCulloch, Tooke and William Newmarch (1820–82), Tooke's collaborator on his History of Prices (1838–57). More formal statistical techniques, including correlation and regression analysis, were developed in the late nineteenth century by Francis Galton (1822–1911), Karl Pearson (1857–1936), and Edgeworth. Jevons had speculated that it might one day be possible to calculate demand curves using statistical data, and early in the twentieth century several economists tried to do this, in both Europe and the United States. In the period before the First World War, economists began to address the problem of how to choose between the different curves that might be fitted to the data.
Despite these long histories of the use of mathematics in deductive and inductive arguments, the mathematization of economics since the 1930s represents a major new departure in the subject. The reason is that it has led to a profound change in the way in which the subject has been conceived. Economics has come to be structured not around a set of real-world problems, but around a set of techniques. These include both theoretical and empirical techniques. Theoretical techniques involve not just mathematical techniques such as constrained optimization or matrix algebra but also received assumptions about how one represents the behaviour of individuals or organizations so that it can be analysed using standard methods. Similarly, empirical techniques involve assumptions about how one relates theoretical concepts to empirical data as well as statistical methods.
This development has had profound effects on the structure of the discipline. The subject has come to be considered to comprise a ‘core' of theory (both economic theory and econometric techniques) surrounded by fields in which that theory is applied. Theory has been separated from applications, and, at the same time, theoretical and empirical research have become separated. The same individuals frequently engage in both (mathematical skills are highly transferable), but these are nonetheless separate enterprises. These changes have also loosened the links (very strong in earlier centuries) between economic research and economic problems facing society. Much research has been driven by an agenda internal to the discipline, even where this has not helped solve any real-world problems.
The theoretical basis for this approach to the subject was provided, in 1933, by Lionel Robbins (1898–1984) in The Nature and Significance of Economic Science. In this book, Robbins argued that economics was not distinguished by its subject matter – it was not about the buying and selling of goods, or about unemployment and the business cycle. Instead, economics dealt with a specific aspect of behaviour. It was about the allocation of scarce resources between alternative uses. In essence it was about choice. The theory of choice, therefore, provided the core that needed to be applied to various problems. The message that economics was centred on a common core that could be applied to a variety of problems was also encouraged by Paul Samuelson in his extremely influential The Foundations of Economic Analysis (1947), even though his concerns were in other respects different from those of Robbins. (Unlike Robbins, he did not denigrate data collection and analysis as inferior activities.) Samuelson started by presenting the theory of constrained optimization, and then applied it to problems of the consumer and the firm. By doing this, he emphasized the mathematical structure common to seemingly different economic problems.
Robbins also encouraged the view that the major propositions of economics could be derived without knowing much more than the fact that resources are scarce. This suggested that theory could be pursued largely independently of empirical work. Furthermore, for many years economists found a large research agenda in working out the properties of very general theoretical models; detailed reference to empirical work was frequently thought not to be necessary. It became more common for economists to be classified as theorists, econometricians or applied economists (who were frequently econometricians). Theorists could ignore empirical work, on the grounds that testing theories was a task for econometricians. When economists wrote articles that had both theoretical and empirical content, it became standard practice for these articles to be divided into separate sections, one on theory and another on empirical work.
These changes in the structure of the discipline came about at the same time as another major change was taking place. This was the large-scale, systematic collection of economic statistics and national accounts. In the 1920s, comprehensive national-income accounts did not exist for any country. The pioneering attempts by people such as Petty and King had involved inspired guesses as much as detailed evidence, and were not based on any systematic conceptual framework. Even in the nineteenth and early twentieth centuries, when estimates of national income were made in several countries, including the United States and Britain, gaps in the data were so wide that detailed accounts were impossible. In the United States, the most comprehensive attempt was The Wealth and Income of the People of the United States (1915) by Willford I. King (1880–1962), a student of Irving Fisher's. King showed that national income had trebled in sixty years, and that the share of wages and salaries in total income had risen from 36 to 47 per cent. He concluded that, contrary to what socialists were claiming, the existing economic system was working well. In Britain, A. L. Bowley (1869–1957) was producing estimates based on tax data, population censuses, the 1907 census of production, and information on wages and employment. However, this work, like that being undertaken elsewhere, remained very limited in its scope. In complete contrast, by the 1950s, national-income statistics were being constructed by national governments and coordinated through the United Nations. By 1950, estimates existed for nearly a hundred countries.
In the inter-war period, national-income statistics were constructed right across Europe. Interest in them was stimulated by the immense problems of post-war reconstruction, the enormous shifts in the relative economic power of different nations, the Depression of the 1930s, and the need to mobilize resources in anticipation of another war. During the 1930s Germany was producing annual estimates of national income with a delay of only a year. The Soviet Union constructed input–output tables (showing how much each sector of the economy purchased from every other sector) through most of the 1920s and the early 1930s. Italy and Germany had worked out a conceptual basis for national accounting that was as advanced as any in the world. By 1939, ten countries were producing official estimates of national income. However, because of the war, the countries that had most influence in the long term were Britain and the United States. Unlike these two, Germany never used national income for wartime planning, and stopped producing statistics.
In the United States there were three strands to early work on national-income accounting. The first was that associated with the National Bureau of Economic Research, established by Mitchell in 1920. Its first project was a study of year-to-year variations in national income and the distribution of income. Published in 1921, its report provided annual estimates of national income for the period 1909–19. These were extended during the 1920s, and were supplemented in 1926 by estimates made by the Federal Trade Commission. The FTC, however, failed to continue this work. With the onset of the Depression, the federal government became involved. In June 1932 a Senate resolution proposed by Robert La Follette, senator for Wisconsin, committed the Bureau of Foreign and Domestic Commerce to prepare estimates of national income for 1929, 1930 and 1931.
In January 1933, after six months in which little was achieved, the BFDC's work was handed to Simon Kuznets (1901–85), who had been working on national income at the NBER since 1929. At the NBER he had prepared plans for estimating national income, later summed up in a widely read article on the subject in the Encyclopedia of the Social Sciences (1933). Within a year, Kuznets and his team produced estimates for 1929–32. (Recognizing the importance of up-to-date statistics, they had included 1932 as well as the years required by La Follette's resolution.) Kuznets moved back to the NBER, where he worked on savings and capital accumulation, and subsequently on problems of long-term growth. The BFDC study of national income became permanent under the direction of Robert Nathan (1908– ). The original estimates were revised and extended, and new series were produced (for example, monthly figures were produced in 1938).
At this time, the very definition of national income was controversial. Kuznets and his team published two estimates: ‘national income produced’, which referred to the net product of the whole economy, and ‘national income received’, which covered payments made to those who produced the net product. In order to base estimates on reliable data, they had excluded many of the then controversial items. These estimates of national income covered only the market economy (goods that were bought and sold), and goods were valued at market prices. The basic distinction underlying Kuznets's framework was between consumers' outlay and capital formation.
At the same time, Clark Warburton (1896–1979), at the Brookings Institution, produced estimates of gross national product (a term he was the first to use, in 1934). This was defined as the sum of final products (i.e. excluding products that are remanufactured to make other products) that emerge from the production and marketing processes and are passed on to consumers and businesses. This was much larger than Kuznets's figure for national income, because it also included capital goods purchased to replace ones that had been worn out, government services to consumers, and government purchases of capital goods. Warburton argued that GNP minus depreciation was the correct way to measure the resources available to be spent. He produced, for the first time, evidence that spending on capital goods was more erratic than spending on consumers' goods. Economists had long been aware of this, but had previously had only indirect evidence.
The third strand in American work on national income was the work associated with Laughlin Currie. In 1934–5 he began calculating the ‘pump-priming deficit’. This was based on the idea that, for the private sector to generate enough demand for goods to cure unemployment, the government had to ‘prime the pump' by increasing its own spending. Currie and his colleagues focused on the contribution of each sector to national buying power – the difference between each sector's spending and its income. A positive contribution by the government (i.e. a deficit) was needed to offset net saving by other sectors.
In Britain, the calculation of national-income statistics was the work of a small number of scholars with no government assistance throughout the inter-war period. Of particular importance was Colin Clark (1905–89). In 1932 Clark used the concept of gross national product and estimated the main components of aggregate demand (consumption, investment and government spending). This work increased in importance after the publication of Keynes's General Theory (1936), and soon after its publication Clark estimated the value of the multiplier. His main work was National Income and Outlay (1937). One of his followers has written of this book that it ‘restored the vision of the political arithmeticians [Petty and Davenant]… [It] brought together estimates of income, output, consumers' expenditure, government revenue and expenditure, capital formation, saving, foreign trade and the balance of payments. Although he did not set his figures in an accounting framework it is clear that they came fairly close to consistency.’1
Clark's work was not supported by the government. (When he had been appointed to the secretariat of the Economic Advisory Council in 1930, the Treasury had even refused to buy him an adding machine.) Questions of income distribution were too sensitive for the government to want to publish figures. Industrialists did not want figures for profits revealed. The government did calculate national-income figures for 1929, but denied their existence because the estimates of wages were lower than those already available. Official involvement in national-income accounting did not begin until the Second World War. Keynes used Clark's figures in How to Pay for the War (1940).
In the summer of 1940 Richard Stone (1913–91) joined James Meade (1907–94) in the Central Economic Information Service of the War Cabinet. During the rest of the year, encouraged and supported by Keynes, they constructed a set of national accounts for 1938 and 1940 that was published in a White Paper accompanying the Budget of 1941. The lack of resources available to them is illustrated by a story about their cooperation. They started with Meade (the senior partner) reading numbers which Stone punched into their mechanical calculator, but soon discovered that it was more efficient for their roles to be reversed. Though the Chancellor of the Exchequer said that the publication of their figures would not set a precedent, estimates were from then on published annually.
During the Second World War, estimates of national income were transformed into systems of national accounts in which a number of accounts were related. Its position in the war effort, together with the work of Kuznets and Nathan at the War Production Board, ensured that the United States was the dominant country in this process. However, the system that was eventually adopted owed much to British work. In 1940 Hicks introduced the equation that has become basic to national-income accounting: GNP = C + I + G (income equals consumption plus investment plus government expenditure on goods and services). He was also responsible for the distinction between market prices and factor cost (market prices minus indirect taxes). Perhaps more important, Meade and Stone provided a firmer conceptual basis for the national accounts by presenting them as a double-entry production account for the entire economy. In one column were factor payments (national income), and in the other column expenditures (national expenditure). As with all double-entry accounts, when calculated correctly the two columns balanced.
From 1941 the United States moved away from national accounts as constructed by Kuznets and Nathan to ones constructed on Keynesian lines, using the Meade–Stone framework. This was the work of Martin Gilbert (1909–79), a former student of Kuznets's, who was chief of the National Income Division of the US Commerce Department from 1941 to 1951. One reason for this move was the rapid spread of Keynesian economics, which provided a theoretical rationale for the new system of accounts. There was no economic theory underlying Kuznets's categories, which derived from purely empirical considerations. The change also appeared desirable for other reasons. In wartime, when the concern was with the short-term availability of resources, it was not necessary to maintain capital, which meant that GNP was the relevant measure of output. In addition, it was important to have a measure of income that included government expenditure. Finally, the Meade–Stone system provided a framework within which a broader range of accounts could be developed. After the war, in 1947, a League of Nations report, in which Stone played an important role, provided the framework within which several governments began to compile their accounts so that it would be possible to make cross-country comparisons. Subsequently, Stone was also involved in the work of the Organization for European Economic Cooperation and the United Nations, which in 1953 produced a standard system of national accounts.
The Econometric Society was formed in 1930, in Chicago, at the instigation of Charles Roos (1901–58), Irving Fisher and Ragnar Frisch (1895–1973). Its constitution described its aims in the following terms:
The Econometric Society is an international society for the advancement of economic theory in its relation to statistics and mathematics… Its main object shall be to promote studies that aim at a unification of the theoretical-quantitative and the empirical-quantitative approach to economic problems and that are penetrated by constructive and rigorous thinking similar to that which has come to dominate in the natural sciences.2
In commenting on this statement, Frisch emphasized that the important aspect of econometrics, as the term was used in the Society, was the unification of economic theory, statistics and mathematics. Mathematics, in itself, was not sufficient.
In its early years the Econometric Society was very small. Twenty years before, Fisher had tried to generate interest in establishing such a society but had failed. Thus when Roos and Frisch approached him about the possibility of forming a society he was sceptical about whether there was sufficient interest in the subject. However, he told them that he would support the idea if they could produce a list of 100 potential members. To Fisher's surprise, they found seventy names. With some further ones added by Fisher, this provided the basis for the Society.
Soon after the Society was formed, it was put in touch with Alfred Cowles (1891–1984). Cowles was a businessman who had set up a forecasting agency but who had become sceptical about whether forecasters were doing any more than guessing what might happen. He therefore developed an interest in quantitative research. When he wrote a paper under the title ‘Can stock market forecasters forecast?’ (1933), he gave it the three-word abstract ‘It is doubtful.’ His evidence came from a comparison of the returns obtained from following the advice offered by sixteen financial-service providers and the performance of twenty insurance companies with the returns that would have been obtained by following random forecasts. Over the period 1928–32 there was no evidence that professional forecasts were any better than random ones. With Cowles's support, the Econometric Society was able to establish a journal, Econometrica, in 1933. In addition, Cowles supported the establishment, in 1932, of the Cowles Commission, a centre for mathematical and statistical research into economics. From 1939 to 1955 it was based at the University of Chicago, distinct from the economics department, after which it moved to Yale. This institute proved important in the development of econometrics.
Econometrics grew out of two distinctive traditions – one American, represented by Fisher and Roos, and the other European, represented by Frisch (a Norwegian). The American tradition had two main strands. One was statistical analysis of money and the business cycle. Fisher and others had sought to test the quantity theory of money, seeking to find independent measures of all the four terms in the equation of exchange (money, velocity of circulation, transactions, and the price level). Mitchell, instead of finding evidence to support a particular theory of the cycle, had redefined the problem as trying to describe what went on in business cycles. This inherently quantitative programme, set out in his Business Cycles and their Causes (1913), was taken up by the National Bureau of Economic Research, under Mitchell's direction. It resulted in a method of calculating ‘reference cycles' with which fluctuations in any series could be compared. An alternative approach was the ‘business barometer' developed at Harvard by Warren Persons (1878–1937) as a method of forecasting the cycle. There was also Henry Ludwell Moore (1869–1958) at Columbia University, who sought, like Jevons, to establish a link between the business cycle and the weather. A few years later, in 1923, he switched from the weather to the movement of the planet Venus as his explanation. Moore's work is notable for the use of a wider range of statistical techniques than were employed by other economists at this time. The other strand in the American tradition was demand analysis. Moore and Henry Schultz (1893–1938) estimated demand curves for agricultural and other goods.
None of this work brought mathematical economic theory together with statistical analysis. Fisher's dissertation had involved a mathematical analysis of consumer and demand theory, but this remained separate from his statistical work, which was on interest rates and money. Mitchell was sceptical about the value of pursuing simplified business-cycle theories that emphasized one particular cause of the cycle. For him, statistical work provided a way to integrate different theories and suggest new lines of inquiry. Mitchell was also, like Moore, sceptical about standard consumer theory. He hoped that empirical studies of consumers' behaviour would render obsolete theoretical models, in which consumers were treated as coming to the market with ready-made scales of bid and offer prices. In other words, statistical work would replace abstract theory rather than complement it. Moore criticized standard demand curves for being static and for their ceteris paribus assumptions (assumptions about the variables, such as tastes and incomes, that were held constant). As long as the attitude of statisticians was one of scepticism concerning mathematical theory, this theory was unlikely to be integrated with statistical work. This unlikelihood was reinforced by the scepticism expressed by many economists (including Keynes and Morgenstern – see p. 263) about the accuracy and relevance of much statistical data.
The European tradition, which overlapped with the American at many points, including research on business cycles and demand, had different emphases. Work by a variety of authors in the late 1920s led to an awareness of some of the problems involved in applying statistical techniques, such as correlation, to time-series data. George Udny Yule (1871–1951), a student of Karl Pearson's, explored the problem of ‘nonsense correlations' – seemingly strong relationships between time series that should bear no relation to each other, such as rainfall in India and skirt lengths in Paris. He argued that such correlations often did not reflect a cause common to both variables but were purely accidental. He also used experimental methods to explore the relationship between random shocks and periodic fluctuations in time series. The Russian Eugen Slutsky (1880–1948) went even further in showing that adding up random numbers (generated by the state lottery) could produce cycles that looked remarkably like the business cycle: there appeared to be regular, periodic fluctuations. Frisch also tackled the problem of time series, in a manner closer to Mitchell and Persons than to Yule or Slutsky, by trying to break down cycles into their component parts.
The first econometric model of an entire economy was constructed by the Dutch economist Jan Tinbergen (1903–94), who came to economics after taking a doctorate in physics and spent much of his career at the Central Planning Bureau in the Netherlands. However, to understand what Tinbergen was doing with this model, it is worth considering the theory of the business cycle that Frisch published in 1933. He took up the idea (taken from Wicksell) that the problem of the business cycle had to be divided into two parts – the ‘impulse' and ‘propagation' problems. The impulse problem concerned the source of shocks to the system, which might be changes in technology, wars, or anything outside the system. The propagation problem concerned the mechanism by which the effects of such shocks were propagated through the economy. Frisch produced a model which, if left to itself with no external shocks, would produce damped oscillations – cycles that became progressively smaller, eventually dying out – but which produced regular cycles because it was subject to periodic shocks. Following Wicksell, he described this as a ‘rocking-horse model’. If left to itself, the movement of a rocking horse will gradually die away, but if disturbed from time to time the horse will continue to rock. Such a model, Frisch argued, would produce the regularly occurring but uneven cycles that characterize the business cycle.
The distinction between propagation and impulse problems translated easily into the mathematical techniques that Frisch was using. The propagation mechanism depended on the values of the parameters in the equations and on the structure of the economy. In 1933 Frisch simply made plausible guesses about what these might be, though he expressed confidence that it would soon be possible to obtain such numbers using statistical techniques. The shocks were represented by the initial conditions that had to be assumed when solving the model. Using his guessed coefficients and suitable initial conditions, Frisch employed simulations to show that his model produced cycles that looked realistic.
In 1936 Tinbergen produced his model of the Dutch economy. This went significantly beyond Frisch's model in two respects. The structure of the Dutch economy was described in sixteen equations plus sufficient accounting identities to determine all of its thirty-one variables. The variables it explained included prices, physical quantities, incomes and levels of spending. It was therefore much more detailed than Frisch's model, which contained only three variables (production of consumption goods, new capital goods started, and production of capital goods carried over from previous periods). Most important, whereas Frisch had simply made plausible guesses about the numbers appearing in his equations, Tinbergen had estimated most of his using statistical techniques. He was able to show that, left to itself, his model produced damped oscillations, and that it could explain the cycle.
Three years later Tinbergen published two volumes entitled Statistical Testing of Business-Cycle Theories, the second of which presented the first econometric model of the United States (which contained three times as many equations as his earlier model of the Netherlands). This work was sponsored by the League of Nations, which had commissioned him to test the business-cycle theories surveyed in Haberler's Prosperity and Depression (1936). However, although Tinbergen managed to build a model that could be used to analyse the business cycle in the United States, the task of providing a statistical test of competing business-cycle theories proved much too ambitious. The available statistical data was limited. Most theories of the cycle were expressed verbally and were not completely precise. More important, most theories discussed only one aspect of the problem, which meant that they had to be combined in order to obtain an adequate model. It was impossible to test them individually. What Tinbergen did manage to do, however, was to clarify the requirements that had to be met if a theory was to form the basis for an econometric model. The model had to be complete (containing enough relationships to explain all the variables), determinate (each relationship must be fully specified) and dynamic (with fully specified time lags).
With the outbreak of the Second World War in 1939, European work on econometric modelling of the cycle ceased and the main work in econometrics was that undertaken in the United States by members of the Cowles Commission. However, many of those working there were European émigrés. A particularly important period began when Jacob Marschak (1898–1977) became the Commission's director of research in 1943. (Marschak illustrates the extent to which many economists' careers were changed by world events. A Ukrainian Jew, born in Kiev, he experienced the turmoil of 1917–18. He studied economics in Germany and started an academic career there, but in 1933 the prospect of Nazi rule made him move to Oxford. In 1938 he visited the United States for a year, and when war broke out he stayed.) Research moved away from seeking concrete results towards developing new methods that took account of the main characteristics of economic theory and economic data, of which there were four. (1) Economic theory is about systems of simultaneous equations. The price of a commodity, for example, depends on supply, demand and the process by which price changes when supply and demand are unequal. (2) Many of these equations include ‘random' terms, for behaviour is affected by shocks and by factors that economic theories cannot deal with. (3) Much economic data is in the form of time series, where one period's value depends on values in previous periods. (4) Much published data refers to aggregates, not to single individuals, the obvious examples being national income (or any other item in the national accounts) and the level of employment. None of these four characteristics was new – they were all well known. What was new was the systematic way in which economists associated with the Cowles Commission sought to develop new techniques that took account of all four of them.
Though many members and associates of the Cowles Commission were involved in the development of these new techniques, the key contribution was that of Trygve Haavelmo (1911–). Haavelmo argued that the use of statistical methods to analyse data was meaningless unless they were based on a probability model. Earlier econometricians had rejected probability models, because they believed that these were relevant only to situations such as lotteries (where precise probabilities can be calculated) or to controlled experimental situations (such as the application of fertilizer to different plots of land). Haavelmo disputed this, claiming that ‘no tool developed in the theory of statistics has any meaning – except, perhaps, for descriptive purposes – without being referred to some stochastic scheme [some model of the underlying probabilities]’.3 Equally significant, he argued that uncertainty enters economic models not just because of measurement error but because uncertainty is inherent in most economic relationships:
The necessity of introducing ‘error terms' in economic relations is not merely a result of statistical errors of measurement. It is as much a result of the very nature of economic behaviour, its dependence upon an enormous number of factors, as compared with those which we can account for, explicitly, in our theories.4
During the 1940s, therefore, Haavelmo and others developed methods for attaching numbers to the coefficients in systems of simultaneous equations. The assumption of an underlying probability model meant that they could evaluate these methods, asking, for example, whether the estimates obtained were unbiased and consistent.
In the late 1940s this programme began to yield results that were potentially relevant for policy-makers. The most important application was by Lawrence Klein (1920–), who used models of the US economy to forecast national income. Klein's models were representative of the approach laid down by Marschak in 1943. They were systems of simultaneous equations, intended to represent the structure of the US economy, and they were devised using the latest statistical techniques being developed by the Cowles Commission. Klein's approach led to the large-scale macroeconometric models, often made up of hundreds of equations, that were widely used for forecasting in the 1960s and 1970s.
The founders of the Econometric Society and the Cowles Commission sought to integrate mathematics, economics and statistics. This programme was only partly successful. Mathematics and statistics became an integral part of economics, but the hoped-for integration of economic theory and empirical work never happened. Doubts about the value of trying to model the structure of an economy using the methods developed at Cowles remained. It was not clear whether structural models, for all their mathematical sophistication, were superior to simpler ones based on more ‘naive' methods. The aggregation problem (how to derive the behaviour of an aggregate, such as market demand for a product, from the behaviour of the individuals of which the aggregate is composed) proved very difficult. The outcome was that towards the end of the 1940s the Cowles Commission shifted towards research in economic theory. (Research into econometrics continued apace, mostly outside Cowles, but without the same optimism as had characterized earlier work.) The Commission's motto, ‘Science is measurement' (adopted from Lord Kelvin), was changed in 1952 to ‘Theory and measurement’. As one historian has expressed it, ‘By the 1950s the founding ideal of econometrics, the union of mathematical and statistical economics into a truly synthetic economics, had collapsed.’5 There are, however, two other strands to this story that need to be considered.
In the 1930s the British Air Ministry started to employ civilian scientists to tackle military problems. Though some of the problems related to physics and engineering, it was increasingly realized that certain questions had an economic aspect, and from 1939 the scientists turned to economists for advice. For example, the question of whether it was worth producing more anti-aircraft shells involved balancing the numbers of enemy bombers shot down (and the damage these might have inflicted) against the resources required to produce the shells. This was an economic question. The US forces followed, employing economists through the Office of Strategic Services (the forerunner of the CIA). These economists became engaged in a wide range of tasks, ranging from estimating enemy capacity and the design of equipment to problems of military strategy and tactics. The last of these included problems such as the selection of bombing targets and the angle at which to fire torpedoes. These were not economic problems, but they involved statistical and optimization problems that economists trained in mathematics and statistics proved well equipped to handle. This was, of course, in addition to the role of the economist in planning civilian production (see pp. 291–2), price control and other tasks more traditionally associated with economics.
Many of these tasks involved optimization and planning how to allocate resources. These required the development of new mathematical techniques in order to obtain precise numerical answers. As many of the problems involved random errors, statisticians were particularly important. The result was intense activity on problems that are best classified as statistical decision theory, operations research and mathematical programming. After the war, the US military, in particular, continued to employ economists and to fund economic research.
These activities by economists had a significant effect on post-war economics. They raised economists' prestige. Many of them were directly related to the war effort and, though less obvious than the achievements of natural scientists, who had produced new technologies such as nuclear weapons, they were widely recognized to have been important. In addition, the economists involved in these activities worked in close proximity with physicists and engineers. The boundaries between statisticians and economists were blurred. Much of these professionals' work was closer to engineering than to what had been traditionally thought of as economics.
Some of the research undertaken to solve problems of specific interest to the military proved to have wider applications. The most important example was linear programming. This is most easily explained using some examples. If goods have to be transported from a series of factories to a set of retail stores, how should transport be arranged in order to minimize total transport costs? If a person needs certain nutrients to survive, and different foods contain these in different proportions, what diet supplies the required nutrients at minimum cost? To solve these problems and others like them, it was assumed that all the relationships involved (such as between cost and distance travelled, or health and nutrient intake) were straight lines.
Linear programming was developed independently by two statisticians, George Dantzig (1914–), working for the US Air Force, and Tjailing Koopmans (1910–85), a statistician with an interest in transportation problems who also made significant contributions to econometrics at the Cowles Commission. During the war, Koopmans was involved with planning Allied freight shipping, and Dantzig was trying to improve the efficiency with which logistical planning and the deployment of military forces could be undertaken. After the war, linear programming and the related set of techniques that went under the heading of ‘activity analysis' proved to be of wide application.
The development of such techniques depended on developments before the war. Dantzig's starting point was the input–output model developed by Wassily Leontief. By assuming that each industry obtained inputs from other industries in fixed proportions, this had reduced technology to a linear structure. Koopmans's interest in transport dated from before the war. Unknown to either of them, Leonid Kantorovich (1912–86), at Leningrad, where input–output techniques had a comparatively long history, had arrived at linear programming as a way to plan production processes. Other techniques developed during the war arose even more directly out of pre-war civilian problems. Statistical methods of quality control, for example, had been used in industry before the war, but were taken up and developed by the military.
In the 1940s and 1950s general-equilibrium theory (also termed competitive-equilibrium theory) became seen as the central theoretical framework around which economics was based. It remained a minority activity, requiring greater mathematical expertise than most economists possessed, but one with great prestige. Its roots went back to Walras and Pareto, but during the 1920s, when Marshall's influence was dominant, it had been neglected. Interest in general-equilibrium theory remained low until the 1930s, when several different groups of economists began to investigate the subject.
One of these groups was based on the seminar organized in Vienna in the 1920s and early 1930s by the mathematician Karl Menger (1902-85) – not to be confused with his father, Carl Menger. The so-called Vienna Circle's manifesto, The Scientific View of The World, was published in 1929, and Vienna was attracting mathematicians and philosophers from all over Europe. One of these was Abraham Wald (1902–50), a Romanian with an interest in geometry. He was put in touch with Karl Schlesinger (1889–1938), whose Theorie der Geld-und Kreditwirtschaft (Theory of the Economics of Money and Credit, 1914) had developed Walras's theory of money. They discussed the simplified version of Walras's set of equations for general equilibrium found in The Theory of Social Economy (1918), written by the Swedish economist Gustav Cassel (see p. 276). Cassel had simplified the set of equations by removing any reference to utility. Schlesinger noted that, if a good was not scarce, its price would be zero, which led him to reformulate the equations as a mixed system of equations and inequalities. For those goods with positive prices, supply was equal to demand, but where goods had a zero price, supply was greater than demand. In a series of papers discussed at Menger's seminar, Wald proved that, if the demand functions had certain properties, this system of equations would have a solution. Using advanced mathematical techniques (in particular a fixed-point theorem, a mathematical technique developed in the 1920s), and using Schlesinger's reformulation of the equations, Wald had been able to achieve what Walras had tried to do by counting equations and unknowns. He proved that the equations for general equilibrium were sufficient to determine all the prices and quantities of goods in the system. In 1937 Wald (like Menger) was forced to leave Austria and he moved to the Cowles Commission, where he worked on mathematical statistics.
Another mathematician to take an interest in general equilibrium was John von Neumann (1903–57), a Hungarian who, after several years in Berlin, joined Princeton in 1931, having spent the previous year there as a visitor. In 1932 he wrote a paper in which he proved the existence of equilibrium in a set of equations that described a growing economy. He discussed this work at Menger's seminar in 1936, after which it was published in Ergebnisse eines mathematischen Kolloqui-ums (Results of a Mathematical Colloquium, 1937) in an issue edited with Wald. Von Neumann focused on the choice of production methods, and he developed a novel way of treating capital goods. This was in contrast to Wald's focus on the problem of allocating given resources. However, they had used similar mathematical techniques to solve the problem of existence of equilibrium.
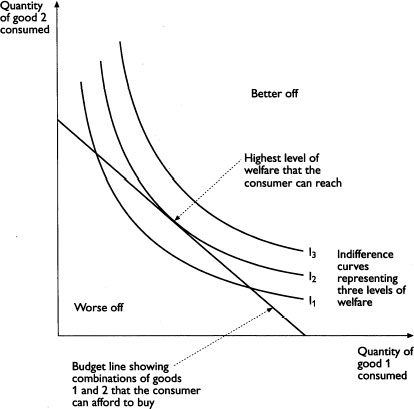
It was, however, not mathematicians such as Wald and von Neumann who revived interest in general-equilibrium theory. At the London School of Economics, Lionel Robbins, who had a greater knowledge of Continental economics than most British economists of his day, introduced John Hicks to Walras and Pareto. In the early 1930s Hicks, with R. G. D. Allen (1906–83), reformulated the theory of demand so as to dispense with the concept of utility, believed to be a metaphysical concept that was not measurable. Individuals' preferences were described instead in terms of ‘indifference curves’. These were like contours on a map: each point on the indifference-curve diagram represented a different combination of goods, and each indifference curve joined together all the points that were equally preferred (that yielded the same level of welfare). In the same way that moving from one contour on a map to another means a change in altitude, moving from one indifference curve to another denotes a change in the consumer's level of welfare – the consumer is moving to combinations of goods that are either better or worse than the original one. The significance of indifference curves was that, in order to describe choices, it was not necessary to measure utility (how well off people were – the equivalent of altitude). So long as one knew the shape of the contour lines and could rank them from lowest to highest, it was possible to find the highest point among those that were available to the consumer. Hicks and Allen argued that this was sufficient to describe behaviour.
This was followed by Hicks's Value and Capital (1939). This book contained an English-language exposition of general-equilibrium theory. It restated the theory in modern terms (albeit using mathematics
Fig. 5 Indifference curves
that was much simpler than that used by Wald, von Neumann or even Samuelson), basing it on the Hicks–Allen theory of consumer behaviour. It also integrated it with a theory of capital and provided a framework in which dynamic problems could be discussed. Though Hicks did not refer to the IS–LM model in Value and Capital, most readers, at least by the end of the 1940s, understood him to have shown how macroeconomics could be viewed as dealing with miniature general-equilibrium systems. In short, the book showed that general equilibrium could provide a unifying framework for economics as a whole.
There was, however, the problem that general-equilibrium theory was a theory of perfect competition. Hicks dealt with this by arguing that there was no choice: imperfect competition raised so many difficulties that to abandon perfect competition would be to destroy most of economic theory – a response that was virtually an admission of defeat. He followed Marshall in relegating the algebra involved in his work to appendices, confining the mathematics in the text to a few diagrams, so that the book was accessible to economists who would be unable to make sense of a more mathematical treatment. Value and Capital was very widely read, and was instrumental in reviving interest in general-equilibrium theory in many countries.
At the same time as Hicks was working on Value and Capital, Paul Samuelson (1915–) was working on what was to become The Foundations of Economic Analysis. (The book was completed in 1941, but publication was delayed for six years because of the war.) After studying economics at Chicago, Samuelson did postgraduate work at Harvard, learning mathematical economics from E. B. Wilson (1879–1964). As well as being a mathematical economist and statistician, Wilson had an interest in physics, having been the last protégé of Willard Gibbs, a physicist who laid the foundations of chemical thermodynamics and contributed to electromagnetism and statistical mechanics. (Irving Fisher had previously been taught by Gibbs.) Samuelson was also influenced by another physicist, Percy Bridgman (1882–1961), who proposed the idea of ‘operationalism’, according to which any meaningful concept could be reduced to a set of operations – concepts were defined by operations. Although Bridgman was responding to what he saw as ambiguities in electrodynamics, Samuelson applied operationalism to economics. In the Foundations, he interpreted this idea as meaning that economists should search for ‘operationally meaningful theorems’, by which he meant ‘hypotheses about empirical data which could conceivably be refuted, if only under ideal conditions’.6 Much of the book was therefore concerned to derive testable conclusions about relationships between observable variables.
Samuelson's starting point was two assumptions. The first was that there was an equivalence between equilibrium and the maximization of some magnitude. Thus the firm's equilibrium (chosen position) could be formulated as profit maximization, and the consumer's equilibrium could be formulated as maximization of utility. The second assumption was that systems were stable: that, if they were disturbed, they would return to their equilibrium positions. From these, Samuelson claimed, it was possible to derive many meaningful theorems. The book therefore opened with chapters on mathematical techniques – one on equilibrium and methods for analysing disturbances to equilibrium, and another on the theory of optimization – and these techniques were then applied to the firm, the consumer and a range of standard problems.
Unlike Value and Capital, Foundations placed great emphasis on mathematics. Like his teacher, Wilson, Samuelson believed that the methods of theoretical physics could be applied to economics, and he sought to show what could be achieved by tackling economic problems in this way. However, there were important similarities between the two books. Hicks and Samuelson both emphasized that all interesting results in the theory of the consumer could be derived without assuming that utility could be measured. They both discussed dynamics and the stability of general equilibrium. Samuelson's assessment of the relationship between the two books was that ‘Value and Capital (1939) was an expository tour de force of great originality, which built up a readership for the problems Foundations grappled with and for the expansion of mathematical economics that soon came.’7
One of the most significant features of the revival of general-equilibrium theory in the 1930s and 1940s was that those involved came to it from very different backgrounds. Hicks approached it as an economist, bringing ideas influenced by Robbins and Continental economists into the British context, then dominated by Marshall. Samuelson's background was mathematical physics as developed by Gibbs and Wilson, whose techniques he sought to apply to economics. He emphasized dynamics and predictions concerning observable variables. In contrast, the way in which Wald and von Neumann approached general equilibrium arose directly from their involvement in mathematics.
In the first three decades of the twentieth century, enormous changes in mathematical thinking had taken place. Acceptance of non-Euclidean geometry (discovered early in the nineteenth century but not fully axiomatized until 1899) raised questions concerning the foundations of mathematics. It became impossible to defend the idea that geometry simply formalized intuitive notions about space. Non-Euclidean geometries violated everyday experience, but were quite acceptable from a mathematical point of view. Euclidean geometry became only one of many possible geometries, and after the theory of relativity it was not even possible to argue that it was the only geometry consistent with the physical world. Another blow to earlier conceptions of how mathematics related to the real world came with quantum mechanics. It was possible to integrate quantum mechanics and alternative theories, but only in the sense that it was possible to provide a more abstract mathematical theory from which both could be derived. Mathematics was, in this process, becoming increasingly remote from everyday experience.
David Hilbert (1862–1943) responded to this situation by seeking to reduce mathematics to an axiomatic foundation. In his programme, in which he hoped to resolve several paradoxes in set theory, mathematics involved working out the implications of axiomatic systems. Such systems included definitions of basic symbols and the rules governing the operations that could be performed on them. An important consequence of this approach is that axiomatic systems are independent of the interpretations that may be placed on them. This means that when general-equilibrium theory is viewed as an axiomatic system it loses touch with the world. The symbols used in the theory can be interpreted to represent things like prices, outputs and so on, but they do not have to be interpreted in this way. The validity of any theorems derived does not depend on how symbols are interpreted. Thus when Wald and von Neumann (whose earlier work included axiomatizing quantum mechanics) provided an axiomatic interpretation of general-equilibrium theory, the way in which the theory was understood changed radically.
From the point of view of economists, Wald and von Neumann were on the periphery of the profession. In the late 1940s, however, the Cowles Commission, having moved away from econometric theory, encouraged work on general-equilibrium theory. Two economists working there, Kenneth Arrow (1921–) and Gérard Debreu (1921–), published, in 1954, an improved proof of the existence of general equilibrium. The Arrow–Debreu model has since come to be regarded as the canonical model of general equilibrium. Its definitive statement came in Debreu's Theory of Value (1959). In the preface, Debreu wrote:
The theory of value is treated here with the standards of rigor of the contemporary formalist school of mathematics… Allegiance to rigor dictates the axiomatic form of the analysis where the theory, in the strict sense, is logically entirely disconnected from its interpretations.8
It is no coincidence that Debreu came to economics from mathematics, and that as a mathematician he was involved with the so-called Bourbaki group, a group of French mathematicians concerned with working out mathematics with complete rigour, who published their work under the pseudonym ‘Nicolas Bourbaki’. Theory of Value could be seen as the Bourbaki programme applied to economics.
Debreu's Theory of Value provided an axiomatic formulation of general-equilibrium theory in which the existence of equilibrium was proved under more general assumptions than had been used by Wald and von Neumann. The price of this generality and rigour was that the theory ceased to describe any conceivable real-world economy. For example, the problem of time was handled by assuming that futures markets existed for all commodities, and that all agents bought and sold on these markets. Similarly, uncertainty was brought into the model by assuming that there was a complete set of insurance markets in which prices could be attached to goods under every possible eventuality. Clearly, these assumptions could not conceivably be true of any real-world economy.
In the early 1960s, confidence in general-equilibrium theory, and with it economics as a whole, was at its height, with Debreu's Theory of Value being widely seen as providing a rigorous, axiomatic framework at the centre of the discipline. The theory was abstract, not describing any real-world economy, and the mathematics involved was understood only by a minority of economists, but it was believed to provide foundations on which applied models could be built. Interpretations of the Arrow–Debreu model could be applied to many, if not all, branches of economics. There were major problems with the model, notably the failure to prove stability, but there was great confidence that these would be solved and that the theory would be generalized to apply to new situations. The model provided an agenda for research. However, this optimism was short-lived. There turned out to be very few results that could be obtained from such a general framework. Most important, it was proved, first with a counter-example and later with a general proof, that it was impossible to prove stability in the way that had been hoped. The method was fundamentally flawed.
In addition, there were problems that could not be tackled within the Arrow–Debreu framework. These included money (attempts were made to develop a general-equilibrium theory of money, but they failed), information, and imperfect competition. In order to tackle such problems, economists were forced to use less general models, often dealing only with a specific part of the economy or with a particular problem. The search for ever more general models of general competitive equilibrium, that culminated in Theory of Value, was over.
Though economists have moved away from general-equilibrium theory, they have continued to search for a unifying framework on which economics can be based. They have found it in game theory. Though this has a longer history, modern game theory goes back to work by von Neumann in the late 1920s, in which he developed a theory to explain the outcomes of parlour games. The simplest such game involves two players who cannot cooperate with each other, each of whom has a choice of two strategies. In such a game, there are four possible outcomes. Von Neumann was able to prove that there will always be an equilibrium, defined as an outcome in which neither player wishes to change his or her strategy. To ensure this, however, he had to assume that players can choose strategies randomly (for example by tossing a coin to decide which strategy to play). There was thus a parallel between social interaction and the need for probabilistic theories in physics. Such work was an attempt to show that mathematics could be used to explain the social world as well as the natural.
From 1940 to 1943 von Neumann cooperated with Oskar Morgenstern (1902–77) on what became The Theory of Games and Economic Behavior (1944). Morgenstern was an economist who succeeded Hayek as director of the Institute for Business Cycle Research in Vienna from 1931, until he moved to Princeton in 1938. In the course of his work on forecasting and uncertainty, he introduced the Holmes–Moriarty problem, in which Sherlock Holmes and Professor Moriarty try to outguess each other. If Holmes believes that Moriarty will follow him to Dover, he gets off the train at Ashford in order to evade him. However, Moriarty can work out that Holmes will do this, so he will get off there too, in which case Holmes will go to Dover. Moriarty in turn knows this… It is a problem with no solution. Though expressed in different language from the problems that von Neumann was analysing, it is a two-person game with two strategies.
In Vienna, Morgenstern became involved with Karl Menger and came to accept that economic problems needed to be handled formally if precise answers were to be obtained. Unlike many Austrian economists, he believed that mathematics could play an important role in economics (he had received tuition in the subject from Wald), and he had an eye for seeing points where mathematics would be able to contribute. However, unlike von Neumann, he was critical of general-equilibrium theory and did not believe that it could provide a suitable framework for the discipline. Game theory provided an alternative. In the course of his cooperation with von Neumann, during which he continually put pressure on him to get their book out, he asked provocative questions and offered ideas on equilibrium and interdependence between individuals that von Neumann was able to develop. In developing their theory, von Neumann and Morgenstern were responding to the same intellectual environment – formalist mathematics – that lay behind the developments in general-equilibrium theory during the same period. Indeed, some of the key mathematical theorems involved were the same.
The Theory of Games and Economic Behavior was a path-breaking work. It analysed games in which players were able to cooperate with each other, forming coalitions with other players, and ones in which they were not able to do this. It suggested a way in which utility might be measured. Most significant of all, it offered a general concept of equilibrium that did not depend on markets, competition or any specific assumptions about the strategies available to agents. This concept of equilibrium was based on the concept of dominance. One outcome (call it x) dominates another (call it y) ‘when there exists a group of participants each one of whom prefers his individual situation in – to that in y, and who are convinced that they are able as a group – i.e. as an alliance – to enforce their preferences’.9 Equilibrium, or the solution to a game, comprises the set of outcomes that are not dominated by any other outcome. In other words, it is an outcome such that no group of players believes it can obtain an alternative outcome that all members of the group prefer. Given that the notion of dominance could be interpreted in many different ways, this offered an extremely general concept of equilibrium.
The Theory of Games and Economic Behavior was received enthusiastically, but by only a small group of mathematically trained economists. One of the main reasons was that, even as late as 1950, many economists were antagonistic towards the use of mathematics in economics. Another was the dismissive attitude of von Neumann and Morgenstern to existing work in economics. (Morgenstern had published a savage review of Value and Capital, and von Neumann was privately dismissive of Samuelson's mathematical ability.) The result was that for many years game theory was taken up by mathematicians, particularly at Princeton, and by strategists at the RAND Corporation and the US Office of Naval Research, but was ignored by economists. The main source of mathematically trained economists was the Cowles Commission, several of whom wrote substantial reviews of The Theory of Games, but even they did not take up game theory.
One of the Princeton mathematicians to take up game theory was John Nash (1928–). In a series of papers and a Ph.D. dissertation in 1950–51, Nash made several significant contributions. Starting from von Neumann and Morgenstern's theory, he too distinguished between cooperative games (in which players can communicate with each other, form coalitions and coordinate their activities) and non-cooperative games (in which such coordination of actions is not possible). He proved the existence of equilibrium for non-cooperative games with an arbitrary number of players (von Neumann had proved this only for the two-player case), and in doing this he formulated the concept that has since come to be known as a Nash equilibrium: the situation where each player is content with his or her strategy, given the strategies that have been chosen by the other players. He also formulated a solution concept (now called the Nash bargain) for cooperative games.
During the 1950s there were many applications of game theory to economic problems ranging from business cycles and bank credit expansion to trade policy and labour economics. However, these remained isolated applications that did not stimulate further research. The main exception was due to Martin Shubik (1926–), an economist at Princeton, in touch with the mathematicians working on game theory. His work during the 1950s culminated in Strategy and Market Structure (1959), in which he applied game theory to problems of industrial organization. It was not until industrial economists became disillusioned with their existing models (notably what was termed the structure–conduct-performance paradigm, which assumed a hierarchical relationship between these three aspects of markets) that game theory became widespread in the subject. During the 1970s, industrial economics came to rely more and more on game theory, which displaced the earlier, empirically driven approach which contained relatively little formal theory. By the 1980s game theory had become the organizing principle for underlying theories of industrial organization. From there it spread to other fields, such as international trade, where economists wanted to model the effects of imperfect competition and strategic interaction between economic agents.
In the 1960s and 1970s, economics was transformed. The mathematization of the subject, which had gained momentum in the 1930s, became almost universal. Though there were exceptions, training in advanced mathematics came to be considered essential for serious academic work – not least because without it it was impossible to keep up with the latest research. It became the norm for articles in academic journals to use mathematics. The foundations for this change, which was so profound that it can legitimately be described as a revolution, were laid in the preceding three decades and encompassed econometrics, linear models, general-equilibrium theory and game theory. Ideas and techniques from these four areas spread into all branches of economics.
The use of mathematical models enabled economists to resolve many issues that were confusing for those who used only literary methods and simple mathematics. Topics on which economists had previously been able to say little (notably strategic interaction) were opened up. However, the cost was that economic theories became narrower, in the sense that issues that would not fit into the available mathematical frameworks were ignored, or at least marginalized. Theories became simpler as well as logically more rigorous and more numerous. There were equally dramatic changes in the way in which economic theories were related to empirical data. Though older, more informal, methods never died out, statistical testing of a mathematical model became the standard procedure.
The variety of economists involved is evidence against any very simple explanation of this process. The motives and aims of Tinbergen, Frisch, Hicks, Samuelson, von Neumann and Morgenstern were all very different. However, some generalizations are possible. The subject saw an enormous influx of people who were well trained in mathematics and physics. They brought with them techniques and methods that they applied to economics. More than this, their experience in mathematics and physics affected their conception of economics. This extended much more widely than the obvious example of von Neumann. The mathematization of economics was also associated with the forced migration of economists in the inter-war period. In the 1920s the main movement was from Russia and eastern Europe, and in the 1930s from German-speaking countries, with some economists being involved in both these upheavals. By the 1950s there had been an enormous movement of economists from central and eastern Europe to the United States. The mathematicians involved in Menger's seminar in Vienna (including Menger himself) were merely the tip of an iceberg. In 1945 around 40 per cent of contributors to the American Economic Review, most of whom lived in the United States, had been born in central and eastern Europe, and a large number of these were highly trained in mathematics.
The aim of the Econometric Society, which fostered much of the early work involving mathematics and economics, was to integrate mathematics, statistics and economics. In a sense, its goals were realized, perhaps more conclusively than its founders had hoped. It became increasingly difficult to study economics without knowledge of advanced mathematics and statistics. However, less progress was made in integrating economic theory with empirical work. From the late 1940s econometrics and mathematical theory developed as largely separate activities within economics. There have been times when they have come together, and there has been considerable cross-fertilization; however, the goal that econometric techniques would make it possible for economic theory to be founded securely on empirical data, instead of on abstract assumptions, has not been achieved. In part this reflects the influence of formalist mathematics. In part it reflects the overconfidence of the early econometricians and their failure to appreciate the difficulty of the task they had set themselves. The main justification for the key assumptions used in economic theory remains, as for Marshall and his contemporaries, that they are intuitively reasonable.
Economists have responded to this situation in different ways. The one most complimentary to economic theory is to argue that theory is ‘ahead of' measurement. This implies that the challenge facing economists is to develop new ways of measuring the economy so as to bring theories into a closer relationship with evidence about real economic activity. An alternative way to view the same phenomenon is to argue that economic theory has lost contact with empirical data – that the theoretical superstructure rests on flimsy foundations. From this perspective the onus is on theorists to develop theories that are more closely related to evidence as much as on empirical workers to develop new evidence.
Doubts about the mathematization of economics have gone in cycles. In the long post-war boom, confidence in economics grew and reached its peak in the 1960s. General-equilibrium theory was the unifying framework, affecting many fields, and, as the cost of computing power fell, econometric studies were becoming much more common. As inflation increased and unemployment rose towards the end of the decade, however, doubts were increasingly expressed. With the emergence of stagflation (unemployment and inflation rising simultaneously) in the mid-1970s, and the failure of large-scale econometric models to forecast accurately, confidence in economics was shaken even further. In the 1980s confidence returned as game theory provided a new unifying framework for economic theory and the advent of powerful personal computers revolutionized econometrics. However, this increased confidence in the subject has been accompanied by persistent dissent. Outsiders and some extremely influential insiders have argued that the assumptions needed to fit economics into the mathematical mould adopted since the 1930s have blinded economists to important issues that do not fit. These include problems as diverse as the transition of the Soviet Union from a planned to a free-market economy or the environmental catastrophe that will result from population growth and policies of laissez-faire.