Instruction-Level Parallelism and Its Exploitation
“America.”
“Who’s second?”
“Sir, there is no second.”
Dialog between two observers of the sailing race later named “The America’s Cup” and run every few years—the inspiration for John Cocke’s naming of the IBM research processor as “America.” This processor was the precursor to the RS/6000 series and the first superscalar microprocessor.
3.1 Instruction-Level Parallelism: Concepts and Challenges 148
3.2 Basic Compiler Techniques for Exposing ILP
3.3 Reducing Branch Costs with Advanced Branch Prediction
3.4 Overcoming Data Hazards with Dynamic Scheduling
3.5 Dynamic Scheduling: Examples and the Algorithm
3.6 Hardware-Based Speculation
3.7 Exploiting ILP Using Multiple Issue and Static Scheduling
3.8 Exploiting ILP Using Dynamic Scheduling, Multiple Issue, and Speculation
3.9 Advanced Techniques for Instruction Delivery and Speculation
3.10 Studies of the Limitations of ILP
3.11 Cross-Cutting Issues: ILP Approaches and the Memory System
3.12 Multithreading: Exploiting Thread-Level Parallelism to Improve Uniprocessor Throughput
3.13 Putting It All Together: The Intel Core i7 and ARM Cortex-A8
3.14 Fallacies and Pitfalls
3.15 Concluding Remarks: What’s Ahead?
3.16 Historical Perspective and References
Case Studies and Exercises by Jason D. Bakos and Robert P. Colwell
3.1 Instruction-Level Parallelism: Concepts and Challenges
All processors since about 1985 use pipelining to overlap the execution of instructions and improve performance. This potential overlap among instructions is called instruction-level parallelism (ILP), since the instructions can be evaluated in parallel. In this chapter and Appendix H, we look at a wide range of techniques for extending the basic pipelining concepts by increasing the amount of parallelism exploited among instructions.
This chapter is at a considerably more advanced level than the material on basic pipelining in Appendix C. If you are not thoroughly familiar with the ideas in Appendix C, you should review that appendix before venturing into this chapter.
We start this chapter by looking at the limitation imposed by data and control hazards and then turn to the topic of increasing the ability of the compiler and the processor to exploit parallelism. These sections introduce a large number of concepts, which we build on throughout this chapter and the next. While some of the more basic material in this chapter could be understood without all of the ideas in the first two sections, this basic material is important to later sections of this chapter.
There are two largely separable approaches to exploiting ILP: (1) an approach that relies on hardware to help discover and exploit the parallelism dynamically, and (2) an approach that relies on software technology to find parallelism statically at compile time. Processors using the dynamic, hardware-based approach, including the Intel Core series, dominate in the desktop and server markets. In the personal mobile device market, where energy efficiency is often the key objective, designers exploit lower levels of instruction-level parallelism. Thus, in 2011, most processors for the PMD market use static approaches, as we will see in the ARM Cortex-A8; however, future processors (e.g., the new ARM Cortex-A9) are using dynamic approaches. Aggressive compiler-based approaches have been attempted numerous times beginning in the 1980s and most recently in the Intel Itanium series. Despite enormous efforts, such approaches have not been successful outside of the narrow range of scientific applications.
In the past few years, many of the techniques developed for one approach have been exploited within a design relying primarily on the other. This chapter introduces the basic concepts and both approaches. A discussion of the limitations on ILP approaches is included in this chapter, and it was such limitations that directly led to the movement to multicore. Understanding the limitations remains important in balancing the use of ILP and thread-level parallelism.
In this section, we discuss features of both programs and processors that limit the amount of parallelism that can be exploited among instructions, as well as the critical mapping between program structure and hardware structure, which is key to understanding whether a program property will actually limit performance and under what circumstances.
The value of the CPI (cycles per instruction) for a pipelined processor is the sum of the base CPI and all contributions from stalls:
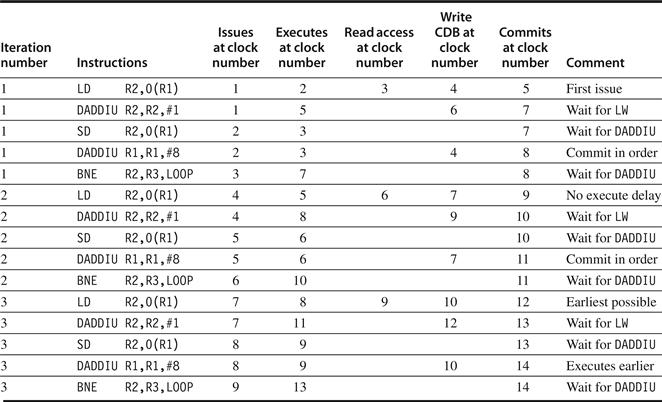
The ideal pipeline CPI is a measure of the maximum performance attainable by the implementation. By reducing each of the terms of the right-hand side, we decrease the overall pipeline CPI or, alternatively, increase the IPC (instructions per clock). The equation above allows us to characterize various techniques by what component of the overall CPI a technique reduces. Figure 3.1 shows the techniques we examine in this chapter and in Appendix H, as well as the topics covered in the introductory material in Appendix C. In this chapter, we will see that the techniques we introduce to decrease the ideal pipeline CPI can increase the importance of dealing with hazards.
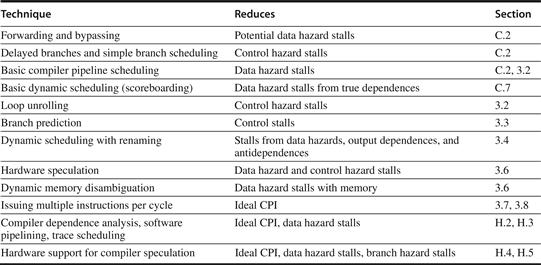
Figure 3.1 The major techniques examined in Appendix C, Chapter 3, and Appendix H are shown together with the component of the CPI equation that the technique affects.
What Is Instruction-Level Parallelism?
All the techniques in this chapter exploit parallelism among instructions. The amount of parallelism available within a basic block—a straight-line code sequence with no branches in except to the entry and no branches out except at the exit—is quite small. For typical MIPS programs, the average dynamic branch frequency is often between 15% and 25%, meaning that between three and six instructions execute between a pair of branches. Since these instructions are likely to depend upon one another, the amount of overlap we can exploit within a basic block is likely to be less than the average basic block size. To obtain substantial performance enhancements, we must exploit ILP across multiple basic blocks.
The simplest and most common way to increase the ILP is to exploit parallelism among iterations of a loop. This type of parallelism is often called loop-level parallelism. Here is a simple example of a loop that adds two 1000-element arrays and is completely parallel:
x[i] = x[i] + y[i];
Every iteration of the loop can overlap with any other iteration, although within each loop iteration there is little or no opportunity for overlap.
We will examine a number of techniques for converting such loop-level parallelism into instruction-level parallelism. Basically, such techniques work by unrolling the loop either statically by the compiler (as in the next section) or dynamically by the hardware (as in Sections 3.5 and 3.6).
An important alternative method for exploiting loop-level parallelism is the use of SIMD in both vector processors and Graphics Processing Units (GPUs), both of which are covered in Chapter 4. A SIMD instruction exploits data-level parallelism by operating on a small to moderate number of data items in parallel (typically two to eight). A vector instruction exploits data-level parallelism by operating on many data items in parallel using both parallel execution units and a deep pipeline. For example, the above code sequence, which in simple form requires seven instructions per iteration (two loads, an add, a store, two address updates, and a branch) for a total of 7000 instructions, might execute in one-quarter as many instructions in some SIMD architecture where four data items are processed per instruction. On some vector processors, this sequence might take only four instructions: two instructions to load the vectors x and y from memory, one instruction to add the two vectors, and an instruction to store back the result vector. Of course, these instructions would be pipelined and have relatively long latencies, but these latencies may be overlapped.
Data Dependences and Hazards
Determining how one instruction depends on another is critical to determining how much parallelism exists in a program and how that parallelism can be exploited. In particular, to exploit instruction-level parallelism we must determine which instructions can be executed in parallel. If two instructions are parallel, they can execute simultaneously in a pipeline of arbitrary depth without causing any stalls, assuming the pipeline has sufficient resources (and hence no structural hazards exist). If two instructions are dependent, they are not parallel and must be executed in order, although they may often be partially overlapped. The key in both cases is to determine whether an instruction is dependent on another instruction.
Data Dependences
There are three different types of dependences: data dependences (also called true data dependences), name dependences, and control dependences. An instruction j is data dependent on instruction i if either of the following holds:
■ Instruction i produces a result that may be used by instruction j.
■ Instruction j is data dependent on instruction k, and instruction k is data dependent on instruction i.
The second condition simply states that one instruction is dependent on another if there exists a chain of dependences of the first type between the two instructions. This dependence chain can be as long as the entire program. Note that a dependence within a single instruction (such as ADDD R1,R1,R1) is not considered a dependence.
For example, consider the following MIPS code sequence that increments a vector of values in memory (starting at 0(R1) and with the last element at 8(R2)) by a scalar in register F2. (For simplicity, throughout this chapter, our examples ignore the effects of delayed branches.)
Loop: L.D F0,0(R1) ;F0=array element
ADD.D F4,F0,F2 ;add scalar in F2
S.D F4,0(R1) ;store result
DADDUI R1,R1,#-8 ;decrement pointer 8 bytes
BNE R1,R2,LOOP ;branch R1!=R2
The data dependences in this code sequence involve both floating-point data:
and integer data:
In both of the above dependent sequences, as shown by the arrows, each instruction depends on the previous one. The arrows here and in following examples show the order that must be preserved for correct execution. The arrow points from an instruction that must precede the instruction that the arrowhead points to.
If two instructions are data dependent, they must execute in order and cannot execute simultaneously or be completely overlapped. The dependence implies that there would be a chain of one or more data hazards between the two instructions. (See Appendix C for a brief description of data hazards, which we will define precisely in a few pages.) Executing the instructions simultaneously will cause a processor with pipeline interlocks (and a pipeline depth longer than the distance between the instructions in cycles) to detect a hazard and stall, thereby reducing or eliminating the overlap. In a processor without interlocks that relies on compiler scheduling, the compiler cannot schedule dependent instructions in such a way that they completely overlap, since the program will not execute correctly. The presence of a data dependence in an instruction sequence reflects a data dependence in the source code from which the instruction sequence was generated. The effect of the original data dependence must be preserved.
Dependences are a property of programs. Whether a given dependence results in an actual hazard being detected and whether that hazard actually causes a stall are properties of the pipeline organization. This difference is critical to understanding how instruction-level parallelism can be exploited.
A data dependence conveys three things: (1) the possibility of a hazard, (2) the order in which results must be calculated, and (3) an upper bound on how much parallelism can possibly be exploited. Such limits are explored in Section 3.10 and in Appendix H in more detail.
Since a data dependence can limit the amount of instruction-level parallelism we can exploit, a major focus of this chapter is overcoming these limitations. A dependence can be overcome in two different ways: (1) maintaining the dependence but avoiding a hazard, and (2) eliminating a dependence by transforming the code. Scheduling the code is the primary method used to avoid a hazard without altering a dependence, and such scheduling can be done both by the compiler and by the hardware.
A data value may flow between instructions either through registers or through memory locations. When the data flow occurs in a register, detecting the dependence is straightforward since the register names are fixed in the instructions, although it gets more complicated when branches intervene and correctness concerns force a compiler or hardware to be conservative.
Dependences that flow through memory locations are more difficult to detect, since two addresses may refer to the same location but look different: For example, 100(R4) and 20(R6) may be identical memory addresses. In addition, the effective address of a load or store may change from one execution of the instruction to another (so that 20(R4) and 20(R4) may be different), further complicating the detection of a dependence.
In this chapter, we examine hardware for detecting data dependences that involve memory locations, but we will see that these techniques also have limitations. The compiler techniques for detecting such dependences are critical in uncovering loop-level parallelism.
Name Dependences
The second type of dependence is a name dependence. A name dependence occurs when two instructions use the same register or memory location, called a name, but there is no flow of data between the instructions associated with that name. There are two types of name dependences between an instruction i that precedes instruction j in program order:
1. An antidependence between instruction i and instruction j occurs when instruction j writes a register or memory location that instruction i reads. The original ordering must be preserved to ensure that i reads the correct value. In the example on page 151, there is an antidependence between S.D and DADDIU on register R1.
2. An output dependence occurs when instruction i and instruction j write the same register or memory location. The ordering between the instructions must be preserved to ensure that the value finally written corresponds to instruction j.
Both antidependences and output dependences are name dependences, as opposed to true data dependences, since there is no value being transmitted between the instructions. Because a name dependence is not a true dependence, instructions involved in a name dependence can execute simultaneously or be reordered, if the name (register number or memory location) used in the instructions is changed so the instructions do not conflict.
This renaming can be more easily done for register operands, where it is called register renaming. Register renaming can be done either statically by a compiler or dynamically by the hardware. Before describing dependences arising from branches, let’s examine the relationship between dependences and pipeline data hazards.
Data Hazards
A hazard exists whenever there is a name or data dependence between instructions, and they are close enough that the overlap during execution would change the order of access to the operand involved in the dependence. Because of the dependence, we must preserve what is called program order—that is, the order that the instructions would execute in if executed sequentially one at a time as determined by the original source program. The goal of both our software and hardware techniques is to exploit parallelism by preserving program order only where it affects the outcome of the program. Detecting and avoiding hazards ensures that necessary program order is preserved.
Data hazards, which are informally described in Appendix C, may be classified as one of three types, depending on the order of read and write accesses in the instructions. By convention, the hazards are named by the ordering in the program that must be preserved by the pipeline. Consider two instructions i and j, with i preceding j in program order. The possible data hazards are
■ RAW (read after write)—j tries to read a source before i writes it, so j incorrectly gets the old value. This hazard is the most common type and corresponds to a true data dependence. Program order must be preserved to ensure that j receives the value from i.
■ WAW (write after write)—j tries to write an operand before it is written by i. The writes end up being performed in the wrong order, leaving the value written by i rather than the value written by j in the destination. This hazard corresponds to an output dependence. WAW hazards are present only in pipelines that write in more than one pipe stage or allow an instruction to proceed even when a previous instruction is stalled.
■ WAR (write after read)—j tries to write a destination before it is read by i, so i incorrectly gets the new value. This hazard arises from an antidependence (or name dependence). WAR hazards cannot occur in most static issue pipelines—even deeper pipelines or floating-point pipelines—because all reads are early (in ID in the pipeline in Appendix C) and all writes are late (in WB in the pipeline in Appendix C). A WAR hazard occurs either when there are some instructions that write results early in the instruction pipeline and other instructions that read a source late in the pipeline, or when instructions are reordered, as we will see in this chapter.
Note that the RAR (read after read) case is not a hazard.
Control Dependences
The last type of dependence is a control dependence. A control dependence determines the ordering of an instruction, i, with respect to a branch instruction so that instruction i is executed in correct program order and only when it should be. Every instruction, except for those in the first basic block of the program, is control dependent on some set of branches, and, in general, these control dependences must be preserved to preserve program order. One of the simplest examples of a control dependence is the dependence of the statements in the “then” part of an if statement on the branch. For example, in the code segment
if p1 {
S1;
};
if p2 {
S2;
}
S1 is control dependent on p1, and S2 is control dependent on p2 but not on p1.
In general, two constraints are imposed by control dependences:
1. An instruction that is control dependent on a branch cannot be moved before the branch so that its execution is no longer controlled by the branch. For example, we cannot take an instruction from the then portion of an if statement and move it before the if statement.
2. An instruction that is not control dependent on a branch cannot be moved after the branch so that its execution is controlled by the branch. For example, we cannot take a statement before the if statement and move it into the then portion.
When processors preserve strict program order, they ensure that control dependences are also preserved. We may be willing to execute instructions that should not have been executed, however, thereby violating the control dependences, if we can do so without affecting the correctness of the program. Thus, control dependence is not the critical property that must be preserved. Instead, the two properties critical to program correctness—and normally preserved by maintaining both data and control dependences—are the exception behavior and the data flow.
Preserving the exception behavior means that any changes in the ordering of instruction execution must not change how exceptions are raised in the program. Often this is relaxed to mean that the reordering of instruction execution must not cause any new exceptions in the program. A simple example shows how maintaining the control and data dependences can prevent such situations. Consider this code sequence:
DADDU R2,R3,R4
BEQZ R2,L1
LW R1,0(R2)
L1:
In this case, it is easy to see that if we do not maintain the data dependence involving R2, we can change the result of the program. Less obvious is the fact that if we ignore the control dependence and move the load instruction before the branch, the load instruction may cause a memory protection exception. Notice that no data dependence prevents us from interchanging the BEQZ and the LW; it is only the control dependence. To allow us to reorder these instructions (and still preserve the data dependence), we would like to just ignore the exception when the branch is taken. In Section 3.6, we will look at a hardware technique, speculation, which allows us to overcome this exception problem. Appendix H looks at software techniques for supporting speculation.
The second property preserved by maintenance of data dependences and control dependences is the data flow. The data flow is the actual flow of data values among instructions that produce results and those that consume them. Branches make the data flow dynamic, since they allow the source of data for a given instruction to come from many points. Put another way, it is insufficient to just maintain data dependences because an instruction may be data dependent on more than one predecessor. Program order is what determines which predecessor will actually deliver a data value to an instruction. Program order is ensured by maintaining the control dependences.
For example, consider the following code fragment:
DADDU R1,R2,R3
BEQZ R4,L
DSUBU R1,R5,R6
L: …
OR R7,R1,R8
In this example, the value of R1 used by the OR instruction depends on whether the branch is taken or not. Data dependence alone is not sufficient to preserve correctness. The OR instruction is data dependent on both the DADDU and DSUBU instructions, but preserving that order alone is insufficient for correct execution.
Instead, when the instructions execute, the data flow must be preserved: If the branch is not taken, then the value of R1 computed by the DSUBU should be used by the OR, and, if the branch is taken, the value of R1 computed by the DADDU should be used by the OR. By preserving the control dependence of the OR on the branch, we prevent an illegal change to the data flow. For similar reasons, the DSUBU instruction cannot be moved above the branch. Speculation, which helps with the exception problem, will also allow us to lessen the impact of the control dependence while still maintaining the data flow, as we will see in Section 3.6.
Sometimes we can determine that violating the control dependence cannot affect either the exception behavior or the data flow. Consider the following code sequence:
DADDU R1,R2,R3
BEQZ R12,skip
DSUBU R4,R5,R6
DADDU R5,R4,R9
skip: OR R7,R8,R9
Suppose we knew that the register destination of the DSUBU instruction (R4) was unused after the instruction labeled skip. (The property of whether a value will be used by an upcoming instruction is called liveness.) If R4 were unused, then changing the value of R4 just before the branch would not affect the data flow since R4 would be dead (rather than live) in the code region after skip. Thus, if R4 were dead and the existing DSUBU instruction could not generate an exception (other than those from which the processor resumes the same process), we could move the DSUBU instruction before the branch, since the data flow cannot be affected by this change.
If the branch is taken, the DSUBU instruction will execute and will be useless, but it will not affect the program results. This type of code scheduling is also a form of speculation, often called software speculation, since the compiler is betting on the branch outcome; in this case, the bet is that the branch is usually not taken. More ambitious compiler speculation mechanisms are discussed in Appendix H. Normally, it will be clear when we say speculation or speculative whether the mechanism is a hardware or software mechanism; when it is not clear, it is best to say “hardware speculation” or “software speculation.”
Control dependence is preserved by implementing control hazard detection that causes control stalls. Control stalls can be eliminated or reduced by a variety of hardware and software techniques, which we examine in Section 3.3.
3.2 Basic Compiler Techniques for Exposing ILP
This section examines the use of simple compiler technology to enhance a processor’s ability to exploit ILP. These techniques are crucial for processors that use static issue or static scheduling. Armed with this compiler technology, we will shortly examine the design and performance of processors using static issuing. Appendix H will investigate more sophisticated compiler and associated hardware schemes designed to enable a processor to exploit more instruction-level parallelism.
Basic Pipeline Scheduling and Loop Unrolling
To keep a pipeline full, parallelism among instructions must be exploited by finding sequences of unrelated instructions that can be overlapped in the pipeline. To avoid a pipeline stall, the execution of a dependent instruction must be separated from the source instruction by a distance in clock cycles equal to the pipeline latency of that source instruction. A compiler’s ability to perform this scheduling depends both on the amount of ILP available in the program and on the latencies of the functional units in the pipeline. Figure 3.2 shows the FP unit latencies we assume in this chapter, unless different latencies are explicitly stated. We assume the standard five-stage integer pipeline, so that branches have a delay of one clock cycle. We assume that the functional units are fully pipelined or replicated (as many times as the pipeline depth), so that an operation of any type can be issued on every clock cycle and there are no structural hazards.
Figure 3.2 Latencies of FP operations used in this chapter. The last column is the number of intervening clock cycles needed to avoid a stall. These numbers are similar to the average latencies we would see on an FP unit. The latency of a floating-point load to a store is 0, since the result of the load can be bypassed without stalling the store. We will continue to assume an integer load latency of 1 and an integer ALU operation latency of 0.
In this subsection, we look at how the compiler can increase the amount of available ILP by transforming loops. This example serves both to illustrate an important technique as well as to motivate the more powerful program transformations described in Appendix H. We will rely on the following code segment, which adds a scalar to a vector:
for (i=999; i>=0; i=i−1)
x[i] = x[i] + s;
We can see that this loop is parallel by noticing that the body of each iteration is independent. We formalize this notion in Appendix H and describe how we can test whether loop iterations are independent at compile time. First, let’s look at the performance of this loop, showing how we can use the parallelism to improve its performance for a MIPS pipeline with the latencies shown above.
The first step is to translate the above segment to MIPS assembly language. In the following code segment, R1 is initially the address of the element in the array with the highest address, and F2 contains the scalar value s. Register R2 is precomputed, so that 8(R2) is the address of the last element to operate on.
The straightforward MIPS code, not scheduled for the pipeline, looks like this:
Loop: L.D F0,0(R1) ;F0=array element
ADD.D F4,F0,F2 ;add scalar in F2
S.D F4,0(R1) ;store result
DADDUI R1,R1,#-8 ;decrement pointer
;8 bytes (per DW)
BNE R1,R2,Loop ;branch R1!=R2
Let’s start by seeing how well this loop will run when it is scheduled on a simple pipeline for MIPS with the latencies from Figure 3.2.
In the previous example, we complete one loop iteration and store back one array element every seven clock cycles, but the actual work of operating on the array element takes just three (the load, add, and store) of those seven clock cycles. The remaining four clock cycles consist of loop overhead—the DADDUI and BNE—and two stalls. To eliminate these four clock cycles we need to get more operations relative to the number of overhead instructions.
A simple scheme for increasing the number of instructions relative to the branch and overhead instructions is loop unrolling. Unrolling simply replicates the loop body multiple times, adjusting the loop termination code.
Loop unrolling can also be used to improve scheduling. Because it eliminates the branch, it allows instructions from different iterations to be scheduled together. In this case, we can eliminate the data use stalls by creating additional independent instructions within the loop body. If we simply replicated the instructions when we unrolled the loop, the resulting use of the same registers could prevent us from effectively scheduling the loop. Thus, we will want to use different registers for each iteration, increasing the required number of registers.
In real programs we do not usually know the upper bound on the loop. Suppose it is n, and we would like to unroll the loop to make k copies of the body. Instead of a single unrolled loop, we generate a pair of consecutive loops. The first executes (n mod k) times and has a body that is the original loop. The second is the unrolled body surrounded by an outer loop that iterates (n/k) times. (As we shall see in Chapter 4, this technique is similar to a technique called strip mining, used in compilers for vector processors.) For large values of n, most of the execution time will be spent in the unrolled loop body.
In the previous example, unrolling improves the performance of this loop by eliminating overhead instructions, although it increases code size substantially. How will the unrolled loop perform when it is scheduled for the pipeline described earlier?
The gain from scheduling on the unrolled loop is even larger than on the original loop. This increase arises because unrolling the loop exposes more computation that can be scheduled to minimize the stalls; the code above has no stalls. Scheduling the loop in this fashion necessitates realizing that the loads and stores are independent and can be interchanged.
Summary of the Loop Unrolling and Scheduling
Throughout this chapter and Appendix H, we will look at a variety of hardware and software techniques that allow us to take advantage of instruction-level parallelism to fully utilize the potential of the functional units in a processor. The key to most of these techniques is to know when and how the ordering among instructions may be changed. In our example we made many such changes, which to us, as human beings, were obviously allowable. In practice, this process must be performed in a methodical fashion either by a compiler or by hardware. To obtain the final unrolled code we had to make the following decisions and transformations:
■ Determine that unrolling the loop would be useful by finding that the loop iterations were independent, except for the loop maintenance code.
■ Use different registers to avoid unnecessary constraints that would be forced by using the same registers for different computations (e.g., name dependences).
■ Eliminate the extra test and branch instructions and adjust the loop termination and iteration code.
■ Determine that the loads and stores in the unrolled loop can be interchanged by observing that the loads and stores from different iterations are independent. This transformation requires analyzing the memory addresses and finding that they do not refer to the same address.
■ Schedule the code, preserving any dependences needed to yield the same result as the original code.
The key requirement underlying all of these transformations is an understanding of how one instruction depends on another and how the instructions can be changed or reordered given the dependences.
Three different effects limit the gains from loop unrolling: (1) a decrease in the amount of overhead amortized with each unroll, (2) code size limitations, and (3) compiler limitations. Let’s consider the question of loop overhead first. When we unrolled the loop four times, it generated sufficient parallelism among the instructions that the loop could be scheduled with no stall cycles. In fact, in 14 clock cycles, only 2 cycles were loop overhead: the DADDUI, which maintains the index value, and the BNE, which terminates the loop. If the loop is unrolled eight times, the overhead is reduced from 1/2 cycle per original iteration to 1/4.
A second limit to unrolling is the growth in code size that results. For larger loops, the code size growth may be a concern particularly if it causes an increase in the instruction cache miss rate.
Another factor often more important than code size is the potential shortfall in registers that is created by aggressive unrolling and scheduling. This secondary effect that results from instruction scheduling in large code segments is called register pressure. It arises because scheduling code to increase ILP causes the number of live values to increase. After aggressive instruction scheduling, it may not be possible to allocate all the live values to registers. The transformed code, while theoretically faster, may lose some or all of its advantage because it generates a shortage of registers. Without unrolling, aggressive scheduling is sufficiently limited by branches so that register pressure is rarely a problem. The combination of unrolling and aggressive scheduling can, however, cause this problem. The problem becomes especially challenging in multiple-issue processors that require the exposure of more independent instruction sequences whose execution can be overlapped. In general, the use of sophisticated high-level transformations, whose potential improvements are difficult to measure before detailed code generation, has led to significant increases in the complexity of modern compilers.
Loop unrolling is a simple but useful method for increasing the size of straight-line code fragments that can be scheduled effectively. This transformation is useful in a variety of processors, from simple pipelines like those we have examined so far to the multiple-issue superscalars and VLIWs explored later in this chapter.
3.3 Reducing Branch Costs with Advanced Branch Prediction
Because of the need to enforce control dependences through branch hazards and stalls, branches will hurt pipeline performance. Loop unrolling is one way to reduce the number of branch hazards; we can also reduce the performance losses of branches by predicting how they will behave. In Appendix C, we examine simple branch predictors that rely either on compile-time information or on the observed dynamic behavior of a branch in isolation. As the number of instructions in flight has increased, the importance of more accurate branch prediction has grown. In this section, we examine techniques for improving dynamic prediction accuracy.
Correlating Branch Predictors
The 2-bit predictor schemes use only the recent behavior of a single branch to predict the future behavior of that branch. It may be possible to improve the prediction accuracy if we also look at the recent behavior of other branches rather than just the branch we are trying to predict. Consider a small code fragment from the eqntott benchmark, a member of early SPEC benchmark suites that displayed particularly bad branch prediction behavior:
if (aa==2)
aa=0;
if (bb==2)
bb=0;
if (aa!=bb) {
Here is the MIPS code that we would typically generate for this code fragment assuming that aa and bb are assigned to registers R1 and R2:
DADDIU R3,R1,#−2
BNEZ R3,L1 ;branch b1 (aa!=2)
DADD R1,R0,R0 ;aa=0
L1: DADDIU R3,R2,#−2
BNEZ R3,L2 ;branch b2 (bb!=2)
DADD R2,R0,R0 ;bb=0
L2: DSUBU R3,R1,R2 ;R3=aa-bb
BEQZ R3,L3 ;branch b3 (aa==bb)
Let’s label these branches b1, b2, and b3. The key observation is that the behavior of branch b3 is correlated with the behavior of branches b1 and b2. Clearly, if branches b1 and b2 are both not taken (i.e., if the conditions both evaluate to true and aa and bb are both assigned 0), then b3 will be taken, since aa and bb are clearly equal. A predictor that uses only the behavior of a single branch to predict the outcome of that branch can never capture this behavior.
Branch predictors that use the behavior of other branches to make a prediction are called correlating predictors or two-level predictors. Existing correlating predictors add information about the behavior of the most recent branches to decide how to predict a given branch. For example, a (1,2) predictor uses the behavior of the last branch to choose from among a pair of 2-bit branch predictors in predicting a particular branch. In the general case, an (m,n) predictor uses the behavior of the last m branches to choose from 2m branch predictors, each of which is an n-bit predictor for a single branch. The attraction of this type of correlating branch predictor is that it can yield higher prediction rates than the 2-bit scheme and requires only a trivial amount of additional hardware.
The simplicity of the hardware comes from a simple observation: The global history of the most recent m branches can be recorded in an m-bit shift register, where each bit records whether the branch was taken or not taken. The branch-prediction buffer can then be indexed using a concatenation of the low-order bits from the branch address with the m-bit global history. For example, in a (2,2) buffer with 64 total entries, the 4 low-order address bits of the branch (word address) and the 2 global bits representing the behavior of the two most recently executed branches form a 6-bit index that can be used to index the 64 counters.
How much better do the correlating branch predictors work when compared with the standard 2-bit scheme? To compare them fairly, we must compare predictors that use the same number of state bits. The number of bits in an (m,n) predictor is
A 2-bit predictor with no global history is simply a (0,2) predictor.
Example
How many bits are in the (0,2) branch predictor with 4K entries? How many entries are in a (2,2) predictor with the same number of bits?
Answer
The predictor with 4K entries has
How many branch-selected entries are in a (2,2) predictor that has a total of 8K bits in the prediction buffer? We know that
Hence, the number of prediction entries selected by the branch = 1K.
Figure 3.3 compares the misprediction rates of the earlier (0,2) predictor with 4K entries and a (2,2) predictor with 1K entries. As you can see, this correlating predictor not only outperforms a simple 2-bit predictor with the same total number of state bits, but it also often outperforms a 2-bit predictor with an unlimited number of entries.
Figure 3.3 Comparison of 2-bit predictors. A noncorrelating predictor for 4096 bits is first, followed by a noncorrelating 2-bit predictor with unlimited entries and a 2-bit predictor with 2 bits of global history and a total of 1024 entries. Although these data are for an older version of SPEC, data for more recent SPEC benchmarks would show similar differences in accuracy.
Tournament Predictors: Adaptively Combining Local and Global Predictors
The primary motivation for correlating branch predictors came from the observation that the standard 2-bit predictor using only local information failed on some important branches and that, by adding global information, the performance could be improved. Tournament predictors take this insight to the next level, by using multiple predictors, usually one based on global information and one based on local information, and combining them with a selector. Tournament predictors can achieve both better accuracy at medium sizes (8K–32K bits) and also make use of very large numbers of prediction bits effectively. Existing tournament predictors use a 2-bit saturating counter per branch to choose among two different predictors based on which predictor (local, global, or even some mix) was most effective in recent predictions. As in a simple 2-bit predictor, the saturating counter requires two mispredictions before changing the identity of the preferred predictor.
The advantage of a tournament predictor is its ability to select the right predictor for a particular branch, which is particularly crucial for the integer benchmarks. A typical tournament predictor will select the global predictor almost 40% of the time for the SPEC integer benchmarks and less than 15% of the time for the SPEC FP benchmarks. In addition to the Alpha processors that pioneered tournament predictors, recent AMD processors, including both the Opteron and Phenom, have used tournament-style predictors.
Figure 3.4 looks at the performance of three different predictors (a local 2-bit predictor, a correlating predictor, and a tournament predictor) for different numbers of bits using SPEC89 as the benchmark. As we saw earlier, the prediction capability of the local predictor does not improve beyond a certain size. The correlating predictor shows a significant improvement, and the tournament predictor generates slightly better performance. For more recent versions of the SPEC, the results would be similar, but the asymptotic behavior would not be reached until slightly larger predictor sizes.
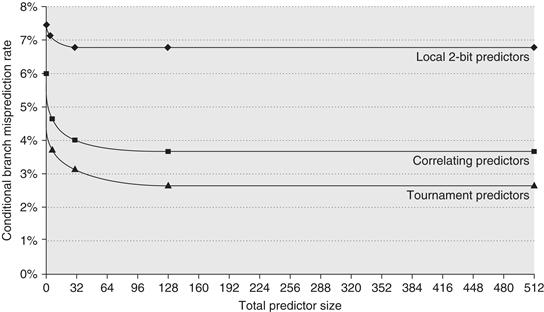
Figure 3.4 The misprediction rate for three different predictors on SPEC89 as the total number of bits is increased. The predictors are a local 2-bit predictor, a correlating predictor that is optimally structured in its use of global and local information at each point in the graph, and a tournament predictor. Although these data are for an older version of SPEC, data for more recent SPEC benchmarks would show similar behavior, perhaps converging to the asymptotic limit at slightly larger predictor sizes.
The local predictor consists of a two-level predictor. The top level is a local history table consisting of 1024 10-bit entries; each 10-bit entry corresponds to the most recent 10 branch outcomes for the entry. That is, if the branch was taken 10 or more times in a row, the entry in the local history table will be all 1s. If the branch is alternately taken and untaken, the history entry consists of alternating 0s and 1s. This 10-bit history allows patterns of up to 10 branches to be discovered and predicted. The selected entry from the local history table is used to index a table of 1K entries consisting of 3-bit saturating counters, which provide the local prediction. This combination, which uses a total of 29K bits, leads to high accuracy in branch prediction.
The Intel Core i7 Branch Predictor
Intel has released only limited amounts of information about the Core i7’s branch predictor, which is based on earlier predictors used in the Core Duo chip. The i7 uses a two-level predictor that has a smaller first-level predictor, designed to meet the cycle constraints of predicting a branch every clock cycle, and a larger second-level predictor as a backup. Each predictor combines three different predictors: (1) the simple two-bit predictor, which was introduced in Appendix C (and used in the tournament predictor discussed above); (2) a global history predictor, like those we just saw; and (3) a loop exit predictor. The loop exit predictor uses a counter to predict the exact number of taken branches (which is the number of loop iterations) for a branch that is detected as a loop branch. For each branch, the best prediction is chosen from among the three predictors by tracking the accuracy of each prediction, like a tournament predictor. In addition to this multilevel main predictor, a separate unit predicts target addresses for indirect branches, and a stack to predict return addresses is also used.
As in other cases, speculation causes some challenges in evaluating the predictor, since a mispredicted branch may easily lead to another branch being fetched and mispredicted. To keep things simple, we look at the number of mispredictions as a percentage of the number of successfully completed branches (those that were not the result of misspeculation). Figure 3.5 shows these data for 19 of the SPECCPU 2006 benchmarks. These benchmarks are considerably larger than SPEC89 or SPEC2000, with the result being that the misprediction rates are slightly higher than those in Figure 3.4 even with a more elaborate combination of predictors. Because branch misprediction leads to ineffective speculation, it contributes to the wasted work, as we will see later in this chapter.
Figure 3.5 The misprediction rate for 19 of the SPECCPU2006 benchmarks versus the number of successfully retired branches is slightly higher on average for the integer benchmarks than for the FP (4% versus 3%). More importantly, it is much higher for a few benchmarks.
3.4 Overcoming Data Hazards with Dynamic Scheduling
A simple statically scheduled pipeline fetches an instruction and issues it, unless there is a data dependence between an instruction already in the pipeline and the fetched instruction that cannot be hidden with bypassing or forwarding. (Forwarding logic reduces the effective pipeline latency so that the certain dependences do not result in hazards.) If there is a data dependence that cannot be hidden, then the hazard detection hardware stalls the pipeline starting with the instruction that uses the result. No new instructions are fetched or issued until the dependence is cleared.
In this section, we explore dynamic scheduling, in which the hardware rearranges the instruction execution to reduce the stalls while maintaining data flow and exception behavior. Dynamic scheduling offers several advantages. First, it allows code that was compiled with one pipeline in mind to run efficiently on a different pipeline, eliminating the need to have multiple binaries and recompile for a different microarchitecture. In today’s computing environment, where much of the software is from third parties and distributed in binary form, this advantage is significant. Second, it enables handling some cases when dependences are unknown at compile time; for example, they may involve a memory reference or a data-dependent branch, or they may result from a modern programming environment that uses dynamic linking or dispatching. Third, and perhaps most importantly, it allows the processor to tolerate unpredictable delays, such as cache misses, by executing other code while waiting for the miss to resolve. In Section 3.6, we explore hardware speculation, a technique with additional performance advantages, which builds on dynamic scheduling. As we will see, the advantages of dynamic scheduling are gained at a cost of significant increase in hardware complexity.
Although a dynamically scheduled processor cannot change the data flow, it tries to avoid stalling when dependences are present. In contrast, static pipeline scheduling by the compiler (covered in Section 3.2) tries to minimize stalls by separating dependent instructions so that they will not lead to hazards. Of course, compiler pipeline scheduling can also be used on code destined to run on a processor with a dynamically scheduled pipeline.
Dynamic Scheduling: The Idea
A major limitation of simple pipelining techniques is that they use in-order instruction issue and execution: Instructions are issued in program order, and if an instruction is stalled in the pipeline no later instructions can proceed. Thus, if there is a dependence between two closely spaced instructions in the pipeline, this will lead to a hazard and a stall will result. If there are multiple functional units, these units could lie idle. If instruction j depends on a long-running instruction i, currently in execution in the pipeline, then all instructions after j must be stalled until i is finished and j can execute. For example, consider this code:
DIV.D F0,F2,F4
ADD.D F10,F0,F8
SUB.D F12,F8,F14
The SUB.D instruction cannot execute because the dependence of ADD.D on DIV.D causes the pipeline to stall; yet, SUB.D is not data dependent on anything in the pipeline. This hazard creates a performance limitation that can be eliminated by not requiring instructions to execute in program order.
In the classic five-stage pipeline, both structural and data hazards could be checked during instruction decode (ID): When an instruction could execute without hazards, it was issued from ID knowing that all data hazards had been resolved.
To allow us to begin executing the SUB.D in the above example, we must separate the issue process into two parts: checking for any structural hazards and waiting for the absence of a data hazard. Thus, we still use in-order instruction issue (i.e., instructions issued in program order), but we want an instruction to begin execution as soon as its data operands are available. Such a pipeline does out-of-order execution, which implies out-of-order completion.
Out-of-order execution introduces the possibility of WAR and WAW hazards, which do not exist in the five-stage integer pipeline and its logical extension to an in-order floating-point pipeline. Consider the following MIPS floating-point code sequence:
DIV.D F0,F2,F4
ADD.D F6,F0,F8
SUB.D F8,F10,F14
MUL.D F6,F10,F8
There is an antidependence between the ADD.D and the SUB.D, and if the pipeline executes the SUB.D before the ADD.D (which is waiting for the DIV.D), it will violate the antidependence, yielding a WAR hazard. Likewise, to avoid violating output dependences, such as the write of F6 by MUL.D, WAW hazards must be handled. As we will see, both these hazards are avoided by the use of register renaming.
Out-of-order completion also creates major complications in handling exceptions. Dynamic scheduling with out-of-order completion must preserve exception behavior in the sense that exactly those exceptions that would arise if the program were executed in strict program order actually do arise. Dynamically scheduled processors preserve exception behavior by delaying the notification of an associated exception until the processor knows that the instruction should be the next one completed.
Although exception behavior must be preserved, dynamically scheduled processors could generate imprecise exceptions. An exception is imprecise if the processor state when an exception is raised does not look exactly as if the instructions were executed sequentially in strict program order. Imprecise exceptions can occur because of two possibilities:
1. The pipeline may have already completed instructions that are later in program order than the instruction causing the exception.
2. The pipeline may have not yet completed some instructions that are earlier in program order than the instruction causing the exception.
Imprecise exceptions make it difficult to restart execution after an exception. Rather than address these problems in this section, we will discuss a solution that provides precise exceptions in the context of a processor with speculation in Section 3.6. For floating-point exceptions, other solutions have been used, as discussed in Appendix J.
To allow out-of-order execution, we essentially split the ID pipe stage of our simple five-stage pipeline into two stages:
1. Issue—Decode instructions, check for structural hazards.
2. Read operands—Wait until no data hazards, then read operands.
An instruction fetch stage precedes the issue stage and may fetch either into an instruction register or into a queue of pending instructions; instructions are then issued from the register or queue. The execution stage follows the read operands stage, just as in the five-stage pipeline. Execution may take multiple cycles, depending on the operation.
We distinguish when an instruction begins execution and when it completes execution; between the two times, the instruction is in execution. Our pipeline allows multiple instructions to be in execution at the same time; without this capability, a major advantage of dynamic scheduling is lost. Having multiple instructions in execution at once requires multiple functional units, pipelined functional units, or both. Since these two capabilities—pipelined functional units and multiple functional units—are essentially equivalent for the purposes of pipeline control, we will assume the processor has multiple functional units.
In a dynamically scheduled pipeline, all instructions pass through the issue stage in order (in-order issue); however, they can be stalled or bypass each other in the second stage (read operands) and thus enter execution out of order. Scoreboarding is a technique for allowing instructions to execute out of order when there are sufficient resources and no data dependences; it is named after the CDC 6600 scoreboard, which developed this capability. Here, we focus on a more sophisticated technique, called Tomasulo’s algorithm. The primary difference is that Tomasulo’s algorithm handles antidependences and output dependences by effectively renaming the registers dynamically. Additionally, Tomasulo’s algorithm can be extended to handle speculation, a technique to reduce the effect of control dependences by predicting the outcome of a branch, executing instructions at the predicted destination address, and taking corrective actions when the prediction was wrong. While the use of scoreboarding is probably sufficient to support a simple two-issue superscalar like the ARM A8, a more aggressive processor, like the four-issue Intel i7, benefits from the use of out-of-order execution.
Dynamic Scheduling Using Tomasulo’s Approach
The IBM 360/91 floating-point unit used a sophisticated scheme to allow out-of-order execution. This scheme, invented by Robert Tomasulo, tracks when operands for instructions are available to minimize RAW hazards and introduces register renaming in hardware to minimize WAW and WAR hazards. There are many variations on this scheme in modern processors, although the key concepts of tracking instruction dependences to allow execution as soon as operands are available and renaming registers to avoid WAR and WAW hazards are common characteristics.
IBM’s goal was to achieve high floating-point performance from an instruction set and from compilers designed for the entire 360 computer family, rather than from specialized compilers for the high-end processors. The 360 architecture had only four double-precision floating-point registers, which limits the effectiveness of compiler scheduling; this fact was another motivation for the Tomasulo approach. In addition, the IBM 360/91 had long memory accesses and long floating-point delays, which Tomasulo’s algorithm was designed to overcome. At the end of the section, we will see that Tomasulo’s algorithm can also support the overlapped execution of multiple iterations of a loop.
We explain the algorithm, which focuses on the floating-point unit and load-store unit, in the context of the MIPS instruction set. The primary difference between MIPS and the 360 is the presence of register-memory instructions in the latter architecture. Because Tomasulo’s algorithm uses a load functional unit, no significant changes are needed to add register-memory addressing modes. The IBM 360/91 also had pipelined functional units, rather than multiple functional units, but we describe the algorithm as if there were multiple functional units. It is a simple conceptual extension to also pipeline those functional units.
As we will see, RAW hazards are avoided by executing an instruction only when its operands are available, which is exactly what the simpler scoreboarding approach provides. WAR and WAW hazards, which arise from name dependences, are eliminated by register renaming. Register renaming eliminates these hazards by renaming all destination registers, including those with a pending read or write for an earlier instruction, so that the out-of-order write does not affect any instructions that depend on an earlier value of an operand.
To better understand how register renaming eliminates WAR and WAW hazards, consider the following example code sequence that includes potential WAR and WAW hazards:
DIV.D F0,F2,F4
ADD.D F6,F0,F8
S.D F6,0(R1)
SUB.D F8,F10,F14
MUL.D F6,F10,F8
There are two antidependences: between the ADD.D and the SUB.D and between the S.D and the MUL.D. There is also an output dependence between the ADD.D and the MUL.D, leading to three possible hazards: WAR hazards on the use of F8 by ADD.D and the use of F6 by the SUB.D, as well as a WAW hazard since the ADD.D may finish later than the MUL.D. There are also three true data dependences: between the DIV.D and the ADD.D, between the SUB.D and the MUL.D, and between the ADD.D and the S.D.
These three name dependences can all be eliminated by register renaming. For simplicity, assume the existence of two temporary registers, S and T. Using S and T, the sequence can be rewritten without any dependences as:
DIV.D F0,F2,F4
ADD.D S,F0,F8
S.D S,0(R1)
SUB.D T,F10,F14
MUL.D F6,F10,T
In addition, any subsequent uses of F8 must be replaced by the register T. In this code segment, the renaming process can be done statically by the compiler. Finding any uses of F8 that are later in the code requires either sophisticated compiler analysis or hardware support, since there may be intervening branches between the above code segment and a later use of F8. As we will see, Tomasulo’s algorithm can handle renaming across branches.
In Tomasulo’s scheme, register renaming is provided by reservation stations, which buffer the operands of instructions waiting to issue. The basic idea is that a reservation station fetches and buffers an operand as soon as it is available, eliminating the need to get the operand from a register. In addition, pending instructions designate the reservation station that will provide their input. Finally, when successive writes to a register overlap in execution, only the last one is actually used to update the register. As instructions are issued, the register specifiers for pending operands are renamed to the names of the reservation station, which provides register renaming.
Since there can be more reservation stations than real registers, the technique can even eliminate hazards arising from name dependences that could not be eliminated by a compiler. As we explore the components of Tomasulo’s scheme, we will return to the topic of register renaming and see exactly how the renaming occurs and how it eliminates WAR and WAW hazards.
The use of reservation stations, rather than a centralized register file, leads to two other important properties. First, hazard detection and execution control are distributed: The information held in the reservation stations at each functional unit determines when an instruction can begin execution at that unit. Second, results are passed directly to functional units from the reservation stations where they are buffered, rather than going through the registers. This bypassing is done with a common result bus that allows all units waiting for an operand to be loaded simultaneously (on the 360/91 this is called the common data bus, or CDB). In pipelines with multiple execution units and issuing multiple instructions per clock, more than one result bus will be needed.
Figure 3.6 shows the basic structure of a Tomasulo-based processor, including both the floating-point unit and the load/store unit; none of the execution control tables is shown. Each reservation station holds an instruction that has been issued and is awaiting execution at a functional unit and either the operand values for that instruction, if they have already been computed, or else the names of the reservation stations that will provide the operand values.
Figure 3.6 The basic structure of a MIPS floating-point unit using Tomasulo’s algorithm. Instructions are sent from the instruction unit into the instruction queue from which they are issued in first-in, first-out (FIFO) order. The reservation stations include the operation and the actual operands, as well as information used for detecting and resolving hazards. Load buffers have three functions: (1) hold the components of the effective address until it is computed, (2) track outstanding loads that are waiting on the memory, and (3) hold the results of completed loads that are waiting for the CDB. Similarly, store buffers have three functions: (1) hold the components of the effective address until it is computed, (2) hold the destination memory addresses of outstanding stores that are waiting for the data value to store, and (3) hold the address and value to store until the memory unit is available. All results from either the FP units or the load unit are put on the CDB, which goes to the FP register file as well as to the reservation stations and store buffers. The FP adders implement addition and subtraction, and the FP multipliers do multiplication and division.
The load buffers and store buffers hold data or addresses coming from and going to memory and behave almost exactly like reservation stations, so we distinguish them only when necessary. The floating-point registers are connected by a pair of buses to the functional units and by a single bus to the store buffers. All results from the functional units and from memory are sent on the common data bus, which goes everywhere except to the load buffer. All reservation stations have tag fields, employed by the pipeline control.
Before we describe the details of the reservation stations and the algorithm, let’s look at the steps an instruction goes through. There are only three steps, although each one can now take an arbitrary number of clock cycles:
1. Issue—Get the next instruction from the head of the instruction queue, which is maintained in FIFO order to ensure the maintenance of correct data flow. If there is a matching reservation station that is empty, issue the instruction to the station with the operand values, if they are currently in the registers. If there is not an empty reservation station, then there is a structural hazard and the instruction stalls until a station or buffer is freed. If the operands are not in the registers, keep track of the functional units that will produce the operands. This step renames registers, eliminating WAR and WAW hazards. (This stage is sometimes called dispatch in a dynamically scheduled processor.)
2. Execute—If one or more of the operands is not yet available, monitor the common data bus while waiting for it to be computed. When an operand becomes available, it is placed into any reservation station awaiting it. When all the operands are available, the operation can be executed at the corresponding functional unit. By delaying instruction execution until the operands are available, RAW hazards are avoided. (Some dynamically scheduled processors call this step “issue,” but we use the name “execute,” which was used in the first dynamically scheduled processor, the CDC 6600.)
Notice that several instructions could become ready in the same clock cycle for the same functional unit. Although independent functional units could begin execution in the same clock cycle for different instructions, if more than one instruction is ready for a single functional unit, the unit will have to choose among them. For the floating-point reservation stations, this choice may be made arbitrarily; loads and stores, however, present an additional complication.
Loads and stores require a two-step execution process. The first step computes the effective address when the base register is available, and the effective address is then placed in the load or store buffer. Loads in the load buffer execute as soon as the memory unit is available. Stores in the store buffer wait for the value to be stored before being sent to the memory unit. Loads and stores are maintained in program order through the effective address calculation, which will help to prevent hazards through memory, as we will see shortly.
To preserve exception behavior, no instruction is allowed to initiate execution until all branches that precede the instruction in program order have completed. This restriction guarantees that an instruction that causes an exception during execution really would have been executed. In a processor using branch prediction (as all dynamically scheduled processors do), this means that the processor must know that the branch prediction was correct before allowing an instruction after the branch to begin execution. If the processor records the occurrence of the exception, but does not actually raise it, an instruction can start execution but not stall until it enters write result.
As we will see, speculation provides a more flexible and more complete method to handle exceptions, so we will delay making this enhancement and show how speculation handles this problem later.
3. Write result—When the result is available, write it on the CDB and from there into the registers and into any reservation stations (including store buffers) waiting for this result. Stores are buffered in the store buffer until both the value to be stored and the store address are available, then the result is written as soon as the memory unit is free.
The data structures that detect and eliminate hazards are attached to the reservation stations, to the register file, and to the load and store buffers with slightly different information attached to different objects. These tags are essentially names for an extended set of virtual registers used for renaming. In our example, the tag field is a 4-bit quantity that denotes one of the five reservation stations or one of the five load buffers. As we will see, this produces the equivalent of 10 registers that can be designated as result registers (as opposed to the four double-precision registers that the 360 architecture contains). In a processor with more real registers, we would want renaming to provide an even larger set of virtual registers. The tag field describes which reservation station contains the instruction that will produce a result needed as a source operand.
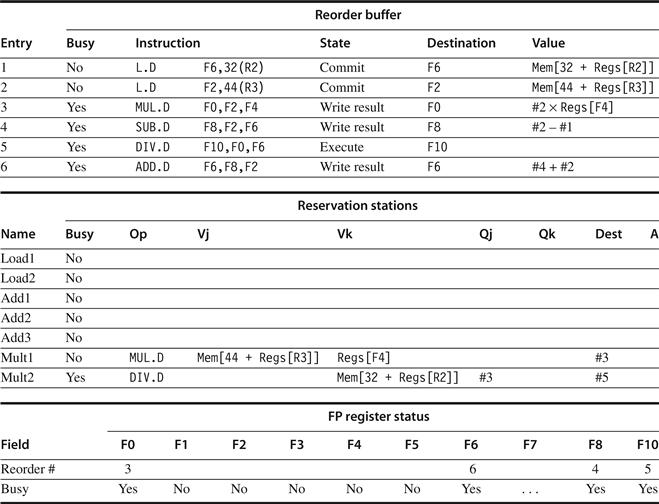
Once an instruction has issued and is waiting for a source operand, it refers to the operand by the reservation station number where the instruction that will write the register has been assigned. Unused values, such as zero, indicate that the operand is already available in the registers. Because there are more reservation stations than actual register numbers, WAW and WAR hazards are eliminated by renaming results using reservation station numbers. Although in Tomasulo’s scheme the reservation stations are used as the extended virtual registers, other approaches could use a register set with additional registers or a structure like the reorder buffer, which we will see in Section 3.6.
In Tomasulo’s scheme, as well as the subsequent methods we look at for supporting speculation, results are broadcast on a bus (the CDB), which is monitored by the reservation stations. The combination of the common result bus and the retrieval of results from the bus by the reservation stations implements the forwarding and bypassing mechanisms used in a statically scheduled pipeline. In doing so, however, a dynamically scheduled scheme introduces one cycle of latency between source and result, since the matching of a result and its use cannot be done until the Write Result stage. Thus, in a dynamically scheduled pipeline, the effective latency between a producing instruction and a consuming instruction is at least one cycle longer than the latency of the functional unit producing the result.
It is important to remember that the tags in the Tomasulo scheme refer to the buffer or unit that will produce a result; the register names are discarded when an instruction issues to a reservation station. (This is a key difference between Tomasulo’s scheme and scoreboarding: In scoreboarding, operands stay in the registers and are only read after the producing instruction completes and the consuming instruction is ready to execute.)
Each reservation station has seven fields:
■ Op—The operation to perform on source operands S1 and S2.
■ Qj, Qk—The reservation stations that will produce the corresponding source operand; a value of zero indicates that the source operand is already available in Vj or Vk, or is unnecessary.
■ Vj, Vk—The value of the source operands. Note that only one of the V fields or the Q field is valid for each operand. For loads, the Vk field is used to hold the offset field.
■ A—Used to hold information for the memory address calculation for a load or store. Initially, the immediate field of the instruction is stored here; after the address calculation, the effective address is stored here.
■ Busy—Indicates that this reservation station and its accompanying functional unit are occupied.
The register file has a field, Qi:
■ Qi—The number of the reservation station that contains the operation whose result should be stored into this register. If the value of Qi is blank (or 0), no currently active instruction is computing a result destined for this register, meaning that the value is simply the register contents.
The load and store buffers each have a field, A, which holds the result of the effective address once the first step of execution has been completed.
In the next section, we will first consider some examples that show how these mechanisms work and then examine the detailed algorithm.
3.5 Dynamic Scheduling: Examples and the Algorithm
Before we examine Tomasulo’s algorithm in detail, let’s consider a few examples that will help illustrate how the algorithm works.
Example
Show what the information tables look like for the following code sequence when only the first load has completed and written its result:
1. L.D F6,32(R2)
2. L.D F2,44(R3)
3. MUL.D F0,F2,F4
4. SUB.D F8,F2,F6
5. DIV.D F10,F0,F6
6. ADD.D F6,F8,F2
Answer
Figure 3.7 shows the result in three tables. The numbers appended to the names Add, Mult, and Load stand for the tag for that reservation station—Add1 is the tag for the result from the first add unit. In addition, we have included an instruction status table. This table is included only to help you understand the algorithm; it is not actually a part of the hardware. Instead, the reservation station keeps the state of each operation that has issued.
Figure 3.7 Reservation stations and register tags shown when all of the instructions have issued, but only the first load instruction has completed and written its result to the CDB. The second load has completed effective address calculation but is waiting on the memory unit. We use the array Regs[ ] to refer to the register file and the array Mem[ ] to refer to the memory. Remember that an operand is specified by either a Q field or a V field at any time. Notice that the ADD.D instruction, which has a WAR hazard at the WB stage, has issued and could complete before the DIV.D initiates.
Tomasulo’s scheme offers two major advantages over earlier and simpler schemes: (1) the distribution of the hazard detection logic, and (2) the elimination of stalls for WAW and WAR hazards.
The first advantage arises from the distributed reservation stations and the use of the CDB. If multiple instructions are waiting on a single result, and each instruction already has its other operand, then the instructions can be released simultaneously by the broadcast of the result on the CDB. If a centralized register file were used, the units would have to read their results from the registers when register buses are available.
The second advantage, the elimination of WAW and WAR hazards, is accomplished by renaming registers using the reservation stations and by the process of storing operands into the reservation station as soon as they are available.
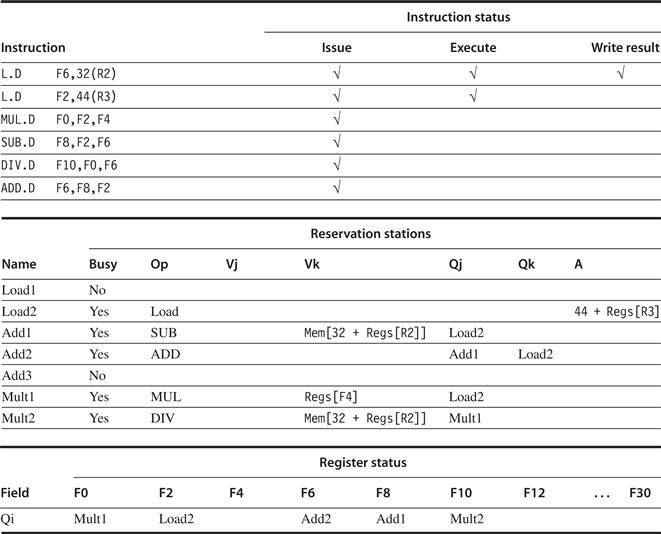
For example, the code sequence in Figure 3.7 issues both the DIV.D and the ADD.D, even though there is a WAR hazard involving F6. The hazard is eliminated in one of two ways. First, if the instruction providing the value for the DIV.D has completed, then Vk will store the result, allowing DIV.D to execute independent of the ADD.D (this is the case shown). On the other hand, if the L.D had not completed, then Qk would point to the Load1 reservation station, and the DIV.D instruction would be independent of the ADD.D. Thus, in either case, the ADD.D can issue and begin executing. Any uses of the result of the DIV.D would point to the reservation station, allowing the ADD.D to complete and store its value into the registers without affecting the DIV.D.
We’ll see an example of the elimination of a WAW hazard shortly. But let’s first look at how our earlier example continues execution. In this example, and the ones that follow in this chapter, assume the following latencies: load is 1 clock cycle, add is 2 clock cycles, multiply is 6 clock cycles, and divide is 12 clock cycles.
Example
Using the same code segment as in the previous example (page 176), show what the status tables look like when the MUL.D is ready to write its result.
Answer
The result is shown in the three tables in Figure 3.8. Notice that ADD.D has completed since the operands of DIV.D were copied, thereby overcoming the WAR hazard. Notice that even if the load of F6 was delayed, the add into F6 could be executed without triggering a WAW hazard.
Figure 3.8 Multiply and divide are the only instructions not finished.
Tomasulo’s Algorithm: The Details
Figure 3.9 specifies the checks and steps that each instruction must go through. As mentioned earlier, loads and stores go through a functional unit for effective address computation before proceeding to independent load or store buffers. Loads take a second execution step to access memory and then go to write result to send the value from memory to the register file and/or any waiting reservation stations. Stores complete their execution in the write result stage, which writes the result to memory. Notice that all writes occur in write result, whether the destination is a register or memory. This restriction simplifies Tomasulo’s algorithm and is critical to its extension with speculation in Section 3.6.
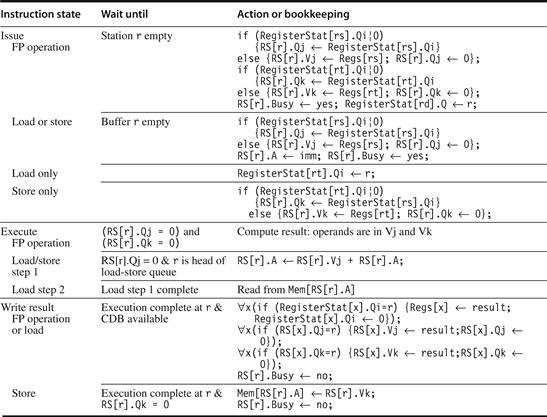
Figure 3.9 Steps in the algorithm and what is required for each step. For the issuing instruction, rd is the destination, rs and rt are the source register numbers, imm is the sign-extended immediate field, and r is the reservation station or buffer that the instruction is assigned to. RS is the reservation station data structure. The value returned by an FP unit or by the load unit is called result. RegisterStat is the register status data structure (not the register file, which is Regs[]). When an instruction is issued, the destination register has its Qi field set to the number of the buffer or reservation station to which the instruction is issued. If the operands are available in the registers, they are stored in the V fields. Otherwise, the Q fields are set to indicate the reservation station that will produce the values needed as source operands. The instruction waits at the reservation station until both its operands are available, indicated by zero in the Q fields. The Q fields are set to zero either when this instruction is issued or when an instruction on which this instruction depends completes and does its write back. When an instruction has finished execution and the CDB is available, it can do its write back. All the buffers, registers, and reservation stations whose values of Qj or Qk are the same as the completing reservation station update their values from the CDB and mark the Q fields to indicate that values have been received. Thus, the CDB can broadcast its result to many destinations in a single clock cycle, and if the waiting instructions have their operands they can all begin execution on the next clock cycle. Loads go through two steps in execute, and stores perform slightly differently during write result, where they may have to wait for the value to store. Remember that, to preserve exception behavior, instructions should not be allowed to execute if a branch that is earlier in program order has not yet completed. Because any concept of program order is not maintained after the issue stage, this restriction is usually implemented by preventing any instruction from leaving the issue step, if there is a pending branch already in the pipeline. In Section 3.6, we will see how speculation support removes this restriction.
Tomasulo’s Algorithm: A Loop-Based Example
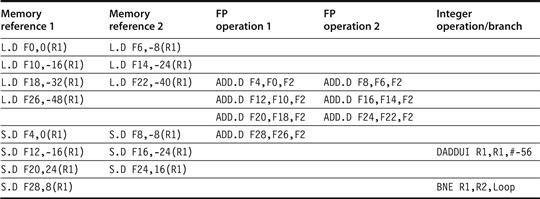
To understand the full power of eliminating WAW and WAR hazards through dynamic renaming of registers, we must look at a loop. Consider the following simple sequence for multiplying the elements of an array by a scalar in F2:
Loop: L.D F0,0(R1)
MUL.D F4,F0,F2
S.D F4,0(R1)
DADDIU R1,R1,−8
BNE R1,R2,Loop; branches if R1|R2
If we predict that branches are taken, using reservation stations will allow multiple executions of this loop to proceed at once. This advantage is gained without changing the code—in effect, the loop is unrolled dynamically by the hardware using the reservation stations obtained by renaming to act as additional registers.
Let’s assume we have issued all the instructions in two successive iterations of the loop, but none of the floating-point load/stores or operations has completed. Figure 3.10 shows reservation stations, register status tables, and load and store buffers at this point. (The integer ALU operation is ignored, and it is assumed the branch was predicted as taken.) Once the system reaches this state, two copies of the loop could be sustained with a CPI close to 1.0, provided the multiplies could complete in four clock cycles. With a latency of six cycles, additional iterations will need to be processed before the steady state can be reached. This requires more reservation stations to hold instructions that are in execution. As we will see later in this chapter, when extended with multiple instruction issue, Tomasulo’s approach can sustain more than one instruction per clock.
Figure 3.10 Two active iterations of the loop with no instruction yet completed. Entries in the multiplier reservation stations indicate that the outstanding loads are the sources. The store reservation stations indicate that the multiply destination is the source of the value to store.
A load and a store can safely be done out of order, provided they access different addresses. If a load and a store access the same address, then either
■ The load is before the store in program order and interchanging them results in a WAR hazard, or
■ The store is before the load in program order and interchanging them results in a RAW hazard.
Similarly, interchanging two stores to the same address results in a WAW hazard.
Hence, to determine if a load can be executed at a given time, the processor can check whether any uncompleted store that precedes the load in program order shares the same data memory address as the load. Similarly, a store must wait until there are no unexecuted loads or stores that are earlier in program order and share the same data memory address. We consider a method to eliminate this restriction in Section 3.9.
To detect such hazards, the processor must have computed the data memory address associated with any earlier memory operation. A simple, but not necessarily optimal, way to guarantee that the processor has all such addresses is to perform the effective address calculations in program order. (We really only need to keep the relative order between stores and other memory references; that is, loads can be reordered freely.)
Let’s consider the situation of a load first. If we perform effective address calculation in program order, then when a load has completed effective address calculation, we can check whether there is an address conflict by examining the A field of all active store buffers. If the load address matches the address of any active entries in the store buffer, that load instruction is not sent to the load buffer until the conflicting store completes. (Some implementations bypass the value directly to the load from a pending store, reducing the delay for this RAW hazard.)
Stores operate similarly, except that the processor must check for conflicts in both the load buffers and the store buffers, since conflicting stores cannot be reordered with respect to either a load or a store.
A dynamically scheduled pipeline can yield very high performance, provided branches are predicted accurately—an issue we addressed in the last section. The major drawback of this approach is the complexity of the Tomasulo scheme, which requires a large amount of hardware. In particular, each reservation station must contain an associative buffer, which must run at high speed, as well as complex control logic. The performance can also be limited by the single CDB. Although additional CDBs can be added, each CDB must interact with each reservation station, and the associative tag-matching hardware would have to be duplicated at each station for each CDB.
In Tomasulo’s scheme, two different techniques are combined: the renaming of the architectural registers to a larger set of registers and the buffering of source operands from the register file. Source operand buffering resolves WAR hazards that arise when the operand is available in the registers. As we will see later, it is also possible to eliminate WAR hazards by the renaming of a register together with the buffering of a result until no outstanding references to the earlier version of the register remain. This approach will be used when we discuss hardware speculation.
Tomasulo’s scheme was unused for many years after the 360/91, but was widely adopted in multiple-issue processors starting in the 1990s for several reasons:
1. Although Tomasulo’s algorithm was designed before caches, the presence of caches, with the inherently unpredictable delays, has become one of the major motivations for dynamic scheduling. Out-of-order execution allows the processors to continue executing instructions while awaiting the completion of a cache miss, thus hiding all or part of the cache miss penalty.
2. As processors became more aggressive in their issue capability and designers are concerned with the performance of difficult-to-schedule code (such as most nonnumeric code), techniques such as register renaming, dynamic scheduling, and speculation became more important.
3. It can achieve high performance without requiring the compiler to target code to a specific pipeline structure, a valuable property in the era of shrink-wrapped mass market software.
3.6 Hardware-Based Speculation
As we try to exploit more instruction-level parallelism, maintaining control dependences becomes an increasing burden. Branch prediction reduces the direct stalls attributable to branches, but for a processor executing multiple instructions per clock, just predicting branches accurately may not be sufficient to generate the desired amount of instruction-level parallelism. A wide issue processor may need to execute a branch every clock cycle to maintain maximum performance. Hence, exploiting more parallelism requires that we overcome the limitation of control dependence.
Overcoming control dependence is done by speculating on the outcome of branches and executing the program as if our guesses were correct. This mechanism represents a subtle, but important, extension over branch prediction with dynamic scheduling. In particular, with speculation, we fetch, issue, and execute instructions, as if our branch predictions were always correct; dynamic scheduling only fetches and issues such instructions. Of course, we need mechanisms to handle the situation where the speculation is incorrect. Appendix H discusses a variety of mechanisms for supporting speculation by the compiler. In this section, we explore hardware speculation, which extends the ideas of dynamic scheduling.
Hardware-based speculation combines three key ideas: (1) dynamic branch prediction to choose which instructions to execute, (2) speculation to allow the execution of instructions before the control dependences are resolved (with the ability to undo the effects of an incorrectly speculated sequence), and (3) dynamic scheduling to deal with the scheduling of different combinations of basic blocks. (In comparison, dynamic scheduling without speculation only partially overlaps basic blocks because it requires that a branch be resolved before actually executing any instructions in the successor basic block.)
Hardware-based speculation follows the predicted flow of data values to choose when to execute instructions. This method of executing programs is essentially a data flow execution: Operations execute as soon as their operands are available.
To extend Tomasulo’s algorithm to support speculation, we must separate the bypassing of results among instructions, which is needed to execute an instruction speculatively, from the actual completion of an instruction. By making this separation, we can allow an instruction to execute and to bypass its results to other instructions, without allowing the instruction to perform any updates that cannot be undone, until we know that the instruction is no longer speculative.
Using the bypassed value is like performing a speculative register read, since we do not know whether the instruction providing the source register value is providing the correct result until the instruction is no longer speculative. When an instruction is no longer speculative, we allow it to update the register file or memory; we call this additional step in the instruction execution sequence instruction commit.
The key idea behind implementing speculation is to allow instructions to execute out of order but to force them to commit in order and to prevent any irrevocable action (such as updating state or taking an exception) until an instruction commits. Hence, when we add speculation, we need to separate the process of completing execution from instruction commit, since instructions may finish execution considerably before they are ready to commit. Adding this commit phase to the instruction execution sequence requires an additional set of hardware buffers that hold the results of instructions that have finished execution but have not committed. This hardware buffer, which we call the reorder buffer, is also used to pass results among instructions that may be speculated.
The reorder buffer (ROB) provides additional registers in the same way as the reservation stations in Tomasulo’s algorithm extend the register set. The ROB holds the result of an instruction between the time the operation associated with the instruction completes and the time the instruction commits. Hence, the ROB is a source of operands for instructions, just as the reservation stations provide operands in Tomasulo’s algorithm. The key difference is that in Tomasulo’s algorithm, once an instruction writes its result, any subsequently issued instructions will find the result in the register file. With speculation, the register file is not updated until the instruction commits (and we know definitively that the instruction should execute); thus, the ROB supplies operands in the interval between completion of instruction execution and instruction commit. The ROB is similar to the store buffer in Tomasulo’s algorithm, and we integrate the function of the store buffer into the ROB for simplicity.
Each entry in the ROB contains four fields: the instruction type, the destination field, the value field, and the ready field. The instruction type field indicates whether the instruction is a branch (and has no destination result), a store (which has a memory address destination), or a register operation (ALU operation or load, which has register destinations). The destination field supplies the register number (for loads and ALU operations) or the memory address (for stores) where the instruction result should be written. The value field is used to hold the value of the instruction result until the instruction commits. We will see an example of ROB entries shortly. Finally, the ready field indicates that the instruction has completed execution, and the value is ready.
Figure 3.11 shows the hardware structure of the processor including the ROB. The ROB subsumes the store buffers. Stores still execute in two steps, but the second step is performed by instruction commit. Although the renaming function of the reservation stations is replaced by the ROB, we still need a place to buffer operations (and operands) between the time they issue and the time they begin execution. This function is still provided by the reservation stations. Since every instruction has a position in the ROB until it commits, we tag a result using the ROB entry number rather than using the reservation station number. This tagging requires that the ROB assigned for an instruction must be tracked in the reservation station. Later in this section, we will explore an alternative implementation that uses extra registers for renaming and a queue that replaces the ROB to decide when instructions can commit.
Figure 3.11 The basic structure of a FP unit using Tomasulo’s algorithm and extended to handle speculation. Comparing this to Figure 3.6 on page 173, which implemented Tomasulo’s algorithm, the major change is the addition of the ROB and the elimination of the store buffer, whose function is integrated into the ROB. This mechanism can be extended to multiple issue by making the CDB wider to allow for multiple completions per clock.
Here are the four steps involved in instruction execution:
1. Issue—Get an instruction from the instruction queue. Issue the instruction if there is an empty reservation station and an empty slot in the ROB; send the operands to the reservation station if they are available in either the registers or the ROB. Update the control entries to indicate the buffers are in use. The number of the ROB entry allocated for the result is also sent to the reservation station, so that the number can be used to tag the result when it is placed on the CDB. If either all reservations are full or the ROB is full, then instruction issue is stalled until both have available entries.
2. Execute—If one or more of the operands is not yet available, monitor the CDB while waiting for the register to be computed. This step checks for RAW hazards. When both operands are available at a reservation station, execute the operation. Instructions may take multiple clock cycles in this stage, and loads still require two steps in this stage. Stores need only have the base register available at this step, since execution for a store at this point is only effective address calculation.
3. Write result—When the result is available, write it on the CDB (with the ROB tag sent when the instruction issued) and from the CDB into the ROB, as well as to any reservation stations waiting for this result. Mark the reservation station as available. Special actions are required for store instructions. If the value to be stored is available, it is written into the Value field of the ROB entry for the store. If the value to be stored is not available yet, the CDB must be monitored until that value is broadcast, at which time the Value field of the ROB entry of the store is updated. For simplicity we assume that this occurs during the write results stage of a store; we discuss relaxing this requirement later.
4. Commit—This is the final stage of completing an instruction, after which only its result remains. (Some processors call this commit phase “completion” or “graduation.”) There are three different sequences of actions at commit depending on whether the committing instruction is a branch with an incorrect prediction, a store, or any other instruction (normal commit). The normal commit case occurs when an instruction reaches the head of the ROB and its result is present in the buffer; at this point, the processor updates the register with the result and removes the instruction from the ROB. Committing a store is similar except that memory is updated rather than a result register. When a branch with incorrect prediction reaches the head of the ROB, it indicates that the speculation was wrong. The ROB is flushed and execution is restarted at the correct successor of the branch. If the branch was correctly predicted, the branch is finished.
Once an instruction commits, its entry in the ROB is reclaimed and the register or memory destination is updated, eliminating the need for the ROB entry. If the ROB fills, we simply stop issuing instructions until an entry is made free. Now, let’s examine how this scheme would work with the same example we used for Tomasulo’s algorithm.
Example
Assume the same latencies for the floating-point functional units as in earlier examples: add is 2 clock cycles, multiply is 6 clock cycles, and divide is 12 clock cycles. Using the code segment below, the same one we used to generate Figure 3.8, show what the status tables look like when the MUL.D is ready to go to commit.
L.D F6,32(R2)
L.D F2,44(R3)
MUL.D F0,F2,F4
SUB.D F8,F2,F6
DIV.D F10,F0,F6
ADD.D F6,F8,F2
Answer
Figure 3.12 shows the result in the three tables. Notice that although the SUB.D instruction has completed execution, it does not commit until the MUL.D commits. The reservation stations and register status field contain the same basic information that they did for Tomasulo’s algorithm (see page 176 for a description of those fields). The differences are that reservation station numbers are replaced with ROB entry numbers in the Qj and Qk fields, as well as in the register status fields, and we have added the Dest field to the reservation stations. The Dest field designates the ROB entry that is the destination for the result produced by this reservation station entry.
Figure 3.12 At the time the MUL.D is ready to commit, only the two L.D instructions have committed, although several others have completed execution. The MUL.D is at the head of the ROB, and the two L.D instructions are there only to ease understanding. The SUB.D and ADD.D instructions will not commit until the MUL.D instruction commits, although the results of the instructions are available and can be used as sources for other instructions. The DIV.D is in execution, but has not completed solely due to its longer latency than MUL.D. The Value column indicates the value being held; the format #X is used to refer to a value field of ROB entry X. Reorder buffers 1 and 2 are actually completed but are shown for informational purposes. We do not show the entries for the load/store queue, but these entries are kept in order.
The above example illustrates the key important difference between a processor with speculation and a processor with dynamic scheduling. Compare the content of Figure 3.12 with that of Figure 3.8 on page 179, which shows the same code sequence in operation on a processor with Tomasulo’s algorithm. The key difference is that, in the example above, no instruction after the earliest uncompleted instruction (MUL.D above) is allowed to complete. In contrast, in Figure 3.8 the SUB.D and ADD.D instructions have also completed.
One implication of this difference is that the processor with the ROB can dynamically execute code while maintaining a precise interrupt model. For example, if the MUL.D instruction caused an interrupt, we could simply wait until it reached the head of the ROB and take the interrupt, flushing any other pending instructions from the ROB. Because instruction commit happens in order, this yields a precise exception.
By contrast, in the example using Tomasulo’s algorithm, the SUB.D and ADD.D instructions could both complete before the MUL.D raised the exception. The result is that the registers F8 and F6 (destinations of the SUB.D and ADD.D instructions) could be overwritten, and the interrupt would be imprecise.
Some users and architects have decided that imprecise floating-point exceptions are acceptable in high-performance processors, since the program will likely terminate; see Appendix J for further discussion of this topic. Other types of exceptions, such as page faults, are much more difficult to accommodate if they are imprecise, since the program must transparently resume execution after handling such an exception.
The use of a ROB with in-order instruction commit provides precise exceptions, in addition to supporting speculative execution, as the next example shows.
Example
Consider the code example used earlier for Tomasulo’s algorithm and shown in Figure 3.10 in execution:
Loop: L.D F0,0(R1)
MUL.D F4,F0,F2
S.D F4,0(R1)
DADDIU R1,R1,#−8
BNE R1,R2,Loop ;branches if R1|R2
Assume that we have issued all the instructions in the loop twice. Let’s also assume that the L.D and MUL.D from the first iteration have committed and all other instructions have completed execution. Normally, the store would wait in the ROB for both the effective address operand (R1 in this example) and the value (F4 in this example). Since we are only considering the floating-point pipeline, assume the effective address for the store is computed by the time the instruction is issued.
Answer
Figure 3.13 shows the result in two tables.
Figure 3.13 Only the L.D and MUL.D instructions have committed, although all the others have completed execution. Hence, no reservation stations are busy and none is shown. The remaining instructions will be committed as quickly as possible. The first two reorder buffers are empty, but are shown for completeness.
Because neither the register values nor any memory values are actually written until an instruction commits, the processor can easily undo its speculative actions when a branch is found to be mispredicted. Suppose that the branch BNE is not taken the first time in Figure 3.13. The instructions prior to the branch will simply commit when each reaches the head of the ROB; when the branch reaches the head of that buffer, the buffer is simply cleared and the processor begins fetching instructions from the other path.
In practice, processors that speculate try to recover as early as possible after a branch is mispredicted. This recovery can be done by clearing the ROB for all entries that appear after the mispredicted branch, allowing those that are before the branch in the ROB to continue, and restarting the fetch at the correct branch successor. In speculative processors, performance is more sensitive to the branch prediction, since the impact of a misprediction will be higher. Thus, all the aspects of handling branches—prediction accuracy, latency of misprediction detection, and misprediction recovery time—increase in importance.
Exceptions are handled by not recognizing the exception until it is ready to commit. If a speculated instruction raises an exception, the exception is recorded in the ROB. If a branch misprediction arises and the instruction should not have been executed, the exception is flushed along with the instruction when the ROB is cleared. If the instruction reaches the head of the ROB, then we know it is no longer speculative and the exception should really be taken. We can also try to handle exceptions as soon as they arise and all earlier branches are resolved, but this is more challenging in the case of exceptions than for branch mispredict and, because it occurs less frequently, not as critical.
Figure 3.14 shows the steps of execution for an instruction, as well as the conditions that must be satisfied to proceed to the step and the actions taken. We show the case where mispredicted branches are not resolved until commit. Although speculation seems like a simple addition to dynamic scheduling, a comparison of Figure 3.14 with the comparable figure for Tomasulo’s algorithm in Figure 3.9 shows that speculation adds significant complications to the control. In addition, remember that branch mispredictions are somewhat more complex as well.
Figure 3.14 Steps in the algorithm and what is required for each step. For the issuing instruction, rd is the destination, rs and rt are the sources, r is the reservation station allocated, b is the assigned ROB entry, and h is the head entry of the ROB. RS is the reservation station data structure. The value returned by a reservation station is called the result. RegisterStat is the register data structure, Regs represents the actual registers, and ROB is the reorder buffer data structure.
There is an important difference in how stores are handled in a speculative processor versus in Tomasulo’s algorithm. In Tomasulo’s algorithm, a store can update memory when it reaches write result (which ensures that the effective address has been calculated) and the data value to store is available. In a speculative processor, a store updates memory only when it reaches the head of the ROB. This difference ensures that memory is not updated until an instruction is no longer speculative.
Figure 3.14 has one significant simplification for stores, which is unneeded in practice. Figure 3.14 requires stores to wait in the write result stage for the register source operand whose value is to be stored; the value is then moved from the Vk field of the store’s reservation station to the Value field of the store’s ROB entry. In reality, however, the value to be stored need not arrive until just before the store commits and can be placed directly into the store’s ROB entry by the sourcing instruction. This is accomplished by having the hardware track when the source value to be stored is available in the store’s ROB entry and searching the ROB on every instruction completion to look for dependent stores.
This addition is not complicated, but adding it has two effects: We would need to add a field to the ROB, and Figure 3.14, which is already in a small font, would be even longer! Although Figure 3.14 makes this simplification, in our examples, we will allow the store to pass through the write result stage and simply wait for the value to be ready when it commits.
Like Tomasulo’s algorithm, we must avoid hazards through memory. WAW and WAR hazards through memory are eliminated with speculation because the actual updating of memory occurs in order, when a store is at the head of the ROB, and, hence, no earlier loads or stores can still be pending. RAW hazards through memory are maintained by two restrictions:
1. Not allowing a load to initiate the second step of its execution if any active ROB entry occupied by a store has a Destination field that matches the value of the A field of the load.
2. Maintaining the program order for the computation of an effective address of a load with respect to all earlier stores.
Together, these two restrictions ensure that any load that accesses a memory location written to by an earlier store cannot perform the memory access until the store has written the data. Some speculative processors will actually bypass the value from the store to the load directly, when such a RAW hazard occurs. Another approach is to predict potential collisions using a form of value prediction; we consider this in Section 3.9.
Although this explanation of speculative execution has focused on floating point, the techniques easily extend to the integer registers and functional units. Indeed, speculation may be more useful in integer programs, since such programs tend to have code where the branch behavior is less predictable. Additionally, these techniques can be extended to work in a multiple-issue processor by allowing multiple instructions to issue and commit every clock. In fact, speculation is probably most interesting in such processors, since less ambitious techniques can probably exploit sufficient ILP within basic blocks when assisted by a compiler.
3.7 Exploiting ILP Using Multiple Issue and Static Scheduling
The techniques of the preceding sections can be used to eliminate data, control stalls, and achieve an ideal CPI of one. To improve performance further we would like to decrease the CPI to less than one, but the CPI cannot be reduced below one if we issue only one instruction every clock cycle.
The goal of the multiple-issue processors, discussed in the next few sections, is to allow multiple instructions to issue in a clock cycle. Multiple-issue processors come in three major flavors:
The two types of superscalar processors issue varying numbers of instructions per clock and use in-order execution if they are statically scheduled or out-of-order execution if they are dynamically scheduled.
VLIW processors, in contrast, issue a fixed number of instructions formatted either as one large instruction or as a fixed instruction packet with the parallelism among instructions explicitly indicated by the instruction. VLIW processors are inherently statically scheduled by the compiler. When Intel and HP created the IA-64 architecture, described in Appendix H, they also introduced the name EPIC—explicitly parallel instruction computer—for this architectural style.
Although statically scheduled superscalars issue a varying rather than a fixed number of instructions per clock, they are actually closer in concept to VLIWs, since both approaches rely on the compiler to schedule code for the processor. Because of the diminishing advantages of a statically scheduled superscalar as the issue width grows, statically scheduled superscalars are used primarily for narrow issue widths, normally just two instructions. Beyond that width, most designers choose to implement either a VLIW or a dynamically scheduled superscalar. Because of the similarities in hardware and required compiler technology, we focus on VLIWs in this section. The insights of this section are easily extrapolated to a statically scheduled superscalar.
Figure 3.15 summarizes the basic approaches to multiple issue and their distinguishing characteristics and shows processors that use each approach.
Figure 3.15 The five primary approaches in use for multiple-issue processors and the primary characteristics that distinguish them. This chapter has focused on the hardware-intensive techniques, which are all some form of superscalar. Appendix H focuses on compiler-based approaches. The EPIC approach, as embodied in the IA-64 architecture, extends many of the concepts of the early VLIW approaches, providing a blend of static and dynamic approaches.
The Basic VLIW Approach
VLIWs use multiple, independent functional units. Rather than attempting to issue multiple, independent instructions to the units, a VLIW packages the multiple operations into one very long instruction, or requires that the instructions in the issue packet satisfy the same constraints. Since there is no fundamental difference in the two approaches, we will just assume that multiple operations are placed in one instruction, as in the original VLIW approach.
Since the advantage of a VLIW increases as the maximum issue rate grows, we focus on a wider issue processor. Indeed, for simple two-issue processors, the overhead of a superscalar is probably minimal. Many designers would probably argue that a four-issue processor has manageable overhead, but as we will see later in this chapter, the growth in overhead is a major factor limiting wider issue processors.
Let’s consider a VLIW processor with instructions that contain five operations, including one integer operation (which could also be a branch), two floating-point operations, and two memory references. The instruction would have a set of fields for each functional unit—perhaps 16 to 24 bits per unit, yielding an instruction length of between 80 and 120 bits. By comparison, the Intel Itanium 1 and 2 contain six operations per instruction packet (i.e., they allow concurrent issue of two three-instruction bundles, as Appendix H describes).
To keep the functional units busy, there must be enough parallelism in a code sequence to fill the available operation slots. This parallelism is uncovered by unrolling loops and scheduling the code within the single larger loop body. If the unrolling generates straight-line code, then local scheduling techniques, which operate on a single basic block, can be used. If finding and exploiting the parallelism require scheduling code across branches, a substantially more complex global scheduling algorithm must be used. Global scheduling algorithms are not only more complex in structure, but they also must deal with significantly more complicated trade-offs in optimization, since moving code across branches is expensive.
In Appendix H, we will discuss trace scheduling, one of these global scheduling techniques developed specifically for VLIWs; we will also explore special hardware support that allows some conditional branches to be eliminated, extending the usefulness of local scheduling and enhancing the performance of global scheduling.
For now, we will rely on loop unrolling to generate long, straight-line code sequences, so that we can use local scheduling to build up VLIW instructions and focus on how well these processors operate.
Example
Suppose we have a VLIW that could issue two memory references, two FP operations, and one integer operation or branch in every clock cycle. Show an unrolled version of the loop x[i] = x[i] + s (see page 158 for the MIPS code) for such a processor. Unroll as many times as necessary to eliminate any stalls. Ignore delayed branches.
Answer
Figure 3.16 shows the code. The loop has been unrolled to make seven copies of the body, which eliminates all stalls (i.e., completely empty issue cycles), and runs in 9 cycles. This code yields a running rate of seven results in 9 cycles, or 1.29 cycles per result, nearly twice as fast as the two-issue superscalar of Section 3.2 that used unrolled and scheduled code.
Figure 3.16 VLIW instructions that occupy the inner loop and replace the unrolled sequence. This code takes 9 cycles assuming no branch delay; normally the branch delay would also need to be scheduled. The issue rate is 23 operations in 9 clock cycles, or 2.5 operations per cycle. The efficiency, the percentage of available slots that contained an operation, is about 60%. To achieve this issue rate requires a larger number of registers than MIPS would normally use in this loop. The VLIW code sequence above requires at least eight FP registers, while the same code sequence for the base MIPS processor can use as few as two FP registers or as many as five when unrolled and scheduled.
For the original VLIW model, there were both technical and logistical problems that make the approach less efficient. The technical problems are the increase in code size and the limitations of lockstep operation. Two different elements combine to increase code size substantially for a VLIW. First, generating enough operations in a straight-line code fragment requires ambitiously unrolling loops (as in earlier examples), thereby increasing code size. Second, whenever instructions are not full, the unused functional units translate to wasted bits in the instruction encoding. In Appendix H, we examine software scheduling approaches, such as software pipelining, that can achieve the benefits of unrolling without as much code expansion.
To combat this code size increase, clever encodings are sometimes used. For example, there may be only one large immediate field for use by any functional unit. Another technique is to compress the instructions in main memory and expand them when they are read into the cache or are decoded. In Appendix H, we show other techniques, as well as document the significant code expansion seen on IA-64.
Early VLIWs operated in lockstep; there was no hazard-detection hardware at all. This structure dictated that a stall in any functional unit pipeline must cause the entire processor to stall, since all the functional units must be kept synchronized. Although a compiler may be able to schedule the deterministic functional units to prevent stalls, predicting which data accesses will encounter a cache stall and scheduling them are very difficult. Hence, caches needed to be blocking and to cause all the functional units to stall. As the issue rate and number of memory references becomes large, this synchronization restriction becomes unacceptable. In more recent processors, the functional units operate more independently, and the compiler is used to avoid hazards at issue time, while hardware checks allow for unsynchronized execution once instructions are issued.
Binary code compatibility has also been a major logistical problem for VLIWs. In a strict VLIW approach, the code sequence makes use of both the instruction set definition and the detailed pipeline structure, including both functional units and their latencies. Thus, different numbers of functional units and unit latencies require different versions of the code. This requirement makes migrating between successive implementations, or between implementations with different issue widths, more difficult than it is for a superscalar design. Of course, obtaining improved performance from a new superscalar design may require recompilation. Nonetheless, the ability to run old binary files is a practical advantage for the superscalar approach.
The EPIC approach, of which the IA-64 architecture is the primary example, provides solutions to many of the problems encountered in early VLIW designs, including extensions for more aggressive software speculation and methods to overcome the limitation of hardware dependence while preserving binary compatibility.
The major challenge for all multiple-issue processors is to try to exploit large amounts of ILP. When the parallelism comes from unrolling simple loops in FP programs, the original loop probably could have been run efficiently on a vector processor (described in the next chapter). It is not clear that a multiple-issue processor is preferred over a vector processor for such applications; the costs are similar, and the vector processor is typically the same speed or faster. The potential advantages of a multiple-issue processor versus a vector processor are their ability to extract some parallelism from less structured code and their ability to easily cache all forms of data. For these reasons multiple-issue approaches have become the primary method for taking advantage of instruction-level parallelism, and vectors have become primarily an extension to these processors.
3.8 Exploiting ILP Using Dynamic Scheduling, Multiple Issue, and Speculation
So far, we have seen how the individual mechanisms of dynamic scheduling, multiple issue, and speculation work. In this section, we put all three together, which yields a microarchitecture quite similar to those in modern microprocessors. For simplicity, we consider only an issue rate of two instructions per clock, but the concepts are no different from modern processors that issue three or more instructions per clock.
Let’s assume we want to extend Tomasulo’s algorithm to support multiple-issue superscalar pipeline with separate integer, load/store, and floating-point units (both FP multiply and FP add), each of which can initiate an operation on every clock. We do not want to issue instructions to the reservation stations out of order, since this could lead to a violation of the program semantics. To gain the full advantage of dynamic scheduling we will allow the pipeline to issue any combination of two instructions in a clock, using the scheduling hardware to actually assign operations to the integer and floating-point unit. Because the interaction of the integer and floating-point instructions is crucial, we also extend Tomasulo’s scheme to deal with both the integer and floating-point functional units and registers, as well as incorporating speculative execution. As Figure 3.17 shows, the basic organization is similar to that of a processor with speculation with one issue per clock, except that the issue and completion logic must be enhanced to allow multiple instructions to be processed per clock.
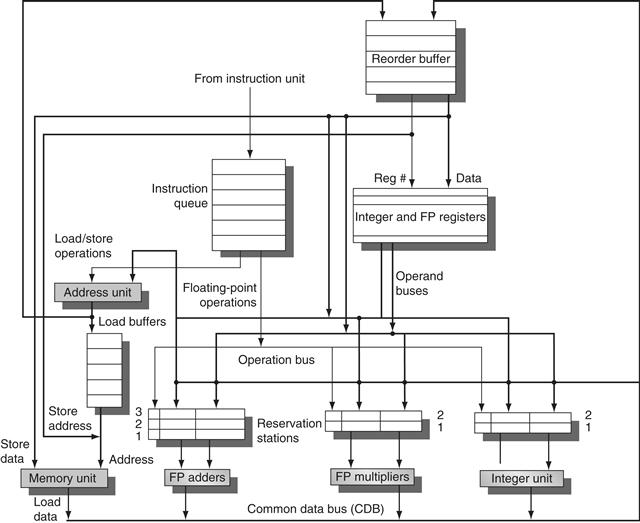
Figure 3.17 The basic organization of a multiple issue processor with speculation. In this case, the organization could allow a FP multiply, FP add, integer, and load/store to all issues simultaneously (assuming one issue per clock per functional unit). Note that several datapaths must be widened to support multiple issues: the CDB, the operand buses, and, critically, the instruction issue logic, which is not shown in this figure. The last is a difficult problem, as we discuss in the text.
Issuing multiple instructions per clock in a dynamically scheduled processor (with or without speculation) is very complex for the simple reason that the multiple instructions may depend on one another. Because of this the tables must be updated for the instructions in parallel; otherwise, the tables will be incorrect or the dependence may be lost.
Two different approaches have been used to issue multiple instructions per clock in a dynamically scheduled processor, and both rely on the observation that the key is assigning a reservation station and updating the pipeline control tables. One approach is to run this step in half a clock cycle, so that two instructions can be processed in one clock cycle; this approach cannot be easily extended to handle four instructions per clock, unfortunately.
A second alternative is to build the logic necessary to handle two or more instructions at once, including any possible dependences between the instructions. Modern superscalar processors that issue four or more instructions per clock may include both approaches: They both pipeline and widen the issue logic. A key observation is that we cannot simply pipeline away the problem. By making instruction issues take multiple clocks because new instructions are issuing every clock cycle, we must be able to assign the reservation station and to update the pipeline tables, so that a dependent instruction issuing on the next clock can use the updated information.
This issue step is one of the most fundamental bottlenecks in dynamically scheduled superscalars. To illustrate the complexity of this process, Figure 3.18 shows the issue logic for one case: issuing a load followed by a dependent FP operation. The logic is based on that in Figure 3.14 on page 191, but represents only one case. In a modern superscalar, every possible combination of dependent instructions that is allowed to issue in the same clock cycle must be considered. Since the number of possibilities climbs as the square of the number of instructions that can be issued in a clock, the issue step is a likely bottleneck for attempts to go beyond four instructions per clock.
Figure 3.18 The issue steps for a pair of dependent instructions (called 1 and 2) where instruction 1 is FP load and instruction 2 is an FP operation whose first operand is the result of the load instruction; r1 and r2 are the assigned reservation stations for the instructions; and b1 and b2 are the assigned reorder buffer entries. For the issuing instructions, rd1 and rd2 are the destinations; rs1, rs2, and rt2 are the sources (the load only has one source); r1 and r2 are the reservation stations allocated; and b1 and b2 are the assigned ROB entries. RS is the reservation station data structure. RegisterStat is the register data structure, Regs represents the actual registers, and ROB is the reorder buffer data structure. Notice that we need to have assigned reorder buffer entries for this logic to operate properly and recall that all these updates happen in a single clock cycle in parallel, not sequentially!
We can generalize the detail of Figure 3.18 to describe the basic strategy for updating the issue logic and the reservation tables in a dynamically scheduled superscalar with up to n issues per clock as follows:
1. Assign a reservation station and a reorder buffer for every instruction that might be issued in the next issue bundle. This assignment can be done before the instruction types are known, by simply preallocating the reorder buffer entries sequentially to the instructions in the packet using n available reorder buffer entries and by ensuring that enough reservation stations are available to issue the whole bundle, independent of what it contains. By limiting the number of instructions of a given class (say, one FP, one integer, one load, one store), the necessary reservation stations can be preallocated. Should sufficient reservation stations not be available (such as when the next few instructions in the program are all of one instruction type), the bundle is broken, and only a subset of the instructions, in the original program order, is issued. The remainder of the instructions in the bundle can be placed in the next bundle for potential issue.
2. Analyze all the dependences among the instructions in the issue bundle.
3. If an instruction in the bundle depends on an earlier instruction in the bundle, use the assigned reorder buffer number to update the reservation table for the dependent instruction. Otherwise, use the existing reservation table and reorder buffer information to update the reservation table entries for the issuing instruction.
Of course, what makes the above very complicated is that it is all done in parallel in a single clock cycle!
At the back-end of the pipeline, we must be able to complete and commit multiple instructions per clock. These steps are somewhat easier than the issue problems since multiple instructions that can actually commit in the same clock cycle must have already dealt with and resolved any dependences. As we will see, designers have figured out how to handle this complexity: The Intel i7, which we examine in Section 3.13, uses essentially the scheme we have described for speculative multiple issue, including a large number of reservation stations, a reorder buffer, and a load and store buffer that is also used to handle nonblocking cache misses.
From a performance viewpoint, we can show how the concepts fit together with an example.
Example
Consider the execution of the following loop, which increments each element of an integer array, on a two-issue processor, once without speculation and once with speculation:
Loop: LD R2,0(R1) ;R2=array element
DADDIU R2,R2,#1 ;increment R2
SD R2,0(R1) ;store result
DADDIU R1,R1,#8 ;increment pointer
BNE R2,R3,LOOP ;branch if not last element
Assume that there are separate integer functional units for effective address calculation, for ALU operations, and for branch condition evaluation. Create a table for the first three iterations of this loop for both processors. Assume that up to two instructions of any type can commit per clock.
Answer
Figures 3.19 and 3.20 show the performance for a two-issue dynamically scheduled processor, without and with speculation. In this case, where a branch can be a critical performance limiter, speculation helps significantly. The third branch in the speculative processor executes in clock cycle 13, while it executes in clock cycle 19 on the nonspeculative pipeline. Because the completion rate on the nonspeculative pipeline is falling behind the issue rate rapidly, the nonspeculative pipeline will stall when a few more iterations are issued. The performance of the nonspeculative processor could be improved by allowing load instructions to complete effective address calculation before a branch is decided, but unless speculative memory accesses are allowed, this improvement will gain only 1 clock per iteration.
Figure 3.19 The time of issue, execution, and writing result for a dual-issue version of our pipeline without speculation. Note that the LD following the BNE cannot start execution earlier because it must wait until the branch outcome is determined. This type of program, with data-dependent branches that cannot be resolved earlier, shows the strength of speculation. Separate functional units for address calculation, ALU operations, and branch-condition evaluation allow multiple instructions to execute in the same cycle. Figure 3.20 shows this example with speculation.
Figure 3.20 The time of issue, execution, and writing result for a dual-issue version of our pipeline with speculation. Note that the LD following the BNE can start execution early because it is speculative.
This example clearly shows how speculation can be advantageous when there are data-dependent branches, which otherwise would limit performance. This advantage depends, however, on accurate branch prediction. Incorrect speculation does not improve performance; in fact, it typically harms performance and, as we shall see, dramatically lowers energy efficiency.
3.9 Advanced Techniques for Instruction Delivery and Speculation
In a high-performance pipeline, especially one with multiple issues, predicting branches well is not enough; we actually have to be able to deliver a high-bandwidth instruction stream. In recent multiple-issue processors, this has meant delivering 4 to 8 instructions every clock cycle. We look at methods for increasing instruction delivery bandwidth first. We then turn to a set of key issues in implementing advanced speculation techniques, including the use of register renaming versus reorder buffers, the aggressiveness of speculation, and a technique called value prediction, which attempts to predict the result of a computation and which could further enhance ILP.
Increasing Instruction Fetch Bandwidth
A multiple-issue processor will require that the average number of instructions fetched every clock cycle be at least as large as the average throughput. Of course, fetching these instructions requires wide enough paths to the instruction cache, but the most difficult aspect is handling branches. In this section, we look at two methods for dealing with branches and then discuss how modern processors integrate the instruction prediction and prefetch functions.
Branch-Target Buffers
To reduce the branch penalty for our simple five-stage pipeline, as well as for deeper pipelines, we must know whether the as-yet-undecoded instruction is a branch and, if so, what the next program counter (PC) should be. If the instruction is a branch and we know what the next PC should be, we can have a branch penalty of zero. A branch-prediction cache that stores the predicted address for the next instruction after a branch is called a branch-target buffer or branch-target cache. Figure 3.21 shows a branch-target buffer.
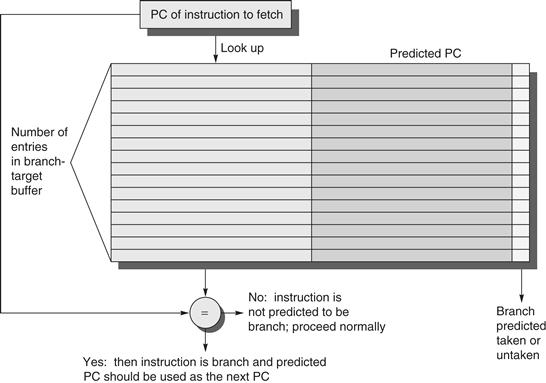
Figure 3.21 A branch-target buffer. The PC of the instruction being fetched is matched against a set of instruction addresses stored in the first column; these represent the addresses of known branches. If the PC matches one of these entries, then the instruction being fetched is a taken branch, and the second field, predicted PC, contains the prediction for the next PC after the branch. Fetching begins immediately at that address. The third field, which is optional, may be used for extra prediction state bits.
Because a branch-target buffer predicts the next instruction address and will send it out before decoding the instruction, we must know whether the fetched instruction is predicted as a taken branch. If the PC of the fetched instruction matches an address in the prediction buffer, then the corresponding predicted PC is used as the next PC. The hardware for this branch-target buffer is essentially identical to the hardware for a cache.
If a matching entry is found in the branch-target buffer, fetching begins immediately at the predicted PC. Note that unlike a branch-prediction buffer, the predictive entry must be matched to this instruction because the predicted PC will be sent out before it is known whether this instruction is even a branch. If the processor did not check whether the entry matched this PC, then the wrong PC would be sent out for instructions that were not branches, resulting in worse performance. We only need to store the predicted-taken branches in the branch-target buffer, since an untaken branch should simply fetch the next sequential instruction, as if it were not a branch.
Figure 3.22 shows the steps when using a branch-target buffer for a simple five-stage pipeline. From this figure we can see that there will be no branch delay if a branch-prediction entry is found in the buffer and the prediction is correct. Otherwise, there will be a penalty of at least two clock cycles. Dealing with the mispredictions and misses is a significant challenge, since we typically will have to halt instruction fetch while we rewrite the buffer entry. Thus, we would like to make this process fast to minimize the penalty.
Figure 3.22 The steps involved in handling an instruction with a branch-target buffer.
To evaluate how well a branch-target buffer works, we first must determine the penalties in all possible cases. Figure 3.23 contains this information for a simple five-stage pipeline.
Figure 3.23 Penalties for all possible combinations of whether the branch is in the buffer and what it actually does, assuming we store only taken branches in the buffer. There is no branch penalty if everything is correctly predicted and the branch is found in the target buffer. If the branch is not correctly predicted, the penalty is equal to one clock cycle to update the buffer with the correct information (during which an instruction cannot be fetched) and one clock cycle, if needed, to restart fetching the next correct instruction for the branch. If the branch is not found and taken, a two-cycle penalty is encountered, during which time the buffer is updated.