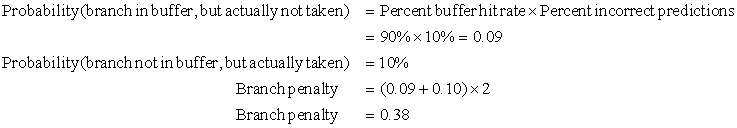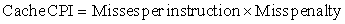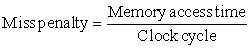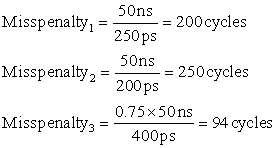One variation on the branch-target buffer is to store one or more target instructions instead of, or in addition to, the predicted target address. This variation has two potential advantages. First, it allows the branch-target buffer access to take longer than the time between successive instruction fetches, possibly allowing a larger branch-target buffer. Second, buffering the actual target instructions allows us to perform an optimization called branch folding. Branch folding can be used to obtain 0-cycle unconditional branches and sometimes 0-cycle conditional branches.
Consider a branch-target buffer that buffers instructions from the predicted path and is being accessed with the address of an unconditional branch. The only function of the unconditional branch is to change the PC. Thus, when the branch-target buffer signals a hit and indicates that the branch is unconditional, the pipeline can simply substitute the instruction from the branch-target buffer in place of the instruction that is returned from the cache (which is the unconditional branch). If the processor is issuing multiple instructions per cycle, then the buffer will need to supply multiple instructions to obtain the maximum benefit. In some cases, it may be possible to eliminate the cost of a conditional branch.
Return Address Predictors
As we try to increase the opportunity and accuracy of speculation we face the challenge of predicting indirect jumps, that is, jumps whose destination address varies at runtime. Although high-level language programs will generate such jumps for indirect procedure calls, select or case statements, and FORTRAN-computed gotos, the vast majority of the indirect jumps come from procedure returns. For example, for the SPEC95 benchmarks, procedure returns account for more than 15% of the branches and the vast majority of the indirect jumps on average. For object-oriented languages such as C++ and Java, procedure returns are even more frequent. Thus, focusing on procedure returns seems appropriate.
Though procedure returns can be predicted with a branch-target buffer, the accuracy of such a prediction technique can be low if the procedure is called from multiple sites and the calls from one site are not clustered in time. For example, in SPEC CPU95, an aggressive branch predictor achieves an accuracy of less than 60% for such return branches. To overcome this problem, some designs use a small buffer of return addresses operating as a stack. This structure caches the most recent return addresses: pushing a return address on the stack at a call and popping one off at a return. If the cache is sufficiently large (i.e., as large as the maximum call depth), it will predict the returns perfectly. Figure 3.24 shows the performance of such a return buffer with 0 to 16 elements for a number of the SPEC CPU95 benchmarks. We will use a similar return predictor when we examine the studies of ILP in Section 3.10. Both the Intel Core processors and the AMD Phenom processors have return address predictors.
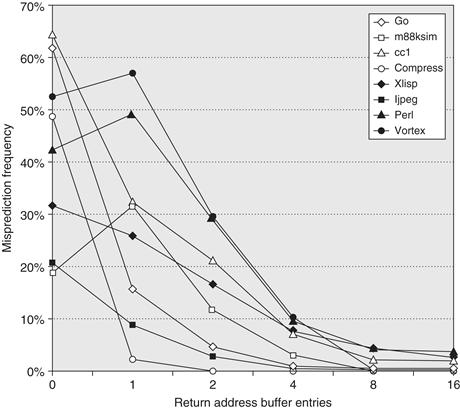
Figure 3.24 Prediction accuracy for a return address buffer operated as a stack on a number of SPEC CPU95 benchmarks. The accuracy is the fraction of return addresses predicted correctly. A buffer of 0 entries implies that the standard branch prediction is used. Since call depths are typically not large, with some exceptions, a modest buffer works well. These data come from Skadron et al. [1999] and use a fix-up mechanism to prevent corruption of the cached return addresses.
Integrated Instruction Fetch Units
To meet the demands of multiple-issue processors, many recent designers have chosen to implement an integrated instruction fetch unit as a separate autonomous unit that feeds instructions to the rest of the pipeline. Essentially, this amounts to recognizing that characterizing instruction fetch as a simple single pipe stage given the complexities of multiple issue is no longer valid.
Instead, recent designs have used an integrated instruction fetch unit that integrates several functions:
1. Integrated branch prediction—The branch predictor becomes part of the instruction fetch unit and is constantly predicting branches, so as to drive the fetch pipeline.
2. Instruction prefetch—To deliver multiple instructions per clock, the instruction fetch unit will likely need to fetch ahead. The unit autonomously manages the prefetching of instructions (see Chapter 2 for a discussion of techniques for doing this), integrating it with branch prediction.
3. Instruction memory access and buffering—When fetching multiple instructions per cycle a variety of complexities are encountered, including the difficulty that fetching multiple instructions may require accessing multiple cache lines. The instruction fetch unit encapsulates this complexity, using prefetch to try to hide the cost of crossing cache blocks. The instruction fetch unit also provides buffering, essentially acting as an on-demand unit to provide instructions to the issue stage as needed and in the quantity needed.
Virtually all high-end processors now use a separate instruction fetch unit connected to the rest of the pipeline by a buffer containing pending instructions.
Speculation: Implementation Issues and Extensions
In this section we explore four issues that involve the design trade-offs in speculation, starting with the use of register renaming, the approach that is often used instead of a reorder buffer. We then discuss one important possible extension to speculation on control flow: an idea called value prediction.
Speculation Support: Register Renaming versus Reorder Buffers
One alternative to the use of a reorder buffer (ROB) is the explicit use of a larger physical set of registers combined with register renaming. This approach builds on the concept of renaming used in Tomasulo’s algorithm and extends it. In Tomasulo’s algorithm, the values of the architecturally visible registers (R0, …, R31 and F0, …, F31) are contained, at any point in execution, in some combination of the register set and the reservation stations. With the addition of speculation, register values may also temporarily reside in the ROB. In either case, if the processor does not issue new instructions for a period of time, all existing instructions will commit, and the register values will appear in the register file, which directly corresponds to the architecturally visible registers.
In the register-renaming approach, an extended set of physical registers is used to hold both the architecturally visible registers as well as temporary values. Thus, the extended registers replace most of the function of the ROB and the reservation stations; only a queue to ensure that instructions complete in order is needed. During instruction issue, a renaming process maps the names of architectural registers to physical register numbers in the extended register set, allocating a new unused register for the destination. WAW and WAR hazards are avoided by renaming of the destination register, and speculation recovery is handled because a physical register holding an instruction destination does not become the architectural register until the instruction commits. The renaming map is a simple data structure that supplies the physical register number of the register that currently corresponds to the specified architectural register, a function performed by the register status table in Tomasulo’s algorithm. When an instruction commits, the renaming table is permanently updated to indicate that a physical register corresponds to the actual architectural register, thus effectively finalizing the update to the processor state. Although an ROB is not necessary with register renaming, the hardware must still track instructions in a queue-like structure and update the renaming table in strict order.
An advantage of the renaming approach versus the ROB approach is that instruction commit is slightly simplified, since it requires only two simple actions: (1) record that the mapping between an architectural register number and physical register number is no longer speculative, and (2) free up any physical registers being used to hold the “older” value of the architectural register. In a design with reservation stations, a station is freed up when the instruction using it completes execution, and a ROB entry is freed up when the corresponding instruction commits.
With register renaming, deallocating registers is more complex, since before we free up a physical register, we must know that it no longer corresponds to an architectural register and that no further uses of the physical register are outstanding. A physical register corresponds to an architectural register until the architectural register is rewritten, causing the renaming table to point elsewhere. That is, if no renaming entry points to a particular physical register, then it no longer corresponds to an architectural register. There may, however, still be uses of the physical register outstanding. The processor can determine whether this is the case by examining the source register specifiers of all instructions in the functional unit queues. If a given physical register does not appear as a source and it is not designated as an architectural register, it may be reclaimed and reallocated.
Alternatively, the processor can simply wait until another instruction that writes the same architectural register commits. At that point, there can be no further uses of the older value outstanding. Although this method may tie up a physical register slightly longer than necessary, it is easy to implement and is used in most recent superscalars.
One question you may be asking is how do we ever know which registers are the architectural registers if they are constantly changing? Most of the time when the program is executing, it does not matter. There are clearly cases, however, where another process, such as the operating system, must be able to know exactly where the contents of a certain architectural register reside. To understand how this capability is provided, assume the processor does not issue instructions for some period of time. Eventually all instructions in the pipeline will commit, and the mapping between the architecturally visible registers and physical registers will become stable. At that point, a subset of the physical registers contains the architecturally visible registers, and the value of any physical register not associated with an architectural register is unneeded. It is then easy to move the architectural registers to a fixed subset of physical registers so that the values can be communicated to another process.
Both register renaming and reorder buffers continue to be used in high-end processors, which now feature the ability to have as many as 40 or 50 instructions (including loads and stores waiting on the cache) in flight. Whether renaming or a reorder buffer is used, the key complexity bottleneck for a dynamically schedule superscalar remains issuing bundles of instructions with dependences within the bundle. In particular, dependent instructions in an issue bundle must be issued with the assigned virtual registers of the instructions on which they depend. A strategy for instruction issue with register renaming similar to that used for multiple issue with reorder buffers (see page 198) can be deployed, as follows:
1. The issue logic pre-reserves enough physical registers for the entire issue bundle (say, four registers for a four-instruction bundle with at most one register result per instruction).
2. The issue logic determines what dependences exist within the bundle. If a dependence does not exist within the bundle, the register renaming structure is used to determine the physical register that holds, or will hold, the result on which instruction depends. When no dependence exists within the bundle the result is from an earlier issue bundle, and the register renaming table will have the correct register number.
3. If an instruction depends on an instruction that is earlier in the bundle, then the pre-reserved physical register in which the result will be placed is used to update the information for the issuing instruction.
Note that just as in the reorder buffer case, the issue logic must both determine dependences within the bundle and update the renaming tables in a single clock, and, as before, the complexity of doing this for a larger number of instructions per clock becomes a chief limitation in the issue width.
How Much to Speculate
One of the significant advantages of speculation is its ability to uncover events that would otherwise stall the pipeline early, such as cache misses. This potential advantage, however, comes with a significant potential disadvantage. Speculation is not free. It takes time and energy, and the recovery of incorrect speculation further reduces performance. In addition, to support the higher instruction execution rate needed to benefit from speculation, the processor must have additional resources, which take silicon area and power. Finally, if speculation causes an exceptional event to occur, such as a cache or translation lookaside buffer (TLB) miss, the potential for significant performance loss increases, if that event would not have occurred without speculation.
To maintain most of the advantage, while minimizing the disadvantages, most pipelines with speculation will allow only low-cost exceptional events (such as a first-level cache miss) to be handled in speculative mode. If an expensive exceptional event occurs, such as a second-level cache miss or a TLB miss, the processor will wait until the instruction causing the event is no longer speculative before handling the event. Although this may slightly degrade the performance of some programs, it avoids significant performance losses in others, especially those that suffer from a high frequency of such events coupled with less-than-excellent branch prediction.
In the 1990s, the potential downsides of speculation were less obvious. As processors have evolved, the real costs of speculation have become more apparent, and the limitations of wider issue and speculation have been obvious. We return to this issue shortly.
Speculating through Multiple Branches
In the examples we have considered in this chapter, it has been possible to resolve a branch before having to speculate on another. Three different situations can benefit from speculating on multiple branches simultaneously: (1) a very high branch frequency, (2) significant clustering of branches, and (3) long delays in functional units. In the first two cases, achieving high performance may mean that multiple branches are speculated, and it may even mean handling more than one branch per clock. Database programs, and other less structured integer computations, often exhibit these properties, making speculation on multiple branches important. Likewise, long delays in functional units can raise the importance of speculating on multiple branches as a way to avoid stalls from the longer pipeline delays.
Speculating on multiple branches slightly complicates the process of speculation recovery but is straightforward otherwise. As of 2011, no processor has yet combined full speculation with resolving multiple branches per cycle, and it is unlikely that the costs of doing so would be justified in terms of performance versus complexity and power.
Speculation and the Challenge of Energy Efficiency
What is the impact of speculation on energy efficiency? At first glance, one might argue that using speculation always decreases energy efficiency, since whenever speculation is wrong it consumes excess energy in two ways:
1. The instructions that were speculated and whose results were not needed generated excess work for the processor, wasting energy.
2. Undoing the speculation and restoring the state of the processor to continue execution at the appropriate address consumes additional energy that would not be needed without speculation.
Certainly, speculation will raise the power consumption and, if we could control speculation, it would be possible to measure the cost (or at least the dynamic power cost). But, if speculation lowers the execution time by more than it increases the average power consumption, then the total energy consumed may be less.
Thus, to understand the impact of speculation on energy efficiency, we need to look at how often speculation is leading to unnecessary work. If a significant number of unneeded instructions is executed, it is unlikely that speculation will improve running time by a comparable amount! Figure 3.25 shows the fraction of instructions that are executed from misspeculation. As we can see, this fraction is small in scientific code and significant (about 30% on average) in integer code. Thus, it is unlikely that speculation is energy efficient for integer applications. Designers could avoid speculation, try to reduce the misspeculation, or think about new approaches, such as only speculating on branches that are known to be highly predictable.
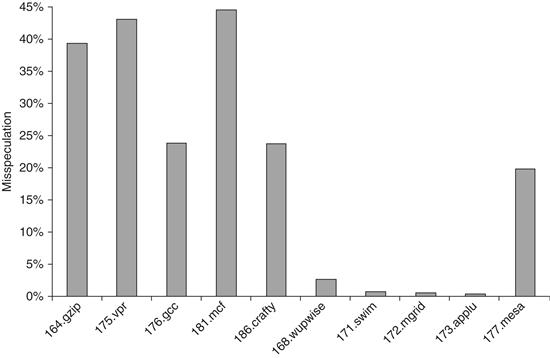
Figure 3.25 The fraction of instructions that are executed as a result of misspeculation is typically much higher for integer programs (the first five) versus FP programs (the last five).
Value Prediction
One technique for increasing the amount of ILP available in a program is value prediction. Value prediction attempts to predict the value that will be produced by an instruction. Obviously, since most instructions produce a different value every time they are executed (or at least a different value from a set of values), value prediction can have only limited success. There are, however, certain instructions for which it is easier to predict the resulting value—for example, loads that load from a constant pool or that load a value that changes infrequently. In addition, when an instruction produces a value chosen from a small set of potential values, it may be possible to predict the resulting value by correlating it with other program behavior.
Value prediction is useful if it significantly increases the amount of available ILP. This possibility is most likely when a value is used as the source of a chain of dependent computations, such as a load. Because value prediction is used to enhance speculations and incorrect speculation has detrimental performance impact, the accuracy of the prediction is critical.
Although many researchers have focused on value prediction in the past ten years, the results have never been sufficiently attractive to justify their incorporation in real processors. Instead, a simpler and older idea, related to value prediction, has been used: address aliasing prediction. Address aliasing prediction is a simple technique that predicts whether two stores or a load and a store refer to the same memory address. If two such references do not refer to the same address, then they may be safely interchanged. Otherwise, we must wait until the memory addresses accessed by the instructions are known. Because we need not actually predict the address values, only whether such values conflict, the prediction is both more stable and simpler. This limited form of address value speculation has been used in several processors already and may become universal in the future.
3.10 Studies of the Limitations of ILP
Exploiting ILP to increase performance began with the first pipelined processors in the 1960s. In the 1980s and 1990s, these techniques were key to achieving rapid performance improvements. The question of how much ILP exists was critical to our long-term ability to enhance performance at a rate that exceeds the increase in speed of the base integrated circuit technology. On a shorter scale, the critical question of what is needed to exploit more ILP is crucial to both computer designers and compiler writers. The data in this section also provide us with a way to examine the value of ideas that we have introduced in this chapter, including memory disambiguation, register renaming, and speculation.
In this section we review a portion of one of the studies done of these questions (based on Wall’s 1993 study). All of these studies of available parallelism operate by making a set of assumptions and seeing how much parallelism is available under those assumptions. The data we examine here are from a study that makes the fewest assumptions; in fact, the ultimate hardware model is probably unrealizable. Nonetheless, all such studies assume a certain level of compiler technology, and some of these assumptions could affect the results, despite the use of incredibly ambitious hardware.
As we will see, for hardware models that have reasonable cost, it is unlikely that the costs of very aggressive speculation can be justified: the inefficiencies in power and use of silicon are simply too high. While many in the research community and the major processor manufacturers were betting in favor of much greater exploitable ILP and were initially reluctant to accept this possibility, by 2005 they were forced to change their minds.
The Hardware Model
To see what the limits of ILP might be, we first need to define an ideal processor. An ideal processor is one where all constraints on ILP are removed. The only limits on ILP in such a processor are those imposed by the actual data flows through either registers or memory.
The assumptions made for an ideal or perfect processor are as follows:
1. Infinite register renaming—There are an infinite number of virtual registers available, and hence all WAW and WAR hazards are avoided and an unbounded number of instructions can begin execution simultaneously.
2. Perfect branch prediction—Branch prediction is perfect. All conditional branches are predicted exactly.
3. Perfect jump prediction—All jumps (including jump register used for return and computed jumps) are perfectly predicted. When combined with perfect branch prediction, this is equivalent to having a processor with perfect speculation and an unbounded buffer of instructions available for execution.
4. Perfect memory address alias analysis—All memory addresses are known exactly, and a load can be moved before a store provided that the addresses are not identical. Note that this implements perfect address alias analysis.
5. Perfect caches—All memory accesses take one clock cycle. In practice, superscalar processors will typically consume large amounts of ILP hiding cache misses, making these results highly optimistic.
Assumptions 2 and 3 eliminate all control dependences. Likewise, assumptions 1 and 4 eliminate all but the true data dependences. Together, these four assumptions mean that any instruction in the program’s execution can be scheduled on the cycle immediately following the execution of the predecessor on which it depends. It is even possible, under these assumptions, for the last dynamically executed instruction in the program to be scheduled on the very first cycle! Thus, this set of assumptions subsumes both control and address speculation and implements them as if they were perfect.
Initially, we examine a processor that can issue an unlimited number of instructions at once, looking arbitrarily far ahead in the computation. For all the processor models we examine, there are no restrictions on what types of instructions can execute in a cycle. For the unlimited-issue case, this means there may be an unlimited number of loads or stores issuing in one clock cycle. In addition, all functional unit latencies are assumed to be one cycle, so that any sequence of dependent instructions can issue on successive cycles. Latencies longer than one cycle would decrease the number of issues per cycle, although not the number of instructions under execution at any point. (The instructions in execution at any point are often referred to as in flight.)
Of course, this ideal processor is probably unrealizable. For example, the IBM Power7 (see Wendell et. al. [2010]) is the most advanced superscalar processor announced to date. The Power7 issues up to six instructions per clock and initiates execution on up to 8 of 12 execution units (only two of which are load/store units), supports a large set of renaming registers (allowing hundreds of instructions to be in flight), uses a large aggressive branch predictor, and employs dynamic memory disambiguation. The Power7 continued the move toward using more thread-level parallelism by increasing the width of simultaneous multithreading (SMT) support (to four threads per core) and the number of cores per chip to eight. After looking at the parallelism available for the perfect processor, we will examine what might be achievable in any processor likely to be designed in the near future.
To measure the available parallelism, a set of programs was compiled and optimized with the standard MIPS optimizing compilers. The programs were instrumented and executed to produce a trace of the instruction and data references. Every instruction in the trace is then scheduled as early as possible, limited only by the data dependences. Since a trace is used, perfect branch prediction and perfect alias analysis are easy to do. With these mechanisms, instructions may be scheduled much earlier than they would otherwise, moving across large numbers of instructions on which they are not data dependent, including branches, since branches are perfectly predicted.
Figure 3.26 shows the average amount of parallelism available for six of the SPEC92 benchmarks. Throughout this section the parallelism is measured by the average instruction issue rate. Remember that all instructions have a one-cycle latency; a longer latency would reduce the average number of instructions per clock. Three of these benchmarks (fpppp, doduc, and tomcatv) are floating-point intensive, and the other three are integer programs. Two of the floating-point benchmarks (fpppp and tomcatv) have extensive parallelism, which could be exploited by a vector computer or by a multiprocessor (the structure in fpppp is quite messy, however, since some hand transformations have been done on the code). The doduc program has extensive parallelism, but the parallelism does not occur in simple parallel loops as it does in fpppp and tomcatv. The program li is a LISP interpreter that has many short dependences.
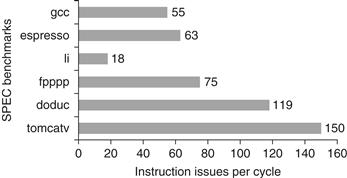
Figure 3.26 ILP available in a perfect processor for six of the SPEC92 benchmarks. The first three programs are integer programs, and the last three are floating-point programs. The floating-point programs are loop intensive and have large amounts of loop-level parallelism.
Limitations on ILP for Realizable Processors
In this section we look at the performance of processors with ambitious levels of hardware support equal to or better than what is available in 2011 or, given the events and lessons of the last decade, likely to be available in the near future. In particular, we assume the following fixed attributes:
1. Up to 64 instruction issues per clock with no issue restrictions, or more than 10 times the total issue width of the widest processor in 2011. As we discuss later, the practical implications of very wide issue widths on clock rate, logic complexity, and power may be the most important limitations on exploiting ILP.
2. A tournament predictor with 1K entries and a 16-entry return predictor. This predictor is comparable to the best predictors in 2011; the predictor is not a primary bottleneck.
3. Perfect disambiguation of memory references done dynamically—this is ambitious but perhaps attainable for small window sizes (and hence small issue rates and load/store buffers) or through address aliasing prediction.
4. Register renaming with 64 additional integer and 64 additional FP registers, which is slightly less than the most aggressive processor in 2011. The Intel Core i7 has 128 entries in its reorder buffer, although they are not split between integer and FP, while the IBM Power7 has almost 200. Note that we assume a pipeline latency of one cycle, which significantly reduces the need for reorder buffer entries. Both the Power7 and the i7 have latencies of 10 cycles or greater.
Figure 3.27 shows the result for this configuration as we vary the window size. This configuration is more complex and expensive than any existing implementations, especially in terms of the number of instruction issues, which is more than 10 times larger than the largest number of issues available on any processor in 2011. Nonetheless, it gives a useful bound on what future implementations might yield. The data in these figures are likely to be very optimistic for another reason. There are no issue restrictions among the 64 instructions: They may all be memory references. No one would even contemplate this capability in a processor in the near future. Unfortunately, it is quite difficult to bound the performance of a processor with reasonable issue restrictions; not only is the space of possibilities quite large, but the existence of issue restrictions requires that the parallelism be evaluated with an accurate instruction scheduler, making the cost of studying processors with large numbers of issues very expensive.
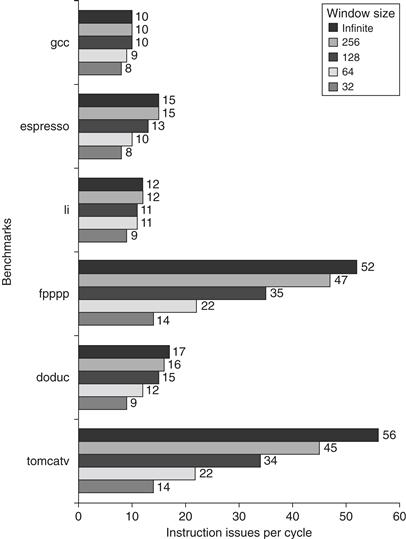
Figure 3.27 The amount of parallelism available versus the window size for a variety of integer and floating-point programs with up to 64 arbitrary instruction issues per clock. Although there are fewer renaming registers than the window size, the fact that all operations have one-cycle latency and the number of renaming registers equals the issue width allows the processor to exploit parallelism within the entire window. In a real implementation, the window size and the number of renaming registers must be balanced to prevent one of these factors from overly constraining the issue rate.
In addition, remember that in interpreting these results cache misses and non-unit latencies have not been taken into account, and both these effects will have significant impact!
The most startling observation from Figure 3.27 is that, with the realistic processor constraints listed above, the effect of the window size for the integer programs is not as severe as for FP programs. This result points to the key difference between these two types of programs. The availability of loop-level parallelism in two of the FP programs means that the amount of ILP that can be exploited is higher, but for integer programs other factors—such as branch prediction, register renaming, and less parallelism, to start with—are all important limitations. This observation is critical because of the increased emphasis on integer performance since the explosion of the World Wide Web and cloud computing starting in the mid-1990s. Indeed, most of the market growth in the last decade—transaction processing, Web servers, and the like—depended on integer performance, rather than floating point. As we will see in the next section, for a realistic processor in 2011, the actual performance levels are much lower than those shown in Figure 3.27.
Given the difficulty of increasing the instruction rates with realistic hardware designs, designers face a challenge in deciding how best to use the limited resources available on an integrated circuit. One of the most interesting trade-offs is between simpler processors with larger caches and higher clock rates versus more emphasis on instruction-level parallelism with a slower clock and smaller caches. The following example illustrates the challenges, and in the next chapter we will see an alternative approach to exploiting fine-grained parallelism in the form of GPUs.
Beyond the Limits of This Study
Like any limit study, the study we have examined in this section has its own limitations. We divide these into two classes: limitations that arise even for the perfect speculative processor, and limitations that arise for one or more realistic models. Of course, all the limitations in the first class apply to the second. The most important limitations that apply even to the perfect model are
1. WAW and WAR hazards through memory—The study eliminated WAW and WAR hazards through register renaming, but not in memory usage. Although at first glance it might appear that such circumstances are rare (especially WAW hazards), they arise due to the allocation of stack frames. A called procedure reuses the memory locations of a previous procedure on the stack, and this can lead to WAW and WAR hazards that are unnecessarily limiting. Austin and Sohi [1992] examined this issue.
2. Unnecessary dependences—With infinite numbers of registers, all but true register data dependences are removed. There are, however, dependences arising from either recurrences or code generation conventions that introduce unnecessary true data dependences. One example of these is the dependence on the control variable in a simple for loop. Since the control variable is incremented on every loop iteration, the loop contains at least one dependence. As we show in Appendix H, loop unrolling and aggressive algebraic optimization can remove such dependent computation. Wall’s study includes a limited amount of such optimizations, but applying them more aggressively could lead to increased amounts of ILP. In addition, certain code generation conventions introduce unneeded dependences, in particular the use of return address registers and a register for the stack pointer (which is incremented and decremented in the call/return sequence). Wall removes the effect of the return address register, but the use of a stack pointer in the linkage convention can cause “unnecessary” dependences. Postiff et al. [1999] explored the advantages of removing this constraint.
3. Overcoming the data flow limit—If value prediction worked with high accuracy, it could overcome the data flow limit. As of yet, none of the more than 100 papers on the subject has achieved a significant enhancement in ILP when using a realistic prediction scheme. Obviously, perfect data value prediction would lead to effectively infinite parallelism, since every value of every instruction could be predicted a priori.
For a less-than-perfect processor, several ideas have been proposed that could expose more ILP. One example is to speculate along multiple paths. This idea was discussed by Lam and Wilson [1992] and explored in the study covered in this section. By speculating on multiple paths, the cost of incorrect recovery is reduced and more parallelism can be uncovered. It only makes sense to evaluate this scheme for a limited number of branches because the hardware resources required grow exponentially. Wall [1993] provided data for speculating in both directions on up to eight branches. Given the costs of pursuing both paths, knowing that one will be thrown away (and the growing amount of useless computation as such a process is followed through multiple branches), every commercial design has instead devoted additional hardware to better speculation on the correct path.
It is critical to understand that none of the limits in this section is fundamental in the sense that overcoming them requires a change in the laws of physics! Instead, they are practical limitations that imply the existence of some formidable barriers to exploiting additional ILP. These limitations—whether they be window size, alias detection, or branch prediction—represent challenges for designers and researchers to overcome.
Attempts to break through these limits in the first five years of this century met with frustration. Some techniques produced small improvements, but often at significant increases in complexity, increases in the clock cycle, and disproportionate increases in power. In summary, designers discovered that trying to extract more ILP was simply too inefficient. We will return to this discussion in our concluding remarks.
3.11 Cross-Cutting Issues: ILP Approaches and the Memory System
Hardware versus Software Speculation
The hardware-intensive approaches to speculation in this chapter and the software approaches of Appendix H provide alternative approaches to exploiting ILP. Some of the trade-offs, and the limitations, for these approaches are listed below:
■ To speculate extensively, we must be able to disambiguate memory references. This capability is difficult to do at compile time for integer programs that contain pointers. In a hardware-based scheme, dynamic runtime disambiguation of memory addresses is done using the techniques we saw earlier for Tomasulo’s algorithm. This disambiguation allows us to move loads past stores at runtime. Support for speculative memory references can help overcome the conservatism of the compiler, but unless such approaches are used carefully, the overhead of the recovery mechanisms may swamp the advantages.
■ Hardware-based speculation works better when control flow is unpredictable and when hardware-based branch prediction is superior to software-based branch prediction done at compile time. These properties hold for many integer programs. For example, a good static predictor has a misprediction rate of about 16% for four major integer SPEC92 programs, and a hardware predictor has a misprediction rate of under 10%. Because speculated instructions may slow down the computation when the prediction is incorrect, this difference is significant. One result of this difference is that even statically scheduled processors normally include dynamic branch predictors.
■ Hardware-based speculation maintains a completely precise exception model even for speculated instructions. Recent software-based approaches have added special support to allow this as well.
■ Hardware-based speculation does not require compensation or bookkeeping code, which is needed by ambitious software speculation mechanisms.
■ Compiler-based approaches may benefit from the ability to see further in the code sequence, resulting in better code scheduling than a purely hardware-driven approach.
■ Hardware-based speculation with dynamic scheduling does not require different code sequences to achieve good performance for different implementations of an architecture. Although this advantage is the hardest to quantify, it may be the most important in the long run. Interestingly, this was one of the motivations for the IBM 360/91. On the other hand, more recent explicitly parallel architectures, such as IA-64, have added flexibility that reduces the hardware dependence inherent in a code sequence.
The major disadvantage of supporting speculation in hardware is the complexity and additional hardware resources required. This hardware cost must be evaluated against both the complexity of a compiler for a software-based approach and the amount and usefulness of the simplifications in a processor that relies on such a compiler.
Some designers have tried to combine the dynamic and compiler-based approaches to achieve the best of each. Such a combination can generate interesting and obscure interactions. For example, if conditional moves are combined with register renaming, a subtle side effect appears. A conditional move that is annulled must still copy a value to the destination register, since it was renamed earlier in the instruction pipeline. These subtle interactions complicate the design and verification process and can also reduce performance.
The Intel Itanium processor was the most ambitious computer ever designed based on the software support for ILP and speculation. It did not deliver on the hopes of the designers, especially for general-purpose, nonscientific code. As designers’ ambitions for exploiting ILP were reduced in light of the difficulties discussed in Section 3.10, most architectures settled on hardware-based mechanisms with issue rates of three to four instructions per clock.
Speculative Execution and the Memory System
Inherent in processors that support speculative execution or conditional instructions is the possibility of generating invalid addresses that would not occur without speculative execution. Not only would this be incorrect behavior if protection exceptions were taken, but the benefits of speculative execution would be swamped by false exception overhead. Hence, the memory system must identify speculatively executed instructions and conditionally executed instructions and suppress the corresponding exception.
By similar reasoning, we cannot allow such instructions to cause the cache to stall on a miss because again unnecessary stalls could overwhelm the benefits of speculation. Hence, these processors must be matched with nonblocking caches.
In reality, the penalty of an L2 miss is so large that compilers normally only speculate on L1 misses. Figure 2.5 on page 84 shows that for some well-behaved scientific programs the compiler can sustain multiple outstanding L2 misses to cut the L2 miss penalty effectively. Once again, for this to work the memory system behind the cache must match the goals of the compiler in number of simultaneous memory accesses.
3.12 Multithreading: Exploiting Thread-Level Parallelism to Improve Uniprocessor Throughput
The topic we cover in this section, multithreading, is truly a cross-cutting topic, since it has relevance to pipelining and superscalars, to graphics processing units (Chapter 4), and to multiprocessors (Chapter 5). We introduce the topic here and explore the use of multithreading to increase uniprocessor throughput by using multiple threads to hide pipeline and memory latencies. In the next chapter, we will see how multithreading provides the same advantages in GPUs, and finally, Chapter 5 will explore the combination of multithreading and multiprocessing. These topics are closely interwoven, since multithreading is a primary technique for exposing more parallelism to the hardware. In a strict sense, multithreading uses thread-level parallelism, and thus is properly the subject of Chapter 5, but its role in both improving pipeline utilization and in GPUs motivates us to introduce the concept here.
Although increasing performance by using ILP has the great advantage that it is reasonably transparent to the programmer, as we have seen ILP can be quite limited or difficult to exploit in some applications. In particular, with reasonable instruction issue rates, cache misses that go to memory or off-chip caches are unlikely to be hidden by available ILP. Of course, when the processor is stalled waiting on a cache miss, the utilization of the functional units drops dramatically.
Since attempts to cover long memory stalls with more ILP have limited effectiveness, it is natural to ask whether other forms of parallelism in an application could be used to hide memory delays. For example, an online transaction-processing system has natural parallelism among the multiple queries and updates that are presented by requests. Of course, many scientific applications contain natural parallelism since they often model the three-dimensional, parallel structure of nature, and that structure can be exploited by using separate threads. Even desktop applications that use modern Windows-based operating systems often have multiple active applications running, providing a source of parallelism.
Multithreading allows multiple threads to share the functional units of a single processor in an overlapping fashion. In contrast, a more general method to exploit thread-level parallelism (TLP) is with a multiprocessor that has multiple independent threads operating at once and in parallel. Multithreading, however, does not duplicate the entire processor as a multiprocessor does. Instead, multithreading shares most of the processor core among a set of threads, duplicating only private state, such as the registers and program counter. As we will see in Chapter 5, many recent processors incorporate both multiple processor cores on a single chip and provide multithreading within each core.
Duplicating the per-thread state of a processor core means creating a separate register file, a separate PC, and a separate page table for each thread. The memory itself can be shared through the virtual memory mechanisms, which already support multiprogramming. In addition, the hardware must support the ability to change to a different thread relatively quickly; in particular, a thread switch should be much more efficient than a process switch, which typically requires hundreds to thousands of processor cycles. Of course, for multithreading hardware to achieve performance improvements, a program must contain multiple threads (we sometimes say that the application is multithreaded) that could execute in concurrent fashion. These threads are identified either by a compiler (typically from a language with parallelism constructs) or by the programmer.
There are three main hardware approaches to multithreading. Fine-grained multithreading switches between threads on each clock, causing the execution of instructions from multiple threads to be interleaved. This interleaving is often done in a round-robin fashion, skipping any threads that are stalled at that time. One key advantage of fine-grained multithreading is that it can hide the throughput losses that arise from both short and long stalls, since instructions from other threads can be executed when one thread stalls, even if the stall is only for a few cycles. The primary disadvantage of fine-grained multithreading is that it slows down the execution of an individual thread, since a thread that is ready to execute without stalls will be delayed by instructions from other threads. It trades an uncrease in multithreaded throughput for a loss in the performance (as measured by latency) of a single thread. The Sun Niagara processor, which we examine shortly, uses simple fine-grained multithreading, as do the Nvidia GPUs, which we look at in the next chapter.
Coarse-grained multithreading was invented as an alternative to fine-grained multithreading. Coarse-grained multithreading switches threads only on costly stalls, such as level two or three cache misses. This change relieves the need to have thread-switching be essentially free and is much less likely to slow down the execution of any one thread, since instructions from other threads will only be issued when a thread encounters a costly stall.
Coarse-grained multithreading suffers, however, from a major drawback: It is limited in its ability to overcome throughput losses, especially from shorter stalls. This limitation arises from the pipeline start-up costs of coarse-grained multithreading. Because a CPU with coarse-grained multithreading issues instructions from a single thread, when a stall occurs the pipeline will see a bubble before the new thread begins executing. Because of this start-up overhead, coarse-grained multithreading is much more useful for reducing the penalty of very high-cost stalls, where pipeline refill is negligible compared to the stall time. Several research projects have explored coarse grained multithreading, but no major current processors use this technique.
The most common implementation of multithreading is called Simultaneous multithreading (SMT). Simultaneous multithreading is a variation on fine-grained multithreading that arises naturally when fine-grained multithreading is implemented on top of a multiple-issue, dynamically scheduled processor. As with other forms of multithreading, SMT uses thread-level parallelism to hide long-latency events in a processor, thereby increasing the usage of the functional units. The key insight in SMT is that register renaming and dynamic scheduling allow multiple instructions from independent threads to be executed without regard to the dependences among them; the resolution of the dependences can be handled by the dynamic scheduling capability.
Figure 3.28 conceptually illustrates the differences in a processor’s ability to exploit the resources of a superscalar for the following processor configurations:
■ A superscalar with no multithreading support
■ A superscalar with coarse-grained multithreading
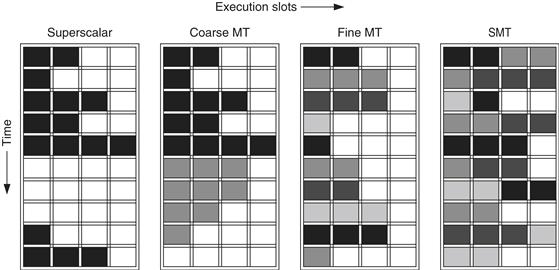
Figure 3.28 How four different approaches use the functional unit execution slots of a superscalar processor. The horizontal dimension represents the instruction execution capability in each clock cycle. The vertical dimension represents a sequence of clock cycles. An empty (white) box indicates that the corresponding execution slot is unused in that clock cycle. The shades of gray and black correspond to four different threads in the multithreading processors. Black is also used to indicate the occupied issue slots in the case of the superscalar without multithreading support. The Sun T1 and T2 (aka Niagara) processors are fine-grained multithreaded processors, while the Intel Core i7 and IBM Power7 processors use SMT. The T2 has eight threads, the Power7 has four, and the Intel i7 has two. In all existing SMTs, instructions issue from only one thread at a time. The difference in SMT is that the subsequent decision to execute an instruction is decoupled and could execute the operations coming from several different instructions in the same clock cycle.
In the superscalar without multithreading support, the use of issue slots is limited by a lack of ILP, including ILP to hide memory latency. Because of the length of L2 and L3 cache misses, much of the processor can be left idle.
In the coarse-grained multithreaded superscalar, the long stalls are partially hidden by switching to another thread that uses the resources of the processor. This switching reduces the number of completely idle clock cycles. In a coarse-grained multithreaded processor, however, thread switching only occurs when there is a stall. Because the new thread has a start-up period, there are likely to be some fully idle cycles remaining.
In the fine-grained case, the interleaving of threads can eliminate fully empty slots. In addition, because the issuing thread is changed on every clock cycle, longer latency operations can be hidden. Because instruction issue and execution are connected, a thread can only issue as many instructions as are ready. With a narrow issue width this is not a problem (a cycle is either occupied or not), which is why fine-grained multithreading works perfectly for a single issue processor, and SMT would make no sense. Indeed, in the Sun T2, there are two issues per clock, but they are from different threads. This eliminates the need to implement the complex dynamic scheduling approach and relies instead on hiding latency with more threads.
If one implements fine-grained threading on top of a multiple-issue dynamically schedule processor, the result is SMT. In all existing SMT implementations, all issues come from one thread, although instructions from different threads can initiate execution in the same cycle, using the dynamic scheduling hardware to determine what instructions are ready. Although Figure 3.28 greatly simplifies the real operation of these processors, it does illustrate the potential performance advantages of multithreading in general and SMT in wider issue, dynamically scheduled processors.
Simultaneous multithreading uses the insight that a dynamically scheduled processor already has many of the hardware mechanisms needed to support the mechanism, including a large virtual register set. Multithreading can be built on top of an out-of-order processor by adding a per-thread renaming table, keeping separate PCs, and providing the capability for instructions from multiple threads to commit.
Effectiveness of Fine-Grained Multithreading on the Sun T1
In this section, we use the Sun T1 processor to examine the ability of multithreading to hide latency. The T1 is a fine-grained multithreaded multicore microprocessor introduced by Sun in 2005. What makes T1 especially interesting is that it is almost totally focused on exploiting thread-level parallelism (TLP) rather than instruction-level parallelism (ILP). The T1 abandoned the intense focus on ILP (just shortly after the most aggressive ILP processors ever were introduced), returned to a simple pipeline strategy, and focused on exploiting TLP, using both multiple cores and multithreading to produce throughput.
Each T1 processor contains eight processor cores, each supporting four threads. Each processor core consists of a simple six-stage, single-issue pipeline (a standard five-stage RISC pipeline like that of Appendix C, with one stage added for thread switching). T1 uses fine-grained multithreading (but not SMT), switching to a new thread on each clock cycle, and threads that are idle because they are waiting due to a pipeline delay or cache miss are bypassed in the scheduling. The processor is idle only when all four threads are idle or stalled. Both loads and branches incur a three-cycle delay that can only be hidden by other threads. A single set of floating-point functional units is shared by all eight cores, as floating-point performance was not a focus for T1. Figure 3.29 summarizes the T1 processor.

Figure 3.29 A summary of the T1 processor.
T1 Multithreading Unicore Performance
The T1 makes TLP its focus, both through the multithreading on an individual core and through the use of many simple cores on a single die. In this section, we will look at the effectiveness of the T1 in increasing the performance of a single core through fine-grained multithreading. In Chapter 5, we will return to examine the effectiveness of combining multithreading with multiple cores.
To examine the performance of the T1, we use three server-oriented benchmarks: TPC-C, SPECJBB (the SPEC Java Business Benchmark), and SPECWeb99. Since multiple threads increase the memory demands from a single processor, they could overload the memory system, leading to reductions in the potential gain from multithreading. Figure 3.30 shows the relative increase in the miss rate and the observed miss latency when executing with one thread per core versus executing four threads per core for TPC-C. Both the miss rates and the miss latencies increase, due to increased contention in the memory system. The relatively small increase in miss latency indicates that the memory system still has unused capacity.
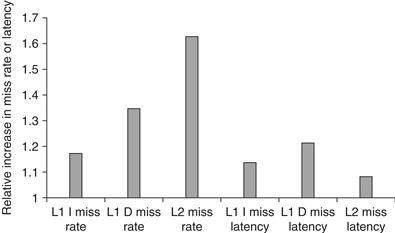
Figure 3.30 The relative change in the miss rates and miss latencies when executing with one thread per core versus four threads per core on the TPC-C benchmark. The latencies are the actual time to return the requested data after a miss. In the four-thread case, the execution of other threads could potentially hide much of this latency.
By looking at the behavior of an average thread, we can understand the interaction among the threads and their ability to keep a core busy. Figure 3.31 shows the percentage of cycles for which a thread is executing, ready but not executing, and not ready. Remember that not ready does not imply that the core with that thread is stalled; it is only when all four threads are not ready that the core will stall.
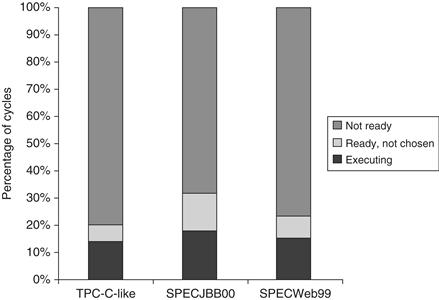
Figure 3.31 Breakdown of the status on an average thread. “Executing” indicates the thread issues an instruction in that cycle. “Ready but not chosen” means it could issue but another thread has been chosen, and “not ready” indicates that the thread is awaiting the completion of an event (a pipeline delay or cache miss, for example).
Threads can be not ready due to cache misses, pipeline delays (arising from long latency instructions such as branches, loads, floating point, or integer multiply/divide), and a variety of smaller effects. Figure 3.32 shows the relative frequency of these various causes. Cache effects are responsible for the thread not being ready from 50% to 75% of the time, with L1 instruction misses, L1 data misses, and L2 misses contributing roughly equally. Potential delays from the pipeline (called “pipeline delay”) are most severe in SPECJBB and may arise from its higher branch frequency.
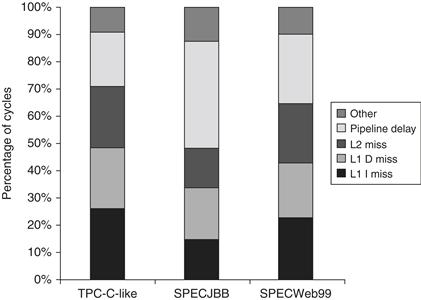
Figure 3.32 The breakdown of causes for a thread being not ready. The contribution to the “other” category varies. In TPC-C, store buffer full is the largest contributor; in SPEC-JBB, atomic instructions are the largest contributor; and in SPECWeb99, both factors contribute.
Figure 3.33 shows the per-thread and per-core CPI. Because T1 is a fine-grained multithreaded processor with four threads per core, with sufficient parallelism the ideal effective CPI per thread would be four, since that would mean that each thread was consuming one cycle out of every four. The ideal CPI per core would be one. In 2005, the IPC for these benchmarks running on aggressive ILP cores would have been similar to that seen on a T1 core. The T1 core, however, was very modest in size compared to the aggressive ILP cores of 2005, which is why the T1 had eight cores compared to the two to four offered on other processors of the same vintage. As a result, in 2005 when it was introduced, the Sun T1 processor had the best performance on integer applications with extensive TLP and demanding memory performance, such as SPECJBB and transaction processing workloads.
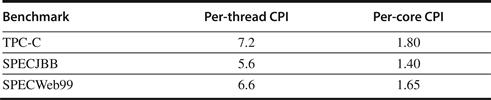
Figure 3.33 The per-thread CPI, the per-core CPI, the effective eight-core CPI, and the effective IPC (inverse of CPI) for the eight-core T1 processor.
Effectiveness of Simultaneous Multithreading on Superscalar Processors
A key question is, How much performance can be gained by implementing SMT? When this question was explored in 2000–2001, researchers assumed that dynamic superscalars would get much wider in the next five years, supporting six to eight issues per clock with speculative dynamic scheduling, many simultaneous loads and stores, large primary caches, and four to eight contexts with simultaneous issue and retirement from multiple contexts. No processor has gotten close to this level.
As a result, simulation research results that showed gains for multiprogrammed workloads of two or more times are unrealistic. In practice, the existing implementations of SMT offer only two to four contexts with fetching and issue from only one, and up to four issues per clock. The result is that the gain from SMT is also more modest.
For example, in the Pentium 4 Extreme, as implemented in HP-Compaq servers, the use of SMT yields a performance improvement of 1.01 when running the SPECintRate benchmark and about 1.07 when running the SPECfpRate benchmark. Tuck and Tullsen [2003] reported that, on the SPLASH parallel benchmarks, they found single-core multithreaded speedups ranging from 1.02 to 1.67, with an average speedup of about 1.22.
With the availability of recent extensive and insightful measurements done by Esmaeilzadeh et al. [2011], we can look at the performance and energy benefits of using SMT in a single i7 core using a set of multithreaded applications. The benchmarks we use consist of a collection of parallel scientific applications and a set of multithreaded Java programs from the DaCapo and SPEC Java suite, as summarized in Figure 3.34. The Intel i7 supports SMT with two threads. Figure 3.35 shows the performance ratio and the energy efficiency ratio of the these benchmarks run on one core of the i7 with SMT turned off and on. (We plot the energy efficiency ratio, which is the inverse of energy consumption, so that, like speedup, a higher ratio is better.)
Figure 3.34 The parallel benchmarks used here to examine multithreading, as well as in Chapter 5 to examine multiprocessing with an i7. The top half of the chart consists of PARSEC benchmarks collected by Biena et al. [2008]. The PARSEC benchmarks are meant to be indicative of compute-intensive, parallel applications that would be appropriate for multicore processors. The lower half consists of multithreaded Java benchmarks from the DaCapo collection (see Blackburn et al. [2006]) and pjbb2005 from SPEC. All of these benchmarks contain some parallelism; other Java benchmarks in the DaCapo and SPEC Java workloads use multiple threads but have little or no true parallelism and, hence, are not used here. See Esmaeilzadeh et al. [2011] for additional information on the characteristics of these benchmarks, relative to the measurements here and in Chapter 5.
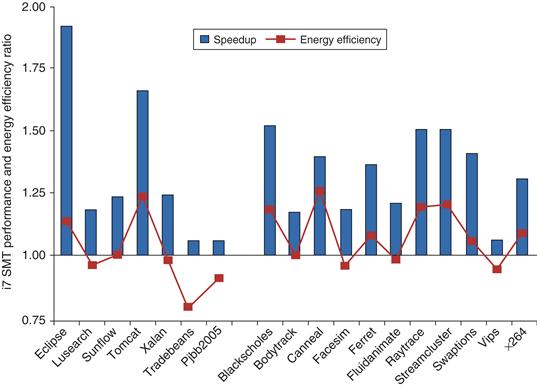
Figure 3.35 The speedup from using multithreading on one core on an i7 processor averages 1.28 for the Java benchmarks and 1.31 for the PARSEC benchmarks (using an unweighted harmonic mean, which implies a workload where the total time spent executing each benchmark in the single-threaded base set was the same). The energy efficiency averages 0.99 and 1.07, respectively (using the harmonic mean). Recall that anything above 1.0 for energy efficiency indicates that the feature reduces execution time by more than it increases average power. Two of the Java benchmarks experience little speedup and have significant negative energy efficiency because of this. Turbo Boost is off in all cases. These data were collected and analyzed by Esmaeilzadeh et al. [2011] using the Oracle (Sun) HotSpot build 16.3-b01 Java 1.6.0 Virtual Machine and the gcc v4.4.1 native compiler.
The harmonic mean of the speedup for the Java benchmarks is 1.28, despite the two benchmarks that see small gains. These two benchmarks, pjbb2005 and tradebeans, while multithreaded, have limited parallelism. They are included because they are typical of a multithreaded benchmark that might be run on an SMT processor with the hope of extracting some performance, which they find in limited amounts. The PARSEC benchmarks obtain somewhat better speedups than the full set of Java benchmarks (harmonic mean of 1.31). If tradebeans and pjbb2005 were omitted, the Java workload would actually have significantly better speedup (1.39) than the PARSEC benchmarks. (See the discussion of the implication of using harmonic mean to summarize the results in the caption of Figure 3.36.)
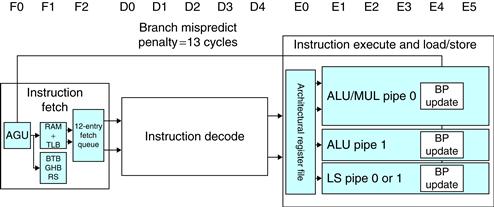
Figure 3.36 The basic structure of the A8 pipeline is 13 stages. Three cycles are used for instruction fetch and four for instruction decode, in addition to a five-cycle integer pipeline. This yields a 13-cycle branch misprediction penalty. The instruction fetch unit tries to keep the 12-entry instruction queue filled.
Energy consumption is determined by the combination of speedup and increase in power consumption. For the Java benchmarks, on average, SMT delivers the same energy efficiency as non-SMT (average of 1.0), but it is brought down by the two poor performing benchmarks; without tradebeans and pjbb2005, the average energy efficiency for the Java benchmarks is 1.06, which is almost as good as the PARSEC benchmarks. In the PARSEC benchmarks, SMT reduces energy by 1 − (1/1.08) = 7%. Such energy-reducing performance enhancements are very difficult to find. Of course, the static power associated with SMT is paid in both cases, thus the results probably slightly overstate the energy gains.
These results clearly show that SMT in an aggressive speculative processor with extensive support for SMT can improve performance in an energy efficient fashion, which the more aggressive ILP approaches have failed to do. In 2011, the balance between offering multiple simpler cores and fewer more sophisticated cores has shifted in favor of more cores, with each core typically being a three- to four-issue superscalar with SMT supporting two to four threads. Indeed, Esmaeilzadeh et al. [2011] show that the energy improvements from SMT are even larger on the Intel i5 (a processor similar to the i7, but with smaller caches and a lower clock rate) and the Intel Atom (an 80×86 processor designed for the netbook market and described in Section 3.14).
3.13 Putting It All Together: The Intel Core i7 and ARM Cortex-A8
In this section we explore the design of two multiple issue processors: the ARM Cortex-A8 core, which is used as the basis for the Apple A9 processor in the iPad, as well as the processor in the Motorola Droid and the iPhones 3GS and 4, and the Intel Core i7, a high-end, dynamically scheduled, speculative processor, intended for high-end desktops and server applications. We begin with the simpler processor.
The ARM Cortex-A8
The A8 is a dual-issue, statically scheduled superscalar with dynamic issue detection, which allows the processor to issue one or two instructions per clock. Figure 3.36 shows the basic pipeline structure of the 13-stage pipeline.
The A8 uses a dynamic branch predictor with a 512-entry two-way set associative branch target buffer and a 4K-entry global history buffer, which is indexed by the branch history and the current PC. In the event that the branch target buffer misses, a prediction is obtained from the global history buffer, which can then be used to compute the branch address. In addition, an eight-entry return stack is kept to track return addresses. An incorrect prediction results in a 13-cycle penalty as the pipeline is flushed.
Figure 3.37 shows the instruction decode pipeline. Up to two instructions per clock can be issued using an in-order issue mechanism. A simple scoreboard structure is used to track when an instruction can issue. A pair of dependent instructions can be processed through the issue logic, but, of course, they will be serialized at the scoreboard, unless they can be issued so that the forwarding paths can resolve the dependence.
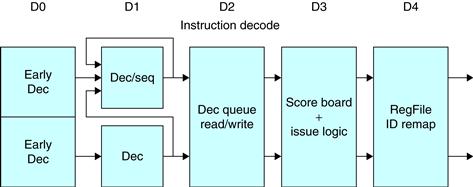
Figure 3.37 The five-stage instruction decode of the A8. In the first stage, a PC produced by the fetch unit (either from the branch target buffer or the PC incrementer) is used to retrieve an 8-byte block from the cache. Up to two instructions are decoded and placed into the decode queue; if neither instruction is a branch, the PC is incremented for the next fetch. Once in the decode queue, the scoreboard logic decides when the instructions can issue. In the issue, the register operands are read; recall that in a simple scoreboard, the operands always come from the registers. The register operands and opcode are sent to the instruction execution portion of the pipeline.
Figure 3.38 shows the execution pipeline for the A8 processor. Either instruction 1 or instruction 2 can go to the load/store pipeline. Fully bypassing is supported among the pipelines. The ARM Cortex-A8 pipeline uses a simple two-issue statically scheduled superscalar to allow reasonably high clock rate with lower power. In contrast, the i7 uses a reasonably aggressive, four-issue dynamically scheduled speculative pipeline structure.
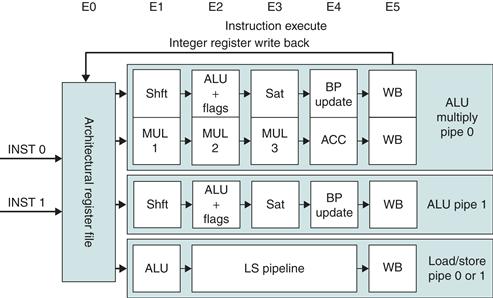
Figure 3.38 The five-stage instruction decode of the A8. Multiply operations are always performed in ALU pipeline 0.
Performance of the A8 Pipeline
The A8 has an ideal CPI of 0.5 due to its dual-issue structure. Pipeline stalls can arise from three sources:
1. Functional hazards, which occur because two adjacent instructions selected for issue simultaneously use the same functional pipeline. Since the A8 is statically scheduled, it is the compiler’s task to try to avoid such conflicts. When they cannot be avoided, the A8 can issue at most one instruction in that cycle.
2. Data hazards, which are detected early in the pipeline and may stall either both instructions (if the first cannot issue, the second is always stalled) or the second of a pair. The compiler is responsible for preventing such stalls when possible.
3. Control hazards, which arise only when branches are mispredicted.
In addition to pipeline stalls, L1 and L2 misses both cause stalls.
Figure 3.39 shows an estimate of the factors that contribute to the actual CPI for the Minnespec benchmarks, which we saw in Chapter 2. As we can see, pipeline delays rather than memory stalls are the major contributor to the CPI. This result is partially due to the effect that Minnespec has a smaller cache footprint than full SPEC or other large programs.
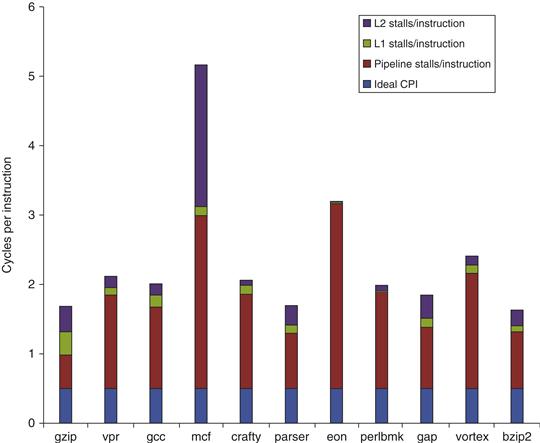
Figure 3.39 The estimated composition of the CPI on the ARM A8 shows that pipeline stalls are the primary addition to the base CPI. eon deserves some special mention, as it does integer-based graphics calculations (ray tracing) and has very few cache misses. It is computationally intensive with heavy use of multiples, and the single multiply pipeline becomes a major bottleneck. This estimate is obtained by using the L1 and L2 miss rates and penalties to compute the L1 and L2 generated stalls per instruction. These are subtracted from the CPI measured by a detailed simulator to obtain the pipeline stalls. Pipeline stalls include all three hazards plus minor effects such as way misprediction.
The insight that the pipeline stalls created significant performance losses probably played a key role in the decision to make the ARM Cortex-A9 a dynamically scheduled superscalar. The A9, like the A8, issues up to two instructions per clock, but it uses dynamic scheduling and speculation. Up to four pending instructions (two ALUs, one load/store or FP/multimedia, and one branch) can begin execution in a clock cycle. The A9 uses a more powerful branch predictor, instruction cache prefetch, and a nonblocking L1 data cache. Figure 3.40 shows that the A9 outperforms the A8 by a factor of 1.28 on average, assuming the same clock rate and virtually identical cache configurations.
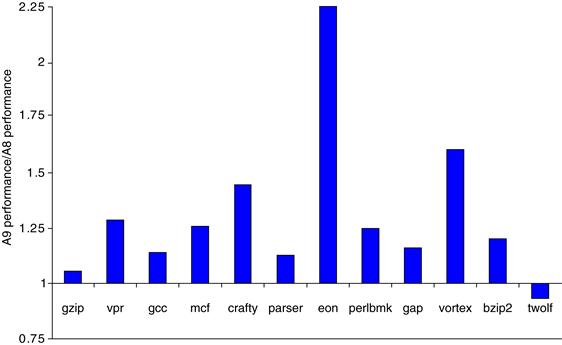
Figure 3.40 The performance ratio for the A9 compared to the A8, both using a 1 GHz clock and the same size caches for L1 and L2, shows that the A9 is about 1.28 times faster. Both runs use a 32 KB primary cache and a 1 MB secondary cache, which is 8-way set associative for the A8 and 16-way for the A9. The block sizes in the caches are 64 bytes for the A8 and 32 bytes for the A9. As mentioned in the caption of Figure 3.39, eon makes intensive use of integer multiply, and the combination of dynamic scheduling and a faster multiply pipeline significantly improves performance on the A9. twolf experiences a small slowdown, likely due to the fact that its cache behavior is worse with the smaller L1 block size of the A9.
The Intel Core i7
The i7 uses an aggressive out-of-order speculative microarchitecture with reasonably deep pipelines with the goal of achieving high instruction throughput by combining multiple issue and high clock rates. Figure 3.41 shows the overall structure of the i7 pipeline. We will examine the pipeline by starting with instruction fetch and continuing on to instruction commit, following steps labeled on the figure.
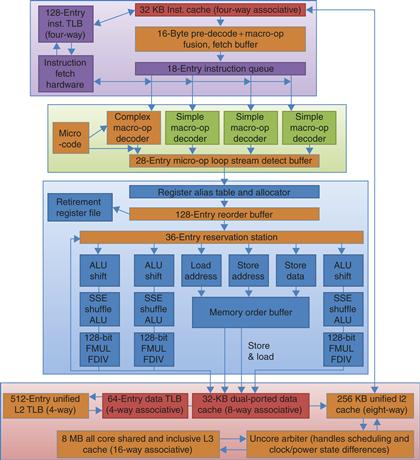
Figure 3.41 The Intel Core i7 pipeline structure shown with the memory system components. The total pipeline depth is 14 stages, with branch mispredictions costing 17 cycles. There are 48 load and 32 store buffers. The six independent functional units can each begin execution of a ready micro-op in the same cycle.
1. Instruction fetch—The processor uses a multilevel branch target buffer to achieve a balance between speed and prediction accuracy. There is also a return address stack to speed up function return. Mispredictions cause a penalty of about 15 cycles. Using the predicted address, the instruction fetch unit fetches 16 bytes from the instruction cache.
2. The 16 bytes are placed in the predecode instruction buffer—In this step, a process called macro-op fusion is executed. Macro-op fusion takes instruction combinations such as compare followed by a branch and fuses them into a single operation. The predecode stage also breaks the 16 bytes into individual x86 instructions. This predecode is nontrivial since the length of an x86 instruction can be from 1 to 17 bytes and the predecoder must look through a number of bytes before it knows the instruction length. Individual x86 instructions (including some fused instructions) are placed into the 18-entry instruction queue.
3. Micro-op decode—Individual x86 instructions are translated into micro-ops. Micro-ops are simple MIPS-like instructions that can be executed directly by the pipeline; this approach of translating the x86 instruction set into simple operations that are more easily pipelined was introduced in the Pentium Pro in 1997 and has been used since. Three of the decoders handle x86 instructions that translate directly into one micro-op. For x86 instructions that have more complex semantics, there is a microcode engine that is used to produce the micro-op sequence; it can produce up to four micro-ops every cycle and continues until the necessary micro-op sequence has been generated. The micro-ops are placed according to the order of the x86 instructions in the 28-entry micro-op buffer.
4. The micro-op buffer preforms loop stream detection and microfusion—If there is a small sequence of instructions (less than 28 instructions or 256 bytes in length) that comprises a loop, the loop stream detector will find the loop and directly issue the micro-ops from the buffer, eliminating the need for the instruction fetch and instruction decode stages to be activated. Microfusion combines instruction pairs such as load/ALU operation and ALU operation/store and issues them to a single reservation station (where they can still issue independently), thus increasing the usage of the buffer. In a study of the Intel Core architecture, which also incorporated microfusion and macrofusion, Bird et al. [2007] discovered that microfusion had little impact on performance, while macrofusion appears to have a modest positive impact on integer performance and little impact on floating-point performance.
5. Perform the basic instruction issue—Looking up the register location in the register tables, renaming the registers, allocating a reorder buffer entry, and fetching any results from the registers or reorder buffer before sending the micro-ops to the reservation stations.
6. The i7 uses a 36-entry centralized reservation station shared by six functional units. Up to six micro-ops may be dispatched to the functional units every clock cycle.
7. Micro-ops are executed by the individual function units and then results are sent back to any waiting reservation station as well as to the register retirement unit, where they will update the register state, once it is known that the instruction is no longer speculative. The entry corresponding to the instruction in the reorder buffer is marked as complete.
8. When one or more instructions at the head of the reorder buffer have been marked as complete, the pending writes in the register retirement unit are executed, and the instructions are removed from the reorder buffer.
Performance of the i7
In earlier sections, we examined the performance of the i7’s branch predictor and also the performance of SMT. In this section, we look at single-thread pipeline performance. Because of the presence of aggressive speculation as well as nonblocking caches, it is difficult to attribute the gap between idealized performance and actual performance accurately. As we will see, relatively few stalls occur because instructions cannot issue. For example, only about 3% of the loads are delayed because no reservation station is available. Most losses come either from branch mispredicts or cache misses. The cost of a branch mispredict is 15 cycles, while the cost of an L1 miss is about 10 cycles; L2 misses are slightly more than three times as costly as an L1 miss, and L3 misses cost about 13 times what an L1 miss costs (130–135 cycles)! Although the processor will attempt to find alternative instructions to execute for L3 misses and some L2 misses, it is likely that some of the buffers will fill before the miss completes, causing the processor to stop issuing instructions.
To examine the cost of mispredicts and incorrect speculation, Figure 3.42 shows the fraction of the work (measured by the numbers of micro-ops dispatched into the pipeline) that do not retire (i.e., their results are annulled), relative to all micro-op dispatches. For sjeng, for example, 25% of the work is wasted, since 25% of the dispatched micro-ops are never retired.
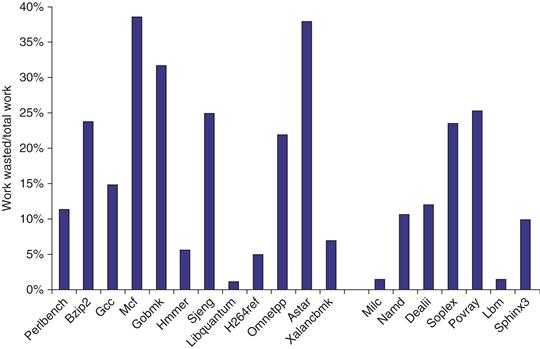
Figure 3.42 The amount of “wasted work” is plotted by taking the ratio of dispatched micro-ops that do not graduate to all dispatched micro-ops. For example, the ratio is 25% for sjeng, meaning that 25% of the dispatched and executed micro-ops are thrown away. The data in this section were collected by Professor Lu Peng and Ph.D. student Ying Zhang, both of Louisiana State University.
Notice that the wasted work in some cases closely matches the branch misprediction rates shown in Figure 3.5 on page 167, but in several instances, such as mcf, the wasted work seems relatively larger than the misprediction rate. In such cases, a likely explanation arises from the memory behavior. With the very high data cache miss rates, mcf will dispatch many instructions during an incorrect speculation as long as sufficient reservation stations are available for the stalled memory references. When the branch misprediction is detected, the micro-ops corresponding to these instructions will be flushed, but there will be congestion around the caches, as speculated memory references try to complete. There is no simple way for the processor to halt such cache requests once they are initiated.
Figure 3.43 shows the overall CPI for the 19 SPECCPU2006 benchmarks. The integer benchmarks have a CPI of 1.06 with very large variance (0.67 standard deviation). MCF and OMNETPP are the major outliers, both having a CPI over 2.0 while most other benchmarks are close to, or less than, 1.0 (gcc, the next highest, is 1.23). This variance derives from differences in the accuracy of branch prediction and in cache miss rates. For the integer benchmarks, the L2 miss rate is the best predictor of CPI, and the L3 miss rate (which is very small) has almost no effect.
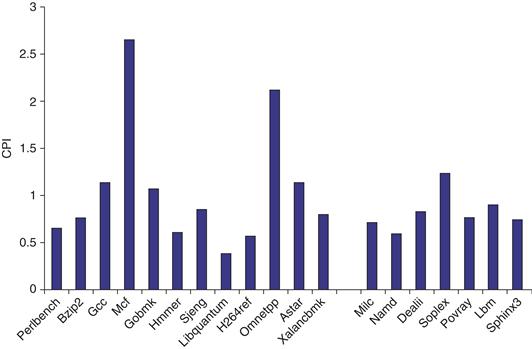
Figure 3.43 The CPI for the 19 SPECCPU2006 benchmarks shows an average CPI for 0.83 for both the FP and integer benchmarks, although the behavior is quite different. In the integer case, the CPI values range from 0.44 to 2.66 with a standard deviation of 0.77, while the variation in the FP case is from 0.62 to 1.38 with a standard deviation of 0.25. The data in this section were collected by Professor Lu Peng and Ph.D. student Ying Zhang, both of Louisiana State University.
The FP benchmarks achieve higher performance with a lower average CPI (0.89) and a lower standard deviation (0.25). For the FP benchmarks, L1 and L2 are equally important in determining the CPI, while L3 plays a smaller but significant role. While the dynamic scheduling and nonblocking capabilities of the i7 can hide some miss latency, cache memory behavior is still a major contributor. This reinforces the role of multithreading as another way to hide memory latency.
3.14 Fallacies and Pitfalls
Our few fallacies focus on the difficulty of predicting performance and energy efficiency and extrapolating from single measures such as clock rate or CPI. We also show that different architectural approaches can have radically different behaviors for different benchmarks.
Fallacy It is easy to predict the performance and energy efficiency of two different versions of the same instruction set architecture, if we hold the technology constant
Intel manufactures a processor for the low-end Netbook and PMD space that is quite similar in its microarchitecture of the ARM A8, called the Atom 230. Interestingly, the Atom 230 and the Core i7 920 have both been fabricated in the same 45 nm Intel technology. Figure 3.44 summarizes the Intel Core i7, the ARM Cortex-A8, and Intel Atom 230. These similarities provide a rare opportunity to directly compare two radically different microarchitectures for the same instruction set while holding constant the underlying fabrication technology. Before we do the comparison, we need to say a little more about the Atom 230.
Figure 3.44 An overview of the four-core Intel i7 920, an example of a typical Arm A8 processor chip (with a 256 MB L2, 32K L1s, and no floating point), and the Intel ARM 230 clearly showing the difference in design philosophy between a processor intended for the PMD (in the case of ARM) or netbook space (in the case of Atom) and a processor for use in servers and high-end desktops. Remember, the i7 includes four cores, each of which is several times higher in performance than the one-core A8 or Atom. All these processors are implemented in a comparable 45 nm technology.
The Atom processors implement the x86 architecture using the standard technique of translating x86 instructions into RISC-like instructions (as every x86 implementation since the mid-1990s has done). Atom uses a slightly more powerful microoperation, which allows an arithmetic operation to be paired with a load or a store. This means that on average for a typical instruction mix only 4% of the instructions require more than one microoperation. The microoperations are then executed in a 16-deep pipeline capable of issuing two instructions per clock, in order, as in the ARM A8. There are dual-integer ALUs, separate pipelines for FP add and other FP operations, and two memory operation pipelines, supporting more general dual execution than the ARM A8 but still limited by the in-order issue capability. The Atom 230 has a 32 KB instruction cache and a 24 KB data cache, both backed by a shared 512 KB L2 on the same die. (The Atom 230 also supports multithreading with two threads, but we will consider only one single threaded comparisons.) Figure 3.46 summarizes the i7, A8, and Atom processors and their key characteristics.
We might expect that these two processors, implemented in the same technology and with the same instruction set, would exhibit predictable behavior, in terms of relative performance and energy consumption, meaning that power and performance would scale close to linearly. We examine this hypothesis using three sets of benchmarks. The first sets is a group of Java, single-threaded benchmarks that come from the DaCapo benchmarks, and the SPEC JVM98 benchmarks (see Esmaeilzadeh et al. [2011] for a discussion of the benchmarks and measurements). The second and third sets of benchmarks are from SPEC CPU2006 and consist of the integer and FP benchmarks, respectively.
As we can see in Figure 3.45, the i7 significantly outperforms the Atom. All benchmarks are at least four times faster on the i7, two SPECFP benchmarks are over ten times faster, and one SPECINT benchmark runs over eight times faster! Since the ratio of clock rates of these two processors is 1.6, most of the advantage comes from a much lower CPI for the i7: a factor of 2.8 for the Java benchmarks, a factor of 3.1 for the SPECINT benchmarks, and a factor of 4.3 for the SPECFP benchmarks.
Figure 3.45 The relative performance and energy efficiency for a set of single-threaded benchmarks shows the i7 920 is 4 to over 10 times faster than the Atom 230 but that it is about 2 times less power efficient on average! Performance is shown in the columns as i7 relative to Atom, which is execution time (i7)/execution time (Atom). Energy is shown with the line as Energy (Atom)/Energy (i7). The i7 never beats the Atom in energy efficiency, although it is essentially as good on four benchmarks, three of which are floating point. The data shown here were collected by Esmaeilzadeh et al. [2011]. The SPEC benchmarks were compiled with optimization on using the standard Intel compiler, while the Java benchmarks use the Sun (Oracle) Hotspot Java VM. Only one core is active on the i7, and the rest are in deep power saving mode. Turbo Boost is used on the i7, which increases its performance advantage but slightly decreases its relative energy efficiency.
But, the average power consumption for the i7 is just under 43 W, while the average power consumption of the Atom is 4.2 W, or about one-tenth of the power! Combining the performance and power leads to a energy efficiency advantage for the Atom that is typically more than 1.5 times better and often 2 times better! This comparison of two processors using the same underlying technology makes it clear that the performance advantages of an aggressive superscalar with dynamic scheduling and speculation come with a significant disadvantage in energy efficiency.
Fallacy Processors with lower CPIs will always be faster.: Processors with faster clock rates will always be faster
The key is that it is the product of CPI and clock rate that determines performance. A high clock rate obtained by deeply pipelining the CPU must maintain a low CPI to get the full benefit of the faster clock. Similarly, a simple processor with a high clock rate but a low CPI may be slower.
As we saw in the previous fallacy, performance and energy efficiency can diverge significantly among processors designed for different environments even when they have the same ISA. In fact, large differences in performance can show up even within a family of processors from the same company all designed for high-end applications. Figure 3.46 shows the integer and FP performance of two different implementations of the x86 architecture from Intel, as well as a version of the Itanium architecture, also by Intel.
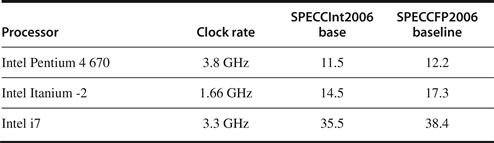
Figure 3.46 Three different Intel processors vary widely. Although the Itanium processor has two cores and the i7 four, only one core is used in the benchmarks.
The Pentium 4 was the most aggressively pipelined processor ever built by Intel. It used a pipeline with over 20 stages, had seven functional units, and cached micro-ops rather than x86 instructions. Its relatively inferior performance given the aggressive implementation, was a clear indication that the attempt to exploit more ILP (there could easily be 50 instructions in flight) had failed. The Pentium’s power consumption was similar to the i7, although its transistor count was lower, as its primary caches were half as large as the i7, and it included only a 2 MB secondary cache with no tertiary cache.
The Intel Itanium is a VLIW-style architecture, which despite the potential decrease in complexity compared to dynamically scheduled superscalars, never attained competitive clock rates with the mainline x86 processors (although it appears to achieve an overall CPI similar to that of the i7). In examining these results, the reader should be aware that they use different implementation technologies, giving the i7 an advantage in terms of transistor speed and hence clock rate for an equivalently pipelined processor. Nonetheless, the wide variation in performance—more than three times between the Pentium and i7—is astonishing. The next pitfall explains where a significant amount of this advantage comes from.
Pitfall Sometimes bigger and dumber is better
Much of the attention in the early 2000s went to building aggressive processors to exploit ILP, including the Pentium 4 architecture, which used the deepest pipeline ever seen in a microprocessor, and the Intel Itanium, which had the highest peak issue rate per clock ever seen. What quickly became clear was that the main limitation in exploiting ILP often turned out to be the memory system. Although speculative out-of-order pipelines were fairly good at hiding a significant fraction of the 10- to 15-cycle miss penalties for a first-level miss, they could do very little to hide the penalties for a second-level miss that, when going to main memory, were likely to be 50 to100 clock cycles.
The result was that these designs never came close to achieving the peak instruction throughput despite the large transistor counts and extremely sophisticated and clever techniques. The next section discusses this dilemma and the turning away from more aggressive ILP schemes to multicore, but there was another change that exemplifies this pitfall. Instead of trying to hide even more memory latency with ILP, designers simply used the transistors to build much larger caches. Both the Itanium 2 and the i7 use three-level caches compared to the two-level cache of the Pentium 4, and the third-level caches are 9 MB and 8 MB compared to the 2 MB second-level cache of the Pentium 4. Needless to say, building larger caches is a lot easier than designing the 20+ -stage Pentium 4 pipeline and, from the data in Figure 3.46, seems to be more effective.
3.15 Concluding Remarks: What’s Ahead?
As 2000 began, the focus on exploiting instruction-level parallelism was at its peak. Intel was about to introduce Itanium, a high-issue-rate statically scheduled processor that relied on a VLIW-like approach with intensive compiler support. MIPS, Alpha, and IBM processors with dynamically scheduled speculative execution were in their second generation and had gotten wider and faster. The Pentium 4, which used speculative scheduling, had also been announced that year with seven functional units and a pipeline more than 20 stages deep. But there were storm clouds on the horizon.
Research such as that covered in Section 3.10 was showing that pushing ILP much further would be extremely difficult, and, while peak instruction throughput rates had risen from the first speculative processors some 3 to 5 years earlier, sustained instruction execution rates were growing much more slowly.
The next five years were telling. The Itanium turned out to be a good FP processor but only a mediocre integer processor. Intel still produces the line, but there are not many users, the clock rate lags the mainline Intel processors, and Microsoft no longer supports the instruction set. The Intel Pentium 4, while achieving good performance, turned out to be inefficient in terms of performance/watt (i.e., energy use), and the complexity of the processor made it unlikely that further advances would be possible by increasing the issue rate. The end of a 20-year road of achieving new performance levels in microprocessors by exploiting ILP had come. The Pentium 4 was widely acknowledged to have gone beyond the point of diminishing returns, and the aggressive and sophisticated Netburst microarchitecture was abandoned.
By 2005, Intel and all the other major processor manufacturers had revamped their approach to focus on multicore. Higher performance would be achieved through thread-level parallelism rather than instruction-level parallelism, and the responsibility for using the processor efficiently would largely shift from the hardware to the software and the programmer. This change was the most significant change in processor architecture since the early days of pipelining and instruction-level parallelism some 25+ years earlier.
During the same period, designers began to explore the use of more data-level parallelism as another approach to obtaining performance. SIMD extensions enabled desktop and server microprocessors to achieve moderate performance increases for graphics and similar functions. More importantly, graphics processing units (GPUs) pursued aggressive use of SIMD, achieving significant performance advantages for applications with extensive data-level parallelism. For scientific applications, such approaches represent a viable alternative to the more general, but less efficient, thread-level parallelism exploited in multicores. The next chapter explores these developments in the use of data-level parallelism.
Many researchers predicted a major retrenchment in the use of ILP, predicting that two issue superscalar processors and larger numbers of cores would be the future. The advantages, however, of slightly higher issue rates and the ability of speculative dynamic scheduling to deal with unpredictable events, such as level-one cache misses, led to moderate ILP being the primary building block in multicore designs. The addition of SMT and its effectiveness (both for performance and energy efficiency) further cemented the position of the moderate issue, out-of-order, speculative approaches. Indeed, even in the embedded market, the newest processors (e.g., the ARM Cortex-A9) have introduced dynamic scheduling, speculation, and wider issues rates.
It is highly unlikely that future processors will try to increase the width of issue significantly. It is simply too inefficient both from the viewpoint of silicon utilization and power efficiency. Consider the data in Figure 3.47 that show the most recent four processors in the IBM Power series. Over the past decade, there has been a modest improvement in the ILP support in the Power processors, but the dominant portion of the increase in transistor count (a factor of almost 7 from the Power 4 to the Power7) went to increasing the caches and the number of cores per die. Even the expansion in SMT support seems to be more a focus than an increase in the ILP throughput: The ILP structure from Power4 to Power7 went from 5 issues to 6, from 8 functional units to 12 (but not increasing from the original 2 load/store units), while the SMT support went from nonexistent to 4 threads/processor. It seems clear that even for the most advanced ILP processor in 2011 (the Power7), the focus has moved beyond instruction-level parallelism. The next two chapters focus on approaches that exploit data-level and thread-level parallelism.
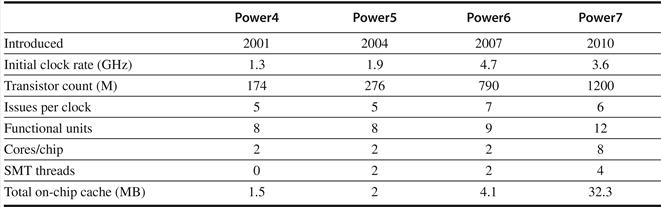
Figure 3.47 Characteristics of four IBM Power processors. All except the Power6 were dynamically scheduled, which is static, and in-order, and all the processors support two load/store pipelines. The Power6 has the same functional units as the Power5 except for a decimal unit. Power7 uses DRAM for the L3 cache.
3.16 Historical Perspective and References
Section L.5 (available online) features a discussion on the development of pipelining and instruction-level parallelism. We provide numerous references for further reading and exploration of these topics. Section L.5 covers both Chapter 3 and Appendix H.
Case Studies and Exercises by Jason D. Bakos and Robert P. Colwell
Case Study: Exploring the Impact of Microarchitectural Techniques
Concepts illustrated by this case study
You are tasked with designing a new processor microarchitecture, and you are trying to figure out how best to allocate your hardware resources. Which of the hardware and software techniques you learned in Chapter 3 should you apply? You have a list of latencies for the functional units and for memory, as well as some representative code. Your boss has been somewhat vague about the performance requirements of your new design, but you know from experience that, all else being equal, faster is usually better. Start with the basics. Figure 3.48 provides a sequence of instructions and list of latencies.
Figure 3.48 Code and latencies for Exercises 3.1 through 3.6.
3.1 [10] <1.8, 3.1, 3.2> What would be the baseline performance (in cycles, per loop iteration) of the code sequence in Figure 3.48 if no new instruction’s execution could be initiated until the previous instruction’s execution had completed? Ignore front-end fetch and decode. Assume for now that execution does not stall for lack of the next instruction, but only one instruction/cycle can be issued. Assume the branch is taken, and that there is a one-cycle branch delay slot.
3.2 [10] <1.8, 3.1, 3.2> Think about what latency numbers really mean—they indicate the number of cycles a given function requires to produce its output, nothing more. If the overall pipeline stalls for the latency cycles of each functional unit, then you are at least guaranteed that any pair of back-to-back instructions (a “producer” followed by a “consumer”) will execute correctly. But not all instruction pairs have a producer/consumer relationship. Sometimes two adjacent instructions have nothing to do with each other. How many cycles would the loop body in the code sequence in Figure 3.48 require if the pipeline detected true data dependences and only stalled on those, rather than blindly stalling everything just because one functional unit is busy? Show the code with <stall> inserted where necessary to accommodate stated latencies. (Hint: An instruction with latency +2 requires two <stall> cycles to be inserted into the code sequence. Think of it this way: A one-cycle instruction has latency 1 + 0, meaning zero extra wait states. So, latency 1 + 1 implies one stall cycle; latency 1 + N has N extra stall cycles.
3.3 [15] <3.6, 3.7> Consider a multiple-issue design. Suppose you have two execution pipelines, each capable of beginning execution of one instruction per cycle, and enough fetch/decode bandwidth in the front end so that it will not stall your execution. Assume results can be immediately forwarded from one execution unit to another, or to itself. Further assume that the only reason an execution pipeline would stall is to observe a true data dependency. Now how many cycles does the loop require?
3.4 [10] <3.6, 3.7> In the multiple-issue design of Exercise 3.3, you may have recognized some subtle issues. Even though the two pipelines have the exact same instruction repertoire, they are neither identical nor interchangeable, because there is an implicit ordering between them that must reflect the ordering of the instructions in the original program. If instruction N + 1 begins execution in Execution Pipe 1 at the same time that instruction N begins in Pipe 0, and N + 1 happens to require a shorter execution latency than N, then N + 1 will complete before N (even though program ordering would have implied otherwise). Recite at least two reasons why that could be hazardous and will require special considerations in the microarchitecture. Give an example of two instructions from the code in Figure 3.48 that demonstrate this hazard.
3.5 [20] <3.7> Reorder the instructions to improve performance of the code in Figure 3.48. Assume the two-pipe machine in Exercise 3.3 and that the out-of-order completion issues of Exercise 3.4 have been dealt with successfully. Just worry about observing true data dependences and functional unit latencies for now. How many cycles does your reordered code take?
3.6 [10/10/10] <3.1, 3.2> Every cycle that does not initiate a new operation in a pipe is a lost opportunity, in the sense that your hardware is not living up to its potential.
a. [10] <3.1, 3.2> In your reordered code from Exercise 3.5, what fraction of all cycles, counting both pipes, were wasted (did not initiate a new op)?
b. [10] <3.1, 3.2> Loop unrolling is one standard compiler technique for finding more parallelism in code, in order to minimize the lost opportunities for performance. Hand-unroll two iterations of the loop in your reordered code from Exercise 3.5.
c. [10] <3.1, 3.2> What speedup did you obtain? (For this exercise, just color the N + 1 iteration’s instructions green to distinguish them from the Nth iteration’s instructions; if you were actually unrolling the loop, you would have to reassign registers to prevent collisions between the iterations.)
3.7 [15] <2.1> Computers spend most of their time in loops, so multiple loop iterations are great places to speculatively find more work to keep CPU resources busy. Nothing is ever easy, though; the compiler emitted only one copy of that loop’s code, so even though multiple iterations are handling distinct data, they will appear to use the same registers. To keep multiple iterations’ register usages from colliding, we rename their registers. Figure 3.49 shows example code that we would like our hardware to rename. A compiler could have simply unrolled the loop and used different registers to avoid conflicts, but if we expect our hardware to unroll the loop, it must also do the register renaming. How? Assume your hardware has a pool of temporary registers (call them T registers, and assume that there are 64 of them, T0 through T63) that it can substitute for those registers designated by the compiler. This rename hardware is indexed by the src (source) register designation, and the value in the table is the T register of the last destination that targeted that register. (Think of these table values as producers, and the src registers are the consumers; it doesn’t much matter where the producer puts its result as long as its consumers can find it.) Consider the code sequence in Figure 3.49. Every time you see a destination register in the code, substitute the next available T, beginning with T9. Then update all the src registers accordingly, so that true data dependences are maintained. Show the resulting code. (Hint: See Figure 3.50.)

Figure 3.49 Sample code for register renaming practice.

Figure 3.50 Hint: Expected output of register renaming.
3.8 [20] <3.4> Exercise 3.7 explored simple register renaming: when the hardware register renamer sees a source register, it substitutes the destination T register of the last instruction to have targeted that source register. When the rename table sees a destination register, it substitutes the next available T for it, but superscalar designs need to handle multiple instructions per clock cycle at every stage in the machine, including the register renaming. A simple scalar processor would therefore look up both src register mappings for each instruction and allocate a new dest mapping per clock cycle. Superscalar processors must be able to do that as well, but they must also ensure that any dest-to-src relationships between the two concurrent instructions are handled correctly. Consider the sample code sequence in Figure 3.51. Assume that we would like to simultaneously rename the first two instructions. Further assume that the next two available T registers to be used are known at the beginning of the clock cycle in which these two instructions are being renamed. Conceptually, what we want is for the first instruction to do its rename table lookups and then update the table per its destination’s T register. Then the second instruction would do exactly the same thing, and any interinstruction dependency would thereby be handled correctly. But there’s not enough time to write that T register designation into the renaming table and then look it up again for the second instruction, all in the same clock cycle. That register substitution must instead be done live (in parallel with the register rename table update). Figure 3.52 shows a circuit diagram, using multiplexers and comparators, that will accomplish the necessary on-the-fly register renaming. Your task is to show the cycle-by-cycle state of the rename table for every instruction of the code shown in Figure 3.51. Assume the table starts out with every entry equal to its index (T0 = 0; T1 = 1, …).

Figure 3.51 Sample code for superscalar register renaming.
Figure 3.52 Rename table and on-the-fly register substitution logic for superscalar machines. (Note that src is source, and dest is destination.)
3.9 [5] <3.4> If you ever get confused about what a register renamer has to do, go back to the assembly code you’re executing, and ask yourself what has to happen for the right result to be obtained. For example, consider a three-way superscalar machine renaming these three instructions concurrently:
ADDI R1, R1, R1
ADDI R1, R1, R1
ADDI R1, R1, R1
If the value of R1 starts out as 5, what should its value be when this sequence has executed?
3.10 [20] <3.4, 3.9> Very long instruction word (VLIW) designers have a few basic choices to make regarding architectural rules for register use. Suppose a VLIW is designed with self-draining execution pipelines: once an operation is initiated, its results will appear in the destination register at most L cycles later (where L is the latency of the operation). There are never enough registers, so there is a temptation to wring maximum use out of the registers that exist. Consider Figure 3.53. If loads have a 1 + 2 cycle latency, unroll this loop once, and show how a VLIW capable of two loads and two adds per cycle can use the minimum number of registers, in the absence of any pipeline interruptions or stalls. Give an example of an event that, in the presence of self-draining pipelines, could disrupt this pipelining and yield wrong results.

Figure 3.53 Sample VLIW code with two adds, two loads, and two stalls.
3.11 [10/10/10] <3.3> Assume a five-stage single-pipeline microarchitecture (fetch, decode, execute, memory, write-back) and the code in Figure 3.54. All ops are one cycle except LW and SW, which are 1 + 2 cycles, and branches, which are 1 + 1 cycles. There is no forwarding. Show the phases of each instruction per clock cycle for one iteration of the loop.
a. [10] <3.3> How many clock cycles per loop iteration are lost to branch overhead?
b. [10] <3.3> Assume a static branch predictor, capable of recognizing a backwards branch in the Decode stage. Now how many clock cycles are wasted on branch overhead?
c. [10] <3.3> Assume a dynamic branch predictor. How many cycles are lost on a correct prediction?

Figure 3.54 Code loop for Exercise 3.11.
3.12 [15/20/20/10/20] <3.4, 3.7, 3.14> Let’s consider what dynamic scheduling might achieve here. Assume a microarchitecture as shown in Figure 3.55. Assume that the arithmetic-logical units (ALUs) can do all arithmetic ops (MULTD, DIVD, ADDD, ADDI, SUB) and branches, and that the Reservation Station (RS) can dispatch at most one operation to each functional unit per cycle (one op to each ALU plus one memory op to the LD/ST).
a. [15] <3.4> Suppose all of the instructions from the sequence in Figure 3.48 are present in the RS, with no renaming having been done. Highlight any instructions in the code where register renaming would improve performance. (Hint: Look for read-after-write and write-after-write hazards. Assume the same functional unit latencies as in Figure 3.48.)
b. [20] <3.4> Suppose the register-renamed version of the code from part (a) is resident in the RS in clock cycle N, with latencies as given in Figure 3.48. Show how the RS should dispatch these instructions out of order, clock by clock, to obtain optimal performance on this code. (Assume the same RS restrictions as in part (a). Also assume that results must be written into the RS before they’re available for use—no bypassing.) How many clock cycles does the code sequence take?
c. [20] <3.4> Part (b) lets the RS try to optimally schedule these instructions. But in reality, the whole instruction sequence of interest is not usually present in the RS. Instead, various events clear the RS, and as a new code sequence streams in from the decoder, the RS must choose to dispatch what it has. Suppose that the RS is empty. In cycle 0, the first two register-renamed instructions of this sequence appear in the RS. Assume it takes one clock cycle to dispatch any op, and assume functional unit latencies are as they were for Exercise 3.2. Further assume that the front end (decoder/register-renamer) will continue to supply two new instructions per clock cycle. Show the cycle-by-cycle order of dispatch of the RS. How many clock cycles does this code sequence require now?
d. [10] <3.14> If you wanted to improve the results of part (c), which would have helped most: (1) Another ALU? (2) Another LD/ST unit? (3) Full bypassing of ALU results to subsequent operations? or (4) Cutting the longest latency in half? What’s the speedup?
e. [20] <3.7> Now let’s consider speculation, the act of fetching, decoding, and executing beyond one or more conditional branches. Our motivation to do this is twofold: The dispatch schedule we came up with in part (c) had lots of nops, and we know computers spend most of their time executing loops (which implies the branch back to the top of the loop is pretty predictable). Loops tell us where to find more work to do; our sparse dispatch schedule suggests we have opportunities to do some of that work earlier than before. In part (d) you found the critical path through the loop. Imagine folding a second copy of that path onto the schedule you got in part (b). How many more clock cycles would be required to do two loops’ worth of work (assuming all instructions are resident in the RS)? (Assume all functional units are fully pipelined.)
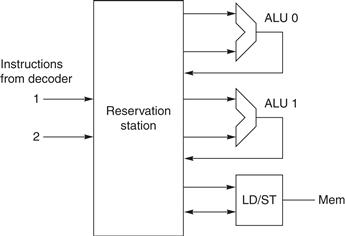
Figure 3.55 An out-of-order microarchitecure.
Exercises
3.13 [25] <3.13> In this exercise, you will explore performance trade-offs between three processors that each employ different types of multithreading. Each of these processors is superscalar, uses in-order pipelines, requires a fixed three-cycle stall following all loads and branches, and has identical L1 caches. Instructions from the same thread issued in the same cycle are read in program order and must not contain any data or control dependences.
■ Processor A is a superscalar SMT architecture, capable of issuing up to two instructions per cycle from two threads.
■ Processor B is a fine MT architecture, capable of issuing up to four instructions per cycle from a single thread and switches threads on any pipeline stall.
■ Processor C is a coarse MT architecture, capable of issuing up to eight instructions per cycle from a single thread and switches threads on an L1 cache miss.
Our application is a list searcher, which scans a region of memory for a specific value stored in R9 between the address range specified in R16 and R17. It is parallelized by evenly dividing the search space into four equal-sized contiguous blocks and assigning one search thread to each block (yielding four threads). Most of each thread’s runtime is spent in the following unrolled loop body:
loop: LD R1,0(R16)
LD R2,8(R16)
LD R3,16(R16)
LD R4,24(R16)
LD R5,32(R16)
LD R6,40(R16)
LD R7,48(R16)
LD R8,56(R16)
BEQAL R9,R1,match0
BEQAL R9,R2,match1
BEQAL R9,R3,match2
BEQAL R9,R4,match3
BEQAL R9,R5,match4
BEQAL R9,R6,match5
BEQAL R9,R7,match6
BEQAL R9,R8,match7
DADDIU R16,R16,#64
BLT R16,R17,loop
Assume the following:
■ A barrier is used to ensure that all threads begin simultaneously.
■ The first L1 cache miss occurs after two iterations of the loop.
■ None of the BEQAL branches is taken.
■ All three processors schedule threads in a round-robin fashion.
Determine how many cycles are required for each processor to complete the first two iterations of the loop.
3.14 [25/25/25] <3.2, 3.7> In this exercise, we look at how software techniques can extract instruction-level parallelism (ILP) in a common vector loop. The following loop is the so-called DAXPY loop (double-precision aX plus Y) and is the central operation in Gaussian elimination. The following code implements the DAXPY operation, Y = aX + Y, for a vector length 100. Initially, R1 is set to the base address of array X and R2 is set to the base address of Y:
DADDIU R4,R1,#800 ; R1 = upper bound for X
foo: L.D F2,0(R1) ; (F2) = X(i)
MUL.D F4,F2,F0 ; (F4) = a*X(i)
L.D F6,0(R2) ; (F6) = Y(i)
ADD.D F6,F4,F6 ; (F6) = a*X(i) + Y(i)
S.D F6,0(R2) ; Y(i) = a*X(i) + Y(i)
DADDIU R1,R1,#8 ; increment X index
DADDIU R2,R2,#8 ; increment Y index
DSLTU R3,R1,R4 ; test: continue loop?
BNEZ R3,foo ; loop if needed
Assume the functional unit latencies as shown in the table below. Assume a one-cycle delayed branch that resolves in the ID stage. Assume that results are fully bypassed.
| Instruction producing result | Instruction using result | Latency in clock cycles |
| FP multiply | FP ALU op | 6 |
| FP add | FP ALU op | 4 |
| FP multiply | FP store | 5 |
| FP add | FP store | 4 |
| Integer operations and all loads | Any | 2 |
a. [25] <3.2> Assume a single-issue pipeline. Show how the loop would look both unscheduled by the compiler and after compiler scheduling for both floating-point operation and branch delays, including any stalls or idle clock cycles. What is the execution time (in cycles) per element of the result vector, Y, unscheduled and scheduled? How much faster must the clock be for processor hardware alone to match the performance improvement achieved by the scheduling compiler? (Neglect any possible effects of increased clock speed on memory system performance.)
b. [25] <3.2> Assume a single-issue pipeline. Unroll the loop as many times as necessary to schedule it without any stalls, collapsing the loop overhead instructions. How many times must the loop be unrolled? Show the instruction schedule. What is the execution time per element of the result?
c. [25] <3.7> Assume a VLIW processor with instructions that contain five operations, as shown in Figure 3.16. We will compare two degrees of loop unrolling. First, unroll the loop 6 times to extract ILP and schedule it without any stalls (i.e., completely empty issue cycles), collapsing the loop overhead instructions, and then repeat the process but unroll the loop 10 times. Ignore the branch delay slot. Show the two schedules. What is the execution time per element of the result vector for each schedule? What percent of the operation slots are used in each schedule? How much does the size of the code differ between the two schedules? What is the total register demand for the two schedules?
3.15 [20/20] <3.4, 3.5, 3.7, 3.8> In this exercise, we will look at how variations on Tomasulo’s algorithm perform when running the loop from Exercise 3.14. The functional units (FUs) are described in the table below.

■ Functional units are not pipelined.
■ There is no forwarding between functional units; results are communicated by the common data bus (CDB).
■ The execution stage (EX) does both the effective address calculation and the memory access for loads and stores. Thus, the pipeline is IF/ID/IS/EX/WB.
■ Loads require one clock cycle.
■ The issue (IS) and write-back (WB) result stages each require one clock cycle.
■ There are five load buffer slots and five store buffer slots.
■ Assume that the Branch on Not Equal to Zero (BNEZ) instruction requires one clock cycle.
a. [20] <3.4–3.5> For this problem use the single-issue Tomasulo MIPS pipeline of Figure 3.6 with the pipeline latencies from the table above. Show the number of stall cycles for each instruction and what clock cycle each instruction begins execution (i.e., enters its first EX cycle) for three iterations of the loop. How many cycles does each loop iteration take? Report your answer in the form of a table with the following column headers:
■ Iteration (loop iteration number)
■ Instruction
■ Issues (cycle when instruction issues)
■ Executes (cycle when instruction executes)
■ Memory access (cycle when memory is accessed)
■ Write CDB (cycle when result is written to the CDB)
■ Comment (description of any event on which the instruction is waiting)
Show three iterations of the loop in your table. You may ignore the first instruction.
b. [20] <3.7, 3.8> Repeat part (a) but this time assume a two-issue Tomasulo algorithm and a fully pipelined floating-point unit (FPU).
3.16 [10] <3.4> Tomasulo’s algorithm has a disadvantage: Only one result can compute per clock per CDB. Use the hardware configuration and latencies from the previous question and find a code sequence of no more than 10 instructions where Tomasulo’s algorithm must stall due to CDB contention. Indicate where this occurs in your sequence.
3.17 [20] <3.3> An (m,n) correlating branch predictor uses the behavior of the most recent m executed branches to choose from 2m predictors, each of which is an n-bit predictor. A two-level local predictor works in a similar fashion, but only keeps track of the past behavior of each individual branch to predict future behavior.
There is a design trade-off involved with such predictors: Correlating predictors require little memory for history which allows them to maintain 2-bit predictors for a large number of individual branches (reducing the probability of branch instructions reusing the same predictor), while local predictors require substantially more memory to keep history and are thus limited to tracking a relatively small number of branch instructions. For this exercise, consider a (1,2) correlating predictor that can track four branches (requiring 16 bits) versus a (1,2) local predictor that can track two branches using the same amount of memory. For the following branch outcomes, provide each prediction, the table entry used to make the prediction, any updates to the table as a result of the prediction, and the final misprediction rate of each predictor. Assume that all branches up to this point have been taken. Initialize each predictor to the following:
| Branch PC (word address) | Outcome |
| 454 | T |
| 543 | NT |
| 777 | NT |
| 543 | NT |
| 777 | NT |
| 454 | T |
| 777 | NT |
| 454 | T |
| 543 | T |
3.18 [10] <3.9> Suppose we have a deeply pipelined processor, for which we implement a branch-target buffer for the conditional branches only. Assume that the misprediction penalty is always four cycles and the buffer miss penalty is always three cycles. Assume a 90% hit rate, 90% accuracy, and 15% branch frequency. How much faster is the processor with the branch-target buffer versus a processor that has a fixed two-cycle branch penalty? Assume a base clock cycle per instruction (CPI) without branch stalls of one.
3.19 [10/5] <3.9> Consider a branch-target buffer that has penalties of zero, two, and two clock cycles for correct conditional branch prediction, incorrect prediction, and a buffer miss, respectively. Consider a branch-target buffer design that distinguishes conditional and unconditional branches, storing the target address for a conditional branch and the target instruction for an unconditional branch.
a. [10] <3.9> What is the penalty in clock cycles when an unconditional branch is found in the buffer?
b. [10] <3.9> Determine the improvement from branch folding for unconditional branches. Assume a 90% hit rate, an unconditional branch frequency of 5%, and a two-cycle penalty for a buffer miss. How much improvement is gained by this enhancement? How high must the hit rate be for this enhancement to provide a performance gain?