Chapter 7
Introduction to matrices
Matrices represent the central algebraic vehicle for advanced computation throughout mathematics as well as in the physical and social sciences. Their introduction in the second half of the 19th century made mathematicians aware that there were important algebraic systems apart from number fields, and their study stimulated the growth of abstract algebra in the early 20th century.
Matrices and their operations
The word ‘matrix’ has a number of meanings in science as one kind of aggregation or another. Its meaning in mathematics is more akin to its use in the film The Matrix, where the characters inhabited a virtual world that was coded as an enormous binary array on a gigantic computer. Indeed, a matrix is simply a rectangular array of numbers of some kind: for example,
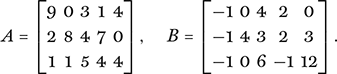
These two matrices, A and B, both have the same size in that each has 3 rows and 5 columns, but a matrix may have any number of rows, m, and columns, n. The matrices A and B are therefore 3 × 5 matrices; an n × n matrix is naturally called a square matrix.
There are some natural and simple operations that can be performed on matrices. First there is scalar multiplication, where all entries in a matrix are multiplied by a fixed number: I am sure the reader can write down the matrices 2A and −3B without difficulty. Two matrices of the same size may be added (or subtracted) by adding (or subtracting) the corresponding entries to form a new matrix of the same size as the original pair. Indeed, we can form linear combinations of the form aA + bB for any multipliers a and b. For example,
for instance, the entry at position (3, 1), meaning the third row and first column, is given here by 2(1) − 3(−1) = 2 + 3 = 5.
This is all very simple, and it is fair to ask why we would want to look at this idea at all. What problems are we hoping to solve by introducing these arrays?
What makes matrices important is the way they are multiplied, for this is a completely new operation that arises in a host of problems involving many variables, which is a feature of complex, real-world situations. Before we move on to that it is worth noting, however, that the definition above allows matrix addition to satisfy the commutative and associative laws, as for m × n matrices A, B, and C,
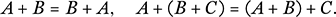
Both these facts are immediate consequences of the corresponding laws holding for ordinary numbers. Also, for scalars a, b, and c we have the rules
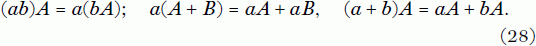
None of this is surprising, but it does give notice that the laws of algebra can be applicable to algebraic systems other than various number fields such as ℚ and ℂ.
Matrix ideas have a very long history. The ancient Chinese text The Nine Chapters on the Mathematical Art (compiled around 250 bc) features the first examples of the use of array methods to solve simultaneous equations, including the concept of determinants (the subject of Chapter 9). The idea first appeared in Europe in Cardano’s 16th-century work Ars Magna, mentioned in Chapter 5 in connection with the solution of the cubic.
From about 1850, the British mathematician James Sylvester did much to establish matrix and determinant theory as a branch of mathematics in its own right, along with his friend Arthur Cayley, who first introduced the formal notion of a group. In the 20th century, matrix theory arose irresistibly in many branches of mathematical physics, particularly in quantum mechanics.
To motivate matrix multiplication, we write our example of a 2 × 2 set of linear equations from Chapter 3 in matrix form. Since the problem is determined by the coefficients of the unknowns together with the right-hand sides of the equations, we isolate the coefficient matrix and write the pair of equations as a single matrix equation in the following fashion:
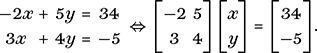
In order that our matrix equation represents a matrix product, we require that
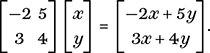
Regarding the RHS as the product of the two matrices on the left, we see that the first entry, −2x + 5y, is equal to −2, the first entry of the first row of the first matrix, times the first entry of the column matrix
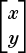, plus the second entry, 5, of the first row times the second entry of the column matrix. On the other hand, 3x + 4y is the result of adding the first entry of the second row of the 2 × 2 matrix times the first entry, x, of the column plus the second entry of the second row times the second entry of the column. This is how matrix products are formed in general, as a sum of products of rows of the first matrix times columns of the second. For that to work, we need the length of the rows of the first matrix to match the length of the columns of the second. Another way of putting this is to say that the number of columns of the first matrix must equal the number of rows of the second.
Having said that, we make this precise as follows. Let A be an m × n matrix and B an n × k matrix. The product C = AB will be an m × k matrix, which is to say the product has the same number of rows as A, the matrix on the left, and the same number of columns as the second matrix, B, on the right. A matrix with just one row is called a row vector and, similarly, a one-column matrix is a column vector.
The next example is of a 2 × 3 matrix, A, multiplied by a 3 × 2 matrix, B, resulting in a 2 × 2 product matrix:
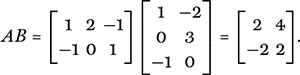
For example, the entry in the top right-hand corner of the product is 4, which comes from taking the so-called scalar product (or dot product) of the first row of A and the second column of B: 1 × (−2) + (2 × 3) + (−1 × 0) = −2 + 6 − 0 = 4.
Let us now compute the reverse product:
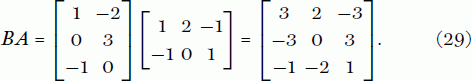
This example shows that matrix multiplication spectacularly fails the commutative law. The matrices AB and BA are certainly unequal, for they do not even have the same dimensions. And this bad behaviour is not just a feature of oblong matrices. If you write down two square n × n matrices A and B, then both AB and BA will also be n × n matrices but they will otherwise probably be quite different from one another.
The general description of the matrix product is as follows. Let A = (aij) be an m × n matrix, meaning that the entry in row i and column j is aij. Similarly, let B = (bij) denote an n × k matrix. Then the product C = AB has entries (cij), where cij is the scalar product of row i of A and column j of B, which is the number
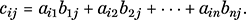(30)
The equation (30) says that cij equals the first entry of row i of A times the first entry of column j of B, plus the second entry of row i times the second entry of column j, and so on.
There is something slightly peculiar about the product BA in (29). If we label the row vectors of BA from top to bottom as r1, r2, and r3, you will notice that
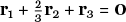, where 0 = (0, 0, 0) is the zero vector. We say that the row set of BA is dependent, in that one row can be expressed in terms of the others: for example, here we might write
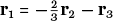. This is an instance of a general phenomenon, as we next explain.
For any matrix M, the row rank of M is the maximum number of rows we can locate in the matrix that form an independent set, meaning that no row is equal to a linear combination, which means a sum of multiples, of the other rows. Of course, we can replace the word ‘row’ in this definition by ‘column’ and in the same way define the column rank of M. For example, the first two rows of BA are independent as neither is a multiple of the other, but, as we have seen, the three rows do not form an independent set, as r1 is a linear combination of r2 and r3. Hence the row rank of BA is 2.
A remarkable theorem says that the row rank and column rank are always equal, and this common value is naturally called the rank of the matrix. What is more, you cannot create independence from dependence, by which is meant that the rank of a matrix can never be increased by taking its product with another matrix, or to put it in symbols,
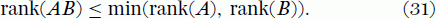
In particular, since our 3 × 3 matrix can be factorized as a product of matrices that have rank at most 2 (because the first only has two columns and the second just two rows), it follows that BA must also have rank no more than 2. Indeed, as we have already noted, rank(BA) is 2.
Before closing this section, however, we hasten to point out that matrices do obey other laws of algebra. Importantly, multiplication is associative and is distributive over addition, so that for any three matrices A, B, and C we have that whenever one side of each of the following equations exists, then so does the other and they agree:
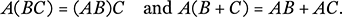
Each of these laws is a consequence of the corresponding law holding over the field of real numbers. The distributive law is easily checked, but associativity of multiplication is less obvious. Careful calculation of the entry in a typical position in each product reveals, however, that the product ABC is independent of how you bracket it, and this is ultimately a consequence of associativity of ordinary multiplication.
Networks
One of the most direct and fruitful lines of application of matrices and their multiplication is to the representation of networks. For example, consider the network in Figure 13, where the four nodes represent cities A, B, C, D and we have drawn an edge joining two nodes if an airline flies on that route. Note that two airlines fly between cities A and B, each represented by an edge in the network.
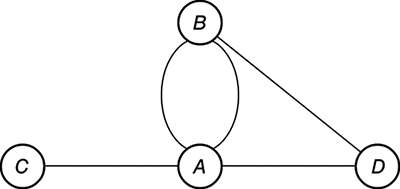
13. Network of cities and airline routes.
It is possible to distil all the information of a network N into what is called the incidence matrix, M, of N. We simply number the nodes in some way; here we follow alphabetical order, and write down what is in this case a 4 × 4 matrix where the entry at position (i, j) is the number of edges connecting node i to node j. Look at what happens when we write down M and calculate its square:
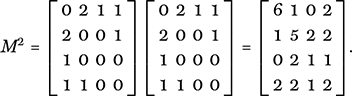
The entries of the matrix product, M2, tell you how many ways there are of travelling from one city to another via a third. For example, there are two ways of getting from D to B (via A). There are five return trips to B (one through D, but there are 2 × 2 = 4 via A as you have two choices of airline for each leg of the journey). In much the same way M3, M4, and, generally, Mn, are matrices whose entry at position (i, j) tells you the number of paths of length n from i to j. Since we are assuming that our edges allow passage equally in both directions, incidence matrices like M and its powers are symmetric, meaning that the entries at (i, j) and (j, i) always agree. But why does matrix multiplication automatically keep track of all this?
Ask yourself how we would count the total number of ways of going from a node i to a node j in a network via any choice of a third node k. For any particular choice of the intermediate node k, we would count all the edges between i and k (which might be zero) and multiply that number by the number of edges from k to our target node, j. This tells you how many paths of length 2 there are from i to j via k. We would then sum these numbers over all possible values of k to find the total number of paths of length 2 from i to j. However, that is exactly the sum that you work out to calculate the entry at (i, j) in the matrix product M2 when you form the product of row i with column j.
Incidence matrices of various types are used to capture information about networks, and algebraic features of these matrices then correspond to and allow calculation of special features of the network. Indeed, network theory is one of the major applications of linear algebra, which is the branch of the subject that is largely represented by matrices and matrix calculations.
For example, we next explain the Kirchhoff matrix K of a network N. First, we define the degree of a node A in a network N to be the number of edges attached to A. In our network of Figure 13, for example, A has degree 4. In fact, the degree of the ith node must equal the sum of the ith row of M (and equally, by symmetry, the sum of the ith column). For a network N with n nodes, let D be the n × n matrix consisting entirely of zero entries except down the principal diagonal, which is the diagonal of the matrix from top left to bottom right, with the diagonal entry at (i, i) being the degree of the ith node. For the network N of our running example, we may write D = diag(4, 3, 1,2), where the notation is self-explanatory. Quite generally, we call a square matrix D a diagonal matrix if its non-zero entries lie exclusively on the principal diagonal. We now define the Kirchhoff matrix K of N to be D − M. In our example, this gives
Note that in any Kirchhoff matrix, the sum of the entries in each row, and by symmetry in each column, is 0.
Through using K it is possible to compute the number of so-called spanning trees in the network N. A tree is a network that contains no cycles but in which there is a path between any two nodes: equivalently, a tree is a network in which there is a unique path between any two nodes. A spanning tree of a network is a tree within the network that contains all of the nodes. For example, the path C–A–D–B represents one spanning tree in N, and the reader should be able to find four others. The matrix K allows you to count the number of spanning trees in N without having to write down all the trees explicitly. To explain how K does this requires the notion of the determinant of a matrix, which is the subject of Chapter 9, where we will revisit this problem.
Geometric applications
Another application of matrices is to the geometry of transformations. We may use any given 2 × 2 matrix A as a means to create a mapping of points P(x, y) in the Cartesian plane by writing the coordinates of P as a column vector, known in this context as a position vector, and multiplying that vector on the left by A to give a new point. For example,
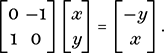
In this instance, the matrix rotates each point (x, y) through 90° anticlockwise about the origin to the point (−y, x) (Figure 14).
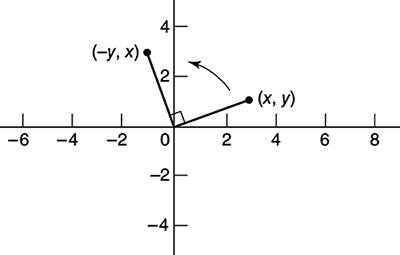
14. Geometric action of a matrix transformation.
The transformations of the plane, also known as mappings, which we can create in this way have very special properties that are a consequence of the algebraic laws that matrices obey.
We first describe these transformations in general without reference to matrices. For convenience, we write the column vector
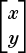as x and, in general, typical column vectors will be denoted by bold letters. A transformation L of the points of the plane is called linear if for any two (column) vectors x and y and for each scalar (i.e. real number) r, the following two rules hold: L(x + y) = L(x) + L(y) and L(rx) = rL(x). Indeed, these rules can be combined into one single rule, that being that for any two vectors x and y and any two scalars r and s,
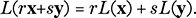(32)
If we let L stand for a 2 × 2 matrix, these rules are satisfied, so that multiplication by such a matrix furnishes a source of linear transformations. More surprisingly, the converse is true: any linear transformation can be realized as multiplication by a suitable matrix, for we proceed as follows. The action of a linear transformation is determined by its action on the two basis vectors
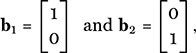
for let us suppose that
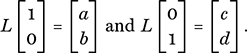
Then, since L is linear, we obtain the following through using (32), with x and y now denoting the multiplying scalars:
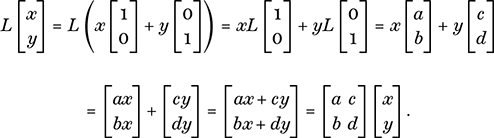
Hence any linear transformation of the plane can be realized by multiplication by a matrix A, the columns of which are the images of the two basis vectors b1 and b2 under L, written in that order.
What is interesting is that if we compose linear mappings, which is to say act with two or more in succession, the outcome is again a linear mapping. This can be verified by working with the abstract definition (32), or we can see it by noting that the composition of two (or more) linear mappings can be realized by multiplying by each of the matrices A and B which represent each linear transformation, one after the other. The bonus here is that, by associativity of matrix multiplication, this composition can be realized by taking the product of the matrices, as B(Ax) = (BA)x. The upshot of this is that, no matter how many linear transformations we act with, we can find a single matrix that has the effect of acting with each of these transformations in turn, in the order that we specify, by taking the corresponding product of matrices.
Two ways in which linear transformations come about are by rotations of the plane about the origin through a fixed angle, and by reflection in a line through the origin. For example, let us find the matrix that has the effect of the following three actions. For each point P(x, y) in the plane, reflect P in the line y = −x, then rotate the resulting point through 90° clockwise about the origin, and finally reflect that point in the x-axis. To find the single matrix that does all this, we need to take the product of the matrices for each of these three transformations, with the first of them on the right and the final one on the left. The three matrices and their product are
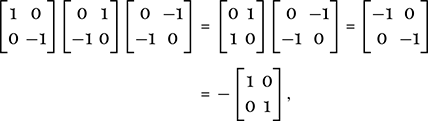
where we have performed the matrix multiplications from left to right. This matrix has the effect that
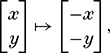
which represents a half turn (180°) about the origin and so that is the net effect of the three transformations. (The symbol ↦ is read as ‘maps to’.)
An important insight stems from how the general linear transformation represented by the matrix
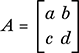
acts on the unit square with corners at the origin, O = (0, 0), and the points (1, 0), (0, 1) and (1, 1). The origin remains fixed while the other three vertices are sent to (a, c), (b, d) and (a + b, c + d), respectively (Figure 15).
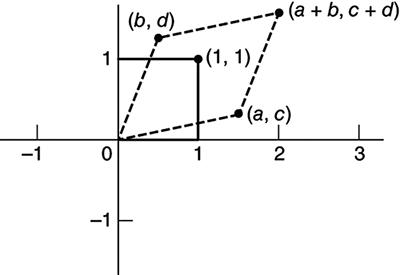
15. Matrix acting on the unit square.
The unit square is then mapped to this parallelogram, the area of which can be shown to equal |ad − bc|. The quantity Δ = ad − bc is known as the determinant of A and it tells us by how much the area of any figure in the plane is magnified (or contracted) when acted on by A. If Δ < 0 then A also reverses the orientation of the figure, in that if a triangle has vertices P, Q, and R, in that order when traced in the anticlockwise direction, then the image triangle will have the respective vertices P′, Q′, and R′ oriented clockwise: it will not be possible to place the original triangle onto its image without breaking out of the plane and flipping it over.
For example, consider our matrices
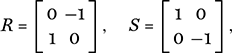
so that R rotates each point through 90° anticlockwise about the origin while S reflects each point in the x-axis. The matrix R does not alter either the area or the orientation of a figure, and so its determinant is det(R) = (0 × 0) − ((−1) × 1) = 0 + 1 = 1. On the other hand, although S does not change areas either, S does swap orientation and this is manifested in the value of its determinant: det(S) = 1 × (−1) − 0 × 0 = −1.
The special case where Δ = 0 is when ad = bc, which occurs if a/c = b/d. In this case the two position vectors from the origin that make up the columns of the matrix both point along the same line through the origin with a common gradient, c/a, and the image parallelogram degenerates to a line segment. The image of any shape is then collapsed along this line and so the area of that image is 0. It remains the case, however, that the absolute value of the determinant of A, |Δ|, is the multiplier of area under the transformation defined by A.
This meeting of the algebraic and geometric worlds is important and we can already see an interesting theorem on offer. If we act with two linear transformations in turn, represented by matrices A and then B, then areas will be multiplied by the multiplier of A followed by that of B, which of course must be the multiplier of the product matrix BA. Moreover, the sign of det(BA) will be the product of the signs of det(A) and det(B), as BA will preserve orientation if both mappings preserve or both reverse orientation but not otherwise. The upshot of this is that the determinant of a product of two square matrices equals the product of their determinants, and since det(A) det(B) = det(B) det(A) we may write
From an algebraic viewpoint, this may seem surprising. It is true nonetheless, extends to higher dimensions, and can be explained in algebraic terms. It is the geometric interpretation, however, that renders the result transparent and, we might even say, ‘obvious’.