3
Domestication in Europe

The domestication of Greek and Arabic physica and mixed mathematics in the Latin West took some 400 years from the first translations in the twelfth century until well into the sixteenth, when Archimedes and Ptolemy were printed and Aristotle’s ancient rivals revitalized. With the generation of Galileo, Kepler, and Francis Bacon, physica’s place in the body of knowledge began to slip, although the Aristotelian world picture still hung securely, if awry, in universities and theological seminaries. The slippage owed much to social factors associated, as in Islamic times, with the bureaucratic needs of newly centralizing states, and also with the discovery of new worlds on the Earth and in the heavens, which revealed that the ancients did not know even half of everything.
At the interface
While Alhazen was solving tough problems in geometrical optics, a polymath, Regimbaldus of Cologne, and a teacher, Rudolphus of Liège, tried to prove that the sum of the angles in a triangle is a straight angle. Not knowing Euclid, they had neither the proof nor the concept of proof, and ended by lining up the angles cut from triangles drawn on parchment. Although their mathematical simplicity was representative of their time and place, savants then existed in the Latin West who could handle hard computations easily. They were masters of computus, the science of the calculation of times of prayer, the dates of movable feasts, and the coordination of calendars. Their master, the Venerable Bede, a Northumbrian monk who died in 735, wrote on physica as well as computus, and dated events anno domini from the year now taken as the first in the Christian era.
Bede’s physica—his understanding of the motions of the planets and the luminaries, of the rotations of the heavens, and the interconvertibility of the elements—came from Pliny’s Natural history and the commentaries on the Hexaemeron by Saints Basil and Ambrose. From the same sources Bede learned that “the ocean tide follows the moon as if the luminary drew the waters behind it and then pushed them back” (thus the saints) and that, owing to the time required for celestial or meteorological events, such as thunder and lightning, to affect the Earth, a delay occurs between high tide and the Moon’s meridianal passage (Pliny). But it was local knowledge that prompted Bede’s important deduction, once acclaimed as the only original contribution to physica from the Latin West in 800 years: the difference in time between the meridian passage of the Moon and the succeeding high tide is a constant at any place. The riddle of the tides, which, according to legend, drove Aristotle to throw himself into the sea, thus acquired an additional complication.
Bede’s knowledge made its way to the Continent via Alcuin of York, who served as Charlemagne’s chief advisor in civilization. Alcuin revived the curriculum of the liberal arts, at least for the court clergy, and stimulated an interest in mathematics, at least of the recreational type. A little book attributed to him comprises 53 perennial problems, for example, river crossings under various restrictions (like the familiar puzzle of the missionaries and the cannibals), and divisions of property. His arithmetical games may have encouraged some students to go on to computus, on which he wrote a tract; but the “Carolingian Renaissance,” which lasted about a century, did not establish a basis on which the likes of Regimbaldus and Rudolphus could build.
One of Alcuin’s tasks was to write against a Christian heresy prospering in Umayyad Toledo. Some of the faithful there entertained unorthodox ideas about the person of Christ. They could not correct themselves as they could not read Latin, although they handled “the Arabic pomposity of language with the greatest erudition.” Umayyad culture beguiled them further with gardens, libraries, and palaces, with scholars, artists, and musicians, and, for the technically minded, with improvements in metalworking, agriculture, waterworks, and trade. The straying sheep were saved from these attractions by the small Spanish kingdoms to the north, which, profiting from the usual divisions within Islamic states, captured Toledo in 1085. The Christian scholars who followed the Christian generals did not care for Arabic poetry. They wanted to learn physica, philosophy, astronomy, and mathematics, partly from curiosity, partly for practical application, and, perhaps mainly, to fortify themselves for arguments with learned Muslims. For, as one of the first scholars to work in Toledo wrote, “our civilization is infantile in comparison with theirs.”
The earliest large-scale translation work in Spain mirrored the effort in Baghdad 400 years earlier. The archbishops of Toledo played the role of the early Abbasid patrons. Translators again invented technical terms via transliteration, bequeathing to English zenith, nadir, azimuth, almanac, algebra, Aldebaran and many other star names, alkali, alembic, elixir, alcohol, a number of things to eat (apricot, artichoke, sherbet), and indications of what made Islamic civilization prosper (bazar, tariff, admiral, arsenal, cotton, muslin, damask). And, as the scholars of al-Mamūn’s House of Wisdom came from many parts of the Islamic world, so Westerners wanting wisdom came from every corner of Christendom. In addition to the Greek corpus, the scientific authorities awaiting their study included, to mention only names already encountered, Albumasar (Abū Ma’shar), Alhazen, Avicenna, Averroes, Avempace, Alfarabus, Alkindus, and Māshā’ Allāh.
“A little learning is a dangerous thing | Drink deep or taste not the Pierian Spring.” The first Latins who tried to apply Islamic astrological physics did not quaff deeply enough before deducing from an upcoming trigon change accompanied by a congregation of planets in Libra (an airy sign) that great winds from the East would dump deserts of sand on European habitations. Consulting their newly acquired authorities, Westerners feared the worst. A friendly Spanish Muslim astrologer wrote the Bishop of Toledo a letter of reassurance. The ignoramuses who made the predictions, “knowing nothing of the virtues of the heavenly bodies and the effects of the five planets and the two luminaries,” had reasoned childishly. There was nothing to fear.
Alma mater
By coincidence, the West had just invented an institution in which to deepen its drinking. This was the universitas or guild organized by teachers accredited for their learning, chartered by the Pope, and supervised by the local bishop. (In a few cases, Bologna being the most prominent, students formed the corporation and hired the professors, see Figure 10.) Although the oldest university in the West, founded by modern consensus in 1088, Bologna dealt primarily in law; the studium generale, comprising at its fullest a preparatory arts faculty and professional schools in theology, medicine, and law, dates from a century or so later, concurrent with the foundations of the universities of Paris and Oxford. To add further dynamism and coincidence, the energetic new mendicant orders, the Dominicans and Franciscans, founded in 1216 and 1223, respectively, soon decided to establish chairs in the arts and theological faculties. Many of the greatest interpreters of Aristotelian physica active in mastering the learning of Greece and Islam were members of these vigorous orders. Thus, in significant contrast to Islam, the Roman Catholic Church embraced rationalistic kalām and produced a scholastic philosophy in which physica had an important place.
Most of the teachers or regent masters in arts were men engaged in the long process of earning a doctorate in theology. The degree they obtained, a bachelor’s (“beginner’s”), conferred the right to teach arts anywhere and thus, with other masters, create a new generation of artists, in a sort of academic apostolic succession. This ius ubique docendi reflected the universal claims of Christendom. Like their Islamic counterparts, Latin scholars had a common language and religion; unlike them, the Westerners had universities that gave institutional continuity and ordered competition in the study of general subjects deemed useful for theology and the lay professions of law and medicine.
Episcopal supervision, clerical professors, and a universal teaching credential did not create uniformity of curriculum or opinion. The arts masters favored Aristotle’s philosophy, as it fell within their domain of knowledge attainable by reason alone. Theologians at first opposed it, not only for its novelty, but also on the sounder ground that it taught many things obnoxious to the Catholic faith. And so, according to its statutes of 1215, the University of Paris required candidates for the bachelor’s degree in arts to have studied Aristotle’s logic and ethics, but prohibited the public reading of his physica and metaphysics. After the studium generale in Toulouse (founded in 1229) advertised that it allowed these works, the Pope, Gregory IX, ordered the University of Paris to separate the useful material in them from the erroneous and scandalous.
Soon the arts masters at Paris were teaching an Averroist Aristotle, literally interpreting the texts and defending their presentations of erroneous and scandalous doctrines as fulfilling a commentator’s duty to his author. This historical method of introducing naturalistic physica, which continued through the time of Galileo’s teachers, did not prevail in thirteenth-century Paris. In 1277 the Bishop, Etienne Tempier, having received the recommendations of a committee of theologians, prohibited over 200 harmful propositions they claimed to have found in Aristotle. With this apparent abrogation of academic freedom, Tempier in fact liberated the Paris faculty from a slavish literal interpretation of the texts and opened the way to wider and wilder speculation. The University of Oxford, which, together with Paris, produced the most advanced physica of the later Middle Ages, adopted proscriptions similar to Tempier’s.
The enduring correction of Aristotelian philosophy through revealed truth was the work of a cosmopolitan Saint, Thomas Aquinas, born in Italy, educated in Paris and Cologne under another saintly exponent of Aristotle, Albertus Magnus, and active as a Dominican master in Paris and Rome. Thomas agreed with Averroes that Aristotle had gone as far as possible on reason alone. To correct for revelation, Thomas replaced the unit Universal Mover by the triune Christian God and the Intelligences by angels, much as the Neoplatonists had done with the One and its emanations, and eliminated the naturalistic errors about Creation, the soul, the vacuum, the displacement of the world, and so on. However, he retained the Aristotelian structure, the quintessential celestial spheres, the four-ring circus of terrestrial elements, the meteorology, and all the paraphernalia of hylomorphism.
Dante took the resultant Christian world picture as the great theater for his journey through Earth to the Devil’s umbilicus and thence through the antipodes, up Mount Purgatory, and past the planets to the divine presence beyond the sphere of the stars. On the way up, Dante stopped at the sphere of the Sun for a talk with the shade of St. Thomas, who appeared in a circle with 11 other sages. Bede was among them, furthest from Thomas; the nearest shades belonged to his teacher Albert and to Siger de Brabant, a champion of Averroist Aristotelianism and Thomas’ unrelenting opponent in life. Their juxtaposition in heaven suggests that the claims of reason deserve a hearing even when in apparent conflict with revealed truth.
University physica
Since most early scholastic writers were theologians, they expounded physica either to clarify obscurities in philosophy or to apply it, after clarification, to doctrinal problems. Take charity. What prompts a philanthropist to give? Since in Aristotelian philosophy the question fell under the category of motion, theologians of charity could make use of concepts developed to analyze physical change. If a shove from the Holy Spirit causes the philanthropist to act, fundraisers should expect giving to slacken just as a ringing bell falls silent. Still, the ringing persists briefly and sometimes so does charity. What causes this persistence? The clapper transfers motion to the bell just as the Holy Spirit conveys a charitable impulse to the philanthropist. Thus the concept of conferred impetus, whether fleeting or enduring, settled into medieval physica. Applied to locomotion, it allowed arrows to fly without being pushed by the air and explained the acceleration of falling bodies as the sum of the impulses acquired in each minute or ell of descent.
The outlawing of Averroistic Aristotelianism at Paris and Oxford encouraged criticism of the fundamental concepts of form and essence. Does “dogginess” exist or is “dog” just the name we give to a group of animals for convenience? The second alternative, nominalism, had its major champion in William of Ockham. His approach to physica in the lectures he gave at Oxford as an inceptor (a bachelor of arts working at theology) irritated the Dominicans and some secular masters. They objected to his conclusions that essences or common natures do not exist, and that general propositions about groups or classes cannot be known to be true. Since the “Venerable Inceptor” (so called because he never finished his degree) held a strict voluntarism (nothing constrains God’s action but the impossibility of compassing a contradiction) he taught that only experience, not a priori deduction, can establish what exists; and that in explaining the apparent relations among things, the fewest possible causes should be invoked (“Ockham’s razor”).
Nominalism favors description over explanation. Hence we find in fourteenth-century Oxford an innovation, introduced by Ockham’s contemporary, Thomas Bradwardine, for discussing the grand question: how does the form of a substance change? Rather than vex themselves over the causes of change, Bradwardine and others at Oxford’s Merton College distinguished between motions at constant speed and at uniform acceleration, and deduced that in locomotion the total distance traversed from rest in a given time at constant acceleration is half the distance that would be traversed at the maximum speed in the same time (the “Mertonian rule”). Although they gave increasingly complicated proofs of their rule, they made no direct applications of it, not even to free fall.
The most distinguished teacher of physica at the University of Paris in the fourteenth century was Jean Buridan, now known primarily for his ass—a donkey with a mind so logical and rigorous that it starved to death for lack of a sufficient reason to choose between two equally attractive bales of hay. Buridan was a nominalist concerned to carve a space for a living Aristotelian physica between the stultifications of Averroism and voluntarism. In a bold step he applied the concept of impetus to the celestial spheres. They would not need angels or Intelligences to inspire them if God gave them an initial push and the quintessence conserved the impetus. Buridan observed further that the Earth must jiggle. Owing to the unequal distribution of land and water, its center of gravity does not coincide with its center of figure. The ongoing processes of erosion and the self-movement of living creatures constantly shift the center of gravity, which in consequence hops about the center of the universe. Perhaps the Earth might even revolve around the center and allow the heavens to rest? Buridan did not build a systematic physics from these fragments. They should be appreciated, rather, as indications of the sorts of things that free thinking within an Aristotelian framework could produce.
Buridan’s prize student, Nicole Oresme, invented a convenient and influential, though misleading, representation of the Mertonian rule. In it a horizontal axis or “longitude” represents space or time, its associated vertical axis or “latitude” the corresponding degree of an accidental quality like place, heat, or color (see Figure 11). In locomotion, the accident was place, the latitude velocity, and the longitude indifferently space or time. The “latitude-of-forms” picture of motion at constant velocity is a rectangle, at constant acceleration a triangle or trapezoid.
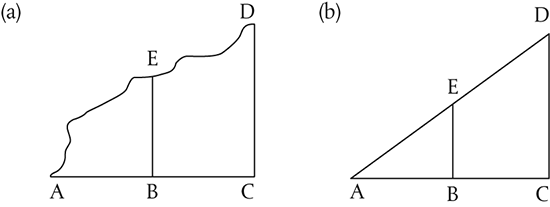
Fig. 11. Motion pictured. (a) AB the “longitude,” usually time or space, BE the corresponding “latitude,” or intensity of a changing form; ABCDE, the “total change” of the form over the entire longitude AC. (b) The case of motion at constant acceleration.
One of Aristotle’s arguments against the possibility of a void makes velocity proportional to the mover’s push P and inversely proportional to the resistance R of the medium, from which the absurdity would follow that velocity in a vacuum would be infinite. To avoid this consequence and a finite velocity P/R when the resistance exceeds the push, Avempace had proposed an arithmetical rule, v∝(P−R). Bradwardine and, after him, Oresme, considered a complicated alternative that can be rendered anachronistically as v∝log(P/R). It had no practical application apart from preserving Aristotle’s argument against the void and making v=0 when P=R.
The teaching that, according to later judges, made the fourteenth century the “Age of Buridan” occurred entirely in the Arts Faculty of Paris. A secular cleric rather than a regular, Buridan did not go on to theology but stayed in arts. In a development of first importance for all liberal studies, arts faculties strengthened against professional ones. A career in arts made long-term cultivation of special subjects possible and offered advancement with age, reputation, and administrative responsibilities. Whereas Bradwardine and Oresme pursued clerical careers (Bradwardine served for a month as Archbishop of Canterbury, Oresme for a few years as Bishop of Lisieux), Buridan rose to be Rector of the Arts Faculty and received several benefices to support his studies. But death levels distinctions, and the Black Plague indiscriminately ended the lives of the Rector, the Bishop, the Archbishop, and the Venerable Inceptor.
Mixed mathematics
Like the impetus theory of charity, statics (scientia de ponderibus) and optics (perspectiva) had a bearing on Christian religion. Although medieval statics could not calculate stresses in a cathedral, it provided some understanding of the effort needed to lift or slide weights into place and keep them there. For example, physica solved the problem of gravitas in situm, the tendency T of a body to slide down an inclined plane, which related to arches and domes. Thābit ibn Qurra and Avempace had made the tendency T equal to the weight of a body W diminished by the ratio of the plane’s height h to its length L, T=(h/L)W. The most important of their Western followers, Jordanus Nemorarius, wrote in the early thirteenth century and was often copied and imitated. He combined the dynamic approach of the pseudo-Aristotelian Mechanica, and its virtual displacements of lever arms, with a geometrical analysis in the style of Archimedes; his packaging of ancient and Arabic contributions to the science of weights served the West for two or three centuries. It was said that an expert in the scientia de ponderibus could weigh divine grace if he followed instructions with sufficient accuracy and faith.
The light of Creation, the Rainbow of the Covenant, and the filtered colors within Gothic cathedrals helped direct Christians to the study of optics. Robert Grosseteste, trained in Oxford and Paris, acted as director of studies in physica and mathematics to the Oxford Franciscans. Beginning at the beginning, Grosseteste imagined the light of Creation to have spread itself like a Neoplatonic emanation, creating space, the celestial spheres, and the rest of the cosmos. This lux (created light) is a general power manifested differently depending on where its lumen (propagating light) operates. Grosseteste’s lux found its ideal medium in Roger Bacon, also educated in Oxford and Paris, where he taught Aristotle’s physica and, in 1257, became a Franciscan. This proved to be a major error since the General of the Order, who became Saint Bonaventure, did not support studies not bearing directly on theology, and rejected two branches of physica, alchemy and astrology, that Bacon esteemed. Bacon’s views continued to annoy his superiors, who jailed him in 1277, perhaps in connection with Tempier’s prohibitions.
Bacon’s development of Grosseteste’s optics invoked the “multiplication of species,” the spherical propagation of lumen from points of lux, which served also as a physical model of astrological influence. Bacon’s Perspectiva incorporated Alhazen’s optical principles, including image formation, except for intromission. Attempting to multiply his influence, Bacon designed a project to refute unbelievers. It required knowledge of languages, mechanics, optics, alchemy, and a scientia experimentalis, “wholly unknown to the general run of students.” He wanted to check speculations about magnetic action, ways to extend life, and the projection of gold. Everlasting lamps and irresistible explosives also belonged to the unusual science of experiment, which Bacon did not practice much himself.
But he did make observations, and thereby put a number on Aristotle’s factoid about the limited height of the rainbow. God placed a maximum of 42° on the altitude of the sign of the Covenant, a number that Bacon, who liked numerology, would have been pleased to know is the answer to the riddle of the universe according to the Hitchhiker’s guide to the galaxy. In the first ever account of rainbow physics, God had written, “It shall come to pass, when I bring a cloud over the earth, that the bow shall be seen in the cloud…And the bow shall be in the cloud.” Subtle is the Lord! Did He mean that the bow exists in the cloud or that we only see it there? Bacon chose the second option and deduced that the observer creates the bow from rays undergoing reflection and refraction when passing through the droplets and air of variable density making up the cloud. Variations of this idea occur in influential works by other theologians: in a Perspectiva (largely a paraphrase of Alhazen) by Erazm Ciołek Witelo (a Polish theologian educated at Paris and Padua), and in a treatise De iride by Theodoric of Freiberg (a Dominican who studied and taught in Paris), which traced rainbow rays reverently and geometrically from the Sun through their reflections and refractions to the eye.
Fresh imports
From the Greeks
As the new universities assimilated their inheritance from Muslim writers, other material of equal importance became available from people fleeing a Byzantium wrecked by crusaders and threatened by other barbarians, and from investigation of material preserved in Italian churches and monasteries. Many Greek manuscripts thus emerged in Italy before the Eastern Roman Empire finally fell to the Turks in 1453. They included the works of Plato and the Neoplatonists, Greek versions of Ptolemy and Archimedes, and bits from the Stoics, Skeptics, and atomists. Just as a new institution, the university, coincidentally arose to receive the Arabic heritage, so a new social movement, Italian humanism, which started among learned secretaries serving the princes of new city states, identified itself with Greek language and literature.
The Greek Almagest that the most famous of the scholarly émigrés, Johannes Bessarion, later a Roman Catholic cardinal, carried to Italy, brought down the curtain on ancient astronomy. As we know, Muslim astronomers had pinpointed discrepancies between Ptolemy’s predictions and observations, as well as the gap between his mathematics and his physics, long before 1453. However, as students tend to blame themselves for not understanding their teachers, so the astronomers of the West supposed that Ptolemy had all the answers; everything might be cleared up by consulting a Greek manuscript free from errors of translation and transcription. The outcome, secured mainly through the efforts of Bessarion’s protégés Georg Peurbach and Peurbach’s student Johannes Regiomontanus (University of Vienna), was decisive. The Greek Almagest did not resolve the problems of astronomy any better than versions made from the Arabic.
While the purified Ptolemy was dashing the hopes of humanist astronomers, other translators were recovering the truths preserved in Platonic treatises. Impressed by intellectual émigrés from Byzantium, Cosimo I de’ Medici desired to resurrect the Platonic Academy in Florence. The great project of this revival was the translation not only of Plato but also of Plotinus and other Neoplatonic philosophers. Cosimo confided the task to Marsilio Ficino, who considered himself a Christian sage in the Platonic line. On Cosimo’s orders, Ficino began not with Plato’s dialogues but with the work of Hermes Trismegistus, a hodgepodge of Christian, Neoplatonic, and Gnostic thought put together in the third century ce. Most humanists regarded these writings as very ancient and Ficino, impressed by their apparent anticipation of Scripture, thought that Hermes was contemporary with Moses or, perhaps, Moses himself. Hermes taught among other things that celestial influences both good and bad can be captured in talismans as well as in people, and that, therefore, a physicus willing to experiment might add useful astrological powers to physica.
The Platonic Academy’s Latinized Plato spread the Pythagorean doctrine that made mathematics the queen of physica rather than, as in the standard teaching, at best a handmaiden. In 1464, when Ficino had just started his translations, Regiomontanus promoted the Pythagorean vision in a lecture in Padua on Islamic astronomy and astrology. The lecture, decorated with humanist references, recommends the study of astrology as the highest, noblest, and hardest branch of mathematics, through which “we are brought near to Immortal God no less than through the other arts we are set apart from wild beasts.” Regiomontanus drew from his ability to master the “angelic art” of astrology a confirmation of Hermes’ dictum, “man is a magnum miraculum,” perhaps as high on the scale of being as demons.
Among the astronomers encouraged by this insight was another Northern European perfecting himself as a humanist in Italy. Nicholas Copernicus, born the year Regiomontanus published Peurbach’s epitome of Ptolemaic planetary theory (1473), studied at the University of Cracow and then, in 1496, went to Italy to learn law and medicine in preparation for an ecclesiastical career. He also studied Greek literature. His subsequent position as a cathedral canon in a region contested by Polish and German princes, and also by Prutenic Knights, left him little time to polish his version of proper astronomy. This turned on the objection pushed by Averroes, al-Tūsī, the Marāgha school, and Ibn al-Shātir: Ptolemy’s use of improper devices like the equant point. Copernicus removed it using constructions that convert circular to rectilinear motion probably taken from Arabic astronomers (“al-Tūsī’s couple”), although no persuasive path of transmission has been established. But the boldness and confidence that prompted Copernicus to go beyond removing the supposed blemishes of the equant to place the Sun at the world’s center did not have a counterpart in Islamic astronomy.
The description of the apparent motions of the Sun, Moon, and stars is equivalent whether the Sun or the Earth stands still. By making the Sun the center of motion, however, Copernicus could do what Ptolemy could not: calculate the distance from the Sun to a planet as a multiple of the radius of the Earth’s orbit. His ordering of the planets and his consequent explanations of the limited elongations of Mercury and Venus, and the retrogradations of Mars, Jupiter, and Saturn, were the anchors of his claim to have made a system out of Ptolemy’s bric-a-brac (see Figure 12). Copernicus’ masterpiece, De revolutionibus orbium coelestium, appeared in 1543 with an unsigned preface by a Lutheran controversialist, Andreas Osiander, who saw the manuscript through the press. Anticipating objections from theologians, he rehearsed the usual arguments against taking mathematical constructions as truths of nature. Perhaps in consequence, the book did not excite theologians for 70 years. However, it caused an immediate ruckus among physici, who saw that it disagreed more profoundly with physica than Ptolemy’s fictions.
Copernicus addressed some of the obvious objections, like the removal of the Earth from the universal center of heavy bodies, the lack of a power to move it in orbit, the fact that falling bodies do not land west of the vertical through their drop point, and so on. Some of his answers were physical (separated bits of planets fall to their centers, objects on a rotating planet participate in its motion) and some rhetorical, invoking a spectrum of ancient writers prized by humanists (Plutarch, Pythagoreans, Plato, Virgil, Hermes, Sophocles) who said things favorable to belief in a Sun-centered universe. Although some of Copernicus’ answers pointed toward a viable new physics, they left much to do before an adequate replacement for standard physica, with a suitable role for mathematics, could even be sketched.
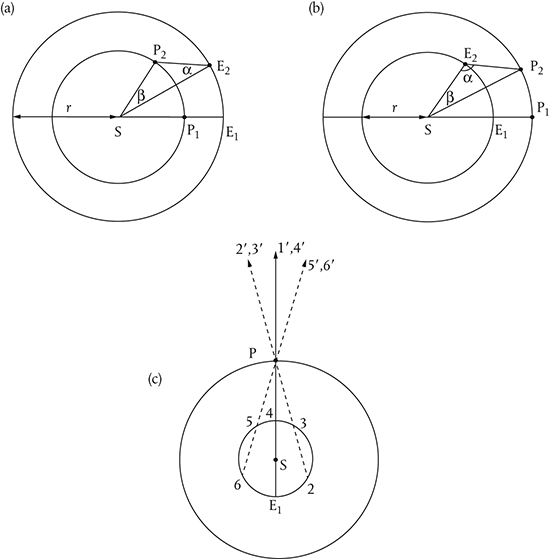
Fig. 12. Heliocentric advantages. Copernicus allows the computation of the solar distances of the planets P in terms of the Sun–Earth distance r. (a) The limited elongations of the “inferior planets” Mercury and Venus is a consequence of Earth’s orbit encircling theirs; (b) the “superior planets” Mars, Jupiter, and Saturn can be seen anywhere because their orbits encircle Earth’s; in both cases, α can be measured and β calculated from the known sidereal periods. (c) The superior planets appear to move backward, or “retrograde,” against their usual cc motion as the Earth overtakes them, as between positions 2 and 4. For convenience, P is pictured as stationary.
While the cause of mathematics as natural philosophy went forward with the help of Plato’s rediscovered eloquence, humanists brought forth another, greater threat to Aristotelian physica in the form of Latin poetry. This was the long-lost work of Lucretius, found in the early fifteenth century and printed for the first time in 1473. The notion that our world is but one of an infinite number composed for no purpose by innumerable atoms tumbling forever through infinite space was not wholesome doctrine for Christians. St. Jerome, who knew the poem, offered the monkish explanation of its perversity that its author went insane from an overdose of aphrodisiac. Nonetheless, the beauty of Lucretius’ descriptions of the couplings of the atoms recommended his poem to all lovers of Latin, and helped to insinuate atomism in its various forms as an alternative to the physica of the schools, the mathematizing of the Platonists, and the Hermetic account of occult influences. Like Averroism, atomism became a dangerous subject during the confessional disputes of the sixteenth century, when the charge of heresy could be leveled to help win philosophical arguments, and Aristotelian physica became officially entangled with theology and the dangerous doctrine of the Eucharist.
From the real world
The tolerance of ambiguity in medieval thought—represented in great matters by compromises between reason and revelation, and in small ones by fuzziness in the concepts of impetus and the latitude of forms—began to give way to more exact forms of knowledge and action during the fifteenth and sixteenth centuries. The main causes of this hardening were the rise of powerful competing orders within the Roman Catholic Church; the Protestant reformation and the Catholic response; the discovery of the new world and its exploration; and the invention of printing. Religious controversy required clear definition of the points at issue among Catholic orders and Protestants sects. The Catholic Church replied not only by strengthening dogma and discipline through the decrees of the Council of Trent, but also by setting up a regime of thought police: the Holy Roman Inquisition (the Holy Office), the Congregation of the Index of Prohibited Books, and the Society of Jesus (the Jesuits).
On the secular side, the European discovery of America intensified the bureaucratic needs of the states competing in the new world. Managing the fleets, keeping track of the influx of precious metals, surveying the new possessions, and teaching and improving navigation, cartography, and geography opened new opportunities for applied mathematicians already in demand as architects, urban planners, and hydraulic engineers. Calculations, whether correct or not, depend on hard edges. Large collections of unfamiliar material brought back from exploratory voyages, and reports of the strange behavior of peoples who did not have the happiness of being European, increased the demand for minds able and energetic in denying and distinguishing. And, to complete this hasty inventory, printing, by replacing costly and imprecise manuscript copying with more-or-less exact reproductions, gave scholars relatively easy access to standard texts. Standardization and definition did not resolve disputes, but made it more likely that the parties to them argued about the same things.
Many consequences for physica of the hardening of the edges and the standardization of texts may be discovered in Galileo’s work. When professor of mathematics at the University of Padua, from 1592 to 1610, he took in private students of aristocratic rank who came to learn the use of surveying and measuring instruments. His expertise in designing practical devices enabled him to transform a spyglass of little magnification into a 30-power telescope in a few months. The printing press helped “the new Columbus” to spread news of his implausible telescopic discoveries—mountains on the Moon, satellites around Jupiter, stars in the Milky Way—as it had given him access to the books of Euclid, Archimedes, Ptolemy, and Copernicus, from which he drew inspiration. When he interpreted his discoveries in ways that conflicted with the views of the Pope and the Inquisition, the hard-edged institutions of the Catholic Counter-Reformation came into play, and condemned the Copernican world picture. Galileo’s conclusions catapulted astronomy into the contested arena of physica and himself from a professorship of mathematics at the tolerant Venetian University of Padua to the dangerous height of “Philosopher and Mathematician to the Grand Duke of Tuscany” in the bigoted Medici court in Florence.
Galileo’s friend Pope Urban VIII was a cultured Florentine and man of the world. Yet he believed on grounds stronger than Plato’s that the unaided human mind cannot arrive at secure truths about the natural world. Urban had followed the logical track of God’s Omnipotence and Freedom to an extreme voluntarism and the conclusion that, however well our theories fit the facts, God could have contrived to bring about the same phenomena in countless other ways. Galileo countered that his business was not to imagine how God might have done things, but to discover the method He chose. His spirited defense of Copernican theory, made in his Dialogue on the two chief world systems (1632) after the Holy Office had found heliocentrism contrary to Scripture and “philosophically absurd” in 1616, precipitated his trial, condemnation, humiliation, and perpetual house arrest.
It was not this suffering that made Galileo a hero to later physicists, however, but his attack on physica under the banner of mathematics. His target at first was the nub of Aristotelian philosophy, the doctrine of motion. When a young professor at the University of Pisa, he replaced the supposedly Aristotelian formula, v∝P/R, with Avempace’s rule, interpreting P−R in Archimedean terms as the difference between the specific gravities of the falling body and the resisting medium. If Galileo dropped weights of different materials from the Leaning Tower as the legend started by his last pupil, Vincenzio Viviani, has it, he would not have expected them to descend at the same speed.
Galileo came to greater enlightenment by abandoning the search for causes. He gave up on Archimedes as he had on Aristotle and entered into a free fall with no goal in sight other than a mathematical description of the journey. He found and confirmed by some mixture of experiment and conjecture that (as he first expressed it in 1604) bodies descending freely from rest cover, in successive intervals of time, spaces proportional to the odd numbers beginning with one. Representing his rule by a graph identical to the medieval picture of the latitude of forms, with instantaneous velocity as the horizontal axis and space traversed as the area, he had, as he wrote it, ΔABE:ΔACD=AB2:AC2 (Figure 11b, rotated 90°). Since he intended the graph not as a qualitative illustration but as a representation of mathematical relationships, he had to decide what the latitudes and the triangles stood for. Initially he fell for the obvious choice, taking the vertical axis to be the distance of fall. Eventually he realized that the choice led to impossibilities. Taking then the vertical axis as time, he had a successful plot, at the major expense, however, of the counterintuitive identification of a line with time and an area with distance. With this sacrifice or advance he achieved the now celebrated, but then not obviously useful, result that distance traversed under constant acceleration from rest is proportional to the square of the elapsed time.
Galileo’s kinematical method, ignoring forces and causes, was perfectly adapted to the contest over world systems and probably owed something to it. The traditional circles and epicycles, which turned without any specified force, and which Copernicus also employed, are kinematical devices. As everyone knowledgeable knew, without a physics (and a theology!) to determine the world’s center, the circles might be referred to the Sun or the Moon and the appearances be saved. Hence neither of the chief world systems, nor their chief competitor—the system worked out by the most exact of observers, Tycho Brahe, in which the planets go around the Sun while the Sun circles the Earth—could be affirmed to be true on the basis of astronomical observations alone. Galileo tried to go further, and to reduce gravitational fall and the effect of the Earth’s rotation to purely kinematical and geometrical relations, and so defeat the standard physical arguments against the Earth’s diurnal rotation. He also devised a kinematical argument to show that only if the Earth moved as Copernicus said it did would there be diurnal, monthly, and annual tides, and published his theory as the provocative conclusion to his Dialogue. To counter the impression that he believed in the condemned Copernican system, Galileo saved the day but not himself by having the dunce of the Dialogue undercut all world systems with Urban’s voluntarist epistemology. The Pope never forgave Galileo for trashing his powerful philosophy of science, with which he had hoped to answer all challenges to Scripture and papal dicta that physica could mount.
Galileo situated his Dialogue in a place fit for a discussion of liberal arts—a palace on the Grand Canal in Venice. He chose the Venetian Arsenal, a shipbuilding complex, for his Discourses on two new sciences (1638), which treated the strength of beams and exterior ballistics. Although his geometrical analyses of these problems were of little practical value, they indicated what a quantitative applied physics might look like; and his technique of compounding a constant velocity imparted by the cannon with an accelerated drop caused by gravity, from which he derived the ideal parabolic trajectory of missiles, became fundamental to analytical mechanics.
In moving his discussants from palace to workshop, Galileo made common cause with a few physicians and other university-trained men who took a sustained interest in the physical principles of practical devices. One of the doctors, Georg Agricola—a learned humanist who practiced in mining regions—illustrated extractive and metallurgical techniques so as almost to thrust the concepts of force, momentum, and pressure into the reader’s mind (see Figure 13). The other doctor, William Gilbert—an English physician fascinated by the magnetic compass that enabled the trade and piracy of London—studied lodestones intensively in what was the first sustained, systematic experimental investigation in the long history of physica (De magnete, 1600). Gilbert invented instruments to measure the dip and declination of a compass needle moved around a spherical lodestone, which performed like a little earth, a terrella, magnetically speaking. His method of arming magnets to increase their power instructed Galileo, and his premise that the Earth was a big magnet inspired Kepler. In vituperation of his opponents, “intoxicated, crazy, puffed-up…lettered clowns,” and his evaluation of his accomplishments, “novel, unheard-of, and opposed to everybody’s opinions,” he almost outdid them both.
A final example, Simon Stevin, made his living as an engineer and state administrator after a late matriculation, in 1583 at the age of 35, at the University of Leyden. The slow start brought him into contact with a fellow student, Maurice of Nassau, who would soon become the head of the United Netherlands. Stevin served Maurice as tutor, military engineer, and quartermaster, and worked with Dutch-reading applied mathematicians as an authority on statics, astronomy, and fortification. Although, unlike Galileo, Stevin made practical devices that worked, they took up many of the same theoretical problems and arrived at similar results, for example, the composition of velocities and the strength of gravity on planes of different slopes. Stevin declared for Copernicus publicly in 1608, before Galileo did, and proposed a method to find the longitude at sea using magnetic data no more practical than Galileo’s scheme using eclipses of Jupiter’s moons. In short, Stevin wrote on almost the entire canon of mixed mathematics, and would have been more influential in his time, and better known in ours, had he not written it in Dutch.

Fig. 13. Applied physics around 1550. A series of pumps removing water from a mine. The series overcame nature’s limit of a 30-foot rise for a single pump. From Georg Agricola’s De re metallica (1556), a coffee-table book describing rough technology in polite Latin.

Fig. 14. Royal Academicians. Louis XIV’s main minister, Jean-Baptiste Colbert, presents the Académie royale des sciences to its master. The unfinished Royal Observatory (completed in 1671) appears in the background.