IN questo capitolo apprenderete la terza capacità fondamentale del disegno, e cioè come valutare e riprodurre i rapporti tra gli oggetti. Imparerete a disegnare «in prospettiva» e «in proporzione», in altre parole «a misurare a vista», capacità forse comparabile all’apprendimento delle regole del leggere e dello scrivere.
Proprio come un corretto uso della grammatica ci permette di formulare parole e frasi nel modo giusto consentendoci di comunicare con chiarezza le nostre idee, una valida misurazione a vista di proporzioni e prospettiva fa sì che contorni, spazi, rapporti, luci e ombre concordino con la logica visiva. Una chiara percezione dei rapporti ci permette di dipingere su una superficie piatta il mondo che vediamo intorno a noi. In più, proprio come imparare a usare la grammatica con perizia ci dà il potere delle parole, capendo come disegnare in prospettiva e rispettando le proporzioni darà forza ai vostri disegni grazie all’illusione dello spazio.
Quando parlo di grammatica mi riferisco ai meccanismi del linguaggio, non all’analisi logica delle parti del discorso, e quando mi riferisco a tali principi intendo la concordanza di verbo e soggetto, secondo le regole della declinazione e la struttura della frase, e così via. Non potrei eseguire l’analisi logica di una frase complicata se non avessi prima assimilato i canoni del linguaggio tanto da farli diventare automatici. Questo è ciò a cui vogliamo arrivare in questo capitolo: imparerete a servirvi della prospettiva e delle proporzioni; non apprenderete terminologie noiose e inutili su punti di fuga, linee parallele convergenti, prospettive di ellissi; studierete i meccanismi della misurazione a vista, che la maggior parte degli artisti utilizza.
Alcuni miei allievi, tuttavia, lamentano che, dopo il piacere di disegnare bordi e spazi negativi tipico della funzione D, la misurazione a vista sembra una funzione dell’emisfero sinistro. In verità, al principio vi sono molti piccoli passi da compiere e brevi istruzioni da seguire. D’altra parte, quasi tutte le attività comportano un’analoga fase preliminare. Per esempio, imparare a guidare un’automobile necessita che voi abbiate assimilato le norme stradali. Noioso? Sì, ma non potete farne a meno, se non volete essere arrestati o avere un incidente. Una volta acquisite tali regole, però, guiderete «automaticamente», senza più pensare al codice della strada.
Lo stesso accade per il disegno. Man mano che passate da un esercizio a quello successivo, avrete imparato le «norme stradali» del disegno. Con un po’ di pratica, la misurazione a vista diventerà un automatismo e non vi renderete conto che state misurando a vista e confrontando dimensioni. Ma soprattutto sarete in grado di riprodurre nei vostri disegni lo spazio tridimensionale.
Alcuni studenti mostrano serie difficoltà nel misurare a vista i rapporti e si trovano a compiere regolarmente errori sconcertanti per quanto riguarda la prospettiva e le proporzioni. Tutto ciò è fonte di preoccupazione per i principianti e, oso aggiungere, talvolta anche per chi è più avanti nell’apprendimento.
Perché acquisire tale capacità sembra così arduo? Anzitutto, la misurazione a vista è una capacità che si compone di due parti: la prima consiste nel misurare gli angoli in rapporto alla verticale e all’orizzontale, la seconda nel misurare il rapporto tra una dimensione e l’altra. Inoltre, tale capacità ha a che fare con rapporti e raffronti, che sembrano tipici dell’emisfero sinistro. E, per finire, non è raro che ci si trovi di fronte a veri e propri paradossi. Per esempio, possiamo sapere che un soffitto è piatto e l’angolo tra soffitto e parete è retto. Ma sul piano d’immagine i bordi del soffitto non sono orizzontali e gli angoli non sono affatto retti. Come potete immaginare, dovrete battere in astuzia la funzione S che ben presto dirà : «Non ha senso!» oppure: «È troppo complicato! Non ce la farò mai» o ancora: «È una cosa stupida!»
Credetemi, imparare a misurare a vista i rapporti tra le cose non è noioso ma stupefacente: è uno spazio che si apre davanti a voi. Certo, non è semplice, ma avete assimilato altre cose complicate prima d’ora, come leggere e scrivere, per esempio. E misurare a vista alla fin fine non è così stupido, anzi è intellettualmente affascinante: ne sono testimoni i più grandi pensatori del Rinascimento che dibattevano su come dipingere lo spazio su una superficie piana.
Una volta che le lamentele della funzione S sono state tacitate, credo che vi divertirete ad apprendere la misurazione a vista, e molto. Sono sicura che possiate già da ora capire il collegamento tra imparare a vedere e disegnare ciò che è davanti ai vostri occhi ed essere una persona più «acuta», capace di far fronte a informazioni contraddittorie e ai molti paradossi del nostro mondo. Siate pronti a ogni tipo di obiezione. La vostra funzione S vivrà una giornata campale, ma abbiate fiducia in me e tutto vi sarà più chiaro.
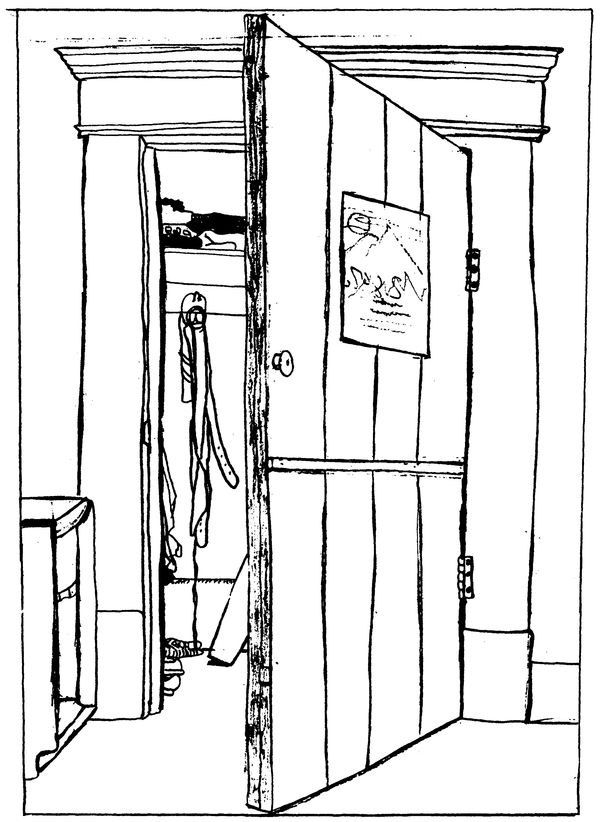
Lupe Ramirez.

Disegno dimostrativo di Grace Kennedy.

Disegno dimostrativo dell’autrice.
Imparare a misurare a vista angoli e dimensioni
Il significato di «misurare a vista» è vedere, ma nel modo dell’artista, i rapporti tra cose diverse sul piano d’immagine (figg. 8-1 e 8-2). Tutto nel misurare a vista è confronto: «Che cos’è quest’angolo in rapporto alla verticale? Quanto è grande la mela paragonata al melone? Qual è la larghezza del tavolo rispetto alla lunghezza?» Gli unici a essere costanti sono i termini di paragone: gli angoli sono confrontati con le costanti verticale e orizzontale, come le dimensioni sono raffrontate con una costante: la nostra unità di base.

Fig. 8-1. Arrotolate un foglio di carta a tubo e controllate il rapporto tra le dimensioni di un oggetto vicino a voi (la testa di qualcuno, per esempio) e di un oggetto simile ma più lontano. Rimarrete stupiti dall’apparente diversità delle dimensioni.

Fig. 8-2. Laurie Kuroyama.
Notate quanto è diversa la grandezza della testa vista da vicino e da lontano.
In matematica, i rapporti sono espressi in numeri – 1:2 significa uno di questo contro due di quell’altro – e il concetto di rapporto sembra essere tipico della funzione S, essendo esso fortemente connesso nella nostra mente alle operazioni matematiche. In realtà, noi ci avvaliamo di rapporti in molte attività quotidiane: nel cucinare, per esempio, il caramello è costituito da una parte di acqua e due parti di zucchero (1:2); nel leggere le carte geografiche, la città X è tre volte più distante rispetto alla città Y (1:3). Nel disegno i rapporti diventano mezzi funzionali per stabilire le relazioni proporzionali tra le parti di una composizione. L’artista sceglie un’unità di base («uno»), e quella unità è rapportata o raffrontata con le altre parti.
Per darvi un’idea, la larghezza di una finestra può essere chiamata «uno», l’unità di base. A confronto, diciamo che l’altezza della finestra è due volte la larghezza (1:2). L’artista disegna la larghezza, la chiama «uno», la misura come «uno» e poi misura due unità, contando: «uno a uno, due». Il rapporto è 1:2. È un modo efficace per classificare e ricordare una proporzione abbastanza a lungo da trasferirla poi nel disegno.
Trattando di paradossi, un tavolo appiattito sul piano d’immagine può sembrare (misurato a vista) più stretto di quanto non ritenete che esso sia (fig. 8-3): il rapporto, per esempio, potrebbe essere di 1:8. In base alle vostre nozioni, quel tavolo non può essere tanto lungo e stretto; ma dovete imparare ad «accettare» il paradosso visivo e disegnare ciò che vedete sul piano. Paradossalmente, soltanto così il tavolo del vostro disegno apparirà delle dimensioni e della forma del tavolo reale. Inoltre, gli angoli del tavolo appaiono diversi da quelli che voi sapete essere angoli retti. Anche in questo caso dovete «accettare» il paradosso.
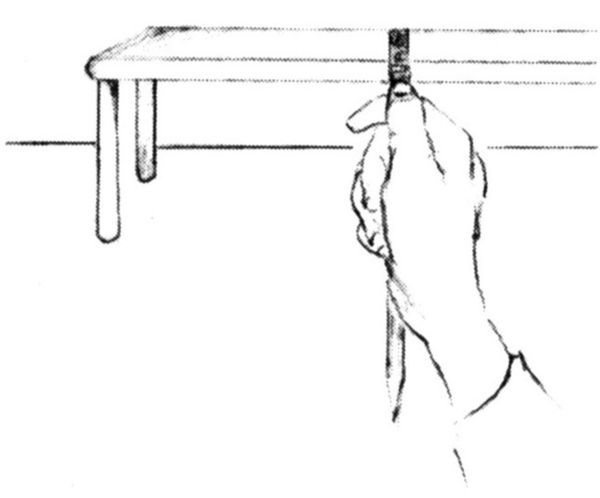
Fig. 8-3.
Prospettiva e proporzione
Per imparare a disegnare in prospettiva bisogna vedere le cose così come appaiono ai nostri occhi. Sia per risolvere un problema sia per fare un disegno dobbiamo accantonare i preconcetti, gli stereotipi e i modelli di pensiero che abbiamo immagazzinato nella memoria. Dobbiamo sconfiggere le false interpretazioni, spesso dovute alla nostra idea di come le cose dovrebbero essere, idea che magari ci siamo fatti senza aver mai guardato bene ciò che abbiamo davanti agli occhi.
Sono sicura che ormai vi è chiara la connessione tra la soluzione di problemi (in ogni campo) e l’arte del disegno. È necessario anzitutto esaminare i fattori importanti e situare le cose «in prospettiva» e «in proporzione». Tale processo richiede la capacità di vedere le varie parti di un problema nel loro reale rapporto.
«Il punto di vista merita otto punti di quoziente intellettivo.»
ALAN KAY
informatico e borsista Disney
La misurazione a vista può essere usata anche per valutare il rapporto tra lunghezza e larghezza. Per disegnare un tavolo visto di scorcio, per esempio, l’artista anzitutto valuta gli angoli, cioè l’inclinazione delle linee rispetto alle costanti verticale e orizzontale, con la misurazione a vista, come nella figura 8-4.
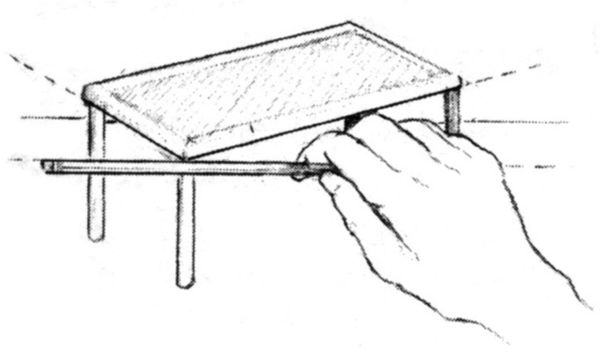
Fig. 8-4.
Il passo immediatamente successivo consiste nel misurare la larghezza del tavolo in rapporto alla lunghezza, come appare da quel particolare punto di vista. Questo rapporto tra larghezza e lunghezza varia a seconda del punto di vista, dipende cioè dal livello degli occhi dell’osservatore.
1. Tenendo la matita parallela al piano degli occhi e con il braccio perfettamente teso per mantenere una scala costante, misurate la larghezza del tavolo. Dovrete far coincidere l’estremità della matita con un angolo del tavolo e mettere il pollice in corrispondenza dell’altro angolo. Questa è la vostra unità di base (fig. 8-5).
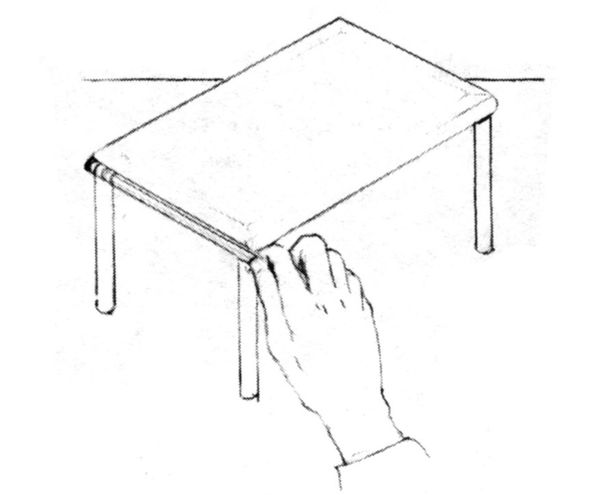
Fig. 8-5.
2. Sempre col braccio teso e la matita parallela al piano degli occhi, riportate quella misura sul lato lungo del tavolo. Quante volte la larghezza sta nella lunghezza? Diciamo, per esempio, una volta e mezzo (1:1½; fig. 8-6).
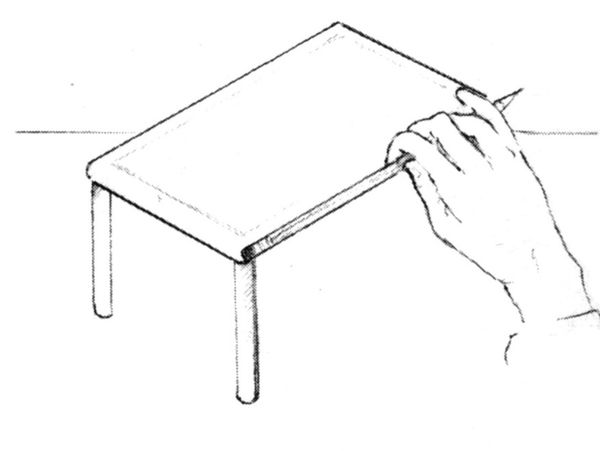
Fig. 8-6.
3. Passate ora alle gambe del tavolo. Tenendo la matita verticale, valutate l’angolo creato da una delle gambe in rapporto alla matita stessa. Sono perfettamente verticali o formano un angolo? Cominciate col disegnare le gambe più vicine a voi. La lunghezza di ciascuna gamba andrà misurata a vista sempre in rapporto alla larghezza del tavolo, che rappresenta l’unità di base (fig. 8-7).
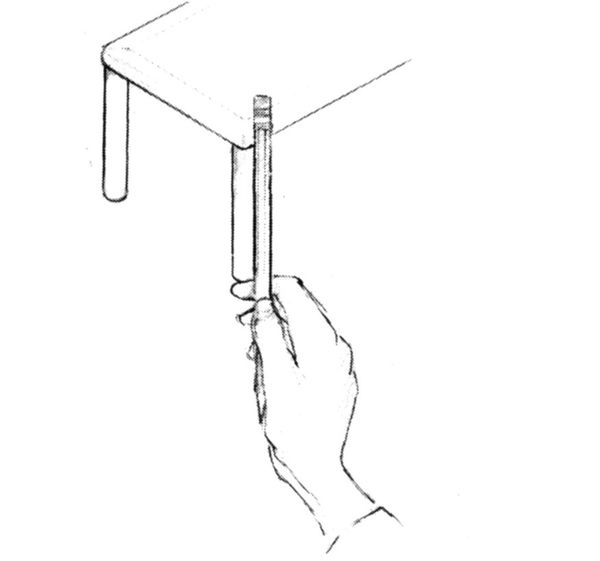
Fig. 8-7.
Definire la prospettiva
Il termine «prospettiva» deriva dal latino prospicere, che significa «guardare innanzi». Il sistema a noi più familiare, quello della prospettiva lineare, fu perfezionato dagli artisti europei durante il Rinascimento; esso consentiva di riprodurre le variazioni visive di linee e forme così come appaiono nello spazio tridimensionale.
Altre culture, come quella egiziana o quella orientale, elaborarono un tipo di prospettiva diverso, a gradini o a livelli sovrapposti, in cui la posizione nello spazio di un oggetto era indicata dalla sua collocazione, più in alto o più in basso, sulla superficie pittorica. Secondo questo sistema, spesso usato in modo intuitivo dai bambini, le forme, indipendentemente dalla loro grandezza, più si trovano in alto nel disegno più sono considerate lontane. In tempi più recenti gli artisti si sono ribellati alle rigide convenzioni prospettiche e hanno ideato nuovi sistemi basati sulle qualità astratte e spaziali del colore, della struttura, della linea e della forma.
Tuttavia, la tradizionale prospettiva rinascimentale è quella che meglio corrisponde al modo occidentale di percepire gli oggetti nello spazio. Le linee parallele sembrano convergere verso uno o più punti di fuga sulla linea dell’orizzonte (che si trova al livello degli occhi di chi guarda) e le forme sono tanto più piccole quanto più sono lontane. Di conseguenza, per eseguire un disegno rigorosamente realistico si dovranno osservare scrupolosamente le leggi della prospettiva. Questo metodo è chiaramente illustrato nella figura 8-8, che riproduce un’acquaforte di Albrecht Dürer.

Fig. 8-8. Albrecht Dürer, Disegnatore che ritrae una donna in prospettiva (1525). The Metropolitan Museum of Art, New York. Dono di Felix M. Warburg, 1918.
Il congegno di Dürer
Albrecht Dürer, grande artista del XVI secolo, ideò un congegno per facilitare la resa corretta delle proporzioni e della prospettiva. Il vostro foglio di plastica trasparente è una versione semplificata del dispositivo di Dürer. Nella figura 8-8, in cui è riprodotto tale congegno, vediamo un disegnatore che, tenendo la testa eretta e immobile (notate lo strumento verticale che serve a fissare il suo punto d’osservazione), guarda attraverso un reticolo posto verticalmente tra lui e il soggetto. Dal suo punto d’osservazione egli ha una visione prospettica della modella, vale a dire che l’asse principale della figura (che va dalla testa ai piedi) è in linea con la direzione dello sguardo dell’artista. In questo modo le parti più distanti della figura (testa e spalle) appaiono più piccole di quanto non siano in realtà, mentre le parti più vicine (le gambe dal ginocchio in giù) appaiono più grandi.
Il disegnatore di Dürer ha davanti a sé, sul tavolo, un foglio di carta delle stesse dimensioni dello schermo verticale e identicamente quadrettato. Egli disegna sul foglio ciò che vede attraverso la griglia, riproducendo sulla carta gli angoli, le curve, le lunghezze dei contorni in rapporto alle linee verticali e orizzontali del reticolo stesso. In realtà, sta copiando ciò che vede appiattito sul piano d’immagine. Se egli copia esattamente ciò che vede, traccerà sulla carta un’immagine in prospettiva della modella. Le proporzioni, le forme e le misure saranno diverse da quelle reali del corpo umano che l’artista conosce, ma solo disegnando proporzioni non reali egli otterrà un’immagine che sembra reale.
Che cosa vede il disegnatore di Dürer attraverso il reticolo? (vedi fig. 8-9). Egli osserva il punto 1, il ginocchio sinistro, e disegna questa parte sul foglio reticolato. Poi osserva il punto 2, il dorso della mano sinistra, il punto 3, il ginocchio destro. Dopo queste parti, osserva il busto e la testa. Alla fine, dopo aver collegato tutti questi punti, otterrà un disegno in prospettiva dell’intera figura.
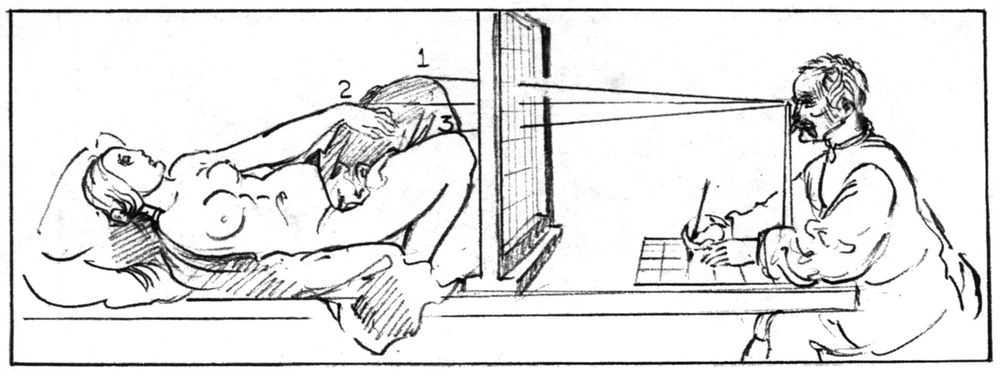
Fig. 8-9. Ciò che vedeva Dürer: misurazione a vista delle parti a una a una.
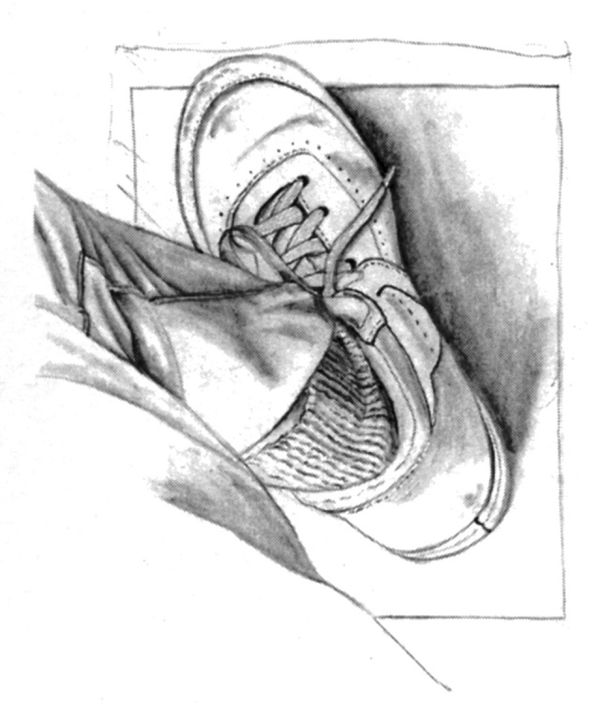
Veduta prospettica di una gamba e di un piede, come vengono visti, appiattiti, sul foglio trasparente.
Quando vogliamo disegnare qualcosa in prospettiva, la nostra difficoltà sta nel fatto che le nostre nozioni sul soggetto in qualche modo interferiscono col nostro lavoro e noi finiamo per disegnare ciò che sappiamo anziché ciò che vediamo. Lo scopo del congegno di Dürer era questo: usando il reticolo e uno strumento che fissasse il punto d’osservazione, l’artista era costretto a disegnare l’immagine esattamente come la percepiva, con tutte le sue proporzioni «sbagliate». Ma poi, paradossalmente, il disegno «appariva giusto». E chi lo vedeva magari si domandava come avesse fatto l’artista a farlo sembrare «così vero».
In sintesi, la conquista della prospettiva rinascimentale fu di codificare e ridurre a sistema un metodo grazie al quale gli artisti aggiravano l’ostacolo costituito dalle nozioni sulle forme e sulle figure. La scienza della prospettiva «formale» forniva gli strumenti mediante i quali essi potevano disegnare le forme così come l’occhio le percepiva, comprese le distorsioni ottiche dovute alla posizione dell’oggetto nello spazio in rapporto al punto d’osservazione.
Il metodo si rivelò molto efficace e rese possibile creare un’illusione di profondità su superfici piane, cioè ri-creare il mondo visibile. Il semplice congegno di Dürer si sviluppò in seguito in un elaborato sistema matematico che dal Rinascimento in poi gli artisti usarono per superare le proprie resistenze mentali alle distorsioni ottiche delle forme reali e per dipingere in modo realistico.
Graham Collier, docente di belle arti, scrive che il sistema prospettico rinascimentale nella fase iniziale del suo sviluppo venne applicato con creatività e immaginazione per offrire nella pittura quella che doveva essere una emozionante impressione di spazio.
«Ma, pur nella sua efficacia, la prospettiva finisce per impoverire la visione naturale dell’artista, una volta che viene accettata come sistema, come formula meccanica.»
GRAHAM COLLIER
Form, Space, and Vision, 1963
Prospettiva formale contro prospettiva «informale»
Il sistema della prospettiva formale, tuttavia, non è senza problemi. Una rigorosa applicazione delle regole della prospettiva può produrre disegni rigidi e piuttosto aridi. Il problema maggiore è però un altro: questo sistema fa appello soprattutto alle facoltà dell’emisfero sinistro, perché comporta processi analitici, computistici, logici, di pensiero propositivo e di calcolo mentale. Si ha a che fare con punti di fuga, linee dell’orizzonte, prospettive di cerchi e di ellissi e così via. È un metodo articolato e ingombrante, del tutto antitetico al modo di procedere dell’artista – il modo della funzione D – che è giocoso/serio e piacevole. Per esempio, in qualsiasi applicazione, esclusa la più semplice prospettiva con un solo punto di fuga (fig. 8-10), i punti di fuga possono trovarsi ben oltre il margine della carta da disegno, richiedendo numerosi strumenti per tracciarli.

Fig. 8-10. Una classica rappresentazione prospettica. Notate che le linee verticali rimangono verticali, mentre le linee che nella realtà sono orizzontali convergono verso un punto di fuga sulla linea dell’orizzonte (che si trova sempre al livello degli occhi dell’artista). Questa in breve è la definizione di prospettiva con un punto di fuga. La prospettiva a due e a tre punti di fuga è assai più complessa e richiede un grande tavolo da disegno, squadre a T e altri strumenti, poiché spesso i punti di fuga sono situati ben al di fuori del foglio. La prospettiva basata sulla misurazione a vista è assai più facile ed è sufficientemente precisa per quasi ogni tipo di disegno.
Fortunatamente, una volta che si è capita la prospettiva «informale» (la misurazione a vista) non è affatto necessario conoscere la prospettiva formale; anzi, lo studio della prospettiva non è né utile né interessante. A mio parere, saper non nuoce, ma la misurazione a vista è sufficiente per fornirci le capacità di base per disegnare.
Un breve esercizio di misurazione a vista prima di disegnare una «vera» prospettiva
Che cosa vi occorre:
- la tavoletta da disegno
- molti fogli di carta per schizzi
- la matita, ben appuntita, e la gomma
- il foglio trasparente e il pennarello con la punta in feltro
- il mirino con l’apertura più ampia
Ecco ciò che farete:
Dapprima vi eserciterete nel misurare a vista le dimensioni e gli angoli, usando la matita come strumento di misurazione. Una volta che avrete fatto un po’ di pratica, eseguirete il disegno «realistico» in prospettiva. Cominciate con il sedervi di fronte al vano di una porta, a una distanza di circa tre metri.
Prendete il mirino applicato al foglio trasparente e inquadrate la vostra composizione in modo da vedere il vano per intero. Tenete ben fermo il mirino e tracciate con il pennarello sul foglio trasparente lo stipite superiore della porta, come nella figura 8-11. Questa è la vostra unità di base. Trasferitela uguale (valutandone la posizione e le dimensioni) su un foglio di carta. Mettete da parte il mirino (fig. 8-12).
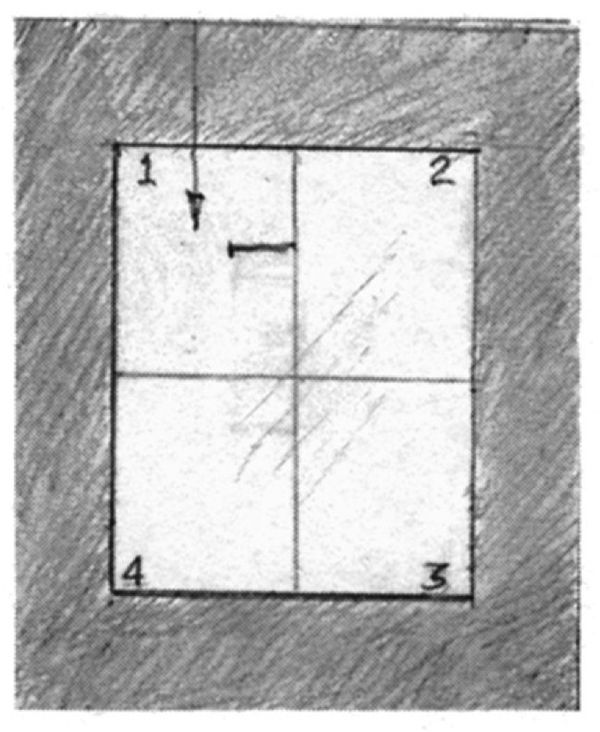
Fig. 8-11. Disegnate lo stipite superiore della porta sul foglio trasparente. Questa sarà la vostra unità di base.
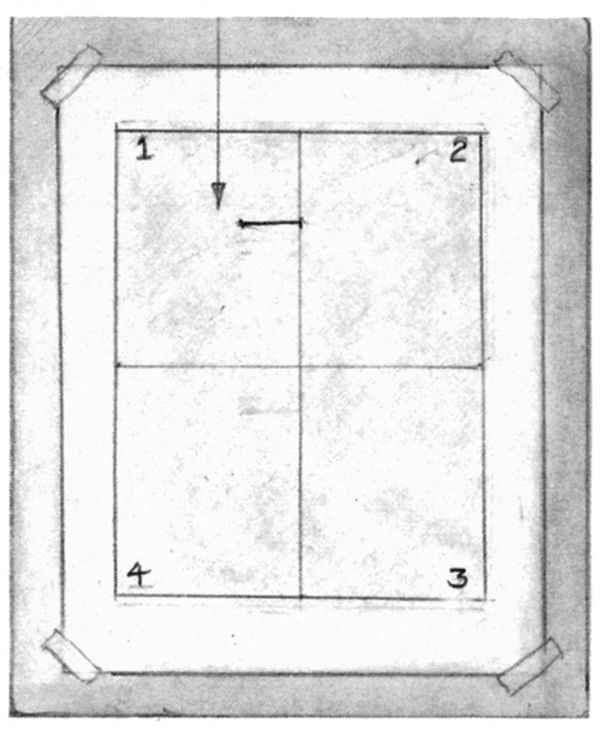
Fig. 8-12. Trasferite l’unità di base sulla carta sfumata con la grafite. Poiché il foglio di carta è più largo del foglio di plastica, dovete riportare in scala (quindi ingrandire, in questo caso) l’unità di base.
Ora, prendete la matita. Tenetela davanti a voi e, con il braccio ben teso, dirigetela verso il soggetto. Chiudete un occhio e spostate la matita in modo che l’estremità coincida con uno dei contorni dello stipite superiore (quello esterno o quello interno). Poi, con l’occhio ancora chiuso, muovete il pollice lungo la matita finché l’unghia coincide con l’estremità dello stipite. Tenete bene a mente questa misura. Avete «misurato a vista» la larghezza del vano della porta.
Una prova: che accade se tenete entrambi gli occhi aperti o se rilassate il gomito?
Tenete il pollice nella stessa posizione e piegate un po’ il gomito, portando leggermente la matita verso di voi. Che cosa accade? Le «misure» sono cambiate, vero? Quindi, la ragione per la quale dovete tenere teso il gomito quando misurate a vista le dimensioni è di mantenere la stessa scala. Se il gomito è ben teso, state prendendo le misure usando sempre lo stesso criterio.
Ora, stendete nuovamente il gomito e tornate a misurare la larghezza del vano con la matita (fig. 8-13). Abbiamo detto che questa è l’unità di base, il vostro «uno». Tenete il pollice nella stessa posizione, girate la matita in verticale e trovate la relazione (il rapporto o la proporzione) tra larghezza e altezza.
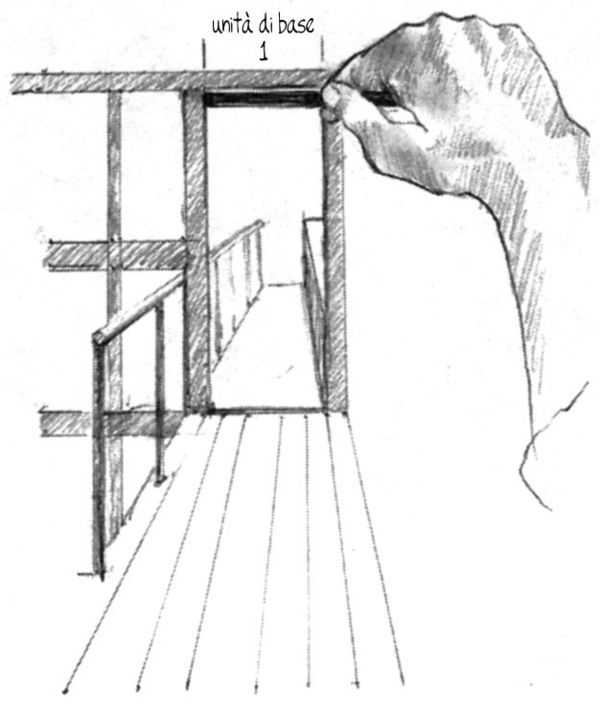
Fig. 8-13. Misurate: «Uno...»
Tenendo sempre la matita davanti a voi, un occhio chiuso e il braccio teso, misurate partendo dall’angolo superiore: «uno (larghezza) a uno (altezza)» (fig. 8-14); scendete con la matita e proseguite: «uno a due» (fig. 8-15), scendete di nuovo e misurate il resto: «uno a due e due terzi» (fig. 8-16). Abbiamo dunque «misurato a vista» la proporzione tra larghezza e altezza. Essa si può esprimere sotto forma di rapporto: 1:2⅔ o, in parole, «uno a due e due terzi».
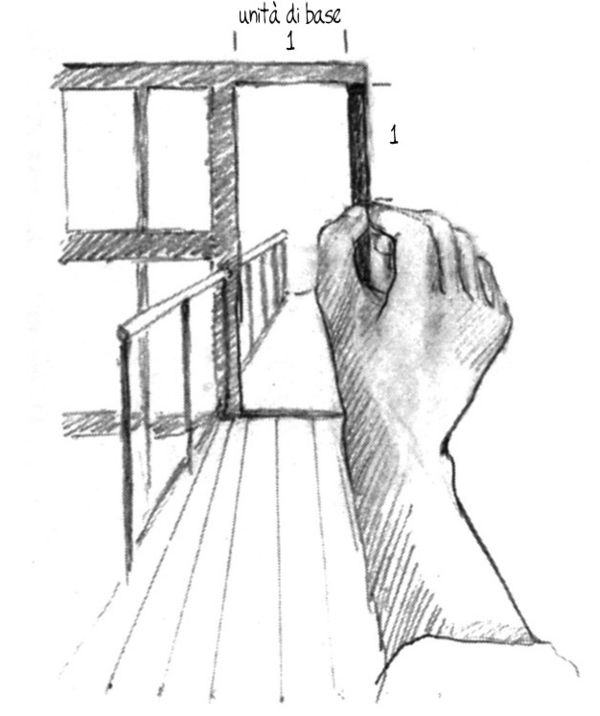
Fig. 8-14. «...a uno...»
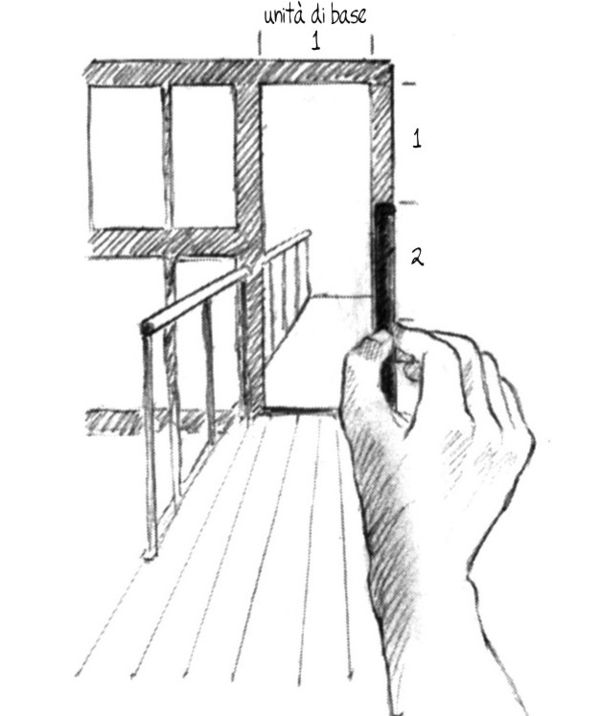
Fig. 8-15. «...due...»
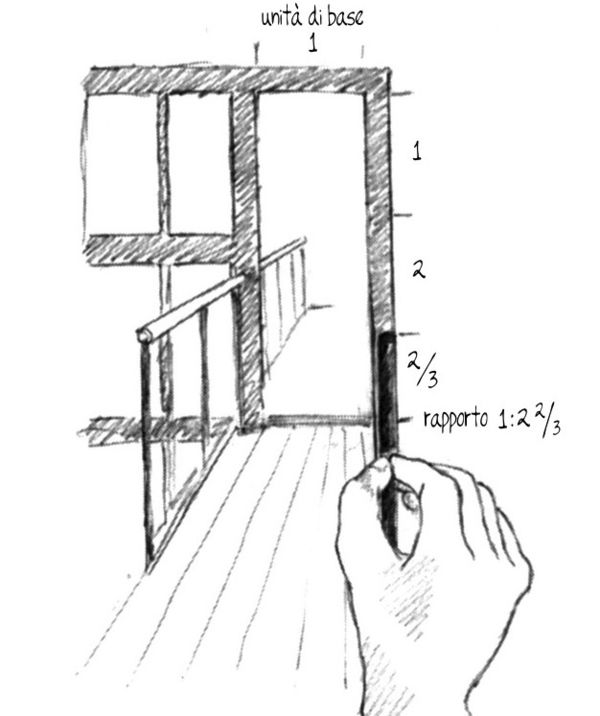
Fig. 8-16. «...e due terzi».
Ora, tornate al vostro schizzo
Misurando a vista il vano della porta avete determinato che la proporzione larghezza-altezza è 1:2⅔. Questo è il rapporto reale, quello che possiamo osservare «là fuori». Il vostro lavoro consiste nel trasferire tale rapporto nel vostro disegno. Ovviamente l’oggetto disegnato sarà più piccolo, molto più piccolo di quello vero, ma il rapporto tra larghezza e altezza sarà lo stesso.
Ora, dunque, aiutatevi con la matita e il pollice per prendere una nuova misura: la larghezza che avete disegnato sulla carta (fig. 8-17). Portate la matita in verticale sul vostro schizzo e valutate «uno a uno, due e due terzi» (figg. 8-18, 8-19, 8-20). Fate un segno e tracciate le due linee (stipite superiore e stipite destro). Quello che avete appena disegnato ha le stesse proporzioni – larghezza e altezza – dell’oggetto reale.
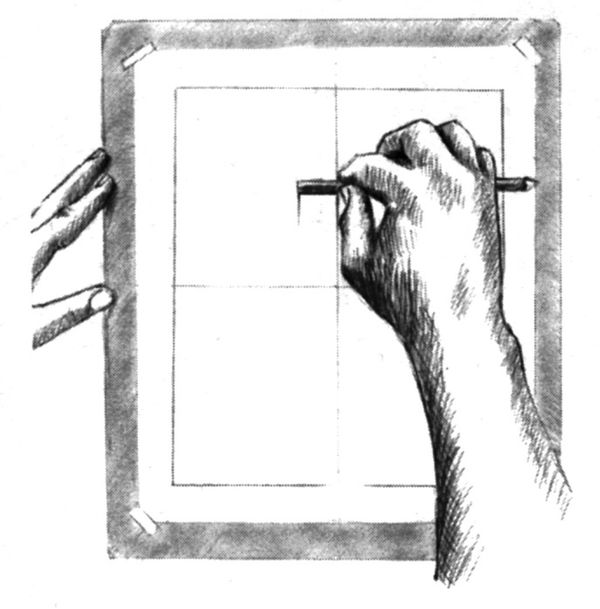
Fig. 8-17. Misurate: «Uno...»
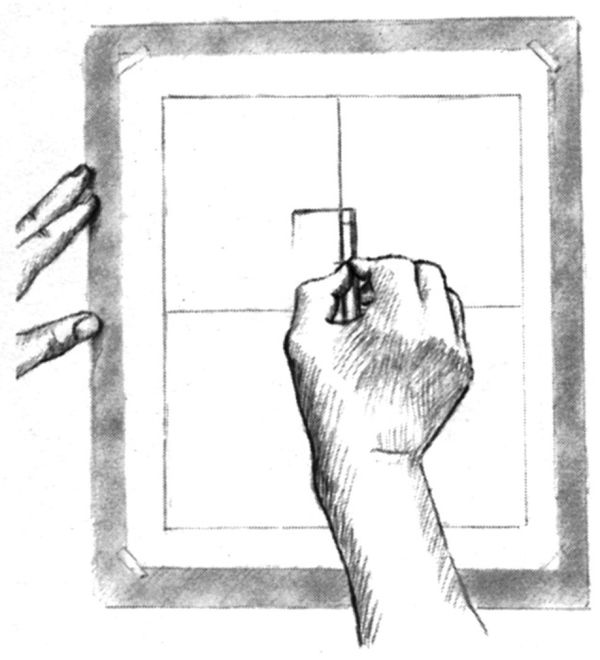
Fig. 8-18. «...a uno...»
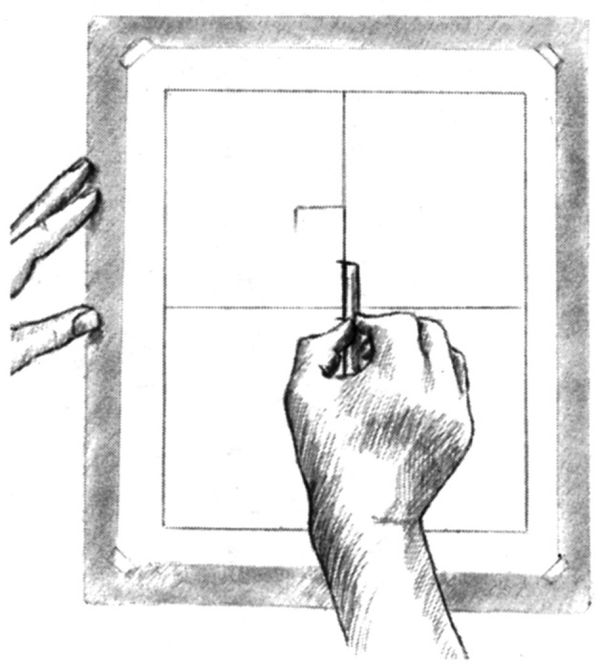
Fig. 8-19. «...due...»
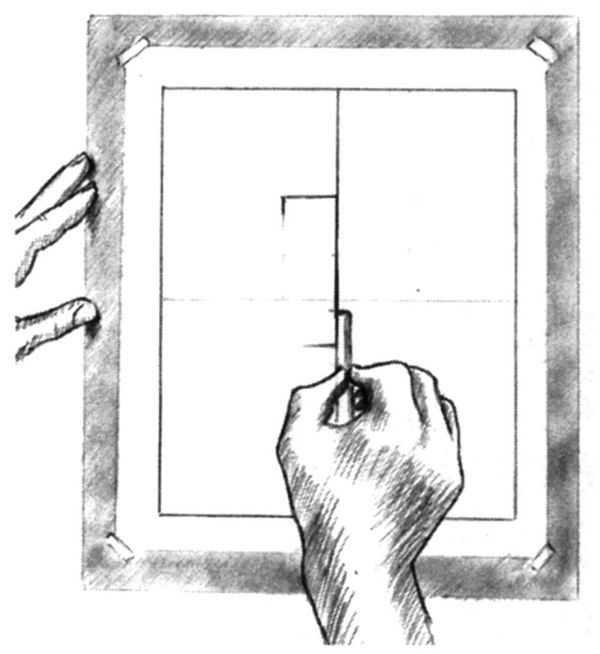
Fig. 8-20. «...e due terzi».
Per afferrare meglio questo concetto, tracciate una nuova unità di base, più piccola della prima. Ora, misurate quella larghezza con la matita e tracciate l’altezza in proporzione. Questo rettangolo sarà più piccolo del precedente, ma avrà le stesse proporzioni sia di quello sia dell’oggetto.
Riassumendo: con la misurazione a vista si scoprono le proporzioni dell’oggetto reale, poi, tenendo a mente quei rapporti (tra l’unità di base, cioè l’«uno», e qualcos’altro), si ripete la misurazione sul foglio, riportando nel disegno gli stessi rapporti proporzionali. Naturalmente gli oggetti disegnati hanno quasi sempre dimensioni diverse da quelli reali (più piccole o più grandi), ma le proporzioni sono le medesime.
Come ha detto, con notevole acume, un mio studente: «Usi la matita per trovare i rapporti reali, li memorizzi, fai sparire la tacca dalla matita, e riprendi le misure con la matita sul disegno».
Il passo successivo: misurare a vista gli angoli
Ricordate, la misurazione a vista è una tecnica costituita da due parti. Avete appena imparato la prima: la misurazione delle proporzioni. Usando la matita si trova la risposta a domande come: «Quanto è grande questo paragonato a quello?», «Quanto è grande questo rispetto alla mia unità di base?» e così via. Si rilevano misure in rapporto l’una all’altra e all’unità di base.
La misurazione a vista degli angoli è differente, perché gli angoli vengono rapportati alla verticale e all’orizzontale. Ricordate, sia gli angoli sia le grandezze devono essere misurati utilizzando il vostro piano d’immagine materiale (il foglio trasparente) e con la matita che vi poggia sopra.
Prendete il mirino applicato al foglio trasparente e il pennarello, e sedetevi di fronte a un qualsiasi angolo di una stanza. Tenendo bene in alto il mirino, osservate l’angolo formato dal soffitto con le due pareti. Il foglio trasparente (piano d’immagine) deve essere perfettamente verticale, parallelo al vostro viso e all’altezza degli occhi. Non inclinatelo in nessuna direzione.
Scegliete ora l’inquadratura e servitevi del pennarello per disegnare sulla plastica lo spigolo tra le due pareti (una linea verticale). Quindi disegnate gli spigoli tra soffitto e pareti e, se possibile, tra pareti e pavimento.
Appoggiate il piano d’immagine su un foglio di carta così da poter vedere il disegno e trasferire le linee su un altro foglio.
Avete appena disegnato un angolo in prospettiva. Ora ripetiamo l’esercizio senza l’aiuto del piano d’immagine.
Scegliete un angolo diverso o una posizione differente. Fissate con nastro adesivo un foglio di carta alla tavoletta da disegno. Osservate l’angolo. Chiudete un occhio e tenete la matita perfettamente verticale protesa verso il soggetto. Tracciate la linea verticale tra soffitto e pavimento (incontro delle due pareti).
Portate ora la matita in posizione perfettamente orizzontale, tenendola parallela al piano degli occhi, per valutare gli angoli che gli spigoli superiori (tra il soffitto e le pareti) formano con la matita stessa (fig. 8-21). Ricordate che per voi questi angoli sono forme. Ripetete la misurazione sul foglio di carta e disegnate gli angoli. Applicate la stessa procedura agli angoli tra il profilo del pavimento e la costante orizzontale (matita) (fig. 8-22).
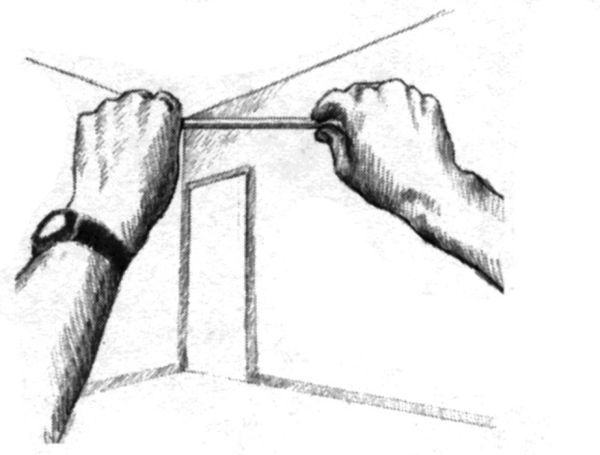
Fig. 8-21.
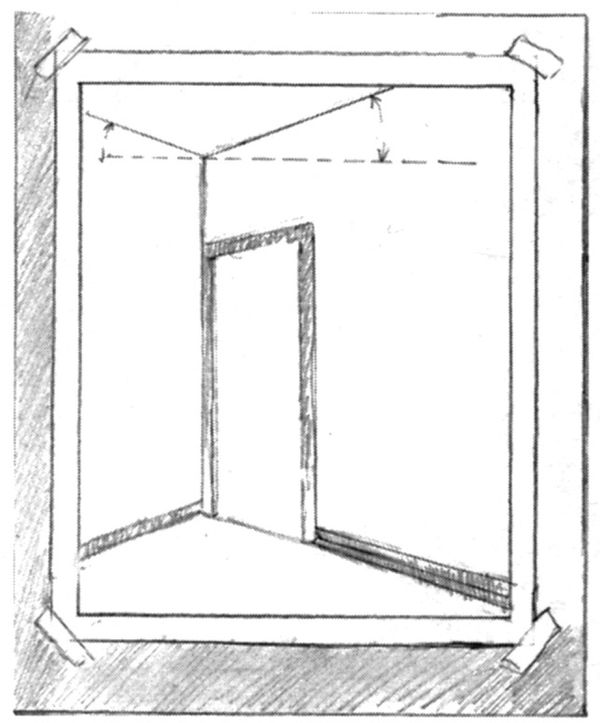
Fig. 8-22.
Le linee verticali di strutture costruite dall’uomo rimangono verticali, mentre le linee orizzontali, cioè parallele alla superficie terrestre, convergono verso un punto di fuga e devono essere misurate a vista. Nel disegno, si può fare abbastanza affidamento sulle verticali, che restano verticali, e saranno parallele ai bordi della carta. Ci sono delle eccezioni, naturalmente. Se siete a livello della strada e guardate verso l’alto per disegnare un edificio a più piani, quei bordi verticali convergeranno e vanno misurati a vista.
Questo, nel disegno, è comunque un caso piuttosto raro.
Queste fondamentali azioni di misurazione a vista non sono difficili da eseguire, una volta che ne abbiate ben compreso lo scopo.
- Chiudere un occhio, come ho spiegato prima, vi aiuta a vedere l’immagine solo a due dimensioni, anziché a tre come nella visione binoculare.
- Tenere ben teso il gomito significa essere sicuri di usare un’unica scala prospettica nella misurazione a vista delle proporzioni. Rilassare il gomito anche di poco può causare errori, modificando la scala dei soggetti. Nella misurazione a vista degli angoli non è necessario tenere il braccio teso, ma è invece importante che la matita rimanga parallela al piano d’immagine.
- Rapportare gli angoli alla verticale e all’orizzontale ha uno scopo evidente. Gli angoli, infatti, possono variare all’infinito e soltanto le linee reali verticale e orizzontale sono costanti e attendibili. E dal momento che i bordi della carta (e i bordi del formato che avete disegnato) rappresentano anche la verticale e l’orizzontale, ogni angolo può essere calcolato sul piano d’immagine e trasferito sulla carta in rapporto a tali costanti.
Alcuni punti fondamentali relativi agli angoli misurati a vista
- Tutti gli angoli sono misurati a vista in rapporto a due costanti: linea verticale e linea orizzontale.
- Nel vostro disegno, i bordi del formato rappresentano le costanti verticale e orizzontale. Una volta che avrete misurato a vista un angolo reale, potrete tranquillamente disegnarlo in rapporto ai bordi del formato.
- Per una valutazione corretta, tutti gli angoli devono essere misurati sul piano d’immagine, che è un piano solido. Non potete trapassare il piano seguendo con la matita l’inclinazione di una linea, per il fatto che questa recede in profondità. L’angolo va misurato così come appare sul piano d’immagine (fig. 8-23).
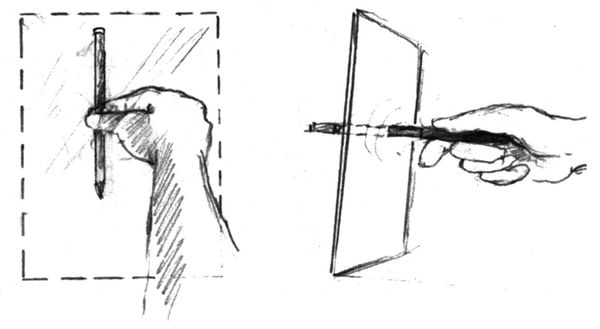
Fig. 8-23. Più avanti, quando avrete imparato a misurare a vista e non avrete più bisogno del piano d’immagine di plastica trasparente, dovrete ricordare di tenere sempre la matita perfettamente parallela all’immaginaria lastra di vetro che sta tra voi e il soggetto: essa non può essere trapassata.
- Potete misurare a vista gli angoli tenendo la matita sia verticale sia orizzontale e comparando l’angolo con il bordo della matita. Potrete anche servirvi delle linee incrociate tracciate sul foglio trasparente o del bordo di uno dei mirini, basta che sia una verticale o un’orizzontale costante, visibile sul piano d’immagine, con cui confrontare l’angolo che intendete disegnare. La matita è comunque lo strumento più semplice da usare e non vi costringe a interrompere il disegno.
- L’informazione visiva che vi viene dal piano d’immagine è quasi sempre diversa dalla vostra conoscenza di come sono le cose. Ad esempio, state guardando l’angolo di una stanza. Sapete che il soffitto è piatto – cioè orizzontale – e che incontra la parete ad angolo retto. Ma se sollevate la matita in orizzontale, chiudete un occhio e, restando sul piano d’immagine, allineate l’angolo in modo che tocchi il centro della matita, vi accorgerete che gli spigoli del soffitto vanno a formare angoli strani. Forse un angolo è più acuto dell’altro (fig. 8-21).
- Dovete disegnare questi angoli proprio come li vedete. Soltanto allora il soffitto sembrerà piatto e gli angoli delle pareti appariranno retti a disegno finito. Questo è uno dei grandi paradossi del disegno.
- Gli angoli che vi sembrano anomali devono essere disegnati proprio come li percepite. Per fare questo, memorizzate la forma di uno dei triangoli formati dal bordo del soffitto con la matita orizzontale. Poi, immaginando una linea orizzontale nel vostro disegno (parallela ai bordi superiore e inferiore del foglio), disegnate lo stesso triangolo. Usate la medesima procedura per disegnare l’altro angolo del soffitto (vedi fig. 8-22).
Di solito raccomando agli studenti di non cercare di definire un angolo in termini di gradi: uno di 45 gradi, l’altro di 30 gradi ecc. È decisamente meglio ricordare la forma che l’angolo assume quando viene rapportato alla verticale o all’orizzontale, e rifarsi a quel costrutto visivo per procedere. Dovrete ritornare spesso sul disegno degli angoli, ma i miei allievi imparano molto velocemente.
Decidere se avvalersi della verticale o dell’orizzontale come costante per valutare un angolo può causare imbarazzo negli studenti. Io vi consiglio di scegliere la linea che, secondo voi, vi permetterà di disegnare l’angolo più stretto.
Capisco che, a questo punto, misurare a vista vi sembri una funzione dell’emisfero sinistro. Ma ricordate che noi stiamo cercando di stabilire delle relazioni.
L’emisfero destro è specializzato nella percezione dei rapporti, dei paragoni. Come ho già detto, la misurazione a vista con i suoi calcoli è soltanto una maniera semplice di dare un’etichetta alle nostre percezioni. L’unità di base è sempre «uno», perché è il primo termine di paragone. Se vi eserciterete nella misurazione a vista, questo processo vi sembrerà istintivo e arriverete a stimare anziché misurare le proporzioni. Ma per ogni percezione problematica, come la prospettiva, un artista esperto ricorre a un’attenta misurazione a vista. Come nel caso degli spazi negativi, misurare a vista facilita il compito.
Cercate di ricordare che il disegno non è che una riproduzione approssimativa del soggetto ritratto, anche per un artista con molta esperienza. Disegnare non è sinonimo di fotografare. Chi disegna, consciamente o inconsciamente, omette, enfatizza (o minimizza) o varia leggermente alcuni aspetti del soggetto. Gli studenti sono spesso molto critici nei confronti del proprio lavoro, perché non lo considerano una raffigurazione fedele, ma il subconscio opera delle scelte mentre si disegna, e queste fanno parte dell’espressività di ognuno.
Un «vero» disegno in prospettiva
Che cosa vi occorre:
- la tavoletta da disegno
- molti fogli di carta riuniti in un blocco morbido
- nastro coprente
- la matita, ben appuntita, e la gomma
- lo stick di grafite e molti fazzoletti di carta
- il foglio di plastica trasparente e il pennarello con la punta in feltro
- il mirino con l’apertura più ampia
Prima di cominciare:
Fissate alcuni fogli di carta alla tavoletta da disegno. Tracciate un perimetro di contorno e preparate un fondo di un tono grigio medio. Disegnate le linee verticale e orizzontale che s’incrociano al centro.
1Scegliete il soggetto. Imparare come disegnare «in proporzione» e «in prospettiva» sono le due sfide maggiori per gli studenti delle scuole d’arte. Sarete impazienti di dimostrare a voi stessi che potete farcela. Quindi, procedete con questo obiettivo in mente: scegliere un soggetto o un luogo che pensate sia difficile da disegnare, per esempio con molti angoli o un soffitto complicato, oppure una veduta prospettica di un lungo corridoio (vedi il disegno più avanti). Il modo migliore per scegliere un soggetto è percorrere lo spazio che vi circonda guardando attraverso il mirino fino a che non trovate un’inquadratura che vi soddisfi, proprio come fareste con una telecamera.
Alcuni suggerimenti:
- un angolo della cucina
- un’anticamera
- una veduta attraverso una porta aperta
- un qualsiasi angolo di una stanza di casa vostra
- un cortile o una balconata
- un angolo di strada dove potete disegnare stando seduti in auto o su una panchina
- l’entrata di un edificio pubblico, sia interna sia esterna
Organizzatevi al meglio. Avrete bisogno di due sedie, una su cui sedervi e l’altra su cui appoggiare la tavola da disegno. Se volete disegnare all’aperto, le sedie pieghevoli sono ideali. Assicuratevi di essere esattamente di fronte al soggetto prescelto.
Se sceglierete di disegnare in luoghi pubblici sarete sicuramente oggetto della curiosità di molti, che verranno da voi e vi rivolgeranno parecchie domande: questa non è una cosa positiva per mantenersi nello stato mentale della funzione D, non verbale. D’altra parte, questo può essere un bel modo per fare nuove amicizie. Chissà come mai, persone che di solito non rivolgerebbero la parola a un estraneo non esitano invece a farlo con un artista.
2Applicate il foglio di plastica trasparente al mirino con l’apertura più ampia. Tracciate il perimetro di contorno sulla plastica con il pennarello, usando come guida il bordo interno della cornice del mirino. Chiudendo un occhio, spostate il foglio avanti e indietro per trovare l’inquadratura migliore o che più vi piace.
3Fatto questo, scegliete un’unità di base, che dovrà essere di media grandezza e di forma non troppo complicata. Potrebbe trattarsi di una finestra, di un disegno su un muro o del vano di una porta. Può essere una forma positiva o uno spazio negativo, una linea singola o articolata. Disegnate la vostra unità di base direttamente sul foglio di plastica con il pennarello.
4Posate il mirino su un foglio bianco, così da poter vedere ciò che avete disegnato. Ora, riportate la vostra unità di base sulla carta. Avrà la stessa forma ma più grande, essendo il foglio più grande dell’apertura del mirino.
5Nel trasferire l’unità di base sulla carta preparata con fondo grigio, usate le due linee incrociate come guida. Sia sulla plastica sia sulla carta da disegno, le linee incrociate dividono l’area in quattro riquadri. Vi rimando alle figure 8-11 e 8-12 per vedere come trasferire l’unità di base dal foglio trasparente alla carta usando questi riquadri.
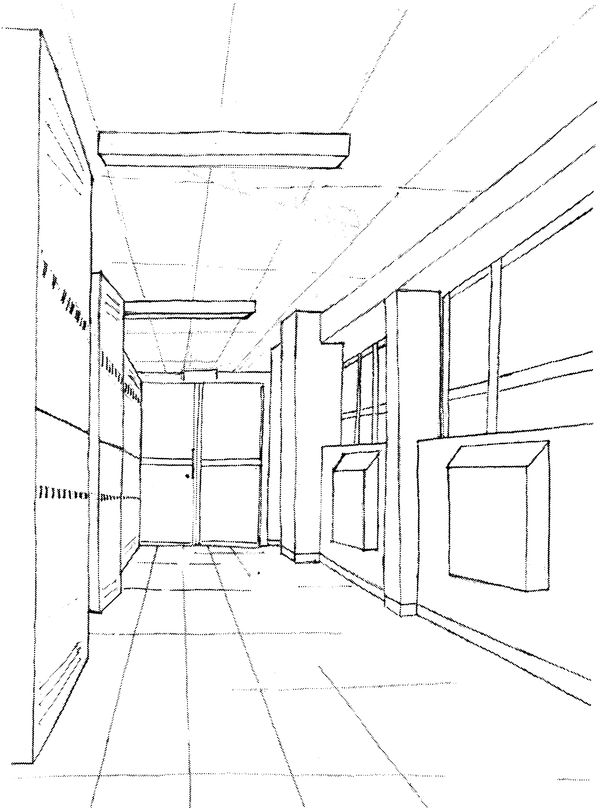
Disegno di un allievo di uno scorcio stimolante e attraente.
Dopo aver riportato la vostra unità di base sul foglio di plastica trasparente, potete anche disegnare, sullo stesso, uno o due contorni principali, ma sappiate che il tratto sarà piuttosto debole e incerto.
L’informazione essenziale cui far riferimento, l’unità di base, è tutto ciò che vi serve.

Un disegno in prospettiva di Cindy Ball-Kingston. Un esempio di come trovare scorci interessanti anche nei luoghi più impensati.
A volte è utile riprendere in mano il mirino con il foglio trasparente per verificare un angolo o una misura. Per ricontrollare la vostra composizione, sollevate semplicemente il mirino e, chiudendo un occhio, muovetelo avanti e indietro fino a che la vostra unità di base «reale» combacerà con il disegno a pennarello della medesima. Controllate quindi ogni angolo o grandezza di cui siete dubbiosi.
So che per molti la parte più ardua è credere alla propria misurazione a vista degli angoli e delle dimensioni. Molte volte ho visto gli studenti guardare, scuotere la testa, guardare di nuovo, scuotere di nuovo la testa, e dire di un angolo: «Non può essere così acuto», o di una dimensione: «Non può essere così piccola».
Però, via via che farete un po’ più di esperienza sarete in grado di fidarvi dei dati rilevati con questa tecnica. Dovete prenderli a scatola chiusa, per così dire, e non tornarci sopra. Ai miei studenti ripeto sempre: «Se lo vedete così, disegnatelo così. Non discutetene con voi stessi».
Naturalmente, bisogna guardare e osservare con il massimo dell’attenzione e dello scrupolo. Quando io eseguo un disegno dimostrativo nel corso di un seminario, gli allievi mi guardano mentre con un movimento deliberato e attento stendo il braccio, blocco il gomito e chiudo un occhio per verificare con precisione una dimensione o un angolo sul piano d’immagine. Ben presto tali movimenti diventeranno pressoché istintivi, proprio come s’impara in breve tempo a fermare la macchina a uno stop.
Per completare il disegno in prospettiva:
1A poco a poco vi accorgerete che potete unire i vari pezzi del vostro disegno come in un puzzle. Passate da una zona a quella adiacente, controllando sempre le proporzioni tra la nuova parte e ciò che avete già disegnato. Tenete bene a mente anche il concetto dei contorni come bordi condivisi, e delle forme positive che, insieme con gli spazi negativi, contribuiscono a creare la composizione. Ricordate che tutte le informazioni di cui avete bisogno per fare questo disegno sono lì, davanti ai vostri occhi. Ora conoscete le strategie che gli artisti usano per «scoprire» quelle informazioni visive e avete i mezzi adeguati per raggiungere ciò cui mirate.
2Usate gli spazi negativi come una parte importante del vostro lavoro (come a fig. 8-24). Aggiungerete forza al vostro disegno se ve ne servirete per vedere e disegnare piccoli oggetti come lampade, tavoli, scritte d’insegne e così via. Concentrandovi infatti solo sulle forme positive il vostro disegno ne uscirebbe estremamente indebolito. Se state raffigurando un paesaggio, gli alberi e il fogliame appariranno rinforzati se enfatizzate gli spazi negativi.

Fig. 8-24. Ricordatevi di enfatizzare gli spazi negativi nel vostro disegno.
3Una volta che avrete completato le parti principali del disegno, potete concentrarvi sulle luci e sulle ombre. Socchiudendo un po’ gli occhi potrete notare molti particolari che vi permetteranno di apprezzare le aree illuminate e quelle in ombra. Potete ricavare le luci con la gomma e stendere le ombre con la matita. Queste forme vanno misurate a vista esattamente come le altre parti del disegno: «Qual è l’angolazione di quell’ombra in rapporto all’orizzontale? Quanto è ampio quel colpo di luce rispetto all’altezza della finestra?»
4Se una parte sembra essere «fuori del disegno», come si suol dire di certi errori, controllate il punto problematico con il piano d’immagine trasparente applicato al mirino. Osservate l’immagine sul piano (con un occhio chiuso, naturalmente) e confrontatela ripetutamente con il disegno, al fine di verificare angoli e dimensioni. Apportate qualsiasi correzione vi sembri ragionevole.
Quando avete terminato:
Congratulazioni! Avete appena completato un compito che molti studenti d’arte dell’università ritengono quasi impossibile.
Misurare a vista significa proprio questo: con un solo sguardo percepire le cose come realmente appaiono sul piano d’immagine. Questa capacità vi permetterà di disegnare qualsiasi cosa abbiate sotto gli occhi. Non dovete cercare soggetti «facili». Siete in grado di disegnare tutto.
La capacità di misurare a vista richiede un po’ d’esercizio, ma ben presto vi scoprirete, quasi per caso, «a disegnare», alle volte persino senza aver bisogno di valutare dimensioni e calcolare angoli. E quando vi troverete ad affrontare le parti di scorcio del soggetto, le capacità che avrete acquisito ve lo faranno sembrare facile.
Il mondo reale è ricco di vedute prospettiche di luoghi, persone, alberi, fiori, che il principiante tende a evitare perché «difficili», preferendo immagini ritenute «più facili». Ma grazie ai metodi che ora avete imparato non sarà più necessario limitare la scelta dei vostri soggetti. Contorni, spazi negativi e misurazione a vista dei rapporti cooperano per far sì che disegnare in prospettiva non solo sia possibile, ma diventi anche piacevole. Come per qualsiasi disciplina, imparare le «parti difficili» è stimolante e divertente.
Robert Henri, artista/insegnante, diede ai suoi studenti questo monito severo:
«Se nei vostri disegni trascurate abitualmente le proporzioni, vi abituerete a una visione distorta e finirete con il perdere la capacità critica. Una persona che vive nello squallore, alla fine ci si abitua».
The Art Spirit, 1923
Guardare avanti
La tecnica che vi ho appena insegnato, detta «prospettiva informale», si affida soltanto a ciò che si vede sul piano d’immagine. La maggior parte degli artisti vi fa ricorso, anche quando conosce bene la tecnica della prospettiva formale. Uno dei vantaggi è che questo metodo può essere usato per ogni soggetto, come vedrete nel prossimo capitolo dedicato al ritratto. Metterete a frutto le capacità acquisite fin qui, di cogliere i rapporti tra contorni, spazi e dimensioni, per raffigurare la testa umana.

Fig. 8-25. Charles White, Predicatore, (1952). Whitney Museum, New York.
Nel disegno di Charles White le forme sono viste di scorcio. Studiatelo. Copiate il disegno, capovolgendolo se necessario.
Potete scegliere come unità di base la lunghezza della mano sinistra dell’uomo (dal polso alla punta dell’indice). Forse vi stupirà sapere che la proporzione tra la testa e la mano sinistra è di 1:1⅔.
Ogni volta che sperimentate il fatto che disegnando esattamente ciò che vedete create quella miracolosa illusione di spazio e di volume sulla superficie piana di un foglio, le tecniche che avete acquisito diventano sempre più parte integrante del vostro modo di vedere, che è il modo di vedere dell’artista.
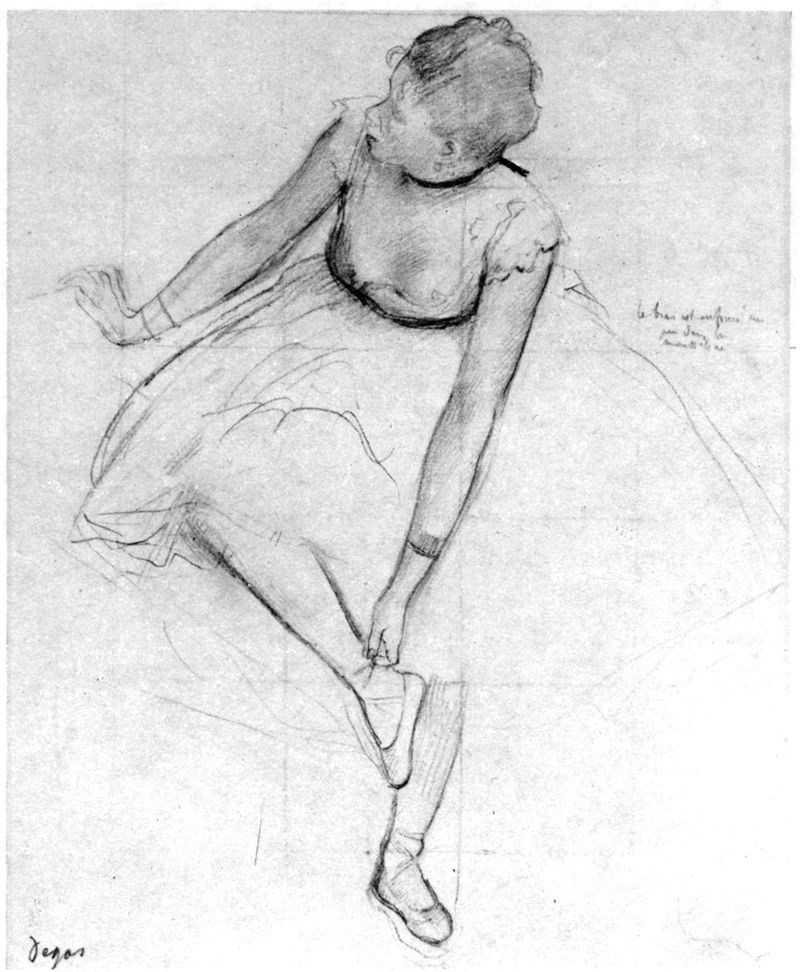
Fig. 8-26. Edgar Degas (1834-1917), Ballerina che si accomoda la scarpetta (1873). The Metropolitan Museum of Art, New York. Lascito di Mrs. H.O. Havemeyer, 1929, collezione H.O. Havemeyer.
Impiego della misurazione a vista nel disegno di figura
Questa tecnica, che consiste nell’utilizzare le costanti verticale e orizzontale per valutare gli angoli, è essenziale non solo nel disegno di oggetti ma anche nel disegno di figura. Spesso negli schizzi sono ancora visibili le linee-guida tracciate dall’artista, come in questo disegno di Edgar Degas. Possiamo presumere che Degas si sia servito della misurazione a vista per valutare per esempio la distanza tra la punta del piede sinistro della ballerina e l’orecchio, o l’angolazione del braccio rispetto alla verticale.
Notate che l’unità di base di Degas andava dal bordo superiore dei capelli al nastrino intorno al collo. L’artista si è servito della stessa unità di base nel disegno riprodotto nelle tavole a colori alla figura 11-6.
Ricordate che il disegno realistico dal vero fa sempre ricorso alle capacità percettive fondamentali: proprio quelle che state imparando ora. Naturalmente, questo è vero anche per altre attività tipiche della funzione D. Per esempio, una volta che avete imparato a guidare non potete forse guidare ogni automobile senza difficoltà?
Il prossimo capitolo vi insegnerà a ritrarre la testa umana, un soggetto particolarmente affascinante e stimolante, e sono certa che vi divertirete.

Randa Cardwell.

Insegnante Dana Crowe.