CHAPTER 9

Oligopolistic Competition, Pricing, and Recoupment of Innovation Outlays

[in] the sacred precincts of theory, the price variable is ousted

from its dominant position. … [I]n capitalist reality, as distinguished from its textbook picture … [the] kind of competition which counts [is] the competition from the new commodity, the new technology, the new source of supply, the new type of organization …—competition which commands a decisive cost or quality advantage and which strikes not at the margins of the profits and the outputs of the existing firms but at their foundations and their very lives.

—Schumpeter, 1947, p. 84

… innovations are rarely the dramatic breakthroughs that Schumpeter may have had in mind but rather small improvements in a new process or product in which genuine novelty and imitation-with-a-difference shade imperceptibly into one another.

—Blaug, 1997, p.110

Part II will, to some extent, look further into the growth process of the free-enterprise economy. Notably in chapter 13, I will return to the discussion of licensing and the voluntary dissemination of proprietary technology, considering the magnitude of license fees, deriving necessary conditions for consistency of this price with economic efficiency, and obtaining an explicit pricing formula. That chapter will also consider whether market forces lead to the adoption of such efficient licensing prices, and will conclude that the market does provide such incentives, though perhaps not always sufficiently powerful, in reality, to lead to prices that approximate optimality.

But the central focus of part II is not the efficiency of the free-market growth process. My main objective, rather, is to illustrate, by means of concrete analyses of a number of significant issues, how readily the standard toolkit and results of microanalysis can be adapted to the study of routine innovation. This evidence invites us to examine the possibility of going one step further: explicitly to incorporate innovation into the basic models of the firm and the industry, not as a mere side issue but as an activity that lies at the heart of the models. In chapter 4, I took a first step toward that goal, in an elementary model of oligopolistic competition as a force that promotes expenditure on invention and innovation. In this chapter and those that follow I continue this sort of analysis. Yet, although I accept the Schumpeterian observation that nowadays it is innovation rather than price that is characteristically the main concern of competing oligopolists, this part of the book will devote a good deal of attention to the interrelation between innovation and pricing. I will consider how innovation affects the price of the final products that employ its technology, how prices are adapted to the requirements of the recoupment of outlays on innovation, and how to set the prices of access to innovations when the proprietor of such intellectual property permits its use to others.

This chapter and the next two will consider the pricing and recoupment of investment in innovation. In this discussion we will find ourselves driven to go beyond the theory to consider an important policy issue. I have already emphasized that the oligopolistic sectors of the economy, and the competition among these large firms, play a major role in the spectacular growth performance of the free-market economies. Oligopolies, traditionally, are nevertheless the prime targets of attention by the antitrust authorities. There is, of course, good reason for this. Market forms populated by smaller firms are unlikely to entail any market power, and so the weak enterprises they contain will be unable to carry out anticompetitive acts or even to attempt to do so. On the other hand, unregulated pure monopoly is a rare bird, if it is to be found at all. So it is the oligopoly markets where any attempt at anticompetitive activity by private and largely unregulated firms is to be expected. Still, exploitation of the public through anticompetitive actions is surely not something undertaken by every oligopoly firm, any one of which must be deemed innocent until proven guilty. It has been common to offer evidence of at least the possession of monopoly power in the form of data showing that an oligopoly firm’s prices differ from the (perfectly) competitive level and, in particular, that it engages in differential (discriminatory) pricing practices. Chapter 10 will end with a discussion of this sort of argument, showing that oligopoly firms, particularly those engaged in substantial innovative activity, may well be forced by competitive pressures and the necessities of survival to adopt prices very different from those that could be expected under perfect competition, and, indeed, prices that are markedly discriminatory. Without this, they might simply be unable to recoup their continuing outlays on innovation. Indeed, rather than constituting manifestations of monopoly power, such investment-recouping prices may well be thrust upon the innovative firms, which may consequently be price takers, not price makers, in the sense that market forces may impose upon them the particular prices they adopt.

WHY INNOVATION IS CRUCIAL FOR MODELS OF OLIGOPOLISTIC COMPETITION

I believe, with Schumpeter, that it is not merely desirable for innovation to be incorporated into the microtheory of oligopolistic competition. Without that component, I believe the theory is deprived of much of its applicability to the modern free-enterprise economy. Anyone with any intimate knowledge of the operation of the firms that constitute the modern sector of an industrialized economy will recognize that pricing is not the primary competitive issue in management’s deliberations. Its hopes and fears instead relate primarily to the redesign of its current products, to the new products it plans to introduce, and to the more productive and reliable production processes it hopes to adopt. In short, the continued exile of innovation to the suburbs of microtheory does not merely mean that there is room for improvement in that body of analysis. Rather, the theory is thereby deprived of what should be one of its most critical components. That is why this book devotes so much attention to suggesting ways in which innovation can be incorporated into the heart of microanalysis, and to emphasizing attributes of the activity that improve the prospects for success in this task. That, then, is the primary purpose of this second part of the book.

THE EFFECTS OF INNOVATION ON FINAL-PRODUCT EQUILIBRIUM: THE COMPARATIVE STATICS

Let us turn now to how the magnitude of the R&D activity determined by competition affects the variables more usually studied in the theory of the firm and industry. I will consider the effects of an increase in the amount of innovation on final-product outputs, prices, and the welfare of consumers and producers.

To obtain determinate results about prices and outputs, the discussion leaves the oligopoly situation discussed up to this point and focuses instead on a single firm whose decision-making is independent of the activities and decisions of other enterprises (and is presumably a pure monopoly).

Definitions

Process and Product Innovations. A product innovation is defined here as one that shifts the demand curve for the affected final product to the right, while a process innovation is one that shifts the pertinent cost curves downward. In the discussion that follows I assume that there is a clear distinction between process and product innovations and that any particular innovation can unambiguously be assigned to one of these two categories.

Successful Innovation. I define an innovation to be successful (commercially) if it increases the producer’s profit. We will see that a successful process innovation can be expected to expand output, reduce product price, and enhance welfare. Thus, it can be considered beneficial in terms of all three of these attributes. A successful product innovation will also increase final-product output, but its general effects on price and welfare can go either way.

The Effects of Process Innovations

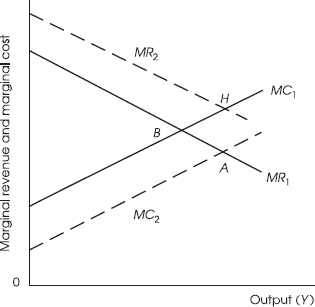
The results for a process innovation now follow trivially on the assumption that it shifts the marginal cost curve downward.1 A graph will suffice to demonstrate them. Figure 9.1 shows the firm’s initial marginal revenue and marginal cost curves, MR₁ and MC₁, this time for the supply of its final product rather than for its investment in R&D, as in chapter 4. The broken lines MR₂ and MC₂ are the corresponding curves after the introduction of an innovation.

We see at once that:

PROPOSITION 9.1. (a) If a process innovation shifts the marginal cost curve downward, it must increase output because of the negative slope of MR, moving the equilibrium point from B to A. (b) Because there is no shift of the demand curve, its presumably negative slope means that the product’s price must fall. (c) If the invention is successful, as defined, it follows that the producer’s surplus will not fall and, because of the fall in price, consumers’ surplus² must rise. This confirms our results for the case of a process innovation.

FIGURE 9.1

Effects of an Innovation

The Effects of a Product Innovation

The case of a product innovation follows the same sort of logic, but the arguments are considerably less straightforward, except for the analysis of the effect on output. The innovation results in an upward shift of the marginal revenue curve to MR₂ (and, presumably, also of the demand curve). That will lead to a rise in output even if the marginal cost curve is downward sloping, so long as its slope is less than that of the marginal revenue curve—as stability of equilibrium requires. All this assumes that the cost curve does not also shift as a result of the product innovation, a possibility that will be considered later.

It will presently be shown that price may either rise or fall as the result of a product innovation. That is because price is now affected by two influences working in opposite directions. The upward shift in the demand curve will push price upward, but the increase in output and the negative slope of the demand curve will have the opposite effect. Once again, the area between the MR and MC curves may well increase, so that, with output expanding, consumers’ surplus may also rise. However, once we consider the possible changes in demand elasticity as well as the sunk costs of the innovation, the effect on welfare is no longer clear. Next, I will look at the price and welfare effects of a product innovation more carefully.

Product Innovation and Price. Let us next prove:

PROPOSITION 9.2. A product innovation may either decrease or increase the firm’s profit-maximizing price, depending at least in part on the effect of the innovation on the price elasticity of demand for the product.

To prove this, it is sufficient to show that either result is possible in the simplest case in which marginal cost does not vary with output in the relevant range. The firm’s objective is to maximize profit

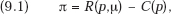
where R and C are, respectively, the total revenue and cost functions, p is the final-product price, and μ is the shift variable representing the contribution of the innovation to total revenue.

Next, we note that first-order and second-order maximum conditions are

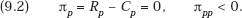
By our simplifying assumption, we have C_p = C_y y_p = a constant. Setting the total differential of the first-order condition in (9.2) equal to zero, we have

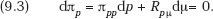
Thus,

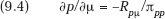
has the same sign as R_pμ.

But R_p = y + py_p = y(1 − E), where E is the initial (absolute value) elasticity of demand at the initial price, p. We know that profit maximization requires E > 1. And we have

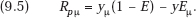
This, and therefore ∂p/∂μ, is clearly positive iff E_μ < (1 − E)y_μ/y < 0, which is our result. Thus, a product innovation can, indeed, either raise or reduce price, as Proposition 9.2 asserts. The role of demand elasticity is clear intuitively. If the innovation substantially increases the elasticity of the demand curve, the increased direct revenue contribution of a rise in price is more than offset by the loss in quantity sold resulting from the price increase.

Product Innovation and Welfare. A product innovation can, indeed, add to welfare but, like all innovations, the validity of this result depends on the real cost of the innovation. Other things being equal, if it has a sufficiently large sunk cost it can obviously cause a net loss in welfare. In the case of a process innovation we avoided this difficulty by assuming that the innovation was successful, meaning that it must still yield an increase in the producer’s surplus, however small. Since in the process innovation case it is trivial to show, as we did, that consumers’ surplus must also increase, the rise in welfare then becomes unambiguous.

The same can be shown for product innovation in special, but not necessarily unrepresentative, cases. However, because of the plausible resulting rise in price that has just been demonstrated, total consumers’ surplus will not necessarily rise, as will be shown presently. Consequently, even if the producer’s surplus is increased slightly, it is possible for a product innovation to reduce welfare. Further, a product innovation can lead to shifts in the cost curves as well as in the revenue curves, unlike a process innovation, which can reasonably be assumed to affect only the cost side. Since costs as well as revenues are affected by product innovation, and those costs can either be raised or lowered, we have a second influence that prevents unambiguous results about the welfare effects.3

Before demonstrating the negative result, let us prove:

PROPOSITION 9.3. Where the marginal and average curves are all linear and the shift in the marginal and average revenue curves as the result of a product innovation does not change any slope or affect the marginal cost curve, then consumers’ surplus must be raised. In that case, a successful innovation (as defined here) must be welfare enhancing.

Proof: Let

a − by + μ = p =	the average revenue function
c + ky =	the average cost function.

Then the firm’s total profit function is

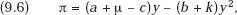
whose first-order maximum condition yields as the profit-maximizing value of y

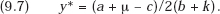
Marshallian consumers’ surplus at that output is given by

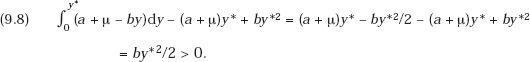
Thus, under the linear and parallel shift assumptions, a product innovation must increase Marshallian consumers’ surplus. Therefore, if it is successful, meaning that it increases the producer’s surplus, it must enhance welfare.

Product Innovations and Welfare: The Generally Ambiguous Result.

A graphic counterexample will suffice to prove:

PROPOSITION 9.4. Even if a product innovation is successful, it can decrease welfare.

This will happen if the innovation reduces consumers’ surplus because of its effect on the slope of the demand curve, and the sunk cost incurred by the innovation yields a negligible contribution to the producer’s surplus.

I will, once again, deal with linear average and marginal revenue curves (in the graph the marginal cost curve will also be drawn as a line segment, but that is unnecessary for the argument). However, in this case I will take the innovation not to shift the left-hand end of the revenue curves. In figure 9.2 I assume that, without the innovation, the marginal and average revenue curves are HMR₁ and HAR₁, respectively. With the innovation, the right-hand end of the old marginal revenue curve moves rightward, so that the new marginal revenue curve, HMR₂, coincides with the old average revenue curve. Consumers’ surplus then clearly changes from triangle ABH to triangle abH, where B is the point on AR₁ directly above the intersection of MC with MR₁, and b is the corresponding point for MC and MR₂. It is clear that if the MC curve were vertical then the second triangle would be considerably smaller than the first: the horizontal sides would be identical but the vertical side of the second triangle would be much smaller than that of the first. By continuity, this must still be true (though the difference will be smaller) if the MC curve is upward sloping but not quite vertical. Thus, in this case, the product innovation will reduce consumers’ surplus by a substantial amount (call it s), because it will raise the profit-maximizing price considerably, reduce the slope of the demand curve, and not add much to the quantity purchased. Let r represent the corresponding increment in the producer’s surplus. Then, so long as r > 0, no matter how small, the innovation will be successful on our criterion. By increasing the sunk cost, the magnitude of r can be reduced as close to zero as desired without making the innovation unsuccessful. In particular, there will be a magnitude of sunk cost beyond which s > r > 0. This proves Proposition 9.4: a successful product innovation can yield not only a negative consumers’ surplus but also a welfare loss.

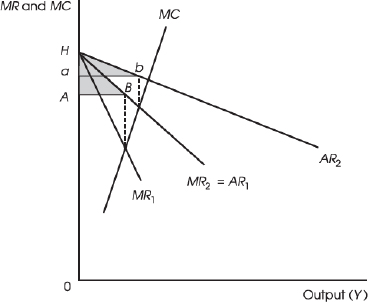
FIGURE 9.2

Effects of Product Innovation on Welfare

The key to construction of the counterexample is a resulting shift in the demand curve that reduces its absolute slope, rather than leaving it unchanged as before, and a rapidly rising marginal cost curve. The decreased slope of the demand curve means that the innovation will increase price considerably, while keeping the rise in the area under the AR curve to a minimum. The sharply rising marginal cost curve ensures that any contribution to consumers’ surplus resulting from an increase in sales will remain small. The graph shows that these two conditions together can ensure that the innovation will decrease welfare. Obviously, if the product innovation increases marginal cost because it provides a better product that is more costly to supply, that can exacerbate any resulting loss in welfare, or it can transform what would otherwise have been a net gain into a net loss.

The next chapter continues the use of elementary microtheory, returning to the implications of routinized innovation for the pricing of final products. In particular, it will focus on the influence of the repeatedly sunk outlays that routinization requires of the firm, and will show the crucial role of discriminatory (differential) pricing in this process, demonstrating that in these circumstances differential prices do not imply possession of monopoly power by the enterprise. Indeed, it will be shown that in these conditions not only may the firm be forced by market pressures to engage in differential prices, but it may have little choice in the magnitudes of those prices.

 

 

___________

1. Of course, there can be exceptions—cases in which a rise in marginal cost is accepted in return for a large cut in fixed costs.

2. Here, I obviously refer to the simplest measure of the surplus, that of Alfred Marshall (1920, pp. 125–33).

3. If the new product has a lower marginal cost than the old product, that may lead to a fall in the product price, further weakening Proposition 9.2. Thus, shifting cost curves can make the price effect of a product innovation even more ambiguous.