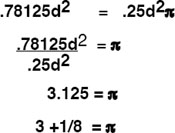In most sciences one generation tears down what another has built and what one has established another undoes. In mathematics alone each generation adds a new story to the old structure. — Hermann Hankel
In these days of conflicts between ancient and modern studies, there must surely be something to be said for a study which did not begin with Pythagoras and will not end with Einstein, but is the oldest and youngest of all.
—G.H. Hardy
Discovering mathematical magic is not confined to present day things. History and ideas from the past hold a wealth of the magic of mathematics. One often wonders how the ancients made use of such ideas as irrational numbers, proofs, conic sections. If it were not for human curiosity and the desire to learn, would mathematics have progressed to where it is today? This chapter presents a few of the multitude of mathematical ideas that have surfaced over the centuries.

Collage of mathematical ideas and their creators.
History shows that mathematical creativity is not privy to any particular culture, time period, civilization, or gender. The wealth of amazing ideas and contributions that were developed over the centuries is truly incredible and exciting to explore. Such an exploration would take the reader on a trip that traverses time and countries all over the world. Such a voyage would reveal that some ideas were discovered almost simultaneously in different countries, as was the case with the development of hyperbolic geometries. We know that numbers and numeration systems of some form are indigenous to all peoples. We find that the use of place value and the number zero was developed in many parts of the world —first by the Babylonians with their base 60, later the Maya with a modified base 20 system and by the Hindu when they developed and evolved a positional notation for the base 10 system. We find that their system was later improved upon and standardized by the Arabs. The Chinese also developed a place value system and used zero with their rod numerals, which they evolved into a sophisticated base ten numeration system used especially in performing calculations. Only a few of the many thousands of mathematicians and ideas are mentioned in this chapter. Those I discuss in no way reflect their superiority or stature over those not appearing. I urge you to use these sections as spring boards for further study and to enhance your understanding of the magic of the past. This is the spirit in which illustrations of the array of famous mathematicians, of the collage of mathematicians and their ideas, and of the diagram of numbers systems is presented. We are in the midst of many new mathematical discoveries. One does not have to be a mathematician to understand the essence of these ideas or appreciate their creativity. Seek out the magic in the past and the present.

An array of some famous mathematicians from the past.

We often think of ancient mathematics as just that — ancient and remote! Yet looking back, it is surprising to discover you may be using a similar idea, value, or concept that people used thousands of years ago. What we have learned about Babylonian mathematics comes mainly from a few clay tablets of cuneiform text from archeological excavations. The tablets date around 3000 to 200 B.C.. They reveal that the Babylonians dealt with the following mathematical concepts—
• equations in one unknown
• systems of equations in two unknown, tables of approximations2
• volumes and areas
• calculation of the area of a triangle and a trapezoid
• the approximation of π, 3 was used in determining the area of the circle— 3r2
• the volume of prisms and cylinders by multiplying area of the base times it height
• the Pythagorean theorem
• aspects of number theory, for example :
1+2+4+…29 = 29 + (29-1)
This Babylonian tablet1 illustrates an astonishingly accurate approximation for √2. It is equally amazing to learn that the Babylonian sexagesimal positional number system lent itself to such accuracies. The Babylonians updated the Sumerian number system to a sexagesimal positional number system.2 It was the first positional number system of its time. Initially lacking a zero and a sexagesimal point, it relied on the context to indicate the intended value of the number. For example, this number
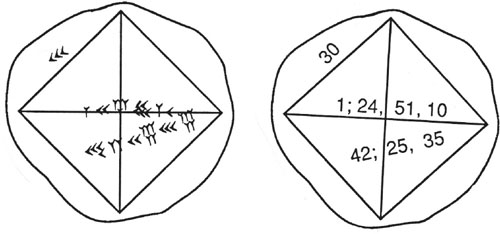
could represent 
11(60) + 12 = 672 or 11 + 12/60.
The Babylonians later developed  or
or  for a zero place holder.
for a zero place holder.
What were the Babylonians doing with such accurate approximations for √2? Examining this cuneiform tablet closely we see that the figure is a square with diagonals drawn. One side of the square has the symbol  which is how they wrote 30. Along the horizontal diagonal they wrote
which is how they wrote 30. Along the horizontal diagonal they wrote  which represents 1, 24, 51, 10. By assuming the sexagesimal point is between 1 and 24, the number converts to
which represents 1, 24, 51, 10. By assuming the sexagesimal point is between 1 and 24, the number converts to
1 +(24/60) +(51/602) +(10/603) = 1+(2/5)+(51/3600)+(1/216000) ≈ 1.4142129+
which compares to the √2 = 1.414213562… To arrive at their estimate the Babylonians probably used a repetitive approximation method often used by the Greeks.3
We know the Babylonians had a good understanding of the Pythagorean theorem. The value they calculated for the vertical diagonal is an accurate approximation for the length of the square’s diagonal. Namely, the diagonal numbers 42; 25; 35 convert to 42+(25/60)+(35/3600) ≈ 42.42638889 while 30√2 ≈ 42.42640687. In addition to working with right triangles whose sides were rational numbers (e.g. {3, 4, 5}, {5, 12, 13}), they also used the Pythagorean theorem on right triangles whose sides were not all rational numbers. This explains their use of approximations for such irrational numbers as √2. 6

The ancient Greeks discovered how to construct the lengths of irrational numbers using the Pythagorean theorem. They used inscribing and circumscribing regular polygons and the concepts of infinities and limits to close in on the area of a circle. They also developed a type of ladder arithmetic using ratios to approximate the value of irrational numbers. Here’s how it worked for √2.

Starting with the 1 and 1 from the top of the ladder, the rest of the numbers in the first column are generated in the following way:
1+1 = 2
2+3 = 5
5+7 = 12
12+17 = 29
29+41 = 70
Here is how the numbers from the first column generate the the numbers in the second column.
1+2 = 3
2+5 = 7
5+12 = 17
12+29 = 41
29+70 = 99
The ratio 1: √2 is squeezed in on by the ratios of the numbers on the same rung of the ladder. The ratios continually come closer and closer to 1/√2. The limit of ratios is the value of 1/√2.
NOTE: The two numbers at each rung of the ladder solve the equation— y2-2x2 = ±1. The x values are the numbers on the right side of the ladder.
1/√2 = .707106781…
1/1 = 1
2/3 = .666…
5/7 = .71428571429…
12/17 = .70588235294…
29/41 = .70731707317…
70/99 = .7070…
Finding experts who are able to translate ancient Chinese writing is difficult. Finding experts able to translate manuscripts that deal with mathematical ideas is even more difficult. This explains why Chinese examples of mathematical themes are scarce. Hsuan-thu, the piling of squares, was a technique that Chinese mathematicians used in order to arrive at algebraic conclusions using geometric and arithmetic means. This particular illustration is from the Chinese manuscript, Chou Pei. The date of Chou Pei is disputed, with possible dates ranging from 1200 B.C. to 100 A.D.. If 1200 B.C. is accurate, it would be one of the earliest known demonstrations of the Pythagorean theorem, predating Pythagoras and the Pythagoreans. The Pythagorean theorem has appeared in many civilizations throughout history. In architecture, it was one means of assuring the formation of a right angle. In mathematics is has been and is an indispensable tool crossing many mathematical disciplines
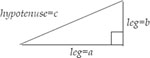
The Pythagorean theorem states that for any right triangle the sum of the squares of its two legs equals its the square of its hypotenuse (a2 + b2 = c2). (The converse is also true.)
In the left diagram below, the interior square’s area is indicated as 5x5 or 52 = 25 square units. It has been subdivided into 4 right triangles, each of area (1/2)(3x4) and a square of area 1x1, totaling 25 square units. In the right diagram below, the square is divided into two smaller overlapping squares, one 3x3 and the other 4x4. The part they overlap has the same area as the vacant part of the 5x5 square they do not occupy, which illustrates that the area of larger square (52) equals the sum of the two smaller squares’ area, namely 32 and 42.
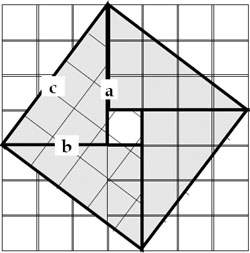
This diagram explains how to find the area of the interior shaded square by summing the areas of 4 triangles and the unit square in the middle. In general it shows —
c2 = 4(1/2)ab + (a-b)2
= 2ab + (a2-2ab+b2
= a2+b2
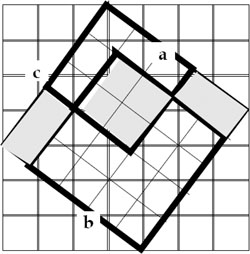
The two shaded rectangles ‘area equals the area of the shaded square ( this is the square created by two overlapping squares). Letting 5, 4, and 3 take on the variable c, a and b, it shows
a2 + b2 = c2.
Although this die was not referred to as random number generator during ancient Greece, it still gets credit for being one of the earliest remaining die. Today it appears in the National Archeological Museum in Athens, Greece. Dice have played many roles over the centuries. They have been used to foretell the future, to implement moves of various games such as backgammon and monopoly, or, as in craps, they are the main elements of the game. Mathematicians have long been intrigued with dice from the viewpoint of probability. In fact, dice can be considered responsible for getting Blaise Pascal and Pierre de Fermat to focus their attention on probability. While gambling, Pascal was asked by a friend how the pot should be split if the game were to be stopped before it was over. Pascal wrote Fermat about the problem. In 1654 the two men worked out their theory of probability in their correspondences, and thus launched this new branch of mathematics. Today dice and other shaped random number generators are used to teach various aspects of the theory of probability.

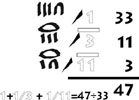
The Egyptian method of multiplication survived and spread over centuries and civilizations. In ancient Greek schools it was taught as Egyptian calculation. In the Middle Ages its techniques were taught and referred to by specific names such as duplatio for doubling and mediatio for halving. Here is an example, from the Rhind papyrus, how an Egyptian scribe would multiply 12×12. One first starts with 12. Then it is doubled to give 24, which is then doubled to give 48, which in turn is doubled giving 96. Slashes are drawn next to the 4 and the 8, indicating their sum of twelve. Then their corresponding amounts are added, giving the answer, 144. The Egyptian method of multiplication eliminates the need for memorizing multiplication tables, since it relies mainly on addition.

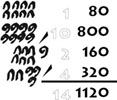
Division is done similarly. To divide 1120 by 80, you find what you would multiply 80 by to get 1120. Depending on how large a number you are dividing, the divisor is either doubled, or multiplied by 10, 100, 1000, etc. The results can then be doubled until a sum is found that equals 1120. If the problem does not come out even, the Egyptians used fractions. As in the example 47÷33.
Ancient Greek mathematicians and scholars are often considered to be predominately theorists and philosophers. Now new research1 has revealed that the first recorded laboratory for experimentation was set up by Pythagoras or the Pythagoreans (6th century B.C.). It is not surprising that there are no records from the Pythagoreans to support this claim, since the Pythagoreans were sworn to secrecy. On the other hand, there is supportive evidence from later scholars. This illustration is from the writings of the Roman scholar Boethius (5th century A.D.). It shows Pythagoras experimenting with sound, specifically the relationship between an object’s proportions (in this case bells) and the tones they produce. Theon of Smyrna (2nd century A.D.), along with other ancient authors, wrote of similar types of experimentations by other Greeks as well as the Pythagoreans. If one just considers the inventions of the Greek mathematician Archimedes (287-212 B.C.)— laws of lever and pulleys, methods for comparing volumes of objects by submergence in water, the Archimedean screw, the catapult—one realizes the importance of experimentation.

AΓEΩMETPHTOΣMHΔEIΣEIΣITΩ
Let no one ignorant of geometry enter here.
These words were over the doors at the Academy of Plato in Athens. Although Plato (428-348 B.C.) is not famous for his mathematical contributions, he is renowned for providing a center where he guided, encouraged and inspired mathematical thought. This elegant method for doubling the area of a square appears in Plato’s dialogue Meno. The diagram both illustrates how to double a square and how not to double a square.
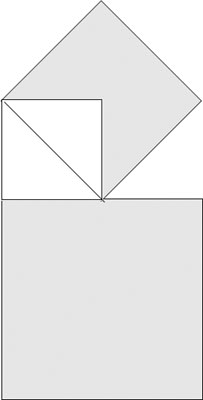
The upper shaded square’s area is double that of the white square. The lower shaded square has area four times that of the white square. Note that although its side is twice the size of the white square’s side, its area is quadrupled.
To find the area of any given circle, the Romans used the area of a square whose diagonal was 1/4 longer than the circle’s diameter.
Here’s how it worked, and its accuracy.
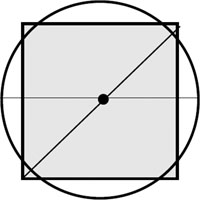
Suppose this circle’s diameter is d.
Then this makes the square’s diagonal d+.25d = 1.25d.
The square’s side is 1.25d/√2. Squaring the side of the square gives the square’s area as
1.5625d2/2.
Since the circle’s radius is .5d, and the area formula for any circle is Πr2, the actual area of this circle is (.5d)2Π = .25d2Π.
Using 3.1416 for the approximation of π. We get —
ROMAN METHOD vs ACTUAL AREA METHOD
1.5625d2/2≈.78125d2 .25d2Π ≈ .785d2
Equating .78125d2 & .25d2Π and solving this relation for Π
we get what approximation the Romans had for Π, namely—
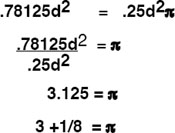
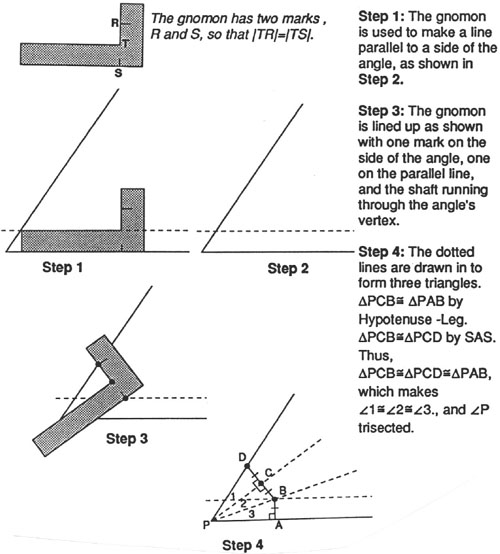
Trisecting an angle was one of the three famous impossible construction problems of antiquity which launched many mathematical discoveries. Although an angle cannot be trisected using only a compass and straight edge, it can be trisected using a tool the Greeks referred to as the gnomon. The gnomon can be used to make and determine right angles. And was used by the ancient Greeks to trisect an angle in the following way:
Mathematics certainly offers an abundance of problems. In fact, mathematics and problems are inseparable. History shows that mathematical ideas have been catalysts for mathematics problems, and that math problems have stimulated many mathematical ideas and discoveries. The three impossible construction problems of antiquity1; the Königsberg Bridge Problem2 and the Parallel Postulate Problem3 are historic examples of problems that have been resolved and in the process stimulated mathematical thought, ideas and discoveries. The posing and pondering of mathematical problems and questions and the scrutinizing of solutions and proofs are driving forces for mathematicians.
Here are a few famous “unsolved” mathematics problems:
THE UNSOLVED PRIME NUMBER PROBLEMS_______
• Is there one formula or a test to determine whether or not a given number is prime?
• Is there an infinite number of prime pairs? A prime pair is a pair of consecutive primes whose difference is two. For example, 3 and 5, since 5 - 3 = 2. Some others are 5 & 7, 11 & 13, 41 & 43.
• The odd perfect number mystery. A perfect number is one which is equal to the sum of its proper divisors (a proper divisor is a divisor other than the number itself).
The number 6 is an example of an even perfect number because 6 = 1+2+3. Other examples are 28, 496, and 8128. Circa 300 B.C., Euclid showed that if 2n-1 was a prime number that 2n-1(2n-1) is a perfect number. Then, in the 18th century, Leonhard Euler proved that any even perfect number must comply with Euclid’s form. For example, 8128 = 26(27-1).
But odd perfect numbers remain a mystery. As yet no one has found an odd perfect number, nor has anyone proved that all perfect numbers are even.

GOLDBACH’S CONJECTURE_____________________________
Is every even number greater than 2 the sum of two primes?
In 1742 German mathematician Christian Goldbach (1690-1764) wrote to Leonhard Euler (1707-1783) the conjecture that every even number except 2 was the sum of two primes. Examples: 4 = 2+2; 6 = 3+3; 8 = 3+5; 10 = 5+5; 12 = 7+5, … Although Goldbach’s conjecture is believed to be true, no one has proven it so as yet. Thus far the following ideas have been shown — In 1931, Soviet mathematician L. Schnirelmann apparently proved that any even number can be written as the sum of not more than 300,000 primes—a far cry from two primes. Ivan M. Vinogradov(1891-1983) proved that all sufficiently large odd integers are the sum of three primes. In 1973, Chen Jing-run showed that every sufficiently large even number is the sum of a prime and a number that is either prime or has two prime factors.
In the 1600’s Pierre de Fermat (1601-1665) wrote in the margin of one of his books—
To divide a cube into two cubes, a fourth power, or in general any power whatever above the second, into two powers of the same denomination, is impossible, and I have assuredly found an admirable proof of this, but the margin is too narrow to hold it.
restated: If n is a natural number greater than 2, there are no positive whole numbers x, y, y such that xn+yn = zn. Fermat’s note went out as a challenge. For centuries the proof or disproof had eluded even the most prominent mathematicians.
The next section gives additional background and discusses the latest information on Fermat’s Last Theorem. Some of the discoveries that have been an outgrowth of efforts to prove Fermat’s Last Theorem are probably more important than the theorem.
__________________
The study of mathematical ideas that have not been resolved is as interesting as delving into what we do know. This is but a small sample of unsolved mathematical mysteries. Although a few are simple enough to explain to someone with no mathematical background, their solutions are elusive.
There are no positive whole numbers that solve xn+yn = zn when n is a natural number greater than 2.

When 17th century mathematician Pierre de Fermat scribbled this note in a margin of a translation of Arithmetica by Diophantus, little did he know the impact his comment would have on the development of mathematics for the next 350 years. Had he really solved it? Was he just playing a joke? No one will ever know for sure, but what we do know is that it became one of the famous unsolved problems in the history of mathematics. Like the three famous construction problems of antiquity, the Königsberg bridge problem, and Euclid’s 5th Postulate, Fermat’s last theorem has stimulated mathematical thought and discoveries for centuries.
The mathematical community is very excited and enthusiastic about Modular Elliptic Curves and Fermat’s Last Theorem, the 200 page work of Andrew J. Wiles, professor of mathematics at Princeton University. Presenting his work at talks at Cambridge (June 1993), he climaxed his last talk with the announcement that he had proven the Shimura-Taniyama-Weil conjecture, which mathematicians felt held a key to proving Fermat’s last theorem. In mathematical circles the feelings are very positive that Wiles work has put Fermat’s Last Theorem to rest.
Over the centuries there have been thousands of “proofs” of Fermat’s problem, but none thus far has held up to scrutiny. It is not that Fermat’s last theorem is so extraordinary, but as Fermat said “I have found a truly wonderful proof” —the solution (its proof) is the beauty of this theorem. It has sparked new discoveries in such areas as number theory, cryptology and codes.

Czech Republic issued this postage stamp in 2000 commemorating Wiles’ work on Fermat’s Last Theorem.
Wiles had been intrigued with Fermat’s theorem as a teenager. But did not delve into its proof until he saw a possible means. Wiles considers his proof a collaboration of the many mathematicians and efforts that went before him. Among historical plateaus toward this end we have 18th century mathematician Leonhard Euler who proved the theorem for n = 3. German mathematician Ernst E. Kummer proved the theorem for all but three numbers less than 100. Present day computer proofs have shown that no solutions exist for the first four million natural numbers n. In the 1950’s Yuktaka Taniyama made his conjecture involving elliptic curves and their structures in a hyperbolic plane. In the 1980’s Gerhard Frey posed that if Taniyama’s conjecture was true for a certain type of elliptic curves (called semi-stable), then Fermat’s theorem could be proven. When Kenneth A. Ribet proved Frey’s proposition, Wiles decided to undertake Fermat’s theorem. From that time on he worked intensively for seven years. In May of 1993, a paper by Barry Mazur of Harvard came to Wiles’ attention. The paper described a numerical technique that was over a hundred years old which was very important in the finalization of his proof.
There are many mathematical concepts that have no restrictions in the realm of mathematics, but have limits when applied to the real world. The idea of proportion is one such idea that is a very useful tool in solving many types of problems. For example, if three identical boxes of marbles weigh 42 pounds, how many boxes are needed for 168 pounds? Setting up a proportion is one way to solve this— (3 boxes/42 lbs = ? boxes/168 lbs). But not all problems of proportion may be realistic to solve. Can any tree be scaled down to any size and be functional? Can a person of any size exist? The composition of an object, be it a tree or the bones of a person, play vital roles in deciding the upper and lower limits of its size. A hundred foot person is not possible, since the structure and materials that make up the human body were not intended for such mammoth sizes. Even giant redwoods have limits to their heights, dictated by their roots system and the properties of wood. One of the first records of the problem of scaling an object up or down was tackled by Galileo Galilei in 1638 in his work Dialogues Concerning Two New Sciences.

Here he states “…if one wants to maintain in a great giant the same proportion of limb as that found in an ordinary man he must either find harder and stronger material for making the bones, or he must admit a diminution of strength in comparison with men of medium stature; for if his height be increased inordinately he will fall and he crushed under his own weight. Whereas, if the size of a body be diminished, the strength of that body is not diminished in proportion; indeed the smaller the body the greater its relative strength.”*
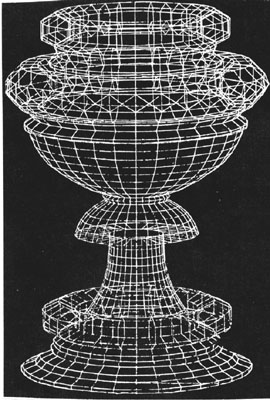
It is often startling and amazing to discover how objects and ideas were mathematized in the past. There are numerous examples of varied vases, containers, and vessels for storage that have been designed into many forms. This design and drawing of a chalice by Paolo Uccello is from the collection on display in the Uffizi Gallery of Florence, Italy. Although it was done during the first part of the 1400s, its precision and exactness is reminiscent of a computer analysis of a goblet, and illustrates linear perspective, constant ratios of proportional measurements, and use of geometric solids.
I have discovered such wonderful things that I was amazed.…out of nothing I have created a strange new universe.
—János Bolyai
from a letter to his father, 1823.
When most of us think of geometry, we think of our high school geometry course — all those “deadly” theorems we had to “memorize”, the excitement of doing our first proof, points, lines, triangles, quadrilaterals, circles, solids, area, volume. The beautiful thing about geometry is that one can visualize its elements. Little did we realize that a silent evolution of ideas had been taking place from ancient times to the present. Those of us who continued the study of mathematics learned that there was more, much more to geometry than Euclidean geometry. We learned how geometry and algebra were linked via the coordinate system by Rène Descartes. We saw how Euclid’s 5th (Parallel) postulate was challenged by mathematicians for centuries. Many mathematicians felt the Parallel postulate was not an independent idea, but could be proven from the existing materials of geometry. As history has shown, the Parallel postulate definitely was independent in Euclidean geometry — but the unsuccessful attempts led to discoveries of non-Euclidean geometries. It is impossible to really separate one field of mathematics from the rest, for as mathematicians get ideas they rely on their entire mathematics knowledge. A time line of the evolution of geometries is too intriguing to pass up. Space limits this time line to an evolving of the fields of geometries rather than specific ideas within a particular geometry. Hopefully it will serve as a springboard for your own research.
600 BC—Thales introduces deductive geometry. It was developed over the years by such mathematicians and philosophers as Pythagoras, the Pythagoreans, Plato, Aristotle.
300 BC—Euclid compiles, organizes and systematizes geometric ideas, which had been discovered and proven, into thirteen books, called The Elements.
140 BC—Posedonius restates Euclid’s 5th postulate.
3rd century AD—Proclus (410-495 AD) is one of the first recorded critics of Euclid’s 5th postulate.
Countless attempts are made over the centuries to prove Euclid’s 5th postulate.
1637—Renè Descartes formulates analytic geometry.
Gerolamo Saccheri (1667-1733) is the first to try an indirect proof of Euclid’s Parallel postulate. Unfortunately, he does not accept the results of his work. Prior to his death he publishes a book, Euclides ab omni naevo vindicatus (Euclid Freed of Every Flaw), which came to the attention of Eugenio Beltrami one and a half centuries later. Had Saccheri not rejected his findings he would have sped up the discovery of a non-Euclidean geometry by about a century.
1639—Girard Desargues (1591-1661) publishes a work on conics in which he discusses his new work on his discoveries of projective geometry.
1736—Leonhard Euler (1707-1783). His study and solution to the Königsberg bridge problem launches the field of topology.
1795—Gaspard Monge (1746-1818) describes structures by plane projections.
1822 Jean Victor Poncelet (1788-1867) revives projective geometry with his treatise and formulates the duality principle.
1843—Arthur Cayley (1821-1895) begins the study of n-dimensional spaces in analytic geometry.
Georg Cantor (1845-1918). His set theory provides a basis for topology, which is presented in 1895 by Henri Poincaré (1854-1912) in his Analysis Situs. Develops the Cantor set, an early fractal.
1871—Christian Felix Klein (1849-1925) does extensive work in projective geometry and topology, and proves consistency of Euclidean, elliptic and hyperbolic geometries.
19th century—Nicolai Lobachevsky (1793-1856), Jonas Bolyai (1802-1860), and Carl Gauss (1777-1855) independently discover hyperbolic geometry.
1854 —G.F. Bernhard Riemann (1826-1866) presents elliptical geometry.
1858 —August Möbius & Johann Listing independently discover one-sided surfaces, e.g. Möbius strip.
1888—Guiseppe Peano (1858-1932) creates Peano space-filling curve (fractal).
1904—Helge von Koch (1870-1924) creates Koch snowflake curve (fractal).
1919—Felix Hausdorff defines fractional dimensions in fractal geometry. A.S. Besicovitch generalizes Hausdorff’s work.
1971—Vladimir Arnold links algebraic (n-dimensional analytic geometry) geometry and topology.
1951-75 —Benoit Mandelbrot coins the word fractal and works nearly singlehandedly on its development.

Ever wonder how certain mathematical fields get their names? For example, consider hyperbolic and elliptic geometries. In both cases their creators had nothing to do with the names that were eventually adopted. Hyperbolic geometry was discovered independently by both Nikolai Lobachevsky (1793-1856) and Janos Bolyai (1802-1860). Euclidean geometry’s fifth postulate states that one and only one parallel line can pass through a given point P not on a given line L. Mathematicians unsuccessful efforts to show this postulate was provable, and thus a theorem, led to the discovery of non-Euclidean geometries. In hyperbolic geometry it was discovered that there exists more than one line passing through P and parallel to L. Hyperbolic comes from the Greek word hyperbole, meaning excessive. In this case it applies to the number of parallel lines passing through P and parallel to L. Lobachevsky had originally referred to his geometry as imaginary geometry and pangeometry. But the name by which it is called today — hyperbolic geometry — was given by the well known geometer Felix Klein, creator of the Klein bottle. In addition, Klein also coined the term elliptic geometry for Georg Riemann’s non-Euclidean geometry in which no lines exist parallel to L passing through P. The Term elliptic is from the Greek term elleiptis, meaning to lack or fall short.

The special thing about mathematics ideas is that once they have been established as true, they should hold for all cases. For example, to sum the first k counting numbers, 1+2+3+…+k, all one needs to do is plug into the formula k(k+1)/2. This formula has been proven mathematically by a method call induction. It is physically impossible to test this formula for every possible set of consecutive counting numbers starting with 1, but the beauty of mathematical proofs is that they do not require brute force. Swiss mathematician Leonard Euler is credited with many mathematical discoveries, especially in the field of topology. His solution to the Königsberg bridge problem is said to have launched the study of topological networks. Topology studies properties of objects that do not change as the object is distorted. For example, a cube can be distorted into a tetrahedron by stretching and squashing the cube, or vice versa. The size of the cube obviously changed, as did its number of faces, vertices and edges. As a result, one might wonder, what type of properties are left to observe and remain unchanged? One observation is that any point on the interior of the cube remains an interior point of the tetrahedron. Outside of topology, a fascinating theorem that Euler proved about a type of invariant property of polyhedra, is that if you add the number of faces of the polyhedra, to the number of its vertices and then subtract the number of its edges, the result is always 2. F+V-E = 2. Try it out on the Platonic solids shown. If you are feeling energetic try it on the rhombicosidodecahedron.

tetrahedron
cube(hexahedron)
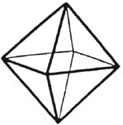
octahedron
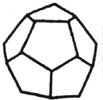
dodecahedron

icosahedron

rhombicosidodecahedron

Three musicians gracing the walls of the tomb of an ancient Egyptian official. Reproduction from the tomb of Nakht, Thebes.

Gregorian chant from 14th century manuscript.

Old musical notes and lyrics from the song ‘Skänelagen” written in the early Middle Ages.

From a 19th century encyclopedia showing Greek alphabet notes transposed to musical scales notes.
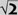






 or
or  for a zero place holder.
for a zero place holder. which is how they wrote 30. Along the horizontal diagonal they wrote
which is how they wrote 30. Along the horizontal diagonal they wrote  which represents 1, 24, 51, 10. By assuming the sexagesimal point is between 1 and 24, the number converts to
which represents 1, 24, 51, 10. By assuming the sexagesimal point is between 1 and 24, the number converts to
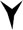 for one and
for one and  for ten. The position of these symbols determined their value.
for ten. The position of these symbols determined their value.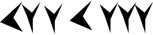 translates to 11, 1, ; 10, 3
translates to 11, 1, ; 10, 3