
THE COMPUTER, 21ST CENTURY S TOOL FOR CREATIVITY
A LOOK AT THE PAST
OBSOLETE CALCULATORS
A LOOK AT THE PRESENT
COMPUTERS ARE IN OUR TREES
MATHEMATICS BECOMES A PRIVATE EYE
CRYPTOGRAPHY, ANARCHY, CYBERPUNKS, & REMAILERS
COMPUTERS, IRRIGATION & WATER CONSERVATION
A LOOK AT THE FUTURE
CYBERSPACE/VIRTUAL REALITY
To err is human, but to really foul things up requires a computer.—Anonymous
Whether we are ready or not or whether we like it or not, the computer is the tool of the 21st century. The computer is impacting all facets of our lives both positively and negatively. It has sped up the gears of change. For today’s writers the computer can be the pen, pencil, or typewriter. For the accountant or bank teller it can be the calculator and keyboard. For the artist —a paintbrush and palette, for the scientist a laboratory, for the architect the drafting table, for the engineer design tools, for the professor a research tool, for the librarian a card catalog and reference desk, for the mathematician an incredibly fast and accurate calculator/computer. However, when things don’t go exactly as planned, the computer becomes the scapegoat, and we are told—”it lost your file,” “the system is down,” “there seems to be a glitch.” Nevertheless having touched almost every aspect of our daily lives, we are now dependent on computers.

Some computers languages developed to communicate with computers.
• The ten digits of our hands were our earliest counting devise.
• The Chinese devised a segmented box to use with their rod numerals. This box was used to write systems of equations.

• The abacus was used in calculation by many cultures including the Chinese, the Greeks, the Romans, and the Japanese.
• The Incas used the knotted quipu as their accounting device.
• Napier’s rods were invented by John Napier in the 1600s to aid computation.
• The slide rule was invented around 1620 by Edmound Gunter.
• The first adding machine was invented by Blaise Pascal in 1642. And in 1673, Gothfried Wilheim von Leibniz invented one that could also multiply and divide.
• In the early 1800s Charles Babbage’s designs and work on the difference and analytical engine furnished the foundation for the modern computer.
This illustration is a reproduction from the early English arithmetic book The Grounde of Artes, by Robert Recorde. In addition to the lines representing 0s, 10s, 100s, etc, the places between these lines were also used to represent 5s, 50s, 500s following the Roman numerals. The “x” on the line was initially used to mark the 1000s line, but later it was used to indicate a comma when writing such numbers as 23,650. When five counters accumulated on a line those beads would be removed and one counter would be carried to the above space. Hence, the possible origin of the term “carry”. In addition to writing this book, Robert Recorde (circa 1510-1558) introduced the symbol “=” for equality, wrote an important algebra text book called The Whetstone of Witte and the geometry book, Pathway to Knowledge.
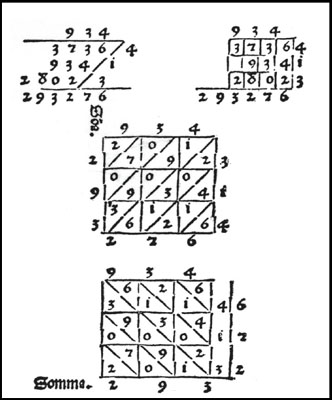
These tables are from a book that was printed in 1478 in Treviso, Italy. It shows four methods for multiplying 934 and 314.

The binary system (base two), which uses only 0s and 1s to write its numbers, held the key to communicating with electronic computers — since 0s and 1s could indicate the “off” and “on” position of electricity. The famous Scottish mathematician John Napier (1550-1617) utilized the concepts of base two before the advent of electricity. Napier is best known for revolutionizing computation by his invention of logarithms. His calculating rods, known as Napier’s rods (or bones) were based on logarithms and were used by merchants to perform multiplication, division, and could be used to find square roots and cube roots. Less well known is his chess board method of calculating. Although he did not use binary notation to write numbers, the board does illustrate how he expressed the numbers in base two. For example, to add 74 + 99+ 46, each number is written out in a row of the chess board by placing markers in the appropriate squares of the row so that the sum of the markers values (indicated along the bottom line) total the number they represent. 74 has markers at 64, 8 and 1 since 64+ 8+1 = 74. After each number is expressed on the chess board, the numbers are added by gathering the markers’ vertically down on the bottom row. Two markers sharing the same square equal one marker to their immediate left. So two “2” markers, produce one “4” marker. Working from right to left, any two markers sharing the same square are removed and replaced by one marker in the adjacent square at the left. At the end of this process, no square will have more than one marker. The sum of the values of the remaining markers represents the sum of the numbers.
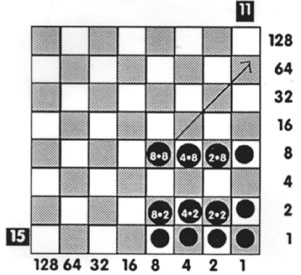
To multiply using Napier’s chess board calculator, the number representations along the horizontal and vertical column are used. Suppose we want to multiply 15 x11. One number is expressed with markers along the bottom row and the other along the vertical column at the right. Then a new marker is placed at the intersecting square where a row with a marker meets a column with a marker. After this is done, the multiplication process is simply done by sliding the markers from the bottom row diagonally to the vertical row. As with addition, any place two markers occupy the same square, they are removed and one marker is placed in the square above them. The resulting vertical column will represent the product of 15 × 11.
It is unworthy of excellent men to lose hours like slaves in the labor of calculation which could safely be relegated to anyone else if machines were used. —Gottfried Wilhelm
von Liebniz
“I’m a dinosaur.” “I refuse to have anything to do with them.” “I can’t understand how a person can spend so much time in front of one.” “They’re so impersonal.” “I’m just computer illiterate.” How many times have you heard or perhaps made some of these statements? But it must be accepted, regardless of how some people may feel, that computers are here to stay. They are making our lives easier in some ways, more complicated in others, and invading our privacy. In fact, it is difficult to remember the days before computers. Now computers are even in our trees!
The growth of trees can be patterned using mathematical networks or drawn using fractals. Computers can be used to model forest fires, and thereby develop strategies to either put out fires or create controlled burns. In addition, computers are now being used extensively to log urban forests. Many cities, in efforts to preserve and maintain the health of their trees are resorting to computers. Washington D.C. has a database of about 109,000 street trees, while Paris, France also has its 100,000 trees on computer. What kind of information is entered? Each city usually decides what data is essential for its particular situation. The Paris database includes—the tree’s location (each tree is consecutively numbered along the street, and its distance from the building, curb and adjacent trees are noted), its vital statistics (species, sex, age, trunk size, height), type of pruning received, environmental statistics (includes soil type, planter dimensions, drainage, mulching), tree’s health (status and diseases noted), environmental pollutants and effects. The initial logging of such information is very time consuming, as is the updating of files. Since trees are an invaluable asset to any community, both aesthetically and environmentally, the time invested ºand long range outcome make such databases worthwhile. In San Francisco, California, the city gardeners maintain the city’s inventory using laptop computers. Paris followed a method used in Washington D.C., in which the initial inventorying was done by junior forestry engineers using hand-held computers. Without computers, such sophisticated databases would not have been possible. Storage and filing space would have been too formidable, let alone the necessary updating, searching and sorting of data.

Bar codes for labeling & tracking such things as trees, groceries and packages.
As the computer evolved, computer functions slowly invaded aspects of our lives. Even as early merchants and navigators, wondered how they had functioned without a set of Napier rods, and Inca scribes must have speculated how they had kept inventory of the population and products of the Inca empire without the quipu, so today we are at a similar point.
As we see with the urban forest, computers play an incredible role in storing, processing, and retrieving data. Today, data imput devices are used by restaurants to process orders, bar codes are used by stores and businesses for sales, inventory, and tracking. Computers are invaluable in the sciences for analyzing, comparing and computing information, thereby saving tremendous amounts of time with fewer errors. This evolving tool’s influence on civilization will be as great as was the impact of the electric light bulb.
The mathematics of wavelets are now being used as a crime fighting technique and tool. Mathematicians have developed wavelets analysis to process images in a quicker more accurate fashion. The method divides an image into basic components. It then isolates the important and relevant information needed to reconstruct the image and discards the non-essential information.

Consequently, wavelets reduce the amount of data necessary to store, transmit and retrieve the image. This data compression saves time and money. In addition, the wavelets do not distort the image as other methods do. This allows the FBI to more efficiently process, identify and match the image of a person’s fingerprints.
Governments, financiers and revolutionaries have always needed to send and receive confidential information. Many methods of coding and decoding messages have been devised over the centuries. Among these are the Spartan scytale1, Polybius’ square cipher2, Julius Caesar’s letter substitution, Thomas Jefferson’s cipher wheel, and the German military code Enigma. There are also many examples in literature where cryptography is important to the plot, as in Edgar Allan Poe’s The Gold Bug, Jules Verne’s La Jangada, Conan Doyle’s The Adventure of the Dancing Men.

A portion of Thomas Jefferson’s cipher wheel. It was made with 36 wooden wheels of the same dimension. Each wheel had the letters of the alphabet printed in various arrangements. A message would be lined up along the metal cross-bar. Then the sender would write the letters of any other horizontal line and send it off. The recipient would line up these nonsense letters along their horizontal cross-bar, and look around the cylinder until a line of letters was found that made sense.
For the past twenty years the encryption formula, DES 3 (Data Encryption Standard), has been used by banks, government agencies and private companies to secure information. This method uses 56 bits of computer data which theoretically would take 200 years to decode using a super computer. Intelligence and law enforcement agencies fear that the present methods are not adequate and would not be able to intercept communications from criminals, terrorist and foreign governments. Consequently, a new system is being proposed with a new formula using 80 bits that would theoretically take more than one billion years to crack. This approach uses a special microchip which would be inserted in telephones, satellites, fax machines, modems etc. to scramble secret communications. The chip would use classified mathematical formulas developed by the National Security Agency. In addition, mathematical keys that unscramble the coded data would be kept by the FBI and other agencies determined by the Attorney General of the United States. The manufacturing process of the chip makes it nearly impossible to take apart and decode. There are people, such as Mitchell Kapor of the Electronic Frontier Foundation (a public policy group in Washington D.C.), who say “A system based on classified secret technology will not and should not gain the confidence of the American public”.4

The substitution cipher in Edgar Allan Poe’s The Gold Bug.
______________________
The translation is: A good glass in the bishop’s hostel in the devil’s seat twenty-one degrees and thirteen minutes northeast and by north main branch seventh limb east side shoot from the left eye of the death’s-head a bee line from the tree through the shot fifty feet out.
1Plutarch describes how messages were exchanged by winding a narrow band of parchment or leather in a spiral manner around a cylindrical shaft. A message would then be written, and the band removed and sent to the recipient who had a cylindrical shaft of the exact same size to wind the band around and decipher the message.
2(Circa200 B.C.-118 B.C.) the Greek Polybius devised a substitution cipher designed around a 5×5 square, which converted each letter of the alphabet into a two digit number using only the digits for 1 through 5.
3In 1999 this code was cracked in 22 hours and 15 minutes, and has been replaced by AES(Advanced Encryption Standard), which was adopted by the US government in 2002. AES is composed of three cipher blocks with 128-bit size with different key sizes. AES publicly available in various packages.
4Secret Phone Scheme Under Fire, by Don Clark, San Francisco Chronicle, May, 1993.
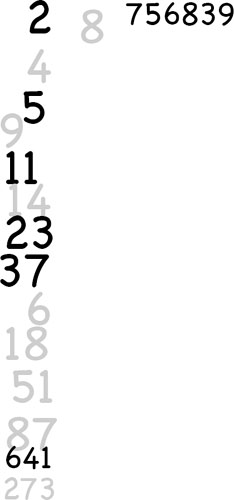
One of the earliest methods for finding prime numbers was devised by the Greek mathematician Eratosthenes (275-194 B.C.). He created a numerical sieve that would eliminate multiples of numbers up to some given number. Ever since then mathematicians have been devising new means for seeking out and identifying prime numbers.
In 1640 Pierre de Fermat claimed that all the numbers of the form Fn = 22n +1 (for n = 0, 1, 2, 3,…) were prime. This is true for the first five Fermat numbers (for n = 0, 1, 2, 3 and 4). But the following century Leonhard Euler factored the 6th Fermat number (F5) into 641 times 6700417. Then in 1880 the Fermat number, F6, was factored into 274177 times 67280421310721. Currently no other Fermat numbers have been found to be prime, and as of 1993 the 22nd Fermat number (F22) was shown to be composite.1 In 1644, the French monk Marin Mersenne wrote an expression– 2p-1, with p a prime number– that would yield primes. But not all the numbers produced by this expression are prime. There are currently 33 known Mersenne primes. Working with expressions (such as those for Mersenne numbers, Fermat numbers, Carmichael numbers, and others), number theory, and computer programming techniques, mathematicians using either supercomputers or strings of revved-up personal computers seek out larger and larger prime numbers – and look for quirky characteristics or patterns.
WHY ALL THE INTEREST IN PRIMES? –mathematical curiosity–setting new records–testing the efficiency and hardware of new computers–using prime numbers to form multidigit numbers for encoding confidential material. Today’s computers, along with ingenious programming and problem solving have made it possible to find literally enormous prime numbers. As of 1993, LARGEST EXPLICIT PRIME is 2859433-1.2
1Projects in Scientific Computation by Richard E. Crandall.
Springer-Verlag, Santa Clara, CA 1994.
2Found by David Slowinski in 1993. Verified at his request by Richard Crandall.
Ever wonder, irritatedly, how it i you receive so much junk mail — catalogues you never requested, offers for “super” buys? How was your name and address accessed? Welcome to the electronic age and the loss of privacy. Most individuals have considerable electronic data about them, which can be accessed by a computer/modem user to create a profile of you based on things you have bought, your travel tickets, your medical records, your traffic tickets, outstanding loans, etc. Although the loss of privacy was created by today’s new technological methods for storing and accessing information, perhaps there is a way to restore that privacy by using these same methods. Cyberpunks, as they call themselves, have come to the rescue. They advocate restoring the privacy of the individual, by using sophisticated cryptographic methods to encode one’s information, and hinder its ready availability. Naturally there are pros and cons to this cryptographic anarchy. Some feel that government and law enforcement agencies have a right to eavesdrop, and cyberpunks new methods would present obstacles. Remailer is an example of one new method developed using advanced cryptography which allows one to send information via modem without leaving any “footprints” to trace the sender. Many feel that if governments can use methods and devices to encode important information, an individual also has a right to use similar methods to insure personal privacy.
It is eerie to observe lush crops growing from dry, sometimes cracked earth. But now with the use of computerized subsurface drip irrigation, water, fertilizer and occasionally pesticides can be delivered directly to the roots of plants. With subsurface drip irrigation, raisin grape farmer Lee Simpson of Fresno, California has cut his water consumption in half and doubled the yield of his farm while cutting back the use of pesticides to one-sixth. A California Department of Water Resource test project on a 160-acre cotton field of Harris Farms, also in Fresno, produced 1600 pounds of cotton per acre as opposed to 930 pounds per acre from previous years, and used 7 inches less water per acre. Claude Phené has been at the cutting edge of this “new” type of farming (drip irrigation has actually been around for over 30 years). Phené had been advocating conserving water and improving yields by this method for years, but it was not until 1987 that some farmers took notice. Phené tested his methods on his tomato crops in California. Acres that formerly produced 26 tons per acre, now produced 100 tons per acre. Phené points out that it does not make sense to flood a room to water a potted plant. His statistics claim that California agriculture uses 85% of the state’s water supply, and if subsurface computerized drip irrigation1 were used with just one crop— e.g. cotton—the 6 inches of water saved on each of the 1.4 million acres would be enough water to supply Los Angeles. The method also reduces the use of herbicides, since weeds do not grow as readily between the furrows because plants are watered at the roots and not flooded. In addition, the amounts of fertilizers and pesticides used would be cut by more than half. His computerized techniques allowed his operation to discover the interaction between different nutrients, timing of nutrient applications and their affects on crops yields, the optimum amount of fertilizer for optimizing plant quality, and numerous factors from soil texture to rooting characteristics.
1Crops are irrigated by underground pipes placed 18 inches below the surface. The very sensitive lysimeters detect morning dew, measure amounts of water that plants absorb and emit, measure surface weather conditions. The computer gathers and analyzes data, and delivers minute amounts of water throughout the day and occasionally fertilizer, herbicides, and pesticides. Without investing in a computer system, small farms could monitor their fields via modems at a centralized computer location.
Today’s computer modeling is a very powerful tool, used by scientists and professionals across a spectrum of fields. It can be used by economists to predicts economic cycles, by doctors to monitor and predict the spread of a contagious disease or with chaos theory to describe heart arrythmias. It has been used by sociologists along with statistics to observe a social trend. The list seem almost unending.

Not too long ago firefighters’ tools were protective garments, axes, pike poles, ropes, chain saws, fireproof blankets, water, chemicals. Today some firefighters are also equipped with laptop computers or even a tent/laboratory in the middle of the forest complete with personal computers. In addition to keeping track of people and supplies, the computers are also used for forest fire analysis.
While working for the United States Forest Service’s Intermountain Fire Sciences Laboratory in Montana, mathematician Patricia Andrews developed the program Behave in 1984. The location of the fire, the typography of the area, the climate conditions (wind speed and direction, dryness, etc.), the types of burning trees or grasses and much more information is fed into the computer. The program then predicts how the fire “might” behave, thereby helping fire managers decide how to best fight the blaze. Naturally, it cannot predict all possible outcomes, but Behave can be continually modified to become more comprehensive as new predicaments occur, such as the Yellowstone “crown fires” in which the fires spread from treetop to treetop. Effects is a companion program now being used to help forest management with decisions for controlled burns. These high tech firefighting tools are now being used in China, have been translated into Spanish, and information has been requested by Italy.
It is the perennial youthfulness of mathematics itself which marks it off with a disconcerting immortality from the other sciences.
—Eric Temple Bell
In the 1500s people were treated to the marvels of the camera obscura. Actual moving scenes from things taking place outside a room were projected on the wall of a darkened room. No electronic devices were needed to bring these scenes into the room. Then, in the second half of the 19th century, there was a surge of interest in optical illusions. Physicists and psychologists studied and wrote about how our minds were tricked by what we perceived. The physical structure of the eye and the analysis of how our minds process information from the eye were studied in efforts to explain distortions which tricked our minds into believing they existed.
Some of their findings were—
(1) The placement of certain angles and segments can lead our eyes inward and outward and thereby make an object appear to be shorter or longer.
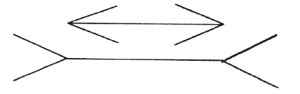
(2) Horizontal objects have a tendency to appear shorter because the retinas of our eyes are curved.

(3) A light region’s image on the retina radiates into the dark region’s image thus making the dark region appear smaller.

4) Identical objects in different locations in a perspective drawing appear to be different in size.
(5) If an image can be interpreted in more than one way, then our mind oscillates the image back and forth between interpretations.

(6) Diagonal segments on parallel lines make them appear non-parallel.

(7) An empty space and an identically filled space appear different in size.
(8) A diagonal broken by a vertical bar does not appear to be aligned.

Now, in the 20th century, computer scientists, mathematicians and inventors are carrying optics, computer technology and optical illusions to new heights with the creation of artificial worlds. Equipped with various paraphernalia, the observer is no longer simply an observer— but actually enters worlds created by the computer.
In these artificial worlds, one can be a participant. For example, one may choose to be:
— an “Olympic” runner experiencing the thrill of running for the gold metal
— an air traffic controller directing planes flying around in the 3-dimensions
— a weather forecaster flying around the world experiencing first hand weather conditions that have been programmed and processed into the computer.
— an atom about to be bonded with other atoms into a molecule
— an architect viewing his or her most recent design by actually walking through the computerized image room by room.

Here a cyberspacenaut enters the racquetball court of the computer, and the game begins. The players actually feel they are playing on the computer court. Photograph courtesy of Autodesk, Inc. Sausalito, California.
Virtual reality, cyberspace, and artificial reality are a few of the expressions coined to describe this form of optical illusions. In the confines of a small room one can don computer gear,1 and suddenly find oneself walking in the English countryside, inspecting a project’s progress thousands of miles away, or learning how a bee collects pollen by becoming the bee. The applications of such technology are mind boggling. Cyberspace is still in its initial stages with much yet to be developed and refined2. Hopefully its evolution and popularity will not serve as a means of mind control, but rather of mind expansion. Computer scientists and mathematicians are breaking new ground in computer graphics, especially by using fractal geometry to create these special effects. Perhaps the holodeck of Star Trek— The Next Generation is not so far fetched.

Computer generated living room awaiting a visitor to virtual reality. Photograph courtesy of Autodesk, Inc. Sausalito, California.
1The computer gear comes in many forms which can include special eye gear, data gloves, data body suit.
2A few of the universities and businesses involved in these artificial worlds are University of North Carolina; Autodesk, Inc. of Sausalito, CA; HITL at the University of Washington; VPL Research Co. of Redwood City, CA; Carnegie Mellon University. Connecticut State Museum of Natural History has an installation created by Myron Krueger called Video Place. At U.C. Berkeley’s ASUC, one can play Dactyl Nightmare, a virtual reality game.
Speculations on the fourth dimension surfaced in the 19th century when August Möbius noticed that a shadow of a right hand could be made into a left handed shadow simply by passing one’s hand through the third dimension. Little did one realize that the term hypercube1 would lead to a generation of such terms as hyperspace, hyperbeing, hypercard2 and now hypertext. Though the last two terms are not directly related to the 4th-dimension, they are related to the computer and its ability to jump from one idea to another — interactive computing. It can be thought of as analogous to moving from one dimension to another. The participants decide where to go and the computer transports them there. For example, with interactive computing, after you decide what you want to do, read or view, the computer immediately brings before you information on that topic, which may include a sound tract, graphics and even a video. Suppose you want to learn something about V-E day of World War II. The computer is able to present historical information, maps showing the invasion and how it proceeded, newsreels from that period, and even songs that were popular during that time. You choose topics by clicking your choice3.

Hypertext draws on interactive computing by allowing even more active participation. A hypertext is not read from beginning to end in the traditional manner. Instead, the computer functions as a tool to explore other possible outcomes, and thereby a new story evolves. With hypertext the reader spins his/her own tale by clicking on highlighted ideas that are interconnected in a story called a web, which has been spun into the original program. While reading the story on the computer, you can choose the direction in which you want the story line to move. You do not create the storyline, but rather choose options along the way, and see what they unfold. A click on a key word or image may take you to a new location, a new idea or even a new plot line. You are able to see how the author unfolded the story along the paths you chose. The reactions to interactive literature are mixed. Some feel it is a novel curiosity that is far more interesting in theory than practice. It is in its initial stages, and thus far once a story has been “altered” by the reader, it can not be undone. In addition, it may also be difficult for the novice to tell when the story is finished, since there may be key words or phrases available throughout the web allowing the reader to continually go off to something new or perhaps even around in a circle by mistake. The web stories may require time and/or practice for inexperienced hypertext readers to orient themselves to this form of reading. Improved programming and writing techniques for this media need to be refined if it is to work optimally and if the reader is to have unencumbered freedom to explore its potentials. As English professor George P. Landow of Brown University says,”It really has the potential to be the next wave of storytelling…The next question is, is this total chaos and anarchy, or is it a new reading form that makes the reader a kind of creator?”4 There are many who feel hypertext is introducing a new way of writing, and consider it an art form. Most of the focus thus far has been on the reader who now helps shape the direction of the story. But consider what such story writing entails for the author. The writer does not develop a single plot line, but instead a family of possible plot lines and their relative outcomes, called the web. As with interactive computing, the web can be enhanced by computer graphics, sound and video. It is too early to pass judgement on interactive literature, especially since the hypertext stories are just being released or posted on electronic bulletin boards, but it will be fascinating to follow the outcome. Will it catch on as a new craze? One thing is certain, hypertext would not exist if it were not for the modern computer.
1 Hypercube is the term coined for a 4th-dimensional cube.
2 Hypercard has two meanings. It can be the trade name for a computer program, which allows you to access and create stacks of cards with information in various forms (including graphics, video, sound) simply by clicking on a particular topic. Hypercard can also be a card (which is 2-dimensional) that has been cut and folded into a 3-dimensional model, similar to the book illustrated on the computer screen. It is hard for one to pass up trying to recreate a hypercard from a 3x5 file card.
3 It seems an easy way to pursue learning. What are some drawbacks? You have to depend on the material that is accumulated in that particular piece of software. Sources other than those on that program are not at hand. If you are using the program for more than just general knowledge, you have to be careful not to rely on this as your sole research material. Hopefully this form of available information will not hinder creativity or the ambition to do additional research, but rather stimulate it.
4 A New Way To Tell Stories, San Francisco Chronicle, San Francisco, CA, April 1993.
One often gets the feeling that the layperson now feels that computers have evolved to their ultimate state, but computer scientists, mathematicians and scientists know this isn’t so. In the spirit of Charles Babbage, M.M. (Monty) Denneau, George V. and David V. Chudnovsky and Saed G. Younis created Little Fermat, a computer designed to handle gigantic computation problems without the number errors associated with conventional computers. Using ideas from number theory—specifically modular arithmetic and Fermat numbers—the computer can carry out computations virtually error free. Little Fermat is programmed in a language called Younis. By utilizing Fermat numbers as divisors in modular arithmetic, it can speed up certain kinds of calculations and avoid the use of real numbers. Thus far Little Fermat is a one-of-a-kind computer, but its creators feel it is ideally suited for digital signal and imaging processes and the solving of various problems from hydrodynamics, chemistry and aerodynamics that require differential equations. Furthermore, they hope it will serve as a model to enhance the performance of the supercomputers.

The keyboard punch for the 1890 Herman Hollerith tabulating machine, which revolutionized the procedure for taking the census in the United States.
With technology changing at such a rapid rate and with new ideas and applications springing-up overnight, computers seem to be impacting every aspect of our lives whether we are aware of it or not. Many scientific laboratories are now the computer, utilizing its modeling and simulation abilities.

A-life, as it is often referred to, is a way to simulate lifelike forms, their behavior, reproduction and evolution. One recent example of its uses were the lifelike computer generated bats in Batman Returns. How was it done? Utilizing logic, mathematics and computers, the habits of a living thing, such as a bat, are analyzed into basic logical steps. These steps are developed into a computer simulation which captures the movements and habits of the life form. The applications are far reaching. One example is the research in disease done at Scripp Research Institute. Here Gerald Joyce uses computer simulations and develops a laboratory procedure in which enzymes evolve according to how they slice in the genetic code of an AIDS virus. By trial and error, these enzymes explore a cure. Computers can develop their own programs based on how well they solve certain problems. Programs designed by this method include steering a vehicle, predicting economic outcomes, predicting planetary motion. Computer pioneer, John von Neuman, contended that machines could not only process information, but reproduce themselves. Some proponents of A-life feel that the essence of life is a set of rules directing the interaction of cells, atoms, molecules, etc. A close connection between A-life and fractal mathematics is also developing. For example, computer simulations have been developed of plant cells that grow and divide according to a set of instructions. One such grew into cell formations almost identical to those of a fern. Studying how different insects navigate, such as ants simulations of miniature robots have been created that are instructed to move and change direction only when they come to an obstacle they cannot traverse. These robots outperform the traditional larger designs when it comes to finding their way around obstacles. In fact, Attila, designed by MIT’s Mobot Lab, weighs 3.6 pounds and will hopefully be used to explore Mars.
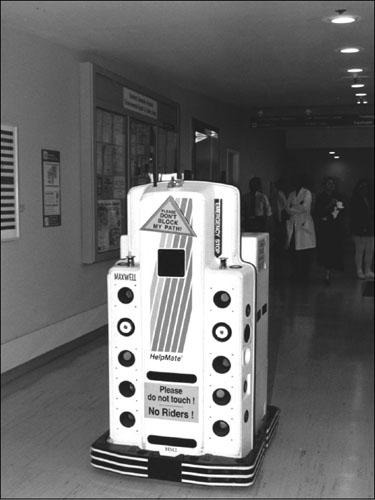
The robot used at Stanford University Hospital (Stanford, California) to carry records back and forth. Photograph courtesy of Stanford University Medical Center, Visual Arts Services.
Our present computers run on electricity. But some scientists are working on the development of a new type of computer. A computer that is made up of optical fibers, lasers and switches that process data and perform calculations via light1 rather than electricity. Unlike electronic computers in which data and programs are stored either on memory chips, hard drives, or disks the optical computer circulates data as light pulses through the optical fibers. “For the first time, we have a computer in which the program and data are always on the move in the form of light, eliminating the need for static storage,” says Harry F. Jordan of the Optoelectronic Computing Systems Center at the University of Colorado at Boulder, Colorado. Over three miles of optic fiber serve as the computers main memory, where instructions and data are encoded in light pulses and circulate the optical fibers. Jordan and Vincent P. Heuring head the development at the University of Colorado. The computer that they have developed thus far does “demonstrates the principle that all of the components of a general-purpose machine can be done in optics.”2

1The only time light is not used occurs when the optical switches are activated and light pulses momentarily converted to electrical current.
2Harry Jordan, quoted from Science News, January 23, 1993.
Suppose I take a log and add it to the fire in my wood burning stove. It begins to burn immediately. At what precise instance will it no longer be considered a log? One person might say right after it caught fire. Someone else might feel when half of it is burned away, and yet another person might contend it’s a log until its last ember. No matter how logical one tries to be about answering this question, there is no definite answer. There is no right or wrong answer. There is no way to quantify the answer. It is all a matter of degree. A 5:00 pm appointment means the same for everyone. But an appointment set for late afternoon may mean 3:30 pm to one person, 5:30 pm to another. In fact, there are a host of possible times depending upon whom you asked. And such is the case with so many things in life, for there is a subjective nature to life and the universe. True or false, yes or no logic cannot deal with such situations or with the ever changing status of everything on earth and in the universe. These are the things that fuzzy logic deals with.
Fuzzy logic may be inside—
•your washing machine, if your machine determines the best washing cycle from your input of water level, load size, fabric, and dirt and stain levels. After a wash cycle. The machine will repeat the cycle if the water is not clean enough.
• your vacuum cleaner, if it can automatically adjust suction based on information gathered through its infrared sensors.


The Mitsubishi HSR-IV is designed to avoid accidents by utilizing a neural fuzzy inference system.
Fuzzy logic is a different way of looking at things and analyzing the world. The termed “fuzzy” logic was coined in the 1960s by Berkeley professor Lofti Zadeh. But paradoxes can probably be blamed for the birth of this new logic. Over the centuries paradoxes have created cliches in traditional logic. True or false logic could not be used to explain such paradoxes as Eublides’ pile of sand paradox 1 or Bertrand Russell’s class membership paradox.2 These paradoxes go hand-in-hand with so many real life situations which cannot be answered by a simple yes or no. Traditional logic does not have room for gradations of a situation. Although fuzzy logic had its origins in the United States, it has been embraced by Eastern philosophy and scientists. Just as mathematical objects do not precisely describe things in our world, so traditional logic cannot be perfectly applied to the real world and real world situations. Traditional logic and computer programming rely on statements being either true or false (electricity being “on” or “off” — “1” or “0” of the binary system). To humanize computers, fuzzy logic must come into the picture. Fuzzy logic tries to imitate how the human brain would work. In other words it attempts to make artificial intelligence real intelligence. Japanese and Korean companies are leading the way with innovations that make use of fuzzy logic. Among other things, they are producing computers, air conditioners, cameras, dishwashers, automobile parts, televisions and washing machines, which are enhanced with fuzzy logic technology. In the October 1993 Tokyo Motor Show, the computer in Mitshubishi’s prototype HSR-IV uses fuzzy logic to imitate the information processing of the driver’s brain. The computer studies the driver’s normal driving habits, and then selects a response for various situations that might occur. For example, if built-in radar detects an obstacle, the fuzzy logic system decides if the driver is aware of it or not (based on past driving patterns). If the driver does not respond as predicted, it can then automatically control the brakes to avoid a collision.
Up until now many Western scientists have been reticent to use fuzzy logic. Some feeling that it threatened the integrity of scientific thought. Other scientists feel it enhances and expands the possibilities of computer programming by considering a broader scope of variables for the solution of a specific problem or the design of a particular product. In the past the National Science Foundation rejected proposals that dealt with fuzzy logic, but perhaps future projects will be considered in another light, especially since more United States companies, such as Ford, Otis Elevator, Pacific Gas & Electric, Motorola, and General Electric are expressing interests in its uses.
14th century B.C. Greek philosopher Eublides considered how many grains of sand make a pile.
2Russell’s paradox —Bertrand Russell’s ( 1872-1970) paradox deals with the idea of membership of a set. A set is either a member of itself or not a member of itself. Refer to a set which does not contain itself as a member as regular. For example, the set of people does not include itself as a member, since it is not a person. Refer to a set which does contain itself as a member as irregular. An example is the set of sets with more than say five elements. Is the set of all regular sets regular or irregular? If it is regular, it cannot contain itself. But it is the set of all regular sets, thus it must contain all regular sets, namely itself. If it contains itself, it is irregular. If it is irregular, it contains itself as a member, but it is supposed to contain only regular sets.