“Wave theory? We don’t need no stinking wave theory!”
Don’t worry, we are not going to get too technical right off the bat. Waves are simply a means of transferring energy from one place to another. Sound energy, once initiated, travels in all directions meaning three dimensionally.
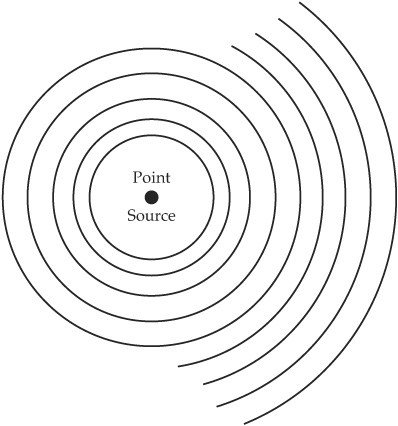
Now the wave surface, which indicates where a pressure change has gotten to at a particular time, will, in anechoic or free-field conditions (that is without any acoustics involved), be spherical (see Fig. 1.1).
FIGURE 1.1 Sound waves are spherical.
Imagine two people sitting on the top of two poles a mile up in the sky, as shown in Fig. 1.2. There are virtually no acoustics involved in this situation. Say the poles are 100 feet apart. When person A’s voice is heard by person B, the distance it has traveled (100 feet) is just the radius of the area that energy has covered. Therefore, the sphere surface would be 4 × pi × 100 feet squared, or 125,000 square feet, upon its arrival at person B. Even if person B’s ears were one square foot each, they would still be receiving only 1/62,500 of the total energy given off by person A. And if person B were to move his pole twice the distance away to 200 feet, the energy received would be only one half of that. This is called the inverse square law and it states that, in nonreflective environments, the level will be halved (or drop by 6 dB) with each doubling of the distance between the source and receiver.
FIGURE 1.2 Two people on poles (with no acoustics involved).
In practice, even if the surface reflecting sound is hard and smooth, it will not be as perfect as that of light bouncing from a mirror. Therefore, the example we will use of a wall giving a mirror image of the wave to the listener is true to an extent, but cannot be taken at face value because no surface is a perfect sound reflector.
Now let’s drop those two people to the ground, and for the sake of this explanation, we’ll assume that the ground’s surface is as reflective of sound as a mirror is of light. As shown in Fig. 1.3, person B will now receive two sets of waves, one direct as above and another that goes from person A to the ground and is then reflected to person B. The reflected wave would not be as strong as the direct, but the increase in level it causes would be noticeable and helpful.
FIGURE 1.3 Two people on the ground.
What happens when we add a wall behind the speaker (see Fig. 1.4)? Now three more paths in addition to the direct one are possible, giving B a total of four waves:
FIGURE 1.4 Two people on the ground with an added wall.
1. The direct path from A to B (no acoustics involved)
2. The reflected path from the floor (one surface)
3. The reflected path from the wall (one surface)
4. The reflected path from the wall reflected once again by the floor (two surfaces)
If we add a surface parallel to one of the first ones, the waves would bounce back and forth (as per our theoretical mirror reflections) setting up an infinite number of paths (infinite additional sound sources). Picture two mirrors parallel to each other—if you look at an object placed in between them, the reflections would continue indefinitely. If we completely enclose the two people in a room with everything parallel—walls front–back, left–right and floor–ceiling—we would be setting up three paths of infinite reflections, and those two people would find it quite difficult to communicate.
To illustrate this differently, we’ll leave our theoretical mirror image reflections and return to reality. About the closest we will ever get to the above perfectly reflective room is an empty indoor swimming pool. Here, the length of time that all the reflected paths last (reverberation time) might be several seconds. This is enough reverberation to make communication difficult because it takes sound longer to travel along multiple reflective paths to the listener and this will cause each syllable to be overlapped by the ones preceding it, causing speech to become garbled, slurred, or at least confusing.
So where has all this stinking theory gotten us? No reflections make hearing more difficult and so do too many reflections. Obviously good acoustics lies somewhere between the two. Take your living room for example, with its carpet, curtains, furniture and possibly an open window or two; it can make conversation quite pleasing. This is due to the fact that this room has softer and more irregular surfaces and, therefore, is quieter sounding than an enclosed empty swimming pool.
On the other hand, everyone knows about singing in the shower. Here the surfaces are hard and smooth with the tiles causing a good deal of reflection. Therefore, it’s easier to reach a higher level of volume; and because the surfaces are fairly close together (showers being relatively small in size), the lengthening of syllables here tends to even out the imperfections of even the most amateurish singing. As compared with our previous examples of either no reflections (lacking of volume or level) or too much reverberation (confusion), showers seem to be closer to ideal, that is, until you put a microphone on that singer and find that there is no control in this particular acoustic situation. That is why every studio that utilizes the bathroom as an additional “reverb chamber” uses the speaker level along with the microphone gain so they, at least, get a handle on the reverberation level and time.
By deciding what materials the walls are made of and where they are placed, we can arrive at a compromise reverberation time that is acoustically suitable to the intended use of a room. As you will see, small rooms tend to amplify some frequencies more than others, while large rooms, or rooms with complex shapes, have more complex reflection paths so they end up having a flatter response. Volume, reverberation time, paths, energy, reflections, standing waves, and all those other mysterious, “scientific” aspects of acoustic theory that cannot be overlooked are actually not that terribly complex.
Let’s take a look at acoustics on the molecular level.
“Molecular level now? Oh Nooooooooooo!”
It’s really not all that bad and it will help you to understand why some materials work as acoustic absorbers and others are just an acoustical rip-off. So by diving into the fundamentals you’ll end up saving yourself both money and self-esteem. Any discussion about acoustic materials boils down to whether sound coming into contact with it is reflected off, absorbed by, transmitted through, or some combination of all three. That is pretty much the whole ball of wax as far as everyday acoustics goes. However the job of the acoustician not only involves the design stage, but also specifying the materials to be used. It is necessary to know about properties to determine how vibrations or airborne sounds will be transmitted, dampened, or attenuated by them. A material’s stiffness or “modulus of elasticity” and resonant frequency are important to its ability to isolate vibration, while its peak Sound Transmission Loss (STL) is important to its ability to stop airborne sound transmission.
But in order to understand how acoustic materials function, you must first understand the physics of sound. Energy that causes a variation in pressure is a result of molecular movement. Sound energy starts at its source, travels along some path, and reaches the receiver. The path must be an elastic medium. Molecular movement is constant for each medium. The magnitude of the movement depends on the pressure and temperature of the medium. In any medium, molecules are constantly in motion, smashing into each other and bouncing around. Sound energy is superimposed on this random motion. To see what effect sound has on molecular motion, you must freeze or stop all the continuous movement for an instant.
Figure 1.5 shows what happens to a molecule when force is exerted upon it by sound. A is displaced to one side and strikes B, setting it in motion. More important than its bouncing back is the fact that A not only returns to its original position, but continues past it to a location opposite the initial direction of movement. Then it returns to its original position. If this movement is repeated at regular intervals, it is a vibration. The areas where A+B, B+C, C+D, and D+E are close together are called compressions. The voids in pressure those compressions cause are called rarefactions. The distance between two adjacent points of rarefaction or for that matter two adjacent points of compression equals the wavelength of the frequency in that particular medium. This holds true for sound power through air as well as mechanical vibration in solids.
FIGURE 1.5 Molecular motion caused by wave incident or vibration. Molecule A’s complete movement, from top to bottom, is one cycle.
Sticking with the molecular example of Fig. 1.5, the sequence of A’s movement from top to bottom is one cycle, or a complete excursion of that molecule. Its frequency is the number of these cycles that occur during the period of one second. The maximum displacement of A is equal to the amplitude of motion, and with audible sound, the excursion or movement is a very small amount.
The important aspects of the path or the medium the sound passes through are elasticity and density. Greater mass causes greater inertia. Elasticity or stiffness is also a factor along with hysteresis (internal friction). Therefore, in any consistent medium, the speed of sound traveling through it will be fixed. The velocity or speed of sound is proportional to the elasticity and inversely proportional to the density of the material through which it is passing.
In other words, the more a material weighs, the slower sound will pass through it; while the stiffer it is, the faster sound will travel through it. These two seemingly simple relationships can become quite complex. As examples, the speed of sound through lead, which is very dense, is approximately 4000 feet per second, while in soft wood it is 11,000 feet per second, and in even less dense air, 1130 feet per second (water: 1,128 / concrete: 10,000 / glass: 12,000 / hard wood: 14,000 / iron and steel: 17,000). These facts would not appear to make sense unless the hardness of the material is taken into consideration.