
The Multiverse of Parmenides
A major breakthrough in the story of quantum physics begins with a young man holed up in a rain pipe—in order to find a quiet place for reading. It is the year 1919, in Munich, shortly after the end of World War I. The chaotic rioting in the streets that followed the revolution driving the German emperor out of office has finally calmed down, and now eighteen-year-old Werner Heisenberg can find some leisure time again.1 He had been working as a local guide, assisting a vigilante group that was trying to reestablish order in the city, but now he could retreat, after the night watch on the command center’s hotline, onto the roof of the old seminary where his cohort was accommodated. There he would lie, in the warm morning sun, in the rain pipe, reading Plato’s dialogues. And on one of these mornings, while Ludwig street below him and the university building across the way with the small fountain in front slowly came to life, he came across that part in Timaeus where Plato philosophizes about the smallest constituents of matter, and the idea that the smallest particles can finally be resolved into mathematical structures and shapes, that one would encounter symmetries as the basic pillar of nature—an idea that will fascinate him so deeply that it will capture him for the rest of his life.2
Werner Heisenberg (Fig. 3.1) was to become one of the most important physicists of his generation. When just turned forty, he was the head of the German nuclear research program, which in World War II examined the possibilities for utilizing nuclear power, including the feasibility of nuclear weapons. In this position he was on the assassination list of the US Office of Strategic Services, but a special agent who had permission to kill Heisenberg in a lecture hall decided against it, after he heard Heisenberg’s lecture on abstract S-matrix theory and concluded that the practical usefulness of Heisenberg’s research was marginal.3 Even today, historians debate Heisenberg’s role in Nazi Germany. His opponents criticize his remaining in Germany and his commitment to the nuclear research project, the so-called Uranverein, which, according to these critics, failed to build a nuclear weapon for Hitler only because Heisenberg was unable to do it.4 Extreme admirers, such as Thomas Powers in Heisenberg’s War,5 argue that Heisenberg used his position to prevent the construction of a German nuclear bomb by exaggerating its difficulties when questioned by officials, bestowing a moral mantle on Heisenberg he never had claimed for himself.
What is well documented is that Heisenberg traveled to Copenhagen, Denmark, in the fall of 1941 to visit his fatherly friend and mentor Niels Bohr. According to Heisenberg, his intention was to inform Bohr that the construction of a nuclear bomb was possible but that the German physicists would not try to build it and to suggest that physicists in the allied nations should follow the same policy.6 This epic conversation, however, only resulted in a lasting breakdown of their friendship. Bohr, the son of a Jewish mother and the citizen of an occupied country, could not have much sympathy for any agreement with the German physicist.

Figure 3.1. From left to right: Enrico Fermi, godfather of the neutrino; Werner Heisenberg, a creator of quantum mechanics; and Wolfgang Pauli, the father of the neutrino. (Photo by Franco Rasetti, courtesy AIP Emilio Segre Visual Archives, Segre Collection, Fermi Film Collection)
In 1998, the British author Michael Frayn wove different perceptions of this meeting into a play that essentially deals with the parallel existence of different realities, both in psychology and in quantum mechanics.7 After all, among all his other activities, Heisenberg was famous for one thing: He was one of the masterminds of a revolutionary new theory.
Just six years after the sunny morning in the rain pipe, Heisenberg, now twenty-three years old and a postdoc at the University of Göttingen, was forced by his hay fever to leave his institute for two weeks, and he spent some sleepless time on Helgoland, a tiny and once holy red rock off Germany’s coast in the North Sea—days that would shatter the most basic grounds of physics. One-third of the day the young man climbed in the famous cliffs; one-third he memorized the works of Goethe, the poet who served as a national idol in Germany and who followed the classical paradigm of the ancient Greeks; and the last third he worked on his calculations. In these calculations he developed a formalism that would be the bedrock of modern quantum physics and would do nothing less than change the world: “In Helgoland there was one moment when it came to me just as a revelation.… It was rather late at night. I had finished this tedious calculation and at the end it came out correct. Then I climbed a rock, saw the sun rise and was happy.”8
Nowadays the technical applications of quantum physics account for about one-third of the US gross domestic product. Nevertheless, Richard P. Feynman commented some forty years after Heisenberg’s work that the theory is so crazy that nobody can actually comprehend it,9 and Einstein had earlier declared bluntly: this is obvious nonsense.10 What makes quantum physics special is that this theory breaks radically with the concept of causality. In our daily lives we are used to ordered sequences of cause and effect: You and a friend clink your glasses with just a little bit too much verve; one glass breaks; beer runs down to the floor; your significant other/roommate/parents cry out. One event causes the next one. This is exactly where quantum physics is different, where this strict connection between cause and effect no longer exists. For example, how a particle reacts to an influence can be predicted only in terms of probabilities. But this is not the end of the story: Unless the effect on the particle is actually observed, all possible consequences seem to be realized simultaneously. Particles can reside in two different locations at once! And particles exhibit properties of waves while waves behave in certain situations like particles. An object thus has both properties of a particle and of a wave, depending on how it is observed. The particle corresponds to an indivisible energy portion of the wave, a so-called quantum. On the other hand, the wave describes the probability for the particle to be located at a certain place. This property of quantum mechanics can be depicted most easily with the famous double-slit experiment (Fig. 3.2).
When a particle beam hits a thin wall with two narrow slits in it, the corresponding wave penetrates both slits and spreads out on the other side as a circular wave. On a screen situated behind the wall, in accordance with the wave nature of the electrons, an interference pattern appears, resulting from the superposition of the waves originating from the two slits in the wall. Where a crest meets another crest or a trough meets another trough the wave gets amplified. A crest encountering a trough, on the other hand, results in little or no amplitude (left side). This pattern appears, however, only as long as it is unknown through which slit a single electron passed. As soon as this is determined, for example by blocking one of the slits or by irradiating the electrons with light, the two-slit interference pattern gets destroyed and the electrons behave just like classical particles. To be more accurate, a new wave emanates from the slit, and the pattern exhibited on the screen is the one for a wave passing through a single slit, which resembles a smooth probability distribution (right side).
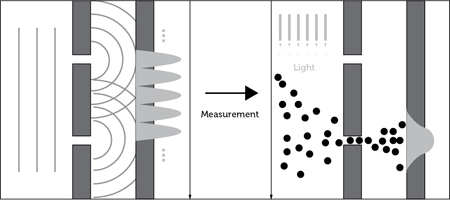
Figure 3.2. Double-slit experiment. As long as no measurement determines which slits the particles are passing through, they behave like interfering waves, which pass simultaneously though both slits (left side). Where two wave crests coincide, the probability of detecting a particle is largest; where a crest coincides with a trough, the probability is very small or zero. The resulting image is called an interference pattern. As soon as an external measurement disturbs the system—for example, if one uses irradiation with light to determine which path the electrons take through the slits—the wave collapses into single particles, which accumulate in narrow bands behind the slits they were flying through (right side).
Heisenberg and Bohr interpreted this as a collapse of the wave function due to the measurement process in which one gets a result with the probability given by the amplitude squared of the wave. This is the so-called Copenhagen interpretation of quantum physics, which is still taught at universities around the globe. According to this interpretation, a particle is located in many places simultaneously until finally a measurement assigns it a concrete location. And this is true not only for position; it applies to other measurable quantities such as momentum, energy, the instant of a nuclear decay, and other properties as well. Erwin Schrödinger, both collaborator with and competitor of Heisenberg in the development of quantum physics, carried this idea to an extreme: “One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat).” In Schrödinger’s experiment the death or life of the cat depends on whether a radioactive isotope does or doesn’t decay in a particular time period. As long as we do not check whether the isotope did decay or not, nor how the cat is doing, Schrödinger’s cat is simultaneously dead and alive, or as Schrödinger phrased it: “[The wave function of the system would have] in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts.”11
There are two reasons why we don’t observe such bizarre phenomena in our daily lives: One is that the wavelengths of ordinary objects around us are tiny compared with the sizes of the objects themselves. The other is that the objects we deal with every day are always interacting with their environment and thus are being measured all the time. A beer bottle, for example, may very well be situated in two different locations, but only for an extremely short time and for an extremely small separation (too short and too small to measure).
Bohr summarized the apparent paradox of particles and waves under the concept of complementarity. After a guest lecture he gave at Moscow University, he left the following aphorism on the blackboard where famous visitors were supposed to leave comments: “Contraria non contradictoria sed complementa sunt” (Opposites do not contradict but rather complement each other).12
But back to Heisenberg, Plato, and the ancient Greeks: As the American philosopher of science Thomas S. Kuhn realized, science in times of scientific revolutions is particularly vulnerable to nonscientific influences.13 When changes to the scientific paradigm cause a shift in the generally accepted problems and solutions and thus also in the general perception and scientific world view, rational reasons like conformity with facts, consistency, scope, simplicity, and usefulness are not sufficient to understand the evolution of a new theory. During these times, personal factors such as cultural background can also play a decisive role. And Heisenberg’s background was almost as Greek as it was German: As the son of a professor of Greek language, he became accustomed to Greek philosophy and culture and their reception in early twentieth-century Germany long before he himself learned Latin and ancient Greek in school. His biographer Armin Hermann suggests that the encounter with Plato’s philosophy influenced Heisenberg more than anything else.14 And not long after Heisenberg studied, climbed, and calculated in Helgoland, Paul Dirac in Cambridge and Erwin Schrödinger in Vienna worked out different but mathematically equivalent versions of quantum physics. Since the standard interpretation of these works was developed basically in the inner circle around Bohr and Heisenberg, Heisenberg’s background seems particularly relevant for its appreciation. Also, Schrödinger made statements such as “Almost our entire intellectual heritage is of Greek origin” and “science can be correctly characterized as reflecting on the Universe in a Greek way.”15 And Dirac left on the blackboard in Moscow, right next to Bohr’s principle of complementarity, only the laconic remark, “A physical law has to have mathematical beauty,”16 a statement that reminds us strongly of Goethe’s transfiguration of the classical worldview:
Nature and art, they seem each other to repel
Yet, they fly together before one is aware;
The antagonism has departed me as well,
And now both of these seem to me equally fair.17
And sure enough, quantum physics seems to be a Greek theory after all. This becomes evident when reading the thoughts in the book Die Einheit der Natur (The Unity of Nature) by Heisenberg’s student and friend, Carl Friedrich von Weizsäcker,18 the brother of the subsequent German president, on the centerpiece of quantum physics—the wave-particle duality—and how it can be traced back to the arguments in Plato’s dialogue Parmenides.
Parmenides of Elea (Fig. 3.3) was a Greek philosopher in the pre-Socratic era around the fifth century BCE. Of his writing only the fragment of a philosophical poem remains;19 it deals with the unity of all being. It describes how an unnamed goddess—often understood as Persephone—invites the poet to perceive the truthful being—again a likely reference to the mystical experience in the mystery cults of Eleusis. The truthful being then is distinguished from mere appearances and described as the all-embracing One—uncreated and indestructible, alone, complete, immovable, and without an end20—reminiscent of Aldous Huxley’s stage of egolessness.21 “Éν τó ![]() αν” (One is the All) is correspondingly the central statement followed up by Weizsäcker22 when he discusses the argument between Socrates and Parmenides chronicled by Plato,23 which, according to the Italian author Luciano De Crescenzo, was the “most boring and complicated discussion in the entire history of philosophy.”24
αν” (One is the All) is correspondingly the central statement followed up by Weizsäcker22 when he discusses the argument between Socrates and Parmenides chronicled by Plato,23 which, according to the Italian author Luciano De Crescenzo, was the “most boring and complicated discussion in the entire history of philosophy.”24

Figure 3.3. Parmenides of Elea (center) in Raphael’s The School of Athens.
In this battle of words, which supposedly took place on the occasion of a visit of Parmenides to Athens, Socrates tried to refute the identity of One and All. To this end Socrates argued that One is not Many and thus has no parts. On the other hand All refers to something which does not miss any of its parts. Consequently the One would consist of parts if it were All, and thus finally One cannot be the All.25
At this point Weizsäcker comes to Parmenides’s defense by stressing the connection with quantum mechanics. And it is really astounding how the quantum mechanical interpretation of the One suddenly bestows this incomprehensible debate with lucidity and meaning. After all, in quantum mechanics the All is the wave function and, in its fullest manifestation, the all-embracing wave function of the universe.
Moreover, in quantum mechanics the analysis of the individual parts of an object without destroying the object is impossible, since the measurement, as explained above, affects the object and thus distorts the unity of its parts. And of all possible states an object can assume, only an infinitesimally small fraction are states in which the parts of the object actually correspond to a clearly defined outcome of a measurement. Only in these states can one truthfully assign reality or existence to these parts. For example, only two among the infinitely many possible states that Schrödinger’s cat can assume (such as 90 percent alive and 10 percent dead or 27.3 percent alive and 72.7 percent dead)—namely totally dead or totally alive—correspond to possible outcomes in a measurement. But quantum mechanically, a pair of two cats, half of them dead and the other half alive, is realizable not only with one living and one dead but also with two half-dead cats or one being 70 percent alive and one being 30 percent alive. Consequently, in quantum physics the All is really more than its parts, the partial objects actually constituting through their association a new entity, or, just as postulated by Parmenides, a new unity, a new One. Now Parmenides, according to Plato, required further that the One possesses no properties: It has no beginning, no center and no end, no shape and no location; it is neither in itself nor in anything else; it is neither at rest nor is it moving. Weizsäcker can argue that a quantum mechanical object fulfills these requirements perfectly. After all, a determination of any of these properties relies on a measurement, which implies a collapse of the wave function and thus destroys the unity of the collective object. On the other hand, isolation of the object from the surrounding universe is impossible:26 The object would not exist in the universe if it were not connected to the universe via some kind of interaction.
Thus, strictly speaking, only the universe as a whole can constitute a real quantum mechanical object. Then, however, nobody would remain who could observe it from outside. Next Weizsäcker and Parmenides follow the discussion backward: how the One—meaning the all-embracing universe barring all properties—unfurls into the colorful and multifaceted appearances of our everyday life. The argument relies here on the quirky assumption that the One, in the instant where it “is”—in the sense of exists—is already two things. It is the One and it is the Is. This argument can be iterated. Again both the One and the Is are two things: the Is is and is the One, and the One is and is the One. By repetition of this consideration the One acquires an infinite multiplicity: The being One unfolds itself into the universe. And again Weizsäcker clarifies the discourse by referring to the quantum mechanical object. After all, the way an object can exist is via interaction with other objects, which again results in the collapse of the wave function and the loss of quantum mechanical unity: In order to establish that an object exists, the object has to be measured and thus is affected in a way that implies that it is no longer one object according to the meaning of Parmenides’s One. In summary, Weizsäcker arrives at an amazing conclusion, that the notion of complementarity has its source in ancient Greece: “We find … the foundation of complementarity already foretold in Plato’s Parmenides.”27 We actually can recover the feel of what the ancient Greeks experienced in their mystery cults in modern twentieth-century physics!
But this is not the end of the story: The atomism of Democritus, the idea that the world is not continuously divisible but made out of indivisible particles, makes sense only in the context of quantum mechanics, where matter consists of compound objects that correspond to standing waves and thus can absorb or emit energy only in indivisible portions—the quanta. Also, the idea of tracing the laws of nature back to fundamental symmetries, as proposed in Plato’s Timaeus, is, as we will see in Chapter 5, an integral part of contemporary particle physics. Finally, consider Einstein’s objection to the fundamental importance of probabilities. Because of that objection, he remained a lifelong opponent of quantum mechanics: God doesn’t play dice with the world.28 This statement appears as a direct response to the 2,500-year-old fragment of Heraclitus: “Eternity is a child moving counters in a game; the kingly power is a child’s.”29
How can one really comprehend the lack of causality inherent in quantum physics and in particular the role of the puzzling quantum collapse, which are not described by the mathematical formalism and remain controversial today? The most modern and consistent interpretation of these puzzling phenomena seems to be at the same time the craziest one: Everything that can happen does happen—albeit in different parallel universes. This idea was formulated for the first time in 1957 by Hugh Everett III while he was working on his doctoral dissertation at Princeton University. With the bizarre concept of parallel universes he asked too much of his contemporary physicists, even though Everett—like Richard Feynman, a founder of quantum electrodynamics, and Kip Thorne, the father of the wormhole time machine—was a student of the eminent John Archibald Wheeler, who was himself a rather unorthodox and creative associate of Einstein and who, among many other achievements, coined the term black hole for the timeless star corpses in the universe. But even with this first-class mentor, Everett’s colleagues didn’t take him seriously. Everett left the academic world shortly after finishing his dissertation. During a frustrating visit in Copenhagen, during which Everett tried to convince Niels Bohr to take some interest in his work, he (Everett) transformed a standard approach in classical mechanics into a method for optimization that he could apply to commercial and military problems and that helped him to become a multimillionaire—but didn’t make him happy. He became a chain-smoking alcoholic and died of a heart attack when he was only fifty-one years old. According to his explicit wish, his ashes were disposed of in the garbage. Fourteen years after his death, his daughter Elizabeth, who suffered from schizophrenia, committed suicide. In her suicide note she wrote that she was going into a parallel universe, to meet her father. His son Mark Everett became the famous rock star E, lead singer of the Eels. He described his father as distant, depressed, and mentally absent, and his own childhood as strange and lonely. Only his music saved him. But he also expressed sympathy for his father: “These guys, I don’t think they should be held to subscribe to normal rules. I think that about rock stars, too.”30
Hugh Everett’s ideas about quantum physics were finally popularized in the 1970s by his advisor Wheeler and Bryce DeWitt, who had also worked with Wheeler. It was DeWitt who added the “many-worlds” label, a term that Wheeler never liked. The interpretation essentially states that every measurement results in a split of the universe. Every possible outcome of a measurement—or more generally of any physical process—is being realized, but in different parallel universes. If a guy chats up a girl in a dance club, there is always a universe where the two of them get happily married and remain in love until they die, but also another one where she tells him to back off, he has too much to drink, and he wakes up the next morning with a serious hangover. This very insight made me particularly nervous when I prepared to jump out of an airplane 4,000 meters above O‘ahu’s north shore. After all, even if I survived in this universe, there are always countless universes where the parachute did not open. So somewhere one loses, every time. But somewhere there is also a parallel universe where Everett still lives happily together with his daughter.
The major advantage of the many-worlds interpretation, compared with the classical Copenhagen interpretation, is that no collapse of the wave function—which, in any case, is not really part of the theory—has to be assumed. Even after the measurement has been performed, both possible outcomes—like an electron at place A and an electron at place B—coexist, but they decouple, so that an observer who measures the electron at place A does not notice the alternative reality with the electron at place B. In contrast to the collapse of the wave function, this process of decoupling can be described within the formalism of quantum mechanics. Perhaps this process—so-called decoherence—is the only reason we witness so little quantum weirdness in our everyday lives. The drawback of the many-worlds interpretation, however, is that we have to give up the concept of a unique reality. The interaction of different parallel universes is suppressed after a measurement, but not totally lost. So even in our daily lives we don’t reside in clearly defined conditions such as dead or alive. The parallel universes in which we and our fellow human beings experience totally different fates instead resonate as unobservable tiny admixtures of alternative realities into our universe. Thus the many-worlds interpretation exhibits the Parmenidic-neo-Platonic nature of quantum mechanics most clearly. According to this point of view, the unity of the different realities is not completely lost. It is actually possible to recognize the multiverse—the collection of all of Everett’s parallel universes—directly as Parmenides’s primeval One: the unity of the world the ancient Greeks felt they had lost in the charted modern world, and for whose reunification with the individualized ego they looked in the ecstasy of their mystery cults, in their Dionysian arts, or in the flush induced by psychedelic drugs.
The bizarre properties of quantum physics naturally inspired the fantasies of both journalists and authors. The parallel existence of different realities in quantum physics, for example, became the subject of a Physics World cover in 1998, which depicts a couple on the phone arguing as follows: “Oh Alice … you’re the one for me”—“But Bob … in a quantum world … How can we be sure?” An even more radical take on the many-worlds interpretation can be found in Douglas Adams’s The Hitchhiker’s Guide to the Galaxy.31 Whenever the extraterrestrial crackpot Zaphod Beeblebrox, double-headed and addicted to Pan Galactic Gargle Blasters, starts the Infinite Improbability Drive, his stolen spaceship gets located in all places in the universe simultaneously, and tiny probabilities are amplified. In the novel this allows the spaceship to travel faster than light, and also causes various strange incidents, such as when a threatening pair of rockets gets suddenly transformed into a dumbfounded whale and a flowerpot.
Finally, and now I am serious again, the many-worlds interpretation could protect time travelers from ludicrous paradoxes, and in this way make time travel a meaningful physics concept. But we’ll get to that later.