
When you were working with LEDs, you tried to keep the current limited to 30 milliamperes. You got this number by looking at the specifications of the LED on the back of the package. But sometimes you get parts that have no detailed specifications, or you are reusing a part from some scavenged bit of electronics. How can you make sure you don’t damage the part by using too much current?
Use a pocket laser pointer as an example. These little devices normally run on tiny button-cell batteries. Small batteries like this might have the same output voltage (about 1.5 volts) as larger cells such as C or D flashlight batteries, but they can’t supply the same amount of current as the larger cells. If you wanted to power a laser pointer from a larger battery, in order to get longer battery life (or because the larger batteries are cheaper and easier to find), you could burn out the laser immediately if you connected it to the larger cells.
Pocket laser pointers are similar to LEDs in many ways. They use diode lasers, which are made of the same materials as LEDs. In fact, if you use low currents, a laser will just glow like an LED. But the laser diode chip is built in a special way, with the faces of the chip cut to make mirrors that bounce the light back and forth, allowing the light to be amplified until it is so bright that it escapes through the mirrors in a bright beam. This laser amplification happens only when the current is so high that the chip is very close to burning out. This makes controlling the current all the more important.
Now see how much current the laser pointer uses when in normal operation. To do this, you need to put your meter in series with the batteries (between the battery and the rest of the circuit), as you did with the LEDs. Simply use some tape to bind the three little batteries together and some alligator clips to connect them to the little spring inside the laser’s battery compartment and to the case of the laser. Use a bit of tape to hold down the power button so the laser stays on.
The current (in this case, for this laser and these batteries) is a little under 12 milliamperes. Compared with the LEDs, it is using only about a third as much current.
If you have two meters, you can measure the current and the voltage drop across the laser diode at the same time.

Here you can see I’ve made a few changes. Instead of the little batteries, I am using flashlight cells. I have added some resistance to keep the current to something close to what the laser normally encounters. I started with one resistor for safety, so the current would be too low to operate the laser. Then I added more resistors in parallel (instead of in series), which reduces the resistance (and thus increases the current) gradually. Adding resistors in parallel gives the electrons more ways to get through, so the current increases and the resistance decreases. (For more information on resistors in parallel, see page 29.)
The voltage drop is about 2.85 volts. When you learned Ohm’s law in the previous experiments, you saw that if you double the voltage going through a resistor, the current doubles as well. Since this makes a straight line when graphed, the relationship is linear. With a diode, the relationship is definitely not linear. As you double the voltage, the current through a diode goes up exponentially. This is what is really going on with that forward voltage drop. The diode seems to let all the current go through it once the voltage reaches the forward voltage drop level.
This is why it is important to limit the current using the resistors. Otherwise, the diode will allow all the current the battery can generate to go through it, and it will heat up until it fails.
Different diodes have different behavior with respect to voltage and current. They are exponential, but some more than others. The laser diode I’m using is not just a diode—it has a resistor built into the circuit inside it to limit the current from the tiny batteries. So as you increase the current, the forward voltage drop also increases.
Let’s risk burning out the laser and see if it can handle the same 30 milliamperes that the LED could.

It can, although for how long we don’t know. It may last years at its normal current but only days or weeks at this higher current. But it is three times brighter than it was before.
Lasers have a voltage called the threshold voltage, below which there is not enough current for them to act as lasers. They act like ordinary LEDs below that current.

Here I have lowered the current to 9.4 milliamperes, and suddenly the laser is much dimmer. When a laser beam hits a rough surface, you can see many tiny sparkles. These are called laser speckles, and they’re caused by the reflected light from the high points interfering with the reflected light from lower points on the rough surface. They are a hallmark of laser activity. But below the threshold current, you won’t see the speckles. This fancy laser is now just an ordinary LED. It is suddenly much dimmer because the light is not being amplified by the laser activity in the diode.
Once the voltage is above the threshold, the light output of the laser is linear with the current. So if you let three times the current go through, then the laser will be three times brighter. It looks like the manufacturers of this laser pointer kept the current very close to the threshold. This lowers the brightness (making the laser safer to use as a toy) and increases the battery life.
Here is the laser operating at 60 milliamperes. It is well over five times as bright as when using the normal batteries. I had to use a 9-volt battery to get to this current level.
The 9-volt battery will last only an hour or so at a discharge rate of 60 milliamps before its voltage drops so much that it can’t drive the laser. In the few minutes I was driving the laser at this rate, I could see the current steadily dropping as the battery discharged. And I would not expect the laser to last very long either.
So far, you have been using resistors to limit the current in LEDs and lasers. In this section I used resistors in parallel to get a lower resistance. I could have simply found a resistor with a lower value and used that. But when experimenting, it is handy to know how to quickly change resistances by putting resistors in series to increase the resistance, or in parallel to reduce it.

If you put one resistor after another, in series, then they both reduce the current flow. If they are both the same value, the resistance of both together is twice that of either one. In fact, you can place any number of different-valued resistors in series, and the resulting resistance is just the sum of all their individual resistances.
Resistors allow fewer electrons to flow than a plain wire would. If you place two resistors together in parallel, the current has twice as many routes it can take. If the resistors have the same value, it is easy to see that together they will have half the resistance.
Before this discussion of resistors ends, there is one more neat trick you can do with them. If you have one voltage, perhaps the voltage of a 9-volt battery, but you need a smaller voltage, you can use two resistors to divide the voltage in half:

But it gets better. The voltage in the middle can be any voltage from 0 to 9 volts. Divide the resistance of the bottom resistor by the total resistance (both resistors added together). Multiply that by the input voltage to get the output voltage. So if you wanted 3 volts, you could make the bottom resistor 10,000 ohms and the top resistor 20,000 ohms, because 10,000 ohms divided by 30,000 ohms is 1/3, and 1/3 of 9 volts is 3 volts. Or you can ask Google to do the arithmetic.
(9 volts * (10000 ohms)) / (30000 ohms) =

So why did I suddenly start using such large values for resistance? Look at what the circuit does. It connects one side of the battery to the other, through two resistors. If the resistance was low, a lot of current would flow. That would heat up the resistors, and they might even catch fire. But with 30,000 ohms of resistance and 9 volts, Ohm’s law tells you that you will have a current of 0.3 milliamps. The resistors won’t heat up much at all, and the battery won’t quickly drain.
When selecting an LED, you might like to know just how bright it will be when you get it built into your circuit. And the package tells you—it might say something like “10,000 millicandelas.” But how bright is that?
To describe how bright something is, it helps to have something to compare it to. Illumination is measured in units called lux. Walking outside in the sun, you are experiencing between 30,000 to 100,000 lux. In a well-lit office, you are in about 1,000 lux. Walking in the moonlight, you are getting only about 1 lux.
If you are trying to light your office with a lamp, and you want 1,000 lux on your desk, you will need to know how much light the lamp produces and how far away from your desk it is. How much light a lamp produces is measured in lumens. A 60-watt incandescent bulb might produce 850 lumens. A 100-watt incandescent might produce 1,700 lumens. To get an illumination level of 1,000 lux on your desk, you can put a 60-watt bulb about 12 feet away.
An LED might put out about half a lumen. That doesn’t sound like a lot. But the LED has a little lens in front of it that focuses the light in one direction. So now, all of the light is falling in a smaller area, giving better lighting to that area. To take into account that focusing of the light, LEDs are measured in candelas (or millicandelas), which are lumens focused on a spot.
All of this sounds complicated. So I have built a little gadget to help out. You can find the gadget on the website that accompanies this book (http://artists.sci-toys.com/how_bright).
With the gadget (an example follows), you can move the sliders back and forth to play with the different lighting concepts. You can change the amount of light, how far away it is, and how focused it is. At the right, you will see the resulting illumination, in lux, and the size of the illuminated spot.

STUDENT ART PROJECT
In Dark Ride by Bethany Carlson Mann, the tiny dancers inside the animal’s mouth move as the viewer turns the hand crank in the front. The LEDs and fiber optics give the piece the required magical aspect when the house lights dim.
If you have many resistors in parallel, the arithmetic is easier if you work with conductance instead of resistance. The two concepts are really just different ways of looking at the same thing—conductance is how easily the electrons can flow, and resistance is how difficult it is for the electrons to flow.
Resistance is measured in ohms, and conductance is measured in siemens. Normally you won’t be using siemens, but I introduce it here because it makes calculating parallel resistances easier. To convert resistance to conductance, you simply take the reciprocal—that is, you divide 1 by the number of ohms.
To get the value for the conductance of parallel resistors, you simply add them. This makes parallel resistors as simple as series resistors, as long as you are using conductance instead of resistance.
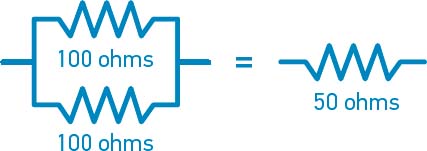
Take a look at the earlier example of two 100-ohm resistors in parallel (page 26). Each resistor has a conductance of 0.01 siemens (1 ÷ 100 ohms). Adding them together in parallel makes the combination more conductive, yielding 0.02 siemens (1 ÷ 100 ohms + 1 ÷ 100 ohms). Taking the reciprocal of that to convert back to ohms yields 50 ohms (1 ÷ 0.02 siemens).
If you like, you can still just work in ohms. To find out the resistance of a 100-ohm resistor in parallel with a 200-ohm resistor, add 1 ÷ 100 ohms and 1 ÷ 200 ohms and then divide 1 by that. To put it in a simple formula:
resistance = 1 ÷ (1 ÷ resistor 1 + 1 ÷ resistor 2)
It’s only a bit more complicated than working with conductances, but it is easy to enter into a scientific calculator, yielding a result of 66.67 ohms.
In mathematical form, it looks like this:

Which can be rearranged as:

This latter form is called the product over sum method, and many electronics students memorize it and have no idea how it comes about, or that understanding parallel resistances is really as easy as adding the conductances.
You can mentally check the result by realizing that the resistors in parallel will always have less resistance than the smallest of the parallel resistors. In this example, you got 66 2/3 ohms, which is less than the smaller of the two resistors (100 ohms).
If you have more than two resistors in parallel, you just add up all of their conductances and divide that into 1 to convert back to ohms.