11
An Historical Intermezzo

This chapter shows how the watershed concept and the algorithms for constructing it emerged progressively.

11.1. Watersheds: the early days

Christian Lantuejoul, in order to model a polycrystalline alloy, defined and studied the skeleton by zones of influence of a binary collection of grains in his thesis [LAN 78]; he studied the geodesic metric used for constructing a SKIZ in [LAN 81]. The shortest distance d_Z (x, y) between two pixels x and y in a domain Z is the length of the shortest path linking both pixels within the domain. If X is a subset of Z, we likewise define the geodesic distance between a point x ∈ Z and the set X, as the shortest path between x and a pixel belonging to X.

Consider now a set X ⊂ Z, union of a family of connected components X_i. The skeleton by zone of influence of X, or skiz (X, Z) assigns to each connected component X_i the pixels which are closer to X_i than to any other set X_j for the geodesic distance d_Z.

The first implementation of the SKIZ was made on the TAS, a hardwired processor developed at the CMM and used homotopic thickenings for constructing the SKIZ. With the advent of cheaper memories and the personal computer, it was possible to represent images on random access memories (whereas the TAS only allowed raster scan access to the images). Luc Vincent proposed a very efficient implementation of a SKIZ [VIN 91c]; the growing of the various germs being governed by a FIFO. The algorithm for constructing the SKIZ skiz(X, Z) of a family of particles X = (X_i) within a domain Z is the algorithm “ geodskiz”.

---

Algorithm 7: Geodesic skeleton by zones of influence (SKIZ)

Input: A family of seeds (K_i)_i∈I within a domain Z

Result: The geodesic SKIZ of the seeds (K_i)_i∈I within Z

1. 1 Initialization:

   Create the first in first out queue Q

   Introduce the inside boundary pixels of the seeds (K_i)_i∈I into Q

2. 2 Core of the algorithm:

   while Q not empty do

   

---

11.1.1. The level-by-level construction of watersheds

The watershed partition π_f of a gray tone image represented by a function f, defined on a domain D and taking its value in the interval [0, N] is then easily obtained by iteratively constructing a series of SKIZ in increasing domains depending on the successive thresholds of f [BEU 82]. In the following algorithm, the notation {f ≤ λ } means the set of pixels of D for which f takes a value below or equal to λ.

---

Algorithm 8: A level-by-level watershed algorithm

Input: A function f

Result: A watershed partition π_f of f

1. 1 Initialization:

   Create the first in first out queue Q

   Initialize the set π_f with the regional minima of f

2. 2 Core of the algorithm:

   for for grey levels λ = 1, Ndo

   

---

We get the watershed algorithm by successively applying the algorithm “geodskiz” for increasing thresholds λ of the function f. L. Vincent and P. Soille completed the algorithm by adding a clever mechanism for finding these successive thresholds of a gray tone function [VIN 91c].

11.1.2. A hierarchical queue watershed algorithm

The algorithm proposed by Lantuéjoul and Beucher [BEU 82] for constructing a watershed repeats the SKIZ construction for the successive levels of the gray tone function. For each level, it uses the algorithm geodskiz. The principal innovation of the hierarchical queue algorithm (HQ algorithm) presented in the previous chapter [MEY 91] is to create all FIFOs at once, each being devoted to a distinct gray tone, with the advantage to put all pixels which are met in a waiting position before they flood neighboring pixels. When a node x is dequeued, all its neighbors may be processed: the neighbors with the same gray tone as x are put in the same FIFO as x, the others are put in the FIFOs corresponding to their gray tone. The resulting algorithm is particularly simple and has been presented in the previous chapter.

11.2. A watershed as the SKIZ for the topographic distance

Each image defined on a grid may be considered as a particular graph. The pixels are the nodes of the graph; neighboring pixels are linked by an edge. All algorithms defined so far immediately apply to node-weighted graphs. We now give a short review of graphs.

11.2.1. The topographic distance

In chapter 3 we introduced an erosion operator between nodes of a node-weighted graph. If p is a node of G, the erosion (ε _N ν)_p is the weight of the lowest neighboring node of p.

Consider an arbitrary path 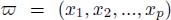of the node-weighted graph G(ν, nil) between two nodes x₁ and x_p. The weight ν_p at node x_p can be written:

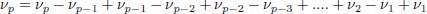
The node k – 1 is not necessarily the lowest neighboring node of node k, therefore ν_k–1 ≥ ε_Nν_k and ν_k – ν_k–1 ≤ ν_k – ε_Nν_k.

Replacing each increment ν_k – ν_k–1 with ν_k – ε_Nν_k will produce a sum ν_p – ε_Nν_p + ν_p–1 – ε_Nν_p–1 + …. + ν₂ – ε_Nν₂ + ν₁, which is larger than ν_p. It is called the topographic length of the path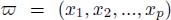

The path with the shortest topographic length between two nodes is called the topographic distance [MEY 94b] between these nodes. It will be equal to ν_p if and only if the path (x₁, x₂,…, x_p) is precisely a path of steepest descent, from each node to its lowest neighbor. The equivalent for continuous functions has been proposed by Laurent Najman and Michel Schmitt [NAJ 94b].

Consider again the “HQ algo”. The regional minima are labeled. During the execution of the algorithm, each node p, when dequeued, assigns its label to its neighbors without labels. If a node q has no label when its neighboring node p is dequeued, it means that q has no other neighbor, which has been dequeued before. If the nodes p and q have distinct weights, it means that p is one of its lowest neighbors: between nodes with distinct gray tones, it is the topographic distance which prevails. If the nodes p and q have the same weight, it means that both p and q belong to the same plateau and p is closer to the lower border of the plateau than q. Thus, we obtain a more restrictive lexicographic distance, where the first term is the topographic distance and the second term the distance to the lower boundaries of the plateaus.

11.3. Convergence into a unique algorithm of three research streams

11.3.1. Three formulations of watershed partitions, one algorithm

There are thus three milestones in the formulation of a watershed as a SKIZ of the regional minima. The first one is due to Lantuejoul and Beucher and constructs a watershed partition sequentially as a series of geodesic SKIZ in increasing thresholds of the function. The second defines a watershed as the SKIZ for the topographic distance. The last one defines a watershed as the SKIZ for an ∞ – steep lexicographic distance. It happens that the HQ algorithm implements all three formulations of a watershed.

We developed the HQ algorithm in 1991, in order to implement the level-by-level construction proposed by Lantuejoul and Beucher. The HQ structure was a way to schedule the operations in order to flood a topographic surface. If a watershed is expressed in terms of flooding, the FIFO of level λ permits to flood the plateaus of level λ starting from the already flooded nodes. The order between the FIFOs permits to flood higher nodes after the flooding of lower nodes.

But the scheduling proved to be more subtle: each node which quits a FIFO floods all its neighbors which are not flooded yet. Like that each node is flooded by one of its lowest neighbors, which ensures that the flooding follows the geodesics of the topographic distance.

Finally, it was a surprise that the same structure also implements the flooding along geodesics of an ∞ – steep lexicographic distance. This is due to the fact that the nodes are not stored loosely in each FIFO but in a very precise order, reflecting their ∞ – steep lexicographic distance to the regional minima.

The fact that the algorithm is compatible with the three successive formulations of a watershed should in fact not be a surprise: if you can move mountains you can move molehills. It turns out that the HQ algorithm implements an ∞ – steep lexicographic distance to the minima. But the level-by-level formulation of the watershed of Lantuejour and Beucher implements in fact an 1 – steep lexicographic distance and the formulation based on the topographic distance expresses a 2 – steep lexicographic distance.

Last but not least, the HQ algorithm remains one of the simplest and fastest algorithm for constructing a watershed partition.

11.3.2. Discussion

The 1991 HQ algorithm propagates the labels of the minima along the ∞ − steep flowing paths. It produces a partition of catchment basins, which are, in fact, a dead leaves tessellation of catchment zones. However, since the catchment zones are associated with an infinite pruning of the graph, their overlapping is minimum, with a maximum thickness of one node. More precisely, there are no double arcs remaining in an ∞ − steep digraph. The existence of button holes is nevertheless possible, when a node at the origin of two flowing paths towards distinct regional minima has a non-empty upstream.

The algorithm produces a partition as it attributes the nodes belonging to an overlapping zone to one adjacent catchment zone or another, depending on the flooding schedule. The node which is flooded first takes the label.

Note that if all regional minima have distinct weights, then two ∞ − steep flowing paths linking the same origin with two distinct regional minima are necessarily different. In this case, the catchment zones never overlap and form a partition.