Chapter 19
Integrated Reasoning: Strategies

GMAC has devised four new question types for the Integrated Reasoning section. As with any section on a standardized test, doing well requires a blend of content knowledge and strategy. Test takers who approach the Integrated Reasoning section with a firm grasp of strategy will do better than those who haven’t thought about strategies for the section.

We’ll be looking at two types of strategies in this chapter. Some strategies apply to most or all of the question types that you’ll see. Other strategies will apply to specific questions types. We’ll start by reviewing strategies and pointers for the section and then move on to examine some methods for the individual question types.

GENERAL STRATEGIES

Some strategies apply to the entire section and you’ll use these methods on almost every question. The more consistently you apply these pointers, the better you’ll do and the more efficiently you’l use your time.

Get Your Bearings

Before you can use a chart, graph, or table to answer questions, you need to understand the information on it. So, before you evaluate any statements or answer any questions, take a few moments to review the charts, graphs, and tables.

For charts and graphs, make sure you look at the axes. You’ll want to take note of what each axis measures and the units used to make the measurements. You’ll also want to read any headings or titles because those can provide valuable insight into the purpose of the graph. There may be a legend. If there is, take a moment to identify the different items that the chart or graph compares. For tables, make sure that you look at each column heading. This sort of review is essential before you start working on evaluating the statements or answering the questions that go with Table Analysis and Graphics Interpretation questions.

For Multi-Source Reasoning questions, you need to review the information that is on each tab. It’s also a good idea to look for connections between the charts on one tab and those on the others. One way that you can do so is to think about what quantities you’d be able to calculate if you used the information from two charts. For example, if one chart shows the number of cars per day that several factories produce and another chart shows the number of days those factories were active in a year, you know that you could calculate the total number of cars each factory produced that year.

Read What You Need When You Need

Both Table Analysis and Graphics Interpretation questions include a blurb of text that explains the table or chart. While GMAC includes this information to help you to understand the table or chart, you may not need to take the time to read it.

Most of the charts and tables are understandable without the explanatory text. So, if your review of the chart or table doesn’t turn up any unusual quantities or units that need further explanation, you’re most likely ready to get to work on the actual questions. You can also be guided by the questions. If something about the question or statement isn’t making sense, then you can always go back and read the explanatory information at that time.

Valid Inferences

Both Table Analysis and Multi-Source Reasoning items include statement style questions. (Reread Chapter 18 to see examples of statement style questions.) In some cases, you’ll be asked to decide whether the statement is true or false. But, in other cases, you’ll be asked whether the information supplied supports the inference as stated and asked to respond yes or no. That’s a little different from asking whether the statement is true or false. After all, there’s the possibility that there is insufficient information to conclude whether the statement is true or false. If that’s the case, you need to pick “no” as your answer.

It’s also important to remember that a valid inference is something that you know to be true. The way you know something is true is that you have evidence you can point to. GMAC knows, however, that most people think “interpret” or “read into” when they hear the word “infer.” So, some statements provided on Table Analysis and Multi-Source Reasoning questions attempt to read into the information on the chart or table to come up with a conclusion. For example, there may be a clear trend on a chart showing that a company has increased its sales for every year between 2000 and 2008. The statement may try to get you to conclude that the company also increased its sales in 2009 even though 2009 is not shown on the chart. That’s not a valid inference! Be careful that you don’t mix up “true” and “very likely” when evaluating what can be inferred from the data.

TABLE ANALYSIS

Table Analysis questions always include one table to display data. You’ll be asked to evaluate four statements. You may be asked whether the statements are true or false based on the data in the table. You may also be asked whether the statements represent valid inferences based on the table.

While you won’t be called upon to provide numerical answers as part of Table Analysis question, you may need to perform some calculations to evaluate the statements. For example, you may be asked to verify that a certain percentage of the items in the table have a certain characteristic.

The Sort Function

As mentioned in our chapter covering the basics of the Integrated Reasoning
section, the sort function allows you to sort the data in the table by any column. However, the sort function will only sort by one column at a time. So, forget all those fancy multiple column sorts that you can do with Excel.

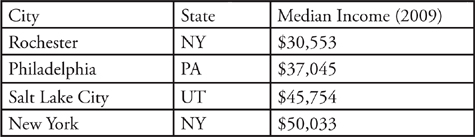
To see how the sort function works for Table Analysis questions, let’s look at a very simple table. This table is really too simple for a GMAT question but it will help us to illustrate how the sort function works.

When you first see the table, it is typically sorted by one key statistic from the table. All numerical sorts are always smallest to largest. This table, for example, is sorted by Median Income (2009) and represents the original sort for this table.

Now, here’s what you’ll see if you sort by state.

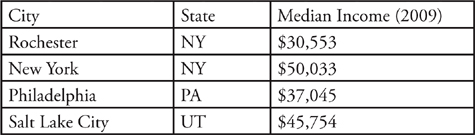
If you sort next by City, you might expect that Rochester and New York would exchange positions. That’s particularly true if you are used to the way that Excel lets you sort by multiple columns.

However, what you’ll really get is an alphabetical listing by City. Here’s what the sort by City looks like.

To Sort or Not To Sort

While the sort feature can be a huge help when answering some questions, you may not need to use it to answer every question. In some cases, you may only need to find one piece of information on the table. In other cases, the table may not have that many rows. Table Analysis questions can have as few as six rows of data. It may be faster to simply scan the table for the information that you need.

On the other hand, remember that sorting the table only takes a few seconds. If you think sorting will help, do it! One thing you shouldn’t do, however, is spend time trying to organize the statements so that you do as little sorting as possible. You’re actually likely to waste more time trying to come up with the perfect order in which to evaluate the statements than you would if you wind up sorting the same way twice in evaluating the statements.

Let’s look at a sample Table Analysis question. Here’s the question that we discussed in Chapter 18.

Here’s How To Crack It:

As with any Table Analysis question, the first step is to make sure that you take a moment to understand the information presented by the table. While it might be tempting to jump straight to the statements, you’ll be able to evaluate the statements more efficiently when you first take a moment to understand the information on the table. Looking at the column headings can also help you to decide whether you need to read the explanatory information under the table.

The first two columns of this table—National Park Name and National Park State—are self-explanatory. More importantly, however, the first column— National Park Name—tells you that this table provides information about national parks. Next, you get information about visitors to the national parks included in the table. The third column heading—Visitors Number—is pretty clear. However, you don’t know the time period for the visitation numbers. The next column—Visitors % Change—shows increases or decreases from some previous time period. Again, you don’t know the time period just by looking at the table. Do the time periods matter? Probably not. You’ll probably learn the time period from the statements. If the statements seem to indicate that the time periods matter, you can read the explanatory text at that time.

The next column—Visitors Rank—is potentially more confusing, however. Does the rank refer to the number of visitors or the percent change? That’s an important distinction for understanding the information in the table. There are two ways to figure out what’s being ranked. You could scan the table looking for evidence. Of course, that could be time consuming. Or, you could scan the explanatory text beneath the table. If you don’t understand one of the column headings shown in the table, that’s when you want to read the explanatory text. The explanation indicates that the rank refers to the total number of visitors. As a bonus, you now also know that the visitation numbers are for 2010.

The last two column headings—Area Acres and Area Rank—are also pretty clear. Note that the inclusion of Area Rank means that you won’t need to deal with the larger number in the Area Acres column if all you need to do is compare the size of one park to another. The same is also true of the inclusion of the Visitors Rank column. The inclusion of these columns makes it much easier to make some types of comparisons about the parks in the table. That’s definitely something to make note of as you finish reviewing the information presented by the chart.

We’ll just evaluate the statements in order. First, we’ll evaluate:

The park that experienced the greatest percent increase in visitors from 2009 to 2010 also had the least total acreage.

This statement is typical of the sorts of statements that you are called upon to evaluate for Table Analysis questions. Note that there are two possible sorts that you could perform to evaluate this question. First, you could sort by Visitors % Change. But, you could also sort by Area Acres. So, what’s the best? Sort by only one of those columns? Sort by both? Sort by neither?

With 11 rows of data, you’ll probably find it safer to sort by at least one of the columns. But, which one? Well, note that the table provides you with ranking information for the areas of the parks. The smaller numbers used to rank the parks by area make it easier to identify the smallest park by area without sorting.

However, you might reasonably be worried about missing which park had the greatest percent increase by visitors. So, sort by Visitors % Change. Here’s what the sorted table looks like:

Now, it’s clear that Acadia had the greatest percent increase in the number of visitors from 2009 to 2010. Acadia was ranked 47th in terms of overall acreage. You could sort the chart by Area Acres or by Area Rank at this point to finish evaluating the statement. However, since you know Acadia’s rank for acreage, it’s probably slightly faster to simply scan to see if any park had a higher rank for area. In this case, Bryce was ranked 50th, so this first statement is false.

Now, let’s take a look at the second statement, which states:

The park with the median rank by the number of visitors is larger than only one other park by acreage.

Again, you may be considering several different ways to sort the chart. So, start by asking yourself “What’s hardest to see right now?” Remember that your chart will still be sorted as shown above, which is the sort that you did to evaluate the first statement. This sort makes it pretty hard to see which park had the median rank for visitors, so it makes sense to sort by Visitors Rank.

Here’s what the sorted chart looks like:

With the table sorted by Visitors Rank, it’s now fairly easy to find the park with the median rank. To find a median, you start by putting the items on a list into numerical order, which we just did by sorting the list. Then, you can just choose the middle number. In this case, Acadia is the park in the middle position since there are 5 parks ranked before it and 5 parks ranked after it.

Note that you could have also sorted the list by Visitors Number. Since data is always sorted from least to greatest, Canyonlands would have been the first row of the table and Grand Canyon would have been the last row. But, Acadia still would have been in the middle. We chose to sort by Visitors Rank because that term was mentioned in the question and it’s easier to work with smaller numbers.

Having identified Acadia as the park with the median rank, you now need to decide whether to sort the table again. Since the table provides ranks for the total acreage of the parks on the list, you likely don’t need to sort again. Acadia is 47th by acreage. One park, Bryce with a rank of 50, is smaller. So, Acadia, the median park by visitation, is larger than only one other park on the list. The second statement is true.

Note, however, that if the table had not provided ranks for the parks by total area, then you most likely would have wanted to sort by Area Acres. After all, it’s a lot easier to see that only one number is greater than 47 than to see that only one number is less than 47,390. Remember that sorting only takes a few seconds and you should sort whenever you think doing so will help you to accurately find what you need on the table.

Now, it’s time to finish the question by evaluating the third statement. The third statement claims:

The total number of visitors at Arches in 2009 was less than 1,000,000.

Because this statement involves only a single data point, you don’t really need to worry about doing any sorting. Even the most involved GMAT tables will have fewer than 30 rows of data. So, it will never be an issue to quickly scan the table, no matter how it is currently sorted, to find one data point. Just use the current sort which has Arches in the 8th row.

Next, you need some information about Arches to evaluate the statement. The table shows that Arches had 1,014,405 visitors in 2010. The table also shows that the number of visitors in 2010 was 1.8% greater than it was in 2009. To find the number of visitors in 2009, use the percent change formula:

Next, put the numbers that you know into the formula to get:

We’ve called the 2009 number that we’re trying to find x. A little rearranging gives:

101.8x = 101,440,500

Finally, just divide through by 101.8 to find that x, the 2009 visitation at Arches, was 996,469 rounded to the nearest integer. So, statement four is true.

Here’s what your answers should look like just before you click next to move onto the next question in the Integrated Reasoning section:

GRAPHICS INTERPRETATION

Graphics Interpretation questions provide you with one chart, graph, or image. Each chart is followed by two statements. The statements each contain one drop- down list from which you choose one answer. Your job is to pick the answer that makes the statement true. Each drop-down list typically contains between three to five answer choices.

You’ll find a few sentences of explanatory text to the right of the chart or graph. As with Table Analysis questions, you may not need to read this explanatory information. Just as with Table Analysis questions, you can be guided by how well you understand the chart or graph. If you understand the chart or graph, then you probably don’t need to read the explanatory text.

So, what should you look for when you review the chart or graph? Start by looking at any labels on the axes. Are quantities being measured in common, easily understood units? You should also look to see if the chart or graph has any titles that help to explain the data it shows. Finally, see if there’s any sort of legend that helps to differentiate different types of data.

Let’s take a look at the sample Graphics Interpretation question that we discussed in Chapter 18.

Here’s How To Crack It:

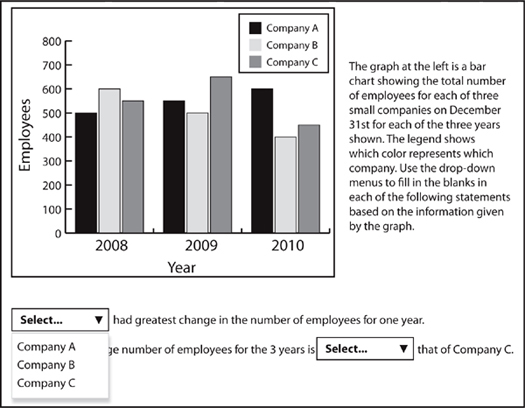
Before we get started discussing this question, note that we’ve expanded the drop down list for the first statement. When the question first appears on the screen, none of the drop-downs are expanded. Here, we just wanted to show what the expanded drop-downs look like in the context of a question.

The first step in working any Graphics Interpretation question is to review the chart or graph. In this case, there’s a bar chart. The vertical axis shows employees in hundreds, which seems fairly easy to understand. The horizontal axis shows results for three years. The different colored bars are explained by the legend—there are three companies. So, this chart seems fairly straightforward. It shows the number of employees for three companies for three different years.

With everything on the chart so clearly marked, there’s little reason to read the explanatory text to the right of the chart. Note that the only piece of information that the explanatory text really adds is that the number of employees for each company was tallied on December 31st of each year. That’s the sort of detail that often turns out to be irrelevant in answering the questions. Remember that you can always go back and read the explanatory text if it seems like you need to know something that wasn’t clearly reflected on the chart or graph.

Let’s take a look at the questions. As with Table Analysis questions, it’s best to just evaluate the statements in order. If one of them gives you trouble or seems particularly time-consuming, you can always skip over it and evaluate the other statements first. Of course, you’ll need to pick an answer for all three statements before you can move to the next question in the Integrated Reasoning section.

Here’s the first statement again:

For this statement, the task is to determine which company had the greatest overall changes in employees in any one year period. You’ll probably find it helpful to write down the changes on your noteboard. You may even want to construct a rough table to keep track of the changes. In that way, you can easily spot the largest overall change.

Here’s a table that shows the changes for each company:

For this statement, it’s important to note that the question asked for the greatest change. So, you need to include overall decreases in looking for the greatest change. Employment at Company C declined by 200 between 2009 and 2010. The correct answer to statement one is “Company C”.

Here’s the second statement showing the possible answers:

To evaluate this statement, you need to calculate the average number of employees for Companies A and C. Questions that ask you to perform calculations such as finding an average are fairly common for Graphics Interpretation questions. Just be sure to read the information from the chart carefully. Common errors for questions such as this one usually involve reading the information for the wrong company or mixing the information for two companies.

For Company A, the total number of employees for each year was 500, 550, and 600. To find the average, take the sum of the three numbers to get 1,650. Now, just divide by 3 because you want the average over three years. So, the average number of employees for Company A is 550.

For Company C, the total number of employees for each year was 550, 650, and 450. The average number of employees per year for Company C is also 550. So, the correct answer for the second statement is ‘the same as’.

Here’s what your answers should look like just before you click next to move on to the next question in the Integrated Reasoning section:

TWO-PART ANALYSIS

Most two-part analysis questions will remind you of the word problems that are part of the Quantitative section of the GMAT. The only difference is that you’ll need to pick two answers rather than one! It’s likely that you’ll need to do some calculations to solve most Two-Part Analysis questions. For the most part, the math you’ll need to do will be fairly straightforward arithmetic. You may find that it’s faster to do the calculations without the calculator. However, remember that the calculator is available. Just remember to set up your calculations before entering them into the calculator.

For most Two-Part Analysis questions, the two answers that you need to pick are related or linked in some way. When that’s the case, you may be able to identify one part as easier to solve than the other. If so, do the easier part first. It’s also important to remember that working with the answer choices is often easier for these questions. While some Two-Part Analysis questions can be solved algebraically, it’s very often faster to just test out the answer choices. In other words, you’ll be able to use a form of PITA (Plugging In The Answers, discussed in our Algebra Chapter) to solve most of these questions. Let’s take a look at how to solve the question we saw in Chapter 18.

Here’s How to Crack It

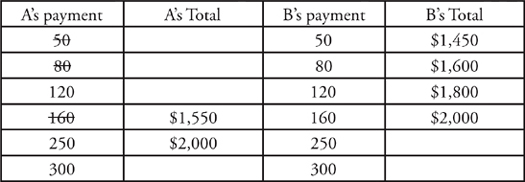
For this problem, one of the first things to notice is that there is a connection between the payments that each family makes. Since Family B’s initial payment is $450 more than that of Family A, Family A’s monthly payment is larger than that of Family B. That can help when you start testing the answer choices. Moreover, you can also see that the answer for Family A cannot be either $50 or $80. If Family A’s monthly payment were $80, then they would have only paid an additional $400 after 5 months. That’s not even enough to make Family A’s total payment equal to Family B’s initial payment. Of course, Family B makes monthly payments, too.

You can set the problem up just like you would a PITA question with one change. So that you can keep track of your process of elimination, write the answer choices down twice leaving some space between the answers to show any quantities that you needed to calculate. Of course, you’ll label your answer choices just like with any other PITA question. For this problem, you can label your columns of numbers as “A’s payment” and “B’s payment.” Here’s what your initial setup should look like:

Note that we’ve already crossed off 50 and 80 as possible payments for Family A. As discussed, these answers are too small for A’s payment. As with any other PITA question, it makes sense to start with a number in the middle. We’ll start with $160 for Family A’s payment.

If Family A’s payment is $160, what can you find? The problem states that Family A makes 5 payments, so the total of those 5 payments is $800. Moreover, the problem also states that Family A made an initial payment of $750. So, if Family A made payments of $160, then the refrigerator cost $750 + $800 = $1,550. That’s what goes into the next column for Family A.

What about Family B? If Family A makes payments of $160, then Family B’s payments must be less than that amount. So, Family B could make payments of $50, $80 or $120. For each of those numbers, calculate how much Family B would have paid for the refrigerator. Here’s what your table should look like at this step:

So, how do you know if you’ve found the correct answers? Remember that the problem states that both families pay the same amount for their refrigerators. Since Family B cannot pay $1,550 for their refrigerator, you can eliminate 160 as an answer for Family A.

It’s not that clear whether Family A’s payment needs to be larger or smaller. So, just pick a direction and try it. Let’s try $250 for Family A’s payment. If Family A’s payment is $250, then their refrigerator costs $750 + (5 × $250) = $2,000. For Family B, none of the answers we’ve already worked out make their refrigerator cost $2,000. However, we can also check what happens if Family B makes monthly payments of $160. In that case, Family B’s refrigerator costs $1,200 + (5 × $160) = $2,000. So, the answers are 250 for Family A and 160 for Family B.

Here’s what your completed table looks like:

Here’s what your answers should look like just before you click next to move on to the next question in the Integrated Reasoning section:

We used a form of Plugging In the Answers (PITA) to solve the previous question. You can use that approach for most of the Two-Part Analysis questions that you see. Here’s a recap of the steps.

PITA for Two-Part Analysis Questions

1. Write down the answer choices on your noteboard. Make two columns leaving some space between.

2. Decide which variable is easier to work with. For example, you might be able to eliminate some answers for one variable because those answers are too big or too small.

3. Write a label over each column of numbers. Label the first column as the easier variable to work with.

4. Starting with an answer in the middle for the first column, work the steps of the problem. For the second column, remember that you may only need to test the answers that are bigger or smaller than the number you worked with in the first column.

5. Check for a match between the first and second column that makes a condition in the problem true.

For some Two-Part Analysis questions, however, you won’t be able to use PITA. For the problem we just discussed, the two monthly payments were linked because both families needed to pay the same amount for a refrigerator. For some Two-Part Analysis questions, however, the variables are either unlinked or, at least, less linked.

Let’s look at an example:

Here’s How to Crack It

For this question, note that there’s no common condition that needs to be satisfied. Rather, there are two independent calculations. That’s how you know that you can’t use PITA to solve this question.

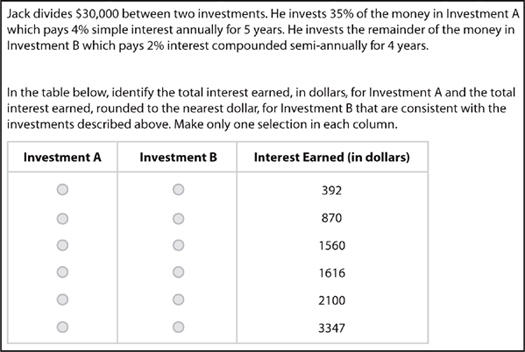
The solution to this question starts with calculating how Jack divides the $30,000 between the two investments. Start by calculating 35% of $30,000. Remember that you can just use the onscreen calculator: 30,000 × 0.35 = 10,500. So, $10,500 is invested in Investment A and the rest, or $19,500, is invested in Investment B.

Next, it’s time to calculate the interest earned on each investment. Investment A earns simple interest at a rate of 4% per year for 5 years. To find simple interest, you multiply the principal amount, $10,500, by the interest rate, 0.04, by the time period, 5 years. Here’s what the calculation looks like:

$10,500 × 0.04 × 5 = $2,100

The onscreen calculator makes doing the calculation an easy, one-step operation. Just make sure that you use the right numbers from the problem!

For Investment B, the interest is compounded semi-annually. That means that every six months the interest is added to the principle so that interest can be earned on the combined amount. There are several ways to calculate compound interest. One of the easiest is to divide the yearly interest rate by the compounding period. For this problem, the investment pays 2% per year but the interest is compounded twice per year.

So, that’s 1% every six months. In four years, there are 8 compounding periods. So, to find the account balance at the end of 4 years, you’d calculate the interest for the first six months by multiplying by 0.01. Then, you’d add that amount to the principal and repeat the calculation. Keep calculating until you’ve done all 8 compounding periods. Of course, since you are multiplying each time, there’s a shorter way. Here’s what the overall calculation looks like.

$19,500 × (1.01)⁸ = $21,115.71

Now, to find the interest just subtract $19,500 from the account balance. The interest earned is $1,616 rounded to the nearest dollar.

Here’s what your answers should look like just before you click next to move onto the next question in the Integrated Reasoning section:

MULTI-SOURCE REASONING

For Multi-Source Reasoning questions, you’ll be given a variety of information that can include text, charts, tables, and graphs. The information is arranged on 2 or 3 tabs. Multi-Source Reasoning questions typically come in sets. So, you’ll probably get two sets of statement style questions and perhaps one standard multiple choice question.

When a new Multi-Source question appears on your screen, you should take a minute to review the information on each tab. As usual, you’ll want to check out things like the axes on graphs and any headings for the charts. But, for Multi-Source Reasoning questions, you also want to see how the information on one tab relates to the information on the other tabs.

Let’s look at the example that we saw in the previous Integrated Reasoning chapter. This time, we’ll take a look at the information on all three tabs. We’ll also discuss how to evaluate statements and answer questions.

Here’s How to Crack It

We’ll review the information one tab at a time before we start evaluating the statements. The first tab, Text #1, provides some background information about the ways in which a country’s population can affect its participation in the global economy. This tab also presents a table with population and growth rates for five countries. Notice that you need to read the included information on this tab to determine that the table displays data from 2005. Unlike the other question types that we’ve discussed, you should always read any text that’s included on a tab in a Multi-Source Reasoning question.

Now, here’s the information for the second tab:

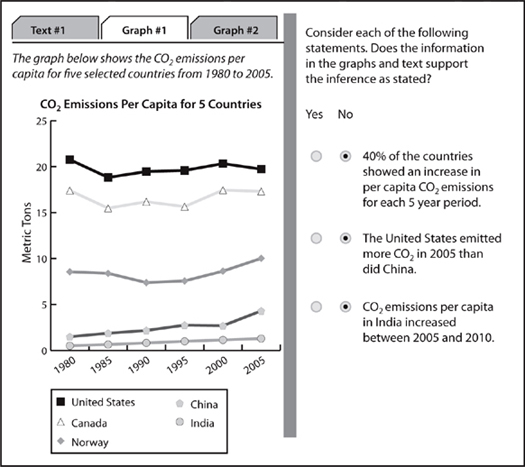
This tab shows CO₂ emissions for five countries over a 25 year period. Notice that the countries on this tab are the same as the countries on the first tab. It’s also important to note that the CO₂ emissions on this tab are per capita emissions. Since the first tab provided information about populations for 2005, it would be possible to calculate approximate total CO₂ emissions for these five countries for 2005. While you don’t necessarily need to consider all the calculations you could perform, thinking about what you could calculate is an excellent way to notice connections between the data provided on the tabs.

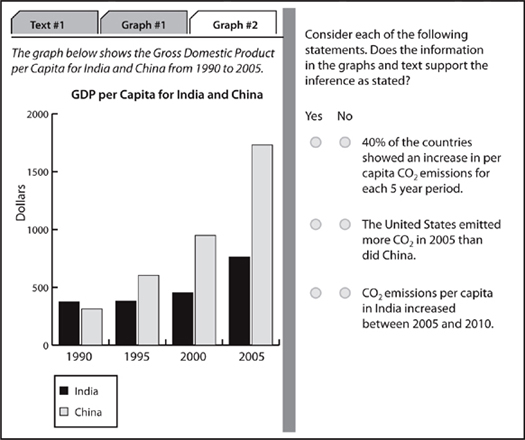
Next, let’s take a look at the information on the third tab:

This tab provides GDP information about two of the countries, India and China, discussed on the first two tabs. The information on this tab is provided for a subset of the timespan from the second tab. The second tab showed the 25 year range from 1980 to 2005 while this information is only for the 15 year timespan from 1990 to 2005. The GDP information is provided as per capita information. Again, that means that the information on the first tab could be used to calculate the overall GDP for India and China. Of course, that calculation can only be completed for 2005.

Now, that we’ve reviewed the information on each tab, it’s time to start evaluating the statements. But first, we need to consider the directions carefully. The directions state that you are supposed to consider “Does the information in the graphs and text support the inference as stated?” Remember our discussion of valid inferences. An inference is a statement that you know to be true because you can back it up with proof.

There are really three cases to consider when evaluating these statements. If the graphs and other information on the tabs are sufficient to show that the statement is true, answer “yes.” If the graphs and other information on the tabs are sufficient to show that the statement is false, answer “no”. But, what if there is simply insufficient information to conclusively show that the statement is either true or false? In that case, you answer “no” because the information did not support the inference. In other words, the task here is a little different than simply evaluating whether the statements are true or false. After all, GMAC could have made the answer choices True and False rather than Yes and No.

Remember, however, that most GMAC statements won’t try to trick you that way. But, it is important to remember that you need proof to claim that something can be inferred. You will see statements that try to get you to read into or interpret the information. Such activities do not lead to valid inferences!

Let’s take a look at the first statement:

40% of the countries showed an increase in per capita CO₂ emissions for each five year period.

The first step in evaluating a statement for a Multi-Source Reasoning question is to determine which tab or tabs contain the information that you need. For this statement, the second tab contains information about per capita CO₂ emissions so select that tab. Next, start checking out the trend lines on the graph. We’ve reprinted the chart from the second tab below.

The trend lines for the United States, Canada, and Norway clearly show both increases and decreases between five year periods. So, none of those countries fit the requirements of the statement. The trend line for China needs to be examined carefully. China’s CO₂ emissions per capita increase for four out of the five five-year periods shown. However, China’s emissions decreased slightly between 1995 and 2000. So, China also does not fit the requirements of the statement. Only India’s trend line shows an increase for every five-year period depicted on the graph. But, that means that only 1 out of 5 or 20% of the countries showed an increase in CO₂ emissions for each five year period. So, the answer to the first statement is no.

Next, let’s take a look at the second statement:

The United States emitted more CO₂ in 2005 than did China.

Evaluating this statement is a little trickier than evaluating the first statement. First, be careful of the wording. The statement is about total CO₂ emissions rather than the per capita emissions that are shown by the chart on the second tab. So, while the emissions chart does show that per capita emissions for the US were greater than those for China in 2005, you cannot base your answer only on that piece of information. Remember that the test-writers will try to get you to make hasty conclusions so always check out the wording of the statement carefully.

Since none of the provided charts allows you to simply look up the information for this statement, you need to determine if you have sufficient information to evaluate the statement. To go from per capita CO₂ emissions in 2005 to total CO₂ emissions in 2005, you need to know the populations for China and the United States in 2005. That information is provided by the table on the first tab. As discussed above, if there had been insufficient information, you could have clicked “no” right away for your answer.

Since there is sufficient information, however, you’ll need to calculate the total 2005 CO₂ emissions for both China and the United States. To do so, multiply the per capita emissions for each country from the chart on the second tab by the population for that country from the table on the first tab. We’ve duplicated the relevant information from the first two tabs below.

Of course, you won’t be able to split the view on your computer screen this way. So, you’ll need to write down some of the relevant information on your noteboards. You should use your noteboards to take notes whenever you need information from two different tabs. Simply trying to remember the numbers can cause errors and waste time. For example, to evaluate this statement, you might jot down the 2005 per capita CO₂ emissions for the United States and China. Then, go to the first tab to get the population numbers for each country.

For the US, per capita CO₂ emissions in 2005 were approximately 20 metric tons. The US population in 2005 was 295,753,000. So, the total 2005 CO₂ emissions for the United States was 20 × 295,753,3000 = 5,915,060,000 metric tons. For China, the per capita CO₂ emissions are approximately 4.8 and the population was 1,304,000,000. So, China’s total CO₂ emissions for 2005 were 4.8 × 1,304,000,000 = 6,259,200,000, greater than those of the United States. Therefore, the answer to the second statement is no.

It’s time to tackle the third statement:

CO₂ emissions per capita in India increased between 2005 and 2010.

In contrast with the second statement, evaluating this statement is certainly less time consuming. However, as we’ll see, you’ll need to remember what is necessary for a valid inference. The necessary information is displayed on the graph on the second tab. Again, we’ve duplicated the necessary information below.

Now, it’s time to be careful. Notice that the chart only displays data up to 2005. While India’s per capita CO₂ emissions have shown a steady increase over the 25 year period shown on the chart, that’s not sufficient for a valid inference. Since the chart does not display the actual numbers for 2010, the answer to the third statement is “no.”

Here’s what your answers should look like just before you click next to move on to the next question in the Integrated Reasoning section:

As mentioned, Multi-Source Reasoning questions usually come in sets. Typically, you’ll get two statement style questions and one multiple choice style question. The questions on the right change but the tabbed information on the left stays the same.

Let’s take a look at a multiple choice question for the tabbed information that we just used to evaluate a statement style question.

Here’s How to Crack It

As with any other Multi-Source Reasoning question, your first step is to determine which chart or charts contain the relevant data. For this question, you certainly need the bar chart on the third tab because that chart shows information about GDP. The bar chart is shown above. However, the bar chart displays data about GDP per capita and the question asks about overall Gross Domestic Product. So, you’ll also need the 2005 population numbers from the table on tab one. We’ve reproduced the relevant table below.

To answer the question, you need to multiply each countries GDP per capita from 2005 by its population from 2005. Then, subtract India’s GDP from that of China.

Based on the bar chart, China’s 2005 per capita GDP was approximately $1,750. Since China’s population in 2005 was 1,304,000,000, China’s 2005 GDP was approximately $1,750 × 1,304,000,000 = $2,282,000,000,000. (Remember that you can use the onscreen calculator to perform the calculation.) For India, the 2005 per capita GDP was approximately $750 while India’s population was 1,095,000,000. That means that India’s GDP was approximately $750 × 1,095,000,000 = $821,250,000,000. Now, just subtract to find that China’s 2005 GDP was approximately $1,460,750,000 more than that of India. That’s closest to Answer Choice B.

Complex Calculations and the Memory Keys

The problem just discussed featured several longer calculations. Your calculator probably has parentheses which makes entering such a calculation a one step operation. Is there a way to do this calculation in one step using the onscreen calculator which doesn’t have parentheses? Sure, use the memory keys!

Enter the following keystrokes:

1750 * 1304000000 =

750 * 1095000000 =

These keystrokes will minimize the number of times you need to enter the large numbers which helps to avoid errors.

Summary

Before you jump into the Integrated Reasoning questions, get your bearings and peruse each tab or piece of information.
On Table Analysis questions, know that you can only sort by one column at a time. If you think that sorting will help, go for it. But don’t waste time devising the perfect order to evaluate statements.
On Graphics Interpretation questions, start by looking for labels on the axes and finding the legend if there is one.
On Two-Part Analysis questions, do some algebra or PITA to get to the right answer. Careful that you select the right button in the right column when answering these questions.
On Multi-Source Reasoning questions, take a minute to review the information on each tab before you jump in. Think about how the information on one tab relates to the information on other tabs.

Chapter 19Integrated Reasoning: Strategies

GENERAL STRATEGIES

Get Your Bearings

Read What You Need When You Need

Valid Inferences

TABLE ANALYSIS

The Sort Function

To Sort or Not To Sort

GRAPHICS INTERPRETATION

TWO-PART ANALYSIS

MULTI-SOURCE REASONING

Summary

Chapter 19
Integrated Reasoning: Strategies