DRILL 1 (AD/BCE)
1. BCE. From Statement (1) all we know is a value for y. There is no telling what the value of x will be.
2. BCE. From Statement (1) we know that 2y is an integer, but does that mean y must be an integer? Not necessarily. What if y were  ?
?
3. D. If we know from the question that there are 12 children in a room and Statement (1) tells us there are 3 girls, then we know there are 9 boys, and we can answer the question.
4. AD. Statement (1) gives us an equation that we could solve to get the value of x (not that we need to). If we can solve for x, then we can answer the question.
DRILL 2
1. 77
2. 79
3. 10
4. 16
5. choice B
6. Statement (1) gives us one unique value for x: x = 2. We’re down to AD. Statement (2) on the other hand gives us two possible values for x: 2 or –2. The correct answer is choice A.
DRILL 3
1. 80 + 40 = 120
2. 55 × 100 = 5,500
3. ab + ac – ad
4. c (ab + xy)
5. 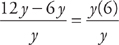 = 6, choice B
= 6, choice B
6. Statement (1) gives us a value for x, but we need x + y + d. Statement (1) is not sufficient. We’re down to BCE. Statement (2) might not have seemed much more helpful, BUT using the distributive property, we can rewrite the original equation to read a (x + y + z) = 15. If a is 5, then x + y + z must equal 3. The correct answer is choice B.
DRILL 4
1.  or 6
or 6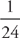
2. 
3. 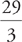
4. 18
5. choice C
DRILL 5
1. 33.30
2. 266.175
3. 6.09
4. 800
5. choice C
6. You were probably very tempted by choice (C) since Statement (1) gives us a value for x and Statement (2) gives us a value for y. However, if x and y are reciprocals (meaning that when multiplied together, their product must equal 1), then Statement (1) not only gives us a value for x ( or
or  ), but it also gives us a value for y: the reciprocal of
), but it also gives us a value for y: the reciprocal of  , which is 5.0. We’re down to AD. Statement (2) does exactly the same thing in reverse. The correct answer is choice D.
, which is 5.0. We’re down to AD. Statement (2) does exactly the same thing in reverse. The correct answer is choice D.
DRILL 6 (Angles and Lengths)
1. x = 110°
2. x = 50° y = 130° z = 130°
3. x = 60° y = 120° z = 120°
4. 
5. choice D
6. Statement (1) by itself gives us a mystery angle y not related to angle x, so we’re down to BCE. Statement (2) by itself relates angles x and y: together, they add up to 180 degrees. But by itself, Statement (2) is still not sufficient because we don’t have either individual angles. We’re down to C or E. However, when we put both statements together, we can answer the question: if x + y = 180, and y = 40, then x must equal 140. The correct answer is choice C.
DRILL 7 (Triangles)
1. x = 8
2. x = 60
3. x = 5
4. x must be less than 11 and greater than 3
5. 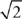
6. 
7. choice B
8. Choice C. Statement (1) tell us that y = 80. Remember, however, that figures in data sufficiency problems are not necessarily drawn to scale. So, don’t assume that angles x and y are equal! We are down to BCE. Statement (2) tells us that sides AB and BC are equal, so angles x and y are also equal. However, we don’t know the degree measure of those angles, so cross off B. Combining the statements, we know that x and y are equal and that y = 80. So, x = 80. The correct answer is choice C.
DRILL 8 (Circles)
1. area = 25π, circumference = 10π
2. circumference = 12π
3. 60°
4. choice B
5. Statement (1) by itself would allow you to find the area of circle Q, but that’s not what the question is asking; we want circle P. We’re down to BCE. Statement (2) by itself gives us a way to compare the two circles, but gives us no specific dimension. We’re down to C or E. Combining the statements gives us both a specific dimension and a way to compare the circles. The correct answer is choice C.
DRILL 9 (Data Sufficiency Parts and Wholes)
1. Choice C. Statement (1) tells us only how many people paid a deposit. This is not sufficient to answer the question, and we are down to BCE. Statement (2) tells us only what percent of the people who paid deposits actually showed up. Again, by itself, this does not give us the number of people who attended, so we can eliminate B. But if we put the two statements together, we now know how many people paid deposits (70), and what percentage of those people actually attended (60%), which means we can figure out how many people attended.
2. Choice D. You might think you need both statements together, but in fact, either is sufficient by itself. Statement (1) tells us there are 7 ounces of pigment in a 12-ounce can. Because there are only two ingredients, this means the other ingredient must make up the rest, or 5 ounces. This is sufficient to figure out the ratio (7 : 5) and we are down to a fifty-fifty choice: A or D. Similarly, Statement (2) tells us there are 5 ounces of alcohol in a 12-ounce can. Because there are only two ingredients, this means the other ingredient must make up the rest, or 7 ounces. Again, this is sufficient to figure out the ratio, so the answer must be D.
3. Choice C. To answer this question, we need the total number of miles. Statement (1) does not give us any concrete figures—just a fraction, so it is not sufficient, and that narrows our options down to BCE. Statement (2) gives us a concrete number, but it is only for part of the distance, so we can eliminate B. However, if we combine the two statements, we learn that those 12 miles must make up the remaining  of the entire trip. From this we can learn the entire distance of the trip by setting up the equation
of the entire trip. From this we can learn the entire distance of the trip by setting up the equation  =
= 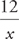 . The correct answer is C.
. The correct answer is C.
DRILL 10 (Strange Powers of Powers)
1. Choice C. Statement (1) might seem to be sufficient, but remember, if x2 = 4, then x could be either 2 or –2. The question asks for the one and only value of x. Statement (1) is not sufficient. Statement (2) by itself is not sufficient either, because the question is asking for the one and only value of x. But together, the two statements are sufficient because Statement (1) gets us down to two possibilities, 2 and –2, and Statement (2) eliminates the positive number.
2. Choice B. If x2 = 4, then x could be either 2 or –2, so Statement (1) is not sufficient. You might not think Statement (2) is sufficient by itself, because it only gives us a value for y, not for x. However, the question is asking for the value of x times y. If y = 0, then we know the value of xy. Zero times any number equals zero.
3. Choice E. If x2 = 4, then x could be either 2 or –2, so Statement (1) is not sufficient. If y2 = 9, then y could be either 3 or –3. The question is asking for the one and only value of x, so Statement (2) is not sufficient by itself either. You might think that putting the two statements together would help us arrive at an answer, but in fact, we don’t know. If x = 2 and y = 3, then xy = 6, but what if either x or y was negative? Then xy could also equal –6.
DRILL 11 (Yes or No)
1. Choice A. To answer this yes-or-no question, plug values into the statements. The only condition of the question itself is that x is positive. The only positive numbers that will make Statement (1) true are positive fractions less than  . This means Statement (1) always answers this question “yes” and we are down to AD. Plugging positive numbers into Statement (2), we could have
. This means Statement (1) always answers this question “yes” and we are down to AD. Plugging positive numbers into Statement (2), we could have  , which gives us a “yes,” or 1, which gives us a “no.” Therefore, the answer must be choice A.
, which gives us a “yes,” or 1, which gives us a “no.” Therefore, the answer must be choice A.
2. Choice B. When we plug normal numbers 3 and 2 into Statement (1), x is positive. But if we plug in –3 and –2, x is negative, so we are down to BCE. Now, when we plug normal numbers 3 and 2 into Statement (2), we get a “yes.” But when we try to plug weird numbers into Statement (2), we realize that (y2) must always be positive—which means that x must always be positive as well, giving us a definitive “yes.”
3. Choice C. To answer this yes-or-no question, plug values into the statements. Let’s begin with Statement (1) and let’s begin with normal numbers. How about 2 and 3? We get a “yes.” Now, let’s try some weird numbers. How about 2 and  ? This time, we get a “no,” which means we’re down to BCE. Let’s try Statement (2). Plugging in normal numbers 2 and 3 again, we get a “yes.” Plugging in weird numbers 3
? This time, we get a “no,” which means we’re down to BCE. Let’s try Statement (2). Plugging in normal numbers 2 and 3 again, we get a “yes.” Plugging in weird numbers 3 and 1
and 1 we get a “no,” and we’re down to C or E. Now, to consider C, we must pick numbers that make both statements work at the same time. The regular numbers give us a “yes.” But when we try to plug weird numbers into the two statements, we realize it can’t be done. Only integers will make both statements true at the same time. The answer is choice C.
we get a “no,” and we’re down to C or E. Now, to consider C, we must pick numbers that make both statements work at the same time. The regular numbers give us a “yes.” But when we try to plug weird numbers into the two statements, we realize it can’t be done. Only integers will make both statements true at the same time. The answer is choice C.
DRILL 12 (Spotting Critical Reasoning Question Types)
1. Strengthen-the-argument question. To find the correct answer, look for the gap in the argument, and try to close it.
2. Inference question. To find the correct answer, use scope and POE to rule out any answer choice that goes too far.
3. Evaluate-the-argument question. To find the correct answer, look for the unspoken assumptions in the passage.
4. Assumption question. To find the correct answer, look for the gap in the argument.
5. Weaken-the-argument question. To find the correct answer, look for the gap in the argument and try to widen it.
6. Resolve/explain question. To find the correct answer, look for the answer choice that allows both of the facts from the passage to be true at the same time.
7. Identify-the-reasoning question. To find the correct answer, identify the conclusion and the premises, and see how they relate to each other.
8. Parallel-the-reasoning question. To find the correct answer, simplify the argument (if A, then B), and look for an answer choice that matches.
INTEGRATED REASONING DRILLS:
Section 1
1-1. True
This question asks about the median, so first list the data in order of Riders and note the median (fifth) in the list: 34th St/Penn Station (Red Lines). Next, to find the station with the greatest decrease in passengers from 2009 to 2010, sort the data by % Change and note that the same station shows a percentage decrease of 1.1%, the greatest percentage decrease in the list.
The question, however, asks if the station had the greatest decrease in passengers, which is different from the greatest percent decrease in passengers. Confirm that the actual decrease in passengers was the greatest; since the only other station with a decrease from 2009 was Grand Central/42nd St, calculate the actual decrease for each station and compare them.
The 2010 ridership for 34th St/Penn Station (Red Lines) is 26,892,243, which you can round to 27 million for this purpose. Since the decrease from 2009 to 2010 was 1.1%, the 2010 value is equal to 98.9% (100%-1.1%) of the 2009 value. So, to solve for the 2009 value, the formula would be 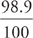 x=27,000,000.
x=27,000,000.
Solving for x gives a 2009 ridership at 34th St/Penn Station (Red Lines) of about 27.3 million for an actual decrease of about 300,000 riders. Calculating the actual decrease for Grand Central/42nd St in the same manner gives a decrease of less than 100,000 riders, and so 34th St/Penn Station (Red Lines) had the greatest decrease in riders, and the statement is true.
1-2. True
Sorting the table by Connecting Subway Lines will make it easy to see which stations have 3 connecting lines and which have 5 connecting lines. The onscreen calculator can be used to find that the average Riders of the two stations with 5 connecting subway lines is 31,307,134; that the average Riders of the three stations with 3 connecting subway lines is 23,434,760; and that the ratio between those two numbers is 1.33. Presented as a fraction, 1.33 is approximately  , so the statement is true.
, so the statement is true.
1-3. False
Sorting the table by % Change will make it easy to identify the station with the highest percent increase in riders from 2009 to 2010: Lexington Ave/59th Street. However, when the table is sorted by Riders, Lexington Ave/59th Street is 8th, not 9th (last), in annual ridership, and so the statement is false.
The problem divides the doctors into two categories: those whose services are, or are not, covered by Frank’s medical plan, and those who graduated from medical school with, or without, honors. The information can be summarized in a group grid as follows:
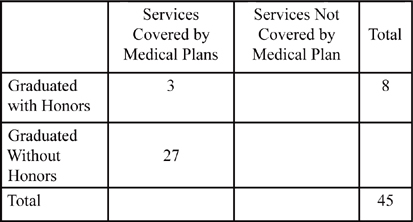
The remaining data in the table can be completed by solving for the missing data elements. The total number of doctors whose services are covered by the medical plan is 27 + 3, or 30, and so the number of doctors whose services are not covered by the medical plan is 45 – 30, or 15. Here’s the group grid with that data filled in:
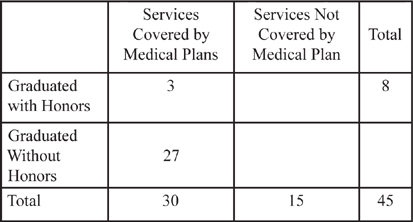
To find the number of doctors who graduated with honors and whose services are not covered by Frank’s medical plan, continue the work from the first part of the question by solving for additional missing elements in the group grid.
In this case, the total number of doctors who graduated without honors is 45 – 8, or 37. The number of doctors, then, who graduated without honors and whose services are not covered by Frank’s medical plan is 37 – 27, or 10.
Here’s the completely filled-in group grid:

Orchids: Choice F, 8
Dahlias: Choice C, 4
The word problem can be expressed in the form of an equation in terms of the price of each flower: 1.35o + 1.8d = 18. Generally, two distinct equations are required in order to solve for two different variables. However, the number of orchids and dahlias must be integers. This restriction makes it possible to solve this equation although there still may be more than one solution.
Since the number of orchids and the number of dahlias must both be integers, Plug In The Answers (PITA). Plug in each answer choice into the equation as the number of orchids and solve the equation for the number of dahlias, looking to see whether the result is also an answer choice.
Start with the first answer choice: 0, giving the equation 1.35(0) + 1.8d = 18, which simplifies to 1.8d = 18, and d = 10. Since 10 is not an available answer choice, 0 is not the correct answer for orchids.
Plugging in the second choice (2) for the number of orchids results in a solution of 8.5 dahlias. Since a whole number of dahlias is required, 2 is not the correct answer for orchids. Using the third choice (4), the solution to the equation is 7 dahlias, but again, 7 is not an available answer choice, so 4 is not the correct answer for orchids.
Plugging in the sixth choice, 8 orchids, to the equation gives 1.35(8) + 1.8d = 18, which can be simplified to 1.8d = 7.2, and when solved, d = 4. Since 4 is also an available response, 8 is the correct number of orchids and 4 is the correct number of dahlias, and no further testing of the answer choices is necessary.
4–1. Choice B, -1.4
The regression line comes close to the points (0,12) and (5,5). Therefore, the approximate slope is  = –1.4.
= –1.4.
4-2. Choice D, 100% greater
After 0 days of training, only two students were able to get within 11 inches of the center of the target. After two days of training, there were four students who were able to get with 11 inches of the center of the target. Since there was clearly an increase, eliminate A and B. Now, to get the percent increase, use the percent change formula: 
Strengthen: Choice B
The stone tools resemble those made and used by Homo erectus and Homo heidelbergensis, human ancestors in the Paleolithic era who lived on the mainland of Greece.
Weaken: Choice E
Approximately 5 million years ago, during the Messinian Salinity Crisis of the late Miocene era, the Mediterranean Sea dried up.
Conclusion:
“… some human ancestors developed nautical skills millions of years earlier than previously discovered.”
Premises:
“… earliest … evidence of seafaring by human ancestors dates to … 130,000 years ago … Archaeologists discovered stone tools on … a Mediterranean island that date to … 2.6 million years ago …” and “40 miles of open
sea separate the island from Greece.”
Assumption:
The only way the stone tools could have gotten to the island is if the human ancestors developed nautical skills and migrated to the island by boat or raft.
Based on the discovery of stone tools on an island that date to 2.6 million years ago, archaeologists hypothesize that human ancestors must have developed nautical skills and migrated to the island by boat. The argument assumes that the evidence is sufficient to support their hypothesis; that there is no alternative explanation that is supported by the data.
The answer that most strengthens the argument will strengthen the link between the premise (finding stone tools on the island) and the conclusion (the human ancestors developed nautical skills and migrated there), or will eliminate alternate explanations supported by the data.
The first answer choice is out of scope because the fact that tools used for fishing were found in the same area does not directly relate to whether the human ancestors had developed nautical skills; they could have fished from land or from the sea.
The second answer choice strengthens the argument by confirming that the stone tools were the same as those used by the human ancestors who lived on the other side of the water, and therefore increases the likelihood that they must have migrated there by boat or raft.
The third answer choice is irrelevant, because the argument is not concerned with the uses of the stone tools.
The fourth answer choice is irrelevant, because the argument is not concerned with whether the stone tools were used to construct boats.
The fifth answer choice weakens the argument by providing an alternate explanation of the migration that does not involve nautical skills: the human ancestors could have migrated to the island while the Mediterranean Sea was dry.
The sixth answer choice is irrelevant, because the argument is not concerned with whether the stone tools were used to construct boats.
(A): No
No 1-year CDs qualify for bonuses, so this $11,000 CD earns an interest rate of 2.2%. Use your calculator. 2.2% of $11,000 is (0.022 × 11,000) $242. Therefore this 1-year CD does not earn at least $250.
(B): No
All 5-year CDs qualify for a 0.1% bonus, so this $9,500 CD will earn 2.6% interest in its first year. Use your calculator. 2.6% of $9,500 is $247, so this CD does not earn at least $250 in its first year.
(C): Yes
All 10-year CDs qualify for a 0.1% bonus, so this $9,500 CD will earn a 2.9% interest rate in its first year. Use your calculator. 2.9% of the $9,500 is $275.50. So this CD does earn more than $250 in its first year.
(A): No
Since the CD has a term of 1 year, no bonus applies. The interest rate is 2.2%. So the interest is 2.2% of $20,000, which is $440. The interest is therefore less than $500.
(B): Yes
Since the CD has a term of 5 years, there is a 0.1% interest bonus. So the interest rate is 2.6%. The interest for the first year is 2.6% of $4,000, which is $104. The interest for each succeeding year will increase by around $2 (2.6% of $104). So the total interest will be a bit more than $520, but certainly less than $600.
(C): No
Since the CD has a term of 2 years, there are no bonuses to consider. The rate for a 2-year CD is therefore 2.4%. The interest from the first year will be $240 and the interest from the second year will be 2.4% of $10,240, which is about $246. So the total interest is $486, less than $500.
(A): No
The memo refers to a revised schedule of penalties for early withdrawal. There must have been a schedule in place previously to revise.
(B): No
It is true that the stated policy offers a bonus available to preferred customers but not to new customers. There is no reference however to this being a reward for loyalty. Rather, the stated purpose is to increase the overall stability of the bank’s portfolio. This statement introduces outside information.
(C): Yes
The stated intention is to shift the CD investments towards those with longer maturation periods. For each type of CD, this means paying higher interest rates to customers. So if the bank succeeds in making this shift, it will pay higher overall average interest rates than it will if a greater proportion of investments remain in shorter term CDs. This statement is well-supported by the evidence.
9-2. False
There are six Democrats and seven Republicans. To find the average electoral vote for each party, add the electoral votes of the Presidents in that party with your calculator and divide by the number of Presidents. The six Democrats add up to 2,200, which gives an average or about 367. The seven Republicans add up to 2,818, which gives an average of about 403. So the Democratic Presidents do not have the higher average.
9-3. True
Sort the chart by % of Popular Vote to make it easy to scan down the list. Now compare the % of Popular Vote and the % of Electoral Vote columns for each line in the table. Look for those lines in which the two values are closest together. There are three elections, 2000, 1976, and 2004, in which the two values are within about 5 points of each other. In 1976, the difference was slightly greater than 5, but in 2000 and 2004 it was closer to 3 points difference, (48.87% vs. 50.4% in 2000 and 50.73% to 53.2% in 2004). So 2000 and 2004 are the two years in which the percentages differ the least. Since George W. Bush was elected both years, it is true that the same President was elected in the two years in which the percentages were the closest.
(A): Yes
Memo #2 lists the regions and their respective average airfares. At $200 the Midwest and the West are tied for the lowest. This means that no region has lower average airfares than the Midwest.
(B): No
Memo #1 states that Regional Office Managers will be responsible for the travel reservations for Level 2 managers, but we don’t know that they will be the only persons in attendance. Therefore we cannot infer this to be true.
(C): Yes
Memo #1 states that Regional Office Managers may delegate that task, meaning that they do not have to do it themselves.
(A): True
Memo #1 states that regions will receive a “Budget Bonus” of 50% of the difference between the ticket price and the average airfare for tickets priced more than 1 standard deviation below the mean. Memo #2 states that the mean for the West is $200 and the standard deviation is $25. Thus the West will get a bonus for all tickets priced less than $175. Since there are 18 tickets priced at $150, the West will get a bonus of 50% of
(18)(200 – 150) = 50% of 900 = $450.
(B): False
Memo #2 states that the sample size for the Mid-Atlantic was 500. Since the standard deviation is $50, $450 is two standard deviations from the mean of $350. In a normally distributed sample, approximately 2% of the data points are more than two standard deviations from the mean. 2% of 500 is 10, which is half of 20.
(C): True
Memo #2 states that the sample size for the Northeast was 400. Since the standard deviation is $50, $250 is one standard deviation below the mean of $300. In a normally distributed sample, approximately 16% of the data points are more than one standard deviation below the mean. 16% of 400 is 64, which is more than 50.
(C): 
Memo #1 states that tickets will be fully reimbursed if it either falls within 1 standard deviation or below 1 standard deviation of the mean. Since the mean is $200 and the standard deviation is $25, 4 tickets fall within 1 standard deviation and 18 fall below 1 standard deviation. Thus 22 tickets out of 30 will be fully reimbursed, which gives a probability of  .
.
INTEGRATED REASONING DRILLS:
Section 2
1-1. Choice A, 15 to 8
The number of clocks produced on Tuesday is 75 and the number of clocks produced on Wednesday is 40. Therefore, the ratio of these two numbers is 75 to 40. Since both numbers are multiples of 5, you can reduce by a factor of 5 to get an equivalent ratio of 15 to 8.
1-2. Choice D, 36%
To get the percentage, you need to calculate 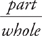 × 100. The part is the sum of the combined clocks produced on Monday and the clocks produced on Wednesday, which is 50 + 40 = 90. Now, you need the total number produced during the entire week. This is 50 + 75 + 40 + 55 + 30 = 250. Therefore, the percentage is
× 100. The part is the sum of the combined clocks produced on Monday and the clocks produced on Wednesday, which is 50 + 40 = 90. Now, you need the total number produced during the entire week. This is 50 + 75 + 40 + 55 + 30 = 250. Therefore, the percentage is 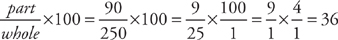
Weakens A’s Argument: Choice F Company X: Portals 8, which was just released, contains bugs and design flaws that will impair Company X’s ability to compete in the modern economy.
Conclusion:
“We have decided to purchase new computers that run Portals 8, the newest version of the world’s best selling operating system, throughout the entire company.”
Premise:
“Our company’s computer technology is out of date. We will be unable to compete effectively in the modern economy if we are not using current computer technology.”
Assumption:
The plan to purchase new computers running Portals 8 will allow Company X to compete effectively in the modern economy.
Company X’s argument uses a planning structure; it describes a problem (the company’s computer technology is out of date, and the company needs current technology to be able to compete effectively), and then proposes a plan to solve that problem (buy new computers running Portals 8).
In a planning argument, the assumption is always that there are no problems with the proposed plan. In this case, Company X assumes that the new computers with Portals 8 will actually help the company to compete effectively in the modern economy.
Because this is a weaken question, the answer will likely suggest a potential problem with the proposed plan (i.e., that the plan will NOT allow the company to compete effectively in the modern economy).
The first answer choice is out of scope, because the argument is not concerned with efficient use of computer resources.
The second answer choice is irrelevant because the argument is concerned with whether the plan will allow the company to compete in the modern economy, not whether GreenCap is the most cutting-edge software.
The third answer choice does not explain in what way the amount of time GreenCap has been available would affect the company’s ability to compete in the modern economy.
The fourth answer choice weakens the Technology Consultant’s argument, because it provides a reason why the consulting firm’s plan may not work, but it has no effect on Company X’s argument.
The fifth answer choice is out of scope, because the fact that Portals 8 is available in several different versions has no impact on the plan.
The sixth answer choice weakens Company X’s argument by providing a potential problem with Company X’s proposed plan (because Portals 8 contains a number of bugs and design flaws that would impair Company X’s ability to compete).
Weaken B’s Argument: Choice D Technology Consultant: GreenCap requires purchase of an annual maintenance agreement, making it more expensive overall than Portals 8.
Conclusion:
“Company X should purchase GreenCap.”
Premise:
“GreenCap costs substantially less than Portals 8, and it provides the same functionality with current computer technology. With the money saved, Company X will be better able to compete effectively in the modern economy.”
Assumption:
Purchasing GreenCap will actually end up saving money for Company X.
The Technology Consultant observes that GreenCap is substantially cheaper than Portals 8, while providing the same functionality, and that if Company X saves money, it will be better able to compete economically. Based on these premises, the consultant concludes that Company X should purchase GreenCap.
The argument assumes that Company X will actually save money by purchasing GreenCap. Since this is a weaken question, the answer will likely provide a potential problem with the proposed plan (for example, a reason purchasing GreenCap would NOT end up saving money for Company X).
The first answer choice is out of scope, because the argument is not concerned with efficient use of computer resources.
The second answer choice is irrelevant because the argument is concerned with whether Company X will actually save money, not whether the GreenCap is the most cutting-edge software.
The third answer choice is out of scope, because the amount of time GreenCap has been available does not affect whether Company X would save money by purchasing GreenCap.
The fourth answer choice weakens the Technology Consultant’s argument, because it provides a reason why purchasing GreenCap will not save money for Company X (because it requires a costly annual maintenance agreement that would eliminate the savings and end up costing more).
The fifth answer choice is out of scope, because the fact that Portals 8 is available in several different versions has no impact on the plan.
The sixth answer choice weakens Company X’s argument by providing a potential problem with Company X’s proposed plan (because Portals 8 contains a number of bugs and design flaws that would impair Company X’s ability to compete).
3-1. Choice C, 6 to 5
This question requires two steps to solve: first, which year had the lowest total per capita consumption of both ice cream and cheese, and second, what was the ratio of ice cream consumption to cheese consumption in that year?
By examining the data points for each year, you can identify that in 1989, the total consumption of ice cream and cheese was less than 53 pounds (because the ice cream consumption was less than 29 pounds, and the cheese consumption was less than 24 pounds.) Testing other years, such as 1990, confirms that 1989 had the lowest total consumption. (In 1990, the total consumption was approximately 53 pounds, based on the data points of approximately 28.5 pounds of ice cream and 24.5 pounds of cheese.)
To calculate the ratio of per capita ice cream consumption to per capita cheese consumption for 1989, divide the data point for ice cream (approximately 29) by the data point for cheese (approximately 24) for a ratio of approximately 1.2 (or, in fractional terms,  ).
).
3-2. Choice B, less than
The regression line for ice cream slopes down, while the line for cheese slopes up; per capita ice cream consumption is reducing over time, while per capita cheese consumption is increasing over time. Thus, the slope of the ice cream line is negative, and is less than the slope of the cheese line, which is positive.
Strengthens: Choice C
Once a geo-engineering innovation has been passed by the committee, the same innovation is automatically approved in all subsequent projects, without further review.
In disagreeing with the XM representative, the federal committee member has based her rebuttal on the statement that if we fail to review your project, we also fail to observe innovations in geo-engineering that may need guidelines drafted for the safety of subsequent projects throughout the industry. Setting a precedent for future projects is therefore the central concern of the committee member. To strengthen her argument, you need additional evidence that supports this assertion. Answer (C) states that once an innovation has been passed, the same innovation in subsequent projects is passed without further review. Including this additional evidence undermines the XM representative’s claim that the project should be passed without review and thus supports the committee member’s rebuttal.
Weakens: Choice A
XM’s latest project is nearly identical to a previous project by XM that had successfully passed the committee review process.
The XM representative claims that the costly and time-consuming review should be waived so that our latest project can be quickly passed and implemented. The federal committee member disagrees because doing what the representative suggests could mean the committee would also fail to observe innovations in geo-engineering that may need guidelines drafted for the safety of subsequent projects throughout the industry. To weaken the committee member’s argument, you need evidence that suggests that no such failure to observe innovations will occur in this case. If XM’s latest project is identical to a previous project by XM that had successfully passed the committee review process, as answer choice (A) states, then there are no innovations to consider. This weakens the federal committee member’s argument, and provides additional support for the XM representative’s request.
Insect Species X: Choice A, 450
Insect Species Y: Choice C, 565
First, note that, if the populations are to become equal in four years, at a 10% and a 15% rate of decrease, respectively, then the two populations are not currently equal. Additionally, the current population of Insect Species Y must be more than the current population of Insect Species X, in order for their totals to converge, at these independent rates of decrease, in four years. Therefore, the current population of Insect Species X cannot be 770, and the current population of Insect Species Y cannot be 450.
The problem requires working with two unknowns: the current population of Insect Species X and the current population of Insect Species Y. Therefore, Plug In The Answers to determine which will satisfy the conditions of the question. To approach the problem most efficiently, recognize that a 10% decrease is the same as taking 90% of the original number. Suppose that the current population of Insect Species X is 450. A 10% decrease from 450 is equivalent to 90% of 450, or (0.9)(450), which is 405. That’s the decrease for one year. To find the decrease for the next year, begin with the adjusted population and decrease from there: a 10% decrease from 405 is equivalent to (0.9)(405), which is 364.5. So, to find the decreased population after two years of 10% decreases from a starting population of 450 is equivalent to calculating (0.9)(0.9)(450) = 364.5. Similarly, to find the decreased population after four years of 10% decreases from a starting population of 450 is equivalent to calculating (0.9)(0.9)(0.9)(0.9)(450) = (0.6561)(450) = 295.245. So, to find the decreased population of Insect Species X after four years of yearly 10% decreases, calculate (0.6561)(current population X).
A 15% decrease is the same as taking 85% of the original number, so to find the decreased population of Insect Species Y after four years of yearly 15% decreases, calculate (0.85)(0.85)(0.85)(0.85)(current population Y), or approximately (0.522)(current population Y).
To determine which starting populations are equal (rounded to the nearest million) after four years, you are looking for values that satisfy the equation (0.6561)(current population X) = (0.522)(current population Y). Now you can simply calculate with each value provided to see what the future populations are:
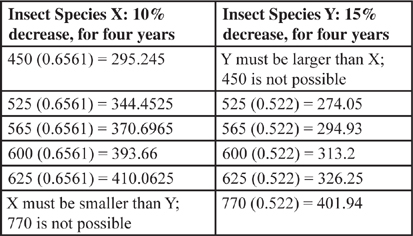
Rounded to the nearest million, the values that satisfy the equation (0.6561)(current population X) = (0.522)(current population Y) are 450 for the current population of Insect Species X and 565 for the current population of Insect Species Y, which both decrease to approximately 295 million, at their independent rates of decrease, after four years.
(A): No
Email #1 asked for the top rated shows among females aged 15–25 and Memo #1 states that Blonde Fury is the most watched program for that group. However, it is still possible that another group watches this show as much or more than do females aged 15–25.
(B): No
Careful. While this is certainly true in the real world, there is not enough information to make that inference here. The emails describe only two programs, thus you can only make inferences about those two.
(C): Yes
Blonde Fury has a ratio of female viewers aged 15–25 to advertising dollars of 45% of viewers to $70,000 or 45/70, which is 9/14, or about 0.643. Hart Attack has a ratio of 35% to $55K or 35/55, or 7/11, or about 0.636, which is less.
Choice D, 9.6
Email #2 states that “80% of the viewers who are females aged 15–25 for Hart Attack also watch Blonde Fury.” If there are 20 million females 15-25, and 35% watch Hart Attack, then 7 million females 15-25 watch Hart Attack. Since 80% of Hart Attack viewers who are females aged 15–25 also watch Blonde Fury, that’s 80% of 7 million, which is 5.6 million. If 45% of 20 million watch Blonde Fury, that’s 45% of 20 million = 9 million. Using the Group Equation, Total = Group 1 + Group 2 – Both + Neither, we get 20 = 7 + 9 – 5.6 + Neither. This gives Neither = 9.6 million. The answer is choice (D).
(A): Yes
In Email #1, the Marketing Director states that the company previously was able in increase revenues by buying advertisement. In stating that if the company increased its advertising expenditures, then we will once again increase our revenues, the Marketing Director assumes that this can work again.
(B): Yes
Memo #1 states that, since increased revenues followed increased advertising, increasing advertising will increase revenues. Therefore, it must be true that the Marketing Director thinks that some of the increased revenues were caused by the increased advertising, and thus assumes that advertising has some effect upon revenues.
(C): Yes
In Email #1, the Marketing Director states that the company previously had increased advertisement expenditures and now plans to increase the number of advertisements. This assumes that the effects are similar.
9-1. Supported
Sort the countries by population in 2010. There are five countries with populations above 150 million: China, India, United States, Indonesia, and Brazil. If China were to have the median foreign-born population, there would be two countries with a higher foreign-born population and two countries with a lower foreign born population. First, estimate China’s foreign-born population. According to the table 0.29% of China’s population of 1,399,725,000 is foreign-born. This is close to 0.3% of 1.4 billion. Multiply 0.003 by 1,400 million: China has 4.2 million foreign-born inhabitants. Now, estimate the foreign-born population of the other four countries. India’s foreign-born population is about 0.5% of 1.2 billion, or is 6 million, which is greater than China’s foreign born population. The foreign-born population of the United States is about 20% of 312 million, about 62 million. This is greater than China’s foreign-born population. Indonesia’s foreign-born population is less than 1% of about 238 million. 1% of 238 million is about 2 million. Therefore, Indonesia’s foreign-born population is less than 2 million and less than China’s. Brazil’s foreign-born population is less than 1% of about 190 million. Since 1% of 190 million is about 1.9 million, Brazil’s foreign-born population is less than 1.9 million. Therefore, Brazil’s foreign-born population is less than China’s. Since two of the countries have a higher foreign born population than China and two of the countries have a lower foreign-born population than China, China’s foreign born population is the median.
9-2. Unsupported
This might appear to be a reasonable conclusion, since 8 million is approximately the average of the population in 2010 and the projected population for 2050. However, there is no information in the table which allows you to assume a uniform population increase from 2010 to 2050. Therefore, this conclusion is unsupported.
9-3. Unsupported
Although Andorra has the highest percentage of its population that is foreign born, this does not mean it has the great number of immigrants. About 20% of Australia’s population of about 20 million is made up of immigrants. Therefore, Australia has about 4 million immigrants. Since this is greater than the entire population of Andorra, the statement is unsupported.
(A): True
The chart on the second tab lists two types of tables for DoxySource, and the first tab mentions the maximum number attending: 400. The cost of the food is (appetizer + entrée + dessert)(400) or ($2.00 + $6.25 + $3.40)(400) = ($11.65)(400) = $4,660.
If the less expensive tables (seating eight) are used, 50 tables are required at $15.50 each, for a total of $775. So, the cost of the tables ($775) is approximately 16.6% of the cost of the food ($4,660). However, if the more expensive tables are used, the table cost rises to $986, which is approximately 21% of the cost of the food ($4,660).
(B): True
The chart on the first tab shows that the punch fountain from BrightRight comes with 40 gallons of punch. To acquire the same amount from DoxySource, the Gala Coordinator would have to order six of the smaller fountains, providing seven gallons of punch each. Thus, the cost per gallon for the BrightRight fountain is $350÷40 or $8.75 per gallon. The cost per gallon for the DoxySource fountains is (6)($47)÷42 gallons=$6.71 per gallon. Since the question states percent less, you figure the percent decrease by calculating the difference over the original: 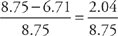 = 0.233, which is approximately 23%.
= 0.233, which is approximately 23%.
(C): True
The first tab states that the present budget is $6,000 and the maximum number of guests is 400. Assume the Gala Coordinator wants to use BrightRight, but to stay within the present budget. The costs are listed on the chart on the second tab. The least expensive food costs for BrightRight is The Classic Western BBQ option, which is $14.00 per person, so total food costs are (400)($14.00) = $5,600.00. Adding in the least expensive costs for the audio ($650) and the punch fountain ($350) brings the cost to $6,600. Lastly, calculate the least expensive table cost: 400 guests at eight guests per table requires 50 tables; (50)($20) = $1,000, and so the total cost is now $7,600, $1,600 over the current budget of $6,000. The percent over budget is  = 0.266 or approximately 27%.
= 0.266 or approximately 27%.
Choice C, $792.00
This question asks about the least possible cost for the tables, using DoxySource. In the chart on the second tab, there are two prices listed for DoxySource tables: $15.50 for a table that seats eight (less expensive), or $17.00 for a table that seats seven (more expensive). The lowest cost way to use at least one of each table is for the Gala Coordinator to use only one of the more expensive tables, and use the less expensive tables for the remaining guests.
Using one of the more expensive tables seats 7 guests, leaving 393 guests who need to be seated at the remaining less expensive tables. Calculate the number of tables needed:
393 ÷ 8= 49.125, meaning that 50 more tables are required, since you can’t have fractions of tables. So, there is one table at $17.00 and 50 tables at $15.50:$17.00 + (50)($15.50) = $792.00.
(A): Yes
Referring to the first email from the Gala Coordinator, the message states Also, I’d like to consider how to justify any over-budget costs from using BrightRight. The Gala Coordinator is considering how to justify any over-budget costs: therefore, she is willing to ask for a budgetary increase.
(B): Yes
Referring to the second tab, the Administrative Assistant mentions both more flexibility in the catering and more hands-on involvement on our end as factors to consider when weighing the benefits of one event planning service against another.
(C): No
On the first tab, the Gala Coordinator states We require: tables, audio, food, and a punch fountain or fountains, meaning that a punch fountain is required. Although she goes on to state a dessert fountain would be a lovely addition, this refers only to a dessert fountain; the punch fountains are necessary.
 ?
?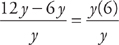 = 6, choice B
= 6, choice B or 6
or 6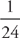

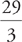
 or
or 
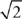

 of the entire trip. From this we can learn the entire distance of the trip by setting up the equation
of the entire trip. From this we can learn the entire distance of the trip by setting up the equation 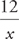 . The correct answer is C.
. The correct answer is C.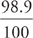 x=27,000,000.
x=27,000,000. , so the statement is true.
, so the statement is true.


 = –1.4.
= –1.4.
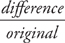 to compare the percent increases in popular vote, rounding to the nearest integer. You should get Bush:
to compare the percent increases in popular vote, rounding to the nearest integer. You should get Bush: 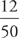 ; Nixon:
; Nixon: 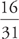 ; Reagan:
; Reagan:  ; Clinton:
; Clinton: 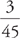 . Clinton’s percentage increase is less than (10%), far lower than the other three. So, of the two-term Presidents, Clinton does have the smallest percent increase in popular vote.
. Clinton’s percentage increase is less than (10%), far lower than the other three. So, of the two-term Presidents, Clinton does have the smallest percent increase in popular vote.
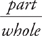 × 100. The part is the sum of the combined clocks produced on Monday and the clocks produced on Wednesday, which is 50 + 40 = 90. Now, you need the total number produced during the entire week. This is 50 + 75 + 40 + 55 + 30 = 250. Therefore, the percentage is
× 100. The part is the sum of the combined clocks produced on Monday and the clocks produced on Wednesday, which is 50 + 40 = 90. Now, you need the total number produced during the entire week. This is 50 + 75 + 40 + 55 + 30 = 250. Therefore, the percentage is 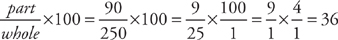
 ).
).
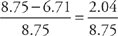 = 0.233, which is approximately 23%.
= 0.233, which is approximately 23%. = 0.266 or approximately 27%.
= 0.266 or approximately 27%.