An atom is composed of a central nucleus (which is itself composed of protons and neutrons) surrounded by a cloud of one or more electrons. The fact that an atom is held together as a single unit is due to the fact that protons and electrons have a special property: They carry electric charge, which gives rise to an attractive force between them.
Electric charge exists in two varieties, which are called positive and negative. By convention, we say that protons carry positive charge and electrons carry negative charge. (Neutrons are well-named: They’re neutral, because they have no electric charge.) The charge of a proton is +e, where e is called the elementary charge, and the charge of an electron is –e. Notice that the proton and the electron carry exactly the same amount of charge; the only difference in their charges is that one is positive and the other is negative.
In SI units, electric charge is measured in coulombs (abbreviated C), and the value of the elementary charge, e, is 1.6 × 10–19 C.
Elementary Charge
e = 1.6 × 10–19 C
When an atom (or any other object) contains the same number of electrons as protons, its total charge is zero because the individual positive and negative charges add up and cancel. So, when the number of electrons (#e) equals the number of protons (#p), the object is electrically neutral. We say that an object is charged when there’s an imbalance between the number of electrons and the number of protons. When an object has one or more extra electrons (#e > #p), the object is negatively charged, and when an object has a deficit of electrons (#e < #p), the object is positively charged. If a neutral atom has electrons removed or added, we say that it has been ionized, and the resulting electrically charged atom is called an ion. A positively charged ion is called a cation, and a negatively charged ion is called an anion. (An object can also become charged by gaining or losing protons, but these are usually locked up tight within the nuclei of the atoms. In virtually all cases, objects become charged by the transfer of electrons.)
Because an object can become charged only by losing or gaining electrons or protons, which can’t be “sliced” into smaller pieces with fractional amounts of charge, the charge on an object can only be a whole number of ±e’s; that is, charge is quantized. So, for any object, its charge is always equal to n(±e), where n is a whole number. To remind us that charge is quantized, electric charge is usually denoted by the letter q (or Q).
It is interesting to note that this quantization of charge applies to all fundamental particles either found in nature or created in the laboratory (e.g., muons, pions, etc.).
In chemistry, it’s common to talk about the charge of an atom in terms of whole numbers like +1 or –2, etc. For example, we say that the charge of the fluoride ion, F–, is –1, and the charge of the calcium ion, Ca+2, is +2. This is just a convenient way of saying that the charge of the fluoride ion is –1 elementary unit (in other words, –1e), and the charge of the calcium ion is +2 elementary units, +2e. When we want to find the electric force between ions, we will express their charges in the proper unit (coulombs), and say, for example, that the charge of the fluoride ion is –1e = –1.6 × 10–19 C and the charge of the calcium ion is +2e = +3.2 × 10–19 C.
Finally, total electric charge is always conserved; that is, the total amount of charge before any process must always be equal to the total amount of charge afterward.1
Example 9-1: When you pet a cat, you rub electrons off the cat’s fur, which are transferred to your hand. Assuming that you transfer 5 × 1010 electrons to your hand, what is the electric charge on your hand? What’s the charge on the cat?
Solution: Because each electron carries a charge of –e = –1.6 × 10–19 C, and you’ve gained 5 × 1010 of them, the charge on your hand will be
(5×1010)(-e) = (5×1010)(−1.6×10−19)=-8×10−9 C
Since the cat has lost 5 × 1010 electrons, the charge on the cat will be
(5×1010)(+e)=(5×1010)(−1.6×10−19)=+8×10−9 C
Notice that the net charge before and after petting the cat was zero; all you’ve done is transfer charge.
Example 9-2: How much positive charge is contained in 1 mole of carbon atoms? How much negative charge? What is the total charge?
Solution: Every atom of carbon contains 6 protons, so the amount of positive charge in one carbon atom is q+ = +6e. Therefore, if NA denotes Avogadro’s number, the total amount of positive charge in 1 mole of carbon atoms is
Q+ = NA × q+ = NA × (+6e) = (6.02×1023)×(6)(+1.6×10−19 C)= +6×105 C
Because every neutral carbon atom also contains 6 electrons, the amount of negative charge in a carbon atom is q− = −6(−e) = −6e = −q+ so the total amount of negative charge in 1 mole of carbon atoms is Q− = NA × q− = −Q+ ≈ −6×105C. The total charge on the carbon atoms, Q+ + Q−, is zero.
If two charged particles are a distance r apart,
then the electric force between them, FE, is directed along the line joining them. The magnitude of this force is proportional to the charges (q1 and q2) and inversely proportional to r2, as given by
Coulomb’s Law
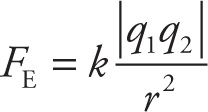
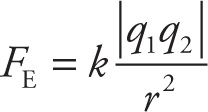
The proportionality constant is k, and in general, its value depends on the material between the particles. However, in the usual case where the particles are separated by empty space (or by air, for all practical purposes), the proportionality constant is denoted by k0 and called Coulomb’s constant. This is a fundamental constant of nature (equal in magnitude, by definition, to 10–7 times the speed of light squared), and its value is k0 = 9 × 109 N.m2/C2:
This is the value of k you should use unless you’re specifically given another value (which would happen only if the charges were embedded in some insulating material that weakens the electric force).
The absolute value sign in the formula gives the magnitude of the force, whether repulsive or attractive. If direction (e.g., + or –) needs to be assigned, it should be done based on the fact that like charges (two positives or two negatives) repel each other, and opposite charges (one positive and one negative) attract. Note that the two electric forces in each of the following diagrams form an action–reaction pair.
Example 9-3: Two charges, q1 = −2 × 10−6C and q2 = +5 × 10−6C, are separated by a distance of 10 cm. Describe the electric force between these particles.
Solution: Using Coulomb’s law, we find that
Since one charge is positive and one is negative, the force is attractive, and each charge feels a 9 N force toward the other.
Example 9-4: A coulomb is a lot of charge. To get some idea just how much, imagine that we had two objects, each with a charge of 1 C, separated by a distance of 1 m. What would be the electric force between them?
Solution: Using Coulomb’s law, we’d find that
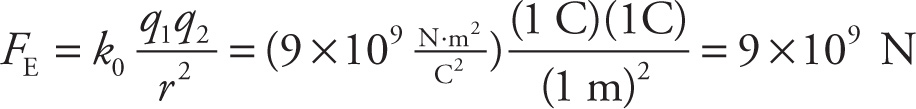
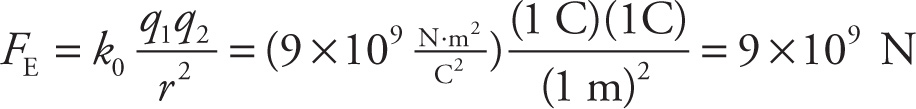
To write this answer in terms of a more familiar unit, let’s use the fact that 1 pound (1 lb) is about 4.5 N, and 1 ton is 2000 lb:
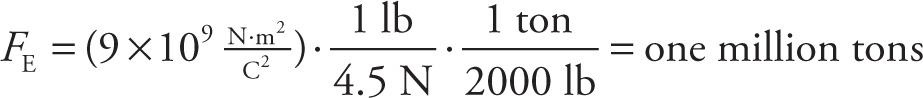
That’s equivalent to the weight of about 2500 Boeing 747s! It’s now easy to understand why most real-life situations deal with charges that are very tiny fractions of a coulomb; the microcoulomb (1 µC =10–6 C) and the nanocoulomb (1 nC =10–9 C) are more common “practical” units of charge.
Example 9-5: Consider a charge, +q, initially at rest near another charge, –Q. How would the magnitude of the electric force on +q change if –Q were moved away, doubling its distance from +q?
Solution: Coulomb’s law is an inverse-square law, FE ∝ 1/r2, so if r increases by a factor of 2, then FE will decrease by a factor of 4 (because 22 = 4).
Example 9-6: Consider two plastic spheres, 1 meter apart: a little sphere with a mass of 1 kg and an electric charge of +1 nC, and a big sphere with a mass of 11 kg and an electric charge of +11 µC.
a) Find the electric force and the gravitational force between these spheres. Which force is stronger?
b) If the big sphere is fixed in position, and the little sphere is free to move, describe the resulting motion of the little sphere if it’s released from rest.
Solution:
a) Using Coulomb’s law, we find that the electric force between the spheres is
Using Newton’s law of gravitation, the gravitational force between them is
Which force is stronger? It’s no contest: The electric force is much stronger than the gravitational force. So, even though the spheres experience an attraction due to gravity, it is many orders of magnitude weaker than their electrical repulsion and can therefore be ignored.
b) The net force on the little sphere is essentially equal to the electrical repulsion it feels from the big sphere (since the gravitational force is so much smaller, it can be ignored). Therefore, the initial acceleration of the little sphere is
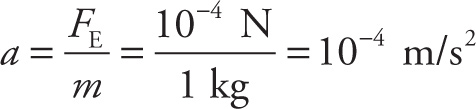
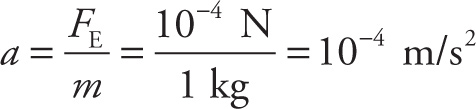
directed away from the big sphere. Notice that as the little sphere moves away, its acceleration does not remain constant. Because the electric force is inversely proportional to the square of the distance between the charges, as the little sphere moves away, the repulsive force it feels weakens, so its acceleration decreases. Therefore, the little sphere moves directly away from the big sphere with decreasing acceleration.
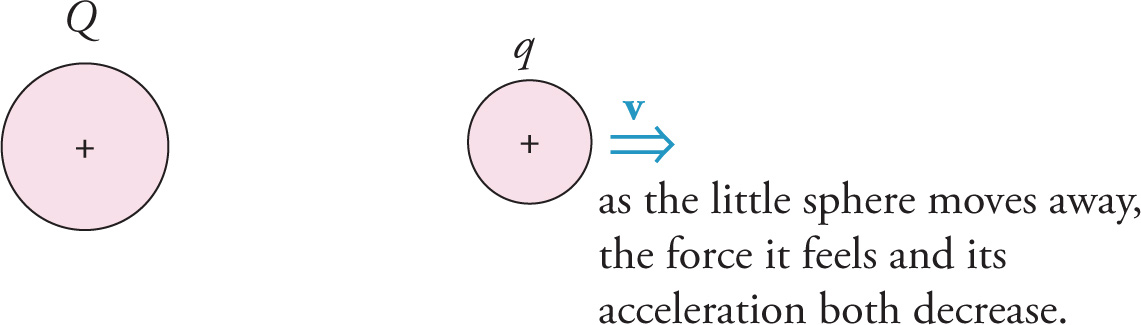
Nevertheless, because the acceleration of the little sphere always points in the same direction (namely, away from the big sphere), the speed of the little sphere is always increasing, although the rate of increase of speed gets smaller as the little sphere gets farther away.
Coulomb’s law tells us how to calculate the force that one charge exerts on another one. What if two (or more) charges affect a third one? For example, what is the electric force on q3 in the following figure?
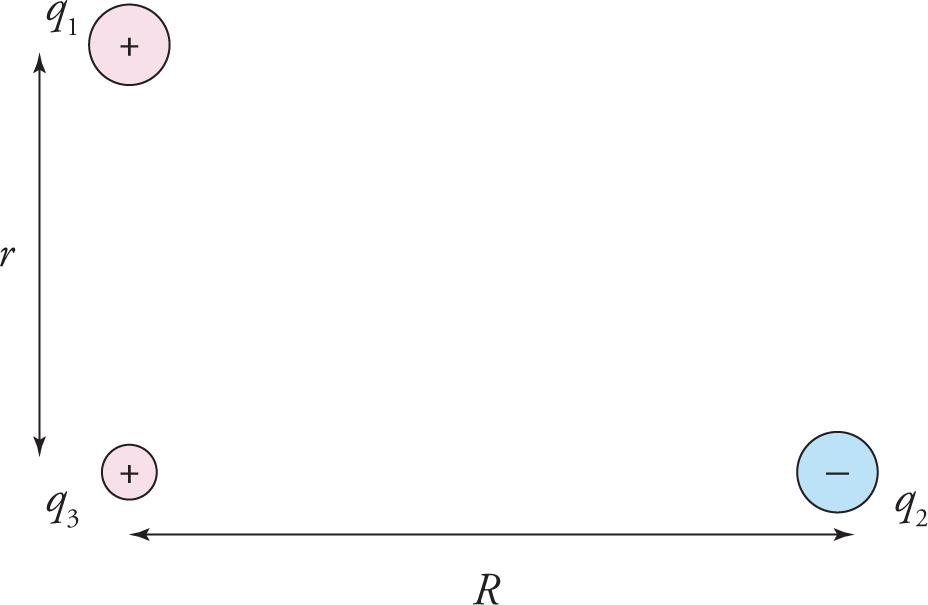
Here’s the answer: If F1-on-3 is the force that q1 alone exerts on q3(ignoring the presence of q2) and if F2-on-3 is the force that q2 alone exerts on q3 (ignoring the presence of q1), then the total force that q3 feels is simply the vector sum F1-on-3 + F2-on-3. The fact that we can calculate the effect of several charges by considering them individually and then just adding the resulting forces is known as the principle of superposition. (This important property will also be used when we study electric field vectors, electric potential, magnetic fields, and magnetic forces.)
The Principle of Superposition
The net electric force on a charge (q) due to a collection of other charges (Q’s)
is equal to
the sum of the individual forces that each of the Q’s alone exerts on q.
Example 9-7: In the figure above, assume that q1 = 2 C, q2 = −8 C, and q3 = 1 nC. If r = 1 m and R = 2 m, which one of the following vectors best illustrates the direction of the net electric force on q3?
Solution: The individual forces F1-on-3 and F2-on-3 are shown in the figure below. Adding these vectors gives Fon 3, which points down to the right, so the answer is C.
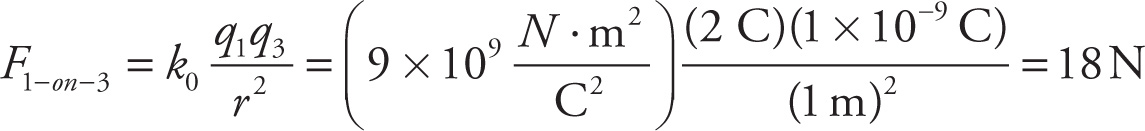
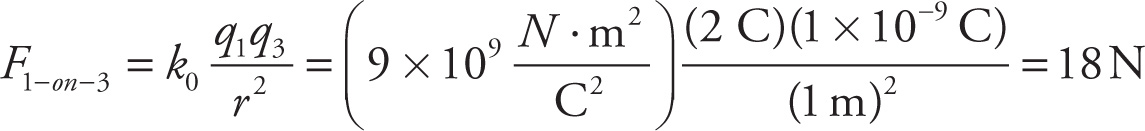
(repulsive; away from q1)
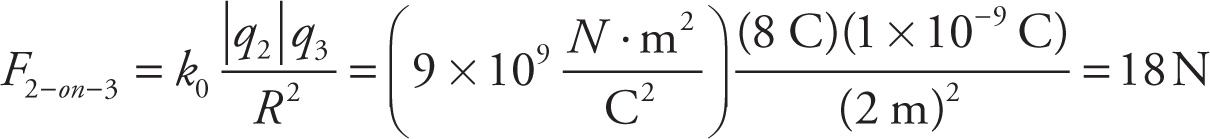
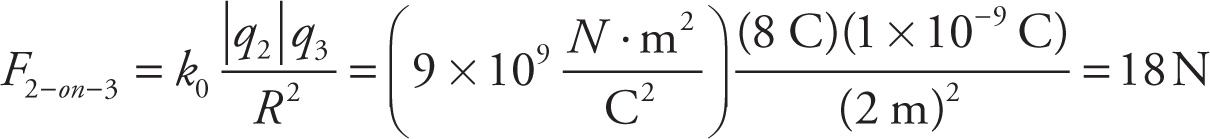
(attractive; toward q2)
If the question had asked for the magnitude of the net electric force on q3, then we’d use the Pythagorean theorem to find the length of the vector Fon 3. The vector Fon 3 is the hypotenuse of the right triangle whose legs are F1-on-3 and F2-on-3, so the magnitude of Fon 3 is found like this:
(Fon 3)2 = F1-on-3)2 + F2-on-3)2
= 182 + 182
= (182)(2)
∴ Fon 3 = 18
≈ 25N
Example 9-8: In the figure below, assume that q1 = 1C, q2 = −1nC, and q3 = 8C. If q4 is a negative charge, what must its value be in order for the net electric force on q2 to be zero?
Solution: The individual forces F1-on-2, F3-on-2, and F4-on-2 are shown in the figure below. Notice that F1-on-2 and F4-on-2 point to the left, while F3-on-2 points to the right.
If we let q4 = xC, then the magnitudes of the individual forces on q2 are
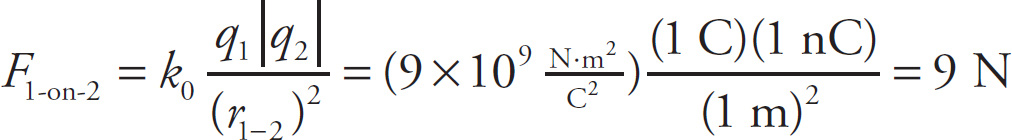
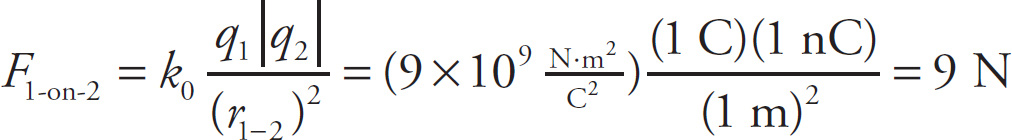
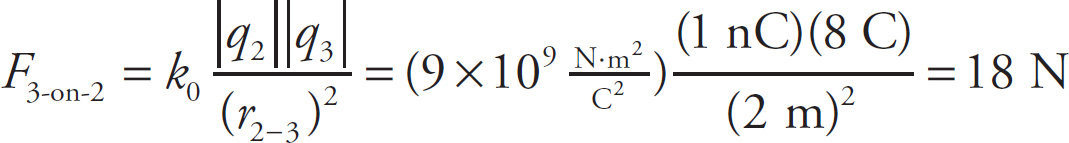
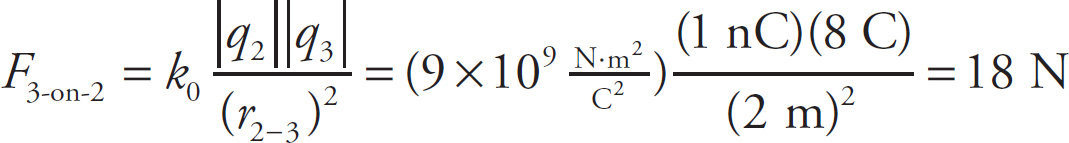
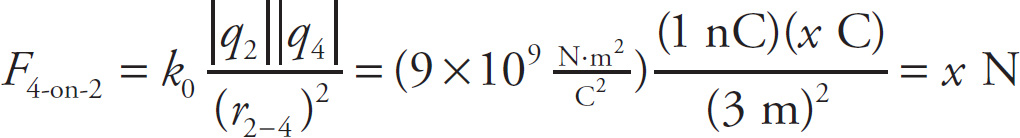
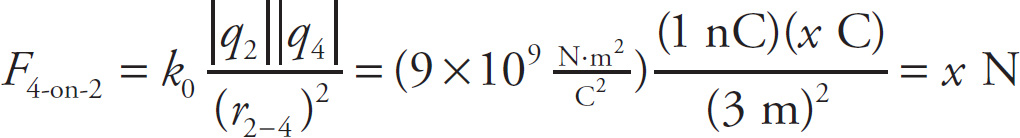
In order for the net electric force on q2 to be zero, the sum of the magnitudes of F1-on-2 and F4-on-2 must be equal to the magnitude of F3-on-2. That is, 9N + xN =18N so x = 9 so. Therefore, q4 = −xC = −9C.
There are several advantages to regarding electrical interactions in a slightly different way from the simple “charge Q exerts a force on charge q” mode of thinking. In this more sophisticated interpretation, the very existence of a charge (or a more general distribution of charge) alters the space around it, creating what we call an electric field in its vicinity. If a second charge happens to be there or to roam by, it will feel the effect of the field created by the original charge. That is, we think of the electric force on a second charge q as exerted by the field, rather than directly by the original charge(s). Qualitatively, we can represent electrical interactions as follows:
The charge(s) creating the electric field is/are called the source charge(s); they’re the source of the electric field. You may like to think of a source charge as a spider and its electric field as the spider’s web. After a spider creates a web, when a small insect roams by, it is the web that ensnares the unfortunate bug, not the spider directly.
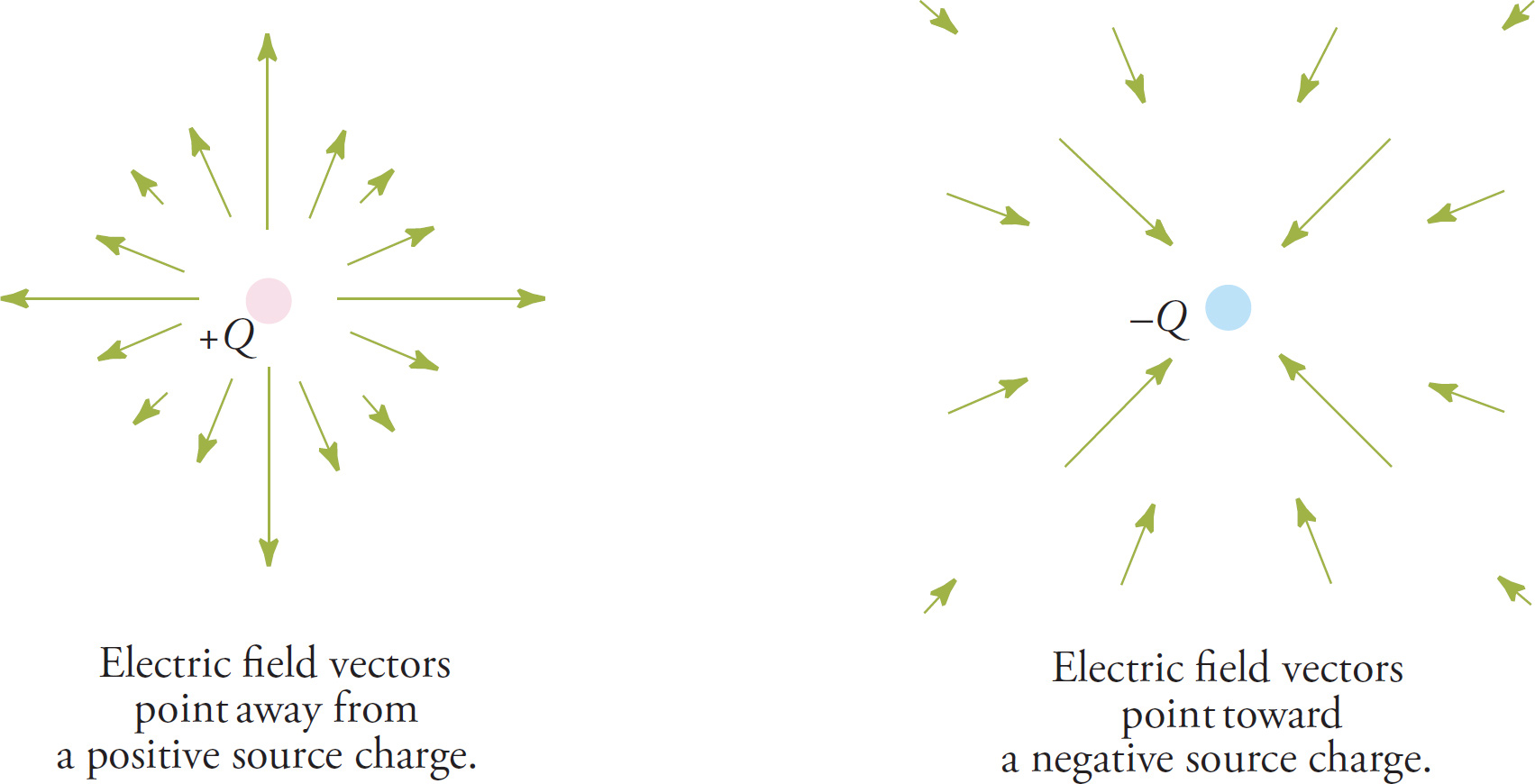
The figure on the right above illustrates one way to picture an electric field, but a few words of explanation are needed. First: An electric field is a vector field, which means that at each point in space surrounding the source charge, we associate a specific vector. The length of this vector will tell us the magnitude, or strength, of the field at that point, and the direction of the vector will tell us the direction of the resulting electric force that a positive test charge would feel if it were placed at that point. That’s the convention: Although the charge that finds itself in an electric field can of course be positive or negative, for purposes of illustrating the field, we always think of a positive test charge. Because of this convention, electric field vectors always point away from positive source charges and toward negative ones. Also, the closer we are to the source charge, the stronger the resulting electric force a test charge would feel (because Coulomb’s law is an inverse-square law). So, we expect the electric field vectors to be long at points close to the source charge and shorter at points farther away. The following figures illustrate the electric field due to a positive source charge and the electric field due to a negative source charge.
We can use Coulomb’s law to find a formula for the strength of the electric field due to a point charge. Remember that a source charge creates an electric field whether or not there’s another charge in the field to feel it. It takes two charges to create an electric force, but it takes only one (the source charge) to create an electric field. So, let’s imagine we have a single source charge, Q, and another charge, q, at a distance r from Q.
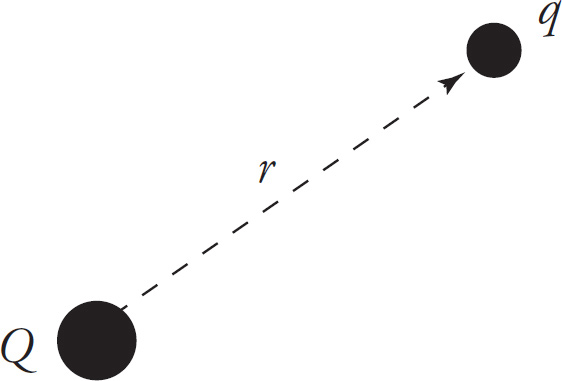
The force by Q, on the charge q, is, by Coulomb’s law,
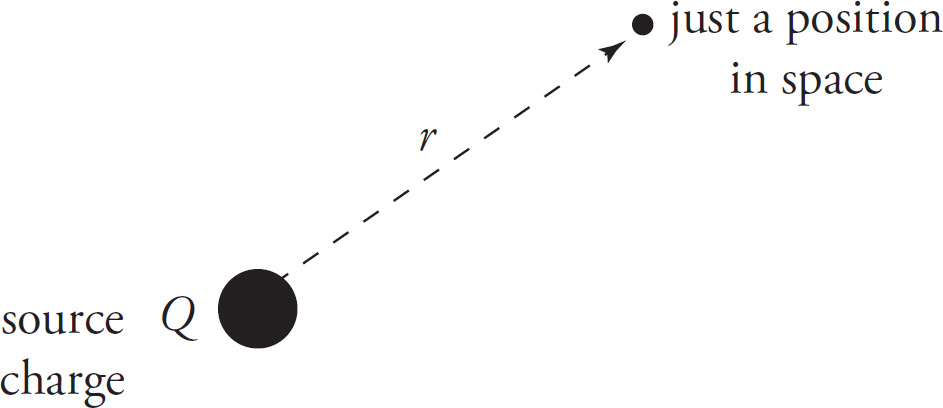
Now we ask, “What if q weren’t there? Do we still have something?” The answer is yes, we have the electric field created by the source charge, Q. “So, if q weren’t there, what if we removed q from the formula for the force exerted on it by Q? Would we still have something?” The answer is yes, we’d have the formula for the electric field, E, created by the single source charge Q.
In the formula for the force by Q on q, the variable r represents the distance from Q to q. However, if q is not there, what does r mean now? Answer: It’s simply the distance from Q to the point in space where we want to know the electric field vector.
Example 9-9: Let Q = +4 nC be a charge that is fixed in position at the origin of an x-y coordinate system. What is the magnitude and direction of the electric field at the point (10 cm, 0)? At the point (–20 cm, 0)?
Solution: In the figure below, the point A is (10 cm, 0), which is 10 cm directly to the right of Q, and B is the point (–20 cm, 0), which is 20 cm directly to the left of Q.
The electric field at point A is
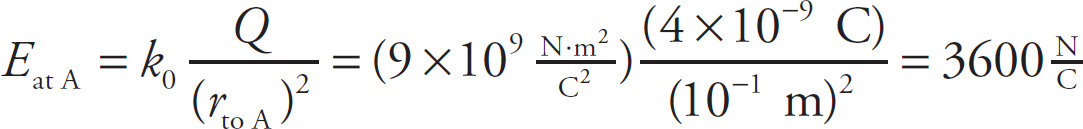
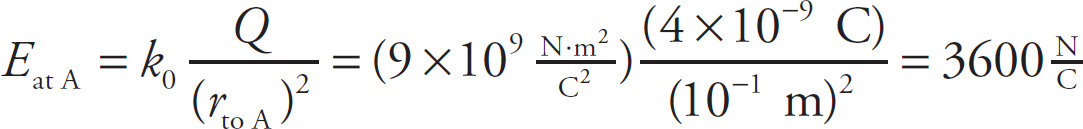
Since Q is positive, this means the electric field vector, EAT A, points away from the source charge. Therefore, EAT A points in the positive x direction, which is usually written as the direction i. So, if we wanted to write the complete electric field vector at point A, we’d write EAT A = (3600N/C)i.
The electric field at point B is
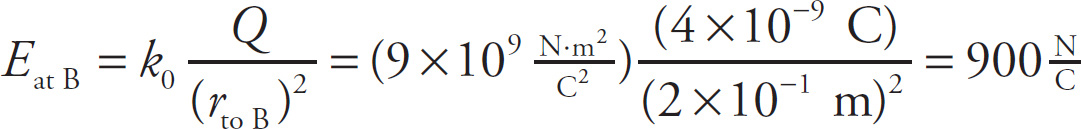
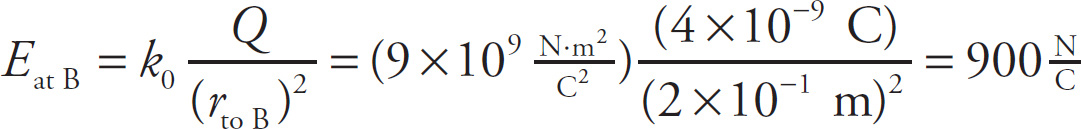
Once again, Eat B points away from the source charge. Therefore, Eat B points in the negative x direction, which is usually written as the direction −i. So, if we wanted to write the complete electric field vector at point B, we’d write Eat B = (900 N/C)(−i) or−(900 N/C)i.
Notice from the formula E = k |Q| /r2 that the electric field obeys an inverse-square law, like the electric force. So the strength of an electric field from a single source charge decreases as we get farther from the source; in particular, E 
1/r2. Also, for a given source charge Q, the electric field strength depends only on r, the distance from Q. So at every point on a circle (or more generally a sphere) of radius r centered on the source charge, the electric field strength is the same. In the electric field vector diagram below on the left, all the field vectors at the points on the smaller dashed circle have the same length, indicating that the electric field magnitude is the same at all points on this circle. Similarly, all the field vectors at the points on the larger dashed circle have the same length, indicating that the electric field magnitude is the same at all points on this circle. (Note that the field vectors at the points on the larger circle are shorter than those at the points on the smaller circle.) However, notice that the magnitude may be the same at every point on each circle (because they’re all the same distance r from the source charge) but the directions of the electric field vectors are all different on each circle. Therefore, we’re forced to say that the electric field isn’t the same at every point a distance r from Q because the directions are all different.
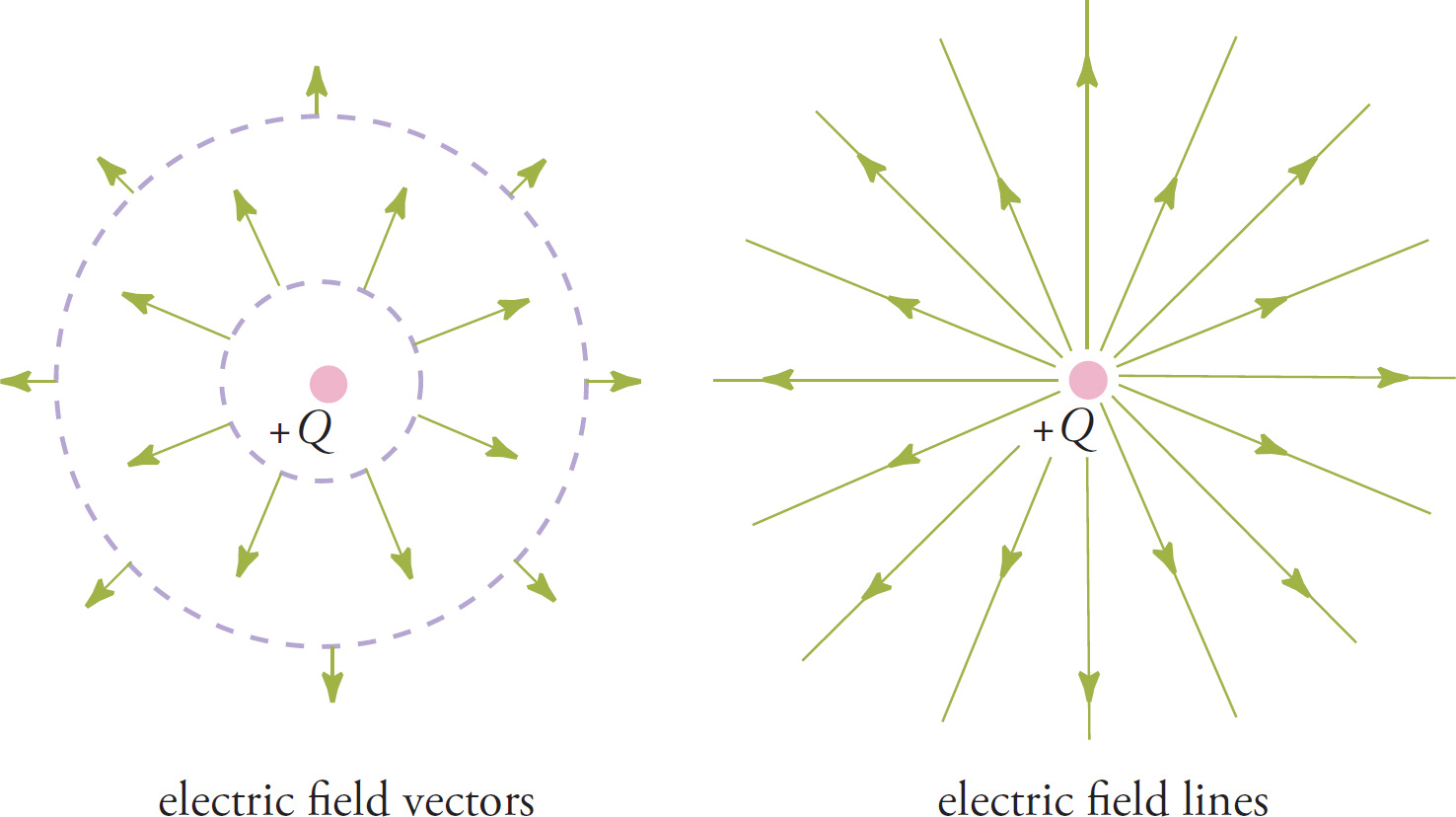
The diagram on the left above and the two given earlier for the electric field produced by a positive source charge and by a negative source charge show the field represented by individual vectors. However, this is not the easiest way to draw an electric field.
Instead of drawing a bunch of separate vectors, we instead draw lines through them, like in the diagram on the right above. This drawing depicts the electric field using field lines. The direction of the field is indicated as usual; remember that, by convention, the electric field points away from positive source charges and toward negative ones and indicates the direction of the electric force that a positive test charge would feel if it were placed in the field.
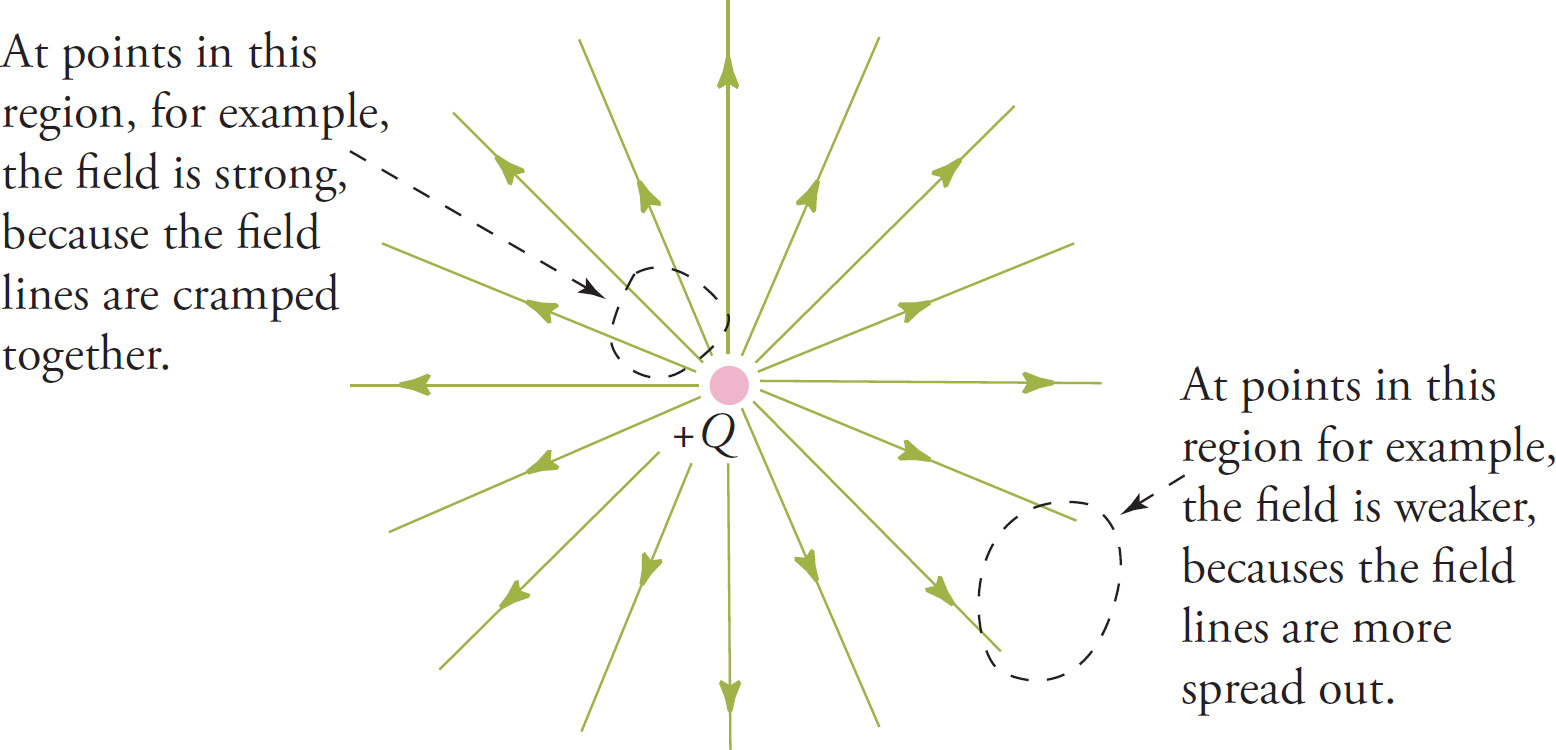
Now that we’ve eliminated the separate vectors, it seems as though we’ve lost some information, namely, where the field is strong and where it’s weak because we got this information from the lengths of the individual vectors. (Where the vectors were long, the field was strong, and where the vectors were shorter, the field was weaker.) However, we can still get a general idea of where the field is strong and where it’s weak by looking at the density of the field lines: Where the field lines are cramped close together, the field is stronger; where the field lines are more spread out, the field is weaker.
Now, let’s imagine that we have a source charge Q creating an electric field, and another charge, q, roams in to the field. What force will q feel? We want to find an equation for the force on q due to the electric field. Recall the formulas above: Fon q = k|Qq|/r2 and Eby Q = k|Q|/r2. What would we need to do to E to get F? Just multiply it by q! That is, Fon q = |q|Eby q. It turns out that this very important formula works not just for the electric field created by a single source charge; it works for any electric field:
Electric Force and Field
Fon q = qE
Note that the absolute value symbol is useful when solving for the magnitude of force and electric field. The vector equation, FE = qE, contains directional information and therefore does not need absolute values. Notice also from this formula that E = F/|q|, so the units of E are N/C, which you saw in Example 7-9. The equation E = F/q also gives us the definition of the electric field: It’s the force per unit charge.
Finally, before we get to some more examples, realize that we’ve had two important (boxed) formulas in this section on the electric field: E = k|Q|/r2 and F = qE. In the first formula, Q is the charge that makes the field, while in the second formula, q is the charge that feels the field.
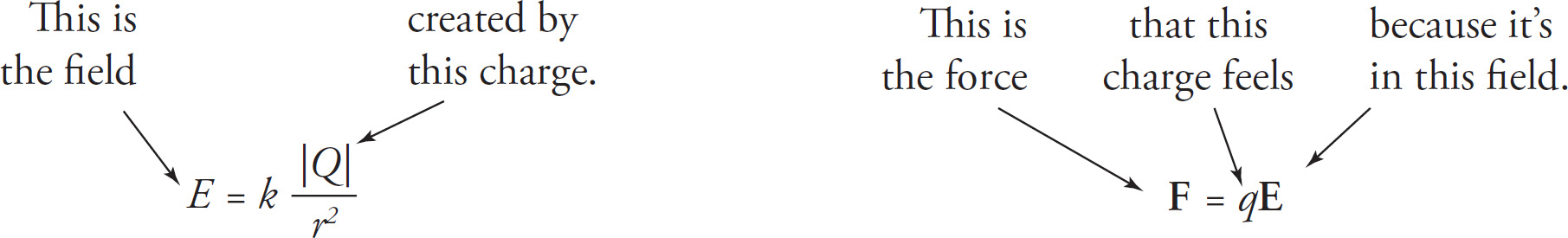
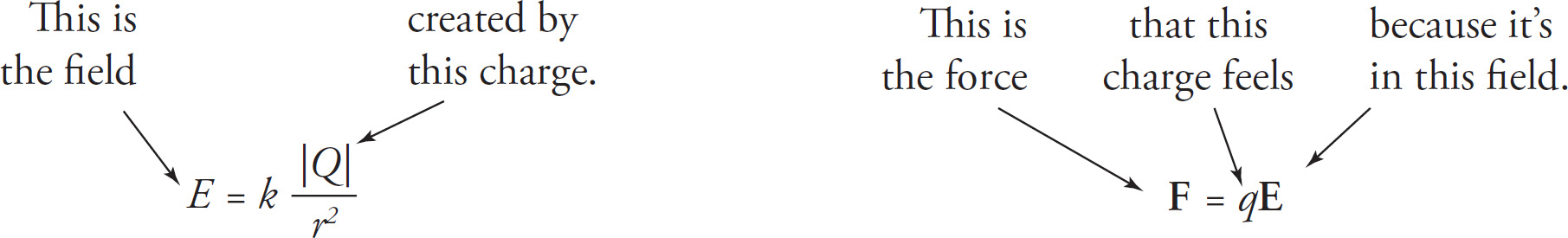
Example 9-10: The magnitude of the electric field at a distance r from a source charge +Q is equal to E. What will be the magnitude of the electric field at a distance 4r from a source charge +2Q?
Solution: The first sentence tells us that kQ / r2 = E. Now, if we change Q to 2Q and r to 4r, we find that E decreases by a factor of 8, because
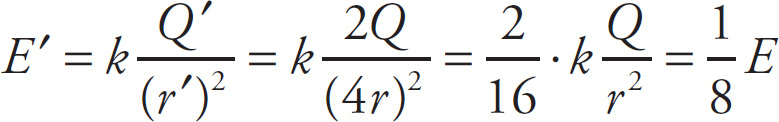
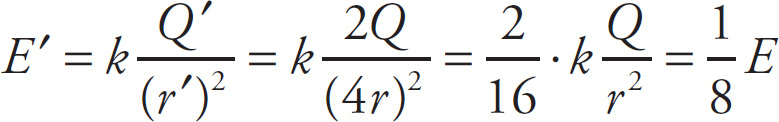
Example 9-11: A particle with charge q = 2 µC is placed at a point where the electric field has magnitude 4 ×104 N/C. What will be the strength of the electric force on the particle?
Solution: From the equation Fon q =qE, we find that
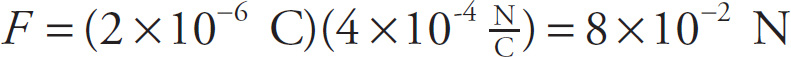
Notice that we didn’t need to know what created the field. If E is given, and the question asks for the force that some charge q feels in this field, all we have to do is multiply, F = qE, and we’re done.
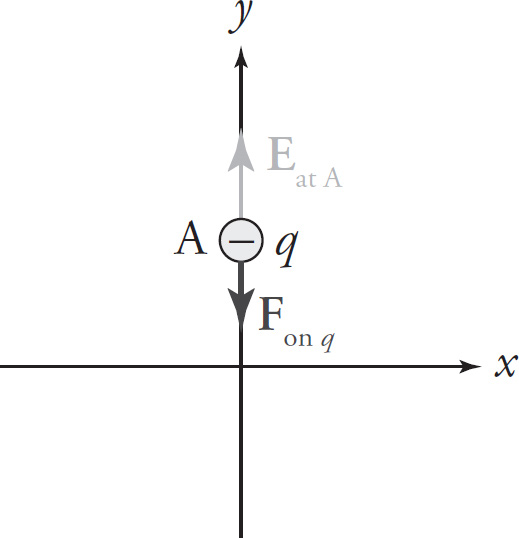
Example 9-12: In the diagram on the left below, the electric field at Point A points in the positive y direction and has magnitude 5 × 106 N/C. (The source charge is not shown.) If a particle with charge q = −3 nC is placed at point A, what will be the electric force on the particle?
Solution: Eat A points in the positive y direction, which is usually written as the direction j, so Eat A = (5 × 106 N/C)j. The equation Fon q = qE then gives us
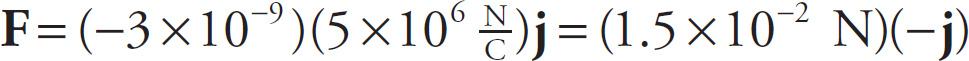
That is, the force will have magnitude 1.2 × 10−2N and point in the negative y direction (−j). Notice that whenever q is negative, the force Fon q will always point in the direction opposite to the electric field.
Example 9-13: A particle of mass m and charge q is placed at a point where the electric field is E. If the particle is released from rest, find its initial acceleration, a.
Solution: The acceleration of the particle is the force it feels divided by its mass: a = F/m. Because F = qE, we get
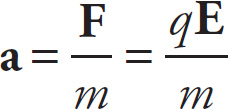
Notice that if q is negative, then F (and, consequently, a) will be directed opposite to the electric field E. Also, the question asked only for the initial acceleration, because once the particle starts moving, it will most likely move through locations where the electric field is different (in magnitude or direction or both), so the force on the particle will change; and if the force on the particle changes, so will the acceleration.
If a region contains a uniform electric field (i.e., same magnitude and direction at all points within the region), then the electrostatic force and the particle’s acceleration will likewise be uniform. The Big 5 kinematics equations can therefore be used to solve for final velocity, time, etc. In addition, the formula W = Fd cosθ can also be used to calculate the work done by or against the electrostatic force to move a charge from one position to another. A large conducting plate that is charged (or a parallel plate capacitor, as detailed in the next chapter) creates an electric field that is approximately uniform.
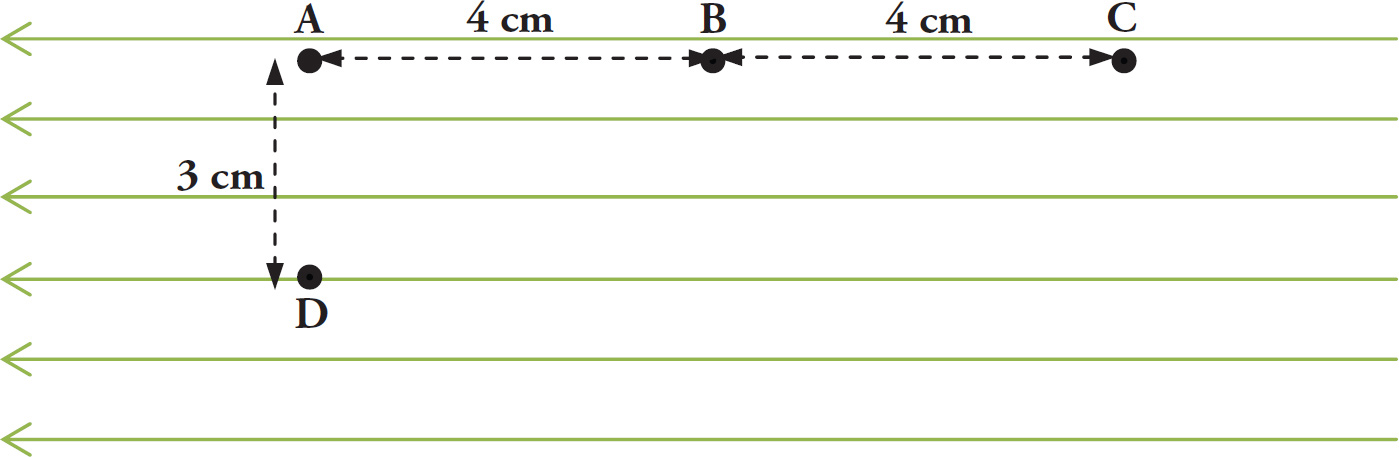
Example 9-14: A uniform electric field of strength 4 × 106 N/C points to the left as shown in the figure on the next page. A particle with charge q = –20 nC and mass m = 10 g is initially placed at point B.
a) If the particle is released from rest, toward which point will it move and how fast will it be traveling when it arrives?
b) If the particle is again placed at point B and is now moved to point D, how much work is done “by the field”? (Note: In reality, forces do work, not fields; work done “by the field” is a commonly used expression.)
Solution:
a) Negatively charged particles feel a force opposite the direction of the electric field, therefore the particle will move to point C. To find the final speed, the acceleration must first be calculated using Newton’s Second Law:
|q|E = ma
a = |q|E / m = (20 × 10–9 C)(4 × 106 N/C) / (10 × 10–3 kg) = 8 m/s2
Using Big 5 #5,
v2 = v02 + 2ad = 0 + 2(8 m/s2)(0.04 m) = 0.64 m2/s2
v is therefore 0.8 m/s.
b) W = Fd cosθ = |q|Ed cosθ. Since q > 90° the work done by the field is negative. ΔBAD is a 3-4-5 triangle, so d = 5 cm. More importantly, cosθ = – 4/5. Therefore,
W = (20 × 10–9 C)(4 × 106 N/C)(0.05 m)(– 4/5) = – 3.2 × 10–3 J
Notice that the work done by the field from point B to point D is the same as if the particle were moved from point B to point A. The field will only do work (whether positive or negative) if there is displacement in the direction of the electric field or opposite the field. This is similar to gravity, which only does work if there is displacement up or down. And as with gravity, the work done by the field is also path independent. This will be discussed in more depth later in the chapter.
The pictures we’ve drawn so far have been of electric fields created by a single source charge. However, we can also have two or more charges whose electric fields overlap, creating one combined field. For example, let’s consider an electric dipole, which, by definition, is a pair of equal but opposite charges:
What if we regarded both of them as source charges; how would we find the electric field that they create together? By using the principle of superposition. If we wanted to find the electric field vector at, say, the point P in the diagram below,
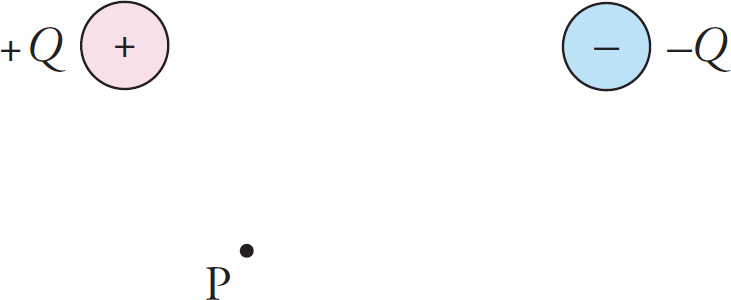
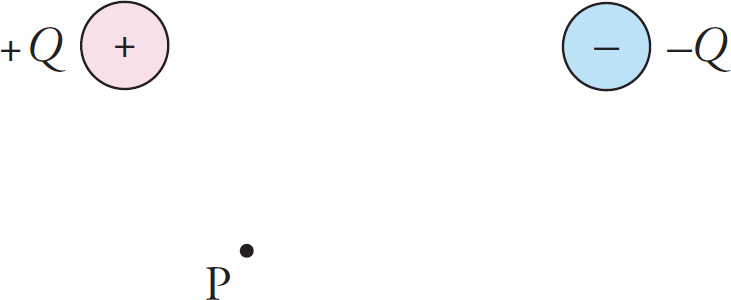
we’d first find the electric field vector, E+, at P due to the +Q charge alone (ignoring the presence of the –Q charge) and then we’d find the electric field vector, E–, at P due to the –Q charge alone (ignoring the presence of the +Q charge). The net electric field vector at P will then be the vector sum, E+ + E–.
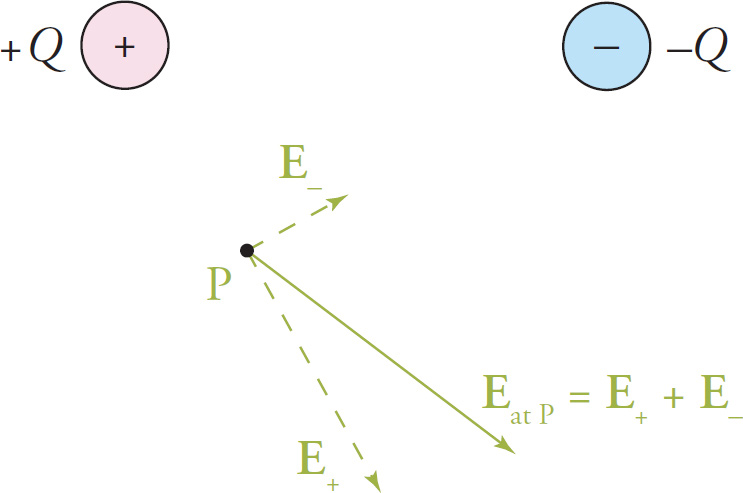
We can do this for as many points as we like and obtain a diagram of the electric field as a collection of vectors. The diagram in terms of electric field lines would look like this:
Notice that between the charges, where the field lines are dense, the field is strong; and as we move away from the charges, the field lines get more spread out, indicating that the field gets weaker.
Example 9-15: An electric dipole consists of two charges, +Q and –Q, where Q = 4 µC, separated by a distance of d = 20 cm. Find the electric field at the point midway between the charges.
Solution: The electric field at P due to the positive charge is 
, pointing away from +Q, and the electric field at P due to the negative charge is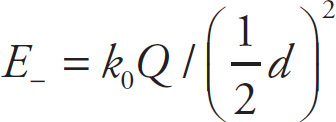 
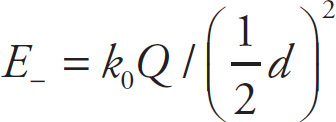, pointing toward –Q (which is in the same direction as E+).
By the principle of superposition, the net electric field at P is the sum: E = E+ + E−. The magnitude of 
:
The direction of Eat P is away from +Q and toward –Q:
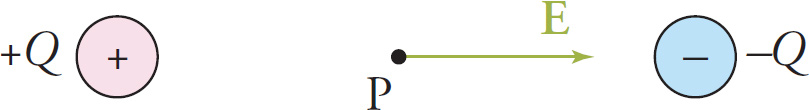
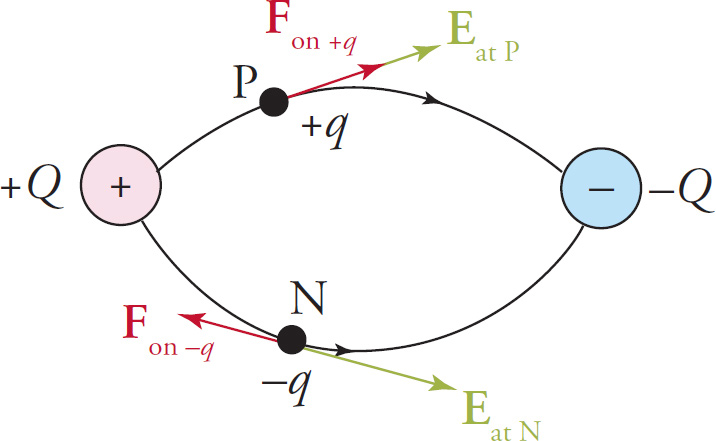
Example 9-16: A positive charge, +q, is placed at the point labeled P in the field of the dipole shown below. Describe the direction of the resulting electric force on the charge. Do the same for a negative charge, –q, placed at the point labeled N.
Solution: The electric field vector at any point is always tangent to the field line passing through that point and its direction is the same as that of the field line. Since F = qE, the force on a positive charge is in the same direction as E and the force on a negative charge is in the opposite direction from E. The directions of Fon q and Fon −q are shown in the figure below.
Most everyday materials can be classified into one of two major categories: conductors or insulators (also known as dielectrics). A material is a conductor if it contains charges that are free to roam throughout the material. Metals are the classic and most important conductors. In a metal, one or more valence electrons per atom are not strongly bound to any particular atom and are thus free to roam. If a metal is placed in an electric field, these free charges (called conduction electrons) will move in response to the field. Another example of a conductor would be a solution that contains lots of dissolved ions (such as saltwater).
Here’s an interesting property of conductors: Imagine that we place a whole bunch of electrons on a piece of metal. It’s now negatively charged. Since electrons repel each other, they’ll want to get as far away from each other as possible. As a result, all this excess charge moves (rapidly) to the surface. Any net charge on a conductor resides on its surface. Since there’s no excess charge within the body of the conductor, there cannot be an electrostatic field inside a conductor. You can block out external electric fields simply by surrounding yourself with metal; the free charges in the metal will move to the surface to shield the interior and keep E = 0 inside.
By contrast, an insulator (dielectric) is a material that doesn’t have free charges. Electrons are tightly bound to their atoms and thus are not free to roam throughout the material. Common insulators include rubber, glass, wood, paper, and plastic.
Now, let’s study this situation: Start with a neutral metal sphere and bring a charge (a positive charge) Q nearby without touching the original metal sphere. What will happen? The positive charge will attract free electrons in the metal, leaving the far side of the sphere positively charged. Since the negative charge is closer to Q than the positive charge, there’ll be a net attraction between Q and the sphere. So, even though the sphere as a whole is electrically neutral, the separation of charge induced by the presence of Q will create a force of electrical attraction between them.
Now what if the sphere was made of glass (an insulator)? Although there aren’t free electrons that can move to the near side of the sphere, the atoms that make up the sphere will become polarized. That is, their electrons will feel a tug toward Q, causing the atoms to develop a partial negative charge pointing toward Q (and a partial positive charge pointing away from Q). The effect isn’t as dramatic as the mass movement of free electrons in the case of a metal sphere, but the polarization is still enough to cause an electrical attraction between the sphere and Q. For example, if you comb your hair, the comb will pick up extra electrons, making it negatively charged. If you place this electric field source near little bits of paper, the paper will become polarized and will then be attracted to the comb2
So far, we have viewed the electric field due to a source charge (or a more general charge distribution, such as a pair of charges or a plate) as a collection of vectors. This point of view allowed us to answer questions about other vector quantities, like force and acceleration. The basic equations for finding these quantities were F = qE and a = F/m = qE/m.
What if we wanted to answer questions about scalar quantities, like energy, work, or speed? It turns out that the easiest way to answer these questions is to view the electric field in a different way, in terms of a scalar field. First, it is useful to review a few facts about gravitational potential energy. As you’ll recall, if an object of mass m is dropped from rest from a height h and hits the ground, Wby grav = +mgh while ΔPEgrav = –mgh. Similarly, if the object is lifted from the ground to a height h, Wby grav = –mgh, Wagainst grav = +mgh and ΔPEgrav = +mgh.
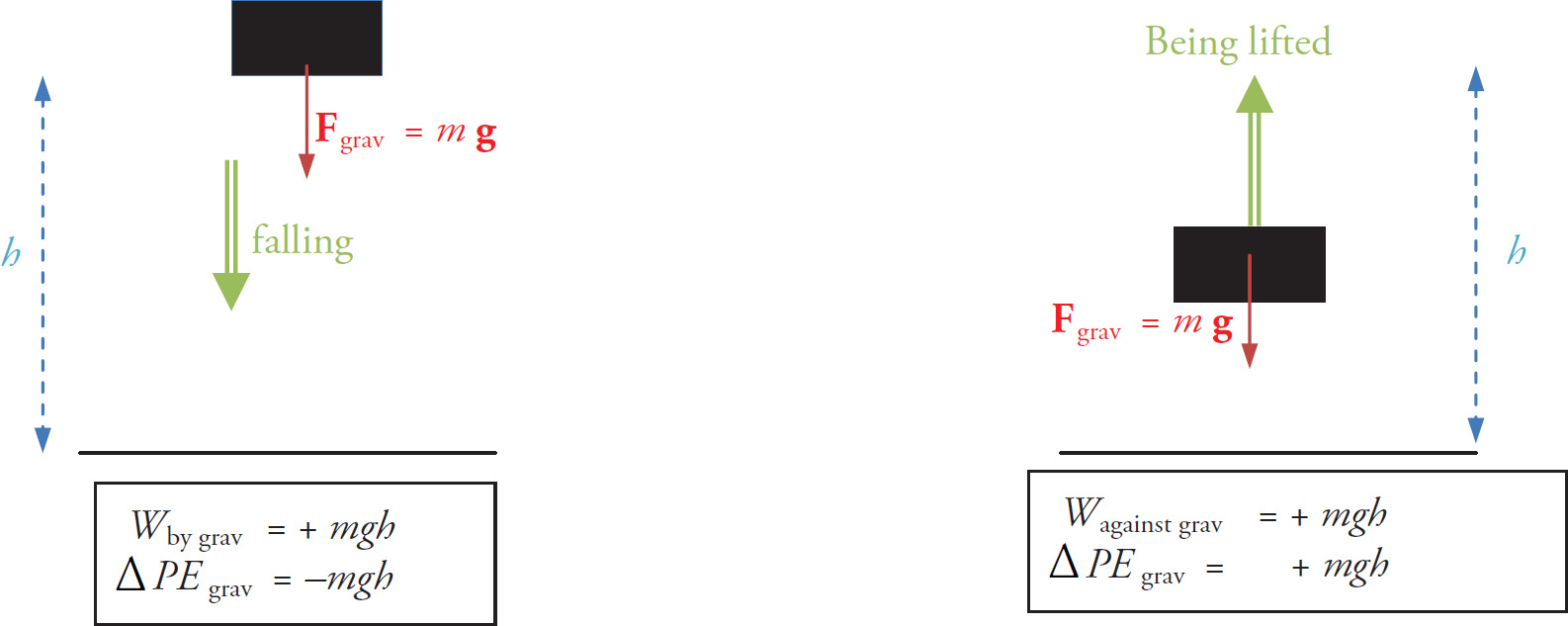
If an object moves “with nature” (i.e., in the direction that gravity points), then potential energy decreases. If an object moves “against nature”, then potential energy increases. This is an important fact to remember going forward, as it will be applied to electric potential energy as well.
In the example below, a positively charged particle is fixed in place and a negatively charged particle is moved from point A to point B.
Without knowing the formula for electric potential energy, we can say that ΔPEelec > 0, since the particle is being moved “against nature”.
Mathematically, we see that Wby grav = –ΔPEgrav and that Wagainst grav = +ΔPEgrav. Similarly, we will be able to make an analogous statement about the relationship between the work done by or against the electric field and the change in electric potential energy. We will also be able to answer questions involving speed by using Conservation of Mechanical Energy.
To find the equation for electric potential energy, it is useful to first consider that charged particles not only create a vector field (i.e., the electric field), they also create a scalar field.
This scalar field has a name: it’s called electric potential (or just potential for short).
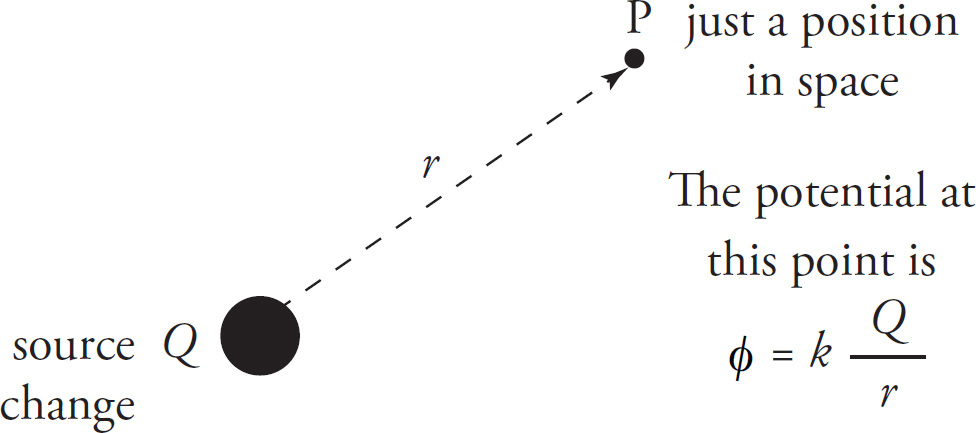
Let Q be a point source charge. At any point P that’s a distance r from Q, we say that the electric potential at P is the scalar given by this formula:
Electric Potential
ϕ= κ
Notice the differences between this formula and the one for the electric field. First, the potential is kQ divided by r, while the electric field is kQ divided by r2. Second, the electric field has a specific direction at each point (because it’s a vector quantity); the potential, on the other hand, is not a vector, so it has no direction. For this reason, no absolute value symbol is needed. The sign of the potential is important in determining the behavior of nearby charges if they are placed in the field. While the electric field has the same magnitude at every point a distance r from Q, the field has a different direction at every point on the circle (or, more generally, the sphere) of radius r centered on Q. Therefore, we’re forced to say that the electric field isn’t the same at every point a distance r from Q because the directions are all different. The potential, however, is easier because it has no direction: The potential is the same at every point that’s a distance r from Q.
The dashed circles shown in the figure on the right above are called equipotentials (“equal potentials”), because the potential is the same at every point on them. For example, the potential is equal to 8 units everywhere on the inner dashed circle, and equal to 3 units everywhere on the outer dashed circle. As we move around on either dashed circle, the electric field changes (because the direction of E changes), but the potential doesn’t change.
The formula given on the previous page for the potential, φ = kQ/r, assumes that the potential decreases to 0 as we move far away from the source charges (that is, as r → ∞); this is the standard, conventional assumption. With this formula, you can see that if Q is a positive charge, then the values of the potential due to this source charge are also positive (if Q is positive, then kQ/r is positive); on the other hand, the values of the potential due to a negative source charge are negative (if Q is negative, then kQ/r is negative). The sign of the potential (that is, whether it’s positive or negative) is not an indication of a direction; remember, potential is a scalar, so it has no direction.
Before we get to some examples, it’s important to mention that while there’s no special name for the unit of electric field, there is a special name for the unit of electric potential:
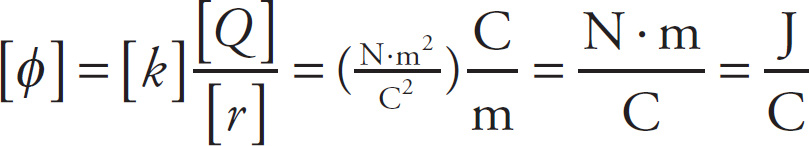
A joule per coulomb (J/C) is called a volt, abbreviated V.
Example 9-17: What is the electric potential at a distance of r = 30 cm from a source charge Q = –20 nC?
Solution: Using the formula φ = k0Q/r, we find that
Example 9-18: In the figure below, the potential at Point A is 1,000 V. What’s the potential at Point B ?
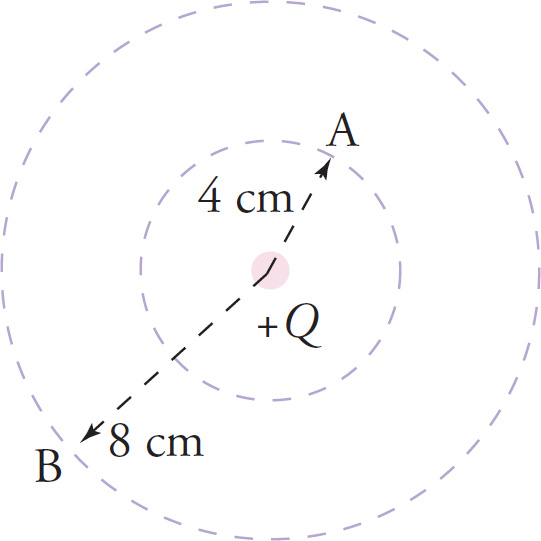
Solution: From the formula φ = k0Q/r, we see that the potential is inversely proportional to r: Thus, φ
1/r. Because the distance from Q to B is twice the distance from Q to A, the potential at B should be half the potential at A. Therefore, φat B =500V. (Notice that because the potential at A is 1,000 V, the potential at every point on the inner circle is 1,000 V; and since the potential at B is 500 V, the potential at every point on the outer circle is 500 V.)
Now that we know how to calculate electric potential, how do we use it to answer questions about the scalar quantities energy, work, and speed? The applications of electric potential all follow from this one fundamental equation:
Change in Electrical Potential Energy
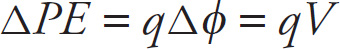
That is, the change in potential energy of a charge q that moves between two points whose potential difference is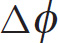 
is just given by the product, 
; it also can be expressed as qV, where V is defined in the change in potential and is known as the voltage. For example, let’s say a charge q = +0.03 C moves from a point on the inner circle to a point on the outer circle in the figure accompanying the preceding example:
Then the change in the electrical potential energy of the charge q is
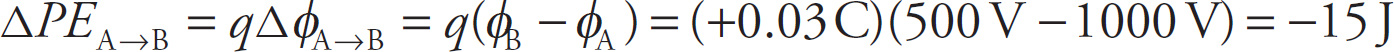
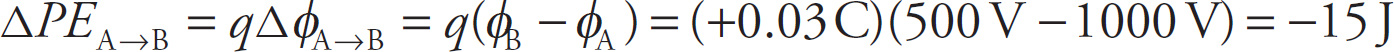
We expected that the change in potential energy would be negative (that is, the potential energy would decrease), because the positive charge is moving farther from the positive source charge (i.e., “with nature”). Because q moves in a way it naturally “wants” to move (since the positive charge q is naturally repelled by the positive charge Q), its potential energy should decrease.
If the charge q were instead pushed (by some outside force) from Point B to Point A (i.e., “against nature”), then its potential energy would increase:
What if the charge q were moved from one point on the outer circle (Point B, say) to another point on the outer circle, B′?
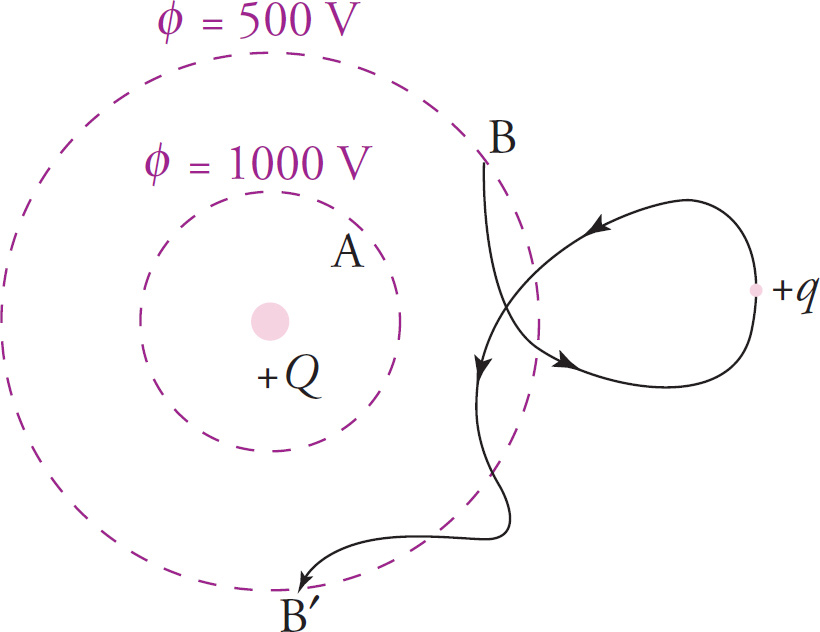
Its potential energy would not change. Because the potential is the same everywhere on the outer circle, the potential at B is the same as the potential at B′, so the potential difference between Points B and B′ is zero; and if 
, then 
as well. A charge experiences no change in potential energy when its initial and final positions are at the same potential.
The figure on the previous page also illustrates that the path taken by the charge is irrelevant. Like the gravitational force, the electric force is conservative; all that matters is where the charge began and where it ended; the specific path it takes doesn’t matter.
Example 9-19: A charge q = –8 nC is moved from a position that’s 10 cm from a charge Q = +2 µC to a position that’s 20 cm away. What is the change in its electrical potential energy?
Solution: Let A be the initial point and B the final point; then the change in potential from Point A to Point B is
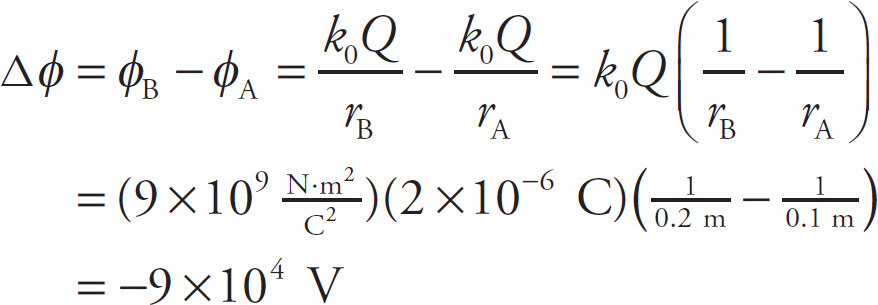
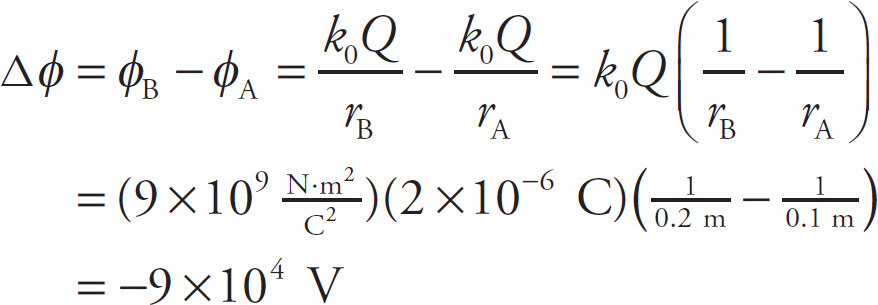
Therefore, the change in potential energy of the charge q is
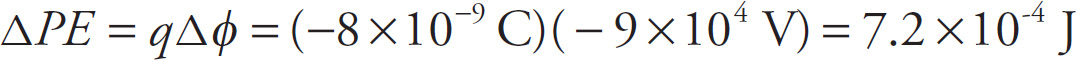
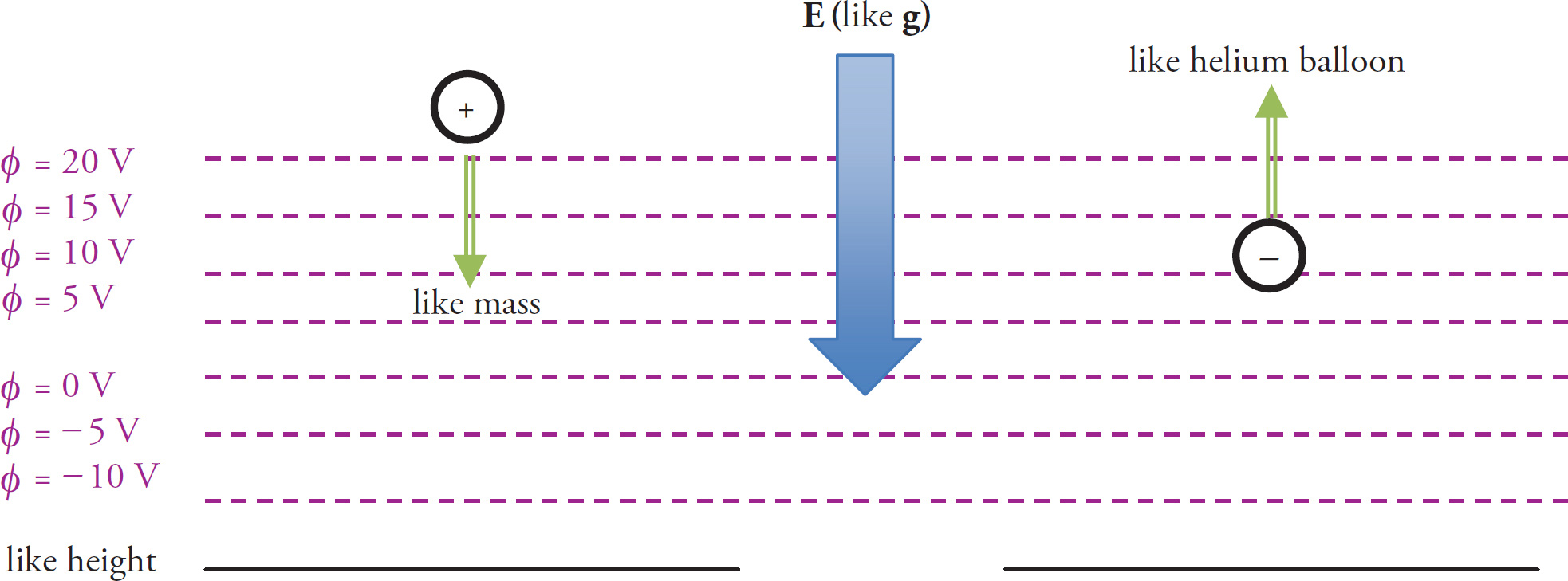
We’ve seen that all charged particles naturally move to positions of lower potential energy. To accomplish this, notice in the preceding examples that positively charged particles naturally tend toward lower potential and negatively charged particles tend toward higher potential. To verify this mathematically, we have learned that ΔPE = qΔφ or Δφ = ΔPE / q. Moving “with nature” means that ΔPE is negative. So if q is positive, then Δφ is (–) / (+) = (–), which means that potential decreases. If q is negative, then Δφ is (–) / (–) = (+), which means that potential increases.
A gravitational analogy may be useful. A positively charged particle can be thought of as any mass: it naturally “falls downward” when released from rest. Conversely, a negatively charged particle can be thought of as a helium balloon—it “rises upward.” The electric field can be thought as g, which is a vector that points downward toward the center of the earth. Positively charged particles therefore naturally move in the direction of E and negatively charged particles naturally move opposite E. Finally, potential can be thought of as height above ground. Positives naturally move toward lower potential and negatives move toward higher potential. Note that negative potentials can be thought of as “heights” below ground. The rules above still apply.
Now that we’ve seen examples of how to calculate changes in potential energy in an electric field by using the concept of electric potential, how do we answer questions about work or kinetic energy? By using equations we already know from mechanics.
What if we want to find the work done by the electric field as a charge moves? If we move objects around in a gravitational field, we remember that the change in gravitational potential energy is equal to the opposite of the work done by the gravitational field. That is, ΔPEgrav = −Wby gravity, which is the same as Wby gravity = −ΔPEgrav Applying this same idea to an electric field, we can say that the work done by the electric field is equal to −ΔPEelec:
Work Done by Electric Field
Wby electric field = −ΔPEelec
Now what about kinetic energy? Well, if there’s no friction (which will be the case for charges moving around in empty space) or other forces doing work as a charge moves, then mechanical energy is conserved; that is KE + PE will remain constant. And if KE + PE is constant, then ∆(KE + PE) will be zero. That is, ∆KE will be equal to –∆PE. Since we know how to calculate ∆PE, we can calculate ∆KE by just changing the sign of ∆PE:
ΔKE = −ΔPE
So, as long as you remember the fundamental formula for potential energy changes in an electric field, ΔPE = qΔφ, you can answer questions about work or kinetic energy in an electric field by just using the formulas above.
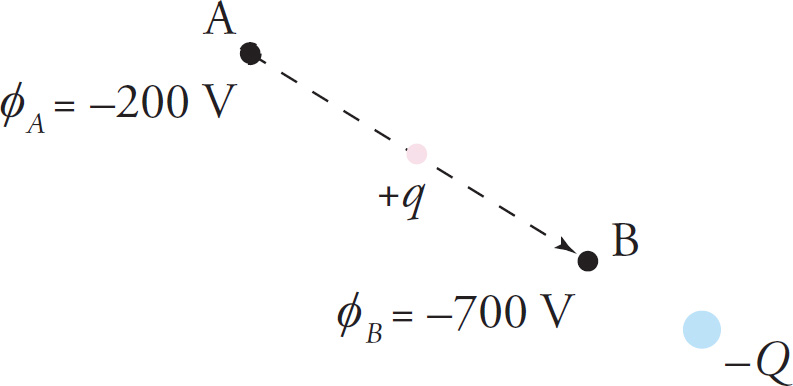
Example 9-20: In the figure below, a particle whose charge q is +4 nC moves in the electric field created by a negative source charge, –Q.
a) the change in potential energy,
b) the work done by the electric field, and
c) the change in kinetic energy of the particle as it moves from position A to position B.
d) If the mass of the particle is 10–8 kg and it started from rest at Point A, what will be its speed as it passes through Point B?
Solution:
a) ΔPE = qΔφ = q(φB − φA) = (4 × 109C)[(−700V)−(−200V)] = −2 ×10−6J
b) Wby electric field = −Δ PEelec = −(−2 × 10−6J) = 2 × 10−6J
c) ΔKE = ΔPEelec = −(−2 × 10−6J) = +2 × 10−6J
d) If the particle started from rest at Point A, then PEat B = ΔKE = +2 × 10−6J, so
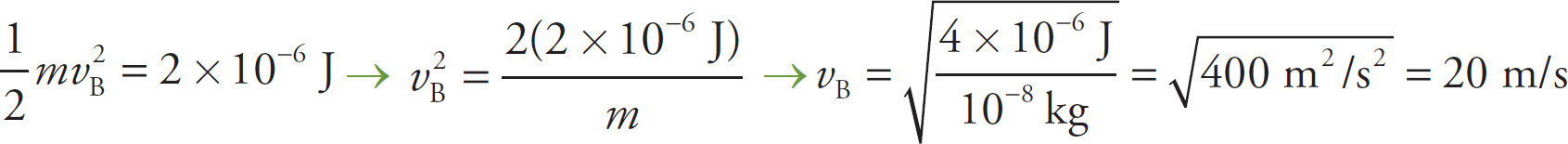
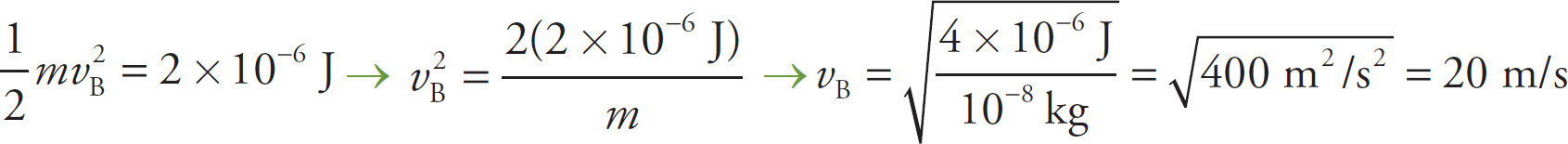
Example 9-21: An electric field pulls an electron from one position to another such that the change in potential is +1 V. By how much does the electron’s kinetic energy change?
Solution: The change in potential energy is
ΔPE = qΔφ = (−1.6 × 10−19C)(+1V) = −1.6 × 10−19J
so the change in kinetic energy is the opposite of this, +1.6×10−19C. This amount of energy is known as 1 electron volt (eV). In fact, the abbreviation for this unit makes the definition easy to remember: An electron (e−) moving through a potential difference of 1 V experiences a kinetic energy change of −qΔ = (e)(1V) = 1.6 × 10−19J = eV. While the joule is the SI unit for energy, it’s too big to be convenient when discussing atomic-sized systems. The electron volt is commonly used instead.
Example 9-22: An electric field pushes a proton from one position to another such that the change in potential is –500 V. By how much does the kinetic energy of the proton increase, in electron volts?
Solution: The change in potential energy is
ΔPE = qΔφ = (+e)(−500V) = −500eV
so the change in kinetic energy, ∆KE, is –∆PE = –(–500 eV) = +500 eV.
The formula φ = kQ / r tells us how to find the potential due to a single point source charge, Q. To find the potential in an electric field that’s created by more than one charge, we use the principle of superposition. In fact, applying this principle is even easier here than for electric forces and fields because potential is a scalar. When we add up individual potentials, we’re simply adding numbers; we’re not adding vectors.
Let’s illustrate with an example. In the figure below, the source charges Q1 = +10 nC and Q2 = –5 nC are fixed in the positions shown; the charges and the two points, A and B, form the vertices of a rectangle. What is the potential at Point A? at Point B?
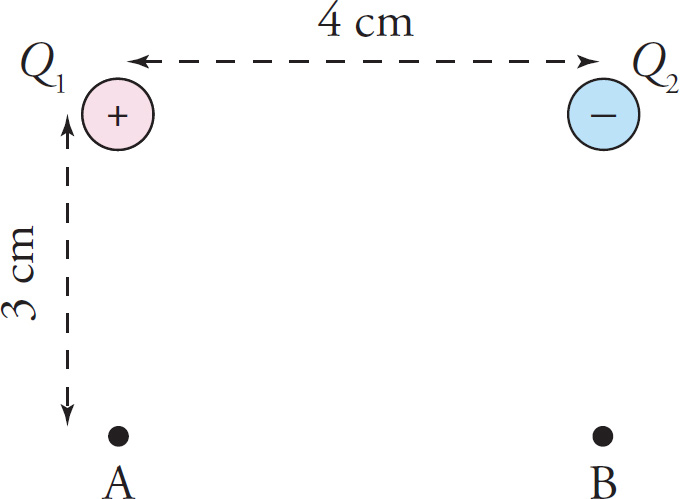
The potential at Point A due to Q1 alone (ignoring the presence of Q2) is
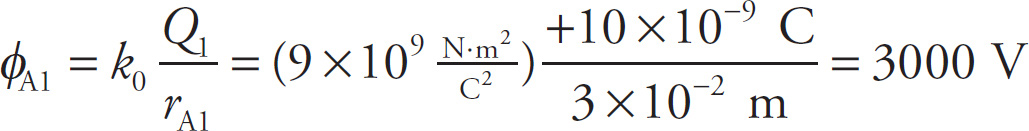
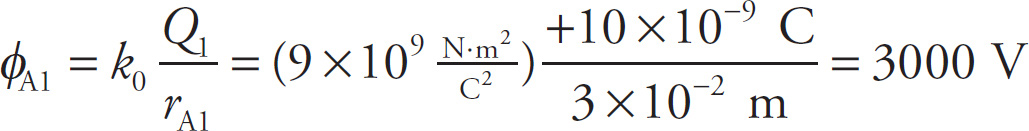
Since Point A is 5 cm from Q2 (it’s the hypotenuse of a 3-4-5 right triangle), the potential at Point A due to Q2 alone (ignoring the presence of Q1) is
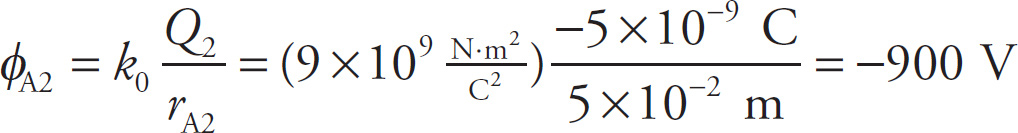
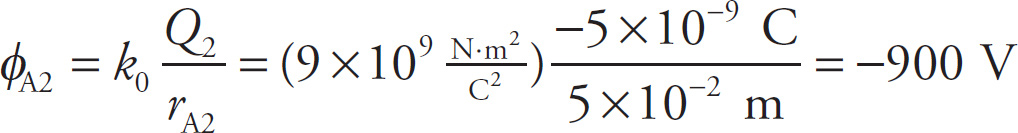
Therefore, the total electric potential at Point A, due to both source charges, is
φA = φA1 + φA2 = (3000V) + (−900V) = 2100V
Similarly, the total electric potential at Point B is
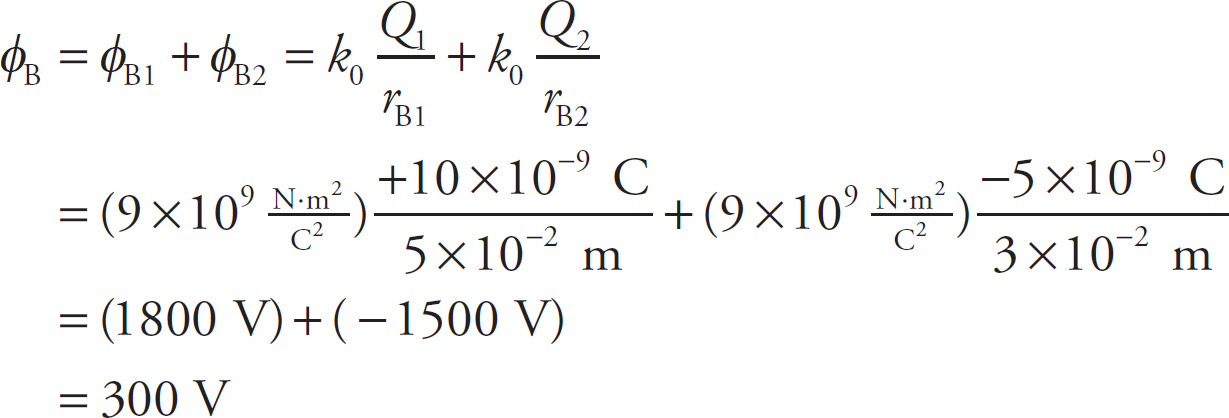
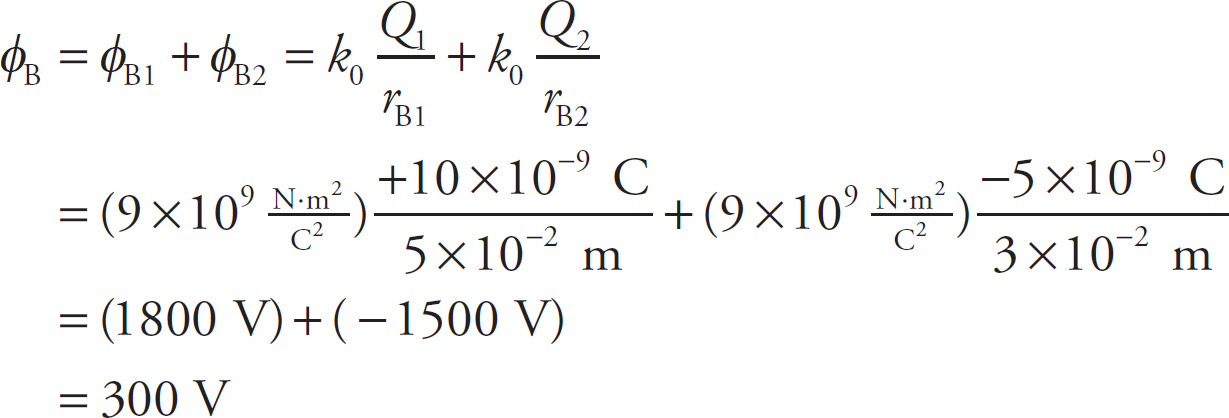
Example 9-23: A charge q = 1 nC is moved from position A to position B, along the path labeled a in the figure below. Find the work done by the electric field. How would your answer change if q had been moved from position A to position B, along the path labeled b?
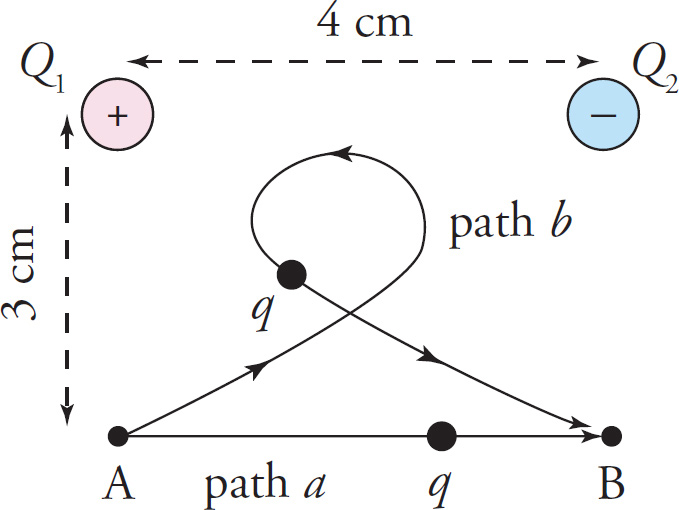
Solution: Path a begins at Point A, where φA = 2100V, and ends at Point B, where φB = 300V, so ΔφA→B = φB − φA = 300V − 2100V = −1800V. Therefore, the change in potential energy of the charge q is
ΔPE = qΔφ = (1×10−9C)(−1800 V) = −1.8×10−6J
This means that the work done by the electric field, Wby E, is equal to −ΔPE = 1.8×10−6J. If q had followed path b, the change in potential energy and the work done by the electric field would have been the same as for path a. The shape or length of the path is irrelevant; all that matters is the initial point and the ending point, and both paths begin at Point A and end at Point B.
We can’t use the formula “work = force × distance” here, because the force is not constant during the object’s displacement. To calculate work in an electric field, we use electric potential and the formula Wby E = −ΔPEelec.
Example 9-24: The figure below shows two source charges, +2Q and –Q. What is the minimum amount of work that must be done by some outside force against the electric field to move a negative charge, –q, from position A to position B along the semicircular path shown?
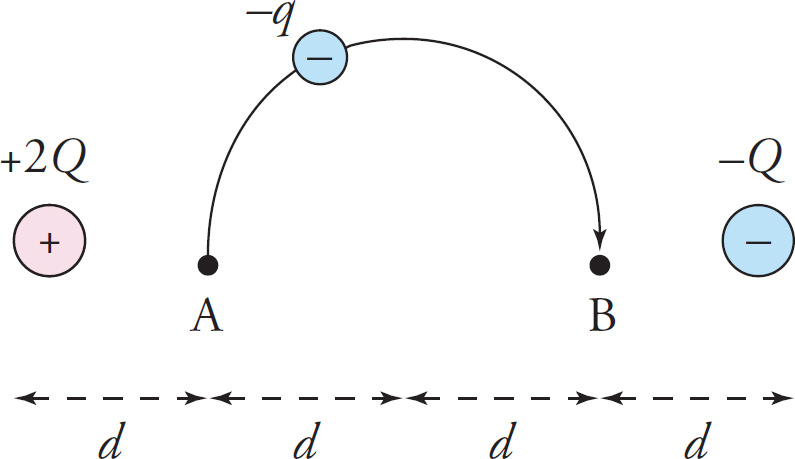
Solution: First, remember that neither the shape nor the length of the path matters; the fact that the path is a semicircle is irrelevant. All that matters is the initial point and the ending point of the path. Using the principle of superposition, the potentials at Points A and B are
and
Therefore, the change in potential energy of the charge –q as it’s moved from A to B is
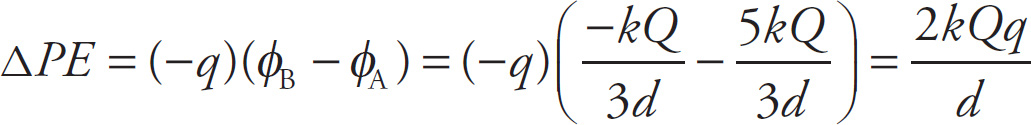
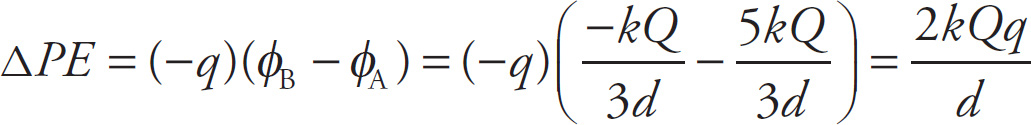
Since the change in PE is positive, we know that the charge –q is not moving as it would naturally on its own (after all, we can see from the figure that it’s being moved from a point near a positive source charge, to which it’s attracted, to a point near a negative charge, from which it’s repelled). Therefore, some outside force is pushing this charge, doing work against the electric field. Since the work done by the electric field is −ΔPE = −2kQq/ d, the work done against the electric field by some outside force must be the opposite of this: 2kQq/ d.
Example 9-25: An electric dipole consists of a pair of equal but opposite charges, +Q and –Q, separated by a distance d. What is the electric potential at the point (call it P) that’s midway between these source charges?
Solution: The potential at P due to the positive charge alone is 
, and the potential at P due to the negative charge alone is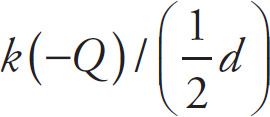 
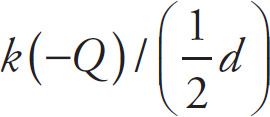. Adding these, we get zero, which is the potential at P due to both charges. (Notice that although the potential at P is zero, the electric field at P is not zero. We can have the “opposite” situation as well; that is, it’s possible to have a point where the electric field is zero, but the potential is not. For example, if we had two equal source charges of the same sign, say +Q and +Q, separated by a distance d, then the potential at the point that’s midway between them would not be zero [it would be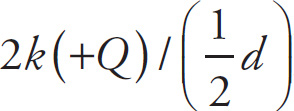 
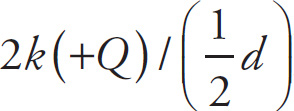] but the electric field there would be zero.)
Example 9-26: An electric dipole consists of a pair of equal but opposite charges, +Q and –Q, separated by a distance d. The dashed curves in the figure below are equipotentials. (Notice that the equipotentials are always perpendicular to the electric field lines, wherever they intersect. This is true for any electrostatic field, not just for the field created by a dipole.)
If a particle of mass m = 1×10−6 and charge q = 5 nC starts from rest at Point A and moves to Point B,
a) How much work is done by the electric field?
b) What is the speed of the particle when it reaches Point B?
Solution:
a) The work done by the electric field is equal to the opposite of the change in the particle’s electrical potential energy Wby E = ΔPEelec. Since the potential at Point A is φA = +300V (because A lies on the φ = +300V equipotential) and the potential at Point B is φB = −100V (because B lies on the φ = −100V equipotential), the change in potential from A to B is φB − φA = (−100V) − (300V) = −400V. Therefore, Wby E = −ΔPEelec = −qΔφ = −(5×10−9C)(−400V) = 2×10−6J
b) Since the total work done on the particle is equal to its change in kinetic energy (the work-energy theorem), we have ΔKE = 2×10−6J Because the particle started from rest at Point A, we have KEat B = ΔKEA→B = 2×10−6J, so
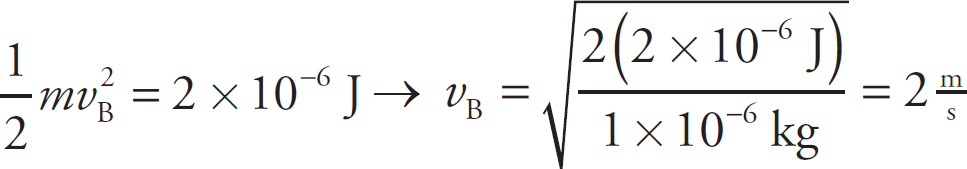
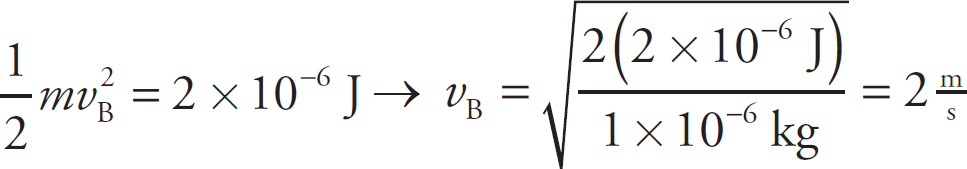
Example 9-27: The figure below shows several point source charges, +Q1, +Q2, –Q3, and –Q4, and the electric potential at various points (A, B, C, Z, Y, and Z) in the electric field they produce:
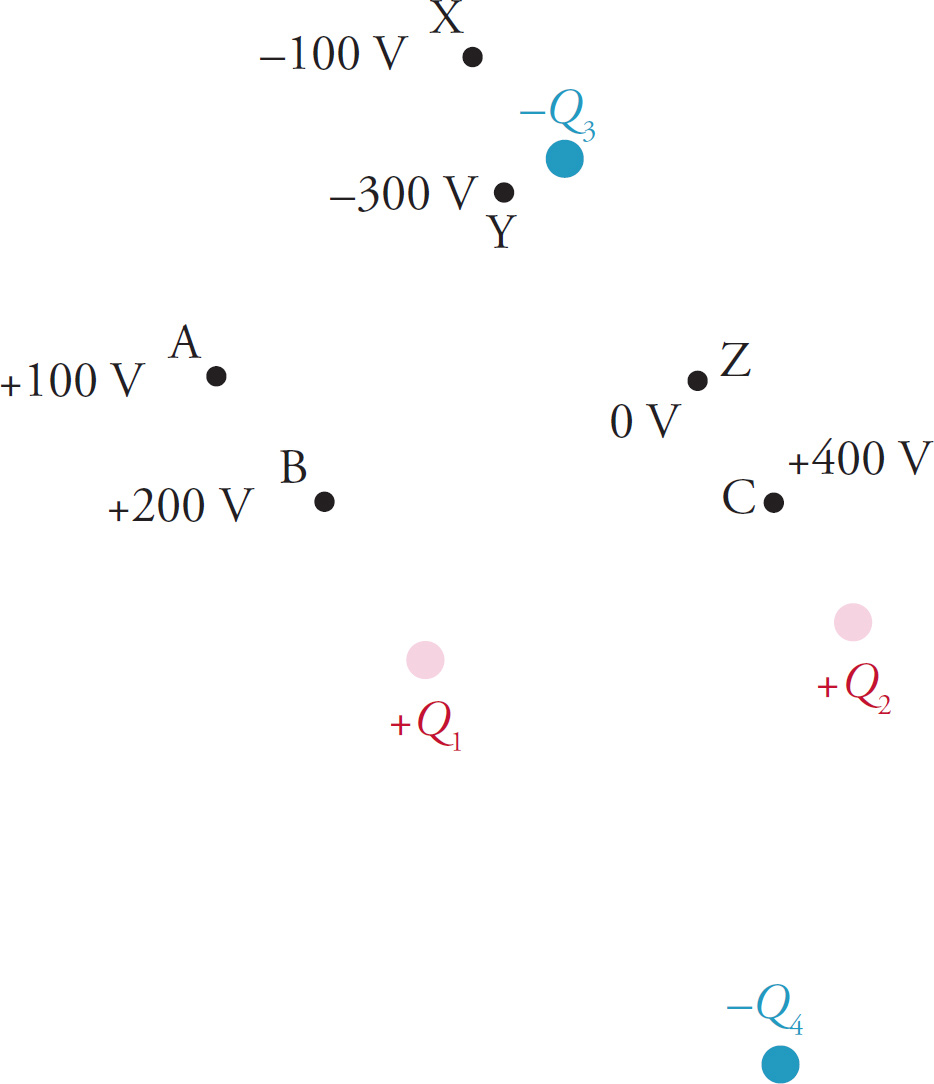
The difference in electric potential between two points is called the voltage, V. That is, V = Δφ. For example, the voltage from Point A to Point B is φB − φA = (+200V)−(+100V)=+100V, and the voltage from X to Y is V = (−300V) − (−100V) = −200V.
a) How much work does the electric field do on a charge q = +2 µC as q is moved from Point X to Point C?
b) True or false? If the charge q is placed at Point Z, it will remain at this point because the electric potential is 0 V.
Solution:
a) The work done by the electric field is equal to the opposite of the change in the electrical potential energy Wby E = ΔPEelec. Since Δφ = V, the fundamental equation ΔPE = qΔφ becomes simply
ΔPE = qV
Since VX→C = φC − φX = (+400V)−(−100V) = +500V, we have
ΔPE = qV = (2×10−6C)(5×102V) = 1×10−3J
Therefore, Wby E = −1×10−3. (Does it make sense that ΔPE is positive and Wby E is negative? Yes, because a positive charge q would have to be pushed by some outside force from Point X (which is near a negative charge) to Point C (which is near a positive charge). When an external force has to do positive work against the electric field, the electrical potential energy increases and the work done by the electric field is negative.)
b) False. If q were placed at a point where the electric field was zero, then it would feel no force and remain there. However, if q is placed at a point where the electric potential is zero, it will be accelerated toward a point where the potential is lower (because q is positive; recall Example 7-21). In this case, q would be accelerated by the electric field toward the negative source charge −Q3
Elementary charge: e = 1.6×10−19 C
charge of proton = +e; charge of electron = –e
Charge is quantized: e = 1.6×10−19C
Coulomb’s law: 
Opposite charges attract, like charges repel.
Coulomb’s constant: 
Principle of Superposition:
The net force, electric field, or electric potential on a charge q (for force) or point P (for electric field or electric potential) due to a collection of other charges (Qs) is equal to the sum of individual effects of each Q.
Electric field due to point charge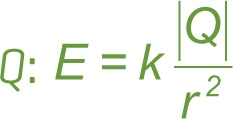 
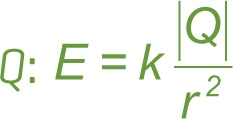
Direction of electric field:
Positive charges want to move in the direction of the electric field (E).
Negative charges want to move opposite the direction of the electric field (E).
Electric force and field: F = qE
(a scalar, not a vector)
Positive charges want to move to regions of lower potential
Negative charges want to move to regions of higher potential
Change in electrical PE: ΔPEelec = qΔφ = qV
Work done by electric field: Wby E = –ΔPEelec
Change in KE = −ΔPE
For conductors, charge rests on the outer surface and the electric field inside is zero.
1. How far apart are two charges (A = 10 µC and B = 12 µC) if the electric potential measured at point C midway between them is 10 V?
A) 2 × 10–5 m
B) 2 × 105 m
C) 4 × 10–4 m
D) 4 × 104 m
2. Two charges (+q and –q) each with mass 9.11 × 10–31 kg are placed 0.5 m apart and the gravitational force (FG) and electric force (FE) are measured. If the ratio of FG/FE is 1.12 × 10–77, what is the new ratio if the distance between the charges is halved?
A) 2.24 × 10–77
B) 1.12 × 10–77
C) 5.6 × 10–78
D) 2.8 × 10–78
3. Two equally positive charges are r distance apart. If the amount of charge on A is doubled and the distance between the charges is doubled, what is the ratio of new electric force to old electric force?
A) 1/4
B) 1/2
C) 2
D) 4
4. The amount of work required to move a charge in an electric field depends:
A) only on the change in potential and not the path traveled.
B) on both the change in potential and the path traveled.
C) only on the path traveled and not the change in potential.
D) on neither the path traveled nor the change in potential.
5. Which of the following pairs of electric forces form an action-reaction pair?
I. Two positive charges, of different masses, placed at a distance d apart.
II. Two negative charges, of equal masses, placed at a distance d apart.
III. One positive charge and one negative charge, of equal masses, placed at a distance d apart.
A) I and II only
B) II and III only
C) III only
D) I, II and III
6. A hollow metal sphere of radius 0.5 m has a net charge of 2.0 × 10–6 C. A solid metal sphere of radius 0.5 m has a net charge of 4.0 × 10–6 C. The centers of the spheres are placed a distance 2 m apart and equilibrium is established. Compared to the electric field at the center of the hollow sphere, the electric field at the center of the solid sphere is:
A) twice the magnitude.
B) four times the magnitude.
C) half the magnitude.
D) equal in magnitude.
7. Starting from rest, a sphere of mass 2 kg and charge –0.1 C slides across a frictionless horizontal plane through a potential difference of 220 V. Determine the instantaneous velocity of the sphere the moment it has rolled through this potential.
A) 4.7 m/s
B) 5.1 m/s
C) 5.5 m/s
D) 6.1 m/s
In the Bohr model of the atom, electrons circle the point-like nucleus similar to the way planets orbit the Sun. Imagining that the atomic model is confined to motion in one plane, the orbit of the electrons can be drawn as circles with the nucleus in the center.
The atomic radius of an atom is defined as the length from the nucleus to the outermost electron and is generally within the tens to hundreds of picometers. The atomic radii of common atoms are as follows: hydrogen = 40 pm, helium = 30 pm, carbon = 80 pm. In the periodic table, atomic radius tends to increase as you go down each column of the table and decrease as you move from left to right across a period.
Current scientific thought suggests that the Bohr model is an oversimplification of atomic structure. Quantum mechanics states that the exact position of an electron at a given point in time cannot be known. Only the probability of electron existence in a region of space is known. However, the Bohr model of the atom wonderfully captures another aspect of quantum mechanics: the quantization of energy. The electrons can only have very specific energy values and the distinct orbitals are a very good visual representation of this. Electrons can only move from one energy level to another if there is the exact energy configuration. When dropping from a higher energy to a lower energy, photons with the exact energy difference are emitted, and electrons can only move to a higher energy level if they absorb a photon of the exact energy difference.
1. What is the magnitude of the electric force a hydrogen nucleus exerts on its only orbiting electron in the Bohr model?
A) 107 N
B) 10 N
C) 10–7 N
D) 10–18 N
2. What is the electric potential a millimeter away from a carbon atom nucleus?
A) 1.4 × 10–9 V
B) 8.6 × 10–6 V
C) 1.4 × 10–6 V
D) 8.6 × 10–3 V
3. If the electric force between the nucleus and the outermost electron in 6Li is F, what is the electric force between the nucleus and the outermost electron in 7Li, given that the mass of a neutron is approximately 1/9th the mass of 6Li?
A) F/9
B) F/3
C) F
D) 9F
4. According to the Bohr model, the atomic radius decreases as you move from left to right in the periodic table. Which of the following helps to explain this phenomenon?
I. The charge of the nucleus decreases as you move from left to right.
II. The electric force between the electrons and the nucleus increases as you move from left to right.
III. The work done by the electrons increases as you move from left to right.
A) I only
B) II only
C) I and II only
D) II and III only
5. An attractive force keeps the electron in 1H orbiting the nucleus. Approximately what is the magnitude of the gravitational force, FG, between the nucleus and the electron in terms of the magnitude of the electric force, FE, between them? (Recall that me = 9 × 10–31 kg, mp = 2 × 10–27 kg, and G = 6 × 10–11 m3kg–1s–2.)
A) 10–10FE
B) 10–20FE
C) 10–30FE
D) 10–40FE
6. Imagine a lithium atom where the two electrons in the first orbital are at exact opposite sides of the nucleus and the electron in the second orbital is in line with the other electrons so that the three electrons and the nucleus all lie on a straight line. How much work would you need to apply to remove the outermost electron if the atomic radius is 100 pm and the distance between the first and second orbital is 50 pm?
A) (ke/150) × 1012 J
B) (ke2/150) × 1012 J
C) (ke/300) × 1012 J
D) (ke2/300) × 1012 J
7. Ionized hydrogen gas is placed in a region with a uniform electric field. All of the following are true EXCEPT:
A) The protons and the electrons will move in opposite directions.
B) The protons and the electrons will have the same magnitude of acceleration.
C) The protons will move in the direction of the electric field.
D) The electrons will move in the direction of higher potential.
1. D This question requires us to remember the electric potential formula. The question stem tells us that C is the midway point between A and B, so if we can determine the distance between A and C (or B and C), we can double that distance to determine the distance between A and B. Since φelec = kQ / r is a scalar quantity, when we use the Principle of Superposition for Electric Potential, it is straight addition. Let C be the distance between A and C (note that it is also the distance between B and C since C is midway between A and B). Thus,
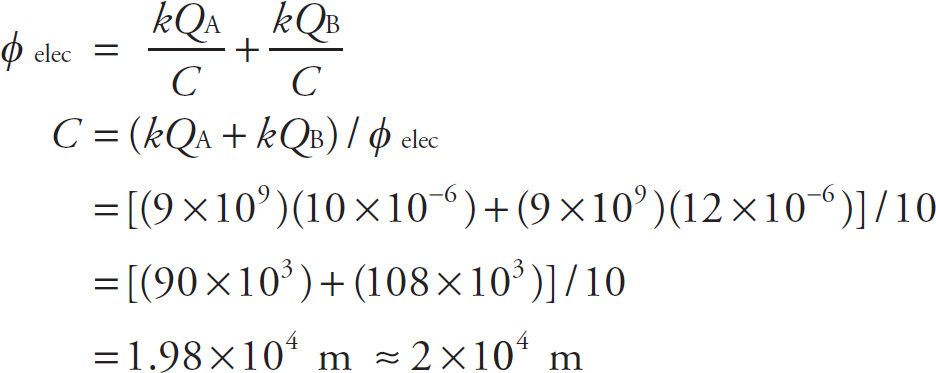
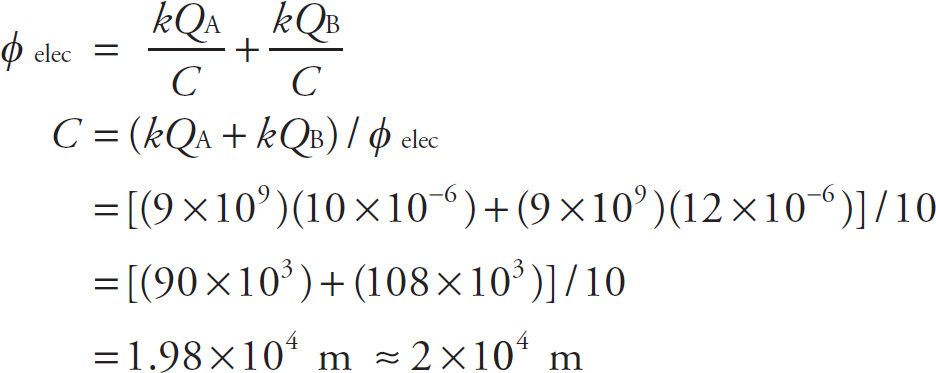
Now that we know how far apart A and C are (and also therefore how far apart B and C are), we double this distance to calculate how far apart A and B are (i.e., 2 × (2 × 104 m) = 4 × 104 m).
2. B To determine how the ratio changes, it is necessary to know the formulae for calculating FG and FE respectively. (FG = GMm/r2 and FE = k|q1||q2|/r2). Both of gravitational force and electric force are inverse square laws with respect to r, the distance between the two charges. Therefore, G and E will vary in the same proportion so the ratio of G/E will be unchanged when the distance between the two charges or masses is varied.
3. B The MCAT loves proportion questions, as they require us to remember the formulae for specific quantities. In this question, we need to recall the formula for electric force and how it varies with respect to the variable of distance. Given that FE =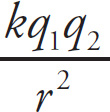 
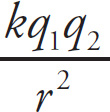, the (original FE) =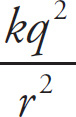 
and the (new FE) =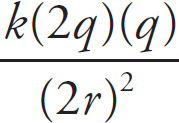 
= 
= 
= 
(
) = 
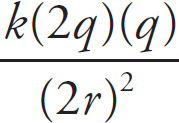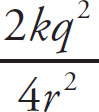
(original FE). Therefore, the ratio of (new FE) / (original FE) = (
original FE) / (original FE) = 
.
4. A The amount of work required to move a charge in an electric field depends only on the change in potential and is independent of the path traveled. Remember, like the gravitational field, the electric field is conservative.
5. D The electric force is a force in the same sense as gravity and friction are forces. In each of these three cases the forces are acting on different objects, thereby satisfying Newton’s third law. As such, each forms an action-reaction pair. Note that the mass in each case is irrelevant as the electric force is independent of the mass.
6. D The electric field inside of an electrostatic conductor is always zero. Therefore, the electric fields at the centers of the solid and hollow sphere are both equal in magnitude.
7. A Since v0 = 0 (the sphere starts at rest), we need to calculate the kinetic energy gained by the sphere and use this to determine vF.ΔPE = qΔφ = −0.1C (220V) = −22J. Using ΔPE = −ΔKE, ΔKE = 22 J. Finally, ΔKE = mv2 / 2, so . The MCAT does not expect you to have this square root memorized, but notice that it is less than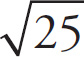 
, which is 5. We know that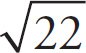 
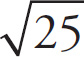
is less than so we can eliminate choices B, C and D.
1. C In this question we just can look at the powers of ten in each term separately from the specific numbers. The electric force is equal to k|q1||q2|/r2, the powers of 10 give (109)(10−19) (10−19)/(10−12)(10−12) = 10−5. Then, the other numbers are approximately (9)(1.6)(1.6)/ (40)(40), which is approximately 25/1600 which is on the order of 10−2. Therefore, the magnitude of the electric force is 10−7.
2. B A carbon nucleus contains six protons, and thus has a charge of Q = 6e. The electric potential one millimeter away from the nucleus is then kQ/r = (9 × 109)(6)(1.6 × 10−19)/(10−3) = 8.6 × 10−6 V.
3. C The formula for electric force is F = k|q1||q2|/r2, and does not depend on mass. Since an isotope does not change the charge of the nucleus, the electric force will not change.
4. B As you move from left to right in the periodic table there are more electrons added in the same shell and the nucleus has a greater positive charge. The added charges increase the electric force between the nucleus and the electrons, hence, attracting them closer together. Item I is not true (choices A and C can be eliminated); as you move from left to right the number of protons in the nucleus increases. Item III is false (choice D can be eliminated) since the electrons do no work as they orbit the nucleus because the electric potential does not change. Thus, Item II is the only correct answer.
5. D In this question you need to work with the powers of 10. The gravitational force is equal to Gm1m2/r2, which is on the order of 10–45, while the electric force is equal to k|q1||q2|/r2, which is on the order of 10–5. Thus, the gravitational force is approximately 10−40FE. (To calculate it more precisely, the electric force is 1.4 × 10–7 N and the gravitational force is 6.75 × 10–47 N.)
6. D First, calculate the electric potential at the point of the outermost electron using the principle of superposition for electric potential:
Removing the electron requires that the final potential is equal to 0 (i.e., the electron is infinitely far away). Therefore, the work required to remove the electron is
Wagainst electric field = ∆PE = q∆ϕ = (–e)(0 – ke / 300 × 10–12) = ke2 / 300 × 10–12.
7. B The direction of the electric field is defined as the direction of force a positive charge would experience. Likewise, negative charges feel a force opposite the direction of the electric field. Choices A and C are true statements, and therefore can be eliminated. Positive charges tend toward lower potential and negative charges tend toward higher potential. This eliminates choice D. The magnitude of the force experienced by a charge in an electric field is given by FE = |q|E. Since protons and electrons have the same magnitude of charge, they will experience the same magnitude of force. Newton’s Second Law tells us that Fnet = ma. Since protons are more massive than electrons, they will experience a smaller acceleration.
1 This does not mean that electric charge cannot be created or destroyed, which happens all the time. For example, in the reaction e– + e+ → γ + γ an electron (e–) and its antiparticle (the positron, e+, which is, in effect, a positively charged electron) meet and annihilate each other, producing energy in the form of two gamma-ray photons (γ), which carry no charge. Charge has been destroyed, but the total charge (zero, in this case) has been conserved. Conversely, charge can be created in the opposite process, when energy is converted to mass and charge (but always with zero total charge).
2 The same phenomenon, in which the presence of a charge tends to cause polarization in a nearby collection of charges, is responsible for a kind of intermolecular force: Dipole-induced dipole forces are caused by a shifting of the electron cloud of a neutral molecule toward positively charged ions or away from a negatively charged ion; in each case, the resulting force between the ion and the atom is attractive.
The London dispersion force, in which electrically neutral molecules temporarily induce polarization in each other, is a much weaker version of the same phenomenon—again, electron clouds shift a little bit to create dipoles.
