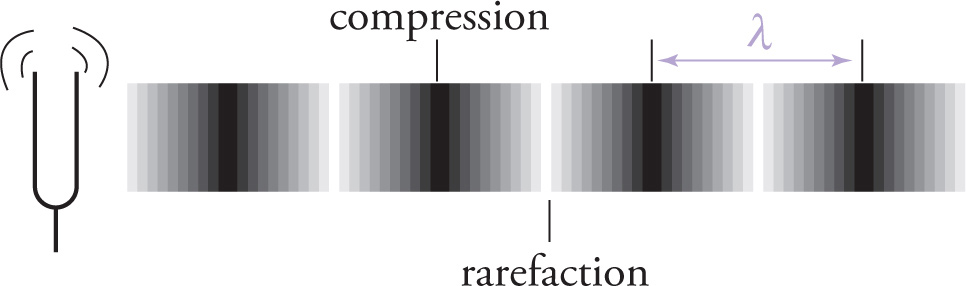

Sound waves don’t travel in the same way that waves on a rope do. The waves we’ve looked at so far are transverse waves: The direction in which the particles of the conducting medium oscillate is perpendicular to the direction in which the wave travels. If, however, the direction in which the particles of the conducting medium oscillate is parallel to the direction in which the wave travels, we call the wave longitudinal. Sound waves (also known as compression waves) are longitudinal waves in gas, liquid, or solid; when a compression wave’s frequency is between 20 Hz and 20 kHz, humans can perceive it as what we commonly call sound.
Let’s take a closer look at sound waves. As a stereo speaker, vocal fold, or tuning fork vibrates, it creates regions of high pressure (compressions) that alternate with regions of low pressure (rarefactions). These pressure waves are transmitted through the air (or some other medium) and can eventually reach our ears and brain, which translate the vibrations into sound.


Like other waves, a longitudinal compression wave has a wavelength, a speed, a frequency, a period, and an amplitude. The equation v = λ f holds, as do the two Big Rules for waves.
Sound can travel in any medium: gas, liquid, or solid. Its speed depends on two things: the medium’s resistance to compression and its density. The greater the medium’s resistance to compression, the faster sound travels in it. On the other hand, the greater the medium’s density, the slower sound travels in it. On the MCAT, you won’t have to figure out the speed of sound in a given medium, though it can be helpful to know that in general, sound travels slowest through gases, faster through liquids, and fastest through solids. The speed of sound in air is about 340 m/s (that’s about 760 miles per hour), but it varies slightly with temperature, pressure, and humidity.
Example 12-1: A sound wave of frequency 440 Hz (this note is concert A, or the A above middle C) travels at a speed of 344 m/s through the air in a concert hall. How fast would a note one octave higher, 880 Hz, travel through the same concert hall?
A. 172 m/s
B. 344 m/s
C. 516 m/s
D. 688 m/s
Solution: Altering the frequency will not affect the wave speed. Remember Big Rule 1 for waves. Therefore, the answer is B.
Example 12-2: A siren produces sound waves in the air. If the frequency of the waves is gradually decreasing, which of the following changes to the waves is most likely also occurring?
A. The wavelength is increasing.
B. The wave speed is decreasing.
C. The amplitude is decreasing.
D. The period is decreasing.
Solution: Because the wave speed is set by the medium (the air, in this case), the wave speed is a constant. Since v = λ f, this means that λ and f are inversely proportional. So, if f is decreasing, then λ must be increasing, choice A.
Example 12-3: What is the wavelength of a sound wave of frequency 170 Hz if the wave speed is 340 m/s?
Solution: Using v = λ f we find that λ = v/f = (340 m/s)/(170 Hz) = 2 m.
Example 12-4: The sound wave in the preceding example was traveling through the air. What would happen to the wave if it passed into water?
A. Its wavelength and speed would both decrease.
B. Its wavelength and speed would both increase.
C. Its wavelength would decrease and its speed would increase.
D. Its wavelength would increase and its speed would decrease.
Solution: When a wave passes into a new medium, its frequency does not change. Therefore, when traveling through the water, the frequency of the sound wave will be the same as it was in the air. However, we know that sound waves generally travel faster through liquids than they do through gases, so we’d expect the wave speed through the water to be faster. Because the equation v = λ f is always true, the same f at a faster v means a greater wavelength. Therefore, the answer is B.
Example 12-5: When a longitudinal compression wave of frequency 700 Hz travels through a brass rod, its wavelength is 5 m. How fast does sound travel through brass?
Solution: Using v = λ f, we find that v = (5 m)(700 Hz) = 3500 m/s.
Just as we can have standing waves on a rope caused by the interference of two oppositely directed transverse waves with equal amplitudes, standing sound waves in a pipe can caused by the interference of two oppositely-directed longitudinal waves of equal amplitude.
The analysis of these standing waves is similar to that of a string attached at each end. In that case, the ends correspond to nodes (because there is no motion). Since the distance between nodes is some whole number of half-wavelengths, this gave us formulas for the different frequencies and wavelengths that the standing waves can have. In the case of pipes, we also need to know what corresponds to each end. The ends of a pipe can either be open to the atmosphere or closed.
It turns out that the open end of a pipe (technically, just beyond it) corresponds to an antinode. To be more specific, these are often referred to as displacement antinodes (maximum displacement). They are also called pressure nodes (constant pressure). The closed end of a pipe corresponds to a displacement node (no motion) or a pressure antinode (maximum pressure fluctuations). The pressure varies most where there is no motion and the motion varies most where there is constant pressure.
Pipes are often classified as open pipes (open on each end) or closed pipes (open on one end and closed on the other).


In the case of the open pipe, the distance between displacement antinodes (or pressure nodes) is equal to a whole number of half-wavelengths. The formulas for wavelength and frequency are therefore the same as for the string attached at each end: λn = 2L / n and fn = nv / 2L, where the harmonic number, n, is any positive whole number, and v now refers to the speed of sound in air.
To visualize the harmonic modes, it is convenient to represent the standing waves as transverse.
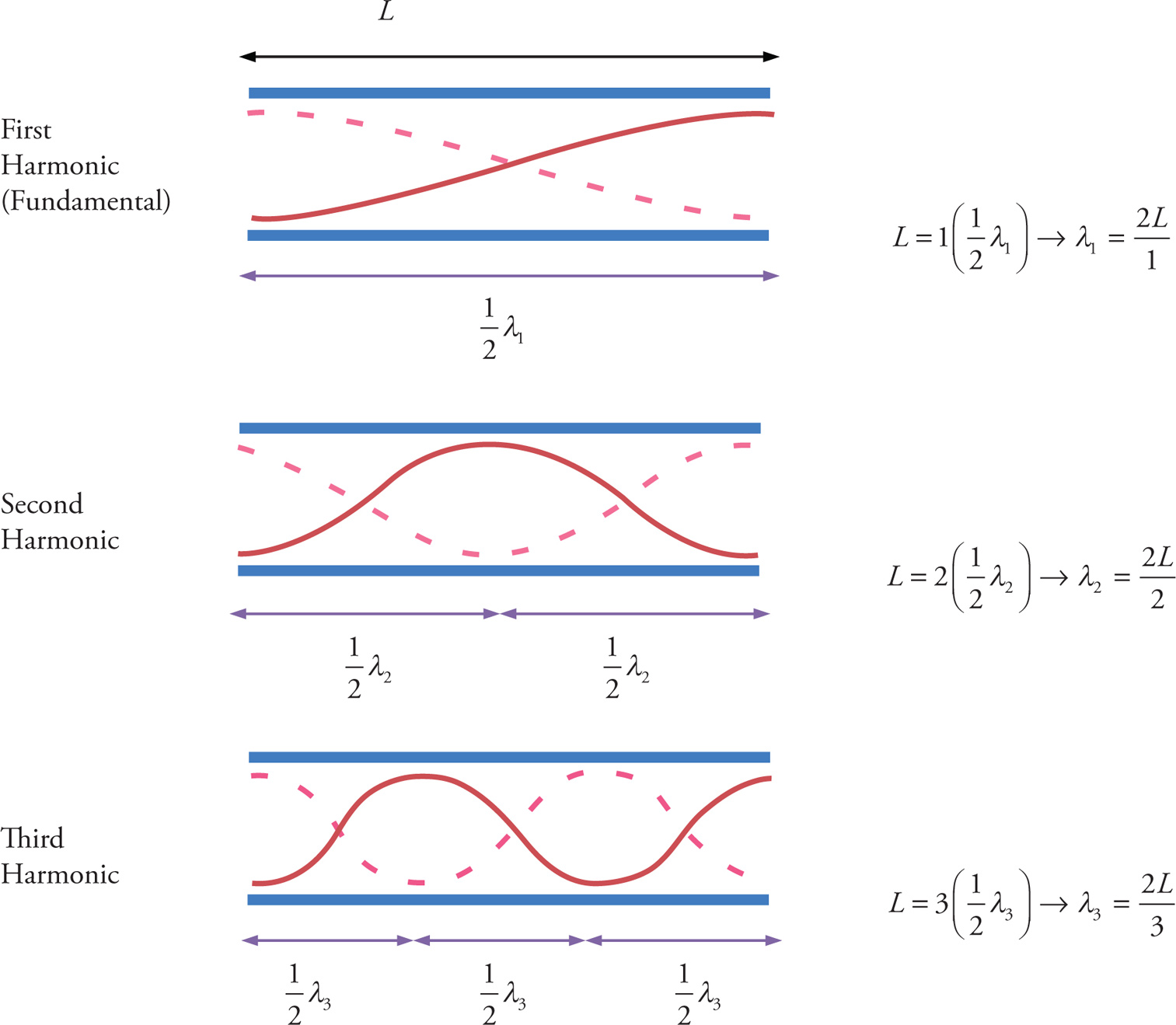

In the case of the closed pipe, the distance between a displacement antinode (or pressure node) and a displacement node (or pressure antinode) is equal to an odd number of quarter-wavelengths. As a result, λn = 4L / n and fn = nv / 4L, where n (which is still called the harmonic) is an odd number.


Note that for all types of resonance, fn = nf1 and λn = λ1 / n.
Example 12-6: An organ pipe that is closed at one end has a length of 3 m. What is the second-longest harmonic wavelength for sound waves in this pipe?
A. 3 m
B. 4 m
C. 6 m
D. 9 m
Solution: Because one end of the pipe is closed, the length of the pipe, L, must be an odd number of quarter-wavelengths: L = 1(λ/4), 3(λ/4), 5(λ/4)…, in order to support standing waves. Therefore, the possible harmonic wavelengths are λ = 4L/1, 4L/3, 4L/5, and so on. The second longest is λ = 4L/3 = 4(3 m)/3 = 4 m, choice B.
Example 12-7: An organ pipe that is open at both ends has a length of 3 m. What is the second-longest harmonic wavelength for sound waves in this pipe?
A. 3 m
B. 4 m
C. 6 m
D. 9 m
Solution: Because both ends of the pipe are open, the length of the pipe, L, must be a whole number of half-wavelengths: L = 1(λ/2), 2(λ/2), 3(λ/2)…, in order to support standing waves. Therefore, the possible harmonic wavelengths are λ = 2L/1, 2L/2, 2L/3, and so on. The second longest is λ = 2L/2 = L = 3 m, choice A.
In the previous chapter, it was mentioned that if two waves with different frequency interfere, the resultant wave will be complicated. If the two waves are sound waves with slightly different frequencies (the difference is less than about 10 Hz), the product is a pulsating, “wobbling” resultant wave. This produces the phenomenon known as beats. Because the frequencies don’t match, sometimes the waves are in phase and sometimes they’re out of phase. When they’re in phase, their amplitudes add; when they’re out of phase, their amplitudes subtract. The combined waveform reaches its maximum amplitude when the waves interfere constructively and its minimum amplitude when they interfere destructively, and these points alternate. Maximum amplitude sounds loud and minimum amplitude sounds soft, so we hear loud, soft, loud, soft, etc. The resulting equally spaced moments of constructive interference (the loud moments) are the beats.
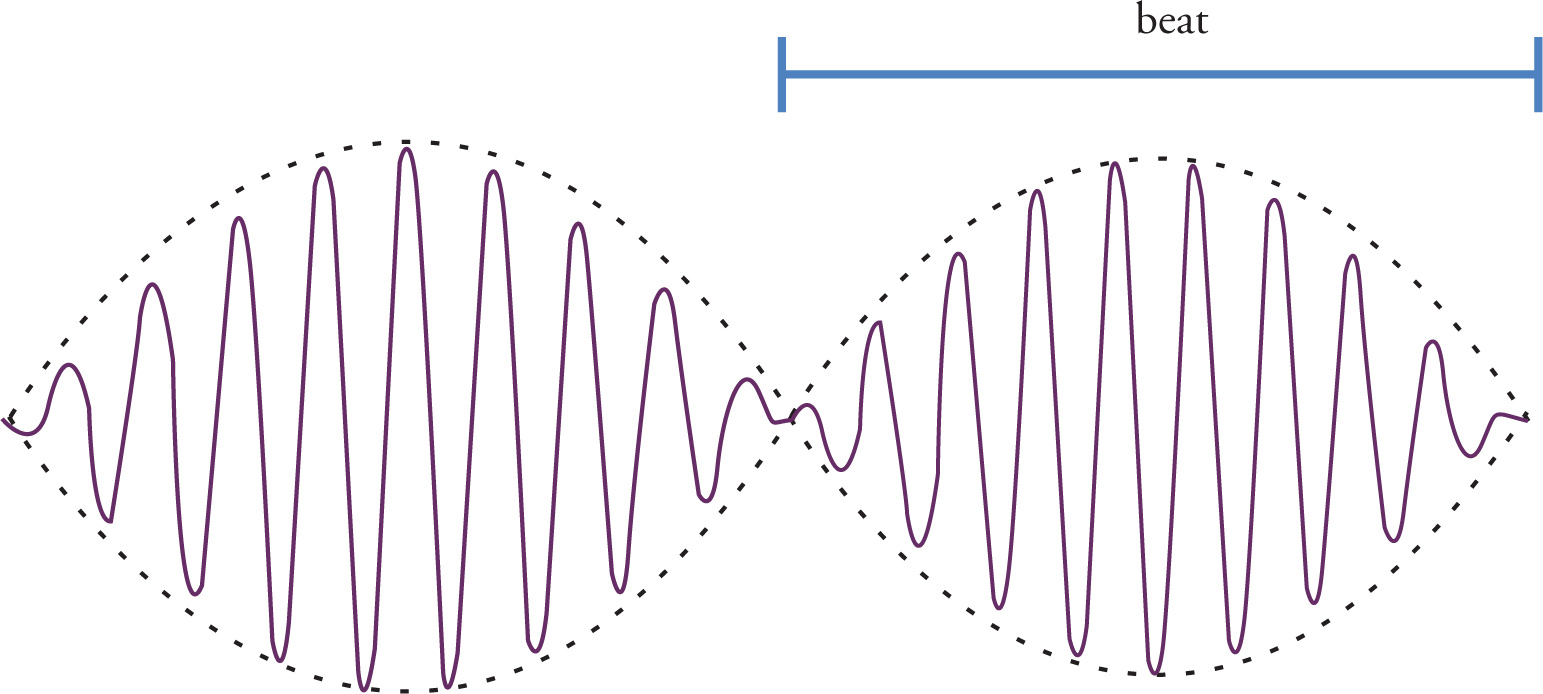

The frequency at which the beats are heard (the beat frequency) is equal to the difference between the frequencies of the two original sound waves. Therefore, if one of these waves has frequency f1 and the other has frequency f2, then fbeat = |f1 − f2|.
Beat Frequency
fbeat = |f1 − f2|
Example 12-8: A piano tuner strikes a tuning fork at the same time he strikes a piano key with a note of similar pitch. If he hears 3 beats per second, and the tuning fork produces a standard 440 Hz tone, then what must be the frequency produced by the struck piano string?
A. 437 Hz
B. 443 Hz
C. 437 Hz or 443 Hz
D. 434 Hz or 446 Hz
Solution: If fbeat = 3 Hz, then the frequencies of the tuning fork and piano string are “off” by 3 Hz. The frequency produced by the piano string might be 3 Hz lower or 3 Hz higher than the tuning fork; without more information, we don’t know which one. If the tuning fork produces a tone of frequency 440 Hz, the piano string produces a frequency of either 440 − 3 = 437 Hz or 440 + 3 = 443 Hz. Choice C is the answer.
Intensity and intensity level are closely related quantities. The intensity of a sound wave (or, indeed, any wave) is the energy it transmits per second (the power) per unit area. It is measured in W/m2. For a point source (i.e., one that creates waves that travel uniformly in all directions), the area in the equation is the surface area of a sphere, which equals 4πr2. Each wavefront in the figure below can be thought of as a bundle of energy that is expanding in size, much like a balloon being blown up. The farther a detector is from the source, the larger the bundle of energy will be, and therefore the detector will receive a smaller fraction of it.
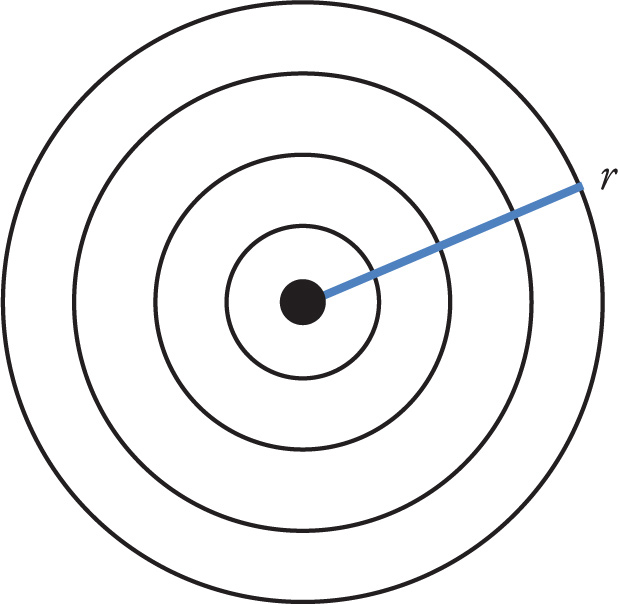

Mathematically, the important fact to remember is that, for a point source, intensity varies inversely as the square of the distance r from that source: I ∝ 1 / r2. If the detector of a wave doubles his distance from the source, the power produced by the wave will spread out over an area that is 22 = 4 times larger, causing the detector to receive ¼ as much. Intensity is also proportional to the square of the amplitude of a wave.
Since the intensity that we can hear spans an impressively large range (about twelve orders of magnitude!), we use logarithms to make the numbers easier to handle. The threshold of hearing, which is roughly the lowest intensity the human ear can perceive as sound at the common middle frequencies, is equal to 10–12 W/m2; this intensity is denoted by I0. The intensity level (or sound level) of a sound wave whose intensity is I is equal to the base-10 logarithm of the ratio I/I0. The unit of intensity level is the bel, abbreviated B. Usually, we multiply this by 10 to get the intensity level, β, in decibels (dB):
Intensity Level in Decibels
β = 10 log10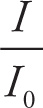
![]()
The most important relationship to get from this equation can be summarized as follows:
Every time we multiply I by 10, we add 10 to β.
Every time we divide I by 10, we subtract 10 from β.
For example, if the intensity is multiplied by 10,000, which is 10 × 10 × 10 × 10, the intensity level in decibels is increased by adding 10 + 10 + 10 + 10 = 40. If we divide by the intensity by, say, 100,000 = 105, then the decibel level decreases by 50.
Example 12-9: At a distance of 1 m, the intensity level of a soft whisper is about 30 dB, while a normal speaking voice is about 60 dB. How many times greater is the power delivered per unit area by a normal-speaking voice than by a whisper?1
A. 2.5
B. 30
C. 1000
D. 3000
Solution: The normal speaking voice has an intensity level that’s 30 dB greater than the whisper. Therefore, the intensity must be 10 × 10 × 10 = 103 = 1000 times greater. Since “power delivered per unit area” is intensity, the answer is C.
Example 12-10: A person listening to music on a stereo system experiences a sound level of 70 dB. If the volume dial is turned up to increase the intensity by a factor of 500, what sound level would this person hear now?
A. 97 dB
B. 105 dB
C. 115 dB
D. 120 dB
Solution: If the intensity had increased by a factor of 100, which is 10 × 10, the sound level would have increased by 10 + 10 = 20 dB. If the intensity had increased by a factor of 1000, which is 10 × 10 × 10, the sound level would have increased by 10 + 10 + 10 = 30 dB. The fact that the intensity increased by a factor of 500, which is between 100 and 1000, means that the sound level increased by between 20 dB and 30 dB. If the original sound level was 70 dB, then the new sound level must be between 70 + 20 = 90 dB and 70 + 30 = 100 dB. Only choice A falls in this range.
Example 12-11: Suppose one moves 10 times further away from a loud siren of constant power. What is the resultant decrease in sound level?
A. 10 dB
B. 20 dB
C. 40 dB
D. 100 dB
Solution: Increasing distance by a factor of 10 decreases intensity by a factor of 100, which is 10 × 10. Therefore, sound level will be reduced by 10 + 10 = 20 dB, choice B.
Suppose a train that is loudly sounding its horn is approaching a passenger waiting on a platform. As the train is approaching, the person hears the pitch at a higher frequency than does the engineer on the train. As the train is moving away, the person on the platform hears a lower frequency than does the engineer. These differences in frequency are the result of the Doppler effect, which arises whenever a source of waves is moving relative to the detector. The result is that the perceived or detected frequency will be different from the frequency of the sound that was emitted from the source.
Normally when a sound is emitted from a source, the rate of the compressions (or frequency, f) is detected as the wave travels at speed v towards the detector. The most important fact to remember is that if the source and detector are moving closer together (no matter which is moving), the detected frequency with be higher than the emitted frequency. Similarly, if the source and detector are moving farther apart, the detected frequency will be lower than the emitted frequency.
Doppler Effect
approaching ↔ higher detected frequency
receding ↔ lower detected frequency
For sound, if the detector moves toward the source or if the source moves toward the detector, the detected frequency will be higher than the emitted frequency. But the reasons are different.
If a detector moves toward (or away from) a stationary source, the relative speed of sound changes. As an example, if a sound wave is moving toward the detector at 340 m/s and the detector moves toward the source at 20 m/s, the wave will appear to be moving at 360 m/s in the detector’s frame of reference. Similarly, if the detector is moving away from the source at 20 m/s, the wave will appear to moving at 320 m/s. The wavelength (i.e., the spacing between wavefronts) will not change. According to the wave equation, v = λf, an increase (or decrease) in perceived wave speed with a constant wavelength will cause an increase (or decrease) in perceived frequency.
If the source moves, the waves themselves become distorted. Say a source emits a pulse that spreads out in all directions. The wavefront is a sphere, though in 2 dimensions it looks like a circle. If the source moves to the right the next pulse it emits would again look like a circle, but whose center is to the right of the previous pulse’s center. The wavefronts bunch up on the right and spread out on the left. The wavelength has therefore changed. If the detector is at rest, then the speed of the wave hasn’t changed. According to the wave equation, v = λf, an increase (or decrease) in wavelength with a constant wave speed will result in a decrease (or increase) in frequency.
No relative motion between the source (S) and detectors (D1 and D2)
Each wave compression emitted by S arrives at the same speed when perceived by D1 and D2. The perceived frequency is the same.
No Doppler shifts.


Here, there is relative motion between the source (S) and detectors (D1 and D2).
D1 is approaching S, so each compression of the wave emitted from S requires less time to reach D1. The perceived wave speed at D1 is faster, and thus the frequency at D1 is higher.
D2 is receding from S, so each compression of the wave requires more time to reach D2. The perceived wave speed at D2 is slower, and thus the perceived frequency is lower.


Here, there is relative motion between the source (S) and detectors (D1 and D2).
S is approaching D1, so the compressions of the wave emitted from S are closer together. The perceived wavelength at D1 is shorter, and thus the frequency at D1 is higher.
S is receding from D2, so the compressions of the wave emitted from S are farther apart. The perceived wavelength at D2 is longer, and thus the frequency at D2 is lower.
To predict exactly what the perceived frequency will be, we need an equation. Despite the fact that there are lots of individual cases to consider (whether the source and/or the detector are stationary or in motion), we can summarize everything in a single equation:
Doppler Effect
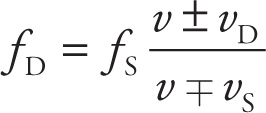
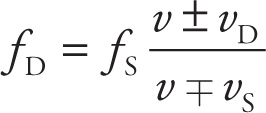
In this equation:
fD = the frequency heard by the detector
fS = the frequency emitted by the source
vD = the speed at which the detector is moving
vS = the speed at which the source is moving
v = the speed of the wave
What we need to do to make this one equation fit all the possible cases is use the conceptual relationships given in the box on the previous page to decide whether to use the + or – in the numerator and whether to use + or – in the denominator.
Notice that we have written ± in the numerator and ∓ in the denominator; one way to memorize the sign conventions for this equation is by the mnemonic “top sign is toward.” When the motion of the detector is toward the source, you use the top of ±, or the “+” sign, in the numerator. When the motion of the source is toward the detector, you use the top of ∓, or the “–” sign, in the denominator.
For example, suppose the source is stationary and the detector is moving toward it. Because vS = 0, there’s no decision to make in the denominator. Now, we know that fD will be higher than fS in this case. Therefore, we choose the + in the numerator, to make the fraction multiplying fS bigger, to give the higher fD we expect:
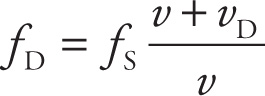
![]() (adding vD makes the numerator bigger)
(adding vD makes the numerator bigger)
If the detector is moving away from the stationary source, we know that fD will be lower than fS in this case. Therefore, we choose the – in the numerator to make the fraction multiplying fS smaller, to give the lower fD we expect:

![]() (subtracting vD makes the numerator smaller)
(subtracting vD makes the numerator smaller)
Now, suppose the detector is stationary and the source is moving toward it. Since vD = 0, there’s no decision to make in the numerator. We know that fD will be higher than fS in this case. Therefore, we choose the—in the denominator, to make the denominator smaller, and thus make the fraction multiplying fS bigger, to give the higher fD we expect:

![]() (subtracting vS makes the denominator smaller)
(subtracting vS makes the denominator smaller)
If the source is moving away from the stationary detector, we know that fD will be lower than fS in this case. Therefore, we choose the + in the denominator, to make the denominator bigger, and thus make the fraction multiplying fS smaller, to give the lower fD we expect:

![]() (adding vS makes the denominator bigger)
(adding vS makes the denominator bigger)
If both the source and the detector are moving, we have two decisions to make (one in the numerator and one in the denominator). The key is to make the two decisions separately. For example, let’s say you’re the detector, driving in your car following a police car whose siren is wailing. In this case, both the source (the police car) and the detector (you) are moving. To decide what to do in the numerator, ask yourself: what’s the detector doing? It’s approaching the source, so its “contribution” to the Doppler effect should be an increase in frequency. Therefore, we’d choose the + in the numerator. Now, what’s the source doing? It’s receding from the detector, so its “contribution” to the Doppler effect should be a decrease in frequency. Therefore, we’d choose the + in the denominator.


If your speed is greater than that of the police car, you’re gaining on it, so the relative motion is motion toward. We’d expect fD to be greater than fS. If vD > vS, then the fraction multiplying fS is bigger than 1, so fD will indeed be greater than fS. On the other hand, if your speed is less than that of the police car, it’s pulling away from you, so the relative motion is motion away. In this case, we’d expect fD to be lower than fS. Further, if vD < vS, then the fraction multiplying fS is less than 1, so fD will indeed be lower than fS. Finally, it’s important to notice what happens if your speed is the same as the police car’s speed. If vD = vS, then the fraction multiplying fS is equal to 1, so fD = fS. Therefore, even though you’re both moving, there’s no Doppler shift because there’s no relative motion between you.
The Doppler effect also applies to electromagnetic waves, such as visible light. The same qualitative relationships continue to hold: motion toward results in a frequency shift upward, while motion away results in a frequency shift downward. An astronomer observing a star moving away from the earth observes the light emitted as being shifted downward in frequency, toward the red end of the visible spectrum (in fact, this is known as the redshift). Furthermore, by measuring the shift, the astronomer can calculate how fast the star is moving away from us.2
Example 12-12: A speaker emitting a sound with a constant frequency approaches a detector. Which of the following wave characteristics will have a greater value at the detector than at the source?
I. Frequency
II. Wavelength
III. Speed
Solution: Since the source is approaching the detector, the detected frequency will be higher than the emitted frequency. The wavelength will be shorter, and the wave speed will be the same. Therefore, only characteristic I will have a greater value at the detector than at the source.
Example 12-13: When you push the “star” key on your cell phone, a tone whose frequency is about 1080 Hz is emitted. However, the button gets stuck and the tone is continuous. Exasperated, you drop the broken phone off a bridge. What is the frequency of the tone you hear at the instant the phone’s speed is 20 m/s (speed of sound in air = 340 m/s)?
Solution: Since you (the detector) are stationary, vD = 0. Now, because the source of the sound (the broken phone) is moving away from you, we use the plus sign on vS in the denominator of the Doppler effect equation to find that


Note that, because the phone is accelerating away from you, the magnitude of vS is increasing as the phone falls, and thus the frequency you detect is decreasing as a function of time.
Example 12-14: As a high-speed chase begins, a police car travels at a speed of 40 m/s directly toward the suspect’s getaway car, which is traveling at a speed of 70 m/s, trying to outrun the pursuing police. The frequency that the suspect hears will be what percentage of the frequency of the police car’s siren? (speed of sound = 340 m/s)
Solution: Use the Doppler effect equation, choosing the signs carefully. The suspect in the getaway car is the detector (so vD = 70 m/s), moving away from the source. The source is the police car (vS = 40 m/s), moving toward the detector. Therefore,
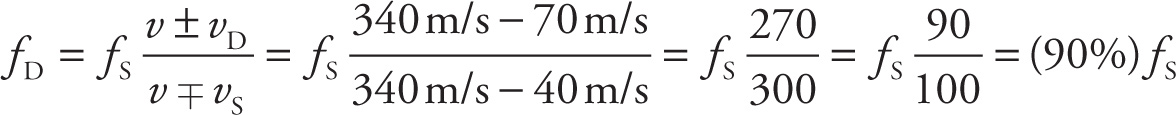
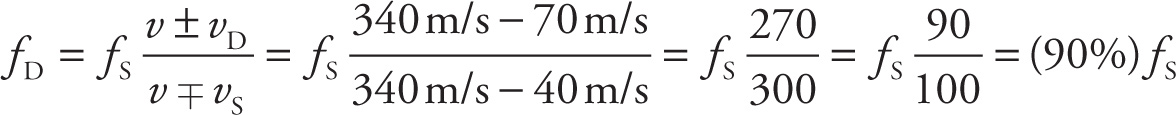
In order to find the correct value of fD, it was necessary to plug in the values for vD and vS, and to change the top and the bottom of the equation separately; we couldn’t just use the relative velocity of 30 m/s. However, if all the problem had asked for was the qualitative effect (i.e., whether the detected frequency was higher or lower than that of the source), then we could have worked out that the frequency was lower simply by noticing that the detector was getting farther away from the source.
Example 12-15: A policeman in a stationary police cruiser is using his radar gun to catch speeders. The radar gun emits microwaves (of frequency 1010 Hz), which then bounce off a passing car and return to a detector in the cruiser. The detector compares the final received frequency, f2, with the original emitted frequency, f1, and converts the difference in frequency into the speed of the car. The difference in frequency, ∆f = f2 – f1, is equal to ±2vf1/c, where v is the speed of the car and c = 3 × 108 m/s is the speed of the microwaves. If ∆f = −2600 Hz, then the observed car is:
A. approaching the police cruiser at 26 m/s.
B. driving away from the police cruiser at 26 m/s.
C. approaching the police cruiser at 39 m/s.
D. driving away from the police cruiser at 39 m/s.
Solution: First, the fact that ∆f is negative means that f2 is lower than f1, and if the final detected frequency is lower than the frequency emitted by the source, then the car must be moving away from the source. This eliminates choices A and C. Now, to figure out the value of the car’s speed, v, we just use the given formula:


Standing Waves in a Tube:
| Both ends open: | λn =  |
fn =  |
|
| One end closed: |   |
fn =  |
Beats, Intensity, Doppler Effect:
| Beat frequency: | fbeat = |f1 − f2| |
| Intensity: |  |
I is inversely proportional to r2 (where r = distance from source), and directly as the square of the wave amplitude.
Sound intensity level (in decibels, dB): β = 10 log10 
![]()
(where I0 = 10–12 W/m2 = 0 threshold of hearing)
multiply I by 10 ↔ add 10 to β.
divide I by 10 ↔ subtract 10 from β.
Doppler effect: describes the change in frequency between a source and a detector due to relative motion of both
relative motion toward ↔ frequency increase (fD > fS)
relative motion away ↔ frequency decrease (fS > fD)
For constant velocities, this shift is constant. The frequency is not increasing or decreasing with time, but is simply a higher or lower constant at the detector than at the source. Relative acceleration creates an increasing or decreasing frequency.
Doppler effect (for waves other than light): fD = fS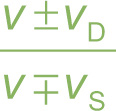
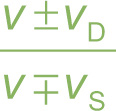
1. When all the finger holes on a clarinet are closed, it can be approximated as a hollow tube with one closed end (mouthpiece) and one open end. When all the finger holes on a clarinet are closed, the lowest pitch that can be produced corresponds to the G below middle C (186 Hz). How long is the clarinet? (assume the speed of sound in air is 340 m/s).
A) 90 cm
B) 70 cm
C) 50 cm
D) 30 cm
2. A 75 cm glass pipe that is open at both ends is placed next to a student a cappella group. It was observed that the pipe first resonates when the choir produces a note at 450 Hz. At which subsequent frequencies will resonance again be observed? (The speed of sound through the pipe is 340 m/s.)
A) 675 Hz and 900 Hz
B) 675 Hz and 1350 Hz
C) 900 Hz and 1350 Hz
D) 900 Hz and 1800 Hz
3. The engine of a small and unmanned airplane produces a known and specific sound frequency (not given). A stationary sound detection device observes that the known emitted sound frequency is 90% of the perceived sound frequency. Relative to the detection device, in which direction and at what velocity is the plane moving?
A) Towards the detector, at 34 m/s
B) Away from the detector, at 34 m/s
C) Towards the detector, at 64 m/s
D) Away from the detector, at 64 m/s
4. An airplane is traveling 157 m/s north on a runway and is producing a sound of frequency f. A woman is seated in a car moving 43 m/s to the south, away from the airplane. What frequency will she observe? (assume the speed of sound in air is 343 m/s)
A) 1/2 f
B) 3/5 f
C) f
D) 2 f
5. A man standing 1 m away from an omnidirectional speaker is exposed to a sound of 140 dB. How far would he have to travel in order to no longer be in pain (the threshold of pain is about 120 dB), given I = P/A and β = 10 log(I / I0), where I0 = 10−12 W/m2.
A) 9 m
B) 10 m
C) 20 m
D) 100 m
6. A stationary cat is purring. Which of the following correctly explains why its owner hears a frequency that is higher than that which is produced by the cat?
A) The owner is moving towards the cat.
B) The owner is moving away from the cat.
C) Both are on an accelerating train.
D) Both are on a decelerating boat.
7. A herpetologist studying alligators at the Kennedy Space Center is 1000 m from the launch pad, when a siren sounds, signaling 30 minutes to launch. After running for 4000 m, the herpetologist turns to watch the launch. How does the intensity of sound produced by the siren at his new location compare to the original intensity, I1, given I = P/A?
A) 5 I1
B) 1/5 I1
C) 1/25 I1
D) 1/50 I1
Sound waves propagate away from a source in spherical wavefronts, lines that connect the points on sound wave that were emitted at the same time. When the source is stationary, these wave fronts are concentric spheres centered about the source. However, when the source begins to move with a velocity v0, the wavefronts get closer together in the direction of v0 and are spread farther apart in the opposite direction.


Figure 1 Wavefronts generated by sound sources that are stationary and moving with a speed less than the speed of sound.
As a result of the change in the distance between wavefronts, a listener standing ahead or behind the object will hear a frequency different from the original emitted frequency, a phenomenon known as the Doppler effect, according to the equation:

![]()
Equation 1
where fD and fS are the detected and emitted frequencies, respectively, v is the speed of sound, and vD and vS are the velocities of the detector and the source, respectively.
Some jets have been designed to fly at speeds greater than the speed of sound. There speeds are usually given as a Mach number, M = v0/v, which indicates the jet’s speed relative to the speed of sound in the surrounding air. Because the speed of sound in air increases as the temperature increases, the jets flying with the same Mach number can be travelling at different speeds. When a jet flies at exactly Mach 1, the wavefronts build up just in front of the object, creating an intense shock wave. Flight at this speed is incredibly turbulent. Interestingly, in this case an observer ahead of the jet would not hear it until the jet itself arrived, since the first wavefront and the jet arrive at the same time. Jets can also fly faster than the speed of sound, at supersonic speeds. When this happens, the jet actually advances ahead of the shock wave it creates. The intense sound heard when a shockwave passes by an observer is known as a sonic boom.


Figure 2 Wavefronts created by a jet flying at the speed of sound and at a supersonic speed.
1. Two jets are flying at Mach 3, one close to sea level, the other at 50,000 ft where the air temperature is cooler. Compared to the jet at sea level, the one flying at 50,000 ft is travelling:
A) at the same speed.
B) at a lower speed because the speed of sound decreases at altitude due to the lower air temperature.
C) at a greater speed because the speed of sound decreases at altitude due to the lower air temperature.
D) at a greater speed because the speed of sound increases at altitude due to the greater air temperature.
2. While driving down the road at 10 m/s, a driver hears 330 Hz siren from police car approaching from behind. If the frequency emitted by the siren is 300 Hz, how fast is the police car going?
A) 9 m/s
B) 10 m/s
C) 20 m/s
D) 40 m/s
3. A stationary observer is standing on a sidewalk when a police car emitting a 300 Hz siren passes by on the road at 20 m/s. Just as the police car passes her, what is the frequency she hears?
A) 283 Hz
B) 300 Hz
C) 318 Hz
D) 340 Hz
4. If the sonic boom that the jet produces when it goes supersonic is 60 dB louder than acceptable limits for the people on the base below, at minimum how many times farther away should it be from the base when it goes supersonic?
A) 103
B) 104
C) 105
D) 106
5. As a siren approaches an observer at a constant velocity, the observer hears a sound that is:
A) increasing in frequency.
B) at a constant frequency that is higher than the emitted frequency.
C) at a constant frequency that is lower than the emitted frequency.
D) decreasing in frequency.
6. What is a possible explanation for why flying at Mach 1 results in incredibly turbulent flight?
A) The transverse motion of the air molecules of the sound wave jostle the vessel up and down.
B) The transverse motion of the air molecules of the sound wave make it difficult for the pilot to steer.
C) The build-up of sound waves in front of the jet creates an extreme pressure front.
D) Jets are increasingly structurally unstable the faster they travel.
7. A jet flying at Mach 2 flies directly over a ship in the ocean. When the observers on the ship hear the jet, the jet is:
A) approaching the ship.
B) directly overhead.
C) already past the ship.
D) somewhere in the vicinity of the ship, but it is impossible know where it is in its path over the ship.
1. C The clarinet with all its finger holes closed approximates a hollow tube with one closed end and one open end can be diagrammed as below:


There is only one quarter (not one half) of a wavelength, and so the length of the pipe must be one-quarter the wavelength of the sound wave. The first (or fundamental) harmonic of a pipe with one closed end is f1 = v/4L, where L is the length of the pipe. Rearranging this formula: L = v/4 f1 = 340 m/s / [(4)(186)]) = 0.5 m.
2. C If the pipe first resonated at 450 Hz, then the fundamental frequency (f1) of the standing wave in the pipe is 450 Hz. The subsequent frequencies that will produce resonance are f2, f3, f4, … fn. These can be calculated using the equation fn = nf1. Since f1 is given to us, the next resonance will be at f2 = (2)(450) = 900 Hz, and the resonance after that will be f3 = (3)(450) = 1350 Hz.
3. A The Doppler effect is measured using the equation fD = fS[v ± vD]/[v ∓ vS]. The prompt tells us that the emitted sound frequency (fS) is 90% of the perceived sound frequency (fD), therefore fD/fS = 10/9. Since the detected sound frequency is greater than the perceived sound frequency (fD/fS > 1), and the sound detector is stationary (vD = 0), then the Doppler effect dictates that the source must be moving towards the detector (v – vS), eliminating choices B and D. To calculate the velocity of the sound source, we must solve for vS using the Doppler effect:
fD/fS = v/(v – vS)
(fD/fS)(v – vS) = v
(fD/fS) × v – (fD/fS) × vS = v
[(fD/fS) − 1] × v = (fD/fS) × vS
vS = (fS/fD) × v × [(fD/fS) − 1]
vS = (340 m/s) × (9/10) × [(10/9) − 1] = 340 / 10 = 34 m/s
4. B This is a Doppler shift question, and thus begins with using the Doppler equation: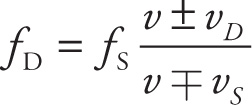
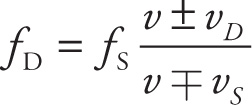
The speed of the detector (vD) is subtracted in the numerator because the car is moving away from the source, and thus the frequency observed will be lower than that produced. Addition is used in the denominator because the source, the airplane, is moving away from the detector and thus the frequency needs to be decreased. Subsequently plugging into the equation yields


which gives choice B as correct. Both choices C and D can be eliminated because when two objects are moving apart, the frequency needs to decrease. (Note that if addition were used in the numerator and subtraction in the denominator, thus reversing the relationship and causing the frequency to increase, the answer would approximate 390/190 or approximately 2 f, which is choice D.)
5. A A difference of 20 dB means a decrease in intensity of 102. This can either be gathered from the given logarithmic equation [20 = 10 log(I/I0) → 2 = log(I/I0) and therefore I = 102)] or by remembering that for every time 10 is added or subtracted from β, 10 is multiplied or divided from I, respectively. Knowing that I decreased by a factor of 100 means that the area would have had to increase by a factor of 100, since the power stays constant (from I = P/A). Since A ∝ r2, the radius must increase by a a factor of 10. Since the man was already 1 m from the source, he will have to travel 9 m. Choice B is a trap answer which ignores the original 1 m. Choice C is simply the number of dB dropped. Choice D is a trap which is equal to the factor that intensity is reduced.
6. A Choices C and D are both incorrect; they will have no effect on the frequency heard since the action is occurring to both the observer and the source. Choice B is backwards, because approaching objects will experience an increase in frequency (choice A is correct).
7. C Since the new radius is 5 times the original radius, the area will increase by 25 times (remembering that A is proportional to r2). Since the area will increase by a factor of 25, the intensity will decrease by that factor (they are inversely proportional), giving choice C. Choice A can be eliminated because it assumes a direct, rather than inverse, relationship between the intensity and the area. Choice B is a trap; it is the correct answer if one forgets to square the multiple of the radius.
1. B Since M = v0/v, for a given Mach number, v0 and v are directly related. The passage indicates that the speed of sound increases with increasing air temperature. Thus, at 50,000 ft where the air is cooler, the speed of sound is lower than at sea level. As a result the jet flying at 50,000 ft must be flying more slowly than the jet flying at sea level, even though they are travelling at the same Mach number.
2. D Since the detected frequency is greater than the emitted frequency, choices A and B be eliminated since these velocities would not result in the siren approaching the observer. Using the fact that the detector is moving away from the source and that the source is approaching the detector, we obtain the equation fD = fS (v – vD)/(v – vS). Plugging the given values into the equation yields 330 Hz = 300 Hz (340 m/s − 10 m/s)/(340 m/s – vS) → 330 = 300 (330)/(340 –vS) → 340 – vS = 300 → vS = 40 m/s.
3. B As the siren is passing the observer, the siren is neither moving towards nor away from the listener. As a result, there is no difference between the detected and the emitted frequencies.
4. A In order to decrease the sound by 60 dB, the intensity of the sonic boom must be decreased by a factor 106. Although this result makes choice D a tempting answer choice, it must be remembered that intensity is proportional to 1/r2. As a result, in order to decrease the intensity by a factor of 106, the radius only has to increase by a factor of 103.
5. B If a sound source is approaching the observer, the frequency should increase, which eliminates choices C and D. If the siren is moving at a constant velocity, then as it approaches, the fraction (v − vD)/(v – vS), which indicates the frequency shift, is constant, not continually increasing, which eliminates choice A.
6. C Since sound is a pressure wave, a buildup of many sound waves does create an extreme pressure front. Choices A and B cannot be correct since sound is not a transverse wave. Although there may be some regime in which jets do become more structurally unstable the faster they fly, it does not answer the question since the passage mentions that the extreme turbulence is felt at exactly Mach 1, not at all speeds greater than Mach 1, indicating that choice D cannot explain this particular phenomenon.
7. C As indicated by the passage, a supersonic jet flies ahead of the shockwave it creates. Therefore, when the observers hear the shockwave as it passes, the jet has already passed by.
1 Our perception of loudness is completely different from both intensity and intensity level. Roughly speaking, a difference in intensity level of 10 dB (and therefore a factor of 10 in intensity) corresponds to a perceived loudness difference of a factor of 2.
2 For light waves, the equation that is used to calculate the magnitude of the Doppler effect is different. This is because of a postulate of special relativity: the speed of light is the same in all frames of reference. The detector, therefore, cannot perceive the speed of light to be faster or slower than 3 × 108 m/s. Another way of saying this is that we can always treat the detector as being at rest while the source may move.