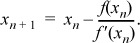
To review Newton’s method very briefly, we are given a differentiable function f of a real variable x and we wish to solve the equation f(x) = 0 for x. Given a current estimate xn of a root of f, Newton’s method gives us a better estimate xn + 1 under suitable conditions, according to the formula
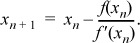
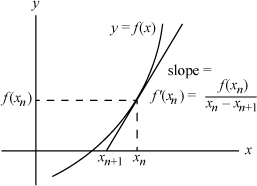
Here, f′(xn) is the derivative of f at x = xn. The derivation of this formula can be read off the figure below (solve for xn + 1).
The method works very well for simple, well-behaved functions such as polynomials, provided the first estimate is quite close. Once an estimate is sufficiently close, the method converges quadratically. That is, if r is the exact value of the root, and xn is a sufficiently close estimate, then
|xn + 1 − r| ≤ (xn − r)2.
Thus, the number of digits of accuracy doubles with each iteration (e.g., if |xn − r| ≤ 0.001 then |xn + 1 − r| ≤ 0.000001).
If the first estimate is way off, then the iterations may converge very slowly, may diverge to infinity, may converge to a root other than the one closest to the first estimate, or may loop among certain values indefinitely.
This discussion has been quite vague because of phrases like “suitable conditions,” “well-behaved,” and “sufficiently close.” For a more precise discussion, consult almost any first-year calculus textbook.
In spite of the caveats surrounding this method, it is occasionally useful in the domain of integers. To see whether or not the method applies to a particular function, you have to work it out, such as is done in Section 11–1, “Integer Square Root,” on page 279.
Table B–1 gives a few iterative formulas derived from Newton’s method, for computing certain numbers. The first column shows the number it is desired to compute. The second column shows a function that has that number as a root. The third column shows the right-hand side of Newton’s formula corresponding to that function.
TABLE B–1. NEWTON’S METHOD FOR COMPUTING CERTAIN NUMBERS
It is not always easy, incidentally, to find a good function to use. There are, of
course, many functions that have the desired quantity as a root, and only a few of
them lead to a useful iterative formula. Usually, the function to use is a sort of
inverse of the desired computation. For example, to find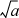 
use f(x) = x2 − a; to find log2a use f(x) = 2x − a, and so on.1
The iterative formula for log2a converges (to log2a) even if the multiplier 1/ln2 is altered somewhat (for example, to 1, or to 2). However, it then converges more slowly. A value of 3/2 or 23/16 might be useful in some applications (1/ln2 ≈ 1.4427).