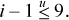
By “bounds checking” we mean to verify that an integer x is within two bounds a and b—that is, that
a ≤ x ≤ b.
We first assume that all quantities are signed integers.
An important application is the checking of array indexes. For example, suppose a one-dimensional array A can be indexed by values from 1 to 10. Then, for a reference A(i), a compiler might generate code to check that
1 ≤ i ≤ 10
and to branch or trap if this is not the case. In this section we show that this check can be done with a single comparison, by performing the equivalent check [PL8]:
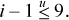
This is probably better code, because it involves only one compare-branch (or compare-trap), and because the quantity i– 1 is probably needed anyway for the array addressing calculations.
Does the implementation
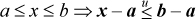
always work, even if overflow may occur in the subtractions? It does, provided we somehow know that a ≤ b. In the case of array bounds checking, language rules may require that an array not have a number of elements (or number of elements along any axis) that are 0 or negative, and this rule can be verified at compile time or, for dynamic extents, at array allocation time. In such an environment, the transformation above is correct, as we will now show.
It is convenient to use a lemma, which is good to know in its own right.
LEMMA. If a and b are signed integers and a ≤ b, then the computed value b – a correctly represents the arithmetic value b − a, if the computed value is interpreted as unsigned.
Proof. (Assume a 32-bit machine.) Because a ≤ b, the true difference b − a is in the range 0 to (231 − 1) − (−231) = 232 − 1. If the true difference is in the range 0 to 231 − 1, then the machine result is correct (because the result is representable under signed interpretation), and the sign bit is off. Hence the machine result is correct under either signed or unsigned interpretation.
If the true difference is in the range 231 to 232 − 1, then the machine result will differ by some multiple of 232 (because the result is not representable under signed interpretation). This brings the result (under signed interpretation) to the range −231 to −1. The machine result is too low by 232, and the sign bit is on. Reinterpreting the result as unsigned increases it by 232, because the sign bit is given a weight of + 231 rather than −231. Hence the reinterpreted result is correct.
The “bounds theorem” is
THEOREM. If a and b are signed integers and a ≤ b, then
Proof. We distinguish three cases, based on the value of x. In all cases, by the lemma, since a ≤ b, the computed value b – a is equal to the arithmetic value b – a if b – a is interpreted as unsigned, as it is in Equation (1).
Case 1, x < a: In this case, x – a interpreted as unsigned is x– a + 232. Whatever the values of x and b are (within the range of 32-bit numbers),
x + 232 > b.
Therefore
x– a + 232 > b−a,
and hence
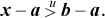
In this case, both sides of Equation (1) are false.
Case 2, a ≤ x ≤ b: Then, arithmetically, x − a ≤ b − a. Because a ≤ x, by the lemma x − a equals the computed value x − a if the latter is interpreted as unsigned. Hence
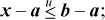
that is, both sides of Equation (1) are true.
Case 3, x > b: Then x − a > b − a. Because in this case x > a (because b ≥ a), by the lemma x − a equals the value of x − a if the latter is interpreted as unsigned. Hence
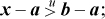
that is, both sides of Equation (1) are false.
The theorem stated above is also true if a and b are unsigned integers. This is because for unsigned integers the lemma holds trivially, and the above proof is also valid.
Below is a list of similar bounds-checking transformations, with the theorem above stated again. These all hold for either signed or unsigned interpretations of a, b, and x.
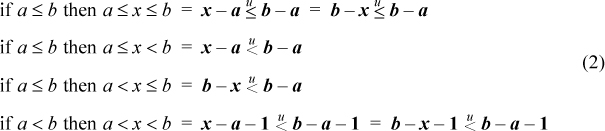
In the last rule, b – a – 1 can be replaced with b + ¬a.
There are some quite different transformations that may be useful when the test is of the form –2n–1 ≤ x ≤ 2n–1 – 1. This is a test to see if a signed quantity x can be correctly represented as an n-bit two’s-complement integer. To illustrate with n = 8, the following tests are equivalent:
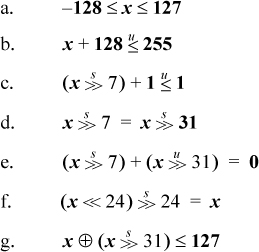
Equation (b) is simply an application of the preceding material in this section. Equation (c) is as well, after shifting x right seven positions. Equations (c) – (f) and possibly (g) are probably useful only if the constants in Equations (a) and (b) exceed the size of the immediate fields of the computer’s compare and add instructions.
Another special case involving powers of 2 is
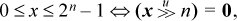
or, more generally,
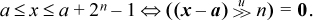
Some optimizing compilers perform “range analysis” of expressions. This is the process of determining, for each occurrence of an expression in a program, upper and lower bounds on its value. Although this optimization is not a really big winner, it does permit improvements such as omitting the range check on a C “switch” statement and omitting some subscript bounds checks that compilers may provide as a debugging aid.
Suppose we have bounds on two variables x and y as follows, where all quantities are unsigned:
Then, how can we compute tight bounds on x + y, x – y, and – x? Arithmetically, of course, a + c ≤ x + y ≤ b + d; but the point is that the additions may overflow.
The way to calculate the bounds is expressed in the following:
THEOREM. If a, b, c, d, x, and y are unsigned integers and
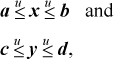
then
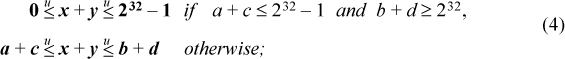
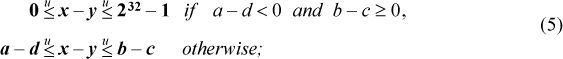
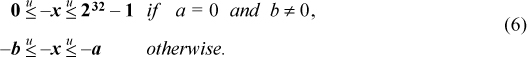
Inequalities (4) say that the bounds on x + y are “normally” a + c and b + d, but if the calculation of a + c does not overflow and the calculation of b + d does overflow, then the bounds are 0 and the maximum unsigned integer. Equations (5) are interpreted similarly, but the true result of a subtraction being less than 0 constitutes an overflow (in the negative direction).
Proof. If neither a + c nor b + d overflows, then x + y, with x and y in the indicated ranges, cannot overflow, making the computed results equal to the true results, so the second inequality of (4) holds. If both a + c and b + d overflow, then so also does x + y. Now arithmetically, it is clear that
a + c−232 ≤ x + y −232 ≤ b + d − 232.
This is what is calculated when the three terms overflow. Hence, in this case also,
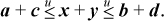
If a + c does not overflow, but b + d does, then
a + c ≤ 232 − 1 and b + d ≥ 232.
Because x + y takes on all values in the range a + c to b + d, it takes on the values 232 − 1 and 232—that is, the computed value x + y takes on the values 232 − 1 and 0 (although it doesn’t take on all values in that range).
Lastly, the case that a + c overflows, but b + d does not, cannot occur, because a ≤ b and c ≤ d.
This completes the proof of inequalities (4). The proof of (5) is similar, but “overflow” means that a true difference is less than 0.
Inequalities (6) can be proved by using (5) with a = b = 0, and then renaming the variables. (The expression – x with x an unsigned number means to compute the value of 232 − x, or of ¬x + 1 if you prefer.)
Because unsigned overflow is so easy to recognize (see “Unsigned Add/Subtract” on page 31), these results are easily embodied in code, as shown in Figure 4–1, for addition and subtraction. The computed lower and upper limits are variables
s and t, respectively.
FIGURE 4–1. Propagating unsigned bounds through addition and subtraction operations.
The case of signed numbers is not so clean. As before, suppose we have bounds on two variables x and y as follows, where all quantities are signed:
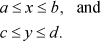
We wish to compute tight bounds on x + y, x − y, and – x. The reasoning is very similar to that for the case of unsigned numbers, and the results for addition are shown below.
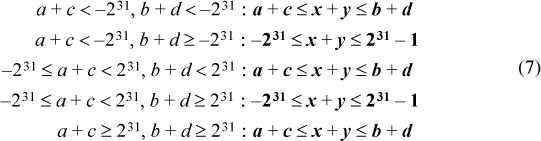
The first row means that if both of the additions a + c and b + d overflow in the negative direction, then the computed sum x + y lies between the computed sums a + c and b + d. This is because all three computed sums are too high by the same amount (232). The second row means that if the addition a + c overflows in the negative direction, and the addition b + d either does not overflow or overflows in the positive direction, then the computed sum x + y can take on the extreme negative number and the extreme positive number (although perhaps not all values in between), which is not difficult to show. The other rows are interpreted similarly.
The rules for propagating bounds on signed numbers through the subtraction operation can easily be derived by rewriting the bounds on y as
− d ≤ – y ≤ – c
and using the rules for addition. The results are shown below.
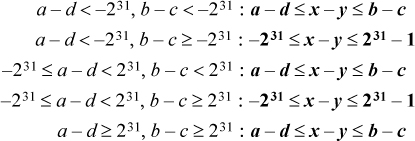
The rules for negation can be derived from the rules for subtraction by taking a = b = 0, omitting some impossible combinations, simplifying, and renaming. The results are as follows:
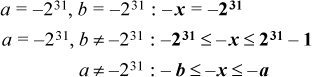
C code for the case of signed numbers is a bit messy. We will consider only addition.
It seems to be simplest to check for the two cases in (7) in which the computed limits
are the extreme negative and positive numbers. Overflow in the negative direction occurs if the two operands are negative and the sum is nonnegative
(see “Signed Add/Subtract” on page 28). Thus, to check for the condition that a + c < –231, we could let s = a + c; and then code something like “if (a < 0 && c < 0 && s >= 0) ....” It will be more efficient,1 however, to perform logical operations directly on the arithmetic variables, with
the sign bit containing the true/false result of the logical operations. Then, we
write the above condition as “if ((a & c & ~s) < 0) ....” These considerations lead to the program fragment shown in Figure 4–2.
s = a + c;
t = b + d;
u = a & c & ~s & ~(b & d &~t);
v = ((a ^ c) | ~(a ^ s)) & (~b & ~d & t);
if ((u | v) < 0) {
s = 0x80000000;
t = 0x7FFFFFFF;}
FIGURE 4–2. Propagating signed bounds through an addition operation.
Here u is true (sign bit is 1) if the addition a + c overflows in the negative direction, and the addition b + d does not overflow in the negative direction. Variable v is true if the addition a + c does not overflow and the addition b + d overflows in the positive direction. The former condition can be expressed as “a and c have different signs, or a and s have the same sign.” The “if” test is equivalent to “if (u < 0 || v < 0)—that is, if either u or v is true.”
As in the preceding section, suppose we have bounds on two variables x and y as follows, where all quantities are unsigned:
Then what are some reasonably tight bounds on x | y, x & y, x ⊕ y, and ¬x?
Combining inequalities (8) with some inequalities from Section 2–3 on page 17, and noting that ¬x = 232 − 1 − x, yields
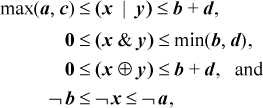
where it is assumed that the addition b + d does not overflow. These are easy to compute and might be good enough for the compiler application mentioned in the preceding section; however, the bounds in the first two inequalities are not tight. For example, writing constants in binary, suppose
Then, by inspection (e.g., trying all 36 possibilities for x and y), we see that 01010 ≤ (x | y) ≤ 10111. Thus, the lower bound is not max(a, c), nor is it a | c, and the upper bound is not b + d, nor is it b | d.
Given the values of a, b, c, and d in inequalities (8), how can one obtain tight bounds on the logical expressions? Consider first the minimum value attained by x | y. A reasonable guess might be the value of this expression with x and y both at their minima—that is, a | c. Example (9), however, shows that the minimum can be lower than this.
To find the minimum, our procedure is to start with x = a and y = c, and then find an amount by which to increase either x or y so as to reduce the value of x | y. The result will be this reduced value. Rather than assigning a and c to x and y, we work directly with a and c, increasing one of them when doing so is valid and it reduces the value of a | c.
The procedure is to scan the bits of a and c from left to right. If both bits are 0, the result will have a 0 in that position. If both bits are 1, the result will have a 1 in that position (clearly, no values of x and y could make the result less). In these cases, continue the scan to the next bit position. If one scanned bit is 1 and the other is 0, then it is possible that changing the 0 to 1 and setting all the following bits in that bound’s value to 0 will reduce the value of a | c. This change will not increase the value of a | c, because the result has a 1 in that position anyway, from the other bound. Therefore, form the number with the 0 changed to 1 and subsequent bits changed to 0. If that is less than or equal to the corresponding upper limit, the change can be made; do it, and the result is the or of the modified value with the other lower bound. If the change cannot be made (because the altered value exceeds the corresponding upper bound), continue the scan to the next bit position.
That’s all there is to it. It might seem that after making the change the scan should continue, looking for other opportunities to further reduce the value of a | c. However, even if a position is found that allows a 0 to be changed to 1, setting the subsequent bits to 0 does not reduce the value of a | c, because those bits are already 0.
C code for this algorithm is shown in Figure 4–3. We assume that the compiler will move the subexpressions ~a & c and a & ~c out of the loop. More significantly, if the number of leading zeros instruction is available, the program can be speeded up by initializing m with
m = 0x80000000 >> nlz(a ^ c);
unsigned minOR(unsigned a, unsigned b,
unsigned c, unsigned d) {
unsigned m, temp;
m = 0x80000000;
while (m != 0) {
if (~a & c & m) {
temp = (a | m)& -m;
if (temp <= b) {a = temp; break;}
}
else if (a & ~c & m) {
temp = (c | m) & -m;
if (temp <= d) {c = temp; break;}
}
m = m >> 1;
}
return a | c;
}
FIGURE 4–3. Minimum value of x | y with bounds on x and y.
This skips over initial bit positions in which a and c are both 0 or both 1. For this speedup to be effective when a ^ c is 0 (that is, when a = c), the machine’s shift right instruction should be mod-64. If number of leading zeros is not available, it may be worthwhile to use some version of the flp2 function (see
page 60) with argument a ^ c.
Now let us consider the maximum value attained by x |y, with the variables bounded as shown in inequalities (8). The algorithm is similar
to that for the minimum, except it scans the values of bounds b and d (from left to right), looking for a position in which both bits are 1. If such a
position is found, the algorithm tries to increase the value of c | d by decreasing one of the bounds by changing the 1 to 0, and setting all subsequent
bits in that bound to 1. If this is acceptable (if the resulting value is greater
than or equal to the corresponding lower bound), the change is made and the result
is the value of c | d using the modified bound. If the change cannot be done, it is attempted on the other
bound. If the change cannot be done to either bound, the scan continues. C code for
this algorithm is shown in Figure 4–4. Here the subexpression b & d can be moved out of the loop, and the algorithm can be speeded up by initializing
m with
unsigned maxOR(unsigned a, unsigned b,
unsigned c, unsigned d) {
unsigned m, temp;
m = 0x80000000;
while (m != 0) {
if (b & d & m) {
temp = (b - m) | (m - 1);
if (temp >= a) {b = temp; break;}
temp = (d - m) | (m - 1);
if (temp >= c) {d = temp; break;}
}
m = m >> 1;
}
return b | d;
}
FIGURE 4–4. Maximum value of x | y with bounds on x and y.
m = 0x80000000 >> nlz(b & d);
There are two ways in which we might propagate the bounds of inequalities (8) through the expression x & y: algebraic and direct computation. The algebraic method uses DeMorgan’s rule:
x & y = ¬(¬x | ¬y)
Because we know how to propagate bounds precisely through or, and it is trivial to propagate them through not (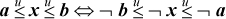
), we have
minAND(a, b, c, d) = ¬maxOR(¬b, ¬a, ¬d, ¬c), and
maxAND(a, b, c, d) = ¬minOR(¬b, ¬a, ¬d, ¬c).
For the direct computation method, the code is very similar to that for propagating bounds through or. It is shown in Figures 4–5 and 4–6.
unsigned minAND(unsigned a, unsigned b,
unsigned c, unsigned d) {
unsigned m, temp;
m = 0x80000000;
while (m != 0) {
if (~a & ~c & m) {
temp = (a | m) & -m;
if (temp <= b) {a = temp; break;}
temp = (c | m) & -m;
if (temp <= d) {c = temp; break;}
}
m = m >> 1;
}
return a & c;
}
FIGURE 4–5. Minimum value of x& y with bounds on x and y.
unsigned maxAND(unsigned a, unsigned b,
unsigned c, unsigned d) {
unsigned m, temp;
m = 0x80000000;
while (m != 0) {
if (b & ~d & m) {
temp = (b & ~m) | (m - 1);
if (temp >= a) {b = temp; break;}
}
else if (~b & d & m) {
temp = (d & ~m) | (m - 1);
if (temp >= c) {d = temp; break;}
}
m = m >> 1;
}
return b & d;
}
FIGURE 4–6. Maximum value of x& y with bounds on x and y.
The algebraic method of finding bounds on expressions in terms of the functions for and, or, and not works for all the binary logical expressions except exclusive or and equivalence. The reason these two present a difficulty is that when expressed in terms of and, or, and not, there are two terms containing x and y. For example, we are to find
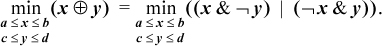
The two operands of the or cannot be separately minimized (without proof that it works, which actually it does), because we seek one value of x and one value of y that minimizes the whole or expression.
The following expressions can be used to propagate bounds through exclusive or:
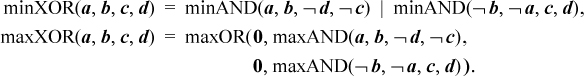
It is straightforward to evaluate the minXOR and maxXOR functions by direct computation.
The code for minXOR is the same as that for minOR (Figure 4–3) except with the two break statements removed, and the return value changed to a ^ c. The code for maxXOR is the same as that for maxOR (Figure 4–4) except with the four lines under the if clause replaced with
temp = (b - m) | (m - 1);
if (temp >= a) b = temp;
else {
temp = (d - m) | (m - 1);
if (temp >= c) d = temp;
}
and the return value changed to b ^ d.
If the bounds are signed integers, propagating them through logical expressions is substantially more complicated. The calculation is irregular if 0 is within the range a to b, or c to d. One way to calculate the lower and upper bounds for the expression x | y is shown in Table 4–1. A “+” entry means that the bound at the top of the column is greater than or equal to 0, and a “–” entry means that it is less than 0. The column labeled “minOR (signed)” contains expressions for computing the lower bound of x | y, and the last column contains expressions for computing the upper bound of x | y. One way to program this is to construct a value ranging from 0 to 15 from the sign bits of a, b, c, and d, and use a “switch” statement. Notice that not all values from 0 to 15 are used, because it is impossible to have a > b or c > d.
TABLE 4–1. SIGNED MINOR AND MAXOR FROM UNSIGNED
For signed numbers, the relation
a ≤ x ≤ b ⇔ ¬b ≤ ¬x ≤ ¬a
holds, so the algebraic method can be used to extend the results of Table 4–1 to other logical expressions (except for exclusive or and equivalence). We leave this and similar extensions to others.
1. For unsigned integers, what are the bounds on x – y if
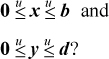
2. Show how the maxOR function (Figure 4–4) can be simplified if either a = 0 or c = 0 on a machine that has the number of leading zeros instruction.
